Glycerol adsorption on a defected Pt₆/Pt(100) substrate: a density functional theory investigation within the D3 van der Waals correction

Abstract

We report an ab initio investigation based on density functional theory calculations within the van der Waals (vdW) correction to obtain an improved atomistic understanding of the adsorption properties of glycerol on a defected Pt₆/Pt(100) substrate, which includes low-coordinated Pt sites and well defined Pt(100) terraces. We found that in the lowest energy structure glycerol weakly adsorbs on a low-coordinated cationic Pt site via one of the anionic O atoms with the central carbonate chain orientated nearly parallel to the surface plane. As expected, the vdW correction enhances the adsorption energy, however, while it does not change the adsorption site preference, it affects the orientation of the CCC frame with respect to the substrate. Our results of the work function and Bader charges suggest a negligible charge transfer between glycerol and the Pt₆/Pt(100) substrate, which can be attributed mostly to polarizations between the atoms of the molecule and of the surface.

---

1 Introduction

Propane-1,2,3-triol (C₃H₈O₃), which is commonly known as glycerol or glycerin (Gly), is formed as a by-product during the production of biodiesel,¹ and the increased biodiesel production in Brazil and worldwide has contributed to generating an oversupply of glycerol in the international market.² The unique combination of its physical and chemical properties makes glycerol an outstanding compound for many technological applications,^3–5 which include food, beverages, pharmaceutical products and cosmetics. Furthermore, it has been considered for hydrogen (H₂) production via a steam reforming reaction for fuel cell applications.^6–8 The ideal glycerol steam reforming reaction can be represented by the following stoichiometric equation, C₃H₈O₃ + 3H₂O → 3CO₂ + 7H₂,^7,8 which is endothermic with a heat of formation of 346 kJ mol⁻¹. As expected, the H₂ production takes several steps such as the dehydrogenation and cleavage of the C–C and C–O bonds at high temperature, and the formation of the desired products is strongly dependent on the selection of the catalysts.^8,9

The performance of several catalysts for H₂ production from glycerol via the steam reforming reaction has been widely tested by employing several experimental conditions. To date, transition-metals (TMs) such as Ni, Pt, Pd and Ru-based catalysts supported on MgO, CeO₂, TiO₂, and La₂O₃ oxides yield some of the best performances for glycerol conversion towards H₂.^6,8–16 For example, Soares et. al.⁶ used various feed rates and temperatures for Pt particles supported on Al₂O₃, ZrO₂, CeO₂/ZrO₂, MgO₂/ZrO₂, and carbon catalysts, and found that Pt/C material possesses the best performance yielding 100% glycerol conversion at 400 °C, 1 bar pressure and a feed rate of 0.32 cm² min⁻¹. A detailed review of different catalysts and operating conditions for glycerol steam reforming reactions can be found elsewhere.^8,13

Although several achievements have been made on the role of TM substrates for the glycerol reactions towards H₂ production, we are still developing our atomistic understanding of the role of defects on the TM substrates, which is essential for further developments. Recently, Fernández et al.¹⁷ prepared a number of well-ordered and disturbed Pt(100) surfaces with various surface defect densities in 0.5 M H₂SO₄ using cyclic voltammetry (CV) and in situ Fourier transform infrared spectroscopy, and showed that defects on the surface play an important role in the onset of the reaction, i.e., the glycerol electron-oxidation reaction occurs at 0.1 V earlier on the well-ordered surfaces than on the Pt(100) surfaces with a high degree of disorder.

Such experimental investigations allow for the development of active, stable and low-cost catalysts for hydrogen production, however, a fundamental understanding of the interaction of glycerol with real TM catalysts is crucial. Up to now, studies using theoretical ab initio calculations based on density functional theory (DFT) have reported only on the interaction of glycerol with perfect close-packed TM surfaces.^18–22 For example, it was found that the glycerol molecule adsorbs via its O atom on the on-top metal atom of close-packed TM surfaces, with the bond formed by its edge carbon atoms nearly parallel to the surface.

Furthermore, the addition of a van der Waals (vdW) correction to the DFT total energy leads to a slight modification of the glycerol structure on close-packed Pt surfaces, e.g., a decrease in the equilibrium Gly–Pt distance and a change in the angle between the molecule and the surface yielding the C–C bond at the edge of the molecule almost parallel to the surface.^17,22 In addition, the vdW correction increases the adsorption energy of the systems, however, the enhancement was found to be dependent on the surface structure.²²

Thus, in order to improve our atomistic understanding of the role of Pt defects on interactions with glycerol, in this work we performed an ab initio DFT investigation of glycerol adsorption on a defect-containing Pt(100) surface, consisting of low-coordinated and terrace sites. We found that in the lowest energy structure, glycerol weakly adsorbs on low-coordinated Pt sites with its edge C atoms nearly parallel to the surface. In addition, we also investigated the role of the vdW correction in a configurational set of glycerol molecules adsorbed on defected Pt(100) surfaces. We found that the performance of the vdW correction varies with the topology of the surface, e.g., the ratio between the adsorption energies from vdW-corrected DFT and plain DFT strongly depends on the position of the molecule over the surface. In order to deeply investigate the interactions between glycerol and the Pt surface, we investigated several properties, such as the change in the work function, Bader charge and the occupied Pt d-states’ center of gravity.

2 Theoretical approach and computational details

Our total energy calculations were based on DFT^23,24 within the generalized gradient approximation²⁵ proposed by Perdew–Burke–Ernzerhof (PBE).²⁶ To improve the description of the long range non-local correlation effects, which play a crucial role in weak interacting systems such as water and ethanol adsorption on TM(111),^27,28 and glycerol adsorption on Pt surfaces,²² we employed one of the van der Waals (vdW) corrections proposed by S. Grimme, namely, the D3 vdW correction.^29–31 The D3 vdW framework has been employed with great success in several studies.^27,29–33 The DFT+D3 total energy, E^DFT+D3_tot, can be obtained as the sum of the DFT-PBE total energy, E^DFT-PBE_tot, and the vdW energy correction, E^vdW_energy, i.e., E^DFT+D3_tot = E^DFT-PBE_tot + E^vdW_energy. Further details on the D3 framework and its implementation in the Vienna ab initio simulation package^34,35 (VASP) are discussed elsewhere.^29–31

The Kohn–Sham equations were solved using VASP version 5.4.1,^34,35 where the electron–ion interactions are described by the all-electron projected augmented wave (PAW) method,^36,37 employing the PAW projectors provided within VASP. For all of the total energy calculations, a plane-wave cutoff energy of 487 eV was used, while for the integration of the Brillouin zone of the Gly/Pt₆/Pt(100)-(4 × 4) systems, we employed a 3 × 3 × 1 k-point mesh. For all of the calculations, we obtained the equilibrium atomic positions once the atomic forces on each atom were smaller than 0.010 eV Å⁻¹ using a total energy convergence of 1 × 10⁻⁶ eV.

By the minimization of the stress tensor, we obtained an equilibrium lattice constant of 3.98 Å (PBE) and 3.93 Å (PBE+D3) for bulk Pt in the face-centered-cubic (fcc) structure, which is in excellent agreement with previous DFT^27,38,39 and experimental, 3.92 Å,⁴⁰ results. As expected, the PBE+D3 lattice constant is smaller than the PBE result due to the attractive nature of the vdW correction, which enhances the magnitude of the cohesive energy, and hence, it decreases the bond lengths (lattice constant). Based on the calculated lattice constants,³⁸ the clean Pt(100) surface was modelled using a slab with a 6 layer thickness and a (4 × 4) surface unit cell (i.e., 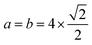), and hence, there are 16 Pt atoms per layer. To minimize the interactions between the slabs, we employed a vacuum region with a 20 Å thickness.

Using the flat Pt(100) model, the defected substrate was designed by removing 10 Pt atoms located in the topmost surface layer, and so there were 6 remaining atoms on the surface, which could be represented using the following notation, Pt₆/Pt(100)-(4 × 4). Thus, the defected Pt substrate has a well defined terrace and a 6-atom island, which can minimise different atomic environments in experimental conditions.¹⁷ Glycerol was adsorbed only on one side of the slab on different adsorption sites, and hence, a dipole correction was employed.⁴¹ Only the bottom layer of the slab was frozen, while glycerol and the remaining surface layers were allowed to relax.

To identify the lowest energy configurations for Gly/Pt₆/Pt(100), we performed standard ab initio molecular dynamics (MD) simulations with a cutoff energy of 300 eV for about 20 ps using an initial temperature of 300 K and decreasing it to 0 K. Then, 15 snapshots were selected along the MD simulation and were optimized using the conjugated gradient algorithm as implemented in VASP. This procedure was employed in previous studies.^27,28 Although the number of configurations is relatively small, it provides a route to improve our atomistic understanding of the interaction of glycerol with defected Pt(100) substrates. Finally, those configurations were re-optimized using the PBE+D3 functional to take into account the vdW corrections.

3 Results

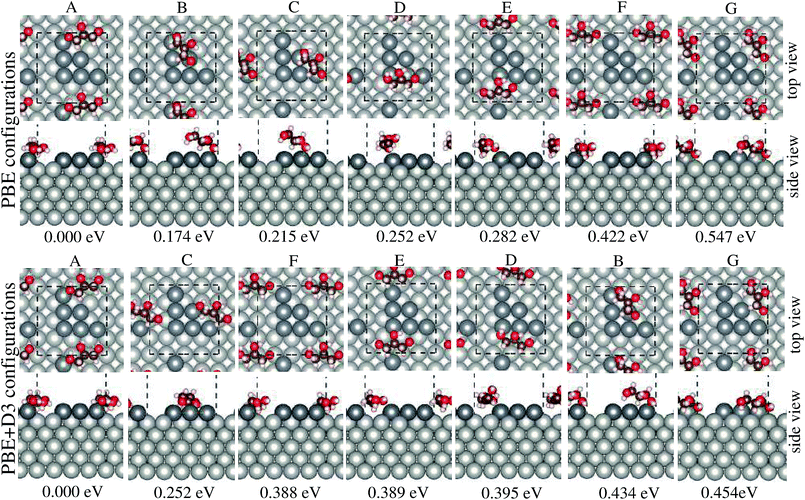
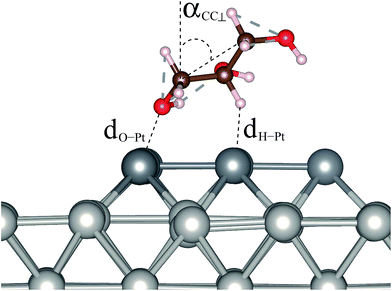
The structures of adsorbed glycerol with the lowest energy and the higher energy isomers for Gly/Pt₆/Pt(100) with their respective relative total energies are shown in Fig. 1, while the most important structural parameters such as the O–Pt bond length, d_O–Pt, the nearest H–Pt bond length, d_H–Pt, and the angle between the edge C atom and the surface normal, α_CC⊥, Fig. 2, are summarized in Table 1, along with the adsorption energies and changes in the work function. All of these results will be discussed below.

Fig. 1 Top and side views of the most important atomic structures of adsorbed glycerol on the Pt₆/Pt(100) substrate that were obtained with the PBE and PBE+D3 functionals. The relative energies are shown below each configuration.

Fig. 2 Structural parameters of glycerol on the Pt₆/Pt(100) surface, such as the O–Pt bond length, d_O–Pt, the H–Pt bond length, d_H–Pt, and the angle between the edge C atoms and surface normal (α_CC⊥).

Table 1 Energetic and structural properties of glycerol on the clean and defected Pt₆/Pt(100) surface (A–G). The adsorption energy, E_ad (in eV), the change in the work function, ΔΦ (in eV), the O–Pt and H–Pt bond lengths, d_O–Pt and d_H–Pt, respectively, and the angle between the edge C atoms and surface normal, α_CC⊥, using PBE and PBE+D3 functionals

	Ead	E^+vdWad	ΔΦ	ΔΦ^+vdW	dO–Pt	d^+vdWO–Pt	dH–Pt	d^+vdWH–Pt	αCC⊥	α^vdWCC⊥
Gly/Pt(100)	−0.45	−1.34	−0.84	−0.85	2.33	2.29	2.02	1.89	78.60	81.84
Gly/Pt6/Pt(100)^A	−0.82	−1.91	−0.29	−0.16	2.19	2.18	2.63	2.24	90.36	90.75
Gly/Pt6/Pt(100)^B	−0.65	−1.48	−0.52	−0.55	2.21	2.21	2.44	1.94	71.36	76.66
Gly/Pt6/Pt(100)^C	−0.61	−1.66	−0.59	−0.54	2.22	2.23	2.11	2.12	68.02	88.63
Gly/Pt6/Pt(100)^D	−0.57	−1.51	−0.62	−0.52	2.28	2.26	2.73	1.97	71.57	89.55
Gly/Pt6/Pt(100)^E	−0.54	−1.52	−0.22	−0.22	2.23	2.29	2.77	2.65	80.53	84.79
Gly/Pt6/Pt(100)^F	−0.40	−1.52	−0.32	−0.33	2.31	2.28	2.12	1.96	79.17	83.08
Gly/Pt6/Pt(100)^G	−0.28	−1.46	−0.18	−0.17	2.29	2.27	2.62	2.41	75.57	81.96

---

3.1 Glycerol adsorbed structures

We found that glycerol preferentially binds on the low-coordinated Pt₆/Pt(100) atoms that are arranged in a triangle. For example, the structures that are labelled from A to E are in the relative total energy window from 0 to 282 meV, whereas structures F and G, in which glycerol is located on the terrace sites, are in the range from 422 meV to 547 meV, higher in energy than the lowest energy PBE structure. Thus, it implies that despite the strong preference of glycerol for the low-coordinated Pt₆ sites, the higher energy isomers can also exist in high temperature experiments, which is the case in the glycerol steam reforming reactions.^7,8 Our results support the electro-chemical experimental findings,¹⁷ in which the importance of the surface defects on the onset of the glycerol electro-oxidation reaction was shown. They can also help in obtaining a fundamental view of the interactions between glycerol and Pt surfaces, which will be discussed below.

The PBE+D3 functional yields the same order of the relative total energies for the lowest energy structure and its highest energy isomer (i.e., the structures for A and G, respectively), but it changes the order of the relative total energies of the other structures. For example, the less preferable structure F (the 5th highest energy isomer obtained from PBE, with a relative total energy of 422 meV), in which glycerol is on the terrace sites, becomes the 2nd highest energy isomer with a relative total energy of 388 meV using PBE+D3. Moreover, structure F has a very close relative total energy to structure E, in which glycerol adsorbed to the low-coordinated sites. This result indicates that there are other factors rather than just the low-coordinated sites that play an important role in the energetic preference of the structures by applying the D3 vdW correction.

In the lowest energy structure, glycerol binds with the low-coordinated Pt₆ atoms, in which the closest carbon chain is above the terrace sites with a O–Pt bond length of 2.19 Å and the edge C atoms are parallel to the surface, i.e., α_CC⊥ = 90.36° (PBE). For the higher energy isomers, glycerol is further away from the Pt surface, i.e., the d_O–Pt bond lengths are spread from 2.21 Å to 2.31 Å, and the carbon chain is less parallel to the surface, i.e., α_CC⊥ is from 68° to 81°. Thus, these findings indicate that the crucial factors that define the lowest energy structure are low-coordinated Pt sites, a short O–Pt distance and a parallel orientation of the molecule to the surface. It is important to notice that due to the stronger binding, the distance between the molecule and the surface ranges from 0.01 Å to 0.10 Å shorter on the low-coordinated sites than on the terrace sites.

Using the PBE+D3 functional, we found that the obtained structures undergo slight modifications, i.e., their carbon chain tends to be above the terrace sites, which can be a consequence of the strengthened bond between H and edge Pt atoms from Pt₆, with the value for the H–Pt bond of 1.94 Å to 2.65 Å. These H–Pt bonds are slightly larger for the structures obtained using PBE, i.e., the d_H–Pt values spread from 2.44 Å to 2.77 Å, except for structures C and F, where d_H–Pt is 2.11 Å and 2.12 Å, respectively. For most of the cases, the addition of the D3 vdW correction leads to smaller O–Pt bond lengths and an increase in the α_CC⊥ angle, i.e., from 4° to 20°, which implies an increased preference for parallel orientations over the surface. These results are supported by our previous findings for alcohol molecules on close-packed TM surfaces.^22,27,28 As expected, the adsorbed structures in which glycerol binds on the terrace sites, e.g., structures F and G, are similar to the adsorbed structure with glycerol bound on the clean Pt(100) surface, that is, d_O–Pt is 2.31 Å and 2.33 Å for structure F and the structure with glycerol bound on the clean Pt(100) surface, respectively.

3.2 Adsorption energy

The glycerol adsorption energy, E_ad, which measures the binding energy of the Gly–Pt interaction, was calculated for all of the systems. We found that E_ad for glycerol on the terrace sites on the defected Pt₆/Pt(100) substrate is closer to the adsorption energy of glycerol on the flat Pt(100) surface, i.e., −0.40 eV and −0.45 eV, respectively, which is almost twice as low as the E_ad value of the lowest energy structure i.e., −0.82 eV. Therefore, there is a strong effect of the low-coordinated Pt sites on the magnitude of the binding of glycerol to the Pt substrate. For the structures in which glycerol is on the low-coordinated Pt sites, changes in the α_CC⊥ angles and O–Pt distances result in a reduction in the adsorption energy of up to 66%.

As found in previous DFT studies with vdW corrections,^22,27,28 the D3 vdW correction increases the adsorption energy. For example, the enhancement factor that is defined as the ratio between the PBE+D3 and PBE adsorption energies ranges from 2.25 to 2.80 for glycerol on the low-coordinated Pt₆ sites. However, the enhancement is even higher on the Pt(100) terrace sites, i.e., it changes from 3.80 to 5.21. Therefore, the adsorption energy enhancement due to the vdW correction is site-dependent. That is, it depends on the coordination of the adsorption site, which is not an unexpected result. For example, the D3 framework employs a coordination-dependent function to estimate the C^AB₆ coefficients, and the function plays a major role in the magnitude of the vdW energy correction. Thus, we cannot exclude the fact that part of the enhancement is related to the selection of the function and its parameterization.

3.3 Role of the vdW correction

As discussed before, the addition of the D3 vdW correction affects the structural and energetic properties. However, it does not change the order of the lowest energy structure, but it slightly modifies the glycerol adsorbed structures on the defected Pt surface. For example, the D3 correction results in a more parallel orientation of the CCC backbone over the surface, the displacement of the glycerol carbon chain to be above the terrace sites, and the strengthening of the bonds between H and the edge Pt atoms, and the O–Pt bond lengths. We found that an increase in the adsorption energy of the systems also occurs upon the addition of the D3 correction, which is dependent on the glycerol position over the surface, with a smaller increase when it binds on low-coordinated Pt₆ sites. This finding is also supported by our previous results, where we investigated the adsorption of glycerol on low-Miller index Pt surfaces, namely the (111), (110), and (100) surfaces.²²

3.4 Change in the work function and Bader charge analysis

The change in the work function, ΔΦ, with respect to the clean Pt(100) substrate (ΔΦ = Φ^{Gly/Pt₆/Pt(100)} − Φ^{Pt₆/Pt(100)}), and Bader charge analysis can help to improve our atomistic understanding of the electron density flows and effective charge on chemical species. The work function of the Pt₆/Pt(100) substrate is smaller than that of the flat Pt(100) substrate by 0.55 eV, i.e., 5.41 eV and 5.96 eV, respectively. It can be explained by the presence of the Pt₆ adatoms on Pt(100), which increases the electron density corrugation on the surface, and contributes to a decrease in the work function of the defected Pt₆/Pt(100) substrate.

Upon glycerol adsorption, we found a reduction in the work function, and the largest change occurs for glycerol adsorbed on the flat Pt(111) surface, i.e., ΔΦ = −0.84 eV, while it ranges from −0.18 eV to −0.62 eV for glycerol on Pt₆/Pt(100). We could not establish a correlation between the adsorption site preference or the adsorption energy values with the magnitude of the change in the work function, beyond the obvious observation that the change in the work function is larger on flat substrates than on defected substrates. The work function reduction can be explained by polarization effects on glycerol and the topmost surface Pt atoms and an effective charge transfer from glycerol to the substrate.²² The D3 vdW correction leads to small differences in the magnitude of the change in the work function, e.g., up to 0.13 eV.

In order to investigate a possible charge transfer in the molecule-substrate layer, we calculated an effective charge on the separated and bound systems using the Bader charge concept.^42,43 For that, we computed the effective charge of every atom in the systems using Bader charge analysis, which is based on a high density Fast Fourier Transform (FFT) grid implemented in VASP.⁴⁴ The average effective charge, Q, was calculated as the difference between the number of valence electrons, Z_val, and the obtained Bader charge, Q_Bader, i.e. Q = Z_val − Q_Bader, for every chemical species with Z_val = 4, 6, 1, and 10e for the C, O, H, and Pt atoms, respectively.

As expected, zero total charge for a glycerol molecule in the gas-phase corresponds to negative and positive charge distributions of the glycerol atoms. These are, for instance, an effective negative charge of −1.11e on the O atoms and an effective positive charge of +0.43e on the C atoms. For those H atoms making bonds with C and O atoms, these effective charges are +0.06e and +0.59e, respectively. The differences in the electronegativity of the elements (2.55 for C, 3.44 for O, and 2.20 for H) are what explain these positive and negative charges on glycerol atoms.⁴⁵

Upon glycerol adsorption, we found a slight charge redistribution among atoms in the system and a small charge transfer between the surface and glycerol. For example, the effective charge of the molecule becomes slightly positive, i.e., +0.11e, which implies that this amount of charge was transferred to the Pt surface. Thus, there is an ionic contribution to the adsorption energy between glycerol and the Pt(100) surface. We found that the low-coordinated Pt₆ atom that is directly bound to glycerol becomes slightly positive (i.e., +0.12e), and hence, these atoms are favoured to bind with the anionic O atoms. Low-coordinated Pt₆ and terrace atoms of the bare Pt₆/Pt(100) substrate are slightly negatively charged with negligible effective charges of −0.05e and −0.01e, respectively, while the effective charge on the remaining layers remains slightly positive.

4 Conclusions

In this article, we reported an ab initio DFT-PBE investigation of the interaction of glycerol with a defected Pt₆/Pt(100) substrate, which includes low-coordinated Pt sites and a terrace Pt(100) region exposed to the vacuum region. In addition to the DFT-PBE calculations, we also investigated the role of the D3 vdW correction on the adsorption properties. In the lowest energy structure, glycerol weakly binds via its anionic O atom with the low-coordinated cationic Pt sites, in which the frame formed by the CCC atoms is nearly parallel to the surface. As found in previous studies and confirmed in this work, the vdW D3 correction yields an increase in the glycerol adsorption energy and only a slight change in the molecule geometry on the surface, i.e., a decrease in the O–Pt bond lengths, an increase in the angle between the edge C–C bond and the surface normal, and movement of the C–C bond to terrace sites. These rearrangements within the configurations tend to strengthen the H–Pt interaction, as expected. Moreover, we found that the ratio between the adsorption energies of PBE+D3 and PBE is different for the molecule bound to lower-coordinated sites and terraces on the surface, i.e., the vdW enhancement is site dependent. Our Bader charge analysis demonstrates that charge transfer between glycerol and the Pt₆/Pt(100) substrate is small, and the change in the work function mostly indicates polarizations between the atoms of the molecule and of the surface.

Acknowledgements

Authors thank the São Paulo Research Foundation (FAPESP) and the National Council for Scientific and Technological Development (CNPq). The authors acknowledge the National Laboratory for Scientific Computing (LNCC/MCTI, Brazil) for providing the HPC resources of the SDumont supercomputer, which have contributed to the research results reported within this paper. URL: http://sdumont.lncc.br. Authors also thank the Laboratory of Advanced Scientific Computing (University of São Paulo) and the Department of Information Technology – Campus São Carlos, for hosting our cluster.

References

1. E. Alptekin, M. Canakci and H. Sanli, Waste Manag., 2014, 34, 2146–2154.
2. M. Ayoub and A. Z. Abdullah, Renewable Sustainable Energy Rev., 2012, 16, 2671–2686.
3. M. A. Dasari, P.-P. Kiatsimkul, W. R. Sutterlin and G. J. Suppes, Appl. Catal., A, 2005, 281, 225–231.
4. C.-H. Zhou, J. N. Beltramini, Y.-X. Fan and G. Q. Lu, Chem. Soc. Rev., 2008, 37, 527–549.
5. M. Pagliaro, R. Ciriminna, H. Kimura, M. Rossi and C. D. Pina, Angew. Chem., Int. Ed., 2007, 46, 4434–4440.
6. R. R. Soares, D. A. Simonetti and J. A. Dumesic, Angew. Chem., 2006, 118, 4086–4089.
7. S. Adhikari, S. D. Fernando, S. D. F. To, R. M. Bricka, P. H. Steele and A. Haryanto, Energy Fuels, 2008, 22, 1220–1226.
8. P. D. Vaidya and A. E. Rodrigues, Chem. Eng. Technol., 2009, 32, 1463–1469.
9. T. Hirai, N.-O. Ikenaga, T. Miyake and T. Suzuki, Energy Fuels, 2005, 19, 1761–1762.
10. S. Adhikari, S. D. Fernando and A. Haryanto, Renewable Energy, 2008, 33, 1097–1100.
11. O. Skoplyak, M. A. Barteau and J. G. Chen, ChemSusChem, 2008, 1, 524–526.
12. E. L. Kunkes, D. A. Simonetti, J. A. Dumesic, W. D. Pyrz, L. E. Murillo, J. G. Chen and D. J. Buttrey, J. Catal., 2008, 260, 164–177.
13. S. Adhikari, S. D. Fernando and A. Haryanto, Energy Convers. Manage., 2009, 50, 2600–2604.
14. A. O. Menezes, M. T. Rodrigues, A. Zimmaro, L. E. P. Borges and M. A. Fraga, Renewable Energy, 2011, 36, 595–599.
15. G. Wu, C. Zhang, S. Li, Z. Han, T. Wang, X. Ma and J. Gong, ACS Sustainable Chem. Eng., 2013, 1, 1052–1062.
16. V. V. Thyssen, T. A. Maia and E. M. Assaf, Fuel, 2013, 105, 358–363.
17. P. S. Fernández, J. F. Gomes, C. A. Angelucci, P. Tereshchuk, C. A. Martins, G. A. Camara, M. E. Martins, J. L. F. Da Silva and G. Tremiliosi-Filho, ACS Catal., 2015, 5, 4227–4236.
18. D. Coll, F. Delbecq, Y. Aray and P. Sautet, Phys. Chem. Chem. Phys., 2011, 13, 1448–1456.
19. B. Liu and J. Greeley, J. Phys. Chem. C, 2011, 115, 19702–19709.
20. B. Liu and J. Greeley, Top. Catal., 2012, 55, 280–289.
21. B. Liu and J. Greeley, Phys. Chem. Chem. Phys., 2013, 15, 6475–6485.
22. P. Tereshchuk, A. S. Chaves and J. L. F. Da Silva, J. Phys. Chem. C, 2014, 118, 15251–15259.
23. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
24. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
25. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
27. P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. C, 2012, 116, 24695–24705.
28. P. Tereshchuk and J. L. F. Da Silva, J. Phys. Chem. C, 2013, 117, 16942–16952.
29. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
30. J. Moellmann and S. Grimme, Phys. Chem. Chem. Phys., 2010, 12, 8500–8504.
31. W. Reckien, F. Janetzko, M. F. Peintinger and T. Bredow, J. Comput. Chem., 2012, 33, 2023–2031.
32. C. R. C. Rêgo, L. N. Oliveira, P. Tereshchuk and J. L. F. Da Silva, J. Phys.: Condens. Matter, 2015, 27, 415502.
33. C. R. C. Rêgo, L. N. Oliveira, P. Tereshchuk and J. L. F. Da Silva, J. Phys.: Condens. Matter, 2016, 28, 129501.
34. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118.
35. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
38. J. L. F. Da Silva, C. Stampfl and M. Scheffler, Surf. Sci., 2006, 600, 703–715.
39. P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104.
40. C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, Inc., New York, 8th edn, 2004.
41. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
42. R. F. W. Bader, Acc. Chem. Res., 1975, 8, 34–40.
43. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1994.
44. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204.
45. L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1960.

---