Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio conical intersections for the Si(1D) + H2 reaction system: a lowest five singlet states study†
Yanan Wuab,
Chunfang Zhangab and
Haitao Ma *a
*a
aBeijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, China. E-mail: mht@iccas.ac.cn
bUniversity of Chinese Academy of Sciences, Beijing 100049, China
First published on 20th February 2017
Abstract
Conical intersection (CI) play a key role in the non-adiabatic processes and the geometric phase (GP) effect associated with CI have a significant influence on the quantum reactive scattering and bound-state calculations. In this work, the CIs and the GP effects associated with the CIs of the Si(1D) + H2 system are investigated using the internally contracted multireference configuration intersection method for the first time. The seams of the CIs (at the linear H–Si–H geometries, linear Si–H–H geometries and C2v geometries) among the lowest five singlet states relative to the Si(1D) + H2 reaction system are searched systematically. The properties of minimum energy crossing points (MECPs) of these intersection seams are determined, the topographies of the potential energy surfaces in the branching spaces of MECPs and the GP effects associated with the CIs are discussed.
1 Introduction
Silylene, SiH2, the prototype radical in silylene family, plays an important role in the organic silicon chemistry,1–3 and it is postulated as a reactive intermediate in the manufacturing process of amorphous silicon films by chemical vapor deposition.4–7 The studies of SiH2 started as early as 1967, when Dubois and co-workers observed electronic absorption spectra belonging to the![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1–Ã1B1 transition of this radical for the first time.8 It was not ascertained that whether the lower 1A1 state of the observed transition was the ground state or there was a lower-lying triplet state, as in CH2, would be the ground state until Milligan and Wirsam's work confirmed that the lower state of the previously observed electronic transition of singlet SiH2, is the ground state9,10 and Apeloig and co-workers explained why CH2 is a ground state triplet while SiH2 is a ground state singlet.11 Most of the studies about this radical concentrated on the
1A1–Ã1B1 transition of this radical for the first time.8 It was not ascertained that whether the lower 1A1 state of the observed transition was the ground state or there was a lower-lying triplet state, as in CH2, would be the ground state until Milligan and Wirsam's work confirmed that the lower state of the previously observed electronic transition of singlet SiH2, is the ground state9,10 and Apeloig and co-workers explained why CH2 is a ground state triplet while SiH2 is a ground state singlet.11 Most of the studies about this radical concentrated on the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and Ã1B1 states. Dubois and co-workers measured the absorption spectrum of the
1A1 and Ã1B1 states. Dubois and co-workers measured the absorption spectrum of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1–Ã1B1 transition of SiH2 and pointed out the existence of a lot of strong and erratic rotational perturbations.8,12,13 The anomalous rotational perturbations were interpreted as the combined effects of the Renner–Teller coupling between the two singlet states and the spin–orbit coupling with the lowest triplet state,13,14 and the large amplitude motion of the bending vibration ν2.14,15 It was reported that fluorescence lifetime of SiH2 in the Ã1B1 state widely vary for each rovibronic level,16,17 and this was interpreted in terms of mixing with adjacent levels of the ã3B1 state,18 and the predissociation to Si(3P) + H2.16,19,20 Ishikawa et al. observed the stimulated emission pumping spectroscopy of the Ã1B1–
1A1–Ã1B1 transition of SiH2 and pointed out the existence of a lot of strong and erratic rotational perturbations.8,12,13 The anomalous rotational perturbations were interpreted as the combined effects of the Renner–Teller coupling between the two singlet states and the spin–orbit coupling with the lowest triplet state,13,14 and the large amplitude motion of the bending vibration ν2.14,15 It was reported that fluorescence lifetime of SiH2 in the Ã1B1 state widely vary for each rovibronic level,16,17 and this was interpreted in terms of mixing with adjacent levels of the ã3B1 state,18 and the predissociation to Si(3P) + H2.16,19,20 Ishikawa et al. observed the stimulated emission pumping spectroscopy of the Ã1B1–![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 transition and obtained information about the ã3B1 state through the spin–orbit interaction.21 Yurchenko et al. first made an ab initio calculation of the potential energy surfaces (PESs) for the
1A1 transition and obtained information about the ã3B1 state through the spin–orbit interaction.21 Yurchenko et al. first made an ab initio calculation of the potential energy surfaces (PESs) for the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1 and Ã1B1 states, and they calculated the rovibronic energies of the two states using this ab initio PESs.22 Researches that refer to higher electronic states than the Ã1B1 state were much fewer. The
1A1 and Ã1B1 states, and they calculated the rovibronic energies of the two states using this ab initio PESs.22 Researches that refer to higher electronic states than the Ã1B1 state were much fewer. The ![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1A1 state of SiH2 and SiD2 radicals was observed for the first time in 2005.23 Before long, Tokue et al. evaluated the transition probabilities of the
1A1 state of SiH2 and SiD2 radicals was observed for the first time in 2005.23 Before long, Tokue et al. evaluated the transition probabilities of the ![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1–Ã1B1 and Ã1B1–
1A1–Ã1B1 and Ã1B1–![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1A1 systems of SiH2 and SiD2,24 and they also investigated the photodissociation process of SiH2(Ã1B1) → SiH2(
1A1 systems of SiH2 and SiD2,24 and they also investigated the photodissociation process of SiH2(Ã1B1) → SiH2(![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 1A1) → Si(1D) + H2.25
1A1) → Si(1D) + H2.25
Conical intersections (CIs),26 not isolated geometries but form a seam,27 are widespread in polyatomic systems and play a key role in non-adiabatic processes,28,29 such as charge-transfer reaction,30,31 nonradiative transition, and electronic quenching. At a CI, the Born–Oppenheimer approximation stipulating that electronic and nuclear motions are separable breaks down.32 Therefore, molecular systems which exhibit such topologies rapidly switch between electronic states through the funnel of the CI.33 Recently, many theoretical and experimental studies about the typical non-adiabatic process associated with CIs, such as electron transfer, isomerization, photoinduced unimolecular decay, and radiationless relaxation of the excited electronic state, have provided lots of valuable new insights into the nature of CIs.30,34–41 There have been some ab initio studies about the CIs in triatomic molecules.42–52 While, the detailed studies of the CIs or PES intersections of the Si(1D) + H2 system have never been reported.
Geometric phases (GP) or Berry phases53 are ubiquitous in physics and chemistry, and some of the most fascinating phenomena in condensed matter science such as topological insulators,54 ferroelectrics,55 the Aharonov–Bohm effect,56 and it is regarded as the signature property and associated non-adiabatic effect of CIs in molecules.57,58 GP may arise when the Hamiltonian of a system depends on a set of parameters R. Consider a physical system described by a Hamiltonian that depends on time through a set of parameters, denoted by R = (R1, R2, …), i.e.,
| H = H(R), R = R(t). | (1) |
We are interested in the adiabatic evolution of the system as R(t) moves slowly along a path C in the parameter space. For this purpose, it is useful to introduce an instantaneous orthonormal basis from the eigenstates of H(R) at each value of the parameter R, i.e.,
| H(R)|n(R)〉 = εn(R)|n(R)〉. | (2) |
However, eqn (2) alone does not completely determine the basis function |n(R)〉, it still allows an arbitrary R-dependent phase factor of |n(R)〉. One can make a phase choice, also known as a gauge, to remove this arbitrariness. Here we require that the phase of the basis function is smooth and single valued along the path C in the parameter space.
According to the quantum adiabatic theorem, the solution of the time-dependent Schrödinger equation is written as
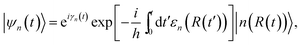 | (3) |
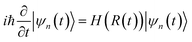 | (4) |
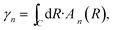 | (5) |
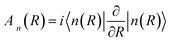 | (6) |
This vector n(R) is called the Berry connection or the Berry vector potential. Eqn (5) shows that, in addition to the dynamical phase, the quantum state will acquire an additional phase γn during the adiabatic evolution. Therefore, for a closed path, γn becomes a gauge-invariant physical quantity, known as the Berry phase or geometric phase in general; it is given by
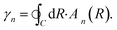 | (7) |
By virtue of the above derivation of GP,55 the GP associated with a CI comes down to the statement that the real adiabatic electronic wave function may acquire a phase which leads to a flip of sign when nuclear configuration traverse a closed path encircling a CI.59,60 Since the total molecular wave function has to remain single-valued, a compensating sign change must occur in the nuclear motion wave function. In order to investigate the GP effects in chemical reaction dynamics and the energy levels of bound-state molecules, the compensating sign of the nuclear motion wave function must be included in quantum reactive scattering and bound-state calculations. The GP effects on the energy levels of bound-state molecules have been well understood,60–62 it has been shown that they are pronounced on the bound-state spectrum of HO2, Na3, and N3.62–64 In recent years, some important theoretical and experimental studies make it more and more apparent that the GP effects can be significant in molecular scattering.65–75 In chemical reactions at thermal energies the GP effects were vanishingly small over a wide range of energies due to the fact that they wash out when a summation or average over all contributing partial waves. While, the situation changes dramatically in an energy regime where only a single partial wave contributes to the reactions, this is the case for ultra-cold chemical reactions in which manifest GP effects occur and it can be modulated by applying an external electric field allowing the possibility of quantum control of chemical reactions in the ultra-cold regime.73–75 In 2014, S. K. Min et al. demonstrated that there exist cases where a nontrivial GP present in BO approximation does not have a topological counterpart in the exact electron-nuclear problem. But they emphasized that it is not known whether these cases are the majority or the exception. Since, in practice, we normally cannot solve the full electron-nuclear problem, it will be extremely important, but difficult, to find simple mathematical criteria by which one can know if a nonvanishing BO-Berry phase survives in the exact electron-nuclear treatment.76
The purpose of this work is to investigate the CIs and the associated GP effects among the five lowest singlet states of Si(1D) + H2 systems. The organization of the present article is as following. The details of the calculations are given in Sec. 2. The results are presented and discussed in Sec. 3. Finally, a brief summary is given in Sec. 4.
2 Theoretical approaches
2.1 Ab initio electronic structure calculations
The ab initio calculations presented in this work are performed with the MOLPRO suite of ab initio programs.77 As the first step, the intersections are searched using the coupled-perturbed multi configuration self-consistent field (SA-CPMCSCF) method. For each calculation of locating the MECP between two electronic states, three vectors were evaluated at SA-CPMCSCF level: (1) non-adiabatic derivative coupling. (2) Gradient of the lower state. (3) Gradient of the upper state. Then, the internally contracted multireference configuration interaction (icMRCI) method was used for more sophisticated calculations of the single point energy. The icMRCI is a direct MRCI procedure performed in an internally contracted configuration basis, and the MRCI wavefunctions include all single and double excitations relative to complete active space self-consistent field (CASSCF) reference functions.78,79 In this work the icMRCI is employed to describe the most correlation energy of single and double electron excitations, and further correlation energy due to higher excitations is approximated by the Davidson correction (+Q).80 The SA-CASSCF is a MCSCF method that the high level multireference SCF energies and wavefunctions for a series of ground and excited states is calculate by a state-averaged variational calculation. In essence, the SA approach included each of the states in question with equal weight and the configuration space is equivalent for all states.81,82 In this work, the state-averaged complete active space self-consistent field (SA-CASSCF) calculation with 0.2, 0.2, 0.2, 0.2, 0.2 weighting on the five states is performed to obtain the orbitals for the icMRCI and SA-CPMCSCF calculations. In the SA-CASSCF calculation, the average energy of the five states, which asymptotically correlate with the five degenerate Si(1D) states, is optimized. The active space consists of six electrons distributed among six orbitals (6e, 6o), which corresponds to all valence electrons and valence orbitals. All the calculations are performed in Cs symmetry, three lowest state of A′ symmetry and two lowest state of A′′ symmetry are used for generating the internally contracted pairs in the icMRCI procedure. The basis set used is Dunning's correlation consistent polarized valence quadruple-zeta set augmented with diffuse functions83–85 (aug-cc-pVQZ).2.2 Characterization of the conical intersections
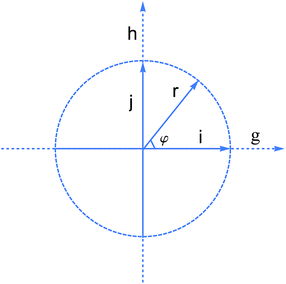
The topography of PES in the vicinity of a CI and the GP effect associated with the CI are discussed in the branching space of the CI. The branching space or g–h plane26,51,86,87 is spanned by the orthonormal vectors![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0069_20d1.gif) =
= ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) /||
/||![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) || and
|| and ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) =
= ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) /||
/||![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) ||, where
||, where ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) is the gradient difference,
is the gradient difference, ![[h with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0068_20d1.gif) is the derivative coupling vectors. The two vectors are determined by the analytic gradient technique in conjunction with the coupled-perturbed multi configuration self-consistent field SA-CPMCSCF method. Nuclear configurations in the branching space are characterized in terms of a set of natural polar coordinates in this plane, as shown in Fig. 1,
is the derivative coupling vectors. The two vectors are determined by the analytic gradient technique in conjunction with the coupled-perturbed multi configuration self-consistent field SA-CPMCSCF method. Nuclear configurations in the branching space are characterized in terms of a set of natural polar coordinates in this plane, as shown in Fig. 1, ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) is the radial coordinate (
is the radial coordinate (![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = x·
= x·![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0069_20d1.gif) + y·
+ y·![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) ), and φ is the angular coordinate or polar angle between
), and φ is the angular coordinate or polar angle between ![[i with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0069_20d1.gif) and
and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) . The CI is located at origin. Each r (we chose r = 0.01
. The CI is located at origin. Each r (we chose r = 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 in this work), together with the angular coordinate changing form 0 to 4π by the step 0.04π, define a trajectory of the nuclear configuration in the branching space. These nuclear configurations in the branching space are transformed into that in the Z-matrix before the electronic structure calculations. The PESs in branching space and the coefficient of the principal electron configuration of the related intersection electronic state are obtained from electronic structure calculations. Then, the double cone topographies of the PESs in the vicinity of the CI are evinced in the branching space, and the coefficient of the principal electron configuration of the related intersection electronic state along the motions of the nuclear configurations in the closed loop path around the CI in the two-dimensional specific branching space give rise to the GP effect.
0.2 in this work), together with the angular coordinate changing form 0 to 4π by the step 0.04π, define a trajectory of the nuclear configuration in the branching space. These nuclear configurations in the branching space are transformed into that in the Z-matrix before the electronic structure calculations. The PESs in branching space and the coefficient of the principal electron configuration of the related intersection electronic state are obtained from electronic structure calculations. Then, the double cone topographies of the PESs in the vicinity of the CI are evinced in the branching space, and the coefficient of the principal electron configuration of the related intersection electronic state along the motions of the nuclear configurations in the closed loop path around the CI in the two-dimensional specific branching space give rise to the GP effect.
3 Results and discussion
3.1 Energy correlation diagram
As an analog of methylene, SiH2 radicals have the similar energy correlation diagram for the lowest singlet states 11A′, 21A′, 31A′, 11A′′ and 21A′′, which correlate with the Si(1D) + H2 asymptote. The energy correlation diagram for the five singlet states is presented in Fig. 2. We can see that the 11A′ and 11A′′ states are bounded relative to the Si + H2 dissociation limit, the depth of them are 60.86 kcal mol−1 and 16.81 kcal mol−1, respectively. While the 21A′, 31A′ and 21A′′ are above this limit. The resolutions of states of linear molecules into those of molecule in the C2v or Cs symmetry, as shown in Table 1, indicate that the 1A′ and 1A′′ states will become the degenerate Δg or Πg pairs at linearity geometries. Our calculations demonstrate that the 11A′, 11A′′ states and the 21A′, 21A′′ states become the degenerate Δg and Πg pairs, respectively, at linearity, and hence there are Renner–Teller coupling between them. The 11A′ and 11A′′ states degenerate in the product asymptote and they are correlated with SiH(X2Π) + H products, the 21A′ and 21A′′ states degenerate in the product asymptote and they are correlated with SiH(X2Δ) + H products. The reaction Si(1D) + H2 → SiH(X2Π) + H have a significant endothermicity of 18.81 kcal mol−1, which is very different from the most researched insertion-type reactions X + H2 → HX + H (X = C, N, O, S) with more or less exothermicity.88,89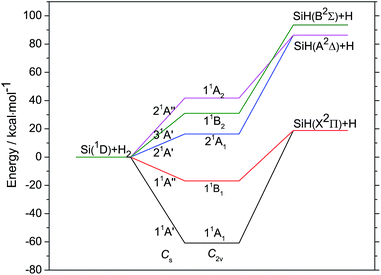 | ||
| Fig. 2 Energy correlation diagram for the Si(1D) + H2 reactive system. It is determined by MRCI + Q method, the energies are relative to Si(1D) + H2 asymptote. | ||
The geometries of minima for the five singlet states of SiH2 radical are summarized in Table 2 and compared with the available experimental and theoretical values.8,12,15,23 The equilibrium SiH distances and the equilibrium HSiH angles of SiH2 11A′, 11A′′, 21A′ and 31A′ states agree well with the available experimental or theoretical values. To our knowledge, it is the first time that the geometry and the relative energy of SiH2 21A′′ are reported in detail.
| Methods | RSiH | ∠HSiH | Energies | |
|---|---|---|---|---|
| a This work.b From ref. 8.c From ref. 12.d From ref. 15.e From ref. 23. | ||||
| SiH2(11A′) | MRCI + Qa | 2.871 | 92.2 | −60.86 |
| MRCIb | 2.870 | 92.2 | ||
| exptc | 2.874 | 92.1 | ||
| exptd | 2.865 | 92.1 | ||
| expte | 2.861 | 92.1 | ||
| SiH2(11A′′) | MRCI + Qa | 2.817 | 122.8 | −16.81 |
| MRCIb | 2.816 | 122.7 | ||
| exptc | 2.806 | 122.0 | ||
| exptd | 2.810 | 123.0 | ||
| SiH2(21A′) | MRCI + Qa | 2.777 | 165.1 | 16.34 |
| MRCIb | 2.776 | 164.8 | ||
| SiH2(31A′) | MRCI + Qa | 3.160 | 180.0 | 36.37 |
| MRCIb | 3.115 | 180.0 | ||
| SiH2(21A′′) | MRCI + Qa | 2.582 | 64.4 | 41.80 |
3.2 Conical intersections
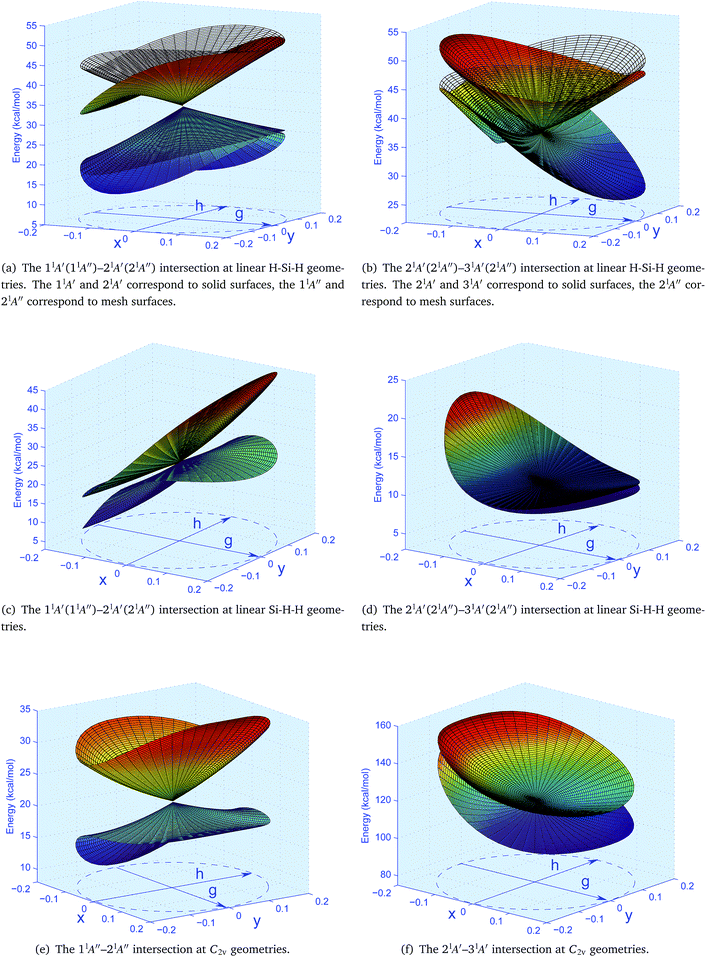
The CIs relative to the five lowest singlet states of Si(1D) + H2 asymptote are investigated systematically. The intersections covers CIs between 11A′ and 21A′ states, CIs between 21A′ and 31A′ states, at linear H–Si–H geometries; CIs between 11A′ and 21A′ states, CIs between 21A′ and 31A′ states, at linear Si–H–H geometries; CIs between 11A′′ and 21A′′ states, CIs between 21A′ and 31A′ states at C2v geometries. The intersection seams of CIs are searched. Minimum energy crossing point (MECP) is an important point of an intersection seam. The energies and geometries of the MECPs on each intersection seams are reported in Table 3. The topographies of the PESs in the branching space of the MECPs and the GP effects associated with the MECPs are discussed. All these intersections are classified in terms of the symmetries of SiH2 geometries and will be discussed in detail below.| Classification | Electronic states | Geometries of MECPs | Energies of MECPs |
|---|---|---|---|
| H–Si–H | 11A′(11A′′)–21A′(21A′′) | RSiH1 = 3.056, RSiH2 = 3.485 | 33.37 |
| H–Si–H | 21A′(21A′′)–31A′(21A′′) | RSiH1 = 3.160, RSiH2 = 3.160 | 36.37 |
| Si–H–H | 11A′(11A′′)–21A′(21A′′) | RSiH1 = 3.578, RHH = 1.952 | 24.06 |
| Si–H–H | 21A′(21A′′)–31A′(21A′′) | RSiH1 = 4.210, RHH = 1.370 | 11.13 |
| C2v | 11A′′–21A′′ | RSiH = 3.165, ∠HSiH = 68.45 | 21.60 |
| C2v | 21A′–31A′ | RSiH = 2.855, ∠HSiH = 60.68 | 118.13 |
![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) , the 21A′ and 21A′′ become non-degenerate states.
, the 21A′ and 21A′′ become non-degenerate states.
The intersection seam between the 21A′ and 31A′ states and the energies along the seam are shown in Fig. S1(b) of the ESI.† The MECP on this seam locates at the geometry with RSiH1 = 3.160 bohrs RSiH2 = 3.160 bohrs, which happen to be a C2v geometry, as shown in Table 3, and the energy of this MECP is 36.37 kcal mol−1. The topographies of the branching space PESs in the vicinity of this MECP are show in Fig. 3(b), it shows that this MECP is actually related to three (21A′, 31A′, 21A′′) states, so as the seam it located on. With that the nuclear configuration moving in the negative direction of ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) , the components of the Πg pair are 21A′ and 21A′′ states before the nuclear configuration reaching the MECP, and switch into 31A′ and 21A′′ states after that. The upper cone of this branching space PESs is also bounded in this region, while the lower cone is lack of bound-states in the vicinity of the MECP. It is obvious that there is a CI which belongs to the intersection seam between the 11A′ and 21A′ states on the lower cone, and the PES in the vicinity of this CI is bounded.
, the components of the Πg pair are 21A′ and 21A′′ states before the nuclear configuration reaching the MECP, and switch into 31A′ and 21A′′ states after that. The upper cone of this branching space PESs is also bounded in this region, while the lower cone is lack of bound-states in the vicinity of the MECP. It is obvious that there is a CI which belongs to the intersection seam between the 11A′ and 21A′ states on the lower cone, and the PES in the vicinity of this CI is bounded.
It has been mentioned that there is a CI point which belongs to the intersection seam between the 21A′ and 31A′ states on the branching space PES in the vicinity of the MECP between 11A′ and 21A′ states, conversely there is a CI point which belongs to the intersection seam between the 11A′ and 21A′ states on the branching space PES in the vicinity of the MECP between 21A′ and 31A′ states. In order to clarify the GP effects of these CIs, we extract the linear H–Si–H geometries out of the geometries of SiH2 that distributing in the branching spaces. The intersection seams and the lines consisting of linear H–Si–H geometries extracted from the corresponding MECP branching spaces are shown in Fig. 4. The MECPs are the centers of the extracted linear geometries lines and other linear geometries with different r (r = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2) are symmetrically distributed with the MECPs. It shows that the cross point between the line that consists of the linear geometries extracted from the branching space of MECP between 11A′ and 21A′ states and the intersection seam that between the 21A′ and 31A′ states is located in the region with 0.09 < r < 0.10 and φ = π in the branching space of the MECP between 11A′ and 21A′ states. The cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 21A′ and 31A′ states and the intersection seam that between 11A′ and 21A′ states is located in the region with 0.10 < r < 0.11 and φ = π in the branching space of the MECP between 21A′ and 31A′ states.
0.2) are symmetrically distributed with the MECPs. It shows that the cross point between the line that consists of the linear geometries extracted from the branching space of MECP between 11A′ and 21A′ states and the intersection seam that between the 21A′ and 31A′ states is located in the region with 0.09 < r < 0.10 and φ = π in the branching space of the MECP between 11A′ and 21A′ states. The cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 21A′ and 31A′ states and the intersection seam that between 11A′ and 21A′ states is located in the region with 0.10 < r < 0.11 and φ = π in the branching space of the MECP between 21A′ and 31A′ states.
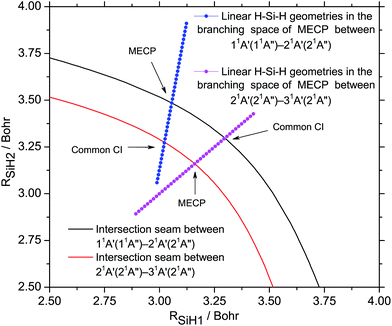 | ||
Fig. 4 The intersection seams at linear H–Si–H geometries and the line of linear H–Si–H geometries in the branching space (r = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2, φ = 0 0.2, φ = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04π 0.04π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2π) of MECP of corresponding seams. 2π) of MECP of corresponding seams. | ||
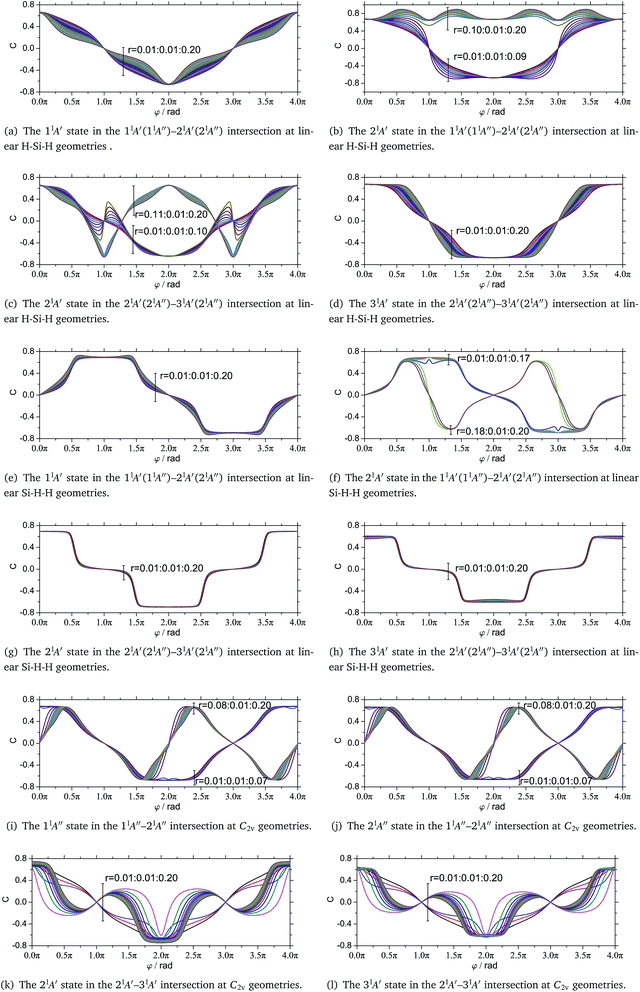
It had been mentioned that with the nuclear configurations completing a closed path encircling a CI odd number of times, the sign of the corresponding real adiabatic electronic wavefunctions will change, which called GP effect. In this work the GP effects are discussed in the branching spaces of corresponding MECPs. Fig. 5 shows the coefficients of principal configuration of the related electronic states change along the closed paths consisting of two loops encircling the MECPs with different r (r = 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2), and it present the GP effects in the title system. Three dimension representation of the GP effects are shown in Fig. S2 of the ESI.†
0.2), and it present the GP effects in the title system. Three dimension representation of the GP effects are shown in Fig. S2 of the ESI.†
As for the 11A′ electronic state corresponding to the lower cone of the branching space PES of 11A′ and 21A′ states, all of the nuclear configuration paths with different r encircle only one CI, that is the MECP between 11A′ and 21A′ states, so the signs of the electronic wavefunctions corresponding to the paths with different r will change with the nuclear configurations completing the first closed loop path and change back to their original states with the second one, C(φ) = −C(φ + 2π), and this is shown in Fig. 5(a).
The 21A′ electronic state corresponding to the upper cone of the branching space PES of 11A′ and 21A′ involves two CIs, one is the MECP between 11A′ and 21A′ states and another is a common CI belonging to the intersection seam between 21A′ and 31A′ states and it is located in the region with 0.09 < r < 0.10 in this branching space. If r ≤ 0.09, the closed nuclear configuration paths encircle only one CI, and the signs of the corresponding electronic wavefunctions will change with the nuclear configurations completing the closed loop path and change back to their original states with the second one, C(φ) = −C(φ + 2π). While, if r ≥ 0.10, the closed paths encircle two CI points, and the signs of the corresponding electronic wavefunctions will not change with the nuclear configurations completing any number of loops, C(φ) = C(φ + 2π), and this is shown in Fig. 5(b).
The 21A′ electronic state corresponding to the lower cone of the branching space PES of 21A′ and 31A′ states, involves two CIs, one is the MECP between 21A′ and 31A′ states and another is a common CI belonging to the intersection seam between 11A′ and 21A′ states and it is located in the region with 0.10 < r < 0.11 in this branching space. If r ≤ 0.10, the closed nuclear configuration paths encircle only one CI, and the signs of the electronic wavefunctions corresponding to the paths with different r will change with the nuclear configurations completing the first loop and change back to their original state after the second one, C(φ) = −C(φ + 2π). While, if r ≥ 0.11, the closed paths encircle two CIs, and the signs of the corresponding electronic wavefunctions will not change with the nuclear configurations completing any number of loops. This is shown in Fig. 5(c).
As for the 31A′ electronic state corresponding to the upper cone of the branching space PES of 21A′ and 31A′ states, all of the nuclear configuration paths with different r encircle only one CI that is the MECP between 21A′ and 31A′, so the signs of the electronic wavefunctions corresponding to the paths with different r will change with the nuclear configurations completing the first loop and change back to their original states with the second one, C(φ) = −C(φ + 2π). This is shown in Fig. 5(d).
The intersection seam between the 21A′ and 31A′ states and the energies along the seam are shown in Fig. S1(d) of the ESI.† The MECP on this seam is located at the geometry with RSiH1 = 4.210 bohrs and RHH = 1.370 bohrs, as shown in Table 3, and the energy of this MECP is 11.13 kcal mol−1. The topography of the branching space PES in the vicinity of this MECP is shown in Fig. 3(d), it should be similar with the intersection between the 21A′ and 31A′ states at the linear H–Si–H geometries that this MECP involve three (21A′, 31A′, 21A′′) states, so as the seam it located on. With the nuclear configuration moving in the negative direction of ![[g with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0067_20d1.gif) , the components of the Πg pair are 21A′ and 21A′′ before the nuclear configuration reaching the MECP, and switch into 31A′ and 21A′′ after that, but this is less obvious compared with that at the linear H–Si–H geometries since that the three relevant states in this region are very close to each other in energy.
, the components of the Πg pair are 21A′ and 21A′′ before the nuclear configuration reaching the MECP, and switch into 31A′ and 21A′′ after that, but this is less obvious compared with that at the linear H–Si–H geometries since that the three relevant states in this region are very close to each other in energy.
The intersection seams and the lines consisting of linear Si–H–H geometries extracted from the MECP branching spaces are shown in Fig. 6. The MECPs are the centers of the extracted linear geometries lines and other linear geometries with different r (r = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01
0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2) are symmetrically distributed with the MECPs. It shows that the cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 11A′ and 21A′ states and the intersection seam that between 21A′ and 31A′ states is located in the region with 0.17 < r < 0.18 and φ = π in this branching space. There is not a cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 21A′ and 31A′ states and the intersection seam that between 11A′ and 21A′ states.
0.2) are symmetrically distributed with the MECPs. It shows that the cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 11A′ and 21A′ states and the intersection seam that between 21A′ and 31A′ states is located in the region with 0.17 < r < 0.18 and φ = π in this branching space. There is not a cross point between the line that consists of linear geometries extracted from the branching space of the MECP between 21A′ and 31A′ states and the intersection seam that between 11A′ and 21A′ states.
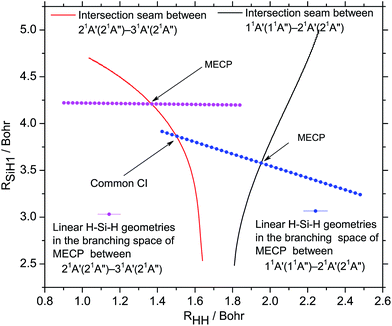 | ||
Fig. 6 The intersection seams at linear Si–H–H geometries and the line of linear Si–H–H geometries in the branching space (r = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.01 0.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2, φ = 0 0.2, φ = 0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.04π 0.04π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2π) of MECP of the corresponding seams. 2π) of MECP of the corresponding seams. | ||
As for the 11A′ electronic state corresponding to the lower cone of the branching space PES of 11A′ and 21A′ states, all of the nuclear configuration paths with different r encircle only one CI that is the MECP between 11A′ and 21A′ states, so the signs of the electronic wavefunctions corresponding to the nuclear configuration paths with different r will change with the nuclear configurations completing the first closed loop path and change back to their original states with the second one, C(φ) = −C(φ + 2π), and this is shown in Fig. 5(e).
The 21A′ electronic state corresponding to the upper cone of the branching space PES of 11A′ and 21A′ states involves two CIs, one is the MECP between 1A′ and 21A′ states and another is a common CI belonging to the intersection seam between 21A′ and 31A′ states located in the region with 0.17 < r < 0.18 and φ = π in this branching space. If r ≤ 0.17, the closed loop paths of nuclear configurations encircle only one CI, so the signs of the electronic wavefunctions corresponding to the nuclear configurations paths with different r will change with the nuclear configurations completing the first closed loop and change back to their original states with the second one, C(φ) = −C(φ + 2π). While, if r ≥ 0.18, the closed loop paths encircle two CIs, and the corresponding electronic wavefunctions will not change sign with the nuclear configurations completing any number of loops, C(φ) = C(φ + 2π). That is shown in Fig. 5(f). All of this confirm that there is a CI on edge the upper cone of branching space PES of 11A′ and 21A′ states, and the CI is one point of intersection seam between 21A′ and 31A′ states.
As for both of the 21A′ and 31A′ electronic states corresponding to the lower cone and the upper cone of the branching space PES of 21A′ and 31A′ states, respectively, all of the nuclear configuration paths with different r encircle only one CI that is the MECP between 21A′ and 31A′ states. So, the signs of the electronic wavefunctions corresponding to the nuclear configuration paths with different r will change with the nuclear configurations completing the first closed loop and change back to their original states after the second one, C(φ) = −C(φ + 2π), and this is shown in Fig. 5(g) and (h).
The GP effects associated with the MECP between 11A′′ and 21A′′ states are shown in Fig. 5(i) and (j). As for both of the 11A′′ state and the 21A′′ state, if r ≤ 0.07, the signs of the corresponding electronic wavefunctions will change with the nuclear configuration completing the first loop and change back to their original states with the second one, C(φ) = −C(φ + 2π). While, if r ≥ 0.08, the corresponding electronic wavefunctions will not change sign with the nuclear configurations completing any number of loops, C(φ) = C(φ + 2π). It indicate that there is a CI on lower and upper cones of the branching space PESs in the vicinity of MECP between 11A′′ and 21A′′ states in the region with 0.07 < r < 0.08, respectively. While this is not apparent in the topography of the branching space PES. We reason that there are some other electronic states that have not been taken into consideration in this work intersecting with the 11A′′, 21A′′ states.
The GP effects associated with the MECP between 21A′ and 31A′ states are shown in Fig. 5(k) and (l). As for both of the 21A′ electronic and 31A′ state, the signs of the corresponding electronic wavefunctions will change with the nuclear configurations completing the first closed loop and change back to its original states after the second one, C(φ) = −C(φ + 2π). It demonstrate that all of the nuclear configuration paths with different r encircle only one CI that is the MECP of intersection seam between 21A′ and 31A′ states. It is true that except the MECP there is not any other CI in the vicinity of the MECP within r ≤ 0.2 in the branching space.
4 Conclusions
CIs among the 11A′, 21A′, 31A′, 11A′′, 21A′′ states of the title system are investigated using the CASSCF or MRCI method. Finally several CI seams at the linear H–Si–H, linear Si–H–H and C2v geometries are determined. The CI seams at the linear H–Si–H, Si–H–H geometries are accompanied by Renner–Teller coupling. The CI seams between 11A′ and 21A′ states actually involve four states: the 11A′, 11A′′ Renner–Teller coupling pair and the 21A′, 21A′′ Renner–Teller coupling pair. The CI seams between 21A′ and 31A′ states simultaneously involve 21A′′ state, for which the components of the Renner–Teller coupling pair are 21A′ and 21A′′ before the MECP, and switch into 31A′ and 21A′′ after the MECP.The geometries and energies of the MECPs on these CI seams are reported, in particular, the MECP of CI seam between 11A′ and 21A′ states at the linear H–Si–H geometries is in the linear H–SiH dissociation direction and it induce the barrier for H + SiH collinear hydrogen exchange reaction with a height of 22.45 kcal mol−1. The MECP of CI seam between 11A′ and 21A′ states at the linear Si–H–H geometries is located on the minimum energy reaction path of the Si(1D) + H2 collinear abstraction reaction, and it determines the energy barrier with a height of 24.06 kcal mol−1.
The topographies of PESs in the vicinities of the MECPs are represented in their branching spaces. The double cone features of the branching space PESs around the MECPs at the linear H–Si–H geometries and the C2v SiH2 geometries are obvious. While, the double cone features of the branching space PESs around the MECPs at the linear Si–H–H geometries are subtle, as the related electronic states are close to each other in energy. In spite of that, the GP effects associated with the MECPs corroborate that the MECPs at the linear Si–H–H geometries are actually CIs, as with that at the linear H–Si–H and C2v SiH2 geometries.
The GP effects of these MECPs are demonstrated. The GP effects associated with the MECPs of intersection between 11A′′, 21A′′ states at the C2v geometries indicate that there are some other electronic states that have not been taken into consideration in this work intersecting with the 11A′′, 21A′′ states.
We hope that this work will be helpful to providing intuitive understanding of the CIs and GP effects, and will contribute to the researches about diabatic dynamics with CIs and GP effects in the title system.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21473218), the Chinese Ministry of Science and Technology (No. 2013CB834601), and the Beijing National Laboratory for Molecular Sciences (No. 20140160, 20150158) and Chinese Academy of Sciences.References
- J. M. Jasinski and J. O. Chu, J. Chem. Phys., 1988, 88, 1678–1687 CrossRef CAS.
- M.-D. Su, J. Am. Chem. Soc., 2002, 124, 12335–12342 CrossRef CAS PubMed.
- M. Denk, J. C. Green, N. Metzler and M. Wagner, J. Chem. Soc., Dalton Trans., 1994, 16, 2405–2410 RSC.
- S. Koseki and M. S. Gordon, J. Mol. Spectrosc., 1987, 123, 392–404 CrossRef CAS.
- R. Escribano and A. Campargue, J. Chem. Phys., 1998, 108, 6249–6257 CrossRef CAS.
- M. Wang, X. Sun and W. Bian, J. Chem. Phys., 2008, 129, 084309 CrossRef PubMed.
- J. Cao, Z. Zhang, C. Zhang, K. Liu, M. Wang and W. Bian, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13180–13185 CrossRef CAS PubMed.
- I. Dubois, G. Herzberg and R. D. Verma, J. Chem. Phys., 1967, 47, 4262–4263 CrossRef CAS.
- D. E. Milligan and M. E. Jacox, J. Chem. Phys., 1970, 52, 2594–2608 CrossRef CAS.
- B. Wirsam, Chem. Phys. Lett., 1972, 14, 214–216 CrossRef CAS.
- Y. Apeloig, R. Pauncz, M. Karni, R. West, W. Steiner and D. Chapman, Organometallics, 2003, 22, 3250–3256 CrossRef CAS.
- I. Dubois, Can. J. Phys., 1968, 46, 2485–2490 CrossRef CAS.
- I. Dubois, G. Duxbury and R. N. Dixon, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 799–806 RSC.
- G. Duxbury, A. Alijah and R. R. Trieling, J. Chem. Phys., 1993, 98, 811–825 CrossRef CAS.
- C. Yamada, H. Kanamori, E. Hirota, N. Nishiwaki, N. Itabashi, K. Kato and T. Goto, J. Chem. Phys., 1989, 91, 4582–4586 CrossRef CAS.
- J. W. Thoman, J. I. Steinfeld, R. I. McKay and A. E. W. Knight, J. Chem. Phys., 1987, 86, 5909–5917 CrossRef CAS.
- M. Fukushima, S. Mayama and K. Obi, J. Chem. Phys., 1992, 96, 44–52 CrossRef CAS.
- J. Thoman and J. Steinfeld, Chem. Phys. Lett., 1986, 124, 35–38 CrossRef CAS.
- M. Fukushima and K. Obi, J. Chem. Phys., 1994, 100, 6221–6227 CrossRef CAS.
- M. Nakajima, A. Kawai, M. Fukushima and K. Obi, Chem. Phys. Lett., 2002, 364, 99–107 CrossRef CAS.
- H. Ishikawa, Y. Muramoto and N. Mikami, J. Mol. Spectrosc., 2002, 216, 90–97 CrossRef CAS.
- S. N. Yurchenko, P. R. Bunker, W. P. Kraemer and P. Jensen, Can. J. Chem., 2004, 82, 694–708 CrossRef CAS.
- Y. Muramoto, H. Ishikawa and N. Mikami, J. Chem. Phys., 2005, 122, 154302 CrossRef PubMed.
- I. Tokue, K. Yamasaki and S. Nanbu, J. Chem. Phys., 2005, 122, 144307 CrossRef PubMed.
- I. Tokue, K. Yamasaki and S. Nanbu, J. Chem. Phys., 2006, 124, 114308 CrossRef PubMed.
- D. R. Yarkony, Acc. Chem. Res., 1998, 31, 511–518 CrossRef CAS.
- T. J. Martinez, Nature, 2010, 467, 412–413 CrossRef CAS PubMed.
- S. Matsika and P. Krause, Annu. Rev. Phys. Chem., 2011, 62, 621–643 CrossRef CAS PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- M. R. Manaa and D. R. Yarkony, J. Chem. Phys., 1992, 97, 715–717 CrossRef.
- A. Perveaux, P. J. Castro, D. Lauvergnat, M. Reguero and B. Lasorne, J. Phys. Chem. Lett., 2015, 6, 1316–1320 CrossRef CAS PubMed.
- D. R. Yarkony, Rev. Mod. Phys., 1996, 68, 985–1013 CrossRef CAS.
- F. Bouakline, S. C. Althorpe and D. Peláez Ruiz, J. Chem. Phys., 2008, 128, 124322 CrossRef PubMed.
- J. P. Villabona-Monsalve, R. Noria, S. Matsika and J. Peón, J. Am. Chem. Soc., 2012, 134, 7820–7829 CrossRef CAS PubMed.
- Y. Asano, A. Murakami, T. Kobayashi, A. Goldberg, D. Guillaumont, S. Yabushita, M. Irie and S. Nakamura, J. Am. Chem. Soc., 2004, 126, 12112–12120 CrossRef CAS PubMed.
- H. Kang, K. T. Lee, B. Jung, Y. J. Ko and S. K. Kim, J. Am. Chem. Soc., 2002, 124, 12958–12959 CrossRef CAS PubMed.
- F. Bernardi, S. De, M. Olivucci and M. A. Robb, J. Am. Chem. Soc., 1990, 112, 1737–1744 CrossRef CAS.
- J. Brazard, L. A. Bizimana, T. Gellen, W. P. Carbery and D. B. Turner, J. Phys. Chem. Lett., 2016, 7, 14–19 CrossRef CAS PubMed.
- C. Schnedermann, M. Liebel and P. Kukura, J. Am. Chem. Soc., 2015, 137, 2886–2891 CrossRef CAS PubMed.
- G. J. Halász, Á. Vibók and L. S. Cederbaum, J. Phys. Chem. Lett., 2015, 6, 348–354 CrossRef PubMed.
- D. Polli, P. Altoe, O. Weingart and K. M. Spillane, Nature, 2010, 467, 440–443 CrossRef CAS PubMed.
- J. G. Atchity, K. Ruedenberg and A. Nanayakkara, Theor. Chem. Acc., 1997, 96, 195–204 CrossRef.
- H. J. Wörner, J. B. Bertrand, B. Fabre and J. Higuet, Science, 2011, 334, 208–212 CrossRef PubMed.
- B. Zhou, C. Zhu, Z. Wen, Z. Jiang, J. Yu, Y.-P. Lee and S. H. Lin, J. Chem. Phys., 2013, 139, 154302 CrossRef PubMed.
- S. Y. Grebenshchikov and R. Borrelli, J. Phys. Chem. Lett., 2012, 3, 3223–3227 CrossRef CAS PubMed.
- M. R. Manaa, J. Chem. Phys., 2000, 112, 8789–8793 CrossRef CAS.
- G. Chaban, M. S. Gordon and D. R. Yarkony, J. Phys. Chem. A, 1997, 101, 7953–7959 CrossRef CAS.
- M. S. Gordon, V.-A. Glezakou and D. R. Yarkony, J. Chem. Phys., 1998, 108, 5657–5659 CrossRef CAS.
- A. Vibók, G. J. Halósz, T. Vèrteśi, S. Suhai, M. Baer and J. P. Toennies, J. Chem. Phys., 2003, 119, 6588–6596 CrossRef.
- D. R. Yarkony, J. Chem. Phys., 1996, 104, 2932–2939 CrossRef CAS.
- N. Matsunaga and D. R. Yarkony, J. Chem. Phys., 1997, 107, 7825–7838 CrossRef CAS.
- X. Liu, W. Bian, X. Zhao and X. Tao, J. Chem. Phys., 2006, 125, 074306 CrossRef PubMed.
- M. V. Berry, Proc. R. Soc. A, 1984, 392, 45–57 CrossRef.
- L. Fu, C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2007, 98, 106803 CrossRef PubMed.
- D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959–2007 CrossRef CAS.
- Y. Aharonov and D. Bohm, Phys. Rev., 1959, 115, 485–491 CrossRef.
- J. W. Zwanziger, M. Koenig and A. Pines, Annu. Rev. Phys. Chem., 1990, 41, 601–646 CrossRef.
- I. G. Ryabinkin and A. F. Izmaylov, Phys. Rev. Lett., 2013, 111, 220406 CrossRef PubMed.
- G. Herzberg and H. C. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77–82 RSC.
- C. A. Mead, Rev. Mod. Phys., 1992, 64, 51–85 CrossRef CAS.
- B. E. Applegate, T. A. Barckholtz and T. A. Miller, Chem. Soc. Rev., 2003, 32, 38–49 RSC.
- B. K. Kendrick and R. T. Pack, J. Chem. Phys., 1997, 106, 3519–3539 CrossRef CAS.
- B. K. Kendrick, Phys. Rev. Lett., 1997, 79, 2431–2434 CrossRef CAS.
- D. Babikov, B. K. Kendrick, P. Zhang and K. Morokuma, J. Chem. Phys., 2005, 122, 044315 CrossRef PubMed.
- B. K. Kendrick, J. Chem. Phys., 2001, 114, 8796–8819 CrossRef CAS.
- B. K. Kendrick, J. Chem. Phys., 2003, 118, 10502–10522 CrossRef CAS.
- B. K. Kendrick, J. Phys. Chem. A, 2003, 107, 6739–6756 CrossRef CAS.
- J. C. Juanes-Marcos and S. C. Althorpe, J. Chem. Phys., 2005, 122, 204324 CrossRef PubMed.
- J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, Science, 2005, 309, 1227–1230 CrossRef CAS PubMed.
- S. C. Althorpe, J. Chem. Phys., 2006, 124, 084105 CrossRef PubMed.
- J. C. Juanes-Marcos, S. C. Althorpe and E. Wrede, J. Chem. Phys., 2007, 126, 044317 CrossRef PubMed.
- J. Jankunas, M. Sneha, R. N. Zare, F. Bouakline and S. C. Althorpe, J. Chem. Phys., 2013, 139, 144316 CrossRef PubMed.
- J. Hazra, B. K. Kendrick and N. Balakrishnan, J. Phys. Chem. A, 2015, 119, 12291–12303 CrossRef CAS PubMed.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Nat. Commun., 2015, 6, 7918 CrossRef CAS PubMed.
- B. K. Kendrick, J. Hazra and N. Balakrishnan, Phys. Rev. Lett., 2015, 115, 153201 CrossRef CAS PubMed.
- S. K. Min, A. Abedi, K. S. Kim and E. K. U. Gross, Phys. Rev. Lett., 2014, 113, 263004 CrossRef PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schutz, MOLPRO, Version 2010.1, a Package of Ab Initio programs, see http://www.molpro.net Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514–522 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053–5063 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- B. C. Hoffman and D. R. Yarkony, J. Chem. Phys., 2000, 113, 10091–10099 CrossRef CAS.
- F. Sicilia, L. Blancafort, M. J. Bearpark and M. A. Robb, J. Phys. Chem. A, 2007, 111, 2182–2192 CrossRef CAS PubMed.
- F. J. Aoiz, L. Banares and V. J. Herrero, J. Phys. Chem. A, 2006, 110, 12546–12565 CrossRef CAS PubMed.
- H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1–68 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Seam lines of the conical intersections and three dimension representation of the geometric phase effect associated with the conical intersection in the Si(1D) + H2 system. See DOI: 10.1039/c7ra01021d |
| This journal is © The Royal Society of Chemistry 2017 |