Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ciprofloxacin intercalated in fluorohectorite clay: identical pure drug activity and toxicity with higher adsorption and controlled release rate
E. C.
dos Santos†
 *ab,
Z.
Rozynek†
*ab,
Z.
Rozynek†
 ac,
E. L.
Hansen†
a,
R.
Hartmann-Petersen
ac,
E. L.
Hansen†
a,
R.
Hartmann-Petersen
 d,
R. N.
Klitgaard
d,
A.
Løbner-Olesen
d,
R. N.
Klitgaard
d,
A.
Løbner-Olesen
 d,
L.
Michels
a,
A.
Mikkelsen
d,
L.
Michels
a,
A.
Mikkelsen
 ac,
T. S.
Plivelic
ac,
T. S.
Plivelic
 e,
H. N.
Bordallo
e,
H. N.
Bordallo
 bf and
J. O.
Fossum
bf and
J. O.
Fossum
 ag
ag
aDepartment of Physics, Norwegian University of Science and Technology (NTNU), Trondheim, Norway. E-mail: everton.santos@ntnu.no
bNiels Bohr Institute (NBI), University of Copenhagen, Copenhagen, Denmark
cFaculty of Physics, Adam Mickiewicz University (AMU), Poznań, Poland
dDepartment of Biology, University of Copenhagen, Copenhagen, Denmark
eMAX IV Laboratory, Lund University, 22100 Lund, Sweden
fEuropean Spallation Source ERIC, Lund, Sweden
gInstitute Pierre-Gilles de Gennes pour la microfluidique, Paris, France
First published on 17th May 2017
Abstract
Different natural clay minerals, including halloysite, montmorillonite and kaolinite, have been proven to be efficient drug carriers providing for high and long lasting drug concentrations owing to their adsorption capacity and ion exchange property. Synthetic clays, however, are advantageous over the natural clay minerals in terms of purity of composition and controllable cation exchange capacity, factors that contribute to improve reproducibility of the host system. Here we studied a synthetic smectite clay as a candidate for high adsorption and controlled release rate. Via X-ray powder diffraction we verified that, under acidic conditions, the antibiotic ciprofloxacin was successfully incorporated in the synthetic clay fluorohectorite, while via UV-VIS spectroscopy we showed that the degree of the drug incorporation is at least 25% higher than for other systems reported in the literature. Furthermore, temperature dependent release studies allowed us to show that the release process is thermally activated and diffusion-controlled. Finally, via bacterial and toxicological tests, we demonstrated that the effectiveness and toxicity of pure ciprofloxacin is unaffected in the clay–drug complex.
Introduction
Controlled drug release systems show several advantages over conventional dosage forms. Besides manipulating the release rate, drug encapsulation offers, among others, protection against drug hydrolysis, chemical degradation as well as decrease in drug toxicity.1–5 Over the last decade, different porous materials have been used as hosts for drug encapsulation,3–12 including natural and synthetic smectite clays.2,13–17 Important factors that facilitate drug intercalation in clay systems are: (i) clay particles undergo crystalline swelling,18–20 (ii) the tunability of their net negative structural charge by isomorphic substitution of the interlayer cation21 and (iii) their non-toxicity for transdermal application and oral administration.11,14–17 Among clay minerals, montmorillonite has been the most commonly studied for drug delivery applications.14,15,22,23 Although, compared with natural smectites, synthetic clays show a number of advantages that contribute to improved reproducibility of the host system, such as purity of composition, controllable cation exchange capacity (CEC) and pore size distributions, not many studies have been devoted to the study of drugs encapsulated in synthetic clays.13,24 It is in this context that the current study focuses on intercalation and release of the antibiotic ciprofloxacin (CIPRO) in the synthetic clay fluorohectorite (Fh).CIPRO, a broad-spectrum antibacterial agent for oral administration, is used to treat bacterial infections.25–28 Like other fluoroquinolones, CIPRO is zwitterionic exhibiting a ‘U-shaped’ pH-solubility profile, with a solubility that increases at high and low pH values. At high pHs CIPRO acquires a negative charge because of the deprotonation of the carboxylic group, whereas at low pHs the CIPRO molecules become positively charged because of the protonation of the amine group. Furthermore, a neutral net charge is observed around neutral pH.14,28,29 Smectite clays, such as Fh, consist of deck-of-card-like particles formed by several negatively charged stacked clay unit layers, including intercalated charge compensating cations. Cations exchange processes are readily achieved in such systems.30,31 Furthermore previous work dealing with the encapsulation of CIPRO in LiFh13 motivated us to investigate the possibility of CIPRO adsorption by intercalation under acidic conditions, where the CIPRO molecules are positively charged and, in this context, might “act” as cations.
In the present study, we use X-ray powder diffraction (XRD) and ultraviolet-visible spectroscopy (UV-VIS) to investigate the suitability of Li-fluorohectorite (LiFh) to incorporate CIPRO, forming a clay–drug composite, hereafter called CPFh. The CIPRO adsorption is studied under acidic conditions and its release by dispersing the clay–drug composite in synthetic gastric acid (SGA). Based on these results we show that at body temperature the drug release is thermally activated. In addition, by means of minimum inhibitory and bactericidal concentration (MIC and MBC, respectively) as well as cell viability tests we show that antibacterial activity and toxicity of the clay–drug complex match that of pure CIPRO.
Experimental
Materials
Fluorohectorite has the unit cell chemical formula Cx(Mg(6−x)Lix)Si8O20F4, with C denoting the exchangeable charge compensating cation.32 In this study we used LiFh, Li1.2(Mg4.8Li1.2)Si8O20F4, purchased from Corning Inc., with Li+ as cation. CIPRO, C17H18FN3O3,28 was purchased from Fluka via Sigma-Aldrich. Both materials were used as received, i.e., without further purification.Preparation of CIPRO intercalated in Fh: the CPFh composite analysed with UV-VIS spectroscopy and synchrotron XRD
The molecular weight of the CIPRO molecule is 331.3 g mol−1, and the molecular weight of the LiFh unit cell is 754 g mol−1. Thus, the formation of CPFh requires at least 0.53 g of ciprofloxacin per 1.00 g of LiFh, assuming that every intercalated Li+ cation in LiFh is exchanged with one CIPRO molecule. Then the molecular weight of the resulting CPFh unit cell, with chemical formula (C17H18FN3O3)1.2(Mg4.8Li1.2)Si8O20F4, would be about 1143 g mol−1.Following this line of reasoning, to investigate the amount of CIPRO needed for complete exchange of Li cations the CPFh composite was prepared by mixing either 0.25 g of CIPRO with 1.00 g of LiFh (hereafter referred to as batch A) or 1.00 g of CIPRO with 1.00 g of LiFh (hereafter referred to as batch B) in 200 mL of an aqueous solution adjusted to pH = 2.0 by adding HCl. At this pH the drug molecules are positively charged, thus facilitating its cationic exchange with the interlayer Li+. Moreover, to examine the drug intercalation in a more environmentally friendly way, i.e. without the use of chemicals for pH control, further sorption tests were conducted in pure deionized aqueous solution (hereafter referred to as batch C).
Considering that temperature might influence the swelling properties of the Fh clay particles,32 the solutions were stirred either at room temperature or at 70 °C.
To assess the degree of CIPRO incorporation, the samples were centrifuged, and the sediment was washed from excess of the drug either through re-dispersion in acidic solution of pH = 2.0 (batches A and B) or in pure deionized water (batch C). The CPFh samples were centrifuged again, and subsequently the supernatant was collected and analysed with UV-VIS spectroscopy using an Agilent 8453 spectrophotometer in a wavelength interval ranging from 200 to 400 nm. This process was repeated 5 times, which proved to be sufficient to reach a stable and minimal CIPRO concentration released into the supernatant, indicating that the remaining drug was adsorbed, either successfully intercalated into the Fh clay particles or attached to its outer particle surfaces.
After washing, the stable sediment was dried at room temperature and analysed with X-rays using the I911-SAXS beamline33 at the MAX-lab Synchrotron Facility in Lund, Sweden. We used a wavelength λ = 0.091 nm covering a scattering vector, Q, in the range from about 1 to 7 nm−1 (corresponding to scattering angles in the range 2θ ≈ 0.85° to 2θ ≈ 5.85°). In order to verify the diffusion rate of the incorporation process, samples were thus collected at several intervals after the initial drug exposure, respectively at 5 hours, 24 hours, 5 days and 13 days.
CIPRO-release from the CPFh composite at pH 1.5 as a function of time and temperature, analysed with UV-VIS spectroscopy
Release studies were conducted in a SGA solution, which was prepared by adding 2.00 g of NaCl to 1.000 L of deionized water adjusted to pH = 1.5 by adding HCl. For the release experiments, 25 mg of washed and dried CPFh from batch B were added to 50 mL of the SGA solution at 24 °C, 37 °C, 55 °C and 70 °C, and stirred. At certain times, the solutions were centrifuged, and aliquots of 0.25 mL were extracted from the supernatant for analysis. The solutions were re-stirred between each centrifugation and extraction.Minimal inhibitory concentration (MIC) and minimal bactericidal concentration (MBC) determination
Standard MIC and MBC assays were done by the micro dilution method essentially as described in standard protocols34 in order to determine the efficiency of the clay–drug complex against Gram-negative (Escherichia coli ATCC® 25922™; Pseudomonas aeruginosa ATCC® 27853™; Acinetobacter baumannii ATCC® 19606™; Klebsiella pneumoniae® 700603™) and Gram-positive (Staphylococcus aureus ATCC® 29213™; Enterococcus faecalis ATCC® 29212™) human pathogens. The same was done for pure CIPRO and LiFh.The diluted bacterial cultures for the MIC and MBC determination were prepared by growing the cultures to OD600 ≥ 0.1 in 10 mL of cation adjusted Mueller–Hinton broth (pH 7.3; CAMHB). Cultures were diluted in CAMHB so that the final concentration was 5 × 105 bacteria per mL during the MIC test. Compounds for antimicrobial activity testing were added as a twofold dilution series.
MBC were determined by plating 100 μl of cells from the 1 × MIC, 2 × MIC and 4 × MIC wells on non-selective LB-agar plates. The MBC was defined as the compound concentration that killed 99.9% of the start inoculum.
Toxicity determination
Human Jurkat cells (ATCC) were maintained in Dulbecco's Modified Eagle medium (Gibco) supplemented with 10% fetal-calf serum (Invitrogen), and 2 mM glutamine (Sigma-Aldrich) at 37 °C in a humidified atmosphere containing 5% CO2. For cell viability assays the cells were seeded in CELLine bioreactor flasks (Sigma-Aldrich). After 48 h cell viability was determined by counting cells stained with Trypan Blue (Sigma-Aldrich) at a final concentration of 0.2%.Results and discussion
CIPRO intercalation
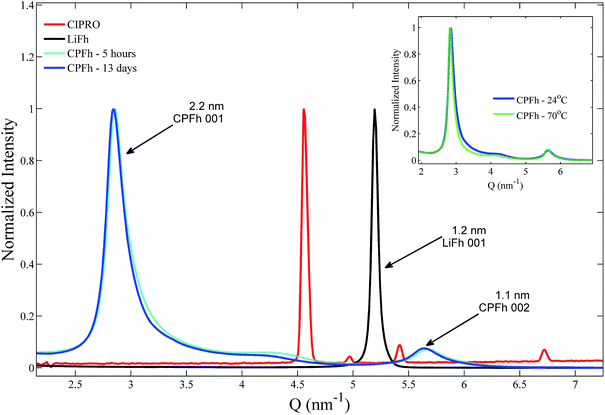
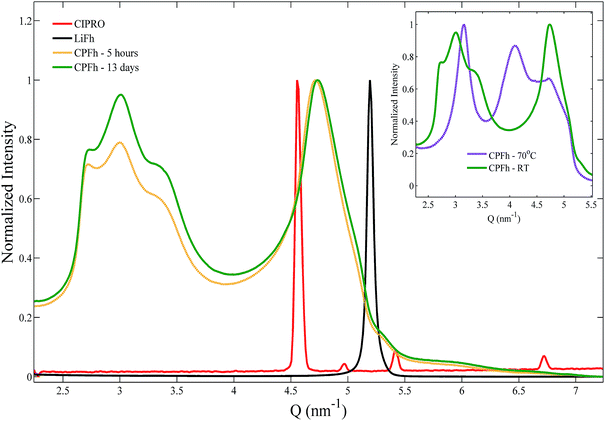
XRD patterns obtained for the CPFh powders, batch A, are shown in Fig. 1. The 001 and 002 Bragg reflections correspond to an interlayer periodicity of 2.2 nm. This is markedly larger than the interlayer periodicity of the native LiFh, which in the monohydrated state is 1.2 nm. Such interlayer expansion is a clear indication of the successful intercalation of CIPRO into the clay interlayers. Under acidic conditions no significant differences between samples prepared at ambient or elevated temperatures were observed (inset of Fig. 1). Because we do not observe significant changes in diffraction profiles from samples extracted after 5 hours (CPFh – 5 hours) and 13 days (CPFh – 13 days), it appears that the intercalation process is completed in less than a day. Under acidic condition, because of the loss of crystallinity of the intercalated drug,35 the Bragg reflections of pure CIPRO are absent in the CPFh diffraction patterns. Samples prepared at pure deionized water, batch C, show a more complex scattering profile, as depicted in Fig. 2, which is in full agreement with the previous studies on CIPRO intercalated into Fh.13The results obtained from the batch C can be understood as follows. At room temperature, when the clay particles are dispersed into deionized water, the pH of the solution is driven towards around 9.36 However, the charge of the CIPRO molecules is pH-dependent, with an acid dissociation constant pKa2 = 8.7.28,37 Thus, in such conditions, the CIPRO molecules might be either in the anionic or neutral forms, and may not intercalate easily. On heating, a very convoluted variation of CIPRO's net charge occurs, most likely due to a different degree of drug intercalation, that gives rise to a more convoluted X-ray pattern (inset of Fig. 2), that could partially be linked to the temperature dependence of the pH.
For the samples prepared under controlled pH, batches A and B, UV-VIS spectroscopy shows that after 24 h of mixing stable CIPRO concentrations are reached, which were measured to be respectively 0.25 ± 0.01 g and 0.49 ± 0.01 g per 1.00 g of LiFh. Although for the batch A all the added CIPRO was retained in the resulting CPFh composite, this is not the optimal situation as the estimated saturation amount is 0.53 g of CIPRO per 1.00 g of LiFh. Therefore, for this batch, not all cations were exchanged by the drug molecules. On the other hand, for batch B the amount of drug retained is not only close to the calculated saturation amount but higher than the amount of CIPRO adsorbed to Fh without pH control (0.350 gCIPRO gHost−1).13 This value is also considerably higher than what is adsorbed by other host systems, such as rectorite: 0.135 gCIPRO gHost−1;23 montmorillonite: 0.395 gCIPRO gHost−1;23 oxidized xerogel: 0.060 gCIPRO gHost−1;38 chemically prepared carbon (wet): 0.133 gCIPRO gHost−1;39 vermiculite modified with amphoteric surfactant of phosphatidylcholine: 0.094 gCIPRO gHost−1.40 Based on these results drug release analysis was performed on batch B only.
CIPRO release
Release studies from samples from the batch B were conducted in SGA at room temperature (24 ± 1 °C), body temperature (37 ± 2 °C) and at 55 ± 2 °C and 70 ± 3 °C. CIPRO release is gradual and temperature dependent, with higher temperatures favouring a faster release (Fig. 3). The release profile shows a plateau in roughly 50 hours at 70 °C, 165 hours at 55 °C and 37 °C, and after more than 200 hours at 24 °C.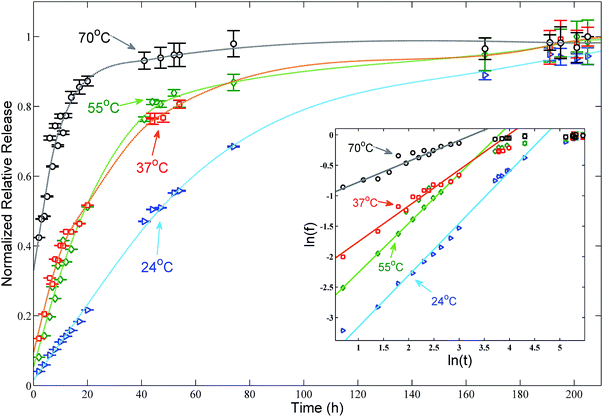 | ||
| Fig. 3 Normalized release profile of CIPRO from solutions of batch B in synthetic gastric acid at four different temperatures. Arrows indicate the temperature at which each set of data was collected and the dashed lines are guide lines to facilitate the viewing. The maximal release concentration of 5.3 mg is achieved after roughly 50 hours at 70 ± 3 °C and after more than 200 hours at 24 ± 1 °C. The resulting continuous lines shown in the inset – log–log plot of the data fitted using eqn (4) – indicate that in the first 20 hours the CIPRO release is mostly thermally activated. | ||
A series of factors can influence the drug release from a given system resulting in different release rates,1,41–43 such as temperature, the host shape and porosity as well as solubility and diffusivity of the drug molecule itself. Over the years, a wide number of models have been derived from the Fick's diffusion law and proposed to explain drug release.41–43 Here we applied the semi empirical Korsmeyer–Peppas model44,45 to describe the CIPRO's release from LiFh. This is a power law which relates the fraction of drug released (ft) to time (t) and is used to fit data within 60% of the fraction of drug released as follows:
| ft = kKPtn | (1) |
If in a particular temperature range, the drug release is mostly thermally activated, all other factors influencing the release can be neglected, i.e. host geometry, solubility and diffusivity of the drug molecule itself as well as concentration of incorporated drug. Therefore, the release rate can be described by the Arrhenius equation
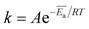 | (2) |
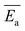 the average activation energy. Then if we define that kKP is related to k by a power law, with n as exponent, eqn (1) becomes
the average activation energy. Then if we define that kKP is related to k by a power law, with n as exponent, eqn (1) becomes| ft = kntn | (3) |
Taking the logarithm in both sides of eqn (3) and reorganizing the terms, we get
ln(ft) = n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(k) + n ln(k) + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(t) ln(t) | (4) |
According to eqn (4), if the assumption that the CIPRO's release is mostly thermally activated, by plotting ln(ft) versus ln(t) a straight line would be obtained and its slope would be numerically equal to the release exponent. Such plot presented as inset in Fig. 3, shows that indeed a straight line can be fitted at least in the first 20 hours of the drug release process, (ln(20) ≅ 3). The fitting results are summarized in Table 1, where one see that n becomes larger than 0.5 as the temperature approaches body temperature, indicating an anomalous drug diffusion from the clay particles.45
| Temperature | n | k (h−1) |
|---|---|---|
| 24 °C | 0.85 ± 0.07 | 0.009 ± 0.004 |
| 37 °C | 0.81 ± 0.06 | 0.024 ± 0.008 |
| 55 °C | 0.59 ± 0.09 | 0.019 ± 0.007 |
| 70 °C | 0.34 ± 0.06 | 0.037 ± 0.009 |
The average activation energy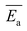 , for the CIPRO's release can be calculated from the slope of the straight line obtained by plotting ln(k) versus 1/T (Arrhenius plot), as depicted in Fig. 4a. According to that,
, for the CIPRO's release can be calculated from the slope of the straight line obtained by plotting ln(k) versus 1/T (Arrhenius plot), as depicted in Fig. 4a. According to that, 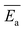 is numerically equal to the slope times the gas constant R, resulting in 22.0 ± 0.5 kJ mol−1 and indicating that the release process is diffusion-controlled.46
is numerically equal to the slope times the gas constant R, resulting in 22.0 ± 0.5 kJ mol−1 and indicating that the release process is diffusion-controlled.46
 | ||
| Fig. 4 (a) Arrhenius plot used to obtain the average activation energy as described in eqn (2), (b) master curve obtained using eqn (5) to further verify if the drug release is mostly thermally activated for the first 20 hours and (c) comparison between the average activation energy obtained using the Arrhenius plot (straight line) and the instantaneous activation energy using eqn (5) (dots). | ||
In order to further verify our assumption that the CIPRO's release is mostly a thermally activated process and thereby confirm the accuracy of the activation energy found from the Arrhenius plot (Fig. 4a), eqn (2) was replaced into eqn (4) giving:
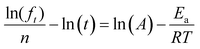 | (5) |
Fig. 4b shows the plot of the left hand of eqn (5)versus 1000/T for the 20 first hours of CIPRO release, when the Arrhenius behaviour is valid (linear dependence shown in the inset of Fig. 3). The dispersion between the points for different times is larger at 70 °C (at 70 °C, 1000/T ≈ 2.91), indicating that in this temperature other factors are influencing CIPRO release, as for example possibly changes in the aspect ratio of the clay particles due to delamination.32 On the other hand, at body temperature, with exception of the data collected after 8 hours of release, the collapsing is almost perfect. This is yet another clear indication that at this temperature the release is mostly thermally activated. From the slopes of each curve at Fig. 4b, an instantaneous activation energy was obtained. These values confirm the average activation energy of 22 kJ mol−1 as depicted in Fig. 4c.
As the activation energy obtained in this work is three times lower than the value previously reported for the CPFh system prepared without pH control (67 kJ mol−1; pH around 8),13 our results show that the release of CIPRO from samples prepared at acidic pH is facilitated. Indeed a faster CIPRO's release at 37 °C in synthetic gastric acid (around 80% of the drug is release after 50 hours, Fig. 3) is observed when comparing the release data from samples prepared without pH control (around 35% of the drug is release after 50 hours (ref. 13)). These differences together with the dissimilarity in the amount of CIPRO captured by Fh with and without pH control, 0.49 gCIPRO ghost−1 (this work) and 0.35 gCIPRO ghost−1,13 further confirm that for samples prepared at pH = 2 the interactions between the drug and the clay are weaker.47
Moreover, the activation energy reported in this work for the CIPRO release is close to the value reported for the adsorption of this drug via cation exchange onto a carbon matrix chemically prepared from palm leaflets39 (17 kJ mol−1) and to the activation energy found by Crosson et. al. for the sorption of denatonium onto the synthetic smectite montmorillonite (25.9 kJ mol−1).48 Furthermore, the obtained 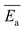 value is within the range of ion exchange in mesoporous and macro porous materials (24–40 kJ mol−1).49 Together these findings support the idea that the CIPRO's release is governed by cation exchange.
value is within the range of ion exchange in mesoporous and macro porous materials (24–40 kJ mol−1).49 Together these findings support the idea that the CIPRO's release is governed by cation exchange.
Toxicity and antibacterial tests
The toxicity of CPFh was determined by analyzing the viability of human Jurkat cells in tissue culture after 48 hours in the presence of the clay-drug complex and comparing with the toxicity of the pure drug. Fig. 5 shows the results for both CIPRO and CPFh. In both cases, only at high concentrations we observe a slight reduction in cell viability. Hence, at 0.1 mg mL−1 approximately 90% of the cells were viable, showing that the clay–drug complex, CPFh, preserve the same toxicity as the pure CIPRO.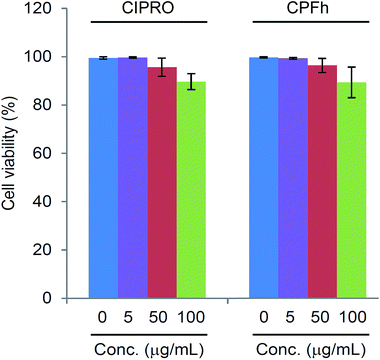 | ||
| Fig. 5 Human Jurkat cells viability in tissue culture after 48 hours in the presence of CIPRO and CPFh. | ||
The minimum inhibitory and bactericidal concentrations of CIPRO and CPFh, together with the minimum inhibitory concentration of LiFh for E. coli, P. aeruginosa, A. baumannii, K. pneumoniae, S. aureus and E. faecalis are presented in Table 2. One may notice that LiFh showed no antimicrobial activity towards any of these pathogens in contrast to CIPRO and CPFh that are effective against the same bacteria. With exception of P. aeruginosa, MIC = MBC for both the pure drug and the clay-drug complex, which is an expected result given the mode of action of CIPRO.50 Comparing the antibactericidal efficacy of CPFh with the pure CIPRO we notice that the concentration of CPFh needed to inhibit bacterial growth is two to four times higher than the pure drug. This does however not indicate a reduced activity of the clay–drug complex relative to that of the pure drug: the UV-VIS results demonstrate that 1.49 g of CPFh contains up to 0.49 g of CIPRO, meaning that about 33% of CPFh is composed of cipro while the remaining 67% is the carrier. Taking this into account, we conclude that the antibacterial efficacy of CPFh is similar to that of pure CIPRO.
| CIPRO MIC (μg mL−1) | CIPRO MBC (μg mL−1) | CPFh MIC (μg mL−1) | CPFh MBC (μg mL−1) | Lifh MIC (μg mL−1) | |
|---|---|---|---|---|---|
| E. coli ATCC 25922 | 0.015 | 0.015 | 0.06 | 0.06 | >128 |
| P. aeruginosa ATCC 27853 | 0.25 | 1.00 | 1.00 | 2.00 | >128 |
| A. baumannii ATCC 19606 | 1.00 | 1.00 | 2.00 | 2.00 | >128 |
| K. pneumoniae ATCC 700603 | 0.50 | 0.50 | 2.00 | 2.00 | >128 |
| S. aureus ATCC 29213 | 0.50 | 0.50 | 2.00 | 2.00 | >128 |
| E. faecalis ATCC 29212 | 2.00 | 2.00 | 8.00 | 8.00 | >128 |
Conclusions
We demonstrated that the antibiotic ciprofloxacin (CIPRO) can be intercalated into the interlayers of the synthetic clay mineral, fluorohectorite (Fh), likely replacing the native Li-cations to produce the clay–drug composite CPFh under different pHs. The intercalation is verified experimentally using X-ray powder diffraction (XRD) and UV-VIS spectroscopy. Under acidic conditions, Fh have retained at least 25% more CIPRO than other hosts systems reported in the literature, being very close to the theoretical prediction. On the other hand, samples prepared without pH control show a more complex XRD profile and a lower degree of drug intercalation.In synthetic gastric acid at temperatures ranging between 24 °C and 70 °C, UV-VIS spectroscopy measurements show that the release profiles of CIPRO from CPFh are strongly temperature dependent. By fitting the release profile curves of CPFh using the semi-empirical Korsmeyer–Peppas model we show that the drug release is mostly thermally activated in the first 20 hours. In addition, at body temperature the release exponent (n = 0.81 ± 0.06), which is related to the release mechanism follows in the range characterizing anomalous diffusion, 0.5 < n < 1. Using the Arrhenius equation an activation energy of 22.0 ± 0.5 kJ mol−1 was obtained, indicating that the CIPRO's release is a diffusion-controlled process. This result differs from the value obtained previously, where the higher activation energy indicates that, for samples prepared without pH control, the release is chemically controlled. Furthermore, these differences in the activation energy, together with the contrasts in the amount of drug captured, indicates that in the case of the samples prepared at pH = 2 the interactions between the drug and the clay particles are weaker. In addition, the higher drug adsorption at acidic pH, where CIPRO is negatively charged, together with the similarities in the activation energy reported in the literature for other cation exchange processes, suggest that the CIPRO capture at acidic pHs occurs via cation exchange.
Antibacterial susceptibility testing demonstrated that the activity of CPFh against E. coli, P. aeruginosa, A. baumannii, K. pneumoniae, S. aureus and E. faecalis was similar to that of pure CIPRO. Along with the observation that the toxicity of the clay–drug complex was low and also similar to that of CIPRO alone, we provide strong evidence that LiFh is a carrier that promotes drug release in a slow and controlled manner without interfering with the drug's action and without causing adverse effects on human cells.
In order to further verify the importance of pH, and consequently the electric charge of CIPRO in the drug delivery process, release studies conducted in basic solutions, obtained for example by adding NaOH to deionized water, are of great interest. In this case, CIPRO should be negatively charged, which could promote its rapid release its replacement by Na+. Therefore, it can be expected that the X-ray scattering profile from the same batch but prepared by adding CPFh to basic NaOH solutions would display a pattern associated with sodium fluorohectorite (NaFh).
To conclude, the high drug adsorption capacity as well as the slow and gradual release reported in this work adds the synthetic smectite fluorohectorite as a promising material within the clay family.
Acknowledgements
E. C. dos Santos research is financed by the Norwegian Research Council (RCN), SYNKØYT Program (project number 228551), and the University of Copenhagen, Niels Bohr Institute. H. N. Bordallo, T. Plivelic and J. O. Fossum acknowledge the financial support by the Norwegian Research Council (RCN), SYNKØYT Program (project number 228551). L. Michels, Z. Rozynek and J. O. Fossum acknowledge the financial support by the Norwegian Research Council (RCN), CLIMIT Program (project number 200041). A. Mikkelsen acknowledges financial support from the European Union's Horizon 2020 research and innovation framework programme under the Marie Skłodowska-Curie grant agreement No. 752896. Zbigniew Rozynek acknowledges the financial support of the Polish National Science Centre through the OPUS programme (2015/19/B/ST3/03055). R. N. Klitgaard and A. Løbner-Olesen were supported by the University of Copenhagen Centre for Control of Antibiotic Resistance (UC-Care) and A. Løbner-Olesen was supported by the Center for Bacterial Stress Response and Persistence (BASP) funded by a grant from the Danish National Research Foundation (DNRF120). The I911-SAXS beamline at MAX IV Laboratory is acknowledged for the beamtime provided, as well as the CALIPSO exchange program for funding E. L. Hansen travels to perform for these experiments. C. Dicko is acknowledged for assistance on the UV-VIS experiments performed at MAX IV Laboratory. We also gratefully thank A. Rivera, L. Valdés, I. Pérez, A. Lam, and E. Altshuler from the University of Havana, Cuba, for very fruitful discussions.References
- M. Andersson Trojer, L. Nordstierna, M. Nordin, M. Nyden and K. Holmberg, Phys. Chem. Chem. Phys., 2013, 15, 17727–17741 RSC.
- L. A. Rodrigues, A. Figueiras, F. Veiga, R. M. de Freitas, L. C. Nunes, E. C. da Silva Filho and C. M. da Silva Leite, Colloids Surf., B, 2013, 103, 642–651 CrossRef CAS PubMed.
- G. Tiwari, R. Tiwari, B. Sriwastawa, L. Bhati, S. Pandey, P. Pandey and S. K. Bannerjee, Int. J. Pharm. Invest., 2012, 2, 2–11 CrossRef PubMed.
- G. Levy, J. Pharm. Sci., 1965, 54, 959–967 CrossRef CAS PubMed.
- H. Rosen and T. Abribat, Nat. Rev. Drug Discovery, 2005, 4, 381–385 CrossRef CAS PubMed.
- Y. Zhang, M. Long, P. Huang, H. Yang, S. Chang, Y. Hu, A. Tang and L. Mao, Sci. Rep., 2016, 6, 33335 CrossRef CAS PubMed.
- X. Li, Q. Yang, J. Ouyang, H. Yang and S. Chang, Appl. Clay Sci., 2016, 126, 306–312 CrossRef CAS.
- Y. Zhang, A. Tang, H. Yang and J. Ouyang, Appl. Clay Sci., 2016, 119(1), 8–17 CrossRef CAS.
- J. Tully, R. Yendluri and Y. Lvov, Biomacromolecules, 2016, 17, 615–621 CrossRef CAS PubMed.
- Y. Lvov, A. Aerov and R. Fakhrullin, Adv. Colloid Interface Sci., 2014, 207, 189–198 CrossRef CAS PubMed.
- A. Rivera and T. Farías, Microporous Mesoporous Mater., 2005, 80, 337–346 CrossRef CAS.
- B. Delalat, V. C. Sheppard, S. Rasi Ghaemi, S. Rao, C. A. Prestidge, G. McPhee, M. L. Rogers, J. F. Donoghue, V. Pillay, T. G. Johns, N. Kroger and N. H. Voelcker, Nat. Commun., 2015, 6, 8791 CrossRef CAS PubMed.
- A. Rivera, L. Valdés, J. Jiménez, I. Pérez, A. Lam, E. Altshuler, L. C. de Ménorval, J. O. Fossum, E. L. Hansen and Z. Rozynek, Appl. Clay Sci., 2016, 124–125, 150–156 CrossRef CAS.
- Q. Wu, Z. Li and H. Hong, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2012, 27, 516–522 CrossRef CAS.
- G. V. Joshi, R. R. Pawar, B. D. Kevadiya and H. C. Bajaj, Microporous Mesoporous Mater., 2011, 142, 542–548 CrossRef CAS.
- G. V. Joshi, B. D. Kevadiya, H. A. Patel, H. C. Bajaj and R. V. Jasra, Int. J. Pharm., 2009, 374, 53–57 CrossRef CAS PubMed.
- T. Takahashi, Y. Yamada, K. Kataoka and Y. Nagasaki, J. Controlled Release, 2005, 107, 408–416 CrossRef CAS PubMed.
- H. Hemmen, E. G. Rolseth, D. M. Fonseca, E. L. Hansen, J. O. Fossum and T. S. Plivelic, Langmuir, 2012, 28, 1678–1682 CrossRef CAS PubMed.
- M. A. S. Altoé, L. Michels, E. C. dos Santos, R. Droppa Jr, G. Grassi, L. Ribeiro, K. D. Knudsen, H. N. Bordallo, J. O. Fossum and G. J. da Silva, Appl. Clay Sci., 2016, 123, 83–91 CrossRef.
- J. K. Park, Y. B. Choy, J.-M. Oh, J. Y. Kim, S.-J. Hwang and J.-H. Choy, Int. J. Pharm., 2008, 359, 198–204 CrossRef CAS PubMed.
- M. M. Herling, H. Kalo, S. Seibt, R. Schobert and J. Breu, Langmuir, 2012, 28, 14713–14719 CrossRef CAS PubMed.
- C. J. Wang, Z. Li, W. T. Jiang, J. S. Jean and C. C. Liu, J. Hazard. Mater., 2010, 183, 309–314 CrossRef CAS PubMed.
- C.-J. Wang, Z. Li and W.-T. Jiang, Appl. Clay Sci., 2011, 53, 723–728 CrossRef CAS.
- L. Valdés, D. Hernández, L. C. de Ménorval, I. Pérez, E. Altshuler, J. O. Fossum and A. Rivera, Eur. Phys. J.: Spec. Top., 2016, 225, 767–771 Search PubMed.
- M. B. Rennels, H. C. Meissner, C. J. Baker, R. S. Baltimore, J. A. Bocchini, J. S. Bradley, P. H. Dennehy, J. R. W. Frenck, C. B. Hall, S. S. Long, J. A. McMillan, K. R. Powell, L. G. Rubin and T. N. Saari, Pediatrics, 2006, 118, 1287–1292 CrossRef PubMed.
- J. S. Wolfson and D. C. Hooper, Am. J. Med., 1991, 91, 153s–161s CrossRef CAS PubMed.
- J. Bertino Jr and D. Fish, Clin. Ther., 2000, 22, 798–817 CrossRef CAS.
- PubChem and C. Database, Ciprofloxacin, https://pubchem.ncbi.nlm.nih.gov/compound/2764.
- M. E. Olivera, R. H. Manzo, H. E. Junginger, K. K. Midha, V. P. Shah, S. Stavchansky, J. B. Dressman and D. M. Barends, J. Pharm. Sci., 2011, 100, 22–33 CrossRef CAS PubMed.
- K. D. Knudsen, J. O. Fossum, G. Helgesen and M. W. Haakestad, Phys. B, 2004, 352, 247–258 CrossRef CAS.
- L. Michels, J. O. Fossum, Z. Rozynek, H. Hemmen, K. Rustenberg, P. A. Sobas, G. N. Kalantzopoulos, K. D. Knudsen, M. Janek, T. S. Plivelic and G. J. da Silva, Sci. Rep., 2015, 5, 8775 CrossRef CAS PubMed.
- E. L. Hansen, H. Hemmen, D. M. Fonseca, C. Coutant, K. D. Knudsen, T. S. Plivelic, D. Bonn and J. O. Fossum, Sci. Rep., 2012, 2, 618 CrossRef CAS PubMed.
- A. Labrador, Y. Cerenius, S. Christe, K. Theodor and T. S. Plivelic, J. Phys.: Conf. Ser., 2013, 425, 072019 CrossRef CAS.
- D. Amsterdam, Antibiotics in laboratory medicine, 1996, vol. 4, pp. 52–111 Search PubMed.
- J. Thiry, F. Krier, S. Ratwatte, J.-M. Thomassin, C. Jerome and B. Evrard, Eur. J. Pharm. Sci., 2017, 96, 590–597 CrossRef CAS PubMed.
- A. Mourchid and P. Levitz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, R4887–R4890 CrossRef CAS.
- S. Babić, A. J. M. Horvat, D. Mutavdžić Pavlović and M. Kaštelan-Macan, TrAC, Trends Anal. Chem., 2007, 26, 1043–1061 CrossRef.
- S. A. C. Carabineiro, T. Thavorn-Amornsri, M. F. R. Pereira and J. L. Figueiredo, Water Res., 2011, 45, 4583–4591 CrossRef CAS PubMed.
- E.-S. I. El-Shafey, H. Al-Lawati and A. S. Al-Sumri, J. Environ. Sci., 2012, 24, 1579–1586 CrossRef CAS.
- S. Liu, P. Wu, L. Yu, L. Li, B. Gong, N. Zhu, Z. Dang and C. Yang, Appl. Clay Sci., 2017, 137, 160–167 CrossRef CAS.
- A. Dokoumetzidis and P. Macheras, Int. J. Pharm., 2006, 321, 1–11 CrossRef CAS PubMed.
- Fundamentals and Applications of Controlled Release Drug Delivery, J. Siepmann, R. A. Siegel and M. J. Rathbone, 1st edn, 2012 Search PubMed.
- P. Costa and J. M. Sousa Lobo, Eur. J. Pharm. Sci., 2001, 13, 123–133 CrossRef CAS PubMed.
- R. W. Korsmeyer, R. Gurny, E. Doelker, P. Buri and N. A. Peppas, Int. J. Pharm., 1983, 15, 25–35 CrossRef CAS.
- P. L. Ritger and N. A. Peppas, J. Controlled Release, 1987, 5, 23–36 CrossRef CAS.
- C. Liu and P. M. Huang, Geochim. Cosmochim. Acta, 2003, 67, 1045–1054 CrossRef CAS.
- W. Xu and Y. Yang, J. Biomater. Sci., Polym. Ed., 2010, 21, 445–462 CrossRef CAS PubMed.
- G. S. Crosson and E. Sandmann, Environ. Eng. Sci., 2013, 30, 311–316 CrossRef CAS PubMed.
- V. J. Inglezakis and A. A. Zorpas, Desalin. Water Treat., 2012, 39, 149–157 CAS.
- K. J. Aldred, R. J. Kerns and N. Osheroff, Biochemistry, 2014, 53, 1565–1574 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2017 |