Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Power loss density of electromagnetic waves in unimolecular reactions
Yinhong Liao *a,
Sanmei Zhangb,
Zhengming Tangb,
Xinpeng Liuc and
Kama Huangd
*a,
Sanmei Zhangb,
Zhengming Tangb,
Xinpeng Liuc and
Kama Huangd
aCollege of Electronics and Information Engineering, Southwest University, Chongqing, China. E-mail: liaoyinhong2006@126.com
bCollege of Electronics and Information Engineering, China West Normal University, Nanchong, China
cCommunication and Information Engineering, Chengdu Technological University, Chengdu, China
dCollege of Electronics and Information Engineering, Sichuan University, Chengdu, China
First published on 17th May 2017
Abstract
Microwave-assisted chemical reactions have been widely used, but the mechanism is still unclear, which limits further applications. For example, when chemical reactions are exposed to electromagnetic waves, some electromagnetic energies dissipate and these processes are poorly understood. In this paper, we investigate the power loss density in unimolecular reactions under exposure of electromagnetic waves. By using the equivalent circuit approach, the energy problem can be transformed into the energy stored or dissipated in equivalent circuit elements. The power loss density of electromagnetic waves in unimolecular reactions can be clearly obtained from an equivalent time-varying resistance, which is related to the amount of substances in reactions. Specifically, when the applied electromagnetic wave is monochromatic and the reaction rate is slow, the derived expression of the power loss density can be reduced to the classical formula in the frequency domain.
1. Introduction
Since Gedye et al.1 found that the use of microwaves can accelerate organic synthesis in 1980s, extensive successful reactions with rapidly enhanced reaction rates have been discovered, including solvent-free reactions,2 cycloaddition reactions,3 the synthesis of radioisotopes and polymers.4 Furthermore, the use of microwaves in chemical industries can benefit from the reduction of energy consumption and the improvement of physical properties of products.5–8 Nevertheless, the further applications of microwaves in chemical reactions are limited by the fact that the mechanisms are still unclear. For example, when chemical reactions are exposed to electromagnetic waves, some electromagnetic energies may dissipate. Nonetheless, as far as we know, the dissipation process is poorly understood. So, the underlying understanding of power dissipation of electromagnetic waves in chemical reactions is essential to clarify the interactions between microwaves and chemical reactions.Generally speaking, the power loss density of electromagnetic waves in media can be calculated by a classic formula in the frequency domain, which depends on complex dielectric constants.9 However, many chemical reactions are non-equilibrium processes. Namely, the concentrations of reactants and products are varying with time until the reactions reach equilibrium. During this process, the dielectric properties of these reactions are time-varying rather than constant.10,11 With consideration of the time-varying characteristics, the classic formula in the frequency domain is possibly inappropriate to describe the power loss density in chemical reactions. Hence, there remains a need for an in-depth investigation that can clearly show the dissipation process of electromagnetic waves in chemical reactions.
Recently, two approaches have been presented to deal with the power loss density in general dispersive media, including the electrodynamic (ED) approach and the equivalent circuit (EC) approach.12–16 In the ED approach, with the aid of electrodynamic equations of constitutive relations, the energy density can be obtained from the energy conservative law. However, it bears the limitation that the derivations of the ED approach can't provide a unique answer.13 This is caused by the fact that there is no unique way to determine whether a term with the dimension of power should be included in the time derivative of the energy density or in the transient power loss density. Furthermore, the polarization involved with chemical reactions increases this complexity. Fortunately, this difficulty can be avoided in the EC approach. In the EC approach, the energy problem can be transformed into the energy stored or dissipated in equivalent circuit elements. In the conventional EC approach, the treatment of a circuit analogy is only in the form of mathematics lacking strict analyses, which is usually used in time-harmonic fields.14,15 We have proposed strict theoretical analyses and extended the EC approach to tackle with the time-domain energy density lately.16
Hence, in this paper, we investigate power dissipation of electromagnetic waves in a unimolecular reaction employing the EC approach, due to the conceptual simplicity.17 Besides, unimolecular reactions widely exist, such as unimolecular elimination reactions, decompositions of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane and unimolecular reactions of organic ions.18–20 This paper is organized as follows. First, the polarization process of unimolecular reactions is studied briefly. Second, the formula of the power loss density of electromagnetic waves in unimolecular reactions is derived from the EC approach. Finally, the difference between the derived formula and the classic formula in the frequency domain is discussed by a numerical model.
2. Polarization of unimolecular reactions under exposure of electromagnetic waves
It is well-known that when chemical reactions are exposed to electromagnetic waves, the polarization depends on not only the current number of dipoles but also on chemical reaction rates. Indeed, the investigation of interactions between electromagnetic waves and chemical reactions can date back to 1960s.21–24 In 1967, Schwarz proved that the chemical reaction rate can affect the polarization, which can be described by modified Smoluchowski–Debye equations.22 Furthermore, he also studied the polarization of chemical reactions in equilibrium processes. Recently, our group have extended Schwarz's work into chemical reactions in non-equilibrium processes with Legendre polynomials.25,26Here, we take a unimolecular reaction as an example to derive the polarization under exposure of electromagnetic waves briefly, due to the conceptual simplicity and wide existence.17–20 For example, an isomerization reaction in practical applications can also be expressed by a unimolecular reaction. Usually, a unimolecular reaction can be shown as
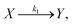 | (1) |
Under exposure of electromagnetic waves, concentration distributions of the reactant X and the product Y can be described by modified Smoluchowski–Debye equations.17,18 In the case where the amplitude of the exposed electric field is less than about 107 V m−1, the distribution concentration functions of the reactants and products can be dominated by the leading order and the first order Legendre polynomials.27 Employing some simple mathematical operations, we can obtain the polarization
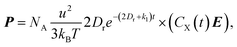 | (2) |
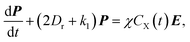 | (3) |
In particular, the frequencies of the applied electromagnetic wave in many practical industrial applications are 915 MHz or 2.45 GHz, which are much larger than most reaction rates. In this case, eqn (2) can be simplified to
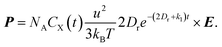 | (4) |
Thus, the complex permittivity of this reaction can be expressed as
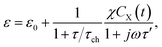 | (5) |
3. Power dissipation of electromagnetic waves in unimolecular reactions
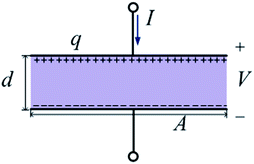
As mentioned above, the amount of reactants and products is varying with time until the reactions reach equilibrium. In this case, it is possibly inaccurate to use the classical formula in the frequency domain describing the power dissipation of electromagnetic waves. Luckily, this problem can be resolved by the EC approach.14–16 Being treated as an equivalent circuit by making analogies with V ↔ E and q ↔ D, the energy problem can be obtained from some basic electric elements, such as resistors, capacitors and inductors.We choose a sample containing many X and Y molecules, whose size is much smaller than a wavelength of the applied electromagnetic wave. It indicates that the electromagnetic field inside the sample is uniform on the macro level. Without loss of generality, a one-dimensional model can be presented. The relationship between the electric field and the displacement can be modeled by a parallel-plate capacitor, which is shown in Fig. 1.
We assume that the width between the parallel plates is d, the length of the plate is A, and the electric field in the parallel-plate capacitor is E. Thus, the voltage between the two plates is
| V = Ed. | (6) |
On the basis of the Gauss's law, the time-varying charge q can be easily obtained
| q = AD, | (7) |
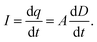 | (8) |
We note that the constitution relationship can be represented as
| D = ε0E + P. | (9) |
Combining eqn (6)–(9) and the scalar form of eqn (3), we obtain
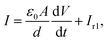 | (10) |
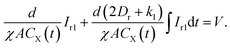 | (11) |
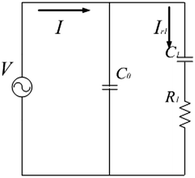
It is easy to see that eqn (10) represents the capacitor C0 in parallel with a first-order circuit whose current is Ir1, as shown in Fig. 2. Eqn (11) represents the transient response of a first-order circuit to the source voltage of V. In Fig. 2, the capacitances of C0 and C1 are ε0A/d and χACX(t)/d(2Dr + k1), respectively, and the resistance of R1 is d/χACX(t). Obviously, both C1 and R1 are time-varying elements.
Usually, the total power dissipated and stored in a circuit element can be expressed as28
| Pcircuit = VI. | (12) |
Thus, we can easily obtain the power in the equivalent circuit
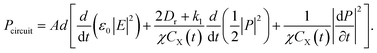 | (13) |
In circuit theory, the electric energy can be stored in capacitors or inductors and dissipated in resistors. Hence, the total power stored in the equivalent circuit can be regarded as the sum of the power stored in C0 and C1, namely
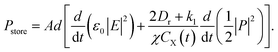 | (14) |
The power dissipated in the equivalent circuit is the power in R1 as
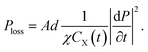 | (15) |
Thus, we obtain the power loss density in this unimolecular reaction
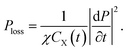 | (16) |
Obviously, the power loss density of electromagnetic waves in a unimolecular reaction is related to a time-varying resistor. It shows that the amount of reaction substances affects power dissipation during the reaction process. Furthermore, if k1 = 0 namely CX(t) is a constant, eqn (16) can be reduced to a general Debye model, which is consistent with the results in ref. 16. It should be highlighted that eqn (16) is a scalar form, whose vector form can be written as
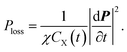 | (17) |
4. Results and discussions
For general media, the power loss density of electromagnetic waves can be usually calculated by the classic formula in the frequency domain, namely9
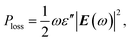 | (18) |
In the following part, we'll use a numerical model to discuss the relationship between the derived formula (17) and eqn (18) in detail. Without loss of generality, the applied electromagnetic wave is set as
| E(t) = sin(2πft), | (19) |
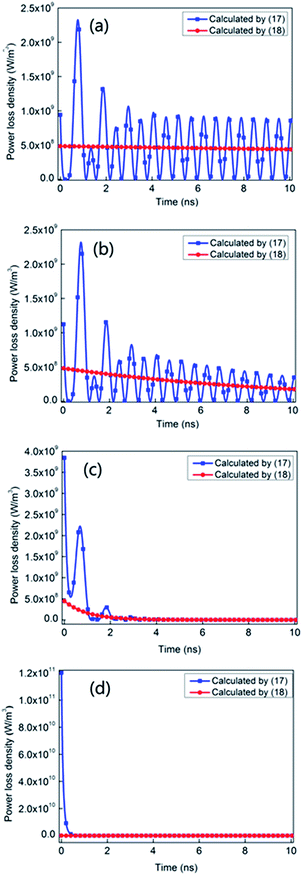 | ||
| Fig. 3 The power loss density calculated by eqn (17) and (18) with different reaction rates: (a) k1 = 1.0 × 107 s−1; (b) k1 = 1.0 × 108 s−1; (c) k1 = 1.0 × 109 s−1 and (d) k1 = 1.0 × 1010 s−1. | ||
In Fig. 3(a), the reaction rate k1 is 1.0 × 107 s−1. In this case, the reaction keeping non-equilibrium lasts about 100 ns and the reaction rate is much less than the frequency of the electromagnetic wave. We can clearly see that the average value of the power loss density calculated by eqn (17) is in good agreement with that calculated by eqn (18), when the electric field tends to steady after t = 3.0 ns. The results show that when the reaction rate is low, the power loss density can be both calculated by eqn (17) and (18), which can also be seen in Fig. 3(b). In Fig. 3(b) with the reaction rate k1 of 1.0 × 108 s−1, the time when the reaction keeps non-equilibrium is about 10 ns and the reaction rate is also much less than the frequency of the electromagnetic wave. In this case, the average value of the power loss density calculated by eqn (17) is also in good agreement with that calculated by eqn (18) after t = 3.0 ns.
However, as the reaction rate increases dramatically, there are some significant differences between eqn (17) and (18). In Fig. 3(c), the reaction rate k1 is 1.0 × 109 s−1. In this case, the time when the reaction keeps non-equilibrium should be about 1.0 ns and the reaction rate can be comparable to the frequency of the electromagnetic wave. We can easily see that, during the reaction process, the power loss density calculated by eqn (18) is significantly different from that calculated by eqn (17) in Fig. 3(c). Specifically, at the initial state of reacting, the power loss density calculated by eqn (17) reaches 3.8 × 109 W m−3, while that calculated by eqn (18) only approaches 5.0 × 108 W m−3. This difference goes up in Fig. 3(d) with the reaction rate of 1.0 × 1010 s−1. In Fig. 3(d), the power loss density calculated by eqn (17) reaches 1.2 × 1011 W m−3 at the beginning of the reaction, while that calculated by eqn (18) approaches 1.1 × 108 W m−3. It indicates that when the reaction rate is fast, the classical formula (18) is inaccurate and the power loss density can only be obtained by the proposed formula (17).
In summary, when the reaction rate is low, the power loss density of electromagnetic waves in unimolecular reactions can be both calculated by eqn (17) and (18). In this case, eqn (3) can be reduced to eqn (4). Namely, the constitution relationship of the reactions can be expressed by the complex permittivity. However, while the reaction rate is fast, the constitution relationship of the reactions can't be expressed by the complex permittivity any more. And, the power loss density in unimolecular reactions can be only calculated by the proposed formula (17).
5. Conclusions
Microwave-assisted chemical reactions have been used in many applications, but the unclear mechanisms limit further applications. The underlying understanding of the power loss density of electromagnetic waves in chemical reactions is critical, which remains rare. In this paper, using the EC approach, we investigate the power loss density in unimolecular reactions under exposure of electromagnetic waves. By transforming the energy problem into the energy stored or dissipated in equivalent circuit elements, we find that the power loss density in unimolecular reactions can be clearly obtained from an equivalent time-varying resistance. The results show the amount of reaction substances affects power dissipation. Specifically, for the cases with slow reaction rates and monochromatic electromagnetic waves, the derived expression of power loss density can be reduced to the classical formula in the frequency domain, which is verified by a numerical model.Acknowledgements
This work was supported by the National Key Basic Research Program of China (No. 2013CB328905) and the Foundation of China West Normal University (No. CXTD2015-12).References
- R. Gedye, F. Smith, K. Westaway, H. Ali, L. Baldisera, L. Laberge and J. Rousell, Tetrahedron Lett., 1986, 27, 279 CrossRef CAS.
- A. Loupy, G. Bram and J. Sansoulet, New J. Chem., 1992, 16, 233 CAS.
- A. Díaz-Ortiz, F. Langa, A. de la Hoz and A. Moreno, Eur. J. Org. Chem., 2000, 4, 3659 Search PubMed.
- N. Elander, J. R. Jones, S. Y. Lu and S. Stone-Elander, Chem. Soc. Rev., 2000, 29, 239 RSC.
- D. A. Jones, T. P. Lelyveld, S. D. Mavrofidis, S. W. Kingman and N. J. Miles, Resour., Conserv. Recycl., 2002, 34, 75 CrossRef.
- X. Zhang and D. O. Hayward, Inorg. Chim. Acta, 2006, 359, 3421 CrossRef CAS.
- D. E. Clark, D. C. Folz and J. K. West, Mater. Sci. Eng., A, 2000, 287, 153 CrossRef.
- X. Zhang, D. O. Hayward and D. M. P. Mingos, Catal. Lett., 2003, 88, 33 CrossRef CAS.
- L. D. Landau, E. M. Lifshitz and P. Pitaevskii, Electrodynamics of continuous media, Elsevier Corporation, Amsterdam, 1960 Search PubMed.
- G. Y. Zhu and K. M. Huang, J. Sichuan Univ., Nat. Sci. Ed., 2001, 48, 849 Search PubMed.
- X. Q. Yang and K. M. Huang, Chinese Journal of Radio Science, 2006, 21, 803 Search PubMed.
- T. J. Cui and J. A. Kong, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205106 CrossRef.
- P. G. Luan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 0466019 CrossRef PubMed.
- P. C. W. Fung and K. Young, Am. J. Phys., 1978, 46, 57 CrossRef.
- P. M. T. Ikonen and S. A. Tretyakov, IEEE Trans. Microwave Theory Tech., 2007, 55, 92 CrossRef.
- K. M. Huang and Y. H. Liao, IEEE Trans. Microwave Theory Tech., 2015, 63, 135 CrossRef.
- F. F. Crim, Annu. Rev. Phys. Chem., 1984, 35(1), 657 CrossRef CAS.
- F. Zamir and R. D. Levine, Chem. Phys., 1980, 52(3), 253 CrossRef.
- R. Shaw and F. E. Walker, J. Phys. Chem., 1977, 81(25), 2572 CrossRef CAS.
- R. D. Bowen, D. H. Williams and G. Hvistendahl, J. Am. Chem. Soc., 1977, 99(23), 7509 CrossRef CAS.
- W. Scheider, Biophys. J., 1965, 5, 617 CrossRef CAS PubMed.
- G. Schwarz, J. Phys. Chem., 1967, 71, 895 CrossRef.
- G. Schwarz, J. Phys. Chem., 1970, 74, 198 CrossRef.
- G. Schwarz, Adv. Mol. Relax. Processes, 1972, 3, 281 CrossRef CAS.
- K. M. Huang and T. Hong, J. Phys. Chem. A, 2015, 119, 8898 CrossRef CAS PubMed.
- X. P. Liu and K. M. Huang, Eur. Phys. J.: Appl. Phys., 2016, 73, 10901 CrossRef.
- W. T. Coffey and B. V. Paranjape, Proc. R. Ir. Acad., Sect. A, 1978, 78, 17 Search PubMed.
- C. K. Alexander and M. N. O. Sadiku, Fundamentals of Electric Circuits, McGraw-Hill, New York, 2000 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |