A quantum chemical study on ˙Cl-initiated atmospheric degradation of acrylonitrile

Abstract

Degradation of acrylonitrile (CH₂=CHCN) by reaction with atomic chlorine was studied using quantum chemical methods. Density functional theory (DFT) (B3LYP, BHandHLYP, M11, MN12SX, M05-2X, and M06-2X) and Møller–Plesset perturbation theory (MP2) with the same basis set 6-311++G(d,p) were employed to obtain the geometries of intermediates and transition states. Potential energy surfaces (PESs) were characterized at the UCCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p) level. The dominant channel is the formation of the intermediate IM1(CH₂ClCHCN) by barrierless addition between ˙Cl and the terminal carbon atom of the C=C double bond of acrylonitrile. Direct hydrogen-abstraction channels are negligible because of higher barriers and the endothermic process. The calculated rate constants were followed by means of the variational transition state theory by Variflex code, and these were in good agreement with the experimental values. The subsequent and secondary reactions for IM1(CH₂ClCHCN) involving NO and O₂ molecules were also investigated in the atmosphere. The atmospheric lifetime of acrylonitrile in ˙Cl is about 18 h in the marine boundary layer. The contribution of ˙Cl to the transformation of acrylonitrile is comparative with that of the ˙OH. Thus, it is necessary to consider ˙Cl initiated tropospheric degradation of acrylonitrile.

---

1. Introduction

Vapor phase ammoxidation of propylene by molecular oxygen and ammonia in the presence of a catalyst is a known method for production of acrylonitrile, an important monomer of synthetic fiber, rubber, and resin. This method is also used to manufacture organic compounds such as acrylamide, acrylic acid, and adiponitrile. In the organic chemicals industry, biomass combustion is an important consideration as a source of emissions to the atmosphere.¹ Experimental and theoretical investigations of acrylonitrile show that it may degrade by a photolysis mechanism to produce poisonous gases such as HCN/HNC, which are detrimental to the atmospheric environment.^2–5

The heterogeneous and multi-phase reaction cycles involving NaCl(cd), HNO₃(g), and N₂O₅(g) can lead to a significant source of ClNO_x, which can undergo photolysis to produce chlorine radicals.⁶ The primary tropospheric sink for acrylonitrile is generally accepted to be reaction with the ˙OH radical because the concentration of ˙Cl is 1–10% of ˙OH levels,^7–9 i.e. [˙OH] = 1.0 × 10⁶ molecules per cm³ vs. [˙Cl] = 1.0 × 10⁴ − 1.0 × 10⁵ molecules per cm³. However, the room temperature rate constants are found to be (1.11 ± 0.33) × 10⁻¹¹ and (1.11 ± 0.23) × 10⁻¹⁰ (in cm³ per molecule per s) for ˙OH and ˙Cl reactions with acrylonitrile, respectively.¹⁰ Thus, the Cl atom could be a tropospheric sink for acrylonitrile, as the acrylonitrile reacts with ˙Cl more rapidly than with ˙OH.

Similar to the reactions with ˙OH, reaction of unsaturated organic pollutants with ˙Cl may proceed via either addition or H-abstraction.^11–13 The favored pathway for reaction of an unsaturated organic compound (such as CH₂=CHR) with ˙Cl is not always the same as that with ˙OH. For example, ˙OH prefers to abstract the hydrogen atoms of propene while ˙Cl prefers to add to the unsaturated bond.^13–15 Theoretical research on reaction of acrylonitrile with ˙OH demonstrates that addition is the dominant reaction over abstraction at temperatures <1000 K, but that abstraction is dominant over addition at higher temperatures.¹⁶ Thus, acrylonitrile reaction with ˙Cl may also follow the addition and H-abstraction mechanism. It is desirable to know which is more important. Only two previous studies have been performed to provide rate constants for the acrylonitrile reaction with ˙Cl, namely, Aranda et al. who used a mass spectrometric discharge-flow method in the temperature range 260–333 K and at a total pressure between 0.5 and 3 Torr at 298 K,¹⁷ and Teruel et al. who predicted rate constants at 298 K and 760 Torr using a relative rate technique method.¹⁰ However, there are still no theoretical studies about the potential energy surface, the temperature and pressure dependence rate constants, and atmospheric implications.

The potential energy surface (PES) is important in theoretical studies of chemical reaction processes. It is well known that the accuracy of molecular dynamics (MD) calculations depends on accurate determination of the PES. Based on Born-Oppenheimer approximation, calculation of the PES must solve the electronic Schroedinger equation of geometries of the reacting molecule. Tremendous improvements in computation methods have made it possible for ab initio methods to provide accurate PESs, even accurate high-dimensional PESs for many-body systems.^18–21 However, construction of ab initio high-dimensional PESs for larger systems remains a challenge. Some of the more important theoretical methods to fit ab initio energies have been used in an attempt to meet this challenge. A brief overview will be provided here. The neural network approach has been applied to fit high-dimensional PESs.^22–24 For large molecules and molecule-surface vibrational analysis, a route is provided by a multimode vibrational self-consistent field (VSCF) method with a fourth-order force field.²⁵ The interpolation method also has been applied to construct a global PES for reactions of a moderate-sized molecule.^26–28 A continuum limit frozen Gaussian approximation was applied to study thermal density in a double-well potential.²⁹ The built-in permutational invariance is the mathematical description of the PES and fits a number of full-dimensional potentials of many-body, non-covalent interactions.^30,31 The related technique of ab initio molecular dynamics gives calculations of quasi-classical trajectory.^32,33

In this paper, ab initio calculations were performed on the reaction of ˙Cl with acrylonitrile, and kinetic calculations were carried out using variational transition-state theory. Comparisons between theoretical and experimental results and atmospheric implications are discussed.

2. Computational methods and details

2.1 Electronic structure calculations

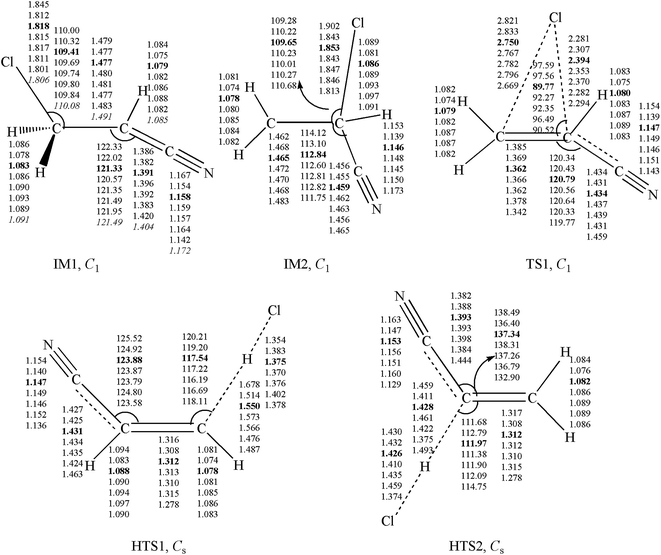
Unrestricted calculations were used for open shell systems. Using the GAUSSIAN 09 suites of programs,³⁴ the geometries of some important intermediates and transition states (IM1, IM2, TS1, HTS1 and HTS2) were optimized with density functional theory (B3LYP,^35,36 BHandHLYP,^35,36 M11,³⁷ MN12SX,³⁸ M05-2X,³⁹ and M06-2X⁴⁰ functionals) and Møller–Plesset perturbation theory (MP2)⁴¹ with the same triple-ζ 6-311++G(d,p) basis set. The other geometries on potential energy surfaces were calculated using the M05-2X/6-311++G(d,p) method. Frequency calculations and intrinsic reaction coordinate (IRC) calculations⁴² were performed. The optimized geometries for the IM1, IM2, TS1, HTS1 and HTS2 at seven levels of theory are depicted in Fig. 1. The optimized geometries for other species are shown in Fig. S1.† For the species C₂H₂, C₂H₃, HCl, and HCN, the bond lengths and angles calculated by the M05-2X/6-311++G(d,p) basis set are in good agreement with the experimental values.⁴³ In addition, the UCCSD(T)/cc-PVTZ and BMC-CCSD⁴⁴ energy calculations were used in conjunction with M05-2X and M06-2X with 6-311++G(d,p) level geometries. All PESs were established at the UCCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p) level. In the following discussion, the M05-2X/6-311++G(d,p) optimized geometric parameters and the UCCSD(T)/cc-PVTZ energies are used, unless otherwise stated.

Fig. 1 Optimized geometries (length in Å and angle in degree) of some important intermediates and transition states. Values obtained at the B3LYP, BHandHLYP, M05-2X (in bold), M06-2X, M11, MN12SX, MP2 and CCSD (in italic) using the 6-311++G(d,p) basis set, respectively.

2.2 Calculations of rate constants

The Variflex code⁴⁵ was employed to perform rate constant calculations based on calculated rotational constants, harmonic frequencies, and energies. Variflex includes the most realistic treatment of loose transition states found in barrierless association reactions. Reactions with loose transition states were treated using variable reaction coordinate–transition state theory (VRC–TST) formalism.^46,47 In estimation of the reactant electronic partition function, two electronic states ²P_3/2 (lowest) and ²P_1/2 of the Cl atom, having degeneracies of 4 and 2, respectively, were considered. Different levels of theory were tested for kinetic calculations of ˙Cl with acrylonitrile. The calculated kinetic data were compared with the reported experimental results (Tables S3–S5†). It is well known that accuracy reaction rate constant calculations strongly depend on the level of electronic structure theory adopted.^48,49 The M05-2X and M06-2X rate coefficients at 298 K and 760 Torr N₂ were found to be 3.80× and 4.02× higher than the Teruel et al. data, respectively. Meanwhile, the rates of M11 and MN12SX were 8.43× and 15.30× higher, respectively, than the experimental rate, and the rates of BHandHLYP and MP2 were 570× and 1090000× lower, respectively, than the experimental rate. The rate constants of UCCSD(T)//M06-2X and BMC-CCSD//M06-2X were about 3.30× and 4.31× higher than the experimental value, respectively. However, B3LYP/6-311++G(d,p) and UCCSD(T)/cc-PVTZ//M05-2X were almost the same as the experimental data. The M05-2X and M06-2X rate coefficients at 260–333 K and 1 Torr He were found to be 1.5× higher than Aranda et al.'s data. UCCSD(T)//M06-2X and B3LYP were found to be four to five times lower than Aranda et al.'s data. The rate constants of UCCSD(T)//M05-2X were about 15 times lower than Aranda et al.'s data. Furthermore, the M05-2X rate coefficients at 298 K and 0.5–3 Torr He were almost the same as Aranda et al.'s data. Based on the results obtained, the calculated overall rate constants at M05-2X/6-311++G(d,p) are in excellent agreement with the experimental data. M05-2X has been proven to calculate kinetic data accurately.^50,51 Reliable wavefunction methods such as CCSD(T) can be used to obtain excellent energies, but incur problems from large spin contamination in the transition states at the UCCSD(T) level of theory. In our system, the S² values, spin contamination before and after annihilation, range from 0.92 to 0.77 for IM1 at UCCSD(T)//M05-2X; this rate error is known to result from spin contamination, or the acceptable instrumental error of two experiments. The UCCSD/6-311++G(d,p) method has been applied to optimize the geometries of IM1. The optimized geometries between M05-2X and UCCSD are different also because of spin contamination. It is well known that UCCSD computational costs are higher than those of M05-2X. According to the results in Table 1, ΔE of IM1 are −19.59 and −20.32 kcal mol⁻¹ at UCCSD(T)//UCCSD and UCCSD(T)//M05-2X, respectively, which are mainly consistent. Therefore, the M05-2X functional gives excellent descriptions for large systems or our small systems in which spin contamination is important.

Table 1 Relative energies (ΔE) for the important intermediates and transition states at various methods

Species	ΔE^a	ΔE^b	ΔE^c	ΔE^d	ΔE^e	ΔE^f	ΔE^g	ΔE^h	ΔE^i	ΔE^k	ΔE^l
a B3LYP/6-311++G(d,p).b BHandHLYP/6-311++G(d,p).c MP2/6-311++G(d,p).d M05-2X/6-311++G(d,p).e M06-2X/6-311++G(d,p).f M11/6-311++G(d,p).g MN12SX/6-311++G(d,p).h BMC-CCSD//M05-2X/6-311++G(d,p).i UCCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p).j UCCSD(T)/cc-PVTZ//UCCSD/6-311++G(d,p).k BMC-CCSD//M06-2X/6-311++G(d,p).l UCCSD(T)/cc-PVTZ//M06-2X /6-311++G(d,p).
R: CH2=CHCN + Cl	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
P1: HCl + CHCHCN	10.46	19.68	26.97	11.87	10.60	10.39	8.06	8.88	11.84	9.15	12.11
P2: HCl + CH2CCN	−0.69	11.16	28.10	3.89	3.72	2.47	−1.85	1.49	5.59	1.69	5.70
IM1	−21.34	−13.85	−9.78	−24.45	−23.61	−24.26	−25.04	−21.73	−19.59(−20.32)^j	−21.65	−19.50
IM2	−8.31	−1.01	−10.05	−12.79	−12.55	−12.25	−12.37	−10.68	−9.11	−10.45	−8.88
TS1	−5.61	5.43	11.19	−6.24	−4.68	−4.07	−6.42	−3.84	−0.67	−3.61	−0.50
HTS1	10.75	22.16	30.33	11.73	11.48	e.44	9.59	9.95	14.12	9.43	13.62
HTS2	3.13	17.40	29.97	6.28	6.48	5.58	3.47	5.35	9.51	5.51	9.81

---

3. Results and discussion

3.1 Potential energy surfaces

3.1.1 Direct hydrogen abstraction paths. A PES for two H-abstraction pathways is presented in Fig. 2. As shown in Fig. 2, H-abstraction from acrylonitrile by ˙Cl proceeds via HTS1 and HTS2, which directly and respectively correlate to P1(HCl + CHCHCN) and P2(HCl + CH₂CCN). Both HTS1 and HTS2 have high relative energies of 14.12 and 9.51 kcal mol⁻¹, and the two pathways are highly endothermic at 11.84 and 5.59 kcal mol⁻¹, respectively.

Fig. 2 Potential energy surface of IM1 and hydrogen abstraction channels predicted at the UCCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p) level.

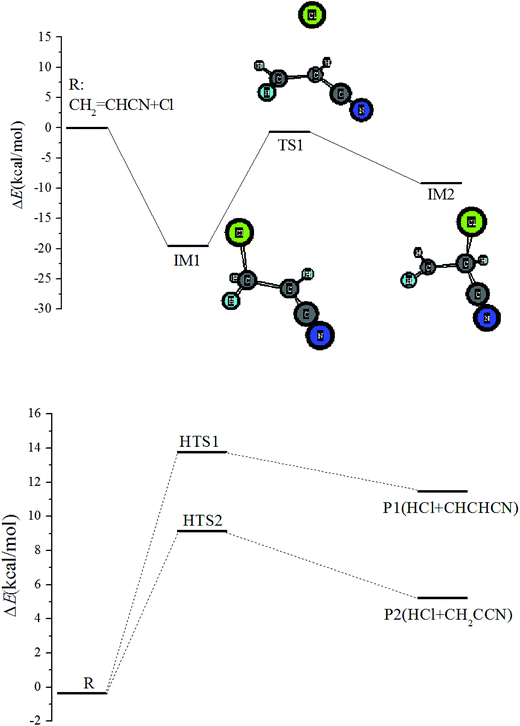
3.1.2 Association paths. The calculated PES for Cl atom addition to acrylonitrile to form IM1 is shown in Fig. 2, with the corresponding ΔE values listed in Table 1. It can be observed that, first, there is barrierless ˙Cl addition to the terminal carbon atom of the C=C double bond of acrylonitrile, with formation of a biradical IM1(ClCH₂CHCN) that lies 19.59 kcal mol⁻¹ below the initial reactants. Starting at IM1, there are four possible reaction pathways: (i) IM1 can dissociate into products P3(H + CHClCHCN) by hydrogen atom dissociation, facing a barrier of 44.9 kcal mol⁻¹; (ii) it can dissociate into the products P4(HCN + CH₂ClC) by breaking the C–C and C–H bonds simultaneously via TS3 with a barrier height of 109.65 kcal mol⁻¹; (iii) IM1 can isomerize to IM3 by cycle addition over a high barrier of 51.5 kcal mol⁻¹ (TS4); (iv) IM1 can isomerize to IM2 by Cl-shift from terminal-C to central-C on the C=C double bond over a high barrier of 18.92 kcal mol⁻¹ (TS1). IM2 lies −9.11 kcal mol⁻¹ relative to reactants. Starting with IM2, direct hydrogen leaving and isomerization have been found. i.e. P5(H + CH₂CClCN), IM4, IM5, and IM6. The involved transition states of TS5-8 have very high barriers. Unimportant channels of schematic potential energy profiles are plotted in Fig. S2.†

In addition, the ˙Cl atom can add to the carbon atom of the –CN group, forming c-IM1(CH₂CHCClN) via transition state c-TS1 with a barrier height of 9.31 kcal mol⁻¹. The energy of c-IM1 is a little lower than the reactant, at 4.28 kcal mol⁻¹. Both P6(CH₂CH + ClCN) and P7(C₂H₂ + ClCNH) are strongly endothermic.

All the PESs show that the Cl atom adds to the terminal-C via the loose transition state, which is the most important step for the title reaction. It could be that direct hydrogen abstraction and other addition pathways are negligible because of the high barriers.

3.2 Kinetics

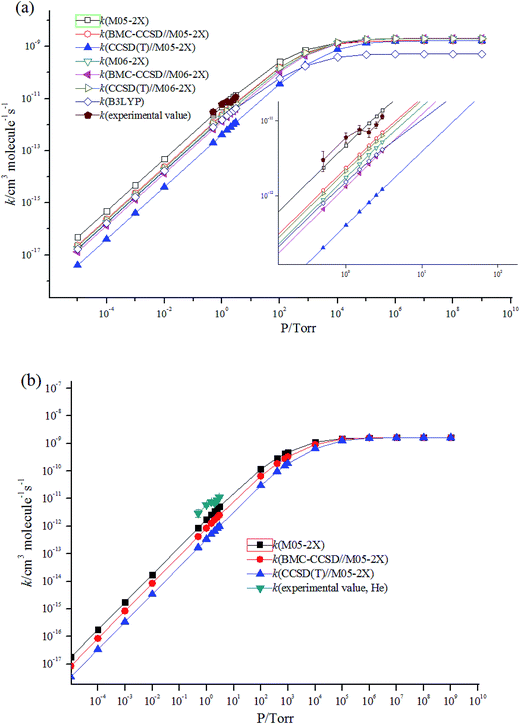
For an essentially barrierless pathway, variational transition state theory was employed to obtain the corresponding microcanonical rate coefficients.⁴⁵ The potential function was computed by scanning the Cl–C bond from 1.8 to 7.8 Å with a step size of 0.1 Å, with other geometric parameters being fully optimized using M05-2X/6-311++G(d,p) and M06-2X/6-311++G(d,p) levels. The results of simulation are shown in Fig. 3. Table S2† lists the rotational constants and harmonic frequencies that were used to calculate rate constants. The E/J (energy E and total angular momentum J) resolved variable reaction coordinate transition state theory (VRC-TST) formalism,⁴⁵ and the master equation formalism⁵² implemented in the Variflex code was used to evaluate the TS partition function. The energy E is from −8552.00 cm⁻¹ to 15 418.00 cm⁻¹ in steps of 30.00 cm⁻¹, and the total angular momentum J covered the range from 1 to 396 in steps of 5. The frequency of collision was derived from the Lennard-Jones (L-J) pairwise potential parameters of N₂ (σ(N₂) = 3.7047 Å, ε/k_B(N₂) = 84.942 K),⁵³ He (σ(He) = 2.5238 Å, ε/k_B(He) = 9.8725 K)⁵³ and i–C₃H₇Cl (σ(i–C₃H₇Cl) =4.81 Å, ε/k_B(i–C₃H₇Cl) = 435 K).⁵⁴ These values were employed for evaluation of the L-J parameters for each collision pair using the approximations σ₁₂ = (σ₁+σ₂)/2 and ε₁₂ = (ε₁ε₂)^1/2. The collision transfer probability was described by the single exponential down model,^55–63 with average transfer energies ΔE_d = 100 and 200 cm⁻¹ for N₂ and He, respectively.

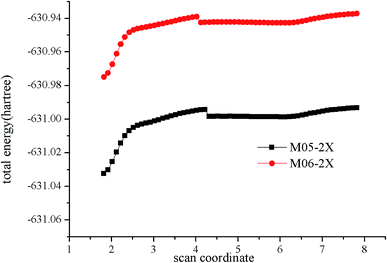Fig. 3 Calculated minimum energy path along the reaction coordinates (R_ClC) at the M05-2X/6-311++G(d,p) and M06-2X/6-311++G(d,p) levels.

Fig. 4 shows the temperature dependence of the rate constants. It can be concluded that the total rate constants have negative temperature dependence. The M05-2X/6-311++G(d,p) method has the best results when simultaneously compared with the two experimental values. The rate constants are mostly sensitive to ΔE_d, scan potential function, and energy of IM1. The calculated total rate constants (k_tot) in N₂ using M05-2X/6-311++G(d,p), CCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p), and B3LYP/6-311++G(d,p) are in good agreement with Teruel et al.'s data¹⁰ (k = 4.27 × 10⁻¹⁰, 1.54 × 10⁻¹⁰, and 9.90 × 10⁻¹¹ cm³ per molecule per s vs. (1.11 ± 0.23) × 10⁻¹⁰ cm³ per molecule per s). At 1.0 Torr He and 298 K, the rate of M05-2X/6-311++G(d,p) of 4.71 × 10⁻¹² cm³ per molecule per s is almost the same as the experimental data of (6.0 ± 0.9) × 10⁻¹² cm³ per molecule per s. The Arrhenius expression for the rate constant using M05-2X/6-311++G(d,p) was obtained at 1.0 Torr He of 200–3000 K, k = 1.28 × 10⁻¹³ × exp(1102/T) cm³ per molecule per s vs. experimental expression k = (5.2 ± 1.6) × 10⁻¹⁴ × exp[(1400 ± 100)/T] cm³ per molecule per s. The following three-parameter expression was fitted over the range 200–3000 K and 1 Torr He and 760 Torr N₂, respectively: k = 3.1 × 10⁻¹² × T^−0.49exp(981/T) and k = 3.45 × 10⁻¹⁰ × T^−0.41exp(755/T) cm³ per molecule per s. The pressure dependence of the rate constants is shown in Fig. 5. The results displayed show that the rate constants have positive pressure dependence. At 298 K and 0.5–3 Torr He, the calculated rate constants at M05-2X/6-311++G(d,p) level are in good agreement with experimental values. For example, the rate of M05-2X/6-311++G(d,p) of 9.29 × 10⁻¹² cm³ per molecule per s is almost the same as the experimental data of (7.0 ± 1) × 10⁻¹² cm³ per molecule per s at 298 K and 2 Torr He.

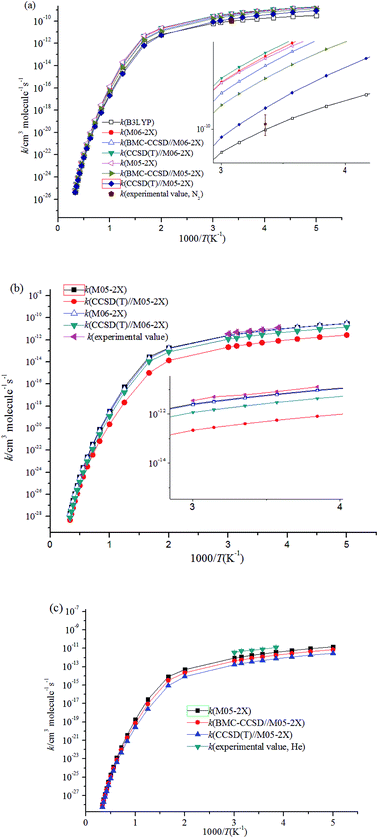Fig. 4 Temperature dependence of the rate constants (a) at 760 Torr N₂; (b) at 1 Torr He; (c) at 1 Torr N₂.

Fig. 5 Rate constants calculated at pressures from 10⁻⁵ to 10⁹ Torr and 298 K in (a) He and (b) N₂.

3.3 Atmospheric implications of IM1(CH₂ClCHCN)

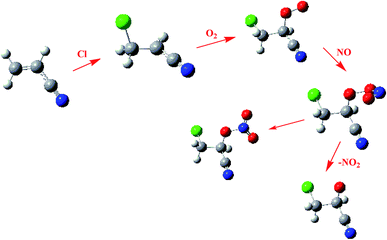
The chemically activated IM1(CH₂ClCHCN) can subsequently react with the main atmospheric oxidants (O₂ and NO_x). Feasible reaction intermediates from the IM1(CH₂ClCHCN) are displayed in Fig. 6. IM1 can react with triplet-O₂ barrierlessly to form O₂IM1. From our calculations, this process is exothermic by 17.38 kcal mol⁻¹. The IM1 + NO reaction can proceed barrierlessly to form NOIM1 adducts with energy of −24.44 kcal mol⁻¹. Meanwhile, IM1 can also react with NO₂ barrierlessly to form NO₂IM1 with energy of −47.81 kcal mol⁻¹. Furthermore, O₂IM1 can easily react with NO to produce the harmful pollutants of ONOOIM1. The produced ONOOIM1 can degrade to a radical OIM1 and NO₂ or isomerize to form an organic nitrate [O2NOIM1], as has been observed in secondary organic aerosols (SOA) in the laboratory with influence on atmospheric chemistry, climate, and human health.^64–67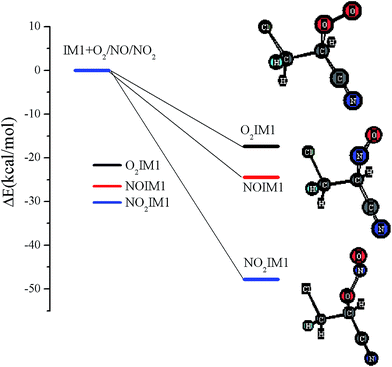

Fig. 6 Energies of the feasible reaction intermediates from IM1(CH₂ClCHCN) in the presence of O₂ and NO_x.

The atmospheric lifetimes (τ) of CH₂=CHCN with the Cl atom were calculated using the expression of τ = (k_Cl[Cl])⁻¹. The global average concentration of the Cl atom from 1.0 × 10⁴ to 1.0 × 10⁵ molecules per cm³ and the calculated k_Cl = 1.54 × 10⁻¹⁰ cm³ per molecule per s was considered. The atmospheric lifetimes of CH₂=CHCN were computed to be 18 h using [Cl] = 1.0 × 10⁵ molecules per cm³. On the basis of the atmospheric concentrations of ˙OH (1.0 × 10⁶ molecules per cm³) and the calculated k_OH = 1.14 × 10⁻¹¹ cm³ per molecule per s,¹⁶ the τ_OH is 24 h. The total tropospheric lifetimes with respect to both reactions with ˙OH and ˙Cl (τ_OH,Cl) were calculated to be τ_OH,Cl = 21 h. Thus, the role of ˙Cl should not be ignored, especially in the huge area of oceans (Fig. 7).

Fig. 7 Degradation and isomerization pathways of IM1 in the presence of O₂ and NO.

4. Conclusions

In the present article, potential energy surfaces were obtained at the UCCSD(T)/cc-PVTZ//M05-2X/6-311++G(d,p) level. Unlike ˙OH reactions with CH₂=CHCN, the ˙Cl reactions are predicted theoretically to proceed predominantly by barrierless addition of the ˙Cl to form the intermediate IM1(ClCH₂CHCN). The reactions are extremely fast with negative temperature dependence and positive pressure rate coefficients. Agreement is excellent between the M05-2X/6-311++G(d,p) results and experimental results. In addition, the lifetimes for CH₂=CHCN were computed as 18 h using the calculated rate coefficients. In the presence of NO and O₂, IM1 can degrade to a radical and NO₂, or isomerize to form an organic nitrate. Reaction with ˙Cl appears to make a non-negligible contribution to destruction of acrylonitrile in the atmospheric environments.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 21507027). The authors acknowledge the Youth Fund Project of Hubei Provincial Department of Education (Q20132501), Hubei Key Laboratory of Pollutant Analysis & Reuse Technology Open Fund (PA160204), and the Scientific Research Starting Foundation of Mianyang Normal University (No. QD2016A007).

References

1. B. R. T. Simoneit, A. I. Rushdi, M. R. B. Abas and B. M. Didyk, Environ. Sci. Technol., 2003, 37, 16–21.
2. D. A. Blank, A. G. Suits, Y. T. Lee, S. W. North and G. E. Hall, J. Chem. Phys., 1998, 108, 5784–5794.
3. S. W. North and G. E. Hall, Chem. Phys. Lett., 1996, 263, 148–153.
4. W. N. Du, C. Luo and Z. S. Li, J. Chem. Phys., 2008, 129, 174309.
5. Z. Homayoon, S. A. Vázquez, R. Rodríguez-Fernández and E. Martínez-Núñez, J. Phys. Chem. A, 2011, 115, 979–985.
6. C. B. Faxon and D. T. Allen, Environ. Chem., 2013, 10, 221–233.
7. O. W. Wingenter, B. C. Sive, N. J. Blake, D. R. Blake and F. S. Rowland, J. Geophys. Res.: Space Phys., 2005, 110, 1–10.
8. J. M. Nicovich, S. Mazumder, P. L. Laine, P. H. Wine, Y. Tang, A. J. C. Bunkan and C. J. Nielsen, Phys. Chem. Chem. Phys., 2015, 17, 911–917.
9. R. G. Prinn, R. F. Weiss, B. R. Miller, J. Huang, F. N. Alyea, D. M. Cunnold, P. J. Fraser, D. E. Hartley and P. G. Simmonds, Science, 1995, 269, 187–192.
10. M. A. Teruel, M. B. Blanco and G. R. Luque, Atmos. Environ., 2007, 41, 5769–5777.
11. C. Sun, B. Xu and S. Zhang, J. Phys. Chem. A, 2014, 118, 3541–3551.
12. M. R. Dash and B. Rajakumar, Atmos. Environ., 2014, 99, 183–195.
13. P. Brana and J. A. Sordo, J. Comput. Chem., 2003, 24, 2044–2062.
14. C. W. Zhou, Z. R. Li and X. Y. Li, J. Phys. Chem. A, 2009, 113, 2372–2382.
15. M. Szori, C. Fittschen, I. G. Csizmadia and B. Viskolcz, J. Chem. Theory Comput., 2006, 2, 1575–1586.
16. J. Y. Sun, R. S. Wang and B. S. Wang, Phys. Chem. Chem. Phys., 2011, 13, 16585–16595.
17. A. Aranda, Y. D. Mera, D. Rodríguez, A. Rodríguez, B. Cabannas and E. Martínez, Chem. Phys. Lett., 2003, 377, 571–576.
18. A. Spielfiedel, M. L. Senent, F. Dayou, C. Balança, L. Cressiot-Vincent, A. Faure, L. Wiesenfeld and N. Feautrier, J. Chem. Phys., 2009, 131, 014305.
19. O. Akin-Ojoa, R. Bukowski and K. Szalewicz, J. Chem. Phys., 2003, 119, 8379–8396.
20. O. Akin-Ojoa and K. Szalewicz, J. Chem. Phys., 2005, 123, 134311.
21. C. Qu, R. Conte, P. L. Houstonbc and J. M. Bowman, Phys. Chem. Chem. Phys., 2015, 17, 8172–8181.
22. J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401.
23. K. Hornik, M. Stinchcombe and H. White, Neural Networks, 1989, 2, 359–366.
24. S. Manzhos, X. G. Wang, R. Dawes and T. Carrington Jr, J. Phys. Chem. A, 2006, 110, 5295–5304.
25. S. Carter, S. J. Culik and J. M. Bowman, J. Chem. Phys., 1997, 107, 10458–10469.
26. M. A. Collins, J. Chem. Phys., 2007, 127, 024104.
27. M. S. Gordon, D. G. Fedorov, S. R. Pruitt and L. V. Slipchenko, Chem. Rev., 2012, 112, 632–672.
28. T. J. Frankcombe and M. A. Collins, Phys. Chem. Chem. Phys., 2011, 13, 8379–8391.
29. R. Conte and E. Pollak, J. Chem. Phys., 2012, 136, 094101.
30. J. Li and H. Guo, J. Chem. Phys., 2015, 143, 214304.
31. R. Conte, C. Qu and J. M. Bowman, J. Chem. Theory Comput., 2015, 11, 1631–1638.
32. R. Conte, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 12304–12317.
33. P. L. Houston, R. Conte and J. M. Bowman, J. Phys. Chem. A, 2016, 120, 5103–5114.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. W. M. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson and J. A. Pople, et al., Gaussian 09, Gaussian Inc., Wallingford, CT, 2009.
35. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
36. C. Lee, W. Yang and R. G. Par, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
37. R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 117–124.
38. R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 10, 13171–13174.
39. Y. Zhao, N. E. Schultz and D. G. Truhlar, J. Chem. Theory Comput., 2006, 2, 364–382.
40. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
41. J. A. Pople, R. Krishnan, H. B. Schlegel and J. S. Binkley, Int. J. Quantum Chem., 1979, 16, 225–241.
42. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
43. NIST Computational Chemistry Comparison and Benchmark Database. http://cccbdb.nist.gov/.
44. B. J. Lynch, Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 1643–1649.
45. S. J. Klippenstein, A. F. Wagner, R. C. Dunbar, D. M. Wardlaw and S. H. Robertson, Variflex: Version 1.00, 1999.
46. (a) S. J. Klippenstein, Chem. Phys. Lett., 1990, 170, 71–77; (b) S. J. Klippenstein, J. Chem. Phys., 1991, 94, 6469–6482; (c) S. J. Klippenstein, J. Chem. Phys., 1992, 96, 367–371.
47. S. H. Robertson, A. F. Wagner and D. M. Wardlaw, Faraday Discuss., 1995, 102, 65–83.
48. J. O. Richardson, J. Chem. Phys., 2016, 144, 114106.
49. A. N. Beyer, J. O. Richardson, P. J. Knowles, J. Rommel and S. C. Althorpe, J. Phys. Chem. Lett., 2016, 7, 4374–4379.
50. A. Vega-Rodriguez and J. R. Alvarez-Idaboy, Phys. Chem. Chem. Phys., 2009, 11, 7649–7658.
51. C. Zavala-Oseguera, J. R. Alvarez-Idaboy, G. Merino and A. Galano, J. Phys. Chem. A, 2009, 113, 13913–13920.
52. (a) R. G. Gilbert and S. C. Smith, Theory of Unimolecular Reactions, Blackwell, 1990; (b) K. A. Holbrook, M. J. Pilling, and S. H. Robertson, Unimolecular Reactions, Wiley, 1996.
53. A. B. Weaver and A. A. Alexeenko, J. Phys. Chem. Ref. Data, 2015, 44, 023103.
54. H. Hippler, J. Troe and H. J. Wendelken, J. Chem. Phys., 1983, 78, 6709–6717.
55. J. R. Barker, L. M. Yoder and K. D. King, J. Phys. Chem. A, 2001, 105, 796–809.
56. A. W. Jasper, K. M. Pelzer, J. A. Miller, E. Kamarchik, L. B. Harding and S. J. Klippenstein, Science, 2014, 346, 1212–1215.
57. A. W. Jasper and J. A. Miller, J. Phys. Chem. A, 2009, 113, 5612–5619.
58. A. W. Jasper and J. A. Miller, J. Phys. Chem. A, 2011, 115, 6438–6455.
59. R. Conte, B. Fu, E. Kamarchik and J. M. Bowman, J. Chem. Phys., 2013, 139, 044104.
60. R. Conte, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2013, 117, 14028–14041.
61. R. Conte, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 7742–7757.
62. P. L. Houston, R. Conte and J. M. Bowman, J. Phys. Chem. A, 2014, 118, 7758–7775.
63. P. L. Houston, R. Conte and J. M. Bowman, J. Phys. Chem. A, 2015, 119, 4695–4710.
64. N. Zhao, Q. Z. Zhang and W. X. Wang, Sci. Total Environ., 2016, 563–564, 1008–1015.
65. A. E. Perring, S. E. Pusede and R. C. Cohen, Chem. Rev., 2013, 113, 5848–5870.
66. J. A. Fisher, D. J. Jacob and K. R. Travis, Atmos. Chem. Phys., 2016, 16, 1–38.
67. M. Glasius and A. H. Goldstein, Environ. Sci. Technol., 2016, 50, 2754–2764.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra01521f

---