Open Access Article
Open Access ArticlePhase stability, elastic and electronic properties of Hf–Rh intermetallic compounds from first-principles calculations
Mingliang Wangab,
Cunjuan Xiaa,
Yi Wua,
Dong Chen *a,
Zhe Chen*b,
Naiheng Mab and
Haowei Wangab
*a,
Zhe Chen*b,
Naiheng Mab and
Haowei Wangab
aState Key Laboratory of Metal Matrix Composites, Shanghai Jiao Tong University, China. E-mail: chend@sjtu.edu.cn
bSchool of Materials Science & Engineering, Shanghai Jiao Tong University, No. 800 Dongchuan Road, Shanghai 200240, China. E-mail: zhe.chen@sjtu.edu.cn; Tel: +86-21-54747597
First published on 7th April 2017
Abstract
The phase stability, elastic and electronic properties of binary Hf–Rh compounds have been studied using first-principles calculations based on density functional theory. The equilibrium lattice constants, formation enthalpies, elastic constants, and elastic moduli are presented. Among the binary Hf–Rh compounds, Hf3Rh5 is the most stable with the lowest formation enthalpy. For the equiatomic HfRh phase, it tends to crystallize in the ZrIr-type structure, followed by L10, and then B2 at the ground state based on the analysis of formation enthalpies. Therefore, the crystal structure of the lower temperature HfRh phase is suggested to be the ZrIr-type. This conclusion is in agreement with the experimental reports in the literature. Besides, Hf3Rh4 are proposed to be the Pu3Pd4-type for the first time. Furthermore, our calculated elastic constants for Hf2Rh, ZrIr-HfRh, L10-HfRh, B2-HfRh, Hf3Rh4, Hf3Rh5 and HfRh3 can all satisfy the Born criteria, indicating their mechanical stabilities. When ZrIr-HfRh is adopted, the bulk modulus (B) increases linearly with the growing Rh atomic concentration. Meanwhile, Young's modulus linearly increases with growing shear modulus, and the compound with a higher Poisson's ratio owns a higher B/G ratio simultaneously. Overall, the results also indicate that all the considered Hf–Rh compounds should be ductile. Finally, the electronic structure is analyzed to understand the essence of structural stability of the binary compound.
1. Introduction
Among the platinum group metals, Rh has the smaller density and better oxidation resistance with a high melting temperature, ensuring it as a promising candidate for industry applications such as developing refractory superalloys.1 During the past decades, Rh-based alloys have received great research interest due to these properties among all the metals, e.g. high melting temperature, the highest corrosion resistance and high strength.2 Meanwhile, Hf is used extensively as an alloying element in transition metal-based superalloys, which are designed to withstand high temperatures and pressures. Hf is a useful addition to transition metals, in which it can form the second phase to improve a material's strength under extreme conditions.3 The investigations on Hf–Rh systems should be of critical importance, which has attracted attention with respect to the superalloys,4–6 the occurrence of superconductivity,7 the amorphization behavior8 and the electrocatalytic hydrogen production ability9 of Hf–Rh alloys.The Hf–Rh phase diagram was studied by Waterstrat et al.,10 and suggested the existence four types of binary compounds, i.e., Hf2Rh, HfRh, Hf3Rh5 and HfRh3. Lately, Eremenko et al.11 reassessed this diagram, and reported seven intermediated phases in this system, including Hf2Rh, HfRh (with three types of polymorphs), Hf3Rh4, Hf3Rh5 and HfRh3. Based on published results,10–15 Okamoto et al.16 has reviewed the Hf–Rh phase diagram, and determined the crystal structure of several binary Hf–Rh compounds. Hf2Rh and Hf3Rh5 should form peritectically at 1723 K and 2168 K and have Ti2Ni- and Ge3Rh5-type structures, respectively. Besides, HfRh3 has a cubic L12 type structure, and can melt congruently at 2278 K at the stoichiometric composition. In addition, the equiatomic HfRh phase has a more complex situation. Initially, the high temperature δ (B2) HfRh phase is confirmed, and should melt congruently at 2453 K at the stoichiometric composition. Secondly, the δ′ (L10) HfRh phase is proposed to be stable at medium temperature from ∼873 K to 973 K. Still, there is a low temperature δ′′ HfRh phase existing below ∼873 K without informing of the crystal structure. The similar situation has also occurred in Hf3Rh4, which should form peritectically at 1718 K and lack of structure information.
Although the Hf–Rh system has been studied for a long time, it is believed that the systematically theoretical study on Hf–Rh system discussing and revealing the crystal structure to the unknown HfRh and Hf3Rh4 phases has been eluded. Also, the experimental studies are also limited. The reliable information, such as formation enthalpies, and elastic properties (i.e., elastic constant, and bulk/shear/Young's modulus) are lacking. Intensive studies are also required to clarify the phase and mechanical stability and the properties of the binary compounds. Therefore, a comprehensive investigation of the ground-state phase stability, elastic and electronic properties of Hf–Rh compounds using first-principles calculations based on the density functional theory (DFT) has been performed in this work. In Section 2, the computational strategies are presented in detail. The calculated results are discussed and compared with the available experimental and theoretical results in Section 3. Finally, the conclusions are summarized in Section 4.
2. Computational methods
All theoretical calculations were carried out by a first-principles plane-wave pseudopotential method based on DFT through the CASTEP package17 in the current work. The ultrasoft pseudopotential was used to model the ion–electron interaction.18 The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was utilized.19–21 The states of Hf5d26s2 and Rh4d85s1 were taken as the basis set in the calculations. The kinetic cutoff energy for plane waves was settled at 400 eV. The special points sampling integration over the Brillouin zone was employed by using the Monkhorst–Pack method22 with determined k-point separation of 0.02 Å−1 in three lattice directions for each structure. The Pulay scheme of density mixing was applied for the evaluation of energy and stress.23,24 The optimization of atom coordinates and lattice constants were made by minimization of the total energy. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization scheme was used in the geometry optimization.25 The tolerances of the geometry optimization were set as follows: the difference of the total energy within 0.001 eV per cell, maximum ionic force within 100 eV Å−1, maximum ionic displacement with in 100 Å, and maximum stress within 100 GPa. The calculation of total energy and electronic structure were followed by cell optimization with SCF tolerance of 1.0 × 10−4 eV per cell. The total energies and the density of states (DOS) under the optimized structures were calculated by means of the corrected tetrahedron Blöchl method.26From the view of thermodynamics, the formation enthalpy (Hf) is defined as the total energy difference between the compound and its constituents in proportion to the composition. The formation enthalpy (Hf) is calculated by the following equation:
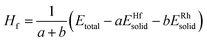 | (1) |
3. Results and discussion
3.1 Crystal structure and stability
Based on the former studies, five chemical compositional HfxRhy compounds (i.e., Hf2Rh, HfRh, Hf3Rh4, Hf3Rh5 and HfRh3) are adopted. The Ti2Ni-type Hf2Rh, Ge3Rh5-type Hf3Rh5, and L12-HfRh3 are used in accordance with the experimental observations. The optimized lattice constants for these compounds are listed in Table 1, along with published lattice constants for comparison from experimental (Ti2Ni-type Hf2Rh,27 Ge3Rh5-type Hf3Rh5,28 L12-HfRh3 (ref. 29)) and theoretical (Ti2Ni-type Hf2Rh9 and L12-HfRh3 (ref. 4, 5 and 30)) results at the ground state. For these three compounds, the differences between the optimized and experimental lattice constants are small accordingly. Thus, the reliability of our calculation method and the chosen parameters have been confirmed, which also assure the credibility of subsequent results.| Composition (at% Rh) | Prototype | Structure | a (Å) | b (Å) | c (Å) | Hf (eV per (atom)) | |
|---|---|---|---|---|---|---|---|
| a Experimental values from ref. 27.b Theoretical values from ref. 46.c Theoretical values from ref. 9.d Theoretical values from ref. 10.e Theoretical values from ref. 30.f Experimental values from ref. 47.g Theoretical values from ref. 48.h Experimental values from ref. 49.i Theoretical values from ref. 44.j Experimental values from ref. 28.k Experimental values from ref. 29.l Theoretical values from ref. 5.m Theoretical values from ref. 4. | |||||||
| Hf2Rh | 33.3 | Ti2Ni | Fd3ms(227) | 12.4719 | −0.6538 | ||
| 12.317a | −0.64b | ||||||
| 12.334c | |||||||
| HfRh | 50 | ZrIr | Cmcm(63) | 3.3695 | 19.8796 | 4.442 | −0.9225 |
| L10 | P4/mmm(123) | 3.309889 | 3.309942 | −0.9059 | |||
| 54 | 3.268d | 3.15d | −0.9539e | ||||
| 55 | 3.12d | 3.41d | |||||
| B2 | Pm3m(221) | 3.3088 | −0.9015 | ||||
| 3.227f | −0.9506e | ||||||
| 3.284g | −0.996 ± −0.0229h | ||||||
| NbRu([39]) | Cmmm(65) | 4.6436 | 4.6437 | 3.3632 | −0.8996 | ||
| 58 | 4.392d | 4.306d | 3.470d | ||||
| B27 | Pnma(62) | 6.0941 | 4.5237 | 5.4062 | −0.8994 | ||
| −0.899i | |||||||
| B33 | Cmcm(63) | 3.2007 | 10.2247 | 4.5364 | −0.8826 | ||
| −0.9433e | |||||||
| B19 | Pmma(51) | 4.6972 | 3.1307 | 4.9632 | −0.8789 | ||
| −0.9402e | |||||||
| B11 | P4/nmms(129) | 3.6268 | 5.8085 | −0.6742 | |||
| Hf3Rh4 | 57.1 | Pu3Pd4 | R3h(148) | 12.3285 | 5.6375 | −0.9284 | |
| Ta3B4 | Immm(71) | 3.2002 | 18.2383 | 4.3887 | −0.669 | ||
| Ti3Cu4 | I4/mmm(139) | 3.4118 | 21.8902 | −0.6099 | |||
| C3Al4 | R3mh(166) | 4.6972 | 24.7277 | −0.2027 | |||
| Co3S4 | Fd3ms(227) | 11.0626 | 0.2877 | ||||
| Th3P4 | I43d(220) | 8.2242 | 27.8134 | ||||
| Hf3Rh5 | 62.5 | Ge3Rh5 | Pbam(55) | 5.5919 | 10.7064 | 4.2877 | −0.9344 |
| 5.58j | 10.73j | 4.25j | −0.9280i | ||||
| HfRh3 | 75 | L12 | Pm3m(221) | 4.007 | −0.791 | ||
| 3.912k, 3.942e | −0.891e | ||||||
| 3.94l, 3.86l | −0.762i | ||||||
| 3.95m | |||||||
For HfRh, Ramam et al.14 reported the L10-HfRh was stable at lower temperature, and B2 HfRh was observed at higher temperatures experimentally. Waterstrat et al.10 confirmed the existence of B2 HfRh, and also reported the occurrence of “tetragonally distorted” B2 phase (Hf46Rh54, a = 3.268 Å, c = 3.150 Å; Hf45Rh55, a = 3.12 Å, c = 3.418 Å). Such phase was ascribed to the L10-HfRh in the Hf–Rh phase diagram generalized by Okamoto.16 In addition, Waterstrat et al.10 also considered the possible formation of HfRh phase in the ZrIr-type12 and/or NbRu-type (Hf42Rh58: a = 4.392 Å, b = 4.306 Å, c = 3.470 Å (ref. 12)) crystal structures.
About the ZrIr-type structure, an earlier X-ray diffraction (XRD) study suggested the ZrIr-type compound may have either B27 or B33 structure.31 In disagreement with this analysis, Semenova et al.32 identified the structure as a monoclinic TiNi (B19′)-type. However, Waterstrat et al.33 considered that the ZrIr-type compound should be a new orthorhombic structure that was resembling to the DyGe3 structure. Stalick et al.34 agreed this idea and determined the crystal structure of orthorhombic ZrIr compound using powder neutron diffraction data. Through first-principles calculations, Chen et al.35 theoretically computed the structural properties of ZrIr compound with the B19′, B27, B33 and ZrIr-type (from ref. 34) structures, and found the calculated lattice constants of ZrIr-type phase were in good agreement with the available experimental results. Therefore, the crystal information of the original ZrIr-type phase is adopted from ref. 34.
Regarding the NbRu-type structure, it is suggested to be an orthorhombic structure.36–41 However, its crystal structure has ever reached consensus yet. For example, Mitarai et al.39 studied the crystal structure of NbRu-type IrTi using XRD analysis experimentally and refined the structure with ab initio calculation theoretically. They proposed that the NbRu-type structure has space group Cmmm (65), and the atomic positions: Nb (1) 0.0 0.5 0.0, (2) 0.5 0.0 0.0; Ru (1) 0.0 0.0 0.5, (2) 0.5 0.5 0.5. Shao et al.40 discussed the structural, thermodynamic and elastic properties of NbRu, and found the Pnma (62)/B27 NbRu structure was both thermodynamically and mechanically stable at the ground state. As a result, both Cmmm (65) and Pnma (62) structures are used for structural optimization in this work. The obtained equilibrium lattice constants for Cmmm (65) HfRh and Pnma (62) HfRh are shown in Table 1. Clearly, the Cmmm (65) HfRh is more approaching to the experimentally reported NbRu-type HfRh (Hf42Rh58: a = 4.392 Å, b = 4.306 Å, c = 3.470 Å (ref. 12)), indicating that Cmmm (65) NbRu structure is more probable.
Resultantly, the HfRh is theoretically inclined to form the crystal structure in the following sequence of ZrIr-type > L10 > B2 > B27 > B33 > B19 > B11 structures based on the Hf values. Our results show good accordance with the experimental observations. For instance, Okamoto et al.16 generalized Hf–Rh phase diagram based on the available experimental data, and concluded there were three phases for equiatomic HfRh, including the high temperature δ (B2) phase, medium temperature δ′ (L10) phase, and low temperature unknown δ′′ phase. Basically, the lower temperature phase at the ground state should possess the more negative Hf value.42,43 Therefore, the Hf values for HfRh phases are in the order of δ′′ > L10 > B2 structures. Theoretically, Xing et al.30 suggested the thermodynamic stability of HfRh was in the order of B33 > L10 > B2 > B19 structure. However, the B33 structure phase has ever reported for HfRh. Similarly, Levy et al.44 considered the Pnma (B27) HfRh should be more stable than the B2 type, where they did not provide lattice constants for evaluation. Nevertheless, we have proved Pnma (B27) HfRh is less possible to form as the NbRu-type structure (Table 1). Conclusively, it is suggested that the unknown δ′′ phase at low temperature should be ZrIr-type, which also corresponds to Waterstrat's work,10 and the HfRh phases are able to crystallize in the order of ZrIr-type > L10 > B2 structures.
For Hf3Rh4, the Pu3Pd4-, Ta3B4-, Ti3Cu4-, C3Al4-, Co3S4-, Th3P4-type structure are considered. Co3S4- and Th3P4-type Hf3Rh4 are unlikely to more due to their positive Hf values. The Pu3Pd4-type Hf3Rh4 should be the favored crystal structure with the most negative Hf value. This is similar to Zr3Rh4 which also possesses the Pu3Pd4-type structure.45
Fig. 1 exhibits the convex hull plot of the formation enthalpies of binary Hf–Rh compounds calculated at the ground state, along with the theoretical values from Levy's work,44 Miedema's model,50 Koteski's work46 and Xing's work,30 and experimental values from Guo's work49 and Gachon's work.51 For Hf2Rh, our calculated value is −0.6538 eV per atom, agreeing well with the experimental value of −0.6934 ± −0.0156 eV per atom (ref. 51) and theoretical value of −0.64 eV per atom.46 About HfRh3, our calculated value is −0.791 eV per atom, which is in good accordance with the theoretical value of −0.762 eV per atom (ref. 44) and −0.891 eV per atom.30 All these values are a bit larger than the experimental value of −0.6063 ± −0.0125,51 although this experimental value is based on the phase Rh0.79Hf0.21. In addition, the enthalpies of formation of HfRh, Hf3Rh4 and Hf3Rh5 at their respective ground-state phases fall on a common straight line, implying that the concentrations ranges for different compounds are quite narrow. Comparably, the convex hull plot of Miedema's model50 shows the lowest point of Hf values at the HfRh phase. However, the convex hull plots of this theoretical work, Levy's theoretical work44 and Gachon's experimental work49 have complied well with each other, and exhibited the similar contours, where the Hf3Rh5 compound has the most negative Hf value, signifying it is the most stable phase among binary Hf–Rh compounds.
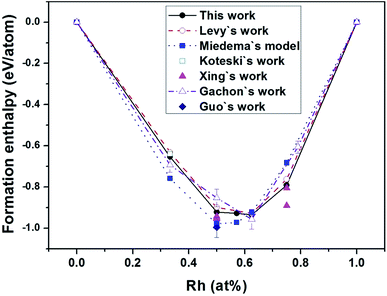 | ||
| Fig. 1 The convex hull plot of the formation enthalpies of binary Hf–Rh compounds calculated at the ground state in comparison with the experimental values from Gachon's work51 and Guo's work,49 and theoretical values from Levy's work,44 Miedema's model,50 Koteski's work46 and Xing's work.30 The tie-line in each work has joined the low enthalpy structures at the vertices of the convex hull. | ||
3.2 Mechanical properties
To investigate the mechanical stability and elastic properties, the single-crystal elastic constants of the binary Hf–Rh phases, as well as pure Hf and Rh, are calculated by the stress–strain method52,53 at their optimized structures. To calculate the elastic constant (Cij), a deformed cell is introduced. The elastic strain energy is presented as following:54
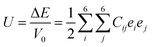 | (2) |
Using the stress–strain methods, the single-crystal elastic constants for seven Hf–Rh binary intermetallics and pure Hf and Rh metals have been derived and summarized in Table 2, in comparison with the available experimental and theoretical values. For pure Hf and Rh metals, our calculated elastic constants are in good agreement with experimental55,56 and theoretical4 values. It has thus indicated the calculation method adopted in the work is effective to predict the elastic properties of metallic compounds. For HfRh3, the derived elastic constants are in good agreement with the available theoretical values.4 However, the experimental and theoretical elastic constants for other six Hf–Rh compounds are not available to the best of our knowledge. Therefore, our calculated elastic constants for Hf2Rh, ZrIr-HfRh, L10-HfRh, B2-HfRh, Hf3Rh4 and Hf3Rh5 compounds should provide useful data for comparison in future experimental and theoretical studies.
| Compound | C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | C14 | C15 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hf | 193.5 | 205.2 | 56.4 | 82.7 | 77.2 | ||||||
| Ref. 55 (exp. values) | 181.0 | 197.0 | 55.7 | 77.0 | 66.0 | ||||||
| Hf2Rh | 245.6 | 55.8 | 125.3 | ||||||||
| HfRh (ZrIr) | 243.7 | 277.9 | 277.6 | 85.7 | 92.5 | 60.6 | 135.5 | 161.1 | 132.4 | ||
| HfRh (L10) | 234.0 | 232.8 | 69.0 | 69.1 | 165.7 | 165.4 | |||||
| HfRh (B2) | 234.6 | 69.4 | 165.9 | ||||||||
| Hf3Rh4 | 292.3 | 313.4 | 27.9 | 157.3 | 130.9 | −17.7 | 26.3 | ||||
| Hf3Rh5 | 330.8 | 304.6 | 301.2 | 96.1 | 85.1 | 47.6 | 116.2 | 149.8 | 168.0 | ||
| HfRh3 | 330.4 | 144.5 | 170.0 | ||||||||
| Ref. 4 (theo. values) | 296.0 | 140.0 | 158.0 | ||||||||
| Ref. 5 (theo. values) | 319.0 | 144.0 | 163.0 | ||||||||
| Rh | 394.7 | 171.7 | 183.6 | ||||||||
| Ref. 55 (exp. values) | 413.0 | 184.0 | 194.0 | ||||||||
| Ref. 56 (exp. values) | 416.0 | 184.0 | 197.0 | ||||||||
| Ref. 4 (theo. values) | 386.0 | 171.0 | 172.0 | ||||||||
In order to evaluate the phase stability of the compound, the mechanical stability is analyzed in combination of the elastic constant and Born's stability criteria.57 For a stable crystalline structure, the elastic constant should satisfy the Born's criteria to prove its mechanical stability. In terms of seven binary Hf–Rh intermetallics considered in this work, Hf2Rh, B2-HfRh, and HfRh3 are ascribed to the cubic structure, ZrIr-HfRh and Hf3Rh5 have the orthorhombic structure, and Hf3Rh4 and L10-HfRh possess the trigonal and tetragonal structure, respectively.
For the cubic crystal, there are three independent elastic constants. The mechanical stability criteria are provided in the following equation:58,59
| C11 > 0; C44 > 0; C11 > |C12|; C11 + 2C12 > 0 | (3) |
In Table 2, the elastic constants of the cubic Hf2Rh, B2-HfRh, and HfRh3 crystals can satisfy the above criteria accordingly, confirming their mechanically stability.
Regarding the orthorhombic phase, it has nine independent elastic constants, and the restrictions of mechanical stability for are presented the following equation:
| C11 > 0; C22 > 0; C33 > 0; C44 > 0; C55 > 0; C66 > 0; C11 + C22 + C33 + 2(C12 + C13 + C23) > 0; C11 + C22 − 2C12 > 0; C11 + C33 − 2C13 > 0; C22 + C33 − 2C23 > 0 | (4) |
It is seen that the elastic constants for ZrIr-HfRh and Hf3Rh5 can both meet the restrictions of mechanical stability, implying both compounds are mechanically stable.
About the trigonal Hf3Rh4 phase with seven independent elastic constants, the mechanical stability criteria are included in the following formula:60
| C11 > 0; C33 > 0; C44 > 0; C11 > |C12|; (C11 + C12)C33 − 2C132 > 0; (C11 − C12)C44 − 2C142 > 0 | (5) |
Clearly, all the elastic constants of Hf3Rh4 exhibited in Table 2 can satisfy Born's criteria for mechanical stability.
For the tetragonal crystal, the stability criteria are shown in the following formula:61
| C11 > 0; C33 > 0; C44 > 0; C66 > 0; C11 − C12 > 0; C11 + C33 − 2C13 > 0; 2(C11 + C12) + C33 + 4C13 > 0 | (6) |
Through the validation of the formula (6), the L10-HfRh phase has six independent elastic constants to ensure its mechanical stability.
Conclusively, the seven Hf–Rh intermetallics considered, i.e., Hf2Rh, ZrIr-HfRh, L10-HfRh, B2-HfRh, Hf3Rh4, Hf3Rh5 and HfRh3, are all suggested mechanically stable.
The elastic constants C11 and C33 should characterize the x direction and z direction resistances to linear compression, respectively.62,63 In Table 2, the ZrIr-HfRh and Hf3Rh4 have larger C33 values, indicating their higher incompressibility under the z direction uniaxial stress. In Hf3Rh5, it is more compressible along z direction than that along x direction due to the larger C11 value. In the case of C44, it is interpreted as the resistance to monoclinic shear in the (100) plane, and is the critical parameter relating to the shear modulus.64,65 In Table 2, the largest C44 for HfRh3 has suggested that HfRh3 has the strongest resistance to shear in the (100) plane, while Hf3Rh4 has the smallest C44 to show the weakest resistance to shear in the (100) plane.
Based on the single-crystal elastic constant, three types of algorithms corresponding to different bounds are adopted to estimate elastic properties of polycrystalline materials. In detail, the Voigt66/Reuss67 method is the larger/smaller value of the actual effective modules on the assumption of uniform strain/stress imposed on the polycrystalline structure. For the cubic structure, the upper and the lower bounds for the bulk (B) and shear (G) modulus related to Voigt and Reuss methods are exhibited in the formula (7-1) to (7-3):59
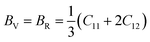 | (7-1) |
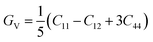 | (7-2) |
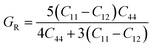 | (7-3) |
Furthermore, the equations used to compute the upper and the lower bounds for the bulk and shear modulus with orthorhombic, trigonal and tetragonal structures can be referred to the ref. 60, 61 and 42, accordingly.
In addition, the arithmetic average of Voigt and Reuss bounds is termed as the Voigt–Reuss–Hill (VRH) method.68 Using the VRH averaging method, the bulk modulus (B) and shear modulus (G) are calculated in the eqn (8):
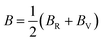 | (8-1) |
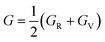 | (8-2) |
Young's modulus (E) and Poisson's ratio (ν) are also major elasticity related parameters, which can be calculated using the following formula:
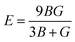 | (9-1) |
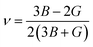 | (9-2) |
The calculated polycrystalline bulk modulus, shear modulus, Young's modulus, Poisson's ratio and B/G values for seven Hf–Rh compounds and pure Hf/Rh metals using VRH methods are calculated and tabulated in Table 3. For pure Hf and Rh metals, the obtained elastic properties are in good agreement with the published experimental55,56 and theoretical4 values, validating the precision of the predicted elastic properties of metallic materials.
| Compound | B (GPa) | G (GPa) | E (GPa) | v | B/G |
|---|---|---|---|---|---|
| Hf | 118.5 | 57.2 | 147.9 | 0.292 | 2.070 |
| Ref. 55 (exp. values) | 108.5 | 55.8 | 142.9 | 0.280 | 1.944 |
| Hf2Rh | 165.4 | 57.5 | 154.5 | 0.344 | 2.877 |
| Ref. 40 (theo. values) | 148.7 | ||||
| HfRh (ZrIr) | 183.8 | 70.5 | 187.5 | 0.330 | 2.609 |
| HfRh (L10) | 188.2 | 52.0 | 142.7 | 0.374 | 3.622 |
| HfRh (B2) | 188.8 | 52.3 | 143.7 | 0.373 | 3.61 |
| Ref. 48 (theo. values) | 173.0 | ||||
| Hf3Rh4 | 192.9 | 39.3 | 110.3 | 0.405 | 4.913 |
| Hf3Rh5 | 200.3 | 76.2 | 202.8 | 0.331 | 2.629 |
| HfRh3 | 223.5 | 114.1 | 292.5 | 0.282 | 1.959 |
| Ref. 4 (theo. values) | 204.0 | 105.4 | 269.7 | 0.280 | 1.936 |
| Ref. 5 (theo. values) | 215.0 | 112.6 | 287.6 | 0.277 | 1.910 |
| Ref. 70 (theo. values) | 274.8 | ||||
| Rh | 254.0 | 141.2 | 357.5 | 0.265 | 1.798 |
| Ref. 55 (exp. values) | 267.0 | 149.4 | 377.8 | 0.264 | 1.787 |
| Ref. 56 (exp. values) | 270.0 | 149.4 | 378.4 | 0.266 | 1.807 |
| Ref. 4 (theo. values) | 243.3 | 141.7 | 356.0 | 0.256 | 1.717 |
The bulk modulus is a measure of resistance to volume change under external pressures. From Table 3, it is observed that the HfRH3 has the strongest resistance to volume change by applied pressure, while Hf2Rh owns the smallest. In addition, the bulk modulus has also been deem as the measure of the average bond strength of atoms for the given crystal.69 Among binary Hf–Rh intermetallics, HfRH3 is suggested have the strongest average bond strength of atoms, and Hf2Rh should be the weakest one. In addition, the B2- and L10-HfRh phases have the similar bulk moduli, and both are a bit larger than the ZrIr-HfRh (Table 3). For Hf2Rh, B2-HfRh and HfRh3, the calculated bulk moduli are in good agreement with those theoretical values for Hf2Rh (Cavor's work9), B2-HfRh (Novakovic's work48), and HfRh3 (Chen's4 and Surucu's5 work), accordingly. Notably, the theoretical bulk modulus for HfRh3 reported by Rajagopalan70 is much larger than other available values, which requires further scrutinizing.
When ZrIr-type HfRh is considered, the relationship between bulk modulus and atomic concentration of Rh has been exhibited in Fig. 2. It is seen that the bulk moduli of Hf–Rh compounds are linearly rising with the increasing Rh atomic concentration (at%), and the fitting line is y = 117.96 + 1.357x with R2 = 0.9961. It is noteworthy that the R2 is quite small to assure the precision of the fitted relationship.
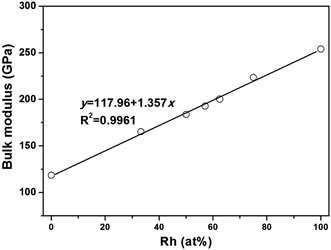 | ||
| Fig. 2 The calculated bulk modulus (B) versus atomic concentration of Rh for the binary Hf–Rh compounds. | ||
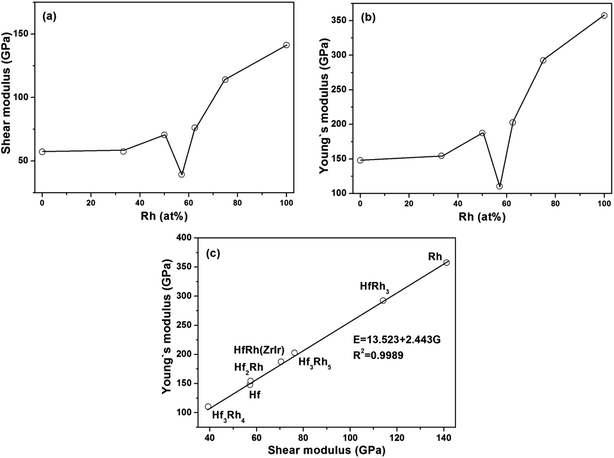
The shear modulus is a measure of resistance to reversible deformations over the shear stress. In Table 3, the HfRH3 has the strongest resistance to reversible deformations over the shear stress, and Hf3Rh4 possesses the smallest among Hf–Rh compounds. Furthermore, the B2- and L10-HfRh phases have the similar shear moduli, and both are smaller than the ZrIr-HfRh (Table 3). Regarding the Young's modulus, it represents the stiffness of materials. Overall, HfRH3 owns the largest, and Hf3Rh4 has the smallest Young' modulus among the Hf–Rh compounds (Table 3). It means HfRH3 and Hf3Rh4 are the most and least stiffest phases among binary Hf–Rh intermetallics, respectively. Besides, the ZrIr-HfRh has the larger Young's modulus than both B2- and L10-HfRh phases (Table 3). Generally, the calculated shear and Young's moduli are both in well compliance with those theoretical values for HfRh3 (Chen's4 and Surucu's5 works).
The obtained shear modulus and Young's modulus are depicted as a function of Rh atomic concentration in Fig. 3a and b, respectively. Since there is not explicit relationship shown in each figure, the connecting lines are only used as the guide for observation in both figures. However, the variations of shear modulus (Fig. 3a) and Young's modulus (Fig. 3b) have exhibited the similar tendencies with increasing Rh concentration, if the ZrIr-HfRh is selected. Therefore, the relationship between shear modulus (G) and Young's modulus (E) has been constructed, as shown in Fig. 3c, showing that E has linearly increased with the growing G. The linear relation can be formulated as E = 13.523 + 2.443G. Clearly, the R2 of the fitted line is 0.9989, which implies good relationship between these two factors.
Poisson's ratio (ν) is used to quantify the stability of the crystal against shear deformation, which usually ranges from −1 to 0.5.71–73 The larger Poisson ratio signifies the better plasticity in materials. The Poisson's ratio for ductile materials is larger than 0.26, while the value of brittle materials is less than 0.26.74 For binary Hf–Rh intermetallics, they are all ductile materials (Table 3). The hardest HfRh3 phase has the Poisson's ratio of 0.282, while the comparatively softest compound of Hf3Rh4 owns a higher Poisson's ratio of 0.405. Poisson's ratio also provides useful information about the characteristic of bonding forces in solids.75,76 The lower and upper limits for central force solids are 0.25 and 0.5, respectively. In this work, the Poisson's ratio for binary Hf–Rh compounds are larger than the lower limit 0.25, indicating that the interatomic forces in these intermetallics are all central forces.
The ratio of shear modulus to bulk modulus (B/G) has been proposed to estimate brittle or ductile behavior of materials.77 A higher B/G ratio is associated with the better ductility, whereas a lower value corresponds to the naturally brittleness. The critical value which separates ductile from brittle material is 1.75. If B/G > 1.75, the material behaves in a ductile manner. Otherwise, the material behaves in a brittle manner. According to Table 3, all the binary Hf–Rh compounds are ascribed to ductile materials, which agrees well with the prediction from the Poisson's ratio.
In the case that the ZrIr-HfRh is adopted, the variations of Poisson's ratio and B/G ratio have exhibited similar trends with the increasing Rh concentration from Fig. 4a and b, respectively. The relationship between Poisson's ratio and B/G ratio are shown in Fig. 4c. It has further confirmed the ductile essence of binary Hf–Rh compounds, and found the compound with a higher Poisson's ratio owns a higher B/G ratio simultaneously.
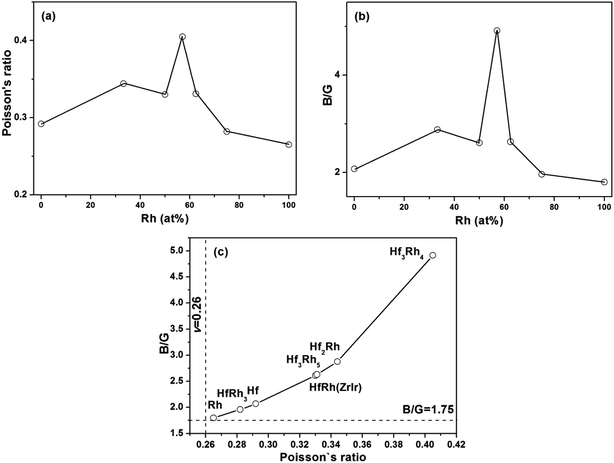 | ||
| Fig. 4 The calculated (a) Poisson's ratio (v) and (b) B/G ratio versus Rh concentration (at%) for binary Hf–Rh compounds; (c) Poisson's ratio versus B/G ratio for binary Hf–Rh intermetallics. | ||
3.3 Density of states
In this work, the calculated electronic structure is helpful to get an insight into the bonding characteristics of binary Hf–Rh compounds, and to reveal the underlying mechanism of structural stability. In Fig. 5a–g, the theoretically calculated total and partial density of states (DOS) for the seven compounds in the Hf–Rh system, where the zero energy in each plotted figure corresponds to Fermi level (EF). Based on the histogram curves, some common features can be identified in these compounds. For example, the peaks of the bonding state below Fermi level are mainly due to the hybridization between Rhd and Hfd electrons in the TDOS. While, the peaks of the antibonding state above the Fermi level are mainly due to the corresponding Hfd electrons. The s electrons of Rh and Hf can make the dominant contributions at deep levels between −8 and ∼−3 eV below the Fermi level. Additionally, The p electrons of Hf are effective around Fermi level in both bonding and antibonding states, and the p electrons of Rh are merely active. Similar featuring properties are identified in TDOS of Zr–Rh system.45 Furthermore, the nonzero TDOS at the Fermi level has symbolized the Hf–Rh system as the metallic material.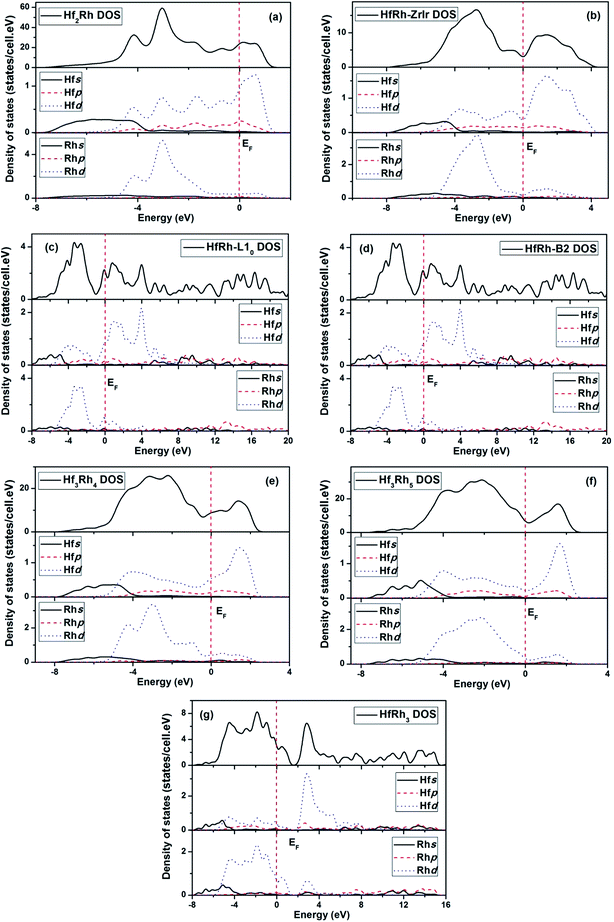 | ||
| Fig. 5 Total and partial density of states for (a) Hf2Rh, (b) ZrIr-HfRh, (c) L10-HfRh, (d) B2-HfRh, (e) Hf3Rh4, (f) Hf3Rh5 and (g) HfRh3 compounds. | ||
The DOS curves of ZrIr-HfRh, L10-HfRh and B2-HfRh are compared in Fig. 5b, c and d, correspondingly. In Fig. 5b, the EF falls exactly on the pseudogap for the TDOS of ZrIr-HfRh structure, indicating its superb stability.78 In comparison, the L10-HfRh and B2-HfRh structures have very similar TDOS profiles, where the Fermi levels are locating at the peaks approaching to the antibonding states. These features have confirmed the conclusion that the ZrIr-HfRh compound is more stable at the ground state.
In order to evaluate the structural stability of the HfRh compounds, the number of bonding electrons per atom is calculated based on the TDOS spectra. Since the charge interaction among bonding atoms is very crucial to the material's stability, the compound possesses higher number of bonding electrons should be more stable structurally.79–81 For the ZrIr-, L10- and B2-HfRh phases, the number of bonding electrons per atom of ZrIr-, L10- and B2- are 6.4974, 6.4943 and 6.494, accordingly. It means the HfRh phases has the stability order of ZrIr-type > L10 > B2, which is in good accordance with the thermodynamic analysis from Table 1. Additionally, for Hf2Rh, ZrIr-HfRh, Hf3Rh4, Hf3Rh5 and HfRh3, the calculated number of bonding electrons per atom have the results of 5.6594, 6.4974, 6.8527, 7.122 and 6.2456 accordingly. Therefore, the sequence of structural stability of the five stable Hf–Rh intermetallics should be Hf3Rh5 > Hf3Rh4 > ZrIr-HfRh > HfRh3 > Hf2Rh. This conclusion is in consistency with the conclusion drawn from formation enthalpies for five intermetallics, as shown in Fig. 1.
4. Conclusions
The phase stability, elastic and electronic properties of binary Hf–Rh compounds have been investigated using first-principles calculations. There are several conclusions are drawn as following:(1) Based on the formation enthalpy analysis, the equiatomic HfRh phase should tend to crystallize in ZrIr-type structure, followed by L10, and then B2 at the ground state. Therefore, the lower temperature HfRh phase is suggested to be the ZrIr-type. This conclusion is in good agreement with the experimental reports in the literature. Besides, Hf3Rh4 is proposed to be Pu3Pd4-type for the first time.
(2) There are seven compounds (i.e., Hf2Rh, ZrIr-HfRh, L10-HfRh, B2-HfRh, Hf3Rh4, Hf3Rh5, and HfRh3) are considered. The optimized lattice constants show a good consistency with available results. Furthermore, Hf3Rh5 is the most stable with the lowest formation enthalpy among the binary Hf–Rh compounds.
(3) The calculated elastic constants for Hf2Rh, ZrIr-HfRh, L10-HfRh, B2-HfRh, Hf3Rh4, and Hf3Rh5 can all satisfy the Born's criteria, indicating their mechanical stabilities.
(4) The elastic modulus of the compound is calculated using the VRH method. When ZrIr-HfRh is considered, the bulk modulus (B) increases linearly with the growing Rh concentration. Besides, it is found Young's modulus has linearly increased with the growing shear modulus, and the compound with a higher Poisson's ratio owns a higher B/G ratio simultaneously. Overall, the analysis made on the Poisson's ratio and B/G ratio have indicated that all the considered Hf–Rh compounds should be ductile.
(5) The number of bonding electrons for each compound has been derived from the DOS analysis. The results show the sequence of structural stability should be Hf3Rh > Hf3Rh4 > ZrIr-HfRh > HfRh3 > Hf2Rh, which is in remarkable agreement with the thermodynamic analysis.
Acknowledgements
This work is sponsored by Research Fund (Project No. 12X100030002 and No. 15X100040018) at Shanghai Jiao Tong University, P. R. China.References
- Y. Yamabe-Mitarai, Y. Koizumi, H. Murakami, T. Maruko, Y. Ro and H. Harada, Scr. Mater., 1997, 36, 393 CrossRef CAS.
- P. M. Clark, S. Lee and D. C. Fredrickson, J. Solid State Chem., 2005, 178, 1269 CrossRef CAS.
- ASM handbook, ed. S. D. Cramer and B. S. Covino, 10th edn, vol. 13B, ASM International, Metals Park (OH), 2005 Search PubMed.
- K. Chen, L. R. Zhao, J. S. Tse and J. R. Rodgers, Phys. Lett. A, 2004, 331, 400 CrossRef CAS.
- G. Surucu, K. Colakoglu, E. Deligoz, N. Korozlu and H. Ozisik, Comput. Mater. Sci., 2010, 48, 859 CrossRef CAS.
- Y. Terada, K. Ohkubo, S. Miura, J. M. Sanchez and T. Mohri, J. Alloys Compd., 2003, 354, 202 CrossRef CAS.
- R. Kuentzler and R. M. Waterstrat, Solid State Commun., 1988, 68, 85 CrossRef CAS.
- Y. Mao and Y. Q. Gao, J. Non-Cryst. Solids, 1988, 105, 134 CrossRef CAS.
- J. Belosevic-Cavor, B. Cekic, V. Koteski and A. Umicevic, Mater. Sci. Eng., A, 2007, 462, 294 CrossRef.
- R. M. Waterstrat and A. A. Giuseppetti, J. Less-Common Met., 1986, 119, 327 CrossRef CAS.
- V. N. Eremenko, T. D. Shtepa, T. A. Velikanova, L. S. Krikiya and V. M. Petyukh, Izv. Akad. Nauk SSSR, Met., 1991, 6, 143 Search PubMed.
- M. V. Nevitt and L. H. Schwartz, Trans. Metall. Soc. AIME, 1958, 212, 700 CAS.
- A. E. Dwight, Trans. Metall. Soc. AIME, 1959, 215, 283 CAS.
- A. Ramam and K. Schubert, Z. Metallkd., 1964, 55, 704 Search PubMed.
- V. N. Eremenko, T. D. Shtepa and T. A. Velikanova, Dokl. Akad. Nauk Ukr. SSR, Ser. B: Geol., Khim. Biol. Nauki, 1985, 10, 72 Search PubMed.
- H. Okamoto, J. Phase Equilib., 1993, 14, 399 CrossRef.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- P. Pulay, J. Chem. Phys., 1983, 78, 5043 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- D. F. Shanno, Math. Comput., 1970, 24, 647 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223 CrossRef.
- N. Ivanovic, S. Koicki, B. Cekic, M. Manasijevic, V. Koteski and D. Marjanovic, J. Phys.: Condens. Matter, 1999, 11, 289 CrossRef CAS.
- Hf3Rh5, ICSD# 104267.
- HfRh3, ICSD #104266.
- W. Xing, X. Q. Chen, D. Li, Y. Li, C. L. Fu, S. V. Meschel and X. Ding, Intermetallics, 2012, 28, 16 CrossRef CAS.
- J. L. Jorda, T. Graf, L. Schellenberg, J. Muller, K. Cenzual, J. C. Gachon and J. Hertz, J. Less-Common Met., 1988, 136, 313 CrossRef CAS.
- E. L. Semenova and Y. V. Kudryavtsev, J. Alloys Compd., 1994, 203, 165 CrossRef CAS.
- R. M. Waterstrat, J. K. Stalick, X. Meng-Burany and M. A. Estermann, Scr. Metall. Mater., 1995, 33, 695 CrossRef CAS.
- J. K. Stalick and R. M. Waterstrat, J. Alloys Compd., 2009, 477, 123 CrossRef CAS.
- B. S. Chen, Y. Z. Li, X. Y. Guan, C. Wang, C. X. Wang and Z. Y. Gao, Comput. Mater. Sci., 2015, 105, 66 CrossRef CAS.
- W. Z. Chen, Z. Y. Jiang, L. Si, L. S. Li and B. Zhou, Solid State Commun., 2011, 151, 1433 CrossRef CAS.
- S. M. Shapiro, G. Xu, G. Gu, J. Gardner and R. W. Fonda, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214114 CrossRef.
- M. Y. Benarchid, N. David, J. M. Fiorani, M. Vilasi and T. Benlaharche, Thermochim. Acta, 2009, 482, 39 CrossRef CAS.
- Y. Yamabe-Mitarai, T. Hara, M. J. Phasha, E. Ngoepe and H. K. Chikwanda, Intermetallics, 2012, 31, 26 CrossRef CAS.
- P. Shao, L. P. Ding, D. B. Luo, J. T. Cai, C. Lu and X. F. Huang, J. Alloys Compd., 2017, 695, 3024 CrossRef CAS.
- B. H. Chen and H. F. Franzen, J. Less-Common Met., 1999, 153, L13 CrossRef.
- J. Li, M. Zhang and X. Luo, J. Alloys Compd., 2013, 556, 214 CrossRef CAS.
- C. Colinet, Intermetallics, 2003, 11, 1095 CrossRef CAS.
- O. Levy, G. L. W. Hart and S. Curtarolo, Acta Mater., 2010, 58, 2887 CrossRef CAS.
- S. Zhang, X. Zhang, Y. Zhu, S. Zhang, L. Qi and R. Liu, Intermetallics, 2014, 44, 31 CrossRef CAS.
- V. Koteski, J. Belosevic-Cavor, B. Cekic, D. Stojic, N. Simic, A. Umicevic and Z. Milosevic, J. Alloys Compd., 2007, 442, 252 CrossRef CAS.
- HfRh, ICSD# 104265.
- N. Novaković, N. Ivanović, V. Koteski, I. Radisavljević, J. Belošević-Čavor and B. Cekić, Intermetallics, 2006, 14, 1403 CrossRef.
- Q. Guo and O. J. Kleppa, J. Alloys Compd., 2001, 321, 169 CrossRef CAS.
- A. Dębski, Arch. Metall. Mater., 2013, 58, 1147 Search PubMed.
- J. C. Gachon, N. Selhaoui, B. Aba and J. Hertz, J. Phase Equilib., 1992, 13, 506 CrossRef CAS.
- W. J. Ding, J. X. Yi, P. Chen, D. L. Li, L. M. Peng and B. Y. Tang, Solid State Sci., 2012, 14, 555 CrossRef CAS.
- G. V. Sin'ko, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104118 CrossRef.
- Y. H. Duan, B. Huang, Y. Sun, M. J. Peng and S. G. Zhou, J. Alloys Compd., 2014, 590, 50 CrossRef CAS.
- Q. Chen and B. Sundman, Acta Mater., 2001, 49, 947 CrossRef CAS.
- N. Singh, Pramana, 1999, 52, 511 CrossRef CAS.
- M. Born and K. Huang, Dynamical Theory of Crystal Lattices, Oxford, Oxford University Press, 1954 Search PubMed.
- D. Shi, B. Wen, R. Melnik, S. Yao and T. Li, J. Solid State Chem., 2009, 182, 2664 CrossRef CAS.
- D. Chen, Z. Chen, Y. Wu, M. Wang, N. Ma and H. Wang, Comput. Mater. Sci., 2014, 91, 165 CrossRef CAS.
- J. Du, B. Wen, R. Melnik and Y. Kawazoe, J. Alloys Compd., 2014, 588, 96 CrossRef CAS.
- Q. J. Liu, H. Qin, Z. Jiao, F. S. Liu and Z. T. Liu, Mater. Chem. Phys., 2016, 180, 75 CrossRef CAS.
- Y. H. Duan, Z. Y. Wu, B. Huang and S. Chen, Comput. Mater. Sci., 2015, 110, 10 CrossRef CAS.
- X. Gao, Y. Jiang, R. Zhou and J. Feng, J. Alloys Compd., 2014, 587, 819 CrossRef CAS.
- S. Chen, Y. H. Duan, B. Huang and W. C. Hu, Philos. Mag., 2015, 95, 3535 CrossRef CAS.
- H. Ozisik, E. Deligoz, K. Colakoglu and G. Surucu, Chin. Phys. B, 2013, 22, 046202 CrossRef.
- W. Voigt, Lehrbuchde Kristallphysik, Terubner, Leipzig, 1928 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- B. Huang, Y. H. Duan, W. C. Hu, Y. Sun and S. Chen, Ceram. Interfaces, 2015, 41, 6831 CrossRef CAS.
- M. Rajagopalan and M. Sundareswari, J. Alloys Compd., 2004, 379, 8 CrossRef CAS.
- B. Mayer, H. Anton, E. Bott, M. Methfessel, J. Sticht, J. Harris and P. C. Schmidt, Intermetallics, 2003, 11, 23 CrossRef CAS.
- M. Pang, Y. Zhan, H. Wang, W. Jiang and Y. Du, J. Appl. Phys., 2011, 110, 033533 CrossRef.
- G. N. Greaves, A. L. Greer, R. S. Lakes and T. Rouxel, Nat. Mater., 2011, 10, 823 CrossRef CAS PubMed.
- S. Chen, Y. Sun, Y. H. Duan, B. Huang and M. J. Peng, J. Alloys Compd., 2015, 630, 202 CrossRef CAS.
- D. Chen, Z. Chen, Y. Wu, M. Wang, N. Ma and H. Wang, Intermetallics, 2014, 52, 64 CrossRef CAS.
- H. Fu, D. Li, F. Peng, T. Gao and X. Cheng, Comput. Mater. Sci., 2008, 44, 774 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823 CrossRef CAS.
- S. Cui, W. Feng, H. Hu, Z. Feng and H. Liu, Scr. Mater., 2009, 61, 576 CrossRef CAS.
- W. C. Hu, Y. Liu, D. J. Li, X. Q. Zeng and C. S. Xu, Comput. Mater. Sci., 2014, 83, 27 CrossRef CAS.
- H. Hou, Z. Wen, Y. Zhao, L. Fu, N. Wang and P. Han, Intermetallics, 2014, 44, 110 CrossRef CAS.
- W. C. Hu, Y. Liu, D. J. Li, X. Q. Zeng and C. S. Xu, Phys. B, 2013, 427, 85 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |