Open Access Article
Open Access ArticleComparison of Li, Na, Mg and Al-ion insertion in vanadium pentoxides and vanadium dioxides†
Vadym V. Kulish and
Sergei Manzhos
and
Sergei Manzhos *
*
Department of Mechanical Engineering, National University of Singapore, Block EA #07-08, 9 Engineering Drive 1, Singapore 117576, Singapore. E-mail: mpemanzh@nus.edu.sg
First published on 28th March 2017
Abstract
Vanadium oxides (VO) are among the most promising electrode materials for advanced electrochemical batteries since they are able to operate in most major types of batteries (Li, Na, Mg and Al-ion). The practical development of VO electrodes, however, is complicated by the presence of multiple VO stoichiometries and phases with distinctly different lattice stabilities, electronic properties and, hence, metal ion insertion thermodynamics and kinetics. We present a systematic comparative ab initio study of four most stable VO phases (α-V2O5, β-V2O5, VO2(R) and VO2(B)) and their interaction mechanism with Li, Na, Mg, and Al atoms. Our results show that among the studied phases, rutile VO2(R) exhibits the largest Al binding energy and a low Al diffusion barrier, which makes it quite promising for Al-ion batteries. At the same time, the β-V2O5 phase exhibits the highest binding energy for Mg insertion and significant reduction of the Mg diffusion barrier compared to conventionally used α-V2O5. Our results highlight the benefits of rational phase engineering and may assist further experimental studies of high performance VO electrodes for Na, Mg, and Al-ion batteries.
1. Introduction
Affordable energy storage is essential for the practical realization of hybrid or all-electric vehicles and grid integration of renewable sources (e.g. solar and wind). Although Li-ion batteries provide the highest energy density among commercial battery technologies, the limited and inhomogeneous global distribution of Li resources may hinder their long-term and large-scale applications. Among the alternative technologies, Na, Mg and Al-ion batteries are attracting an ever-growing research attention due to their advantages in elemental abundance and environment-friendly chemistry. Moreover, Mg-ion and Al-ion batteries can operate with metallic Mg and Al anodes, offering the benefits of low cost, dendrite-free deposition during charging and high volumetric capacity. However, the identification of suitable cathode materials has been a major challenge in the development of Na, Mg and Al-ion batteries. Due to the larger ion size or multivalency, the storage of Na, Mg, and Al is associated with low binding energies to an electrode material (compared with the metal's cohesive energy) and high energy barriers for ionic diffusion.1–6 Thus, identification of suitable cathode materials specific for post-lithium batteries is necessary and requires thorough understanding of the basic insertion mechanisms.Vanadium oxides (VO) are among the few materials that are able to operate as electrodes for the most types of batteries.7–14 For example, layered V2O5 has shown Mg storage capacities of >150 mA h g−1 at 2.3–2.6 V vs. Mg/Mg2+.15 Al insertion in V2O5 has been demonstrated as well, although at a rather low voltage of about 1 V (vs. Al/Al3+).16,17 VO2 exhibits high Li storage capacity (320 mA h g−1) and good stability resulting from edge-sharing VO6 octahedra bilayers.18,19 Despite these promising studies, a systematic understanding of VO electrodes is currently lacking, mainly due to the presence of multiple stoichiometries and phases, such as α-V2O5, β-V2O5, VO2(R), VO2(B), V6O13, V3O7, etc.20,21 The crystalline and electronic structures of VO polymorphs are complex with distinctly different lattice symmetries, electronic properties and, hence, different metal-ion insertion thermodynamics and kinetics. It would be highly desirable to rationally select the best VO phase for a given type of battery. So far, the layered V2O5 has been the most studied VO phase and may serve as a convenient benchmark system.22–28 Carrasco et al. employed van der Waals (vdW)-inclusive methods with nonlocal density functionals to investigate the Li and Na insertion into α-V2O5.29,30 However, vdW-corrected methods may overestimate the voltages and diffusion barriers in electrode materials.4,31 Gautam et al.32–35 and Zhou et al.36 theoretically investigated Mg insertion in orthorhombic V2O5 using DFT+U methods.
While recent studies investigated vanadium pentoxides as cathode materials, there have been no reports on Li, Na, Mg and Al insertion in VO2 compounds. Moreover, there have been no theoretical study comparing with the same computational setup the insertion energetics into multiple VO compounds, such as α-V2O5, β-V2O5, VO2(R), and VO2(B). In this paper, we attempt to fill this knowledge gap, and more importantly, we investigate the potential of VO2 phases as a potential cathode materials for Li, Na, Mg, and Al-ion batteries. Our theoretical work fits very well with the latest experimental advances in controlled growth and epitaxial stabilization of the VO polymorphs as reported recently.11,37 Theoretical insights from our work would help the development of high-performance VO electrodes for Li, Na, Mg, and Al-ion batteries.
2. Computational methods
Calculations were performed within the density functional theory (DFT) framework, as implemented in the VASP 5.3 package.38 The core electrons were treated within the projector augmented wave (PAW) method.39,40 Exchange-correlation effects were described with the generalized gradient approximation and the PBEsol functional.41 For comparison, we have also used PBE functional42 and van der Waals-corrected D2 method of Grimme.43 The following valence electron configurations were used: Li (2s1), Na (3s1), Mg (2p6 3s2), Al (3s2 3p1), V (3p6 3d4 4s1) and O (2s2 2p4). The total energies of the VO supercells were calculated using converged Γ-centered Monkhorst–Pack k-point grids.44 The plane-wave cutoff was 500 eV. The Gaussian smearing with a smearing factor of 0.1 eV was used in all calculations. The optimized structures were obtained by relaxing all atomic positions and lattice parameters using the conjugated gradient algorithm until all forces are smaller than 0.01 eV Å−1. With the selected modeling parameters, the predicted lattice constants of the VO phases agree well with the experimental data (Table 1). The amount of charge transfer between the metal ion atom and VO host is estimated from the grid-based Bader charge analysis.45 Large supercells of VO were used, describing insertion at the dilute concentration (1–1.5 at%). In such a way, metal–metal interactions can be neglected and the interaction of the isolated inserted atom with VO can be studied. We used a (3 × 1 × 3) supercell for α-V2O5 (127 atoms), a (3 × 1 × 1) supercell for β-V2O5 (85 atoms), a (2 × 2 × 4) supercell for VO2(R) (97 atoms), and a (1 × 3 × 2) supercell for VO2(B) (145 atoms). Activation barriers for diffusion are calculated using the climbing-image nudged elastic band (CI-NEB) method.46 The CI-NEB calculations were performed using 3–6 images, and the initial guess of the migration pathway has been generated by linear interpolation between the initial and final points of the diffusion path. The geometry and energy of the images were then relaxed until the largest norm of the force orthogonal to the path was smaller than 0.02 eV Å−1. To account for the on-site Coulomb interactions between the V 3d electrons, we performed DFT+U calculations by adding an effective parameter, Ueff, as introduced by Dudarev et al.47 As suggested by Ceder et al.,48 we have used Ueff = 3.0 eV for vanadium. Spin polarization is included, and all calculations were performed for the ferromagnetic (FM) spin ordering. In fact, it is reported in the literature that lithiated phases with FM ordering are lower in energy than those with AFM ordering.49| Compound | Functional | a (Å) | b (Å) | c (Å) |
|---|---|---|---|---|
| α-V2O5 | PBE | 3.57 | 11.60 | 4.54 |
| PBEsol | 3.54 | 11.55 | 4.32 | |
| D2-vdW | 3.54 | 11.64 | 4.40 | |
| Exp51 | 3.56 | 11.51 | 4.36 | |
| β-V2O5 | PBE | 11.54 | 3.56 | 10.74 |
| PBEsol | 11.50 | 3.53 | 10.69 | |
| D2-vdW | 11.58 | 3.52 | 10.04 | |
| VO2(R) | PBE | 4.59 | 4.59 | 2.85 |
| PBEsol | 4.55 | 4.55 | 2.85 | |
| D2-vdW | 4.55 | 4.55 | 2.84 | |
| Exp52 | 4.55 | 4.55 | 2.86 | |
| VO2(B) | PBE | 12.01 | 3.73 | 6.42 |
| PBEsol | 12.02 | 3.71 | 6.39 | |
| D2-vdW | 12.00 | 3.70 | 6.40 | |
| Exp52 | 12.03 | 3.69 | 6.42 |
The insertion (binding) energy (Eb) per inserted atom is estimated as
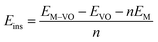 | (1) |
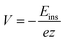 | (2) |
3. Results and discussion
3.1. Crystal structures of pure VO phases
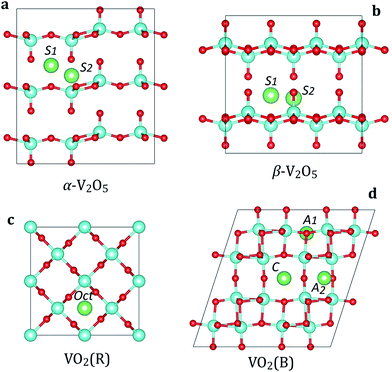
We consider two polymorphs of vanadium pentoxide (V2O5): α-V2O5 and β-V2O5 (Fig. 1a and b). From the experimental studies, α-V2O5 is the most stable bulk phase at temperatures below 400 °C.51 The α-V2O5 has a layered crystal structure (space group Pmmn, no. 59), consisting of layers of alternating corner- and edge-sharing VO5 pyramids. Each V atom is five-coordinated with four V–O bonds of 1.78–1.86 Å and one short double V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of 1.58 Å, which forms the apex of the VO5 pyramid. The key difference between α-V2O5 and β-V2O5 phases is the layer stacking order. In metastable β-V2O5 (space group Cmcm, no. 63), alternate layers are displaced by a/2, leading to considerable changes in the interlayer spacing (which is larger by >0.5 Å). The adjacent layers are interacting by weak van der Waals (vdW) forces along c(z) direction.
O bond of 1.58 Å, which forms the apex of the VO5 pyramid. The key difference between α-V2O5 and β-V2O5 phases is the layer stacking order. In metastable β-V2O5 (space group Cmcm, no. 63), alternate layers are displaced by a/2, leading to considerable changes in the interlayer spacing (which is larger by >0.5 Å). The adjacent layers are interacting by weak van der Waals (vdW) forces along c(z) direction.
The most stable phase of vanadium dioxide (VO2) is rutile (VO2(R), Fig. 1c), which belongs to the space group P42/mnm (136). VO2(R) is stable in the temperature range from 68 °C to 1540 °C.52 It consists of VO6 octahedra which share edges, forming tunnel-like structure along the c axis. Our calculated lattice parameters for VO2(R) are a = b = 4.55 Å and c = 2.85 Å, close to the experimental values.52 Each V atom is six-coordinated with two V–O bonds of 1.93 Å and four V–O bonds of 1.92 Å.
The monoclinic polymorph of vanadium dioxide (VO2(B), Fig. 1d), belonging to the space group C2/m (12), can be synthesized by gentle reduction (hydrothermal treatment) of V2O5. VO2(B) has a larger unit cell as compared to VO2(R), and can be described as stacking of two identical layers of VO6 octahedra along b axis. The second layer is shifted with respect to the first one by ½, ½ and 0 along x, y, and z directions, respectively. The VO6 octahedra are deformed with the V atoms being no longer in their center. Our calculated lattice parameters for VO2(B) are a = 12.02 Å, b = 3.71 Å, c = 6.39 Å, consistent with experimental data.52 The calculated V–O bond lengths are 1.87–2.07 Å. In VO2(B), all VO6 octahedra are aligned along the same crystallographic orientation.
The calculated structural parameters for VO phases are summarized in Table 1. We can notice that lattice parameters in strongly-bonded VO2(R) and VO2(B) phases are reproduced with a good accuracy by all functionals. However, PBE calculations overestimate the interlayer spacing of 4.54 Å in α-V2O5 phase. In contrast, PBEsol calculations show an optimal interlayer spacing of 4.32 Å, in good agreement with the experimental value of 4.36 Å. The effect of van der Waals interactions in α-V2O5 can also be treated by using the semi-empirical correction scheme of Grimme (DFT-D2).43 However, studies show that use of vdW-corrected functionals may potentially lead to overestimated voltages in covalently-bonded phases, such as VO2.4 Therefore, in order to preserve the consistency in the computational setup among both weak and strongly-bonded VO phases, we use the PBEsol functional in all following calculations.
3.2. Energetics of Li, Na, Mg and Al insertion
We first examine the insertion of M atoms (M = Li, Na, Mg and Al) into α-V2O5 at the dilute concentration. There are two possible insertion sites for M ions as shown in Fig. 1a. At the S1 site, the M atom is located at the high-symmetry position with equal distances to four vanadyl oxygens (O1) and two bridging oxygens (O2). At the S2 site, the M atoms are located on the line between vanadyl O1 and V atoms. The M atoms at the S1 and S2 sites are six- and four-coordinated, respectively. We find that the inserted M ions strongly prefer to occupy the S1 site. The lattice distortions caused by M insertion are very small, suggesting good stability of V2O5 host during battery cycling. When M atom is placed at the S1 site, the four vanadyl O1 atoms move towards the M ion with slight increase in the V–O bond lengths. The results for M insertion at the most stable site (S1) are summarized in Table 2. Importantly, we find that all M atoms (Li, Na, Mg and Al) have negative binding energies in α-V2O5. This implies that metal insertion in V2O5 is energetically favorable. The insertion voltage at the low concentration follows the trend Li/Na > Mg > Al.| Compound | Property | Li | Na | Mg | Al |
|---|---|---|---|---|---|
| α-V2O5 | Eins (eV) | −3.13 | −3.17 | −5.50 | −5.11 |
| V (V) | 3.13 | 3.17 | 2.75 | 1.70 | |
| dM–O (Å) | 2.20 | 2.41 | 2.19 | 2.10 | |
| Q (|e|) | 0.86 | 0.88 | 1.60 | 2.43 | |
| Site | S1 | S1 | S1 | S1 | |
| β-V2O5 | Eins (eV) | −3.35 | −3.50 | −6.21 | −5.32 |
| V (V) | 3.35 | 3.50 | 3.10 | 1.77 | |
| dM–O (Å) | 2.31 | 2.55 | 2.32 | 2.12 | |
| Q (|e|) | 0.90 | 0.89 | 1.65 | 2.49 | |
| Site | S1 | S1 | S1 | S1 | |
| VO2(R) | Eins (eV) | −3.65 | −1.09 | −3.96 | −5.97 |
| V (V) | 3.65 | 1.09 | 1.98 | 1.99 | |
| dM–O (Å) | 1.85 | 1.96 | 1.87 | 1.78 | |
| Q (|e|) | 0.92 | 0.87 | 1.61 | 2.45 | |
| Site | Oct | Oct | Oct | Oct | |
| VO2(B) | Eins (eV) | −3.11 | −2.99 | −5.46 | −5.76 |
| V (V) | 3.11 | 2.99 | 2.73 | 1.92 | |
| dM–O (Å) | 2.01 | 2.53 | 2.15 | 1.75 | |
| Q (|e|) | 0.92 | 0.90 | 1.61 | 2.44 | |
| Site | C | C | A1 | A1 | |
| M-oxide | dM–O (Å) | 2.01 | 2.42 | 2.12 | 1.87 |
The insertion sites in β-V2O5 resemble very closely those in α-V2O5 with the same local coordination of M atoms (Fig. 1b). However, we find that M insertion is more energetically favorable in β-V2O5 than in the α phase. Although the difference for the Li is quite small, for Na, Mg and Al atoms it is substantial (Table 2). This is directly related to an extra space available for M insertion (the interlayer spacing in β-V2O5 is >0.5 Å larger than in α-V2O5). We also find that the volume changes in β-V2O5 upon M insertion are smaller than in α-V2O5, as measured by the change in interlayer spacing. This is beneficial for the long-term cycling of batteries.
In contrast to V2O5, the VO2 polymorphs are considerably less studied as electrode materials. To the best of our knowledge, there have been only limited theoretical studies on the insertion of Li, Na, Mg or Al atoms in VO2.53 First, we address the rutile VO2 phase. There are two possible insertion positions for metal ions in the VO2(R) structure (Fig. 1c): octahedral (Oct) and tetrahedral (Td). Our calculations show a strong preference for insertion at the Oct site for all atoms. The Td site is energetically metastable, and can be possibly occupied at larger metal ion concentrations. In the following, we discuss the local coordination of inserted Li, Na, Mg and Al on the example of Li. When placed in the octahedral site, the Li atom is six-fold coordinated with two Li–O bonds lengths of 1.78 Å and four of 2.05 Å. In the Td position, the Li atom adopts four-fold coordination forming Li–O bonds of 1.78–1.85 Å. The larger binding energies at the Oct site (by >0.20 eV) show that metal atoms prefer sites with a higher coordination number. The preference for the Oct site can also be rationalized by much more space available for metal atom insertion, leading to smaller structural deformations.
Next, we examine metal ion insertion in the VO2(B), the second most stable VO2 phase.52 We have considered three stable intercalation sites (Fig. 1d), which are denoted as A1, A2, and C. The unit cell of VO2(B) contains four A1 sites, which are 5-fold coordinated to oxygen atoms; four A2 sites, which are also 5-fold coordinated to oxygen; and two C sites, which have a planar 4-fold coordination. Our calculations show that there is a difference in site preference among metal atoms. Namely, Li and Na favor insertion at the C site. When Li is located at the C site, its position is slightly displaced in the b direction from the ideal coordinates. Similar displacement has also been observed in bronze TiO2.54 In contrast, Mg and Al atoms prefer the A1 insertion site.
The preference of insertion at the particular site in VO2(B) can be rationalized by the interplay of two factors. First, a stable insertion configuration should lead to minimum lattice strains induced by the presence of the cation. This can be achieved by insertion at sites within the more open channel region, such as the C site. Secondly, insertion is favored at sites with effective screening of the electrostatic repulsions due to M–M and M–V ion interactions. Such screening can be enhanced by increasing M–V distances and maximizing the degree of oxygen coordination. The position with the highest degree of oxygen coordination in VO2(B) corresponds to the five-coordinated A1 site. Overall, it seems that the first argument is dominant for Li and Na atoms. Meanwhile, the insertion of multivalent atoms (Mg and Al) with larger polarization is ruled by the second factor.
The calculated binding energies (Table 2) demonstrate several important differences between V2O5 and VO2 phases. First, Li insertion is energetically favorable in all structures with similar estimated voltages (3.13–3.65 V). This is consistent with experimental voltages55–57 achieved by vanadium oxides in Li-ion and Mg-ion batteries at the dilute concentrations studied here, which correspond to 8.19, 12.28, 10.09, and 6.73 mA h g−1 in α-V2O5, β-V2O5, VO2(R), and VO2(B), respectively. However, the binding energies for Na and Mg in VO2(R) are significantly reduced, as compared to V2O5. For instance, Na insertion energy in VO2(R) is only −1.09 eV. Due to the larger ionic radius of Na, there is not enough space to its accommodation within the VO2(R) host. The calculated Na–O bond lengths in VO2(R) are 1.96 Å, much shorter than the equilibrium Na–O bond of 2.42 Å in Na2O oxide. On the other hand, the presence of open channels in VO2(B) leads to the favorable Na insertion with a binding energy of −2.99 eV. Remarkably, the estimated voltage for single Al insertion is greatly increased in VO2(R) and VO2(B) as compared to V2O5: namely, from 1.70 V in α-V2O5 to 1.99 V in VO2(R). In fact, the calculated Al–O bond lengths at the Oct site in VO2(R) (1.78–1.94 Å) are nearly identical to that of 1.87 Å in Al2O3 oxide, suggesting favorable Al insertion. Considering that the low Al insertion voltages have been a major bottleneck for the energy density in Al ion batteries, our results demonstrate that VO2(R) has a good potential as electrode for Al-ion batteries.
3.3. Electronic structure
Vanadium oxides exhibit a variety of distinctly different electronic properties. In particular, we find that V2O5 phases are non-magnetic semiconductors, while VO2 phases are spin-polarized metals as shown in Fig. 2.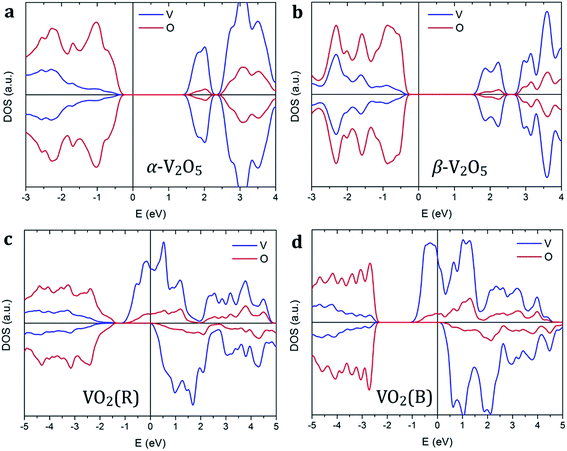 | ||
| Fig. 2 Spin-polarized density of states of (a) α-V2O5, (b) β-V2O5, (c) VO2(R), and (d) VO2(B). The Fermi level is aligned to zero, indicated by the vertical line. | ||
Both pristine α-V2O5 and β-V2O5 show similar electronic structure. Here, the valence band is formed by O 2p bands, while the top of conduction band mainly originates from V 3d states. The DFT+U-calculated DOS of α-V2O5 with Li, Na, Mg and Al inserted atoms are shown in Fig. 3. Upon insertion, the valence shells of the metal atoms are fully ionized, they donate their valence electrons to the host bands. Due to the charge transfer, the Fermi level is shifted towards the conduction band. The insertion of Li, Na, Mg and Al gives rise to midgap state between the conduction and valence bands. These midgap states originate from filling of the lowest-energy nonbonding V 3d states as a result of the electron transfer from the inserted atom. The number of such states is equal to the number of valence electrons transferred. Note that in Li- and Na-inserted systems, the spin-polarized V-3d states are located very near the bottom of the conduction band but are separate from it.
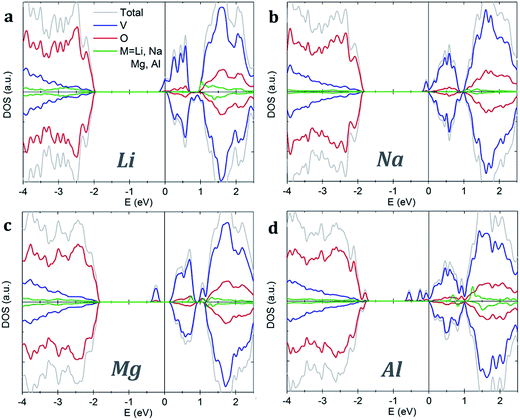 | ||
| Fig. 3 Density of states of α-V2O5 with inserted (a) Li, (b) Na, (c) Mg and (d) Al atoms. The plots are aligned at the Fermi level, indicated by the vertical line. | ||
In contrast, VO2 phases have spin-polarized metallic electronic structure with large density of states at the Fermi level. The states near the Fermi level originate mainly from V 3d bands. The p–d hybridization causes additional O 2p contributions in this energy range resulting from the V 3d–O 2p bonding. Our results for rutile VO2 agree very well with the literature.52 We find that metal ion insertion does not noticeably affect the electronic structure of the VO2 host. In such case, the states originating from the metal ions are covered by the metallic nature of the VO2 host (see Fig. S1 in the ESI†).
We examined the charge redistribution by plotting the spin density difference. Fig. S2† shows it for the case of Mg insertion in α-V2O5, with the number of d-like orbitals equal to the number of valence electrons donated. For all oxides, we found that the charge accumulation on the V atoms, indicating the reduction of V species. Interestingly, the partial V reduction believed to be from V5+ to V4+, as well as the Fermi level shift has been experimentally observed in X-ray photoelectron spectroscopy (XPS) for Na–V2O5.8 A large fraction of the electron donated by the metal ion to the oxide host is not only transferred to V (thus changing the valence of V according to a conventional chemistry point of view) but is also transferred to oxygen. For example, it was found that about 50% of the charge from Li is transferred to oxygen in VO2. The Bader charge analysis shows that the electron transfer from metal ions to the oxide host is very local. In particular, there is a significant increase in the electron density at the oxygen sites immediately surrounding the inserted metal ions.
3.4. Diffusion
Facile electron and ionic transport are desirable for fast charge/discharge rate in electrode materials. Ionic diffusion in α-V2O5 can be presented as a one-dimensional process along the x-axis (the smallest lattice parameter). The calculated diffusion barriers are summarized in Fig. 4a. The energy barrier follows the trend Li < Na < Mg < Al. For all atoms except Li (0.35 eV), the energy barrier is >1 eV, indicating very slow diffusion kinetics. This is consistent with previous works which reported a barrier for Mg diffusion in α-V2O5 of 0.90–1.15 eV.28,35 The slow Na diffusion is attributed to the large size of Na ions. The slow Mg and Al diffusion can be attributed to the polarization effect of Mg2+ and Al3+ and strong Mg–O/Al–O interactions. Remarkably, the diffusion barrier can be lowered by a factor of two in β-V2O5 phase (to 0.52 and 0.65 eV for Na and Mg, respectively). Such reduction will lead to much faster charge/discharge rates in Na-ion and Mg-ion batteries.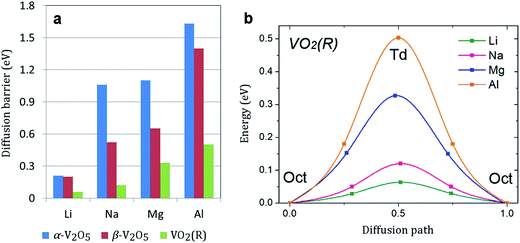 | ||
| Fig. 4 (a) The calculated diffusion barriers (in eV) in α-V2O5, β-V2O5, and VO2(R). (b) The energy profile for the lowest energy diffusion pathway of Li, Na, Mg, and Al in VO2(R). | ||
Metal diffusion in VO2(R) may involve several possible pathways. The pathway with the lowest energy barrier is along the z direction. Most remarkably, we find very low metal ion diffusion barriers in VO2(R). As shown in Fig. 4b, the migration barriers for Mg and Al are only 0.33 and 0.50 eV, respectively. Another possible pathway is located in the xy plane. Here, metal ion diffusion occurs via tetrahedral sites. The energy barrier for this pathway is much higher, which suggests that metal diffusion in VO2(R) is anisotropic. The barrier for Al diffusion is the lowest among all electrode materials for Al-ion batteries reported in the literature. It is comparable to the energy barrier for Li diffusion in high-capacity bulk silicon anode (0.57 eV).6,58 Considering recent experimental advances in surface-oriented, anisotropic growth of VO2 crystals,11 we can expect facile diffusion rates in VO2(R) as a potential anode material for Na-ion batteries.
4. Conclusions
In summary, we presented a comprehensive and truly comparative study of Li, Na, Mg and Al insertion in the most stable VO phases (α-V2O5, β-V2O5, VO2(R) and VO2(B)). We found that the VO2(R) phase exhibits the highest voltage for Al insertion and a low Al diffusion barrier, and may be a potential cathode choice for Al-ion batteries. The β-V2O5 phase may be the most promising VO cathode material for Na-ion and Mg-ion batteries due to much improved diffusion kinetics and sufficiently high voltages. The energy barriers for Na and Mg diffusion in α-V2O5 are rather high (>1 eV). However, we have observed a significant reduction of barriers for Na and Mg diffusion in the β-V2O5 phase (0.52 and 0.65 eV, respectively) leading to potential fast charge/discharge rates. Overall, our study highlights the benefits of rational phase engineering for VO cathode materials in rechargeable batteries.Acknowledgements
This work is supported by the Ministry of Education of Singapore grant MOE2015-T2-1-011.References
- S. P. Ong, V. L. Chevrier, G. Hautier, A. Jain, C. Moore, S. Kim, X. H. Ma and G. Ceder, Energy Environ. Sci., 2011, 4, 3680–3688 CAS.
- V. L. Chevrier and G. Ceder, J. Electrochem. Soc., 2011, 158, A1011–A1014 CrossRef CAS.
- O. Malyi, V. V. Kulish, T. L. Tan and S. Manzhos, Nano Energy, 2013, 2, 1149–1157 CrossRef CAS.
- M. A. Sk and S. Manzhos, J. Power Sources, 2016, 324, 572–581 CrossRef CAS.
- F. Legrain, O. Malyi and S. Manzhos, J. Power Sources, 2015, 278, 197–202 CrossRef CAS.
- V. V. Kulish, O. I. Malyi, M.-F. Ng, Z. Chen, S. Manzhos and P. Wu, Phys. Chem. Chem. Phys., 2014, 16, 4260–4267 RSC.
- D. Kundu, B. D. Adams, V. Duffort, S. H. Vajargah and L. F. Nazar, Nat. Energy, 2016, 1, 16119 CrossRef CAS.
- C. K. Chan, H. L. Peng, R. D. Twesten, K. Jarausch, X. F. Zhang and Y. Cui, Nano Lett., 2007, 7, 490–495 CrossRef CAS PubMed.
- A. M. Cao, J. S. Hu, H. P. Liang and L. J. Wan, Angew. Chem., Int. Ed., 2005, 44, 4391–4395 CrossRef CAS PubMed.
- P. Senguttuvan, S.-D. Han, S. Kim, A. L. Lipson, S. Tepavcevic, T. T. Fister, I. D. Bloom, A. K. Burrell and C. S. Johnson, Adv. Energy Mater., 2016, 6, 1600826 CrossRef.
- S. Park, C. W. Lee, J.-C. Kim, H. J. Song, H.-W. Shim, S. Lee and D.-W. Kim, ACS Energy Lett., 2016, 1, 216–224 CrossRef CAS.
- B. Yan, X. Li, Z. Bai, L. Lin, G. Chen, X. Song, D. Xiong, D. Li and X. Sun, J. Mater. Chem. A, 2017, 5, 4850–4860 CAS.
- Z. Khan, B. Senthilkumar, S. O. Park, S. Park, J. Yang, J. H. Lee, H.-K. Song, Y. Kim, S. K. Kwak and H. Ko, J. Mater. Chem. A, 2017, 5, 2037–2044 CAS.
- Z. Wu, W. Qiu, Y. Chen, Y. Luo, Y. Huang, Q. Lei, S. Guo, P. Liu, M.-S. Balogun and Y. Tong, J. Mater. Chem. A, 2017, 5, 756–764 CAS.
- G. Gershinsky, H. D. Yoo, Y. Gofer and D. Aurbach, Langmuir, 2013, 29, 10964–10972 CrossRef CAS PubMed.
- L. D. Reed and E. Menke, J. Electrochem. Soc., 2013, 160, A915–A917 CrossRef CAS.
- H. Wang, Y. Bai, S. Chen, X. Luo, C. Wu, F. Wu, J. Lu and K. Amine, ACS Appl. Mater. Interfaces, 2014, 7, 80–84 Search PubMed.
- S. Yang, Y. Gong, Z. Liu, L. Zhan, D. P. Hashim, L. Ma, R. Vajtai and P. M. Ajayan, Nano Lett., 2013, 13, 1596–1601 CrossRef CAS PubMed.
- C. Nethravathi, C. R. Rajamathi, M. Rajamathi, U. K. Gautam, X. Wang, D. Golberg and Y. Bando, ACS Appl. Mater. Interfaces, 2013, 5, 2708–2714 CAS.
- N. Bahlawane and D. Lenoble, Chem. Vap. Deposition, 2014, 20, 299–311 CrossRef CAS.
- H. Li, P. He, Y. Wang, E. Hosono and H. Zhou, J. Mater. Chem., 2011, 21, 10999–11009 RSC.
- Z. Y. Li and Q. H. Wu, ChemPhysChem, 2008, 9, 300–304 CrossRef CAS PubMed.
- X. Rocquefelte, F. Boucher, P. Gressier and G. Ouvrard, Chem. Mater., 2003, 15, 1812–1819 CrossRef CAS.
- J. Braithwaite, C. Catlow, J. Gale and J. Harding, Chem. Mater., 1999, 11, 1990–1998 CrossRef CAS.
- Z. Wang, Q. Su and H. Deng, Phys. Chem. Chem. Phys., 2013, 15, 8705–8709 RSC.
- X. Zhao, X. Zhang, D. Wu, H. Zhang, F. Ding and Z. Zhou, J. Mater. Chem. A, 2016, 4, 16606–16611 CAS.
- D. Wang, H. Liu, J. D. Elliott, L.-M. Liu and L. W. M. Lau, J. Mater. Chem. A, 2016, 4, 12516–12525 CAS.
- A. Parija, Y. Liang, J. L. Andrews, L. R. De Jesus, D. Prendergast and S. Banerjee, Chem. Mater., 2016, 28, 5611–5620 CrossRef CAS.
- V. Riffet, J. Contreras-García, J. Carrasco and M. Calatayud, J. Phys. Chem. C, 2016, 120, 4259–4265 CAS.
- J. Carrasco, J. Phys. Chem. C, 2014, 118, 19599–19607 CAS.
- V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 13921–13928 RSC.
- G. S. Gautam, P. Canepa, W. D. Richards, R. Malik and G. Ceder, Nano Lett., 2016, 16, 2426–2431 CrossRef PubMed.
- G. S. Gautam, P. Canepa, A. Abdellahi, A. Urban, R. Malik and G. Ceder, Chem. Mater., 2015, 27, 3733–3742 CrossRef.
- Z. Rong, R. Malik, P. Canepa, G. S. Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Chem. Mater., 2015, 27, 6016–6021 CrossRef CAS.
- G. S. Gautam, P. Canepa, R. Malik, M. Liu, K. Persson and G. Ceder, Chem. Commun., 2015, 51, 13619–13622 RSC.
- B. Zhou, H. Shi, R. Cao, X. Zhang and Z. Jiang, Phys. Chem. Chem. Phys., 2014, 16, 18578–18585 RSC.
- S. Lee, I. N. Ivanov, J. K. Keum and H. N. Lee, Sci. Rep., 2016, 6, 19621 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- D. Wang, L.-M. Liu, S.-J. Zhao, B.-H. Li, H. Liu and X.-F. Lang, Phys. Chem. Chem. Phys., 2013, 15, 9075–9083 RSC.
- M. K. Aydinol, A. F. Kohan and G. Ceder, J. Power Sources, 1997, 68, 664–668 CrossRef CAS.
- R. Enjalbert and J. Galy, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 1467–1469 CrossRef.
- C. Leroux, G. Nihoul and G. Van Tendeloo, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 5111–5121 CrossRef CAS.
- W. Wang, B. Jiang, W. Xiong, H. Sun, Z. Lin, L. Hu, J. Tu, J. Hou, H. Zhu and S. Jiao, Sci. Rep., 2013, 3, 3383 Search PubMed.
- D. Panduwinata and J. D. Gale, J. Mater. Chem., 2009, 19, 3931–3940 RSC.
- A. Moretti, F. Maroni, F. Nobili and S. Passerini, J. Power Sources, 2015, 293, 1068–1072 CrossRef CAS.
- J. Shao, X. Li, Z. Wan, L. Zhang, Y. Ding, L. Zhang, Q. Qu and H. Zheng, ACS Appl. Mater. Interfaces, 2013, 5, 7671–7675 CAS.
- Q. An, Y. Li, H. D. Yoo, S. Chen, Q. Ru, L. Mai and Y. Yao, Nano Energy, 2015, 18, 265–272 CrossRef CAS.
- W. H. Wan, Q. F. Zhang, Y. Cui and E. G. Wang, J. Phys.: Condens. Matter, 2010, 22, 415501 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02474f |
| This journal is © The Royal Society of Chemistry 2017 |