Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Powder metallurgically synthesized Cu12Sb4S13 tetrahedrites: phase transition and high thermoelectricity
Fu-Hua Sun,
Chao-Feng Wu,
Zhiliang Li,
Yu Pan,
Asfandiyar,
Jinfeng Dong and
Jing-Feng Li *
*
State Key Laboratory of New Ceramics and Fine Processing, School of Materials Science and Engineering, Tsinghua University, Beijing 100084, P. R. China. E-mail: jingfeng@mail.tsinghua.edu.cn; Fax: +86 10 62784845; Tel: +86 10 62771160
First published on 29th March 2017
Abstract
Cu12Sb4S13 tetrahedrite with intrinsically low lattice thermal conductivity has been identified as a promising thermoelectric material with earth-abundant and environmental-friendly resource, but as a natural mineral its synthesis process has not been established. This work studied a powder metallurgical process combining mechanical alloying (MA) and spark plasma sintering (SPS) to synthesize Cu12Sb4S13−x (x = 0, 0.1, 0.2, 0.3 and 0.4) compounds. It is found that single-phased Cu12Sb4S13−x bulks could be synthesized by the MA-SPS process, but tended to become powdered naturally in air at room temperature. Interestingly, this weathering-like phenomenon could be effectively suppressed when the MA-SPS process was repeated. Consequently, a high ZT value of up to 0.65 at 723 K was achieved at a nominal composition of Cu12Sb4S12.7, which is close to the best value of 0.70 obtained in Cu12Sb4S13 tetrahedrites prepared by the melting method, although the present process is more simple and cost-effective. In addition, in this study temperature-dependent phase transitions were investigated to explore the reasons for the weathering-like phenomenon observed in synthetic Cu12Sb4S13 tetrahedrites.
Introduction
Recently developed thermoelectric (TE) materials will offer new opportunities to efficiently and economically recover waste heat sources from industrial applications and vehicles using highly reliable and relatively passive systems that produce no noise and vibrations, have rapid response times, or allow for remote operation.1–3 It is well known that thermoelectric efficiency is dominated by the dimensionless figure of merit defined as ZT = (S2σ/κ)T, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the working temperature in Kelvin.4,5 There are two different strategies to further promote thermoelectric applications: increasing the energy conversion efficiency by raising ZT, and/or reducing the cost of the devices. For the ZT enhancement, one effective method is to improve the power factor (PF), S2σ, which has been achieved through regulating the convergence of the electronic band structure, resonance levels, invisible dopants, etc., and the other is to decrease the thermal conductivity by scattering the long wavelength heat-carrying phonons and/or using energy filtering effects of introduced nanoinclusions.6,7 Great progress has been made in PbTe-based TE materials with a record ZT reaching 2.2 at 923 K.8 However, tellurium resources are very limited, so the search for Te-free and/or Pb-free materials has drawn increasing attention in the thermoelectric research community worldwide9–11 and found a niche in high TE performance, i.e., the highest ZT value of 2.6 at 923 K for SnSe single crystals.12Recently, interest has been concentrated on Cu–Sb–S ternary compounds based on Cu12Sb4S13 compositions, which not only meet the requirements of constitution elements with cost-effective merit, but also offer the potential of promising TE materials due to their low lattice thermal conductivity (<0.5 W m−1 K−1 in the entire testing temperature range). Cu12Sb4S13 presents a chemical formula of (Cu12d)12(Cu12e)12(Sb8c)8(S2a)2(S24g)24 in one crystal cell. As theoretically predicted, Cu12e site atoms behave as rattlers based on the Sb(CuS3)Sb triangular bipyramid host frameworks in Cu12Sb4S13 thermoelectrics, which scatter the low-frequency large-amplitude vibration phonons, so as to reduce the thermal conductivity. Simultaneously, the electrical conductivity can be enhanced because of the weakened Cu–Sb bonding energy.13 Given the complex and special Cu–Sb–S crystal structure and low thermal conductivity, a range of single- or co-substituted synthetic tetrahedrite compounds have already been investigated for their relatively high ZT values at middle temperatures, such as 0.7 for Cu10.5Ni1.5Sb4S13 at 665 K,14 1.13 for Cu11MnSb4S13 at 575 K,15 0.98 for Cu11.5Co0.5Sb4S13 at 673 K,16 0.8 for Cu12Sb3.2Te0.8S13 at 665 K,17, 0.8 for Cu11.18Co0.82Sb3.59Te0.41S13 at 673 K,18 etc. However, often the tetrahedrite materials were synthesized by a direct melting reaction combining subsequent heat-treatments, which takes several weeks to obtain the final samples. Lu and Barbier et al.19,20 tried a synthesis using spark plasma sintering (SPS), but only a single phase was obtained in Cu12Sb4S13 with a certain amount of substitution elements like As, Hg and Ag, or using natural minerals as a “seed matrix”.
In this work, we found that high phase-purity Cu12Sb4S13 compounds could be synthesized by repeating mechanical alloying (rMA) and SPS. The phase structure and thermal stability of the synthesized Cu12Sb4S12.7 prepared by MA-SPS and rMA-SPS were also investigated at working temperatures from room temperature to 723 K. It is noted that the coexistence of second phase structures in the parent Cu12Sb4S13, introducing boundaries, interfaces and lattice mismatch, can coordinate the electrical and thermal conductivity, leading to the enhanced thermoelectric property of tetrahedrite compounds. This work validated that single-phase thermoelectric p-type tetrahedrites can be synthesized by a facile rMA-SPS process.
Experimental section
Chemicals and samples preparation
Cu (99.9%) powder and Sb (99.99%) and S (99.99%) shots were mixed according to the nominal compositions of Cu12Sb4S13−x (x = 0, 0.1, 0.2, 0.3 and 0.4) in a dry argon-filled glove box, and charged to a stainless steel jar with balls made of the same materials. Then the sealed jar was set on a planetary ball mill and conducted at 450 rpm for 10 hours for the MA synthesis of compound powders. The MA-derived powders were subsequently put into a graphite die and sintered by SPS at 723 K in vacuum for 10 min under an axial pressure of 50 MPa, which was then cooled down to room temperature at a rate of 10 K min−1. The resultant samples were crushed to powders and consolidated again by SPS at 573 K for 10 min under 100 MPa. The relative densities of all samples were above 98% and 86% after the first and repeated SPS processes, respectively.Structural and thermoelectric characterization
The phase structures of the tetrahedrite samples were analyzed by X-ray diffraction (XRD) on a Bruker D8 Advance diffractometer equipped with a Ge (111) monochromator using Cu Kα radiation (λ = 1.5418 Å). The data were collected at a rate of 4 degree per minute over the angular range 15° ≤ 2θ ≤ 65° with a step increment of 0.02°. The morphology was observed by field emission scanning electron microscopy (SEM, ZEISS Gemini 2, Germany). The phase transition, thermal stability and specific heat capacity were investigated by differential scanning calorimetry (DSC) on a Netsch STA449 apparatus (Germany), and characterized under an argon flow from room temperature to 723 K with a heating rate of 10 K min−1 in the closed-aluminum crucibles.To investigate the thermoelectric properties, bar- and disk-shaped specimens were cut from the SPSed pellets and polished with fine sandpaper. The Seebeck coefficient and electrical resistivity were measured simultaneously by a Seebeck coefficient/electrical resistance measuring system (ZEM-2, Ulvac-Riko, Japan), under partial helium pressure at temperatures from 323 K to 723 K. The thermal diffusivity (D) was measured in the same temperature range using the laser flash model (TC-9000, Ulvac-Riko, Japan). Then, the thermal conductivity (κ) was calculated by κ = DρCp, where ρ is the density, which was measured by the Archimedes method.
Results and discussion
Phase and macrostructure
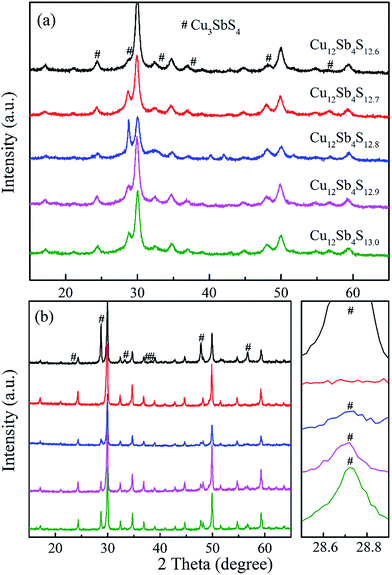
The phase structure data of Cu12Sb4S13−x (x = 0, 0.1, 0.2, 0.3 and 0.4) bulks were recorded at room temperature by X-ray diffraction. As shown in Fig. 1a, although the expected tetrahedrite crystalline phase (space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m, PDF#42-0561) was obtained by a one-step MA process, considerably strong peaks of second phase Cu3SbS4 (PDF#35-0581) were detected, which could not be suppressed even when adjusting the S content. However, as shown in Fig. 1b, the samples have higher phase purity after SPS treatment due to the additional heat treatment. As shown by the enlarged peaks around 2θ = 28.7°, the peaks of the impurity phase Cu3SbS4 weakened with decreasing S content, resulting in a nearly single phase at x = 0.3. These results suggest that single-phased tetrahedrite can be synthesized by MA-SPS. It should be pointed out that second phase Cu3SbS4 was probably formed during the cooling process, which was well confirmed by the following DSC/TG experiments. In fact, it was reported that synthetic tetrahedrites tend to decompose as compared with the natural tetrahedrite mineral, which has been significantly demonstrated in a previous publication.21
3m, PDF#42-0561) was obtained by a one-step MA process, considerably strong peaks of second phase Cu3SbS4 (PDF#35-0581) were detected, which could not be suppressed even when adjusting the S content. However, as shown in Fig. 1b, the samples have higher phase purity after SPS treatment due to the additional heat treatment. As shown by the enlarged peaks around 2θ = 28.7°, the peaks of the impurity phase Cu3SbS4 weakened with decreasing S content, resulting in a nearly single phase at x = 0.3. These results suggest that single-phased tetrahedrite can be synthesized by MA-SPS. It should be pointed out that second phase Cu3SbS4 was probably formed during the cooling process, which was well confirmed by the following DSC/TG experiments. In fact, it was reported that synthetic tetrahedrites tend to decompose as compared with the natural tetrahedrite mineral, which has been significantly demonstrated in a previous publication.21
It is interesting that as-sintered Cu12Sb4S13−x samples presented poor mechanical properties and easily broke into small pieces in air at room temperature, as seen in Fig. 2. The as-sintered bulks (Fig. 2a) would naturally degrade from the outmost surfaces, transforming into rougher appearances and gradually cracking when placed in laboratory conditions for 0 h to 36 h (Fig. 2b and c), and finally decomposing after 120 h (Fig. 2d). This phenomenon might be explained by a temperature-dependent phase transition as discussed later.
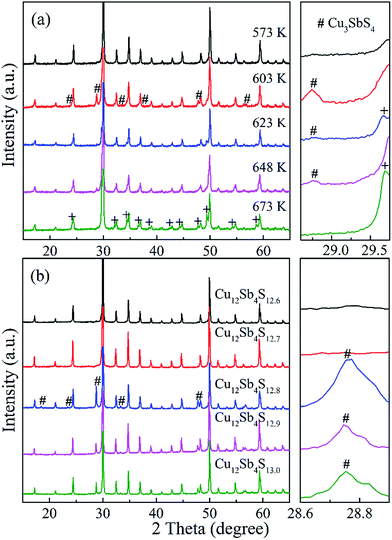
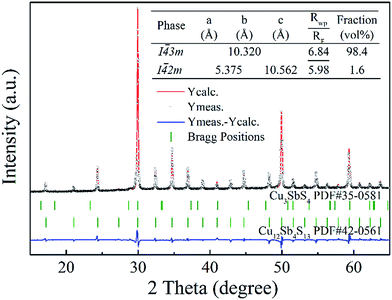
With a motivation to further synthesize robust bulks and improve the phase purity of the Cu12Sb4S13−x samples, a simple repeated MA-SPS method was applied to the synthesis aiming to obtain high thermoelectric property. Fig. 3a shows the XRD patterns of the Cu12Sb4S12.7 sample using the rMA-SPS process at different temperatures ranging from 573 K to 673 K. It was found that the impurity peaks of the Cu3SbS4 crystalline phase weakened or even disappeared as the temperature increased. However, if the temperature exceeds 623 K, the tetrahedrites slightly deviate from the nominal Cu12Sb4S13 compositions (marked with a plus sign + in Fig. 3), which implies volatilization of sulphur at higher temperatures. Also, considering that the synthesis of the x = 0.7 compound has been completed in the first sintering process, we decreased the SPS temperature to 573 K at the repeated step, which can keep the phase purity of rMA-SPS samples by avoiding the further volatilization of sulphur. Additionally, the pressure was accordingly raised to 100 MPa to compensate for the sacrificed sintering driving force due to the lowered SPS temperature. As shown in Fig. 3b, high-quality samples were obtained with phase purity and crystallinity, where no peaks could be detected in the x = 0.3 and 0.4 samples even when enlarging the range around 2θ = 28.7°, as done in Fig. 1b. An estimation of the phase purity for the Cu12Sb4S12.7 bulk was conducted using the Maud software and the Rietveld method. As shown in Fig. 4, a nearly single-phased sample was obtained with only 1.6 volume percent of Cu3SbS4 as a secondary phase, which illustrates well that the rMA-SPS method is a rapid and facile process to fabricate Cu12Sb4S13 tetrahedrites by suppressing the formation of the impurity phase.
Thermal stability and microstructure
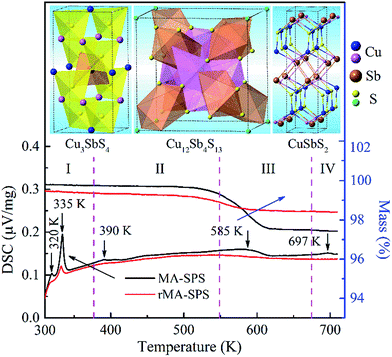
As mentioned above, all the MA-SPS samples easily broke into small pieces at room temperature in air. Therefore, it is necessary to further study the thermal stability through DSC/TG measurement. The DSC curves of the Cu12Sb4S12.7 compound were characterized by four types of exothermic peaks at temperatures from room temperature to 723 K, as shown in the bottom panel of Fig. 5, with the crystal structures corresponding to the phase transitions displayed in the top panel of Fig. 5. Thus, the evolution of the crystal structures here can be divided into four steps.22 (I) At low temperature, the two sharp peaks at 320 K and 335 K for the MA-SPS and rMA-SPS samples can be attributed to the phase decomposition of Cu12Sb4S13 into Cu3SbS4 and CuSbS2. (II) The weak exothermic peak around 390 K was characterized as the interchange of Cu3SbS4 and Cu1.5Sb0.5S2. (III) The broad peak revealed the phase transition from Cu3SbS4 or Cu1.5Sb0.5S2 to Cu12Sb4S13 at a medium temperature of 585 K, which is also consistent with the large weight loss in the TG curves. (IV) At high temperatures, a small broad peak at 697 K was observed for the MA-SPS sample, resulting from the phase decomposition of Cu12Sb4S13 to CuSbS2, and the sulphur probably volatilized when the temperature exceeded 670 K. It is noted that no exothermic peaks were detected for the rMA-SPS sample above 350 K, which indicates the absence of a phase transition at moderate temperatures, suggesting that the thermal stability is enhanced through repeated MA-SPS processing. There are big differences among Cu3SbS4 (tetragonal, a = b = 5.385 Å and c = 10.748 Å), Cu12Sb4S13 (cubic) and CuSbS2 (orthogonal, PDF#00-44-1417, a = 14.501 Å, b = 6.019 Å and c = 3.797 Å),23 so the internal stress accumulated in the sintering process is gradually released as the temperature declines, then leading to the fragmentation of the as-sintered samples, as seen above in Fig. 2.As analyzed above, for the rMA-SPS samples the phase transition from Cu12Sb4S13 to Cu3SbS4/CuSbS2 can also be detected at low temperatures after repeating the MA and SPS process, and it maintained the robust bulks for a quite long time in air at room temperature, even when placed under laboratory conditions (Fig. 2e and f). It is presumed that the micropores among the grains (which have a large amount of crystal defects, as shown in Fig. 6b) might absorb the expansion to some extent, so that the weathering-like phenomenon did not occur in the samples after repeated MA-SPS. In fact, as mentioned above, the relative density became lower after repeating MA-SPS.
 | ||
| Fig. 6 The SEM images for the Cu12Sb4S12.7 sample using different process of (a) MA-SPS and (b) rMA-SPS at temperature of 723 K and 573 K, respectively. | ||
Electrical transport property
Fig. 7a shows the temperature-dependent electrical conductivity (σ) of the Cu12Sb4S13−x samples synthesized by the rMA-SPS method. Their σ values present the same trend, in which they firstly increase until the mid-temperature region and then turns to a decrease for all of the compounds, indicating that the properties change with increasing temperature from those of nondegenerate semiconductors to metal-like materials, as reported by Barbier, Chetty and Lu et al.16,22,24 Moreover, the electrical conductivity increases with the decreasing sulphur element concentration at all testing temperatures and reaches a maximum value (5.91 × 104 S m−1) for the Cu12Sb4S12.6 sample at 573 K.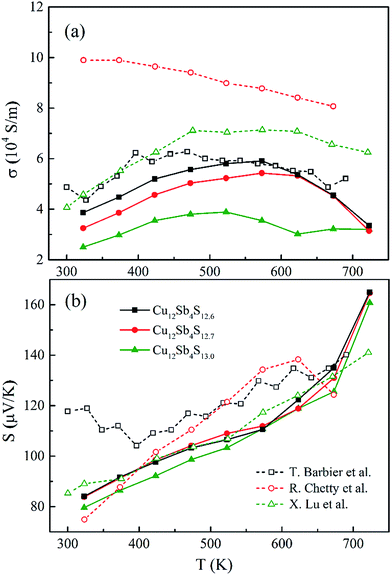 | ||
| Fig. 7 (a) The electrical conductivity and (b) Seebeck coefficient of the Cu12Sb4S13−x (x = 0, 0.3 and 0.4) samples prepared by rMA-SPS, as compared with those of the reported literature16,22,24 (open-symbol dashed lines). | ||
As for tetrahedrite compounds, all the carriers would be activated by the thermal energy with increasing temperature (<500 K), but will be suppressed by the carrier-phonon coupling scattering at high temperatures, which is associated with the impurity scattering-induced Anderson localization25 and the hole-trapping effects for metal-like heavily doped p-type semiconductors. To further investigate the origin and evolution of the electric conductivity, the bonding state of the S atom should be taken into account. The triangular bipyramidal Sb(CuS3)Sb structure was treated as the fundamental unit in the Cu12Sb4S13 cell, and an “extra” S2− 3p4 on the octahedral 2a site provides two unfilled holes per formula unit, which produces a sharp peak at the top of the hybridized valence band (VB).13 From this fact, the lack of sulphur element in stoichiometric Cu12Sb4S13 (from 13.0 to 12.6 atoms) should lead to a decrease in the electrical conductivity (the hole carriers are decreasing), but opposite results were obtained in this work (as shown in Fig. 7a). It might be interpreted that the impurity phase of Cu3SbS4 and large crystal defects largely weakened the carrier-phonon coupling effects. It is also confirmed in the CuFeS2 compound that the electrical conductivity is inversely proportional to sulphur concentration, as reported in our previous research.26
In order to obtain a large Seebeck coefficient, the position of EF should be close to the top of the VB, where hybridization of the Cu 3d and S 3p orbitals can be performed. However, the Fermi level lies in the VB due to the impurity- and defects-induced scattering effect, which could lead to the slightly lower S values than those reported,16,22,24 as shown in Fig. 7b. It was also confirmed that the S values decreased with copper deficiency in the CuFeS2 thermoelectric material, as reported by D. Berthebaud et al.,27 thus the measured Seebeck coefficients range from 80 μV K−1 at 323 K to 165 μV K−1 at 723 K. The limited difference for all samples can be explained by using a model for degenerate semiconductors:28
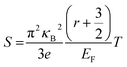 | (1) |
Thermal transport property and ZT
As reported previously,14,29 the heat capacity could be described using one Debye lattice and three Einstein oscillators:
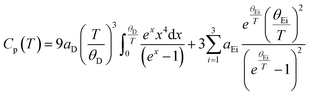 | (2) |
 | ||
| Fig. 8 (a) Temperature dependence of measured and calculated heat capacity (Cp) together with that reported by Heo et al.15 and (b) the relationship between the Lorenz number and temperature for rMA-SPS Cu12Sb4S13−x (x = 0, 0.3 and 0.4) samples including that by Chetty et al.16 | ||
However, the measured Cp values are larger than the calculated results, and also larger than those reported in ref. 15 at temperatures from 323 K to 723 K. This model approximation likely matches the experimental values for the low temperature range from 2 K to 400 K, but underestimates the heat capacity at elevated temperatures due to the perpendicular vibration of the triangular Cu12e site atoms overlapping the Debye parabolic contribution at low energies and/or oversimplifying the three Einstein oscillators model. Additionally, the two short sharp peaks show the phase transition from Cu12Sb4S13 to Cu3SbS4 and CuSbS2 at a low temperature of ca. 330 K, which is consistent with the DSC/TG measurement in Fig. 5. Thus, in this work the Cp value of 0.50 J g−1 K−1 was used as the mean heat capacity for calculating the thermal conductivity, and the results are shown in Fig. 9a.
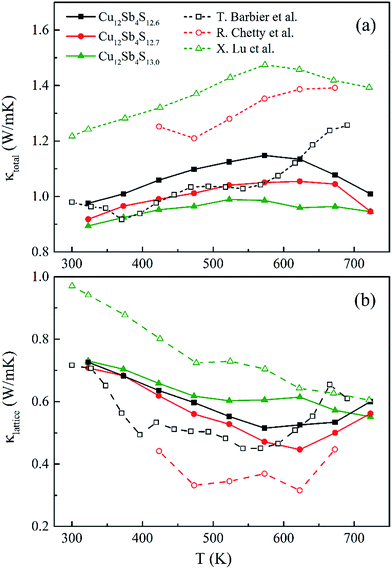 | ||
| Fig. 9 (a) The total (κtotal) and (b) lattice (κlattice) thermal conductivity as a function of temperature for rMA-SPS Cu12Sb4S13−x (x = 0, 0.3 and 0.4) samples, compared with the reported data16,22,24 (open-symbol dashed line). | ||
The total thermal conductivity (κtotal) is quite low, below 1.2 W m−1 K−1, for Cu12Sb4S13−x samples at all temperatures (from 323 K to 723 K) in Fig. 9a, and increases slightly with increasing temperature, then begins to fall above a certain temperature as observed by Lu et al.24 The present samples show lower thermal conductivity than that reported by Lu and Chetty,16,24 and are close to the values reported by Barbier.22 The reduced thermal conductivity resulted from the structural and chemical characteristics of the Cu12Sb4S13−x compounds. The S-deficiency induced carrier defects, the impurities and grain boundary-induced Anderson localization (coupling to other atoms), the Cu3SbS4 phase in Fig. 3b, and the numerous grain boundaries in Fig. 6b can reduce the carrier transport property in the rMA-SPS-processed tetrahedrite compounds, which leads to the low carrier thermal conductivity. This was well illustrated by the results of the lattice thermal conductivity (κlattice). As for the κlattice, it was evaluated by subtracting the carrier contribution (κcarrier) from the κtotal values. The κcarrier values can be estimated by the Wiedemann–Franz relation, κcarrier = LσT (where σ and T are the electrical conductivity and absolute temperature, respectively), in which the value of the Lorenz number (L) can be obtained through an assumption of transport dominated by acoustic scattering, and a single parabolic band using the following formula:16
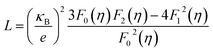 | (3) |
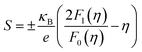 | (4) |
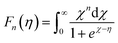 | (5) |
The calculated L values range from 1.70 to 2.05 × 10−8 W Ω K−2 for the rMA-SPS-ed Cu12Sb4S13−x (x = 0, 0.3 and 0.4) samples, as shown in Fig. 8b, which is well consistent with that reported by Chetty et al.16 and less than the metallic limit of 2.45 × 10−8 W Ω K−2. Using the calculated L values, a relatively lower κlattice was obtained in Fig. 9b, which is similar to that reported by Barbier.22 The lowest κlattice reaches 0.45 W mK−1 for the Cu12Sb4S12.7 sample at 623 K.
The ZT values of the Cu12Sb4S13−x samples increase with increasing temperature, as shown in Fig. 10a, and reach the maximum of 0.65 at 723 K for the x = 0.3 sample, which is larger than that of the stoichiometric composition (Cu12Sb4S13) and is almost equal to the best data (0.7, in Fig. 10b) reported for the pure tetrahedrites synthesized by the melting process.16 Compared with the conventional melting method, the repeated MA-SPS process is a facile and cost-effective way for directly synthesizing high purity-phase tetrahedrites. Additionally, the thermal conductivity is reduced by the defect-induced (grain boundary and S deficiency) scattering effect, which has more contribution to the high ZT values obtained in the powder-processed tetrahedrite materials.
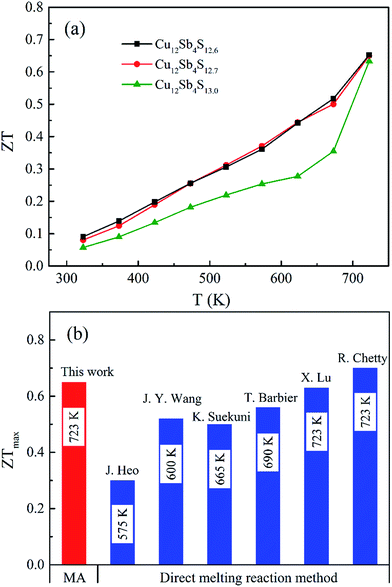 | ||
| Fig. 10 (a) Thermoelectric figure of merit as a function of the temperature for Cu12Sb4S13−x (x = 0, 0.3 and 0.4) samples. (b) The maximum ZT values of the pure-phase tetrahedrites synthesized by the rMA-SPS method in this work and previous reports (using melting and SPS processes)14–16,22,24,30 at their optimal temperatures. | ||
Conclusions
Natural mineral tetrahedrite thermoelectric materials can be synthesized by combining mechanical alloying (MA) and spark plasma sintering (SPS), but it was found that the synthetic Cu12Sb4S13−x bulks tended to become small particles naturally in air at room temperature. Nevertheless, it is possible to suppress the weathering-like phenomenon by simply repeating the MA and SPS processes. Such a process modification effectively facilitates the crystallinity of the parent phase as well as suppresses the impurity phase (like as Cu3SbS4). The DSC/TG measurements revealed that the weathering-like phenomenon was due to a series of phase transitions from Cu12Sb4S13 to Cu3SbS4/CuSbS2/Cu1.5Sb0.5S2. The robust Cu12Sb4S12.7 compound showed a large ZT value, 0.65 at 723 K, because of the largely reduced thermal conductivity. Considering the low-cost and earth-abundant properties of copper and sulphur elements, this study should afford great attention to the synthesis of p-type tetrahedrite TE materials by simple processes.Acknowledgements
This work was supported by the National Basic Research Program of China (Grant No. 2013CB632503) and the National Natural Science Foundation (No. 51172121, 11474176).Notes and references
- S. N. Girard, J. Q. He, C. P. Li, S. Moses, G. Y. Wang, C. Uher, V. P. Dravid and M. G. Kanatzidis, Nano Lett., 2010, 10, 2825–2831 CrossRef CAS PubMed.
- K. Biswas, J. He, Q. Zhang, G. Wang, C. Uher, V. P. Dravid and M. G. Kanatzidis, Nat. Chem., 2011, 3, 160–166 CrossRef CAS PubMed.
- L. G. Chen, F. K. Meng and F. R. Sun, Sci. China: Technol. Sci., 2016, 59, 442–455 CrossRef.
- K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418 CrossRef CAS PubMed.
- Q. H. Zhang, X. Ai, L. J. Wang, Y. X. Chang, W. Luo, W. Jiang and L. D. Chen, Adv. Funct. Mater., 2015, 25, 966–976 CrossRef CAS.
- A. M. Dehkordi, M. Zebarjadi, J. He and T. M. Tritt, Mater. Sci. Eng., R, 2015, 97, 1–22 CrossRef.
- P. Pichanusakorn and P. Bandaru, Mater. Sci. Eng., R, 2010, 67, 19–63 CrossRef.
- H. J. Wu, L.-D. Zhao, F. S. Zheng, D. Wu, Y. L. Pei, X. Tong, M. G. Kanatzidis and J. Q. He, Nat. Commun., 2014, 5, 4515 CAS.
- J.-F. Li, W.-S. Liu, L.-D. Zhao and M. Zhou, NPG Asia Mater., 2010, 2, 152–158 CrossRef.
- W. G. Zeier, A. Zevalkink, Z. M. Gibbs, G. Hautier, M. G. Kanatzidis and G. J. Snyder, Angew. Chem., Int. Ed., 2016, 55, 6826–6841 CrossRef CAS PubMed.
- T.-R. Wei, C.-F. Wu, W. Sun, Y. Pan and J.-F. Li, RSC Adv., 2015, 5, 42848–42854 RSC.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377 CrossRef CAS PubMed.
- W. Lai, Y. X. Wang, D. T. Morelli and X. Lu, Adv. Funct. Mater., 2015, 25, 3648–3657 CrossRef CAS.
- K. Suekuni, K. Tsuruta, M. Kunii, H. Nishiate, E. Nishibori, S. Maki, M. Ohta, A. Yamamoto and M. Koyano, J. Appl. Phys., 2013, 113, 043712 CrossRef.
- J. Heo, G. Laurita, S. Muir, M. A. Subramanian and D. A. Keszler, Chem. Mater., 2014, 26, 2047–2051 CrossRef CAS.
- R. Chetty, A. Bali, M. H. Naik, G. Rogl, P. Rogl, M. Jain, S. Suwas and R. C. Mallik, Acta Mater., 2015, 100, 266–274 CrossRef CAS.
- Y. Bouyrie, C. Candolfi, V. Ohorodniichuk, B. Malaman, A. Dauscher, J. Tobola and B. Lenoir, J. Mater. Chem. C, 2015, 3, 10476–10487 RSC.
- Y. Bouyrie, S. Sassi, C. Candolfi, J. B. Vaney, A. Dauscher and B. Lenoir, Dalton Trans., 2016, 45, 7294–7302 RSC.
- X. Lu and D. T. Morelli, Phys. Chem. Chem. Phys., 2013, 15, 5762–5766 RSC.
- T. Barbier, S. Rollin-Martinet, P. Lemoine, F. Gascoin, A. Kaltzoglou, P. Vaqueiro, A. V. Powell and E. Guilmeau, J. Am. Ceram. Soc., 2016, 99, 51–56 CrossRef CAS.
- X. Lu, D. T. Morelli, Y. Xia and V. Ozolins, Chem. Mater., 2015, 27, 408–413 CrossRef CAS.
- T. Barbier, P. Lemoine, S. Gascoin, O. I. Lebedev, A. Kaltzoglou, P. Vaqueiro, A. V. Powell, R. I. Smith and E. Guilmeau, J. Alloys Compd., 2015, 634, 253–262 CrossRef CAS.
- W. Hofmann, Z. Kristallogr., 1933, 84, 177–203 CAS.
- X. Lu, D. T. Morelli, Y. X. Wang, W. Lai, Y. Xia and V. Ozolins, Chem. Mater., 2016, 28, 1781–1786 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1958, 109, 1492–1505 CrossRef CAS.
- J.-H. Li, Q. Tan and J.-F. Li, J. Alloys Compd., 2013, 551, 143–149 CrossRef CAS.
- D. Berthebaud, O. I. Lebedev and A. Maignan, J. Materiomics, 2015, 1, 68–74 CrossRef.
- H. J. Goldsmid, J. Electron. Mater., 2013, 42, 1482–1489 CrossRef CAS.
- E. Lara-Curzio, A. F. May, O. Delaire, M. A. McGuire, X. Lu, C. Y. Liu, E. D. Case and D. T. Morelli, J. Appl. Phys., 2014, 115, 193515 CrossRef.
- J. Y. Wang, M. Gu, Y. F. Bao, X. Y. Li and L. D. Chen, J. Electron. Mater., 2016, 45, 2274–2277 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |