Open Access Article
Open Access ArticleRenewable DNA seesaw logic circuits enabled by photoregulation of toehold-mediated strand displacement†
Xin Song *a,
Abeer Eshra
*a,
Abeer Eshra bc,
Chris Dwyer
bc,
Chris Dwyer ab and
John Reif
ab and
John Reif ab
ab
aDepartment of Electrical and Computer Engineering, Duke University, Durham, NC, USA. E-mail: xin.song@duke.edu
bDepartment of Computer Science, Duke University, Durham, NC, USA
cDepartment of Computer Science and Engineering, Faculty of Electronic Eng., Menoufia University, Menouf, Egypt
First published on 31st May 2017
Abstract
An important achievement in the field of DNA-based computation has been the development of experimental protocols for evaluation of Boolean logic circuits. These protocols for DNA circuits generally take as inputs single-stranded DNA molecules that encode Boolean values, and via a series of DNA hybridization reactions then release ssDNA strands to indicate Boolean output values. However, most of these DNA circuit protocols are use-once only, and there remains the major challenge of designing DNA circuits to be renewable for use with multiple sets of inputs. Prior proposed schemes to make DNA gates renewable suffered from multiple problems, including waste accumulation, signal restoration, noise tolerance, and limited scalable complexity. In this work, we propose a scalable design and in silico verifications for photoregulated renewable DNA seesaw logic circuits, which after processing a given set of inputs, can be repeatedly reset to reliably process other distinct inputs. To achieve renewability, specific toeholds in the system are labeled with photoresponsive molecules such as azobenzene to modulate the effective rate constants of toehold-mediated strand displacement (TMSD) reactions. Our proposed design strategy of leveraging the collective effect of TMSD and azobenzene-mediated dehybridization may provide new perspectives on achieving synchronized and localized control of DNA hybridizations in complex and scalable reaction networks efficiently and economically. Various devices such as molecular walkers and motors could potentially be engineered reusable, be simulated and subsequently implemented using our simplified design strategy.
1. Introduction
Nucleic acids have been widely recognized as a leading material for nanoscale engineering.1–5 High predictability and programmability6 of nucleic acid reactions have initiated fast development in the field of molecular self-assembly and computing using deoxyribonucleic acids (DNA) and ribonucleic acids (RNA). In recent years, various static7–12 and dynamic nanostructures4,5 have been designed and demonstrated experimentally based on well-understood thermodynamic parameters of DNA hybridization13–25 and relatively simple sets of design metrics. Representative works include successful implementations of DNA walkers26–30 and motors,28,31–33 molecular beacon,34 complex-shaped and functional DNA origami structures.35–37 Furthermore, owing to the naturally biocompatible material, DNA-enabled nanotechnology has expanded its applications to the realm of bio-diagnostics and monitoring,38–41 drug delivery,11,42–46 and cancer therapeutics.47–49Among prior excellent work on functional nucleic acid devices, significant research has been devoted to DNA computing and molecular-scale circuit implementations. By virtue of the highly specific Watson–Crick base pairing6 and the theoretical 0.34 nm addressability,18 DNA could be leveraged as a superior natural computing substrate to pack high density of information into tiny space and provide functionality in a programmable manner at molecular scale. To date, advances on the study of nucleic acids Chemical Reaction Networks (CRNs)50 have facilitated designs and wet lab implementations of a variety of logic circuit devices made with DNA.51–61 Many of these implementations are enzyme-free and take advantage of a well-studied DNA reaction mechanism called Toehold-Mediated Strand Displacement (TMSD),5,31,62 where a short single-stranded DNA (ssDNA) toehold is first hybridized to initiate a subsequent more extensive hybridization reaction.
An example of utilizing TMSD is the remarkable work by Qian and Winfree63 on DNA seesaw circuits, which provides a simple yet robust approach to systematically building enzyme-free catalytic DNA logic architectures. These architectures are scalable, noise tolerant and reasonably fast.64 Recently published research on DNA seesaw technology explored designs and simulations for more complicated constructions such as combinational circuit units and application-specific circuit realizations.65–67 However, not much advances have yet emerged to address the existing problems and challenges with DNA seesaw technology itself. To our knowledge, the non-reusability of circuit components has been a major limiting factor that inhibits further development and applications of DNA seesaw technology beyond what has been demonstrated in literature. Although the seesaw reaction is reversible in its essence, the thresholding reaction and catalytic process of circuit operations inevitably lead to irreversible consumption of seesaw gates. Such limitation makes it difficult to develop sequential logic and memory devices using the seesaw implementation.
1.1 Prior work on renewable DNA logic gates and circuits
A DNA circuit is renewable if after processing a given set of inputs, the circuit can be repeatedly reset to reliably process other distinct inputs. Prior work on renewable DNA logic gates has mostly been focused on achieving asynchronous and time-responsive circuit behavior. This is a desirable feature for DNA computing especially in the realm of therapeutics. A gate is time-responsive if its output varies appropriately with dynamic changes of its inputs. Because the gate output continuously reflects change in inputs, molecular monitoring of biological signals could be achieved using such time-responsive DNA logic gates. Goel and Ibrahimi68 proposed a design of time-responsive DNA logic gates using restriction enzymes. However, such implementation is constrained by the accumulation of wastes and the requirement of identifying specific restriction enzymes to achieve described circuit functionality. Chiniforooshan et al.58 presented a theoretical design of enzyme-free DNA logic gates with focuses on scalability, time-responsiveness, and energy efficiency. However, the time-responsiveness is achieved at the cost of fuel being continuously consumed. In addition, the design relies on the addition of ‘signal restoration gate’ on each signal path between gates to maintain correct digital logic levels. As a result, the implementation suffers from unavoidable complexities due to the involved non-trivial CRNs for constructing signal restoration gates. Genot et al.69 proposed a cleaner design of time-responsive and reversible DNA logic circuits by using TMSD and DNA hairpins. However, the design faces the drawback of being non-catalytic, which limits the gate performance in terms of signal restoration and noise tolerance. More recently, Garg70 demonstrated successful wet lab implementation of asynchronous time-responsive DNA logic gates. However, on one hand, the design faces the challenge of being non-catalytic, which requires special adjustment of reactant concentrations at different circuit levels to mitigate signal degradation. On the other hand, the renewal process of gates depends on collaborative hybridization reactions between multiple DNA species, thus posing restrictions in terms of sequence design difficulty of assembling gates into desired secondary structures.1.2 Contributions of this work
In this work, we aim to address the problem of ‘irreversible depletion of gate components’ in DNA seesaw circuits for the first time by engineering photoresponsive DNA seesaw gates with modifications on the sticky-ends. We harness the effect of azobenzene photoisomerization on nucleotides as the driving force for modulating the ‘effective toehold length’ during the gate renewal process. As a result, the co-contributing effects of TMSD facilitate the circuit regeneration process by ameliorating the issue with unideal yield of azobenzene-mediated DNA dehybridization reported in prior works.71,72 Our design also provides benefits in reducing leaks of seesaw circuit operations due to spurious toehold binding. This not only helps to solve the leakage problem when seesaw circuits scale up, but also makes the seesaw gate regeneration fast and robust.This work provides various analyses and simulations of the photoregulated renewable seesaw circuits, including:
(i) A novel analysis of the dynamics of hybridization reactions involving trans- and cis-azobenzene labeled oligonucleotides, by quantifying the change in effective lengths of toeholds and branch migration domains.
(ii) Based on well-studied thermodynamics of TMSD and azobenzene-mediated DNA dehybridization, Ordinary Differential Equations (ODEs) are used to model the mass-action kinetics of CRNs involved in the operations of renewable seesaw logic gates. Critical reaction rate constants were calculated and verified based on well-known prior studies.62,64,73
(iii) Development of a formal description of the renewable seesaw gates in Language for Biochemical Systems (LBS).74 The renewable DNA logic gates are implemented and deterministically simulated in the software Visual Genetic Engineering of Living Cells (Visual GEC)75 to provide theoretical verification of the design feasibility.
2. Results and discussion
2.1 Modulating the effective rate constants of TMSD reactions
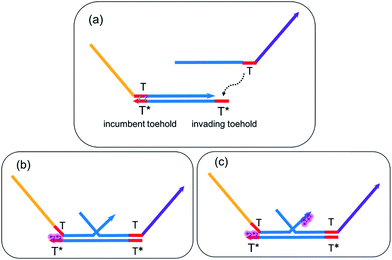
TMSD is a mechanism that facilitates programmable chemical reactions between DNA molecules with fine controllability. Based on well-established principles of DNA hybridization13,14,16,76 and branch migration,77–79 a ssDNA molecule could bind to a double-stranded DNA (dsDNA) complex flanked by a short (3–6 nucleotides) exposed single-stranded sequence called ‘toehold’ or ‘sticky-end’. This toehold is typically the same for all gates, and so is termed ‘universal’. Driving either by standard free energy (i.e. change in base pairings) or entropic free energy (i.e. imbalance of DNA concentrations), the top strand of the dsDNA complex could be displaced either irreversibly or reversibly by the invading ssDNA. DNA seesaw circuits exploit the concept of ‘toehold exchange’,62,80 a special case of TMSD where the dsDNA base strand is flanked on both sides by a toehold of equal length, to reversibly exchange the active toehold from one side to another. All these reactions occur with high precision by taking advantage of the Watson–Crick base pairing specificity and predictable kinetics of the deoxyribose nucleic acids.6 Various factors could affect the dynamics and kinetics of TMSD reactions in reality, for example, temperature, salt composition and concentration, sequence design of DNA molecules, toehold binding energies, etc. For this study, we select DNA sequences verified by Seesaw Compiler63 and Nucleic Acid Package (NUPACK)81 so that any mismatch or undesired secondary structure is eliminated. Under such conditions, we can safely study DNA reactions on the ‘domain’ (consecutive nucleotides on a sequence) level.82 By simply modulating the ‘effective toehold length’, for example, via toehold sequestering51 which limits the rate of toehold hybridization, it is possible to modify the effective rate constants of strand displacement and further initiate the biasing of reaction pathways for circuit regeneration even after the original reactions reach stoichiometric equilibrium.2.2 Understanding the pros and cons of DNA seesaw logic gate implementation
In seesaw circuit, each Boolean value is encoded by a specified range of concentration of a particular ssDNA strand. For example, input is low (i.e. Boolean logic 0) when the concentration is lower than 20 nM and high (i.e. Boolean logic 1) when its concentration exceeds 80 nM but is below a higher bound of 100 nM. A seesaw gate motif is a basic unit of seesaw circuit which executes a single Boolean computation; it takes as inputs one or more ssDNA strands and provides as outputs one or more ssDNA strands. Seesaw gate motifs enable hierarchical abstractions to implement enzyme-free nucleic acid circuits that perform large-scale multi-level digital logic operations.63,64In this study, we adopt the ‘2–2 scheme’ as shown in Fig. 1 for seesaw logic gate implementation, which comprises of two seesaw gate motifs for each functional seesaw logic gate. This scheme supports easy conversion between different digital logic functions by only adjusting the threshold concentration. It is free from threshold crosstalk problems as those present in the ‘1–4 scheme’.63 The first gate motif, called integrating gate, sums up input signal strands. The signal then propagates in the form of a released ssDNA to the next level gate motif, which consists of a threshold complex and an amplifying gate complex. Both complexes have an identical recognition domain (typically approximately 15 nt), but the threshold complex differs in its extended left toehold domain and absence of the right universal toehold domain. This difference facilitates fast DNA strand displacement reaction between the released ssDNA (here we call it ‘invading input strand’ based on naming conventions62) and the threshold complex. The logic function, AND or OR, of the seesaw gate is determined by the concentration of threshold complex. When input level exceeds the threshold, the signal propagation to the amplifying gate is no longer inhibited. With catalytic cycle triggered by fuel strand, sufficient amount of output strand from amplifying gate is released to establish a correct logic level as the circuit output (in the actual seesaw gate implementation, a reporter gate is added to reflect the level of output signal by generating detectable fluorescence). Thresholding and the catalytic cycle are the co-contributing factors of noise resilience and signal restoration that make seesaw logic fast, robust, and reliable for multi-level large-scale circuit implementations.63 Since signals in DNA seesaw circuits are represented by concentrations of corresponding DNA molecules, it is difficult to implement a logic NOT gate due to the indistinguishability between a signal being low versus the absence of the signal. To solve the problem and to be able to implement arbitrary logic functions, DNA seesaw circuits adopt the ‘dual-rail’63,83,84 convention with the downside of approximately doubling the number of required gates for circuit implementation.
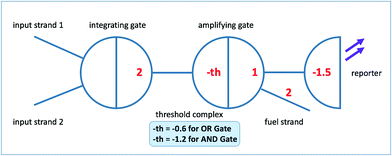 | ||
| Fig. 1 Logic gate implementation based on the ‘2–2 scheme’.63 | ||
According to Qian and Winfree,63 although the seesawing reaction is reversible by the nature of toehold exchange, the significant net change in standard free energy associated with gaining of base pairings during seesaw gate operation leads to irreversible consumption of the threshold complex. For similar reasons, the reporting mechanism also prevents possibility of reforming circuit components including the reporter and the amplifying gate complex. Hence, this poses one of the main limitations of seesaw circuits, which is the irreversible depletion of circuit components. The one-time-use-only nature of seesaw gates presents the largest hurdle of designing and implementing synchronous sequential logic and memory devices using seesaw method.
2.3 Leveraging azobenzene-functionalized oligonucleotides in TMSD reaction networks
One approach to deal with the aforementioned challenge in seesaw circuits is to use azobenzene isomerization to locally initiate and control DNA strand displacement. With azobenzene intercalation at selected positions on DNA strand, the double-helical binding stability could be perturbed by the conformational and polarity change of azobenzene moieties upon photo-isomerization.85 As shown in Fig. 2, an azobenzene molecule consists of a double N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond that links two phenyl functional groups in specific orientations. Azobenzene isomerization is a fast-conformational-change triggered by light irradiation that converts the molecule into one of the two configurations, namely, the trans-form and the cis-form. trans-Isomers refer to the azobenzene molecules whose functional groups are on the opposite side of the N
N bond that links two phenyl functional groups in specific orientations. Azobenzene isomerization is a fast-conformational-change triggered by light irradiation that converts the molecule into one of the two configurations, namely, the trans-form and the cis-form. trans-Isomers refer to the azobenzene molecules whose functional groups are on the opposite side of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, forming a planar structure. cis-Isomers refer to azobenzene molecules whose functional groups are on the same side of the N
N bond, forming a planar structure. cis-Isomers refer to azobenzene molecules whose functional groups are on the same side of the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, forming a non-planar structure. Tethered with trans-form azobenzene isomers, nucleic acids react similarly as unmodified strands in terms of temporal binding and unbinding dynamics. According to experimental evidence,85–87 the melting temperature (Tm) of the modified duplex DNA increases nearly uniformly with increasing number of trans-form azobenzene intercalations. This observed stabilizing effect on the duplex DNA is possibly due to the stacking interactions that lead to favorable enthalpy change between azobenzene trans-isomers and adjacent nucleobases.86,87 Evidently, molecular dynamic simulations and Tm experiments of duplexes have both indicated that the stabilizing effect is sufficient to offset the asymmetric distortion in DNA backbones resulted from the addition of azobenzene residues.88,89 This makes it feasible to use azobenzene as a non-invasive molecular switch for controlling TMSD reactions in DNA seesaw circuits without sacrificing sequence specificity.
N bond, forming a non-planar structure. Tethered with trans-form azobenzene isomers, nucleic acids react similarly as unmodified strands in terms of temporal binding and unbinding dynamics. According to experimental evidence,85–87 the melting temperature (Tm) of the modified duplex DNA increases nearly uniformly with increasing number of trans-form azobenzene intercalations. This observed stabilizing effect on the duplex DNA is possibly due to the stacking interactions that lead to favorable enthalpy change between azobenzene trans-isomers and adjacent nucleobases.86,87 Evidently, molecular dynamic simulations and Tm experiments of duplexes have both indicated that the stabilizing effect is sufficient to offset the asymmetric distortion in DNA backbones resulted from the addition of azobenzene residues.88,89 This makes it feasible to use azobenzene as a non-invasive molecular switch for controlling TMSD reactions in DNA seesaw circuits without sacrificing sequence specificity.
Upon external ultraviolet (UV) light stimuli, trans-to-cis isomerization of azobenzene moieties (Fig. 2) perturbs the local DNA base stacking structure and initiates destabilization of the duplex due to steric hindrance. With properly designed sequences, selected positions of azobenzene intercalations, and well-controlled experimental conditions, a high percentage (∼85%) of photoregulated duplex DNA dissociation could be achieved.88,90 After the azobenzene-initiated duplex dehybridization reaches its equilibrium, the released ssDNA strand would no longer favorably hybridize to its Watson–Crick complementary strand as long as the intercalating azobenzenes stay in the polar non-planar cis-form on the strand. Such condition could be maintained by irradiating the sample continuously with 300–400 nm UV light. To restore hybridization dynamics and reform the DNA duplex, blue light (>400 nm) is supplied to promote the cis-to-trans isomerization of azobenzene molecules back to their planar and non-invasive conformation in the duplex. Furthermore, it has been reported that no side reactions are involved in the azobenzene photo-isomerization process.86,88 This completely reversible regulation could help establish a fast, efficient, and non-invasive pathway towards achieving fine controllability and renewability of circuit components in TMSD reactions including the seesawing, thresholding and reporting mechanism involved in DNA seesaw circuits.
2.4 Reversing and renewing a simplified strand displacement reaction network
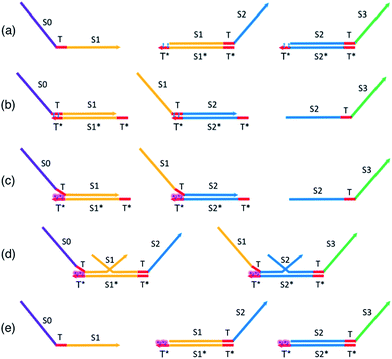
In this section, we present a method to provide renewability and reusability to a TMSD circuit (Fig. 3) built with gate complexes adapted from the original published seesaw paper.63 A key aspect of our design is the limited use of azobenzene-labeling to renew the entire TMSD circuit by modulation of the effective toehold lengths only. We term the resulting system incorporating azobenzene-labeling, A-TMSD circuit. This section serves as the foundation that leads to our complete designs and implementations of renewable seesaw logic gates. Unless otherwise specified, we use the following convention and notations to describe DNA species involved in CRNs: consecutive nucleotides form functional domains on a DNA sequence. The capital letter S with a numeric value indicates a specific domain, and T represents toehold. The Watson–Crick complementary sequence of a domain or toehold is annotated by an asterisk *. Angle brackets enclose the bound duplex formed by a sequence hybridized to its complementary strand. Unique domains and toeholds are illustrated with different colors. A domain or toehold share the same color with its complementary sequence.Assume the following DNA species are present in the system's initial state as shown in Fig. 3a: input sequence S0TS1, gate complex T〈S1T〉S2, and gate complex T〈S2T〉S3. To minimize the scale of modifications to the existing DNA seesaw technology, our design assumes 5 nt universal toeholds, each intercalated by two azobenzene moieties that are two nucleobases apart. The planar and non-polar trans-form azobenzene molecules are represented by the blue cartoons sitting on the toeholds T* of the gate base strand. Based on experimentally demonstrated results,85–88 these trans-form azobenzene isomers would not inhibit regular toehold binding events between the input and gate. Initiated by the exposed universal toeholds, forward reactions involving seesawing, branch migration, and strand displacement would proceed normally to produce the single-stranded S2TS3 output in Fig. 3b. At this point of stoichiometric equilibrium, no more productive reactions could occur in an unmodified seesaw motif cascade network. Any further computational operations would require building all the cascade components from scratch. However, it is not the case with our proposed design of renewable A-TMSD networks.
To initiate the reversal process of the cascade reaction network, external UV light stimulus is supplied (Fig. 3c). Upon this UV light excitation, azobenzene moieties on the toehold photo-isomerize to cis-isomers and induce destabilizing steric repulsion to the incumbent top strand. Structural and polarity changes involved in this photo-isomerization process affect the Tm of the duplex, specifically, more drastic change in Tm has been consistently observed with cis-azobenzene insertions on the oligonucleotide.86,87,90 As a result, the incumbent top strand in the duplex starts to dissociate from the gate base strand at the azobenzene-intercalated toehold domain, and this leads to exposed but unreactive universal toeholds sequestered by cis-form azobenzenes. Such toeholds are not favorable for further binding while azobenzenes stay in the non-planar cis-form.
Now, due to imposed hindrance on toehold binding, we consider the ‘effective length’ of the left toehold is correspondingly reduced. This effect exponentially decreases the bimolecular (BM) reaction rate62,73 for any forward TMSD reactions initiated by the left toehold. In other words, the presence of cis-form azobenzenes resulted in an imbalance of effective toehold lengths on the two sides of gate base strand. Because now the right toehold is effectively a much stronger invading toehold comparing to the sequestered left toehold, there would be a net gain of effective base pairs when the released output strand S2TS3 rebinds to the gate base strand and displaces the incumbent S1TS2 through branch migration. Hence, it is thermodynamically favorable for this reversal process to occur and regenerate seesaw gate motifs to their corresponding initial states. This gate reversal process is illustrated in Fig. 3d.
In Fig. 3e, all species have been reverted to their original form and concentration. Furthermore, the cis-form azobenzenes on the toeholds set a “lock” to the overall reaction network. Because the system already resides in the state of lowest free energy, no forward reactions could favorably proceed as long as the azobenzene isomers remain in cis-form. Depending on the application, one may now choose to extract the input signal strand and introduce a different input to serve new computational needs, or simply disable the “lock” to repeat prior computation using the regenerated circuit. Irradiating the sample with blue light will trigger the cis-to-trans isomerization of azobenzene, and this will start operations of the newly regenerated circuit.
As mentioned earlier, the DNA seesaw gate technology also benefits from our proposed design in terms of circuit leakage reduction. On one hand, trans-form azobenzenes on the toehold stabilizes the toehold binding and makes the forward reaction faster. On the other hand, cis-form azobenzenes on the toehold make the toehold thermodynamically unfavorable to hybridize to its complementary strand during the gate renewal process. Thus, in both trans-form and cis-form, azobenzenes on the toehold prevent spurious toehold binding events and provide an additional layer of leakage reduction.
2.5 Discussion on the yield of azobenzene-mediated DNA dehybridization
It is worth noting that neither the photo-isomerization of azobenzene molecules nor the azobenzene-mediated duplex DNA dehybridization occurs with perfect yield in reality. As investigated in a majority of published literature, the actual yield depends on various factors such as the number of azobenzene moieties incorporated, positions and spacing between azobenzene intercalations, and local mismatches of nucleobases surrounding the intercalation site.71,85–91 However, these studies mainly focused on regulating the hybridization of duplex DNA with ‘blunt ends’, meaning no exposed ssDNA toehold is present to facilitate the dehybridization process. In contrast, our design takes advantage of both the steric hindrance induced by azobenzene and the modulation of effective toehold length to evoke controlled renewability of the seesaw motif cascade reaction network. This makes our approach novel and unlikely to fall into limitations faced by studies done with blunt-ended DNA duplexes.From a theoretical perspective, the problem associated with non-ideal yield of photo-controlled duplex dehybridization could be ameliorated by making use of the exponential dependence of reaction rate on ‘effective toehold length’. With our design, isomerization of azobenzene to cis-form would result in an increased difference between the effective lengths of the invading and incumbent toehold. According to well-known experiments and modeling of the TMSD and toehold exchange mechanism done by Zhang and Winfree,62 such difference could contribute to an exponential increase in the probability of the duplex dissociation. Eventually, all original species in the reaction network should be able to reform at a high yield despite only a small number of azobenzene insertions on the toehold. In this work, we will quantify and analyze the effect of different reaction yields based on empirically-derived and model-verified thermodynamic parameters of A-TMSD. Using rate constants estimated and verified by our model, we will demonstrate the renewability of a full-scale seesaw AND gate as an example.
2.6 Designing a renewable nucleic acid seesaw logic ‘AND’ gate
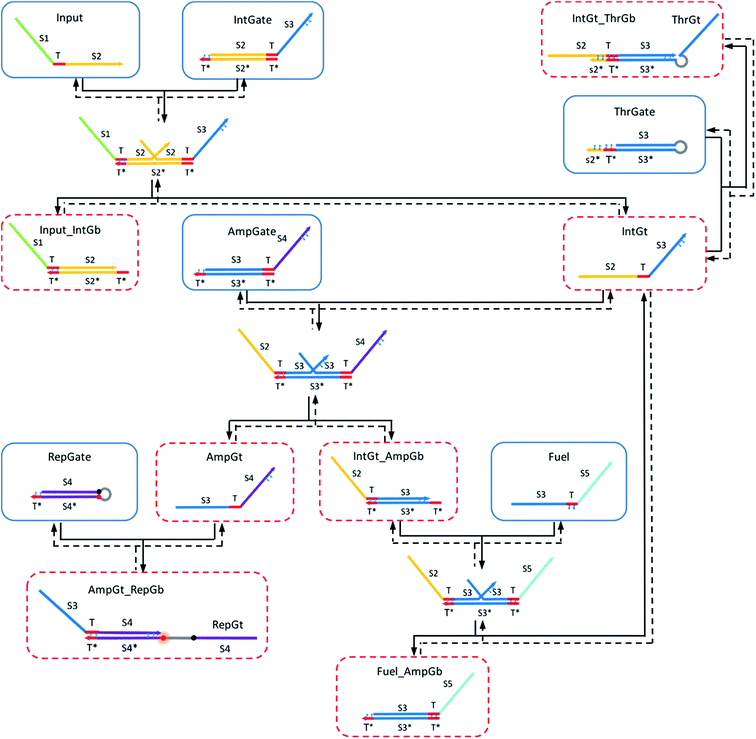
Shown in Fig. 4 is the complete design of a renewable nucleic acid seesaw AND gate. Table S1† explains the naming convention for reactant and product species in the CRN. In this design, universal T* toeholds are 5 nt long, and the extended toehold s2*T* on threshold complex is 10 nt long. We assume a default length of 15 nt for branch migration domain on gates. Initial species are enclosed by blue boxes and red dotted boxes enclose species that need to be reversed during the gate renewal process to reform original gate components. Thermodynamic feasibility of the gate operating with azobenzene in trans-form and in cis-form, respectively, was analyzed quantitatively based on the remarkable work by Zhang and Winfree.62We applied azobenzene functionalization to (i) the left toehold domain of integrating gate base strand, (ii) the left toehold domain of amplifying gate base strand, (iii) the toehold domain of the reporter gate base strand, (iv) the toehold domain on fuel strand, (v) the 3′-end portion of integrating gate top strand, (vi) the 3′-end portion of amplifying gate top strand, and (vii) the extended toehold domain of the threshold gate base strand. Two azobenzene molecules are used in functionalization (i)–(vi), and four azobenzene molecules in functionalization (vii). In addition, hairpin loop was added on the threshold gate to link its top strand to the base strand. In the original seesaw gate implementation, the top strand from threshold gate is rendered as waste after being released from the gate, because the short strand is inactive due to lack of reactive toehold domains. To facilitate fast renewal process of the threshold gate complex, our design requires the top strand to be able to come back to its original gate base strand as easy as possible. The hairpin provides such a linkage preventing the top strand from completely moving away when it is displaced during the forward thresholding reaction. Similarly, a hairpin linkage was added to the reporter gate complex so that its top strand could be easily recycled during the reporter renewal process. The addition of hairpins in our design was only for future experimental consideration and was therefore not directly modeled in our simulations.
2.7 Modeling the forward operation of a seesaw logic ‘AND’ gate functionalized with trans-form azobenzenes
The following types of reactions were considered to model the A-TMSD reaction network when azobenzene molecules are maintained in the planar trans-form. The corresponding CRN reaction graph is shown in Fig. S1.†• Reversible seesawing reactions between inputs and the integrating gate:
 | (1) |
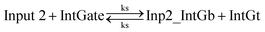 | (2) |
• Fast thresholding reaction between the released integrating gate top strand and the threshold gate:
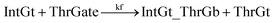 | (3) |
• Reversible seesawing reactions between the released integrating gate top strand and the amplifying gate:
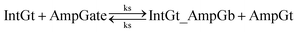 | (4) |
• Reversible seesawing reactions and catalytic cycle triggered by fuel strand:
 | (5) |
• TMSD reaction between released amplifying gate top strand and the reporter gate:
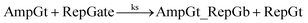 | (6) |
• Gate-fuel leakage due to fuel slowly replacing the top strand from amplifying gate:
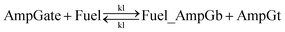 | (7) |
For equations shown above, ks, kf and kl represent BM rate constants for slow A-TMSD, fast A-TMSD, and gate-fuel leakage, respectively. We adapted BM rate constant values in Table S2† as proposed and experimentally verified in prior work.62,64 The mass-action kinetics of the above A-TMSD reactions were modeled with a formal set of ODEs resolved from Dynetica.92 Further verifications of circuit behavior were done by deterministic simulations in Visual GEC.75 Table S3† lists the initial concentrations of DNA species in the seesaw logic AND gate with input condition ON–ON as an example. All possible Boolean input combinations for the forward operation of the seesaw logic AND gate were evaluated, and the final states of the circuit operated under different input conditions are recorded in Table S4.† According to the results, our model demonstrated the desired circuit behavior for computing the logic AND using DNA seesaw gate modified with trans-form azobenzenes.
2.8 Modeling the renewal process of a seesaw logic ‘AND’ gate functionalized with cis-form azobenzenes
Taking the Boolean input combination ON–ON as an example, now let us consider the system has reached equilibrium after completing the forward operation of logic AND on the two inputs. External UV light is now supplied to initiate the trans-to-cis isomerization of azobenzene molecules. As shown in Fig. 5, steric hindrance from the non-planar cis-form azobenzene isomers induces a difference in the ‘effective toehold lengths’ between the new invading toehold and incumbent toehold. Depending on where the azobenzene functionalization resides on the strand, the effect of cis-form azobenzene can either help reduce the effective length of incumbent toehold, or increase the effective length of invading toehold, or both. All of these three mechanisms could provide thermodynamically favorable condition for the regeneration process to occur and proceed, with a different effective BM rate constant for the corresponding A-TMSD reaction. For convenience, we use the following notations for the analysis and modeling of the seesaw gate renewal process:(i) n: effective length of invading toehold under the effect of cis-azobenzene.
(ii) m: effective length of incumbent toehold under the effect of cis-azobenzene.
(iii) b: effective length of branch migration domain in the corresponding A-TMSD.
(iv) k{m,n}: effective BM rate constant of the corresponding A-TMSD.
In the following sections, we will explain, model, and evaluate the renewal process for the integrating gate and inputs, threshold gate, reporter gate, amplifying gate and fuel, respectively.
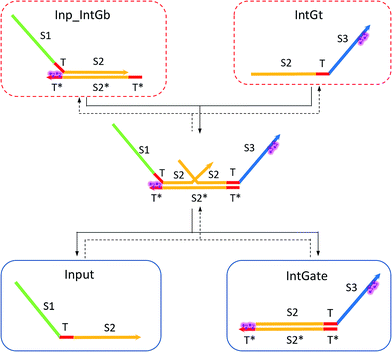
 | (8) |
 | (9) |
In chemical eqn (8) and (9), ksc is the forward slow BM rate constant due to toehold sequestering by cis-azobenzenes on the left T* toehold of IntGb. To model the forward A-TMSD reaction Input 1 + IntGate → Inp1_IntGb + IntGt and Input 2 + IntGate → Inp2_IntGb + IntGt, we apply the bimolecular reaction model62 of toehold exchange, taking the cis-azobenzene functionalized left toehold T* as the invading toehold and the right toehold T* of IntGb as the incumbent toehold. Depending on the strength of toehold sequestering by cis-azobenzene, the effective length of invading toehold could range from the ideal case 0 to the worst case 5. Because the incumbent toehold length remains a constant 5 nt, we could model the BM rate constant ksc by k{5,n}, n = 0, 1, 2, 3, 4, or 5.
Similarly, the reverse A-TMSD reaction Inp1_IntGb + IntGt → Input 1 + IntGate and Inp2_IntGb + IntGt → Input 2 + IntGate could be modeled with a BM rate constant krc. In contrast to the forward A-TMSD reactions modeled above, the azobenzene-sequestered left toehold on IntGb is now considered in the model as the incumbent toehold with an effective length m ranging from 0 to 5 depending on the yield of toehold sequestering. In the case of fully renewing the integrating gate, photoisomerization of azobenzenes leads to complete dissociation of the incumbent toehold domain from its complement. Hence, the effective incumbent toehold length is zero for the ideal case. Consequently, we can model the effective BM rate constant krc by k{m,5}, m = 0, 1, 2, 3, 4, or 5. Because of no azobenzene functionalization on the recognition domain of IntGb, the effective length of branch migration domain remains the default 15 nt for both the forward and reverse reactions modeled by eqn (8) and (9). As shown in Tables S5 and S6,† we calculated the effective rate constant ksc and krc based on the derivation and MATLAB script adapted from prior work.62
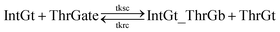 | (10) |
To estimate the forward BM rate constant tksc, we take as invading toehold the cis-azobenzene sequestered s2*T2 domain on ThrGate shown in Fig. 7. In addition, steric repulsion by cis-azobenzenes on IntGt determines the effective length b of the branch migration domain. Meanwhile, upon spontaneous dissociation of ThrGt from ThrGate after branch migration, a temporary incumbent toehold is resulted with an effective binding length equal to m = 15 − b. Therefore, in our model we estimate tksc by k{m,n}, with n ranging from 0 to 10, and with m ranging from 5 to 0 depending on the effective length of branch migration domain. To simplify the modeling, we assume a uniformly distributed effect on DNA dehybridization by cis-to-trans isomerization of azobenzenes, so that any change in b (or m) will correspond to twice that amount of change in n. This linearity could be verified by the fact that our design satisfies the following eqn (11):
 | (11) |
With this assumption, we construct and analyze different scenarios of tksc as shown in Table S7.†
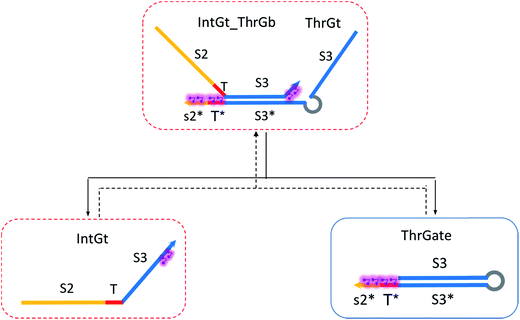
The renewal process of threshold complex is achieved primarily by the reverse reaction IntGt_ThrGb + ThrGt → IntGt + ThrGate with a BM rate constant tkrc. In this case, we take the temporary single-stranded short domain exposed by azobenzenes on the 3′-end of IntGt as the invading toehold, with an effective length n ranging from 5 to 0 depending on the azobenzene isomerization yield. Accordingly, the effective length of branch migration is calculated as b = 15 − n. Lastly, the incumbent toehold has an effective length m between 0 to 10 based on strength of toehold sequestering on the s2*T2 domain, as depicted in Fig. 7. Here we take similar assumptions from the calculation of tksc to simplify the modeling. Overall, tkrc could be theoretically calculated as k{m,n}, with n ranging from 5 to 0 and m between 0 to 10 accordingly. However, empirically speaking, the actual yield of cis-azobenzene-mediated dehybridization would not be so low that the effective length of the incumbent toehold could ever reach 10 nt. To accommodate for this and readily adapt the available data of toehold binding energies from prior published work,62 we restrict our analysis to m = 6 at maximum, which corresponds to roughly a 40% yield of azobenzene-mediated dehybridization in our model. Table S8† summarizes the estimation of rate constant tkrc depending on the yield of toehold sequestering due to cis-azobenzenes. It should be noted that the regeneration of integrating gate is also facilitated, because during the ThrGate renewal process, the IntGt is released from the bound complex and becomes available for the reformation of IntGate.
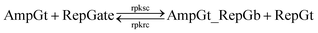 | (12) |
To model the forward reaction AmpGt + RepGate → AmpGt_RepGb + RepGt, we consider left toehold T* on RepGate as the invading toehold, with an effective binding length n between 0 to 5 depending on the sequestering strength of cis-azobenzenes. The cis-azobenzenes on the 3′-end of AmpGt forms a temporary incumbent toehold on RepGb. Specifically, the spontaneous dissociation of RepGt from RepGate after branch migration must occur via the temporary incumbent toehold, with its effective toehold binding length m ranging from 5 to 0. Accordingly, the effective length of branch migration domain is b = 15 − m. In our model we estimate rpksc by k{m,n}, as summarized in Table S9.†
Next we model the reverse reaction AmpGt_RepGb + RepGt → AmpGt + RepGate with an effective BM rate constant rpkrc. cis-Azobenzene-mediated dehybridization on 3′-end of AmpGt forms an invading toehold with an effective length n, which correspondingly results in a branch migration domain with an effective length b = 15 − n. Furthermore, cis-azobenzenes on the left toehold T* of RepGb modulate the effective length m of incumbent toehold, with the relation m = 5 − n. The estimation of rpkrc is shown in Table S10.† Note that the regeneration of amplifying gate is also facilitated as a result of this reaction by releasing AmpGt from the bound complex AmpGt_RepGb.
 | (13) |
 | (14) |
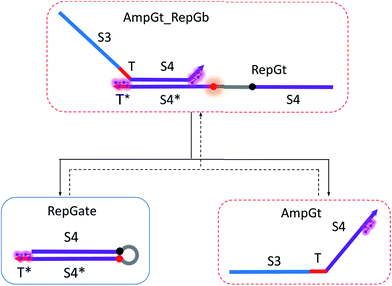
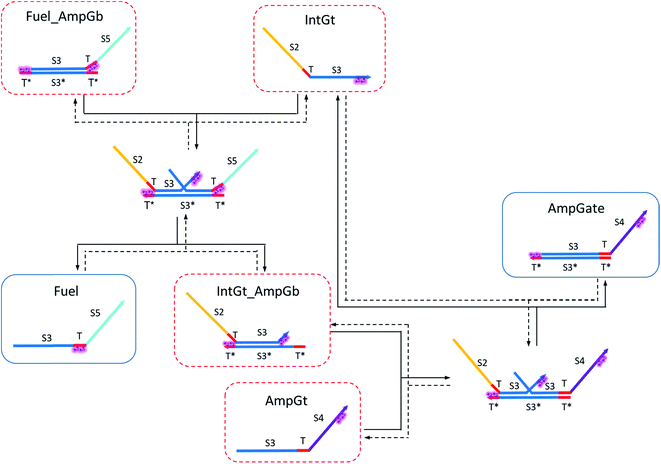 | ||
| Fig. 9 Regeneration of the amplifying gate. Regeneration of the fuel is affected in this CRN. Regeneration of the integrating gate is facilitated. | ||
To estimate the BM rate constant ampksc, we take the left toehold T* on AmpGb as the invading toehold with an effective binding length n from 0 to 5. cis-Azobenzenes on the 3′-end of IntGt modulate the effective length m of the incumbent toehold and b of the branch migration domain. Depending on the cis-azobenzene isomerization yield, b has a value between 10 to 15. The effective length of incumbent toehold is therefore expressed as m = 15 − b + 5 = 20 − b. Here the 5 nt part is contributed by the right toehold T* on AmpGb. Table S11† shows the possible effective values of ampksc estimated from the model. For the case m = 10, 9, or 8, there is no available data in literature for the corresponding toehold binding energy, and N/A is therefore noted in the table. Theoretically for all these three cases, their expected effective BM rate constant should be much smaller than the estimated value from case m = 7 because of their smaller n and larger m. Hence we estimate their ampksc with a value of zero in place of N/A for our modeling purpose.
To model the effective rate constant ampkrc of the reverse reaction IntGt_AmpGb + AmpGt → IntGt + AmpGate, the previously defined incumbent toehold with effective binding length 20 − b is now considered as the invading toehold. Similarly, the previously defined invading toehold is now the incumbent toehold with an effective length m in the range of 0 to 5. Estimated values of ampkrc are shown in Table S12.†
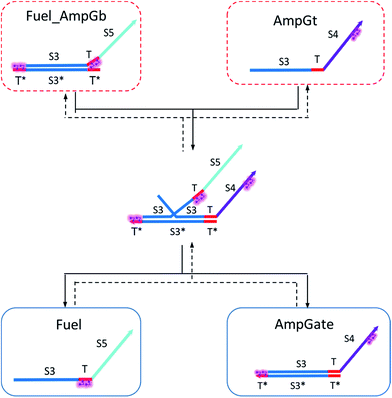
To model the forward BM reaction associated with eqn (14), we first need to estimate the effective length of the invading toehold, which consists of two parts: (i) the right toehold T* of AmpGb effectively sequestered by cis-azobenzenes on the T domain of fuel, and (ii) the exposed portion of AmpGb due to cis-azobenzenes on 3′-end of IntGt of the IntGt_AmpGb complex. With an assumption made earlier, the length of effective binding region sequestered in (i) and exposed in (ii) should be roughly equal. Thus, the counteracting effects result in a constant effective length of n = 5 for the invading toehold but a varying effective length b of branch migration domain depending on the azobenzene isomerization yield, which also modulates the incumbent toehold effective length m. As a result, we model the forward rate constant fksc by k{m,5}, with m ranging from 0 to 5 and b from 10 to 15, as shown in Table S13.†
Analogously, we model the reverse BM reaction in eqn (14) by taking the left toehold T* on Fuel_AmpGb as the invading toehold with an effective length n ranging from 0 to 5. In addition, we model the incumbent toehold with a constant effective length m of 5 nt and the branch migration domain with an effective length b ranging from 10 to 15. As a result, we model the reverse rate constant fkrc by k{5,n}, as shown in Table S14.†
Based on the results from Tables S13 and S14,† the cis-azobenzene functionalization does not actually facilitate the regeneration of fuel strand. However, importantly, one should not forget to account for a new productive reaction between Fuel_AmpGb and AmpGt because of the toehold sequestering by the fuel strand. Mathematically, this reaction could be derived by adding eqn (13) to (14) on both side, resulting in a single bidirectional BM chemical eqn (15) to describe an overall process that effectively regenerates both AmpGate and fuel. A diagram for the corresponding reaction network is shown in Fig. 10.
 | (15) |
As discussed earlier, the un-sequestered blunt-end TMSD reaction between fuel and AmpGate happens in the form of leakage at least 6 orders of magnitude slower than regular TMSD reactions. With cis-azobenzenes on T toehold of the fuel strand, the effective rate constant is even slower.62 As a result, assigning zero to ampfksc is a good approximation for modeling the effective rate constant of forward reaction Fuel + AmpGate → Fuel_AmpGb + AmpGt. To estimate the reverse rate constant ampfkrc, we take the exposed portion of right toehold on AmpGb as the invading toehold, with an effective length n ranging from 5 to 0. Furthermore, the length of branch migration domain is unaffected by azobenzene isomerization, and the left toehold T* on Fuel_AmpGb does not participate in any toehold exchange reaction in this CRN. Thus, we can model the effective rate constant ampfkrc by k{0,n}. Table S15† shows the correlation between the estimated value of ampfkrc and the strength of toehold sequestering by cis-azobenzenes on fuel strand.
2.9 Deterministic simulation results
We carried out deterministic simulations in Visual GEC for the renewal process of a single seesaw AND gate. The efficacy of gate renewal process is quantified by the ‘regeneration yield’, defined as the ratio between the regenerated concentration and the initial concentration for each gate component as defined in Table S3.† Time courses of the simulated kinetics shown in Fig. 11 provide measurements of renewability for individual gate components. Evaluations were based on different effective yields of toehold sequestering by cis-azobenzenes. The resulted renewal yields of AND gate components under the input condition ON–ON are shown in Table 1. Taking 80% as a reasonably achievable yield of toehold sequestering by cis-azobenzenes, we then compared the model-predicted yields of gate renewability corresponding to different input conditions of AND gate, as shown in Table 2.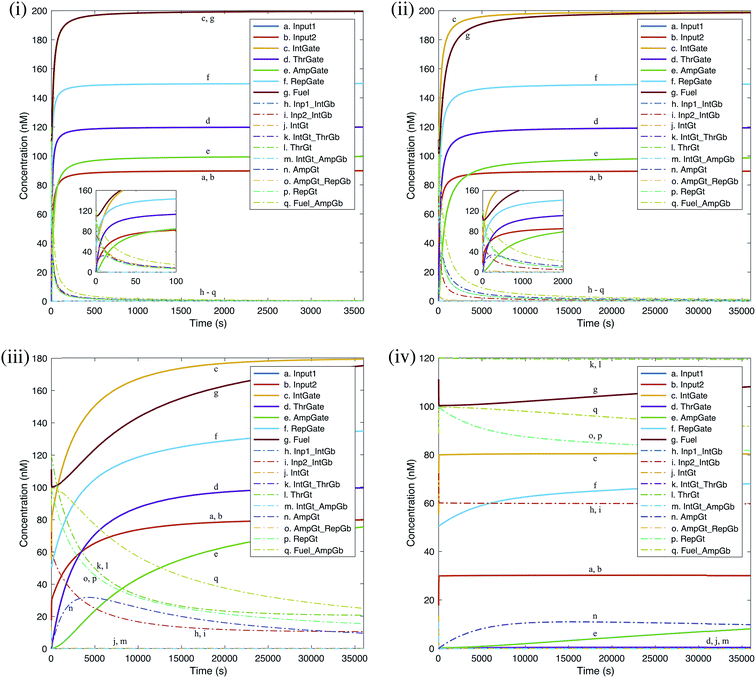 | ||
| Fig. 11 Deterministic simulation for the renewal process of a DNA seesaw logic AND gate as a result of A-TMSD. Starting concentrations were extracted from equilibrium state after evaluating the input condition ‘ON, ON’. Gate renewability was simulated based on different effective yields of toehold sequestering by cis-azobenzenes: (i) 100%, (ii) 80%, (iii) 60%, (iv) 40%. Regeneration of gate species is shown by solid lines. Removal of wastes and intermediate species is shown by dash-dot lines. Insets in (i) and (ii) show enlarged views of the rapid gate renewal process at the beginning of reactions. Graphs generated by Visual GEC75 and MATLAB. | ||
| Species name | Regeneration yield (%), 100% effective toehold sequesteringa | Regeneration yield (%), 80% effective toehold sequesteringb | Regeneration yield (%), 60% effective toehold sequestering | Regeneration yield (%), 40% effective toehold sequestering |
|---|---|---|---|---|
| a Reaction reached equilibrium within 0.5 hour.b Reaction reached equilibrium within 5 hours. | ||||
| Input 1 | 99.7 | 99.4 | 88.4 | 33.5 |
| Input 2 | 99.7 | 99.4 | 88.4 | 33.5 |
| IntGate | 99.8 | 99.6 | 89.6 | 40.2 |
| ThrGate | 99.8 | 99.5 | 82.9 | 0.4 |
| AmpGate | 99.5 | 98.7 | 75.2 | 8.2 |
| Fuel | 99.8 | 99.3 | 87.6 | 54.1 |
| RepGate | 99.9 | 99.6 | 89.8 | 45.4 |
| Species name | Regeneration yield (%), input ON–ON | Regeneration yield (%), input ON–OFF | Regeneration yield (%), input OFF–ON | Regeneration yield (%), input OFF–OFF |
|---|---|---|---|---|
| Input 1 | 99.4 | 99.2 | 99.2 | 96.8 |
| Input 2 | 99.4 | 99.2 | 99.2 | 96.8 |
| IntGate | 99.6 | 99.6 | 99.6 | 99.7 |
| ThrGate | 99.5 | 99.5 | 99.5 | 99.5 |
| AmpGate | 98.7 | 98.9 | 98.9 | 99.6 |
| Fuel | 99.3 | 99.4 | 99.4 | 99.8 |
| RepGate | 99.6 | 99.7 | 99.7 | 99.8 |
3. Conclusion
According to the simulation results, our proposed design is capable of renewing all gate components of a DNA seesaw circuit to near completion with an achieved yield close to or above 97%. Our model also predicted reasonable time windows (<5 hours) for achieving such high yield of circuit renewability in real wet lab experiments, given that our proposed toehold sequestering mechanism could achieve an effective yield of roughly 80% or above. Based on published data and our discussion on the yield of azobenzene-mediated DNA dehybridization, we anticipate that 80% toehold sequestering yield is experimentally achievable because of the collaborative effects of azobenzene-mediated duplex dehybridization and TMSD.In summary, we introduced a novel design strategy for achieving near complete gate renewability in DNA seesaw technology by photonic controls. Due to variations in DNA sequence design and achievable azobenzene isomerization yield on strands, additional experimental studies are needed to fully characterize the efficiency of gate renewability. Nevertheless, our proposed design strategy of leveraging the collective effect of TMSD and azobenzene-mediated dehybridization may provide new perspectives on achieving synchronized and efficient localized control of DNA hybridization in complex and scalable reaction networks. There are much more to explore with our proposed seesaw gate renewal mechanism, for example, by applying DeMorgan's theorems and the ‘dual-rail’ logic representation to implement a complete set of renewable DNA logic gates, including dual-rail AND, OR, NOR, NAND and XOR. Comparing to other prior renewable circuit schemes, one can also exploit the fan-in and fan-out capability of seesaw circuits to construct time-responsive sequential circuits and memory devices with our simplified design strategy and the economical use of photoresponsive molecules on DNA. In theory, our novel modeling strategy presented here could apply to the in silico analysis and verification of any TMSD networks that operate with some type of toehold sequestering mechanism. Various devices such as molecular walkers and motors could potentially be engineered reusable, be simulated and subsequently implemented using our proposed design strategy.
4. Method
4.1 Notes on modeling the forward operation of seesaw ‘AND’ gate functionalized with trans-form azobenzenes
For eqn (1)–(7), three different BM rate constants, namely, ks, kf and kl, were involved in modeling the logic gate operation with trans-form azobenzene modifications in the circuit. Reversible seesawing reactions were modeled with the same forward and reverse rate constant because of equivalent toehold exchange. Despite the slight stabilization effect on toehold binding due to trans-form azobenzene intercalations, we assumed that the non-invasive trans-form azobenzenes had minimal influences on the BM reaction rate constants. This assumption was reasonable considering we only inserted a few azobenzene molecules on the toehold. Hence, in our model we could use BM rate constants defined in Table S2† as previously verified by experimental work.62,64 Other universal toehold binding reactions64 were not incorporated in our model because they were unproductive simulation-wise with regard to their influences on the characterization of the overall CRN. Thus, only three rate constant values were needed for characterizing and evaluating the forward operation of a full-scale seesaw logic AND gate with trans-form azobenzenes.Text S1† lists the set of ODEs for modeling the mass-action kinetics of associated A-TMSD reactions using Dynetica.92 The equations were evaluated with initial conditions listed in Table S3,† taking Boolean input combination ON–ON as an example. These recommended numbers were adapted from the Seesaw Compiler63 and were used to configure the simulation of CRN kinetics for the AND gate forward operation in Visual GEC.75 For all other species that appear in the final state of the gate forward operation, an initial concentration of zero was assigned. These included dsDNA species Inp1_IntGb, Inp2_IntGb, IntGt_ThrGb, IntGt_AmpGb, Fuel_AmpGb, AmpGt_RepGb, and ssDNA species IntGt, ThrGt, AmpGt, RepGt.
4.2 Notes on modeling the renewal process of seesaw ‘AND’ gate functionalized with cis-form azobenzenes
To best apply the well-established three-step model and the bimolecular reaction model of toehold exchange,62 in our design all species were supposed to operate under or near the ‘critical concentration’ as defined in prior literature.62 Typical DNA sequence design as well as standard buffer condition such as salt composition and concentration were assumed so that the calculated toehold binding energies from prior literature62 could be adapted to our model and to predict the reaction kinetics with reasonable accuracy. We assumed typical toehold binding energies, 25 °C temperature, and the energy model of ‘Nupack + Protozanova’ for estimation of BM rate constants using a modified MATLAB script adapted from prior work,62 as listed in Text S2.† MATLAB commands for estimating specific rate constant values for the renewal process of gate components are indicated in Tables S5–S15.† Different sets of effective BM rate constant values were estimated according to specific strengths of toehold-sequestering by cis-azobenzenes estimated for each DNA strand modification in our design. The calculated values were then used in LBS programs to simulate the mass-action kinetics of the renewal process of seesaw logic AND gate in Visual GEC. As an example, Text S3† lists the LBS code for deterministic simulation with the Boolean input condition ON–ON and an assumed effective yield of 80% for the cis-azobenzene toehold-sequestering effect.Acknowledgements
This work was supported by National Science Foundation (CCF1617791) and National Security Science and Engineering Faculty Fellowship (NSSEFF) ONR (N00014-16-1-2512). A. E. was supported by Missions & Cultural Representation Sector, Ministry of Higher Education, Egypt. We thank Prof. Ayman El-Sayed and Prof. Nawal El-Fishawy for insightful suggestions on the revisions of the manuscript.References
- F. A. Aldaye, A. L. Palmer and H. F. Sleiman, Science, 2008, 321, 1795–1799 CrossRef CAS PubMed.
- Y. Lu and J. Liu, Curr. Opin. Biotechnol., 2006, 17, 580–588 CrossRef CAS PubMed.
- I. Willner, B. Shlyahovsky, M. Zayats and B. Willner, Chem. Soc. Rev., 2008, 37, 1153 RSC.
- J. Bath and A. J. Turberfield, Nat. Nanotechnol., 2007, 2, 275–284 CrossRef CAS PubMed.
- D. Y. Zhang and G. Seelig, Nat. Chem., 2011, 3, 103–113 CrossRef CAS PubMed.
- J. D. Watson and F. H. C. Crick, Nature, 1953, 171, 737–738 CrossRef CAS PubMed.
- P. W. K. Rothemund, N. Papadakis and E. Winfree, PLoS Biol., 2004, 2, e424 Search PubMed.
- P. W. K. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS PubMed.
- S. M. Douglas, H. Dietz, T. Liedl, B. Högberg, F. Graf and W. M. Shih, Nature, 2009, 459, 414–418 CrossRef CAS PubMed.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Nature, 2008, 452, 198–201 CrossRef CAS PubMed.
- A. S. Walsh, H. Yin, C. M. Erben, M. J. A. Wood and A. J. Turberfield, ACS Nano, 2011, 5, 5427–5432 CrossRef CAS PubMed.
- N. C. Seeman, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS PubMed.
- J. SantaLucia and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440 CrossRef CAS PubMed.
- R. M. Dirks, J. S. Bois, J. M. Schaeffer, E. Winfree and N. A. Pierce, SIAM Rev., 2007, 49, 65–88 CrossRef.
- M. Zuker, Nucleic Acids Res., 2003, 31, 3406–3415 CrossRef CAS PubMed.
- J. SantaLucia, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465 CrossRef CAS.
- S. Bommarito, N. Peyret and J. SantaLucia Jr, Nucleic Acids Res., 2000, 28, 1929–1934 CrossRef CAS PubMed.
- V. A. Bloomfield, D. M. Crothers and I. Tinoco Jr, Nucleic acids: structures, properties and functions, Sterling Publishing Company, New York, 2000 Search PubMed.
- R. Owczarzy, B. G. Moreira, Y. You, M. A. Behlke and J. A. Walder, Biochemistry, 2008, 47, 5336–5353 CrossRef CAS PubMed.
- E. Protozanova, P. Yakovchuk and M. D. Frank-Kamenetskii, J. Mol. Biol., 2004, 342, 775–785 CrossRef CAS PubMed.
- D. V. Pyshnyi and E. M. Ivanova, Russ. Chem. Bull., 2002, 51, 1145–1155 CrossRef CAS.
- Z.-J. Tan and S.-J. Chen, Biophys. J., 2006, 90, 1175–1190 CrossRef CAS PubMed.
- V. A. Vasiliskov, D. V Prokopenko and A. D. Mirzabekov, Nucleic Acids Res., 2001, 29, 2303–2313 CrossRef CAS PubMed.
- D. V. Pyshnyi and E. M. Ivanova, Nucleosides, Nucleotides Nucleic Acids, 2004, 23, 1057–1064 CAS.
- J. Petruska and M. F. Goodman, J. Biol. Chem., 1995, 270, 746–750 CrossRef CAS PubMed.
- K. Lund, A. J. Manzo, N. Dabby, N. Michelotti, A. Johnson-Buck, J. Nangreave, S. Taylor, R. Pei, M. N. Stojanovic, N. G. Walter, E. Winfree and H. Yan, Nature, 2010, 465, 206–210 CrossRef CAS PubMed.
- T. Omabegho, R. Sha and N. C. Seeman, Science, 2009, 324, 67–71 CrossRef CAS PubMed.
- S. J. Green, J. Bath and A. J. Turberfield, Phys. Rev. Lett., 2008, 101, 238101 CrossRef CAS PubMed.
- J.-S. Shin and N. A. Pierce, J. Am. Chem. Soc., 2004, 126, 10834–10835 CrossRef CAS PubMed.
- W. B. Sherman and N. C. Seeman, Nano Lett., 2004, 4, 1203–1207 CrossRef CAS.
- B. Yurke, A. J. Turberfield, A. P. Mills, F. C. Simmel and J. L. Neumann, Nature, 2000, 406, 605–608 CrossRef CAS PubMed.
- J. Bath, S. J. Green, K. E. Allen and A. J. Turberfield, Small, 2009, 5, 1513–1516 CrossRef CAS PubMed.
- S. Venkataraman, R. M. Dirks, P. W. K. Rothemund, E. Winfree and N. A. Pierce, Nat. Nanotechnol., 2007, 2, 490–494 CrossRef PubMed.
- S. Tyagi and F. R. Kramer, Nat. Biotechnol., 1996, 14, 303–308 CrossRef CAS PubMed.
- H. Dietz, S. M. Douglas and W. M. Shih, Science, 2009, 325, 725–730 CrossRef CAS PubMed.
- D. Han, S. Pal, J. Nangreave, Z. Deng, Y. Liu and H. Yan, Science, 2011, 332, 342–346 CrossRef CAS PubMed.
- E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, R. Subramani, W. Mamdouh, M. M. Golas, B. Sander, H. Stark, C. L. P. Oliveira, J. S. Pedersen, V. Birkedal, F. Besenbacher, K. V. Gothelf and J. Kjems, Nature, 2009, 459, 73–76 CrossRef CAS PubMed.
- E. Graugnard, A. Cox, J. Lee, C. Jorcyk, B. Yurke and W. L. Hughes, IEEE Trans. Nanotechnol., 2010, 9, 603–609 CrossRef PubMed.
- S. Beyer and F. C. Simmel, Nucleic Acids Res., 2006, 34, 1581–1587 CrossRef CAS PubMed.
- S. Modi, M. G. Swetha, D. Goswami, G. D. Gupta, S. Mayor and Y. Krishnan, Nat. Nanotechnol., 2009, 4, 325–330 CrossRef CAS PubMed.
- Y. Benenson, B. Gil, U. Ben-Dor, R. Adar and E. Shapiro, Nature, 2004, 429, 423–429 CrossRef CAS PubMed.
- S. M. Douglas, I. Bachelet and G. M. Church, Science, 2012, 335, 831–834 CrossRef CAS PubMed.
- E. Ruiz-Hernández, A. Baeza and M. Vallet-Regí, ACS Nano, 2011, 5, 1259–1266 CrossRef PubMed.
- Q. Zhang, Q. Jiang, N. Li, L. Dai, Q. Liu, L. Song, J. Wang, Y. Li, J. Tian, B. Ding and Y. Du, ACS Nano, 2014, 8, 6633–6643 CrossRef CAS PubMed.
- Q. Jiang, C. Song, J. Nangreave, X. Liu, L. Lin, D. Qiu, Z. G. Wang, G. Zou, X. Liang, H. Yan and B. Ding, J. Am. Chem. Soc., 2012, 134, 13396–13403 CrossRef CAS PubMed.
- Y.-X. Zhao, A. Shaw, X. Zeng, E. Benson, A. M. Nyström and B. Högberg, ACS Nano, 2012, 6, 8684–8691 CrossRef CAS PubMed.
- E. Shapiro and Y. Benenson, Sci. Am., 2006, 294, 44–51 CrossRef CAS PubMed.
- M. You, G. Zhu, T. Chen, M. J. Donovan and W. Tan, J. Am. Chem. Soc., 2015, 137, 667–674 CrossRef CAS PubMed.
- D. Shangguan, Y. Li, Z. Tang, Z. C. Cao, H. W. Chen, P. Mallikaratchy, K. Sefah, C. J. Yang and W. Tan, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 11838–11843 CrossRef CAS PubMed.
- D. Soloveichik, G. Seelig and E. Winfree, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 5393–5398 CrossRef CAS PubMed.
- G. Seelig, D. Soloveichik, D. Y. Zhang and E. Winfree, Science, 2006, 314, 1585–1588 CrossRef CAS PubMed.
- H. Lederman, J. Macdonald, D. Stefanovic and M. N. Stojanovic, Biochemistry, 2006, 45, 1194–1199 CrossRef CAS PubMed.
- B. M. Frezza, S. L. Cockroft and M. R. Ghadiri, J. Am. Chem. Soc., 2007, 129, 14875–14879 CrossRef CAS PubMed.
- M. N. Stojanovic, S. Semova, D. Kolpashchikov, J. Macdonald, C. Morgan and D. Stefanovic, J. Am. Chem. Soc., 2005, 127, 6914–6915 CrossRef CAS PubMed.
- T. Ran, S. Kaplan and E. Shapiro, Nat. Nanotechnol., 2009, 4, 642–648 CrossRef CAS PubMed.
- M. N. Stojanovic, T. E. Mitchell and D. Stefanovic, J. Am. Chem. Soc., 2002, 124, 3555–3561 CrossRef CAS PubMed.
- A. Lake, S. Shang and D. M. Kolpashchikov, Angew. Chem., Int. Ed., 2010, 49, 4459–4462 CrossRef CAS PubMed.
- E. Chiniforooshan, D. Doty, L. Kari and S. Seki, in Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Springer, LNCS, Berlin, Heidelberg, 2011, vol. 6518, pp. 25–36 Search PubMed.
- R. Weiss, G. E. Homsy and T. F. Knight, Toward in vivo Digital Circuits, in Evolution as Computation, Natural Computing Series, ed. L. F. Landweber, E. Winfree, Springer, Berlin, Heidelberg, 2002, pp. 275–295 Search PubMed.
- H. Jiang, M. D. Riedel and K. K. Parhi, in 2013 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), IEEE, 2013, pp. 721–727 Search PubMed.
- W. Li, F. Zhang, H. Yan and Y. Liu, Nanoscale, 2016, 8, 3775–3784 RSC.
- D. Y. Zhang and E. Winfree, J. Am. Chem. Soc., 2009, 131, 17303–17314 CrossRef CAS PubMed.
- L. Qian and E. Winfree, J. R. Soc., Interface, 2011, 8, 1281–1297 CrossRef CAS PubMed.
- L. Qian and E. Winfree, Science, 2011, 332, 1196–1201 CrossRef CAS PubMed.
- V. A. Ferizani, A. Niknafs and M. Mohammadi, Int. J. Bio-Inspired Comput., 2015, 7, 376 CrossRef.
- X. Liu, J. Suo, J. Liu, Y. Gao and X. Zeng, J. Nanomater., 2015, 2015, 1–11 Search PubMed.
- Z. Wang, G. Tian, Y. Wang, Y. Wang and G. Cui, Bio-inspired Comput.-Theor. Appl., 2014, 472, 463–467 Search PubMed.
- A. Goel and M. Ibrahimi, Nat. Comput., 2011, 10, 467–485 CrossRef.
- A. J. Genot, J. Bath and A. J. Turberfield, J. Am. Chem. Soc., 2011, 133, 20080–20083 CrossRef CAS PubMed.
- S. Garg, PhD thesis, Duke University, 2016.
- Y. Yan, X. Wang, J. I. L. Chen and D. S. Ginger, J. Am. Chem. Soc., 2013, 135, 8382–8387 CrossRef CAS PubMed.
- Y. Ogura, A. Onishi, T. Nishimura and J. Tanida, Biomed. Opt. Express, 2016, 7, 2142 CrossRef CAS PubMed.
- B. Yurke and A. P. Mills Jr, Genet. Program. Evolvable Mach., 2003, 4, 111–122 CrossRef.
- M. Pedersen and G. Plotkin, presented in part at International Conference on Computational Methods in Systems Biology, Berlin Heidelberg, October, 2008 Search PubMed.
- M. Pedersen and A. Phillips, J. R. Soc., Interface, 2009, 6, S437–S450 CrossRef CAS PubMed.
- L. E. Morrison and L. M. Stols, Biochemistry, 1993, 32, 3095–3104 CrossRef CAS PubMed.
- C. M. Radding, K. L. Beattie, W. K. Holloman and R. C. Wiegand, J. Mol. Biol., 1977, 116, 825–839 CrossRef CAS PubMed.
- I. G. Panyutin and P. Hsieh, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 2021–2025 CrossRef CAS.
- C. Green and C. Tibbetts, Nucleic Acids Res., 1981, 9, 1905–1918 CrossRef CAS PubMed.
- D. Y. Zhang, A. J. Turberfield, B. Yurke and E. Winfree, Science, 2007, 318, 1121–1125 CrossRef CAS PubMed.
- J. N. Zadeh, C. D. Steenberg, J. S. Bois, B. R. Wolfe, M. B. Pierce, A. R. Khan, R. M. Dirks and N. A. Pierce, J. Comput. Chem., 2011, 32, 170–173 CrossRef CAS PubMed.
- D. Y. Zhang, Lect. Notes Comput. Sci., 2011, 6518, 162–175 Search PubMed.
- D. E. Muller, Symp. Appl. Switch. Theory Sp. Technol., 1963, 289–297 Search PubMed.
- G. Seelig, B. Yurke and E. Winfree, DNA Comput., 2005, 3384, 329–343 Search PubMed.
- H. Asanuma, T. Ito, T. Yoshida, X. Liang and M. Komiyama, Angew. Chem., Int. Ed., 1999, 38, 2393–2395 CrossRef CAS PubMed.
- H. Asanuma, X. Liang, T. Yoshida and M. Komiyama, ChemBioChem, 2001, 2, 39–44 CrossRef CAS PubMed.
- X. Liang, T. Mochizuki and H. Asanuma, Small, 2009, 5, 1761–1768 CrossRef CAS PubMed.
- H. Asanuma, X. Liang, H. Nishioka, D. Matsunaga, M. Liu and M. Komiyama, Nat. Protoc., 2007, 2, 203–212 CrossRef CAS PubMed.
- M. Biswas and I. Burghardt, Biophys. J., 2014, 107, 932–940 CrossRef CAS PubMed.
- H. Asanuma, Nucleic Acids Symp. Ser., 2005, 49, 35–36 CrossRef PubMed.
- Y. Hachikubo, S. Iwai and T. Q. P. Uyeda, Biotechnol. Bioeng., 2010, 106, 1–8 CAS.
- L. You, A. Hoonlor and J. Yin, Bioinformatics, 2003, 19, 435–436 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed figures, tables, and program scripts for reaction rate constant calculations and deterministic simulations of reaction networks. See DOI: 10.1039/c7ra02607b |
| This journal is © The Royal Society of Chemistry 2017 |