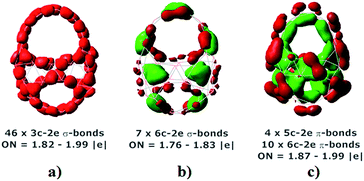Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Aromatic cage-like B46: existence of the largest decagonal holes in stable atomic clusters†
Truong Ba Tai *ab and
Minh Tho Nguyen
*ab and
Minh Tho Nguyen c
c
aComputational Chemistry Research Group, Ton Duc Thang University, Ho Chi Minh City, Vietnam. E-mail: truongbatai@tdt.edu.vn
bFaculty of Applied Sciences, Ton Duc Thang University, Ho Chi Minh City, Vietnam
cDepartment of Chemistry, KU Leuven, Leuven City, Belgium
First published on 21st April 2017
Abstract
The most stable form of B46 has a cage-like structure containing two hexagonal, two heptagonal and two decagonal holes. The intriguing presence of decagonal holes is a remarkable breakthrough since such large holes have never been found before for atomic clusters. This finding not only provides more insights into the growth motif of large-sized boron clusters, but also presents a new family of cage-like boron clusters containing large BN holes with N = 6–10.
Introduction
Exhibiting a wide range and an unpredictability of structural characteristics, boron clusters are of great interest to theoretical and experimental scientists.1–6 The early studies showed that small boron clusters at neutral state Bn (n = 2–19) have planar or quasi-planar structures containing basic triangular units.1–3 At larger sizes, they exhibit more complex geometries, including convex structures or tubular shapes containing either two or three N-membered rings connected together in antiprism bonding motif and quasi-planar geometries containing N-membered holes (N = 5–8).7,8 Interestingly, while their cationic state prefers the double-ring shapes at smaller sizes,5,9 anionic species Bn− remain the quasi-planar geometrical structures up to B40−.10Stimulated by the discovery of carbon fullerene C60 (ref. 11) and its unique properties, the search for cage-like boron clusters has been greatly attractive over the last decade. The buckyball B80, an isoelectronic species of the fullerene C60, was proposed in 2007 (ref. 12) and has received much attention,13,14 although recent theoretical studies reported that core–shell structures are more favourable in energy.15 Recently, the B40 cluster was found as a stable all-boron fullerene containing four heptagonal holes and two hexagonal holes.10,16,17 In the combined experimental and theoretical study, Wang et al.10 reported that this caged structure was somewhat less stable than a quasi-planar structure containing two hexagonal holes and both of them were identified in the photoelectron spectrum. These findings marked a breakthrough in the discovery of boron clusters since the anion B40− is the first cage-like boron cluster which was observed in experiment. A few cage-like systems such as B38,18 B39−, B41+ and B422+ were subsequently reported.19 A common structural feature of these systems is that they are composed of the hexagonal and heptagonal holes. Smaller cage-like structures B14, B280/− and B29− were also reported as smallest boron cages which were almost degenerate with the planar structures.20,21 More recently, we found that the B42+ and B44 also have, for their lowest-energy form, cage-like structures which contain eight- and nine-membered holes, respectively (Fig. 1).22 The neutral cage-like B42 is nearly degenerate with a triple ring tube of 14-atom strings. The presence of such large holes is intriguing since they have been found for the first time in atomic clusters, and has stimulated us to further explore larger sized species Bn to find out elements for the answer to the question as to whether boron clusters with larger holes exist.
In the present work, we report on the existence of the boron cluster B46 which exhibits a cage-like structure containing two hexagonal, two heptagonal and two decagonal (ten-membered) holes. The presence of decagonal holes has never been found before in atomic clusters, of either main group elements or transition metals. The present work does not only provide more insight into the growth motif of boron clusters, but it also shows a new family of cage-like boron clusters containing large hole BN with N = 6–10 (Fig. 1).
Computational methods
Extensive structural searches for B46 were carried out by using stochastic random searching procedures,23 and manual structural construction based on the known structures of smaller sized boron clusters17–19,22 by using the PBE0 functional24 in conjunction with small basis set 3-21G.25 Low-lying isomers B46 with relative energy of 0.0–5.0 eV obtained from initial geometry optimizations at the PBE0/3-21G were fully re-optimized at the higher level PBE0/6-311+G(d).26 To identify a true global minimum, single-point electronic energies of a few lowest-lying B46 isomers were subsequently calculated using the couple-cluster theory CCSD(T)/6-31G(d) method27 at their PBE0/6-311+G(d) optimized geometries. These computational methods were used to effectively establish the energy landscape of boron clusters in the literature.3,4,7–9,22 All calculations were performed using the Gaussian 09 (ref. 28) and Molpro 2009 packages.29Results and discussion
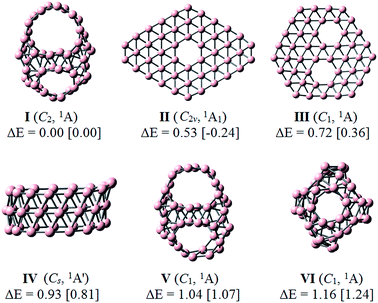
Identification of the global minimum for B46 was carried out using the DFT and CCSD(T) methods. The optimized geometries and relative energies (eV) of a few lowest-lying B46 isomers are depicted in Fig. 2, while those of less stable isomers are shown in Fig. S1 of the (ESI†) file. At the CCSD(T)/6-31G(d)//PBE0/6-311+G(d) level, our computed results show that structure I (C2, 1A) which contains two hexagonal, two heptagonal and two decagonal holes is the most stable form. This structure is composed of 54 triangular units and six polygonal holes. The latter includes two decagonal B10, two heptagonal B7 and two hexagonal B6 holes. This isomer can be constructed by replacing two neighboured heptagonal B7 holes of the B40 fullerene by two decagonal B10 holes and following the Euler's rule for a polyhedron: E(104 edges) = F(54 triangular + 2 hexagonal + 2 heptagonal + 2 decagonal faces) + V(46 vertices) − 2.Although a quasi-planar structure II (C2ν, 1A1) which contains one hexagonal hole is more stable at the PBE0/6-311+G(d) level, it is 0.53 eV less stable than I at the CCSD(T)/6-31G(d). These calculated results are consistent with the early reports that the PBE0 tends to overestimate the cohesive energy of the quasi-planar or planar structures.9,30 The next isomers exhibit different structural characteristics, including a quasi-planar structure III (C1, 1A), a tubular form IV (Cs, 1A′) and cage-like structures V (C1, 1A) and VI (C1, 1A), with relative energies of at least 0.72 eV at the CCSD(T)/6-31G(d) level. The structure III is also quasi-planar structure containing two hexagonal hole, while the structure IV is tubular form which is composed of two fifteen-membered rings and one sixteen-membered ring.
As shown in Fig. 1, the clusters B40, B42, B44 and B46 have similar geometries in which two neighboured B7 holes of B40 were replaced by two B8, B9 and B10 holes to form the B42, B44 and B46, respectively. We expect that these large-sized holes play as stable units in the building up of larger boron clusters.
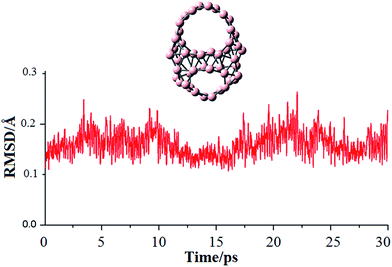
To gain more understanding about the high stability of the isomer I, we performed molecular dynamics (MD) simulation for this system by using the CP2K programs.31 The simulation was carried out at temperature of 500 K during a time of 30 ps using the PBE functional in conjunction with the 6-31G(d) basis set. RMSD values were calculated using the VMD code32 and their plots are depicted in Fig. 3 together with the movie of simulation trajectory at 500 K (ESI†). During the BO-MD simulation at 500 K, the isomer I retains its connectivity pattern and cage-like shape with two decagonal holes. The root mean square deviation (RMSD) varies in range of 0.11 to 0.26 Å. The high stability of decagonal holes is of fundamental characteristic and gives us more understanding about the growth mechanism of boron clusters.
The characteristics of electron delocalization and aromaticity of boron clusters have attracted much attention since they provide us with better understanding about their stability. The aromatic feature of B46 is first evaluated using the nucleus independent chemical shift (NICS)33 which is one common criterion to evaluate the molecular aromaticity. Our NICS calculations at the central position of structure I point out that this cage is highly aromatic with a large negative NICS value of −26 ppm. This value is comparable to the NICS values obtained earlier for boron cages, e.g. −38 ppm for B39−,19a −42 ppm for B40 (ref. 10) and −21 ppm for B44.22a In the previous report, using the profiles of the z-component of the induced magnetic field (Bindz), Merino et al.17a showed that the intensity of Bindz in B40 diminishes gradually along the center to the surface of cage B40. Based on the computed Bindz profiles, these authors also indicated that there is strong delocalization in σ-electron systems of both 6- and 7-membered rings. While the π-electron system of the 6-membered rings presents strong delocalization, the π-electron delocalization of the 7-membered rings is much less.
To have more insight into the high stability and aromaticity of I, we performed a topological analysis of the electron localization function (ELF).34 This approach does not only give us a general view of bonding pattern and electron distribution, but also allows the aromatic feature of the systems to be examined on the basis of their bifurcation values of the ELFσ and ELFπ components.7,22,35 Accordingly, each total ELF map can be partitioned in terms of separate ELFσ and ELFπ components that arise from the contributions of σ and π electrons, respectively. An aromatic system possesses a high ELF bifurcation value, whereas the corresponding bifurcation value is low in an anti-aromatic system. The ELF analysis was carried out by using the Dgrid-4.6 package.36
Our analysis of canonical molecular orbitals (CMOs) for I shows that this species contains a total of 69 valence MOs which are separated into 55 σ-MOs and 14 π-MOs. The ELFπ and ELFσ plots depicted in Fig. 4 emphasize an excellent electron delocalization for both σ and π electron systems of cage-like structure I. At the value of ELFσ = 0.85, the isosurface of the ELFσ is separated into 54 basins that determine the chemical bonding of 54 triangular units. The isosurface of ELFπ is separated at the bifurcation value of ELFπ = 0.70 which consequently indicates a π electron delocalization over the whole system. In general, such an electron distribution with high bifurcation values gives raise to two highly delocalized σ and π bonding systems, which make the isomer I aromatic and thereby highly thermodynamically stable.
To probe a better understanding about the chemical bonding characteristic of the B46, the further analysis was carried out for the most stable isomer I by using adaptive natural density partitioning (AdNDP) method.37 This approach was effectively used to analyze the chemical bonds of boron clusters in the early reports.4c,10,19 As shown in Fig. 5, 69 valence electron pairs of the isomer I are almost delocalized over structure and form 55 σ-bonds and 14 π-bonds. First set includes 46(3c–2e) σ-bonds (Fig. 5a) and 8(6c–2e) σ-bonds (Fig. 5b) which distribute on 54 triangle units. The remaining (6c–2e) σ-bond is located at top of structure (Fig. 5b) that supports for high stability of two ten-membered rings. Interestingly, second set includes 4 (5c–2c) π-bonds and 10 (6c–2e) π-bonds that are delocalized over planar boron double chains (BDCs) of the B46 (Fig. 5c). This delocalized σ and π-bonding pattern agrees well with our above ELF analysis and strongly supports for high stability of the B46 I.
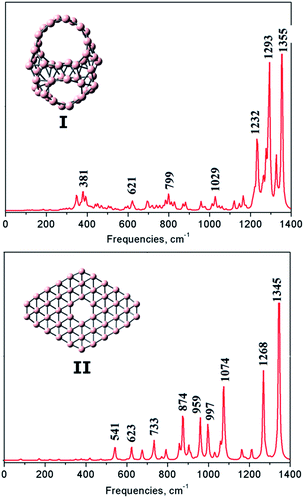
The vibrational spectrum is interesting and helpful since it allows us to identify structural characteristics. To assist future experimental studies, simulations of infrared (IR) spectra of two stable lowest-lying isomers I and II obtained at the PBE0/6-311+G(d) level are shown in Fig. 6. While the IR spectrum of the planar structure II exhibits many intensive peaks in a large range of 500–1400 cm−1, the spectrum of I is more concentrated in the range of 1200–1400 cm−1 and characterized by much less intensive peaks at low frequencies. For isomer I, seven major peaks appear at 381, 621, 799, 1029, 1232, 1293 and 1355 cm−1 which correspond to the intense peaks centered of 380, 713 and 1274 cm−1 of the cage B40,17 and the peaks of 390, 776, 1005, 1231, 1275 cm−1 of the cage-like B44.22
Conclusions
In conclusion, we performed a theoretical study on the B46 cluster by using DFT and CCSD(T) methods, and found that the most stable form of B46 is the cage-like structure I containing two decagonal, two heptagonal and two hexagonal holes. The structure I is composed of two delocalized σ and π bonding systems that rationalize its high stability. BO-MD simulations at 500 K showed that the B46 is both thermodynamically and kinetically stable. The analysis of chemical bonding characteristics showed that the B46 contains two delocalization σ and π electron systems that supports for its enhanced stability. The presence of decagonal holes again marks a breakthrough since it has been never found before in elemental clusters. The present work does not only provide more insight into the growth motif of boron clusters, but it also emphasizes a new family of cage-like boron clusters containing large holes BN with N = 6–10.Acknowledgements
We are indebted to the KU Leuven Research Council (GOA program) and Vlaams Supercomputer Centrum (VSC).Notes and references
- (a) I. Boustani, Z. Zhu and D. Tomanek, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 193405 CrossRef; (b) I. Boustani, Chem. Modell., 2011, 8, 1 CAS; (c) S. Chacko, D. G. Kanhere and I. Boustani, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035414 CrossRef.
- (a) W. L. Li, Y. F. Zhao, H. S. Hu, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 5540 CrossRef CAS PubMed; (b) C. Romanescu, D. J. Harding, A. Fielicke and L. S. Wang, J. Chem. Phys., 2012, 137, 014317 CrossRef PubMed; (c) A. N. Alexandrova, A. I. Boldyrev, H.-J. Zhai and L.-S. Wang, Coord. Chem. Rev., 2006, 250, 2811 CrossRef CAS; (d) Z. A. Piazza, I. A. Popov, W.-L. Li, R. Pal, X. C. Cheng, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2014, 141, 034303 CrossRef PubMed; (e) I. A. Popov, Z. A. Piazza, W. L. Li, L. S. Wang and A. I. Boldyrev, J. Chem. Phys., 2013, 139, 144307 CrossRef PubMed; (f) W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202 CrossRef CAS PubMed.
- (a) A. G. Arvanitidis, T. B. Tai, M. T. Nguyen and A. Ceulemans, Phys. Chem. Chem. Phys., 2014, 16, 18311 RSC; (b) T. B. Tai, A. Ceulemans and M. T. Nguyen, Chem.–Eur. J., 2012, 18, 4510 CrossRef CAS PubMed; (c) H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, Chem. Phys. Lett., 2013, 557, 32 CrossRef; (d) T. B. Tai, D. J. Grant, M. T. Nguyen and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 994 CrossRef CAS PubMed; (e) T. B. Tai, N. M. Tam and M. T. Nguyen, Chem. Phys. Lett., 2012, 530, 71 CrossRef CAS.
- (a) J. O. C. Jimenez-Halla, R. Islas, T. Heine and G. Merino, Angew. Chem., Int. Ed., 2010, 49, 5668 CrossRef CAS PubMed; (b) D. Moreno, S. Pan, L. Liu-Zeonjuk, R. Islas, E. Osorio, G. M. Guajardo, P. K. Chattaraj, T. Heine and G. Merino, Chem. Commun., 2014, 50, 8140 RSC; (c) F. Cervantes-Navarro, G. Martinez-Guajardo, E. Osorio, D. Moreno, W. Tiznado, R. Islas, K. J. Donald and G. Merino, Chem. Commun., 2014, 50, 10680 RSC; (d) G. Martinez-Guajardo, A. P. Sergeeva, A. I. Boldyrev, T. Heine, J. M. Ugalde and G. Merino, Chem. Commun., 2011, 47, 6242 RSC; (e) S. Jalife, L. Liu, S. Pan, J. L. Cabellos, E. Osorio, C. Lu, T. Heine, K. J. Donald and G. Merino, Nanoscale, 2016, 8, 17639 RSC.
- E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503 CrossRef CAS PubMed.
- (a) S. Li, Z. Zhang, Z. Long, G. Sun and S. Qin, Sci. Rep., 2016, 6, 1 CrossRef CAS PubMed; (b) A. B. Rahane and V. Kumar, Nanoscale, 2015, 7, 4055 RSC.
- (a) T. B. Tai, L. V. Duong, H. T. Pham, D. T. T. Mai and M. T. Nguyen, Chem. Commun., 2014, 50, 1558 RSC; (b) T. B. Tai and M. T. Nguyen, Chem. Commun., 2015, 51, 7677 RSC; (c) T. B. Tai and M. T. Nguyen, Phys. Chem. Chem. Phys., 2015, 17, 13672 RSC.
- (a) Z. A. Piazza, H.-S. Hu, W.-L. Li, Y.-F. Zhao, J. Li and L.-S. Wang, Nat. Commun., 2014, 5, 31 Search PubMed; (b) W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 126, 12257 CrossRef PubMed; (c) B. Kiran, S. Bulusu, H.-J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961 CrossRef CAS PubMed.
- T. B. Tai, N. M. Tam and M. T. Nguyen, Theor. Chem. Acc., 2012, 131, 1241 CrossRef.
- H.-J. Zhai, Y.-F. Zhao, W.-L. Li, Q. Chen, H. Bai, H.-S. Hu, Z. A. Piazza, W.-J. Tian, H.-G. Lu, Y.-B. Wu, Y.-W. Mu, G.-F. Wei, Z.-P. Liu, J. Li, S.-D. Li and L.-S. Wang, Nat. Chem., 2014, 6, 727 CAS.
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS.
- N. G. Szwacki, A. Sadrzadeh and B. I. Yakobson, Phys. Rev. Lett., 2007, 98, 166804 CrossRef PubMed.
- (a) A. Ceulemans, J. T. Muya, G. Gopakumar and M. T. Nguyen, Chem. Phys. Lett., 2008, 461, 226 CrossRef CAS; (b) J. T. Muya, E. Lijnen, M. T. Nguyen and A. Ceulemans, Chem. Phys. Chem., 2013, 14, 346 CrossRef CAS PubMed.
- (a) S. De, A. Willand, M. Amsler, P. Pochet, L. Genoverse and S. Grodecker, Phys. Rev. Lett., 2011, 106, 225502 CrossRef PubMed; (b) Y. Li, G. Zhou, J. Li, B.-L. Gu and W. Duan, J. Phys. Chem. C, 2008, 112, 19268 CrossRef CAS.
- H. Li, N. Shao, B. Shang, L. F. Yuan, J. L. Yang and X. C. Zeng, Chem. Commun., 2010, 46, 387 Search PubMed.
- H. T. Pham, L. V. Duong, N. M. Tam, M. P. Pham-Ho and M. T. Nguyen, Chem. Phys. Lett., 2014, 608, 295 CrossRef CAS.
- (a) G. Martinez-Guajardo, J. L. Cabellos, A. Diaz-Celaya, S. Pan, R. Islas, P. K. Chattaraj, T. Heine and G. Merino, Sci. Rep., 2015, 5, 11287 CrossRef CAS PubMed; (b) R. He and X. C. Zeng, Chem. Commun., 2015, 51, 3185 RSC.
- (a) J. Lv, Y. Wang, L. Zhu and Y. Ma, Nanoscale, 2014, 6, 11692 RSC; (b) T. B. Tai and M. T. Nguyen, Nanoscale, 2015, 7, 3316 RSC.
- (a) Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li and L. S. Wang, ACS Nano, 2015, 9, 754 CrossRef CAS PubMed; (b) Q. Chen, S. Y. Zhang, H. Bai, W. J. Tian, T. Gao, H. R. Li, C. Q. Miao, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 8160 CrossRef CAS PubMed.
- (a) L. Cheng, J. Chem. Phys., 2012, 136, 104301 CrossRef PubMed; (b) J. Zhao, X. Huang, R. Shi, H. Liu, Y. Su and R. B. King, Nanoscale, 2015, 7, 15086 RSC.
- (a) Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307 CrossRef PubMed; (b) H. R. Li, T. Jian, W. L. Li, C. Q. Miao, Y. J. Wang, Q. Chen, X. M. Luo, K. Wang, H. J. Zhai, S. D. Li and L. S. Wang, Phys. Chem. Chem. Phys., 2016, 18, 29147 RSC.
- (a) T. B. Tai and M. T. Nguyen, Chem. Commun., 2016, 52, 1652 RSC; (b) T. B. Tai and M. T. Nguyen, Phys. Chem. Chem. Phys., 2016, 18, 11620 RSC.
- T. B. Tai and M. T. Nguyen, J. Chem. Theory Comput., 2011, 7, 1119 CrossRef CAS PubMed.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS; (c) J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef.
- (a) J. S. Binkley, J. A. Pople and W. J. Hehre, J. Am. Chem. Soc., 1980, 102, 939 CrossRef CAS; (b) M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, J. Am. Chem. Soc., 1982, 104, 2797 CrossRef CAS; (c) K. D. Dobbs and W. J. Hehre, J. Comput. Chem., 1987, 8, 861 CrossRef CAS.
- (a) A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639 CrossRef CAS; (b) K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650 CrossRef.
- M. Rittby and R. J. Bartlett, J. Phys. Chem., 1988, 92, 3033 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- H. J. Werner, et al., MOLPRO 09, version 2009.1, 2009, see, http://www.molpro.net Search PubMed.
- F. Li, P. Jin, D. Jiang, L. Wang, S. B. Zhang, J. Zhao and Z. Chen, J. Chem. Phys., 2012, 136, 074302 CrossRef PubMed.
- J. Vande Vonele, M. Krack, F. Mohamed, M. Parrinello, Y. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 8, 1314 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- P. V. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. V. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317 CrossRef CAS.
- A. Becke and K. Edgecombe, J. Chem. Phys., 1990, 92, 5397 CrossRef CAS.
- J. C. Santos, W. Tznado, R. Contreras and P. Fuentealba, J. Chem. Phys., 2004, 120, 1670 CrossRef CAS PubMed.
- M. Kohout, Dgrid-4.6, Radebeul, 2011.
- D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra02870a |
| This journal is © The Royal Society of Chemistry 2017 |