Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Large activation energy in aged Mn-doped Sr0.4Ba0.6Nb2O6 ferroelectric ceramics
Yingying Zhao,
Jiping Wang *,
Lixue Zhang*,
Shujuan Liu,
Dawei Zhang and
Xuan Wang
*,
Lixue Zhang*,
Shujuan Liu,
Dawei Zhang and
Xuan Wang
State Key Laboratory for Mechanical Behavior of Materials, School of Materials Science and Engineering, Xi'an Jiaotong University, Xi'an 710049, China. E-mail: jpwang@mail.xjtu.edu.cn; lxzhang@mail.xjtu.edu.cn
First published on 19th May 2017
Abstract
The properties of ferroelectrics can be significantly enhanced through appropriate doping, and also can be strongly influenced by aging treatment. In this paper, we report a slow aging effect with a large activation energy and an enhanced energy storage density in the aged Mn-doped Sr0.4Ba0.6Nb2O6 ferroelectric ceramics. Mn-doped Sr0.4Ba0.6Nb2O6 (SBN40-xMn) (x = 0.0, 1.0, 2.0, 4.0, 6.0, 8.0 mol%) ferroelectric ceramics were prepared by the conventional solid state reaction method. The dielectric constant of Mn-doped Sr0.4Ba0.6Nb2O6 ceramics shows a decrease after aging in the ferroelectric state. The activation energy derived from the dielectric aging curves shows an obviously large value of 1.87 eV and 2.01 eV for SBN40-4Mn and SBN40-6Mn sample, respectively, compared with the value of 0.55 eV in SBN40-2Mn sample. Besides, the large activation energy is much higher than those values reported in previous literatures for perovskite ferroelectrics such as BaTiO3 and Pb(Ti0.42Zr0.58)O3 based system. The relaxation time (reflecting the aging rate) is also much longer than the cited perovskite systems. The large relaxation time and activation energy both indicate the slow aging process. Moreover, the aging is related to the migration of oxygen vacancies, and the existence of oxygen vacancies in the Sr0.4Ba0.6Nb2O6 ceramics is proved by the dielectric relaxation at high temperature and the XPS spectra investigation. Based on the longer relaxation time and larger activation energy, a different diffusion path of oxygen vacancy in our tetragonal tungsten bronze structure high Mn doped SBN is proposed: a long distance migration path of oxygen vacancies among neighbor oxygen octahedron, in contrasting to the short migration distance of oxygen vacancies within perovskite unit cells. In consequence of the long path oxygen vacancy diffusion, a typical double hysteresis loop appeared and the maximum energy storage density is achieved in aged SBN40-4Mn sample. These results can provide guidance for understanding the dynamic of aging process and improving the energy storage properties of doped ferroelectric materials with the tungsten bronze structure.
Introduction
Ferroelectric materials are widely used in sensors, capacitors, actuators, electro-optical and transducers because of their excellent dielectric, ferroelectric and piezoelectric properties.1–5 The properties of ferroelectrics can be tailored through the addition of dopants.6,7 Besides, some dopant like acceptor can induce aging and aging further strongly influences the properties of ferroelectric materials.8–10 On one hand, during aging the ferroelectric, dielectric and piezoelectric properties of ferroelectric materials will change with time. It is unfavorable to the application of ferroelectric materials.11,12 On the other hand, there are reports showing that the large recoverable electrostrain can be induced by aging.13,14 Therefore, it is so important to study the process of aging behavior in the doped ferroelectric materials.Aging has been reported in many perovskite-type structure ferroelectrics. The deformation of ferroelectric hysteresis loop (including the appearance of constricted or double hysteresis loop) in large signal and the decrease of dielectric properties in small signal are the main characteristic for aged ferroelectrics.12,14 The double hysteresis loop induced by aging effect has been observed in most acceptor-doped perovskite-type structure ferroelectrics, such as Mn-doped BaTiO3, PbTiO3 and KNbO3-based ceramics.15–17 The decrease of dielectric properties has been reported in Ba0.6Sr0.4Nb2O6–Ba0.6Sr0.4TiO3 (SBN–BST),18 Ba0.8Sr0.2TiO3,19 Ba0.77Ca0.23TiO3 (ref. 8) systems. Three models have been proposed in explaining the origin of aging process: volume effect, domain wall effect and grain boundary effect. They are all concerned with the migration of oxygen vacancy, which is influenced mostly by the local structure of ferroelectric materials.11,12,16,20 The investigation of activation energy of oxygen vacancy migration shows that the value is closely related to its moving distance.19,21,22 In reported acceptor-doped perovskite-type structure ferroelectrics, the activation energy value of oxygen vacancy migration is about 1 eV within a short-range distance.19,21–23
Strontium barium niobate, SrxBa1−xNb2O6 (SBN), is a typical lead-free ferroelectric ceramic with a tetragonal tungsten bronze type structure, and has a wide composition range 0.25 ≤ x ≤ 0.75. It has received considerable attention due to its high pyroelectric coefficient and piezoelectric constants.24–26 More importantly, the ferroelectric properties, Curie temperature, as well as the dielectric constant of SBN can be adjusted by changing the Sr/Ba ratio.27,28 The SBN unit cell formula is (A1)2(A2)4(C)4(B1)2(B2)8O30. Its Nb atoms occupy the B1 and B2 sites forming NbO6 octahedral parallel to the polar c-axis, which share corners forming three different interstices (A1, A2, and C). A1 is a 12-coordinated tetragonal site and is occupied only by Sr ion. Ba ion and the residual Sr ion occupy the bigger 15-coordinated pentagonal interstice (A2). While there are only five Sr and Ba ions for six A sites, thus one sixth of A sites and the smallest C site are empty.29–31 For SBN, the study of dopant is mainly about the sintering behavior and the electric properties.32,33 However, there are only two works investigating the aging behavior and the activation energy of oxygen vacancy diffusion in acceptor-doped tungsten bronze structure ferroelectrics, as far as we know.18,34 Therefore, further study about the effects of both the dopant and the oxygen vacancy on the aging dynamic in SBN is necessary for understanding the aging of tungsten bronze structure ferroelectrics.
In this paper, we doped Mn in SBN ferroelectric ceramics, which has a tungsten bronze type structure. Moreover, we found a dielectric and polarization aging in the doped SBN samples. Compared with the perovskite ferroelectrics such as 1 mol% Mn-doped Ba0.8Sr0.2TiO3 (ref. 19) and 6 mol% Mn-doped Pb(Ti0.42Zr0.58)O3 (ref. 22) (more information shown in subsequent Table 1), a larger activation energy value of the oxygen vacancy migration is revealed in our high Mn doped samples. In consequence, a different migration path of oxygen vacancy is proposed in our study. Our results may provide guidance for the research of aging in tungsten bronze structure ferroelectric ceramics.
| Composites | Structure | Dopant and concentration | Activation energy (Ea/eV) | Temperature | Reference | Computing method |
|---|---|---|---|---|---|---|
| Ba0.8Sr0.2TiO3 | Perovskite | 1% Mn | 0.43 | 90–110 °C | 19 | Dielectric permittivity |
| Pb(Ti,Zr)O3 | Perovskite | 0.1% Fe | 0.64 | 40–80 °C | 21 | Phase angle |
| Pb(Ti0.42Zr0.58)O3 | Perovskite | 3% Mn | 0.69 | 35–75 °C | 22 | Internal bias |
| Pb(Ti0.42Zr0.58)O3 | Perovskite | 6% Mn | 0.64 | 35–75 °C | 22 | Internal bias |
| Pb(Ti0.42Zr0.58)O3 | Perovskite | 3% Al | 0.73 | 35–75 °C | 22 | Internal bias |
| Pb(Ti0.42Zr0.58)O3 | Perovskite | 6% Al | 0.83 | 35–75 °C | 22 | Internal bias |
| BaTi0.995Mg0.005O2.995 | Perovskite | 0.5% Mg | 0.47 ± 0.04 | 150–300 °C | 23 | Dielectric losses |
| Sr0.4Ba0.6Nb2O6 | Tungsten bronze | 2% Mn | 0.55 | 40–55 °C | This work | Dielectric permittivity |
| Sr0.4Ba0.6Nb2O6 | 4% Mn | 1.87 | 35–50 °C | This work | ||
| Sr0.4Ba0.6Nb2O6 | 6% Mn | 2.01 | 35–50 °C | This work |
Experimental procedures
Preparation
Sr0.4Ba0.6(Nb1−xMnx)2O6 ceramics were prepared by the conventional solid state reaction method using SrCO3 (99.9%), BaCO3 (99.9%), Nb2O5 (99.9%) and MnO2 (99.9%) as starting raw materials (x = 0.0, 1.0, 2.0, 4.0, 6.0, 8.0 mol%). These highly pure chemicals are all from Alfa Aesar company. For convenience, the formula of compositions Sr0.4Ba0.6(Nb1−xMnx)2O6 is abbreviated as SBN40-xMn. The starting materials were weighed according to the stoichiometric formula and ball milled for 4 h. The dried slurries were calcined at 1200 °C for 2 h and then ball milled again for 6 h. After dried at 80 °C, the calcined powders were combined with 10 wt% polyvinyl alcohol (PVA) solution and pressed into disks with a diameter of 12 mm. The disks were sintered at 1300–1370 °C for 4 h. After sintered, the samples were polished and then Ag paint was applied to both faces of the samples, firing at 800 °C for 30 min.Characterization
The X-ray diffraction (XRD, X'Pert diffractometer with Cu Kα λ – 0.15406 nm) was used to determine the phase structure of the samples at room temperature. Microstructures of the SBN40-xMn ceramics were observed with a scanning electron microscope (SEM, Hitachi S-2700). The temperature dependence of dielectric constant was measured by HIOKI LCR Hitester at different frequencies over a temperature range of −50–200 °C. The time dependence of dielectric constant was measured by HIOKI LCR Hitester at several aging temperatures (at 1 kHz frequency). The time dependence of polarization-electric field hysteresis loops (P–E hysteresis loops) were characterized by Precision Premier II from Radiant Company, together with a high voltage amplifier. Before each hysteresis loop test and dielectric aging test, a deaging treatment was performed by heating the samples to 200 °C, which is above Curie temperature (43.9–133 °C), and the samples were held for 2 h at 200 °C, then quenched to the aging temperature 25 °C. The P–E hysteresis loops aging time ranges from 1 min to 785 h (about 1 month). Hereafter the aging time of 1 min is denoted as fresh sample state, and the long aging time of 785 h is denoted as the final sample state. The X-ray photoelectron spectroscopy (XPS) spectra were obtained by Axis Ultra (UK) using monochromatic Al Kα (150 W, 15 kV, 1486 eV).Results and discussion
Microstructure
Fig. 1 shows the morphologies of SBN40-xMn ceramics doped with different levels of Mn. It is found that the grains are anisometric and most of them show columnar shape. The grain size does not change much with the Mn content increasing. The columnar shape of the grains may be caused by the growth habit of the tungsten bronze structure. Because the grain growth in (001) facet of tungsten bronze structure is faster due to the lower surface energy.35 | ||
| Fig. 1 The morphologies of SBN40-xMn ceramics: (a) SBN40-0Mn, (b) SBN40-1Mn, (c) SBN40-2Mn, (d) SBN40-4Mn, (e) SBN40-6Mn, (f) SBN40-8Mn. | ||
XRD patterns results
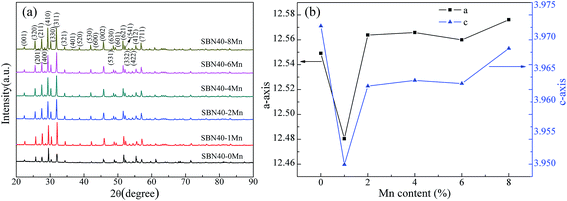
XRD patterns of SBN40-xMn samples are shown in Fig. 2(a). It can be seen that all the samples show a tetragonal tungsten bronze (TTB) phase without any impurity. Fig. 2(b) shows the variation of the lattice parameters of all the samples with Mn content. With the Mn content increasing, both a- and c-axis parameters first decrease and then increase. Compared with the lattice parameters of the undoped SBN samples, the lattice parameters of Mn-doped SBN samples change little. That indicates the impossibility of Mn entering into A site to replace Sr/Ba ion, as the big radius difference between Mn ion and Sr/Ba ion can change the lattice parameter obviously.Temperature dependence of dielectric constant
Fig. 3 shows the temperature dependence of dielectric constant of SBN40-xMn ceramics measured at different frequencies. With the frequency increasing, the dielectric constant of all the samples decreases. With the temperature increasing, the dielectric constant of all the samples first increases and then decreases. The temperature of the maximum dielectric constant is the Curie temperature (TC) corresponding to the phase transition from ferroelectric to paraelectric. When the temperature is below TC, the dielectric constants of all the samples show weak frequency dependence. This is caused by the response of different scale domains under different frequencies. When the temperature is above TC, the frequency dependence of dielectric constant increases with the Mn content increasing. Moreover, the dielectric constant of high Mn samples (x > 2) shows a strong frequency dependence at temperature above TC. It has been reported that the dielectric relaxation at high temperature is related to the movement of oxygen vacancies.36,37 This suggests the existence of oxygen vacancy in SBN, which is induced by doping Mn into B site substituting Nb ion. More Mn dopants, more oxygen vacancy generated, so a strong frequency dependence of high Mn samples (x > 2) is observed. Besides, the values of TC are 133.0 °C, 100.4 °C, 96.2 °C, 62.2 °C, 54.0 °C, 43.9 °C for SBN40-0Mn to SBN40-8Mn samples, respectively, which decrease with increasing the Mn concentration.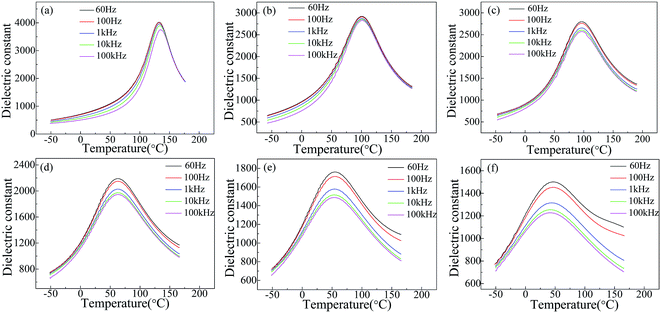 | ||
| Fig. 3 Temperature dependence of dielectric constant of SBN40-xMn ceramics: (a) SBN40-0Mn, (b) SBN40-1Mn, (c) SBN40-2Mn, (d) SBN40-4Mn, (e) SBN40-6Mn, (f) SBN40-8Mn. | ||
Dielectric aging (in a small signal) and the activation energy of oxygen vacancy migration
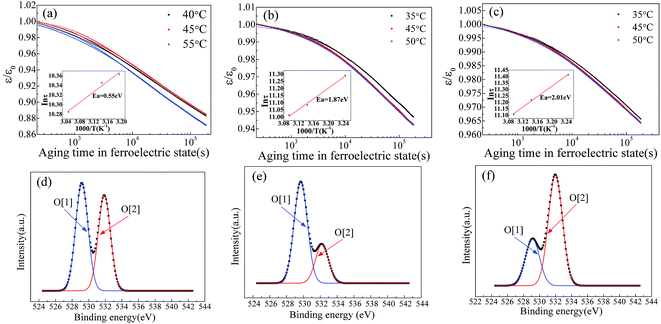
It is well known that the existence of oxygen vacancy in ferroelectric materials will generate aging effect, such as the decrease of dielectric properties. The time dependence of dielectric constant of SBN40-2Mn, SBN40-4Mn, SBN40-6Mn samples at different temperatures (at 1 kHz frequency) was investigated and the results are shown in Fig. 4(a)–(c). Besides, the time dependence of dielectric constant of SBN40-2Mn, SBN40-4Mn, SBN40-6Mn samples with logarithmic scale for the x axis are shown in Fig. 5(a)–(c). It can be seen that the dielectric constant decreases fast first and then decreases slowly, showing a tendency to be gradually stable after aging 55 h (∼200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s).
000 s).
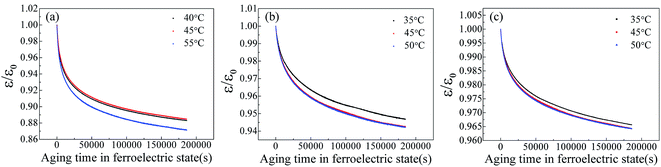 | ||
| Fig. 4 The dielectric aging behavior of SBN40-xMn samples at different temperatures (at 1 kHz) (a)–(c): (a) SBN40-2Mn, (b) SBN40-4Mn, (c) SBN40-6Mn. | ||
As the dielectric aging is related to the oxygen vacancy, in order to verify the existence of oxygen vacancy (OV), the O 1s XPS spectra of SBN40-2Mn, SBN40-4Mn, SBN40-6Mn samples were investigated and the results are shown in Fig. 5(d)–(f). The O 1s XPS spectra of all the three samples can be fitted into two peaks. The fitted peak with lower binding energy of about 529.1 eV, denoted by O[1], represents the oxygen in the lattice, while the higher binding energy at about 531.9 eV, denoted by O[2], is assigned to absorbed oxygen species, relating to the presence of oxygen vacancy.9,38,39 The mole fraction of oxygen vacancy is not given. This is because the oxygen can be affected by many factors such as oxygen in the air, adsorbed oxygen and so on. So the mole fraction of oxygen measured by XPS is inaccurate.
Further, the oxygen vacancy migration influences the dynamics of aging process. It can be seen from Fig. 5(a)–(c) that for different aging temperatures the aging process is different, which indicated that the aging process is thermally activated. The dielectric aging follows the stretched exponential (or Kohlrausch) function as follows,40–42
ε = ε∞ + A1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(t/τ)υ] exp[−(t/τ)υ]
| (1) |
τm = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kBT) exp(Ea/kBT)
| (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus 1/T plots are shown in Fig. 5(a)–(c) insets and they exhibit a typical Arrhenius behavior. It can be seen that the activation energy value changes with the dopant concentration. Moreover, it is worth mentioning that the activation energy value of 1.87 eV and 2.01 eV differs significantly with the reported values for acceptor-doped perovskite ferroelectrics, such as BaTiO3 doped with Mn and Mg,19,23 Pb(Ti,Zr)O3 doped with Fe,21 and Pb(Ti0.42Zr0.58)O3 doped with Mn and Al.22 A summary of the activation energy values of oxygen vacancy diffusion in various reported perovskite systems and our samples are listed in Table 1. It can be found that for perovskite structure ferroelectrics, the activation energy of oxygen vacancy diffusion related to aging is less than 1.0 eV. Meanwhile, in BaTiO3 the activation energy of oxygen vacancy migration is also calculated with a value of 0.91 eV (ref. 46) and 0.99 eV.47 Comparing the activation energy of SBN in our study with the reported values of perovskite structure ferroelectrics, the activation energy value of 1.87 eV and 2.01 eV in SBN is much larger than the 1.0 eV of perovskite ferroelectrics. Besides, for the Pb(Ti0.42Zr0.58)O3 doped with various content of Mn and Al, the activation energy value does not change much with the dopant concentration. This is also contradicted with our results: with Mn content increasing, the activation energy increases from 0.55 eV to 2.01 eV.
τ versus 1/T plots are shown in Fig. 5(a)–(c) insets and they exhibit a typical Arrhenius behavior. It can be seen that the activation energy value changes with the dopant concentration. Moreover, it is worth mentioning that the activation energy value of 1.87 eV and 2.01 eV differs significantly with the reported values for acceptor-doped perovskite ferroelectrics, such as BaTiO3 doped with Mn and Mg,19,23 Pb(Ti,Zr)O3 doped with Fe,21 and Pb(Ti0.42Zr0.58)O3 doped with Mn and Al.22 A summary of the activation energy values of oxygen vacancy diffusion in various reported perovskite systems and our samples are listed in Table 1. It can be found that for perovskite structure ferroelectrics, the activation energy of oxygen vacancy diffusion related to aging is less than 1.0 eV. Meanwhile, in BaTiO3 the activation energy of oxygen vacancy migration is also calculated with a value of 0.91 eV (ref. 46) and 0.99 eV.47 Comparing the activation energy of SBN in our study with the reported values of perovskite structure ferroelectrics, the activation energy value of 1.87 eV and 2.01 eV in SBN is much larger than the 1.0 eV of perovskite ferroelectrics. Besides, for the Pb(Ti0.42Zr0.58)O3 doped with various content of Mn and Al, the activation energy value does not change much with the dopant concentration. This is also contradicted with our results: with Mn content increasing, the activation energy increases from 0.55 eV to 2.01 eV.
For better comparison, the values of relaxation time τ of SBN40-xMn samples in our work and other reported perovskite systems are shown in Table 2. As shown in Table 2, it is noticed that SBN40-xMn samples show a slow dielectric properties aging with a large relaxation time. On one hand, the relaxation time decreases with temperature increasing. On the other hand, the relaxation time increases with the content of Mn dopant increasing. The increase of relaxation time reflects an increase of activation energy with dopant content.41 This is in agreement with the results of Fig. 5. Besides, it is worth noting that the relaxation time of our samples is much longer than other reported perovskite ferroelectrics.40–42
| Composites | Structure | Dopant and concentration | Temperature (°C) | Relaxation time (second) | Reference |
|---|---|---|---|---|---|
| Ba0.8Sr0.2TiO3 | Perovskite | 1% Mn | 90 | 4150 | 19 |
| 100 | 3525 | 19 | |||
| 110 | 2890 | 19 | |||
| BaTi0.99Mn0.01O3 | Perovskite | 1.5% Ta | 40 | 574.48 | 40 |
| Na0.5Bi0.5TiO3 | Perovskite | 1.5% Fe | 25 | 8817 | 41 |
| Ba0.99Na0.01TiO3 | Perovskite | 1.5% Sm | 40 | 677.71 | 42 |
| Sr0.4Ba0.6Nb2O6 | Tungsten bronze | 2% Mn | 40 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 670 |
This work |
| 45 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 113 113 |
This work | |||
| 55 | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
This work | |||
| Sr0.4Ba0.6Nb2O6 | 4% Mn | 35 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 097 097 |
This work | |
| 45 | 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 135 135 |
This work | |||
| 50 | 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 675 675 |
This work | |||
| Sr0.4Ba0.6Nb2O6 | 6% Mn | 35 | 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 577 577 |
This work | |
| 45 | 74![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 527 527 |
This work | |||
| 50 | 66![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 638 638 |
This work |
The explanation of migration path of oxygen vacancy
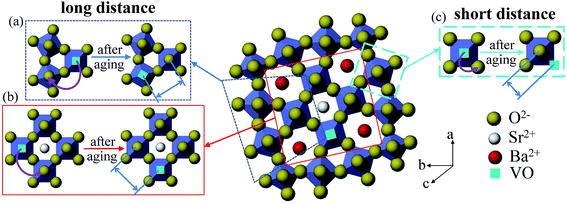
It has been reported that for ferroelectrics the change of properties during aging can be explained by the migration of oxygen vacancy.20,48 Due to the imbalance of valence resulted from the addition of acceptor-dopant Mn ion, the oxygen vacancy would be created.10 Aging rate is related to the migration time of oxygen vacancy. The acceptor dopant and the oxygen vacancy tend to form a defect dipole rather than remaining isolated during aging.7 Here we proposed a possible explanation based on a defect dipole volume effect model. Before aging the oxygen vacancy would randomly occupy one of the six sites in NbO6 octahedron. But this state is not stable and the defect dipoles formed by oxygen vacancy associate with Mn ion prefer to align along the spontaneous polarization, and this process is performed with the migration of oxygen vacancy. In the perovskite structure, the oxygen vacancy migration is processed in an oxygen octahedron and its migration path is short. For PZT, oxygen vacancy migrating from a face center to the neighbouring face center require approximately 0.9 eV of activation energy.49 It can be obtained from reported literatures that the activation energy for oxygen vacancy diffusion in perovskite structure is mostly less than 1 eV or about 1 eV. In ref. 21 and 50, it states that the longer the distance charges move, the larger the activation energy they need. Besides, at high temperature the dielectric relaxation is also involved with the diffusion of oxygen vacancy and the activation energy of oxygen vacancy diffusion is larger with a value between 1–2 eV.36,37,51 This is due to the dissociation of defect dipole at high temperature and thus the oxygen vacancy could move a long distance.23It is well known that the kinetic migration of oxygen vacancy is closely related to the local structure of ferroelectrics.16 Based on the above activation energy results, the activation energy for oxygen vacancy migration in our high Mn doped tungsten bronze structure SBN is much larger than perovskite ferroelectrics. It indicates that the aging process mechanism of tungsten bronze ferroelectrics may be different from the perovskite structure. For perovskite structure ferroelectrics, the structure is simple. While for SBN, due to its complicated structure with three different interstices, it is reasonable to believe that in tungsten bronze structure the migration path of oxygen vacancy may be different from the perovskite ferroelectrics. In SBN, the oxygen vacancy may move a long distance and it may be conducted with several oxygen octahedron in ab plane. The potential migration path of oxygen vacancy in SBN is shown in Fig. 6. For the condition of SBN40-4Mn and SBN40-6Mn samples with activation energy of 1.87 eV and 2.01 eV, respectively, the migration path of oxygen vacancy may cross the triangle and tetragonal interstices as shown in Fig. 6(a) and (b). For the condition of SBN40-2Mn sample with activation energy of 0.55 eV, the migration path of oxygen vacancy is probably similar with perovskite ferroelectrics: (c) within an oxygen octahedron. In addition, because the models interpreting the aging process is still under debate, the oxygen vacancy also may move a long distance to domain walls in the domain boundary model.18,52 This different migration path of oxygen vacancy might be the explanation for the larger activation energy in SBN. However, the fundamental reason for the movement path of oxygen vacancy needs further investigation.
Polarization aging (in a large signal)
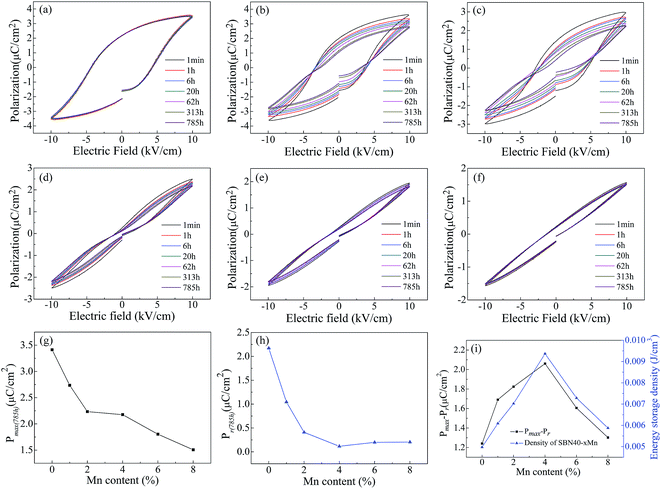
It is well known that double ferroelectric hysteresis loop will appear in acceptor-doped ferroelectrics during aging due to the diffusion of oxygen vacancy.53,54 In order to investigate the polarization aging of SBN, the P–E hysteresis loop evolution after aging different time of all the Mn-doped SBN ceramics are shown in Fig. 7(a)–(f). The samples for measuring P–E hysteresis loop aging were aged at temperature of 25 °C. It can be found that when x < 6% the constrict tendency of P–E hysteresis loop is more and more obvious with increasing the Mn content. This may indicate that the aging effect of doping Mn is strengthened with Mn content increasing. Moreover, when x = 4%, a typical double hysteresis loop induced by migration of oxygen vacancy is observed. Also for all the samples the shape of P–E hysteresis loops is gradually shrinking with the aging time increasing. However, when x > 4%, the P–E hysteresis loops did not show more obvious constricted shape and the shape of P–E hysteresis loop did not change much with the aging time increasing. We consider the reason for the vanishing of double hysteresis loop in higher Mn content sample SBN40-6Mn and SBN40-8Mn is that the aging temperature is close to their Curie temperature. It is well known that the defect polarization PD will align along the spontaneous polarization PS and form an internal bias field during aging for the perovskite ferroelectrics. After being applied with an electric field E, the PS will switch to the direction of electric field, while the PD cannot be switched during such a diffusionless process. After removing the electric field E, the PD will serve as a restoring force making the PS switch to the original state. As a result, the double P–E hysteresis loop appeared.11,13,55 When the measuring temperature is nearby the Curie temperature, the decreased degree of lattice deformation leads to a small defect polarization PD, resulting in a small restoring force. After the electric field removed, the PS cannot switch to the original state with a smaller restoring force, thus the double hysteresis loop is not observed.The changes of Pmax and Pr with Mn content after aging 785 h are shown in Fig. 7(g) and (h), respectively. With the Mn content increasing, the Pmax and Pr decreased. It can be found that SBN40-4Mn sample has the minimum Pr value after aging 785 h. This minimum Pr is considered to be related with the long path oxygen vacancy diffusion. Further analyses on the activation energy of oxygen vacancy diffusion under P–E hysteresis loop measurement are necessary to clarify this consideration. As the polarization is linked to the energy storage density,56–59 Fig. 7(i) gives the value of Pmax−Pr and the energy storage density after aging 785 h of all the samples. The change tendency of Pmax−Pr value is similar with that of energy storage density. It can be seen that the value of Pmax−Pr and energy storage density reach the maximum at x = 4%, which has an obvious double hysteresis loop. The reason for the maximum energy storage density can be attributed to the small Pr induced by the aged double hysteresis loops. Therefore, doping Mn and aging treatment are effective measures improving the energy storage density and it is meaningful to the practical application.
Conclusion
The effects of Mn dopant on the temperature dependence of dielectric properties, dielectric aging (in a small signal) behaviors as well as the fitted activation energy and the polarization aging (in a large signal) of Sr0.4Ba0.6Nb2O6 ceramics with a tetragonal tungsten bronze structure were investigated. The temperature dependence of the dielectric constant shows a dielectric relaxation at high temperature, which is involved with the existence of oxygen vacancy. And the existence of oxygen vacancy in our Sr0.4Ba0.6Nb2O6 ceramics is proved by the XPS spectra investigation. The activation energy value of the oxygen vacancy diffusion deduced from dielectric aging ranges from 0.55 eV to an obviously large value of 2.01 eV. Besides, the relaxation time is also much larger (reflecting the aging rate is slow) than that of the compared perovskite systems. Compared with the short migration distance of oxygen vacancy within perovskite unit cell, the possible different migration path of oxygen vacancy with a longer distance was proposed in higher Mn content SBN samples. A longer migration distance of oxygen vacancy needs a longer time and the corresponding aging rate is slow. The P–E loop of the SBN40-4Mn sample shows a double hysteresis loop as aged acceptor-doped perovskite structure ferroelectrics. The polarization aging revealed that when doped with 4 mol% Mn the energy storage density has the peak value. This may provide guidance for the study of dynamic in aging process and improvement of energy storage properties in tungsten bronze structure ferroelectrics.Acknowledgements
This work was supported by the National Basic Research Program of China (Grant No. 2012CB619401), the National Natural Science Foundation of China (Grant No. 51621063), the Natural Science Foundation of Shaanxi Province of China (Grant No. 2015JM5191), the Innovative Research Team of Ministry of Education of China (Grant No. IRT13034) and the “Fundamental Research Funds for the Central Universities”.References
- J. Chen, Q. Yun, W. Gao, Y. Bai, C. Nie and S. Zhao, Mater. Lett., 2014, 136, 11–14 CrossRef CAS.
- Y. Bai, X. Han, X. C. Zheng and L. Qiao, Sci. Rep., 2013, 3, 2895 CrossRef PubMed.
- Y. Tan, J. Zhang, Y. Wu, C. Wang, V. Koval, B. Shi, H. Ye, R. McKinnon, G. Viola and H. Yan, Sci. Rep., 2015, 5, 9953 CrossRef CAS PubMed.
- X. Hao and Y. F. Yang, J. Mater. Sci., 2007, 42, 3276–3279 CrossRef CAS.
- W. Li, Z. Xu, R. Chu, P. Fu and G. Zang, J. Eur. Ceram. Soc., 2012, 32, 517–520 CrossRef CAS.
- J. Li, R. Huo, R. Guo, F. Li, D. Wang, Y. Tian, Q. Hu, X. Wei, Z. He, Y. Yan and G. Liu, ACS Appl. Mater. Interfaces, 2016, 8, 31109–31119 Search PubMed.
- A. Chandrasekaran, D. Damjanovic, N. Setter and N. Marzari, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 214116 CrossRef.
- Q. Yue, L. Luo, X. Jiang, W. Li and J. Zhou, J. Alloys Compd., 2014, 610, 276–280 CrossRef CAS.
- F. Z. Huang, Z. H. Jiang, X. M. Lu, R. X. Ti, H. R. Wu, Y. Kan and J. S. Zhu, Appl. Phys. Lett., 2014, 105, 022904 CrossRef.
- E. Sapper, R. Dittmer, D. Damjanovic, E. Erdem, D. J. Keeble, W. Jo, T. Granzow and J. Rödel, J. Appl. Phys., 2014, 116, 104102 CrossRef.
- Y. A. Genenko, J. Glaum, M. J. Hoffmann and K. Albe, Mater. Sci. Eng., B, 2015, 192, 52–82 CrossRef CAS.
- L. Zhang and X. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094121 CrossRef.
- Z. Feng and S. W. Or, J. Alloys Compd., 2009, 480, L29–L32 CrossRef CAS.
- Z. Li and H. Fan, Solid State Ionics, 2009, 180, 1139–1142 CrossRef CAS.
- Y. Pu, D. Liu and X. Shi, Vacuum, 2014, 99, 38–41 CrossRef CAS.
- L. Zhang, W. Liu, W. Chen, X. Ren, J. Sun, E. A. Gurdal, S. O. Ural and K. Uchino, Appl. Phys. Lett., 2012, 101, 242903 CrossRef.
- W. Liu, L. Zhang, W. Chen, S. Li and X. Ren, Appl. Phys. Lett., 2011, 99, 092907 CrossRef.
- S. Ke, H. Huang, H. Fan, H. L. W. Chan and L. M. Zhou, J. Phys. D: Appl. Phys., 2007, 40, 6797–6802 CrossRef CAS.
- D. Xue, J. Gao, L. Zhang, H. Bao, W. Liu, C. Zhou and X. Ren, Appl. Phys. Lett., 2009, 94, 082902 CrossRef.
- X. Ren, Nat. Mater., 2004, 3, 91–94 CrossRef CAS PubMed.
- M. I. Morozov and D. Damjanovic, J. Appl. Phys., 2008, 104, 034107 CrossRef.
- K. Carl and K. H. Hardtl, Ferroelectrics, 1977, 17, 473–486 CrossRef.
- S. H. Cha and Y. H. Han, J. Appl. Phys., 2006, 100, 104102 CrossRef.
- Z. Yang, R. Gu, L. Wei and H. Ren, J. Alloys Compd., 2010, 504, 211–216 CrossRef CAS.
- I. Bhaumik, S. Ganesamoorthy, R. Bhatt, N. Subramanian, A. K. Karnal, P. K. Gupta, S. Takekawa and K. Kitamura, J. Alloys Compd., 2015, 621, 26–29 CrossRef CAS.
- A. S. Bhalla, R. Guo, L. E. Cross, G. Burns, F. H. Dacol and R. R. Neurgaonkar, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 2030–2035 CrossRef CAS.
- M. Said, T. S. Velayutham, W. C. Gan and W. H. Abd Majid, Ceram. Int., 2015, 41, 7119–7124 CrossRef CAS.
- J. L. Wang, B. Vilquin, B. Gautier, G. Dezanneau and N. Barrett, Appl. Phys. Lett., 2015, 106, 242901 CrossRef.
- C. S. Dandeneau, Y. Yang, B. W. Krueger, M. A. Olmstead, R. K. Bordia and F. S. Ohuchi, Appl. Phys. Lett., 2014, 104, 101607 CrossRef.
- A. Belous, O. V'yunov, D. Mishchuk, S. Kamba and D. Nuzhnyy, J. Appl. Phys., 2007, 102, 014111 CrossRef.
- T.-T. Fang and H.-Y. Chung, Appl. Phys. Lett., 2009, 94, 092905 CrossRef.
- J. T. Shiue and T. T. Fang, J. Eur. Ceram. Soc., 2002, 22, 1705–1709 CrossRef CAS.
- T.-T. Fang and F.-Y. Chen, J. Appl. Phys., 2006, 100, 014110 CrossRef.
- S. Bu, D. Chun and G. Park, Jpn. J. Appl. Phys., 1997, 36, 4351–4354 CrossRef CAS.
- B. Yang, L. Wei, X. Chao, Z. Wang and Z. Yang, J. Alloys Compd., 2015, 632, 368–375 CrossRef CAS.
- Z. Yu, C. Ang, P. M. Vilarinho, P. Q. Mantas and J. L. Baptista, J. Appl. Phys., 1998, 83, 4874 CrossRef CAS.
- B. S. Kang, S. K. Choi and C. H. Park, J. Appl. Phys., 2003, 94, 1904 CrossRef CAS.
- A. B. Hungría, A. Martínez-Arias, M. Fernández-García, A. Iglesias-Juez, A. Guerrero-Ruiz, J. J. Calvino, J. C. Conesa and J. Soria, Chem. Mater., 2003, 15, 4309–4316 CrossRef.
- C.-M. Pradier, C. Hinnen, K. Jansson, L. Dahl, M. Nygren and A. Flodstrom, J. Mater. Sci., 1998, 33, 3187–3191 CrossRef CAS.
- T. Sareein, M. Unruan, A. Ngamjarurojana, S. Ananta and R. Yimnirun, Ferroelectrics, 2014, 458, 56–63 CrossRef CAS.
- T. Sareein, M. Unruan, A. Ngamjarurojana, S. Jiansirisomboon, A. Watcharapasorn and R. Yimnirun, Phys. Lett. A, 2009, 373, 1583–1587 CrossRef CAS.
- T. Sareein, P. Baipaywad, W. Chaiammad, A. Ngamjarurojana, S. Ananta, X. Tan and R. Yimnirun, Curr. Appl. Phys., 2011, 11, S90–S94 CrossRef.
- A. Tamilselvan, S. Balakumar, M. Sakar, C. Nayek, P. Murugavel and K. S. Kumar, Dalton Trans., 2014, 43, 5731–5745 RSC.
- Y. Zhi, A. Chen, P. M. Vilarinho, P. Q. Mantas and J. L. Baptista, J. Eur. Ceram. Soc., 1998, 18, 1621–1628 CrossRef CAS.
- Y. Zhi, A. Chen, P. M. Vilarinho, P. Q. Mantas and J. L. Baptista, J. Eur. Ceram. Soc., 1998, 18, 1629–1635 CrossRef CAS.
- M. Morozov, Softening and hardening transitions in ferroelectric Pb(Zr,Ti)O3 ceramics, Ph.D. dissertation, École Polytechnique Fédérale de Lausanne, 2005.
- G. V. Lewis, C. R. A. Catlow and R. E. W. Casselton, J. Am. Ceram. Soc., 1985, 68, 555–558 CrossRef CAS.
- L. X. Zhang, W. Chen and X. Ren, Appl. Phys. Lett., 2004, 85, 5658 CrossRef CAS.
- S. Gottschalk, H. Hahn, S. Flege and A. G. Balogh, J. Appl. Phys., 2008, 104, 114106 CrossRef.
- M. I. Morozov and D. Damjanovic, J. Appl. Phys., 2010, 107, 034106 CrossRef.
- O. Bidault, P. Goux, M. Kchikech, M. Belkaoumi and M. Maglione, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7868–7873 CrossRef CAS.
- Y. Zhou, D. Xue, X. Ding, L. Zhang, J. Sun and X. Ren, J. Phys.: Condens. Matter, 2013, 25, 435901 CrossRef PubMed.
- L. Jin, F. Li and S. Zhang, J. Am. Ceram. Soc., 2014, 97, 1–27 CrossRef CAS.
- H. Yan, F. Inam, G. Viola, H. Ning, H. Zhang, Q. Jiang, T. Zeng, Z. Gao and M. J. Reece, J. Adv. Dielectr., 2011, 1, 107 CrossRef CAS.
- L. X. Zhang and X. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 174108 CrossRef.
- B. Qu, H. Du and Z. Yang, J. Mater. Chem. C, 2016, 4, 1795–1803 RSC.
- Q. Zhang, L. Wang, J. Luo, Q. Tang and J. Du, J. Am. Ceram. Soc., 2009, 92, 1871–1873 CrossRef CAS.
- L. Wu, X. Wang and L. Li, J. Am. Ceram. Soc., 2016, 99, 930–937 CrossRef CAS.
- L. Zhao, Q. Liu, S. Zhang and J.-F. Li, J. Mater. Chem. C, 2016, 4, 8380–8384 RSC.
| This journal is © The Royal Society of Chemistry 2017 |