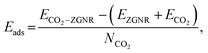Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Asymmetric passivation of edges: a route to make magnetic graphene nanoribbons†
Wen-cai Yi ab,
Wei Liu
ab,
Wei Liu cd,
Lei Zhaob,
Rashed Islamb,
Mao-sheng Miao*bc and
Jing-yao Liu
cd,
Lei Zhaob,
Rashed Islamb,
Mao-sheng Miao*bc and
Jing-yao Liu *a
*a
aLaboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun, 130023, People's Republic of China. E-mail: ljy121@jlu.edu.cn
bDepartment of Chemistry & Biochemistry, California State University, Northridge, CA 91330-8262, USA. E-mail: mmiao@csun.edu
cBeijing Computational Science Research Center, Beijing, 100193, P. R. China
dDepartment of Physics and Astronomy, University of California, Irvine, CA 92697, USA
First published on 26th May 2017
Abstract
Zigzag graphene nanoribbons (ZGNRs) are known to carry interesting properties beyond graphene, such as finite and variable band gaps. More interestingly, the edges of ZGNRs are magnetic due to single occupation of carbon dangling bonds (DB). However, the magnetic moments at two different edge sides couple antiferromagnetically, leading to a zero global moment for ZGNRs. Furthermore, the application of ZGNRs is limited by the high chemical activity of their edges that can be easily oxidized while exposed in air. It has been proposed and intensively studied to protect the edges by passivating them by hydrogenation or adsorption of other molecules such as CO2. In this work, we systematically studied the stability, the structures and the effect of CO2 adsorption at the edges of ZGNRs. Our calculations confirm the experimental observation that the CO2 molecules can be easily absorbed by the ZGNR edges. More interestingly, our calculations show that the asymmetric CO2 adsorption at two edges of ZGNR yields a ferrimagnetic state of ZGNRs that presents a finite global moment. Furthermore, considering the strong bonding between CO2 groups and ZGNRs, we propose that it can be utilized to stitch arrays of ZGNRs together to form new types of 2D materials that inherit the advantageous properties of the nanoribbons, such as finite gaps and novel magnetic properties.
1. Introduction
Zigzag graphene nanoribbons (ZGNRs), synthesized in 2008,1 have attracted much attention as a candidate material for spintronic devices because of their peculiar electronic structures.2–6 It is well known that the ground state of ZGNRs is characterized by spin-polarized electronic states at two edges, which couple through the graphene backbone and result in an antiferromagnetic (AF) arrangement of spins on adjacent atomic sites with zero total magnetic moment.7–11 In this regard, many works reported the electronic properties and chemical properties of the edge states of ZGNRs while the structure is modified by defects,12–15 doping foreign atoms,16–21 hydrogenation,22–30 oxidation,31 adsorption of some gas molecules32–35 and external electric field.36–38 However, it remains a challenge to produce ferrimagnetic ZGNRs with modification of the structures.The pristine ZGNR edges might be oxidized easily when exposed in the air. The unpaired electrons and the dangling bonds (DBs) are very reactive and can be passivated by various gas molecules or functional groups. Recently, an experimental work showed that CO2 can be irreversibly adsorbed on GNRS edges at ambient temperature,36 but structures of the passive edges are not determined. Furthermore, it is not clear how the absorption of CO2 molecules modifies the magnetism of ZGNR edges.
Here, we performed a first-principle study based on density functional theory (DFT) to address the structures and the magnetism of CO2 adsorbed on ZGNRs. Our results confirmed that CO2 can be strongly adsorbed on the edges of ZGNRs with large adsorption energies of −3.75 eV, which is larger than the adsorption energies of many other molecules,39,40 such as NO (−2.29 eV), NO2 (−2.70 eV) and H2O (−2.56 eV). Furthermore, different CO2 concentrations can affect the magnetism of ZGNRs, and in some cases produce ferromagnetic edge states. Additionally, we proposed that –CO2– group can work as bridges to connect ZGNRs by forming C–C and C–O covalent bonds. As a result, a two dimensional ZGNR–CO2–ZGNR structure can be formed, which is metallic and magnetic. This two dimensional material based on ZGNR arrays sewed by –CO2– groups may have good potentials for applications in 2D electronic devices.
2. Calculation method
All the first principles calculations were carried out by density functional theory (DFT) framework as implemented in the Vienna ab initio Simulation Package (VASP code).41–43 The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional within the generalized gradient approximation (GGA) scheme was employed.44,45 The electron-ion interaction is described by projector-augmented-wave (PAW) potentials.46 The energy cutoff is set to 500 eV, the Brillouin Zones (BZ) are represented by Monkhorst–Pack47 special k-point meshes of 9 × 1 × 1 for structural optimizations. A vacuum space of 20 Å in the non-periodic direction was used to remove any interaction between two neighboring images. Structural optimizations were completed until the remnant force on each atom was less than 0.02 eV Å−1. The electron spin-polarization was considered in all calculations. The adsorption energies (Eads) of CO2 on ZGNR were defined by the following formula:where ECO2–ZGNR, EZGNR, ECO2 and NCO2 are the total energies of the CO2 adsorbed ZGNR, the pristine ZGNR, the CO2 molecule and the number of CO2 molecules, respectively. The molecular dynamics (MD) simulation were also performed to evaluate the stability for typical structures. All the simulations ran for 3 ps containing 2000 MD steps at a finite temperature in the NVT ensemble with a large supercell containing about 100 atoms.
3. Results and discussion
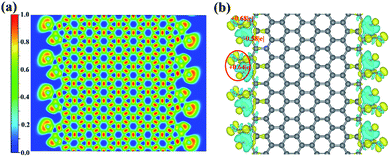
We use 8-ZGNR (containing 8 arrays of C) as the example system to study the adsorption of –CO2. We also tested n-ZGNRs (n = 6, 7, 9, 10, 11, 12) and found negligible difference while comparing with 8-ZGNRs results. In order to study different CO2 coverage, 8 repeated unit cells of 8-ZGNR are included in the model. Several configurations with different adsorption coverages and adsorption sites are constructed and optimized by DFT calculations. These include: (1) on the top of 8-ZGNR (8-ZGNR-t1, Fig. 1a); (2) on both edges of 8-ZGNR and chemically connected with only carbon atoms in CO2 molecules (8-ZGNR-s1, Fig. 1b); (3) on both edges of 8-ZGNR and connected with both carbon atoms and oxygen atoms in CO2 molecules (8-ZGNR-8/8, Fig. 1c); (4) on one edge of 8-ZGNR with 100% coverage (8-ZGNR-4/8, Fig. 1d); (5) single CO2 molecule adsorption on one edge of 8-ZGNR (8-ZGNR-1/8, Fig. 1e). The calculated adsorption energies for all the configurations are listed in Table 1 together with magnetic properties.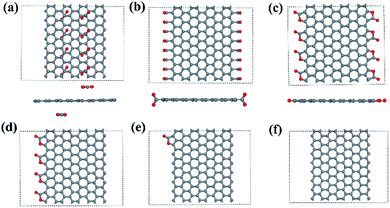 | ||
| Fig. 1 The structures of 8-ZGNR-t1 (a), 8-ZGNR-s1 (b), 8-ZGNR-8/8 (c), 8-ZGNR-4/8 (d), 8-ZGNR-1/8 (e), 8-ZGNR (f). | ||
| Name | Eads (eV per CO2) | EFM − EAFM (meV per unit) | Local magnetic moment (μB per edge) | Total magnetic moment (μB per unit) |
|---|---|---|---|---|
| 8-ZGNR-8-t1 | 0.04 | 22.19 | 0.65 | 0.00 |
| 8-ZGNR-8-s1 | −0.33 | −28.48 | 0.48 | 2.00 |
| 8-ZGNR-8/8 | −3.75 | 20.35 | 0.10 | 0.00 |
| 8-ZGNR-4/8 | −3.78 | 22.17 | 0.65(0.1) | 8.00 |
| 8-ZGNR-1/8 | −3.90 | 60.03 | 0.65(0.1) | 2.00 |
| 8-ZGNR | — | 82.99 | 0.65(0.1) | 0.00 |
For the first adsorption structure 8-ZGNR-t1, the optimization of the structure shows that the distance of the C–C bridge connecting CO2 and ZGNR is 3.44 Å, indicating a physical adsorption by weak interactions such as van der Waals' force. There is no distinct charge transfer between 8-ZGNR and CO2, and the modification to the electronic structure of ZGNR is minor. So the configuration of 8-ZGNR-t1 remain antiferromagnetic (AFM) after adsorption.
For the second adsorption structure 8-ZGNR-s1, the C–C distance of the bridging bond is 1.50 Å, which is a bit shorter than the C–C bond length of 1.54 Å. This indicates chemical adsorption of CO2 molecules on the edges of 8-ZGNR. The adsorption energy is found to be −0.33 eV, showing again the adsorption is chemical. The charges are calculated by the Bader's Quantum Theory of Atoms in Molecules (QTAIM).48–50 The results show that there is 0.17e charge transfer from 8-ZGNR to CO2 molecules. The adsorption also alters the structure of CO2 from a linear molecule to a nonlinear bent OCO group. The O–C–O angle becomes 127.40°, and the length of C–O changes from 1.18 Å of an isolated CO2 molecule to 1.26 Å. The geometry change of CO2 is accompanied by the change of hybridization from sp to sp2. However, the sp2 hybridization plane of CO2 group is perpendicular to the sp2 hybridization plane of ZGNR.
For the third adsorption structure 8-ZGNR-8/8, different from the structure of 8-ZGNR-s1, both carbon and oxygen atoms of the CO2 molecules bind on two edges of 8-ZGNR, with C–O and C–C bonds lengths of 1.35 and 1.48 Å, respectively, which indicate that 8-ZGNR-8/8 may have a stronger adsorption than 8-ZGNR-s1. The adsorption energy is exceedingly large with a value of −3.75 eV, corresponding to very strong chemisorption. The C atom in CO2 converts to sp2 hybridized and the hybridization plane matches that of ZGNR. Therefore, the C and O atoms formed both s and p bonds with neighboring C atoms on ZGNR. The lengths of the C–O bonds in CO2 change from 1.18 Å to 1.21 Å and 1.49 Å, showing one C–O single bond and one C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O double bond and the O–C–O angle becomes 118.72°. The nature of their bonding was probed by calculating the electron localization functions (ELF) of this structure. The result is depicted in Fig. 2a. Basins of electron localization could be found between CO2 molecules and 8-ZGNRs, indicating the formation of covalent bonds between them. The QTAIM charge analysis indicates that each carbon atom at the edges of ZGNR loses 0.58e during the adsorption, and the carbon atom in CO2 molecule gains 0.68e, and the total charge transfer from 8-ZGNR to one CO2 molecule is 0.64e (Fig. 2b).
O double bond and the O–C–O angle becomes 118.72°. The nature of their bonding was probed by calculating the electron localization functions (ELF) of this structure. The result is depicted in Fig. 2a. Basins of electron localization could be found between CO2 molecules and 8-ZGNRs, indicating the formation of covalent bonds between them. The QTAIM charge analysis indicates that each carbon atom at the edges of ZGNR loses 0.58e during the adsorption, and the carbon atom in CO2 molecule gains 0.68e, and the total charge transfer from 8-ZGNR to one CO2 molecule is 0.64e (Fig. 2b).
These results reveal that CO2 molecules can be strongly adsorbed on the edges of 8-ZGNRs while both C and O atoms in CO2 molecule bond with 8-ZGNR. The adsorption energies are larger than 3.0 eV, corresponding to very strong chemisorption. Our results confirm the experimental finding that CO2 can be captured by ZGNR if ZGNR grows under the environment of CO2. In this configuration, the carbon and oxygen atoms were both connected with ZGNR whereas the hybridization of carbon changes from sp to sp2 accompanied by 0.64 electrons transfer from ZGNR to CO2.
The last two configurations represent different CO2 adsorption coverage, based on the coverage, we name them as 8-ZGNR-4/8 (Fig. 1d) and 8-ZGNR-1/8 (Fig. 1e). Fig. 1f shows a ZGNR with pristine edges. The adsorption energies and the geometries of the adsorbed CO2 molecules vary only slightly with the CO2 coverage. This is easy to understand since the adsorbed CO2 molecules do not strongly interact with each other. However, as we will show later, the different adsorption coverage has great influence on magnetism of the edges.
To further evaluate the stability of CO2 adsorption system, two typical adsorption structures of 8-ZGNR-8/8 and 8-ZGNR-4/8 were perform MD simulation at 400 K. As shown in Fig. S1,† all those two adsorption structures become stable after 3 ps and neither experience serious disruption nor break, although the atoms shifted along a perpendicular direction, developing a ripple-like structure like other low dimension materials.51 The MD simulations demonstrate that the adsorption of CO2 does not break the stability of ZGNRs at ambient temperature.
In order to examine the effect of CO2 adsorption to magnetic order, we calculated the energies of three spin configurations, including non-magnetic (NM), ferromagnetic (FM) and antiferromagnetic (AFM) states. The AFM state consists of local moments oriented oppositely at two edge sides. The energy differences between the FM and AFM states, ΔE = EFM − EAFM, of all adsorption models were calculated and listed in Table 1. Negative ΔE values mean that FM coupling is energetically more favorable, whereas positive values correspond to AFM coupling. All ΔE values are positive except 8-ZGNR-8-s1, which indicates that the feature of the antiferromagnetic coupling remains after adsorbing CO2 molecules.
The spin densities of the pristine ZGNR and three CO2 adsorbed ZGNR are plotted in Fig. 3. It is well known that zigzag edges ZGNRs are semiconductors with spin-polarized edge states that are ferromagnetically ordered at each edge and antiferromagnetically coupled between two edges (Fig. 3a). Furthermore, the calculations show that the magnetic ordering of the ZGNR edges fully covered by CO2 adsorption (8-ZGNR-8/8) is the same as that of a pristine ZGNR (Fig. 3b). The major difference is that the local magnetic moments are significantly reduced in passivated edges (Table 1). This results agree well with the previous calculation.31 More interestingly, while the CO2 coverage is asymmetric between the two sides, there will be net magnetic moments in the ZGNR because the adsorption of CO2 will largely reduce the local moment. If only one edge is covered by CO2 molecules (Fig. 4c), the total magnetic moment will be 8.00 μB per cell as used in calculations (8 repeating ZGNR units). As a matter of fact, a single CO2 adsorption at one side will contribute 2.00 μB for the total magnetic moment (Fig. 4d). We also tested the variation of magnetic moments with different adsorption positions of CO2 molecules (Fig. S2†) and found that the total magnetism moment is only determined by different number of CO2 molecules adsorbed on two sides. Therefore, the ZGNR asymmetrically adsorbed CO2 molecules at two edges are ferrimagnetic, since the local moments at two edge sides are antiferromagnetically coupled and yet the system exhibit finite moment.
 | ||
| Fig. 3 The spin-polarized electron density of ZGNR (a), ZGNR-8/8 (b), ZGNR-4/8 (c), ZGNR-1/8 (d). Blue was spin up and yellow was spin down. The isosurface value is set to 1.00 × 10−2 Å−3. | ||
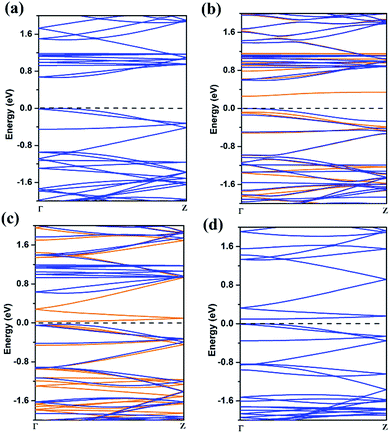 | ||
| Fig. 4 The band structures of 8-ZGNR (a), 8-ZGNR-1/8 (b), 8-ZGNR-4/8 (c), 8-ZGNR-8/8 (d). In (b) and (c), blue and orange lines represent majority spin (down) and minority spin (up) bands. | ||
The band structure of ZGNR is also greatly influenced by the adsorption of CO2. Using PBE functional, we calculated the band structures of ZGNR with different adsorption coverage of CO2 molecules. The results are plotted in Fig. 4. As shown in Fig. 4a, the bare 8-ZGNR has a direct band gap of 0.68 eV at Γ point. Considering the use of semi-local exchange–correlation functional (PBE), the band gap might be greatly underestimated in our work. With the adsorption of CO2 molecules, there are several features in the change of the band structures. For the 8-ZGNR-1/8 and 8-ZGNR-4/8 coverage, the band structures were different between spin-up and spin-down because the system is magnetic. The 8-ZGNR-1/8 can be considered as introducing an impurity at the edge. Its effect to the band structure is the inducing of impurity states in the gap (Fig. 4b). As shown in the figure, this impurity state is a deep acceptor state. For 8-ZGNR-4/8, a full spin polarized band structure has developed (Fig. 4c). The majority-spin bands exhibit similar band structures as the pristine ZGNR (Fig. 4a); however, the minority-spin bands contain features originated from the absorption. Overall, the material is still semiconducting with a very small gap. Therefore, the ZGNR with CO2 passivation at one side is a low-gap magnetic semiconductor and may find its usage in future two-dimensional spintronic devices. 8-ZGNR-8/8 is non-magnetic with overlapping majority and minority bands. While comparing the band structures with the pristine ZGNR, we find that the original conduction bands are pushed upward for about 0.6 eV which is a result of the passivation of the dangling bonds. A few more bands are introduced in the gap, resembling same features as the minority-spin bands in 8-ZGNR-4/8. Overall, the material is a low-gap semiconductor, the values of band gap were showed in Table S1.†
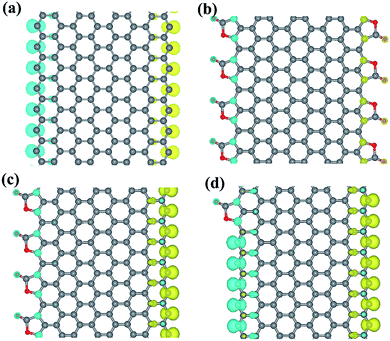
We notice that the CO2 groups can be used to connect two neighbor ZGNR by forming C–C and C–O bonds. Again, we use 8-ZGNR as example nanoribbons to demonstrate this idea. As shown in Fig. 5a, we constructed a model CO2-stitched ZGNR arrays and optimized its structure using DFT method with PBE functional. The structure belongs to Pmm2 symmetry group. The most stable interface structure consists of CO2 groups bonding to one ZGNR edge with two C–O bonds and to another ZGNR edge with one C–C bond. The ELF calculation shows strong covalent features for the interface C–C and C–O bonds. The MD simulations demonstrate this stitched 2D ZGNR arrays are stable up to 700 K. Fig. S3† shows the structures and fluctuations in the temperature as a function of the simulation time at 300 K and 700 K, respectively.
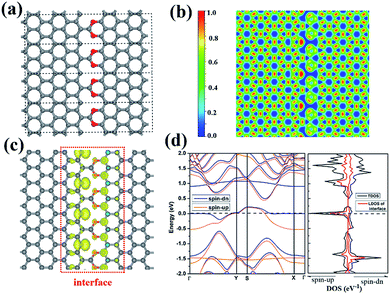 | ||
| Fig. 5 The structure (a), the ELF (b), the spin-polarized electron density (c), the band structure (d) of CO2 stitched ZGNR. | ||
Although most dangle bonds at the edges of ZGNR arrays were passivated by CO2 molecules, some of them remain as shown in Fig. 5a. There are single electrons occupying these DBs and may exhibit large local magnetic moments. As a matter of fact, the spin-polarized calculations show that the CO2-stitched ZGNR arrays are magnetic with a net moment of 1.52 μB per unit. Further calculations indicate the energy of ferromagnetic state is 0.57 eV lower than that of non-magnetic state, and is 0.84 meV lower than the antiferromagnetic state. The spin polarized electron density is plotted in Fig. 5c that shows the magnetism moment mainly come from the edge C atoms containing DB. The local magnetic moments as calculated by the charge density inside the PAW radii is 0.58 μB of the carbon atom with DBs.
The band structure calculation indicates the CO2 stitched ZGNR is metallic with impurity states occupied in the middle of band gap and the Fermi level across those states. The further analysis by LDOS indicates that most of those states come from the interface between CO2 and ZGNR (Fig. 5d).
4. Conclusions
In summary, we have performed first-principles calculations to study the stability, the structures of CO2 molecule adsorption at the edges of ZGNR. Our calculations reveal large adsorption energies, agreeing to the experimental observation of easy adsorption of CO2 molecules at ZGNR edges. The adsorption of CO2 molecules can largely modify the electronic structure of ZGNR. It reduces the overall gap by inducing new edge states in the gap of ZGNR. More interestingly, the adsorption of CO2 at the edges can greatly alter the magnetic properties of ZGNR. Especially, while the adsorption is asymmetric, the ZGNR become ferrimagnetic with large global moment, indicating the fabrication of interesting carbon based low dimensional magnetic materials. Moreover, we propose that the CO2 groups can be used to stitch the ZGNR arrays together to form a new type of 2D materials. The electronic structure calculations show that such materials are ferromagnetic semiconductor with low band gaps.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 21373098). The authors are grateful to the referees for their valuable comments, which have significantly improved the manuscript. Part of the calculations are performed on NSF-funded XSEDE resources (TG-DMR130005) especially on the Stampede cluster run by Texas Advanced Computing Center.Notes and references
- S. Aigner, L. D. Pietra, Y. Japha, O. Entin-Wohlman, T. David, R. Salem, R. Folman and J. Schmiedmayer, Science, 2008, 319, 1226–1229 CrossRef CAS PubMed.
- V. Barone, O. Hod and G. E. Scuseria, Nano Lett., 2006, 6, 2748–2754 CrossRef CAS PubMed.
- D. E. Jiang, B. G. Sumpter and S. Dai, J. Chem. Phys., 2007, 126, 134701 CrossRef PubMed.
- Q. Yan, B. Huang, J. Yu, F. Zheng, J. Zang, J. Wu, B. L. Gu, F. Liu and W. Duan, Nano Lett., 2007, 7, 1469–1473 CrossRef CAS PubMed.
- F. Wu, E. Kan, H. Xiang, S.-H. Wei, M.-H. Whangbo and J. Yang, Appl. Phys. Lett., 2009, 94, 223105 CrossRef.
- W. Y. Kim and K. S. Kim, Nat. Nanotechnol., 2008, 3, 408–412 CrossRef CAS PubMed.
- M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920–1923 CrossRef CAS.
- S. Okada and A. Oshiyama, Phys. Rev. Lett., 2001, 87, 146803 CrossRef CAS PubMed.
- H. Lee, Y.-W. Son, N. Park, S. Han and J. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174431 CrossRef.
- C. Tao, L. Jiao, O. V. Yazyev, Y.-C. Chen, J. Feng, X. Zhang, R. B. Capaz, J. M. Tour, A. Zettl, S. G. Louie, H. Dai and M. F. Crommie, Nat. Phys., 2011, 7, 616–620 CrossRef CAS.
- G. Z. Magda, X. Jin, I. Hagymasi, P. Vancso, Z. Osvath, P. Nemes-Incze, C. Hwang, L. P. Biro and L. Tapaszto, Nature, 2014, 514, 608–611 CrossRef CAS PubMed.
- D. W. Boukhvalov and M. I. Katsnelson, Nano Lett., 2008, 8, 4373–4379 CrossRef CAS PubMed.
- M. Topsakal, E. Aktürk, H. Sevinçli and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235435 CrossRef.
- G.-D. Lee, C. Z. Wang, E. Yoon, N.-M. Hwang and K. M. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195419 CrossRef.
- J. N. B. Rodrigues, P. A. D. Gonçalves, N. F. G. Rodrigues, R. M. Ribeiro, J. M. B. Lopes dos Santos and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 155435 CrossRef.
- T. B. Martins, R. H. Miwa, A. J. da Silva and A. Fazzio, Phys. Rev. Lett., 2007, 98, 196803 CrossRef CAS PubMed.
- S. Dutta and S. K. Pati, J. Phys. Chem. B, 2008, 112, 1333–1335 CrossRef CAS PubMed.
- S. S. Yu, W. T. Zheng, Q. B. Wen and Q. Jiang, Carbon, 2008, 46, 537–543 CrossRef CAS.
- S. Dutta, A. K. Manna and S. K. Pati, Phys. Rev. Lett., 2009, 102, 096601 CrossRef PubMed.
- Y. Li, Z. Zhou, P. Shen and Z. Chen, ACS Nano, 2009, 3, 1952–1958 CrossRef CAS PubMed.
- Z. L. Yu, D. Wang, Z. Zhu and Z. H. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 24020–24028 RSC.
- Y. W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- K. N. Kudin, ACS Nano, 2008, 2, 516–522 CrossRef CAS PubMed.
- T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, Phys. Rev. Lett., 2008, 101, 096402 CrossRef PubMed.
- G. Lee and K. Cho, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 165440 CrossRef.
- S. Bhandary, O. Eriksson, B. Sanyal and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 165405 CrossRef.
- R. Yang, Z. Shi, L. Zhang, D. Shi and G. Zhang, Nano Lett., 2011, 11, 4083–4088 CrossRef CAS PubMed.
- J. Zeng, K.-Q. Chen, J. He, X.-J. Zhang and C. Q. Sun, J. Phys. Chem. C, 2011, 115, 25072–25076 CAS.
- X. Q. Deng, Z. H. Zhang, G. P. Tang, Z. Q. Fan and C. H. Yang, Carbon, 2014, 66, 646–653 CrossRef CAS.
- X. H. Zheng, X. L. Wang, L. F. Huang, H. Hao, J. Lan and Z. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 081408 CrossRef.
- O. Hod, V. Barone, J. E. Peralta and G. E. Scuseria, Nano Lett., 2007, 7, 2295–2299 CrossRef CAS PubMed.
- E. J. Kan, Z. Li, J. Yang and J. G. Hou, J. Am. Chem. Soc., 2008, 130, 4224–4225 CrossRef CAS PubMed.
- A. P. Seitsonen, A. M. Saitta, T. Wassmann, M. Lazzeri and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115425 CrossRef.
- M. Asai, T. Ohba, T. Iwanaga, H. Kanoh, M. Endo, J. Campos-Delgado, M. Terrones, K. Nakai and K. Kaneko, J. Am. Chem. Soc., 2011, 133, 14880–14883 CrossRef CAS PubMed.
- E. Akbari, M. T. Ahmadi, M. J. Kiani, H. K. Feizabadi, M. Rahmani and M. Khalid, J. Comput. Theor. Nanosci., 2013, 10, 1301–1304 CrossRef CAS.
- E.-J. Kan, Z. Li, J. Yang and J. G. Hou, Appl. Phys. Lett., 2007, 91, 243116 CrossRef.
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- S. D. Dalosto and Z. H. Levine, J. Phys. Chem. C, 2008, 112, 8196–8199 CAS.
- B. Huang, Z. Li, Z. Liu, G. Zhou, S. Hao, J. Wu, B.-L. Gu and W. Duan, J. Phys. Chem. C, 2008, 112, 13442–13446 CAS.
- M. Vanin, J. Gath, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195411 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- W. Liu, M. Miao and J.-y. Liu, J. Mater. Chem. C, 2015, 3, 9921–9927 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The spin-polarized electron density of different CO2 concentrations and position, snapshots of the final configurations for molecular dynamics simulation of ZGNR–CO2–ZGNR interface. See DOI: 10.1039/c7ra03461j |
| This journal is © The Royal Society of Chemistry 2017 |