Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Phosphomolybdic acid supported atomically dispersed transition metal atoms (M = Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au): stable single atom catalysts studied by density functional theory†
Shujiao Wanga,
Yingxin Fenga,
Sen Lin *a and
Hua Guob
*a and
Hua Guob
aState Key Laboratory of Photocatalysis on Energy and Environment, College of Chemistry, Fuzhou University, Fuzhou 350002, People's Republic of China. E-mail: slin@fzu.edu.cn; Tel: +86-591-22865872
bDepartment of Chemistry and Chemical Biology, University of New Mexico, Albuquerque, NM 87131, USA
First published on 10th May 2017
Abstract
By means of first-principles calculations, the interaction of twelve different transition metal atoms (M = Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au) of groups VIII–XI with phosphomolybdic acid (H3PMo12O40, PMA), a newly emerging medium for trapping transition metal atoms, has been systematically investigated. The M–PMA systems have very high stability with the binding energies of transition metals higher than those on widely used metal oxide supports. The high diffusion barriers of these single metal atoms on the PMA surfaces suggest that they are sufficiently stable to prevent agglomeration. Based on the electronic structure analysis, the remarkable stability of single atoms is attributed to the strong mixing between the d orbitals of the metal atom and 2p orbitals of PMA oxygens, which results in electron transfer from the metal atoms to PMA, producing positively charged single metal atoms which can be used for catalytic applications. Finally, we test the activity of Pt–PMA as a low-cost, stable, and efficient catalysts for CO oxidation. This work is expected to provide useful insight to the development of new highly efficient heterogeneous single atom catalysts (SACs).
1. Introduction
Single-atom catalysis, in which reactions are catalyzed with extremely high performance efficiencies by metal atoms atomically dispersed on a support, has attracted more and more attention in both experiment and theory.1–27 The atomic form of the catalyst greatly increases the catalytic efficiency, which could potentially lead to a dramatic reduction of precious metal demands and thus costs. In recent reports, most of the single atoms were anchored onto metal oxides or metal surfaces through various experimental techniques. For example, Zhang’ group reported for the first time that isolated single Pt atoms were able to disperse on the surfaces of iron oxide (FeOx) with excellent stability and exhibit high reaction activity for both CO oxidation and preferential oxidation of CO in H2.3 Vilé and the co-workers reported that single Pd atoms anchored to cavities of mesoporous polymeric graphitic carbon nitride can be successfully applied to catalyze hydrogenation of alkynes and nitroarenes with high activity and product selectivity.12 More recently, Datye and coworkers demonstrated that isolated single Pd atoms supported by γ-Al2O3 had large binding energies and strong catalytic activity for CO oxidation, which is supported by density functional theory (DFT) calculations.16It should be noted, however, that the structures of single atom catalysts (SACs) could undergo significantly changes under some catalytic conditions with high temperatures or pressures, leading to partial or complete loss of the expected reaction activity due to the formation of nanoparticles through agglomeration.16 Therefore, searching for effective supports that can provide a sufficient concentration of surface sites for trapping transition metal atoms to prevent agglomeration remains a challenge in the design and synthesis of SACs.
Importantly, the catalytic properties of the trapped metal atoms are often different from those of the corresponding bulk metal, because of their strong interactions with the support. Such interactions can be electrostatic in nature, but more common are transfer of charges.28 In this sense, SACs share some commonalities with homogeneous catalysis, in which the properties of the ligands greatly affect the catalytic properties of the metal center.5 Ultimately, it would be highly desirable to design SACs by varying the metal interactions with the support. Such a goal cannot however be realized unless fundamental understanding of the metal-support interaction is achieved.
Recently, phosphomolybdic acid H3PMo12O40 (denoted as PMA) has emerged as an attractive medium to trap transition metal atoms.14 Zhang et al. developed a stable Pt SAC with a high loading of Pt on PMA. PMA has a classical Keggin structure consisting of molybdenum and oxygen atoms with a phosphorus atom located in the center.29–31 Thanks to the special configuration of PMA, a range of coordination sites containing exposed oxygen atoms exist for metal atoms to be stably anchored. Particularly, a Pt atom has been shown to bind strongly at the four-fold hollow site on PMA in a distorted square-planar geometry and serves as a homogeneous single-atom catalyst for hydrogenation reactions with high selectivity.14 That work provides a new direction for designing stable heterogeneous SACs by utilizing the advantageous aspects of coordination chemistry and homogeneous catalysis.
Given the fact that isolated Pt atoms can be positioned on PMA with high stability, it is natural to ask whether these coordination sites can also trap other transition metal atoms such as Pd, Au, and Cu, thus generating new SACs. As far as we know, there are few reports about the single atoms supported by PMA,14 particularly in theory. In order to obtain a deeper understanding of such specific adsorption characteristics and provide fundamental knowledge for designing and synthesizing stable and effective SACs in experiment, the interaction between transition metal atoms (M = Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au) and PMA coordination sites containing different numbers of oxygen atoms are systematically investigated in this work, using DFT. Our calculation results reveal that the hollow sites formed by four oxygen atoms on PMA facilely trap the transition metal atoms. Interestingly, comparison of the adsorption energies of the M species with PMA to the binding energies of the corresponding atoms in metal nanoparticles indicates high stability of the anchored M species against agglomeration. Clear trends in calculated adsorption energies are found for transition metals in different rows and groups of the periodic table, which help to build general rules for the preparation of stable transition metal SACs. Furthermore, it is shown that the oxygens in the binding site significantly modify the characteristic of the trapped metal atom by charge transfer. Finally, potential catalytic applications of M–PMA catalysts are assessed using CO oxidation as an example. This publication is organized as follows. The calculation details are described in Section 2. The results and discussion are presented in Section 3. The conclusions are given in Section 4.
2. Computational details
All spin-polarization calculations were carried out by using the Vienna ab initio simulation package (VASP)32–34 with the gradient-corrected PW91 exchange–correction functional.35 For valence electrons, a plane-wave basis set was used with the energy cut-off set to 400 eV and the ionic cores were described with the projector augmented-wave (PAW) method.36,37 The cubic unit cell contains a classical Keggin configuration consisting of 12 Mo atoms and 40 O atoms with a P atom located in the center. For the structural optimizations, all the atoms were fully relaxed. In order to avoid the interactions between the complex and its image, the box length was set to 20 Å. Only the Γ-point was used to sample the Brillouin zone.38 The electron density for the ground-state was converged with a 10−4 eV total energy threshold and the geometries were optimized until the maximum force on any ion was less than 0.01 eV Å−1. To explore the oxidation states of the adsorbed transition metals, Bader charge analysis was performed.39The adsorption energy Eads is defined by Eads = E(M–PMA) − (E(M) + E(PMA)), where E(M) is the energy of free transition metal atom, E(PMA) the energy of the free PMA support and E(M–PMA) the total energy of the complex. The charge density difference (Δρ(r)) plots were obtained by subtracting the charge densities of the separated M (ρM(r)) and PMA (ρPMA(r)) from the charge density of the M–PMA complex (ρM+PMA(r)) systems as follows: Δρ(r) = ρM–PMA(r) − [ρPMA(r) + ρM(r)]. In order to obtain the energy barrier, the climbing image-nudged elastic band (CI-NEB) method was employed.40 The highest image along the minimum energy path was denoted as transition state (TS). The energy barrier Ea of each elementary reaction was calculated by the energy difference between the TS and initial state (IS).
3. Results and discussion
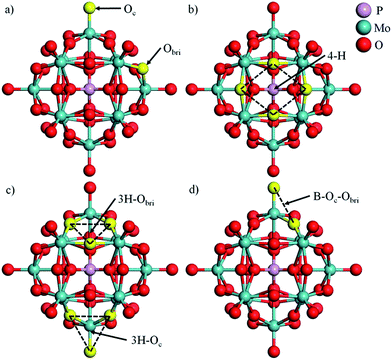
In this work, phosphomolybdic acid, PMA (H3PMo12O40) was selected as the support to trap the single metal atoms. The optimized PMA structure is displayed in Fig. 1 and there are several possible coordination sites on the surface of PMA, including a 4-fold hollow site (4-H), two 3-fold hollow sites (3H–Oc and 3H–Obri) and a bridge site (B–Oc–Obri). The corresponding key geometry parameters are listed in Table 1. The P–O, Mo–Oc and Mo–Obr bond lengths are calculated to be 1.55, 1.70 and 1.94 Å, respectively, which are in good agreement with the values from previous experiment and theories.14,313.1 Geometry and stability of M–PMA
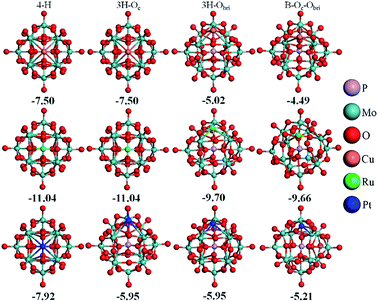
As reported by Zhang et al.,14 Pt atoms can strongly bind at the 4-H sites on PMA. The adsorption energies in Table 2 reveal that PMA can strongly bind not only atomic Pt but other transition metal atoms of groups VIII–XI in the periodic table. Beside the 4-H site, the other sites such as 3H–Oc, 3H–Obri and B–Oc–Obri might also trap the metal atoms. Here, we select one metal from each period (Cu, Ru, and Pt) to systematically investigate all the possible adsorption sites. It can be seen from Fig. 2 that after optimization the metal atoms are located at their initially positioned sites except for Cu and Ru, which migrate from the initial 3H–Oc site to 4-H. Not surprisingly, the calculated adsorption energies (see Table S1†) indicate that the most stable site for all metal atoms is the 4-H site. For Cu, the adsorption energy becomes stronger in the order B–Oc–Obri < 3H–Obri < 4-H with the values of −4.49, −5.02 and −7.50 eV, respectively. The calculated bond lengths for Cu–O are around 1.90 Å. For Ru, the binding energy at 3H–Obri is almost equal to that at B–Oc–Obri with a value of −9.66 eV. At the 3H–Obri site, the calculated Ru–O bond lengths are 1.89, 1.89 and 2.09 Å, respectively; and at the bridge site the values are 1.71 and 1.82 Å. For Pt, the largest binding energy is −7.92 eV at the 4-H site. This atom can be also stable at the 3H–Oc site with an adsorption energy of −5.95 eV and the site of B–Oc–Obri possesses the smallest binding energy of −5.21 eV. In this case, the average Pt–O bond distance is calculated to be about 1.89 Å. Based on the calculation results, it can be concluded that the most stable adsorption site for these three transition atoms is the 4-H site surrounded by four bridge oxygen atoms, which is consistent with the DFT results of the Pt–PMA system reported by Zhang et al.14 In the following sections, only the 4-H site is considered for all transition metals examined.| M | dM–O | dO–O | ∠OMO | Eads | Ecoh20 | q |
|---|---|---|---|---|---|---|
| Group VIII | ||||||
| Fe | 1.81, 1.81, 1.84, 1.84 | 2.55, 2.55, 2.55, 2.55 | 88.6, 88.6, 88.6, 88.6 | −10.90 | −4.28 | 1.42 |
| Ru | 1.90, 1.90, 2.03, 2.03 | 2.55, 2.60, 2.55, 2.60 | 80.8, 82.8, 82.8, 80.9 | −11.04 | −6.74 | 1.34 |
| Os | 1.88, 1.86, 1.96, 2.01 | 2.46, 2.56, 2.46, 3.12 | 79.5, 82.2, 109.6,78.8 | −11.24 | −8.17 | 1.42 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Group IX | ||||||
| Co | 1.81, 1.81, 1.83, 1.83 | 2.53, 2.53, 2.53, 2.53 | 87.9, 87.9, 87.9, 87.9 | −10.41 | −4.39 | 1.26 |
| Rh | 1.88, 1.88, 2.08, 2.08 | 2.61, 2.61, 2.61, 2.61 | 82.3, 82.3, 82.3, 82.3 | −9.11 | −5.74 | 1.11 |
| Ir | 1.86, 1.85, 2.06, 2.04 | 2.52, 3.10, 2.51, 2.65 | 80.1, 105.4, 85.3, 80.2 | −10.08 | −6.94 | 1.21 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Group X | ||||||
| Ni | 1.78, 1.78, 1.87, 1.87 | 2.55, 2.55, 2.55, 2.55 | 88.6, 88.6, 88.6, 88.6 | −9.35 | −4.44 | 1.18 |
| Pd | 1.94, 1.94, 2.04, 2.04 | 2.71, 2.71, 2.71, 2.71 | 85.7, 85.7, 85.7, 85.7 | −6.44 | −3.90 | 1.03 |
| Pt | 1.94, 1.94, 2.04, 2.04 | 2.75, 2.75, 2.75, 2.75 | 87.3, 87.5, 87.5, 87.4 | −7.92 | −5.85 | 1.05 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Group XI | ||||||
| Cu | 1.82, 1.82, 1.84, 1.84 | 2.57, 2.57, 2.57, 2.57 | 89.3, 89.3, 89.3, 89.3 | −7.50 | −3.48 | 1.18 |
| Ag | 2.01, 2.01, 2.02, 2.02 | 2.77, 2.77, 2.77, 2.77 | 86.9, 86.9, 86.9, 86.9 | −4.63 | −2.94 | 1.06 |
| Au | 2.00, 2.00, 2.02, 2.02 | 2.80, 2.80, 2.80, 2.80 | 88.2, 88.2, 88.2, 88.2 | −5.04 | −3.81 | 1.03 |
We also explore whether PMA can still trap transition metal atoms strongly enough with a high loading of metal atoms, since each PMA contains more than one 4-H site. From the calculated results (the configurations and adsorption energies are shown in Fig. S1 and Table S2 in ESI,† respectively), it is found that the adsorption energies for the second and third metal atoms at 4-H sites are somewhat smaller than the those for the first one: −6.14 and −5.23 eV for Pt, −9.49 and −8.56 eV for Ru, −5.11 and −4.36 eV for Cu, respectively. These results suggest that it might be possible to have multiple metal atoms trapped in different sites of a single PMA, further increasing the SAC concentration.
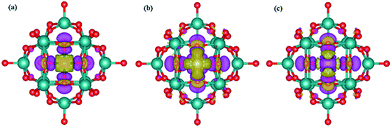
The top views of the optimized structures for the M–PMA systems with a single trapped M are displayed in Fig. 3. It is shown from the side view that all the metal atoms are located at 4-H sites and protrude slightly from the oxygen plane after structural relaxation. As shown in Table 2, the calculated dM–O and dO–O distances of M–PMA reveal that the coordination type is approximately symmetric, except for the cases of Os and Ir. For example, the dFe–O distances are 1.81, 1.81, 1.84 and 1.84 Å and the dO–O distances are all equal to 2.55 Å. The square-planar configurations are significantly distorted for both Os and Ir as the dO–O distances are substantially changed from the initial values of 2.72 Å to 2.46, 2.56, 2.46 and 3.12 Å for Os and 2.52, 3.10, 2.51 and 2.65 Å for Ir, respectively, probably due to their large atomic radii. In addition, the dOs–O values are calculated to be 1.88, 1.86, 1.96 and 2.01 Å and the dIr–O values are 1.86, 1.85, 2.06 and 2.04 Å.
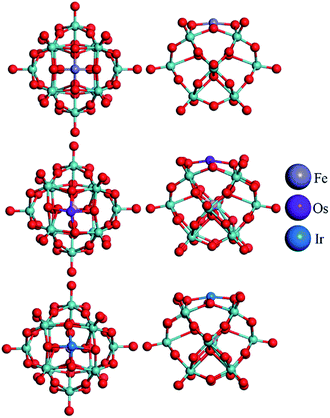 | ||
| Fig. 3 Top and side view of the optimized configurations of the M–PMA (M = Fe, Os, and Ir) systems (the configurations of other M–PMAs are close to that of symmetric Fe–PMA and thus not shown here). The metal atoms are represented with different colors, the oxygen atoms surrounding the adsorption sites (4-H) are highlighted in yellow and the calculated distances of the M–O bonds are listed in Table 2. | ||
Next we look into the stabilization of the trapped metal atoms on PMA. In group VIII, with the increasing of atomic radius in the order of Fe < Ru < Os, their adsorption energies rank in the following descending order: Os > Ru > Fe. However, it is noted that the adsorption energies are quite similar around −11 eV, indicating that these trapped atoms are very stable on PMA. These adsorption energies are comparable to those on the CeO2(100) surface,20 a widely used substrate for trapping single atoms. On CeO2(100), an M atom at the surface Ce4+ vacancy interacts with four lattice oxygen atoms, generating a square-planar configuration, similar to that in M–PMA complexes. For metals in group IX, the Co atom in PMA has the largest binding energy of −10.41 eV. On the other hand, the Rh atom has the smallest binding energy of −9.11 eV, but is still about 2 eV higher than that on CeO2 (−7.03 eV) and Fe2O3 (−7.34 eV).20,23 For group X metals, the interaction between the transition metal atom and PMA support becomes weaker and the binding energy becomes stronger in the order: Pd (−6.44 eV) < Pt (−7.92 eV) < Ni (−9.35 eV). For comparison, these values for Pd and Pt are also a little bit larger than those on CeO2 (−5.22 and −7.02 eV) and FeOx (−5.62 and −6.67 eV),20,23 revealing the ability of PMA to strongly bind these metal atoms. For group XI, in general, the binding energies of Cu, Ag and Au are much weaker when compared with those of other metals. The smallest binding energy is found for Ag with a value of −4.63 eV, however, still higher than that on the CeO2 support (−2.87 eV).20
As displayed in Fig. 4, clear trends in the calculated Eads can also be seen along the periods and groups of the periodic table. From the left to the right of a period, Eads is reduced in magnitude, which is attributed to the more occupied d orbitals of metals forming weaker bonds with the oxygens of PMA. For 4d metals, the trend for Eads is monotonous from Ru to Ag. While the trend along the period for 3d and 5d metals becomes less monotonic. In general, these trends reveal that the single atoms of 4d metals yield the weakest bonds with the oxygen atoms at the 4-H sites, quite similar to that on CeO2.20 However, the 3d metals can interact with the oxygen atoms by forming the strongest bonds with the exception of Fe, contrast to that on CeO2 where 5d metals have largest binding energies.20 As shown in Table 2, the lengths of M–O bonds are less than 1.90 Å, which are shorter than those for 4d and 5d metals. That may be due to the fact that atom radii of 3d atoms are smaller than those of 4d and 5d atoms. This comparison underscores the fact that the trends for the adsorption energy of single metal atoms depend on the selected support. In Fig. 4, the adsorption energies of M on PMA are also compared with those for these atoms in edge positions of the M79 nanoparticles.20 It is also clear that the former are significantly larger in magnitude (more negative) than the latter, indicating that the dispersed single metal atoms at the 4-H sites of PMA nanostructures are energetically favored over the formation of metallic nanoparticles. In addition, we also compare the Ead values with the experimental metal cohesive energies and the propensity of the embedded single metal atom to agglomerate is quite similar (see Table S3†).
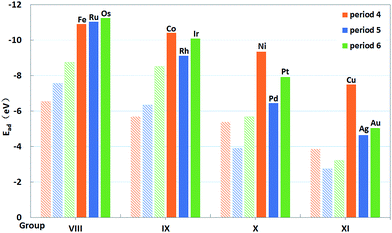 | ||
| Fig. 4 Binding energies (filled columns) of single transition metal atoms (M) trapped on PMA and binding energies20 (shadowy columns) of these atoms in edge positions of the M79 nanoparticles of the same atoms. | ||
The diffusion of an anchored single metal atom on the PMA surface is also investigated. To reduce the computational cost, we only examined the Pt–PMA system as an example. The corresponding geometries as well as the calculated energies of the initial state, transition state, and final state for this process are determined by a NEB calculation and shown in Fig. 5. As expected, the transfer of a Pt metal atom from the most stable 4-H site to the nearest B–Oc–Obri site needs to overcome a rather high energy barrier of 3.04 eV, which is comparable to the calculated values (2.51–6.48 eV) of the corresponding metals on CeO2 and FeOx.20,23 Combining with the large binding energies discussed above, this result practically rules out the possible aggregation of single metal atoms on the PMA surfaces and further confirming the experimental observation that Pt is very stable on PMA.14 Although NEB calculations were not performed for the Cu and Ru atoms, the large endothermicities of 3.01 and 2.45 eV for moving from the 4-H site to B–Oc–Obri site suggest that the energy barriers for the processes should be also very high.
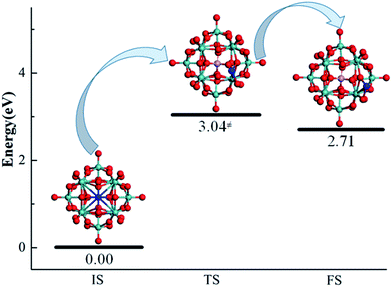 | ||
| Fig. 5 Geometries of the IS, TS, and FS for a Pt atom (color = blue) migrating from the most stable adsorption 4-H site to the nearby B–Oc–Obri site on PMA. | ||
All the above calculation results suggest that the interaction between the metal atoms and the 4-H site on the PMA surface is sufficient strong to prevent metal agglomeration. Thanks to this strong metal–ligand interaction, stable zero- or low-valent transition metal atoms can be supported by satisfying the empirical requirements of coordination chemistry and therefore explaining the capability of the PMA system to trap a relatively high loading of single metal atoms against agglomeration into metal nanoparticles.
3.2 Electronic structure of M–PMA
To provide a deeper understanding why these single atoms stay so stably on the PMA surface and how the ligands modify the trapped metal, we performed calculations of the local density of states (LDOS), Bader charge (q) and charge difference density (Δρ(r)). As shown in Fig. 6a–c, the d orbitals of the Cu (3d), Ru (4d) and Pt (5d) atom are found to strongly hybridize with the 2p orbitals of the PMA oxygen atoms above and below the Fermi level (EF), suggesting a very strong interaction between the metal atom and oxygen atoms at the 4-H site of PMA. Different from that on Cu–PMA, the spin-down DOSs of Ru–PMA and Pt–PMA shift to higher energies due to the effect of spin polarization, making the spin-up and spin-down gap states quite different. Especially, for Ru–PMA, a significant DOS peak can be clearly observed at EF, providing a reasonable explanation for its larger adsorption energy and Bader charge as listed in Table 2. It should also be noted that such a d population near EF might play a crucial role in activating the adsorbates during catalytic reaction.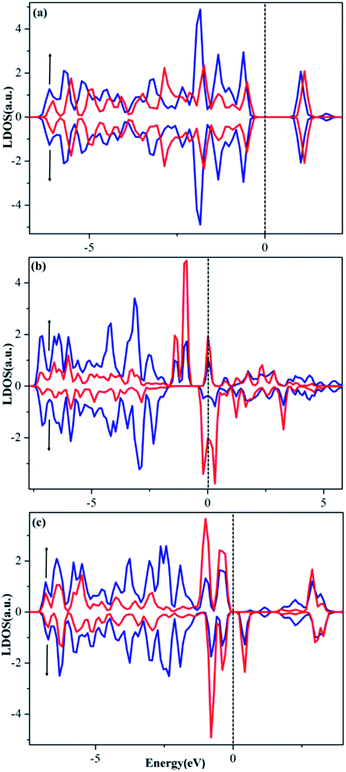 | ||
| Fig. 6 Spin-polarized LDOSs projected on 2p orbitals (blue) of O and d orbitals (red) of Cu (a), Ru (b) and Pt (c) embedded in the 4-H site of PMA. The Fermi level was set to zero. | ||
As listed in Table 2, all metal atoms trapped on PMA have positive charges, clearly indicating significant electron transfer from the metal atom to the PMA substrate. In group VIII, Fe, Ru, and Os have the largest Bader charges with the values of 1.42, 1.34 and 1.42|e|, respectively, consistent with the fact that they possess the largest binding energies. Similarly, the largest positive charges are also found on these atoms on CeO2 among other metal atoms examined.20 In group IX, the Bader charges can be ranked in the following increasing order: Co (1.26|e|) > Ir (1.21|e|) > Rh (1.11|e|). In groups X and XI, the single atoms exhibit moderate positive charges between 1.05–1.18|e|. The transferred electrons are significantly more than those on the FeOx supported metal complexes.23 It is also interesting that from group VIII to IX, X and XI, the charge of the single transition metal atoms on PMA decreased gradually in general. That might be due to the fact that the electronegativity of the transition metal atoms increases from group VIII to IX, X and XI.
As shown in Fig. 7, charges are observed to deplete from the vicinity of the metal (Cu, Ru and Pt) atoms, and accumulate in the vicinity of the surface oxygens at the 4-H site, again indicating the electron transfer from the embedded single metal atoms to PMAs. Importantly, these oxidized states of metal atoms may lead to potential catalytic activities. For Pt, a clear accumulation is shown at the very center where the metal is located and the depletion can be also seen around the Pt center. Differently, for Cu and Ru, it is clear to see depletion at the metal centers but with accumulation which cannot be clearly observed. However, it is believed there is a net depletion in each metal atom, which has been already revealed by the Bader charge calculations that metal atoms are positively charged. For example, it is known that positively charged Pt captures hydrogen easily and exhibits excellent activity in the hydrogenation of nitrobenzene and cyclohexanone.14 In our previous study, it was found that the defected h-BN supported metal atoms such as Fe, Co, Cu and Pt possess positive charges with a range of +0.64–1.02|e|, which are responsible to the predicted high activity of CO oxidation.17,19
3.3 Model CO oxidation
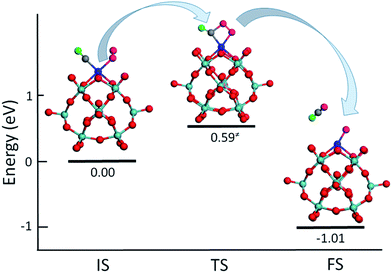
To test the ability of M–PMA SACs, we have computed the reaction energetics for CO oxidation, a prototypical catalysis reaction. The activation of oxygen molecules was investigated first since it is an important step of CO oxidation.3,16,17 The calculated O–O bond of the O2 adsorbed on the metal center of M–PMA is found to be elongated, suggesting O2 activation. For example, as shown in Fig. S2,† the O–O bond length on Ru–PMA is significantly elongated from its equilibrium value of 1.23 Å to 1.36 Å, yielding a binding energy of −1.37 eV for the adsorbed O2 species. While for a non-precious metal such as Fe, the O2 molecule has an adsorption energy of −0.48 eV with the length of the O–O bond changed to 1.33 Å, implying efficient activation of O2 on Fe–PMA. In addition, the reaction of CO + O2 → CO2 + O is investigated on Pt–PMA. As shown in Fig. 8, in IS the CO molecule is co-adsorbed with O2 in which the O–O bond length is about 1.27 Å. At the transition state, the O–O bond distance is further elongated to 1.37 Å and the carbon atom of CO connects to one of oxygen atoms in O2 with a bond length of 1.69 Å. This reaction step for the production of a CO2 molecule requires to overcome an energy barrier of 0.59 eV, which is much lower than those (around 1 eV) on transition metal surfaces such as Pt, Au and Ag.41–43 In addition, this reaction is quite exothermic with ΔE equal to −1.01 eV. For the reaction between the second CO and the remaining O atom (CO + O → CO2), the calculated energy barrier is also quite small (0.22 eV) and the exothermicity is found to be −2.14 eV. In order to find out whether the other supported metal atoms have catalytic activity, we also investigated CO oxidation on PMA supported single Ru atom. The energy barrier for the reaction (CO + O2 → CO2 + O) is about 0.75 eV with a large exothermicity of −3.13 eV, suggesting its strong activity. For Ru–PMA, the CO + O → CO2 step overcomes an energy barrier as high as 0.95 eV, which is much larger than that (0.22 eV) on Pt–PMA. It can be attributed to the fact that the oxygen atom is strongly bounded to the Ru–PMA complex with a binding energy of −3.36 eV, about 3 eV larger than that on Pt–PMA. Our calculation results indicate that the adsorption energy of the intermediate species such as an oxygen atom plays an important role in the oxidation process. If this value is found to be large, the oxygen species might not be facilely taken away by the second CO molecule and the catalyst might be poisoned. Overall, our results suggest that Pt–PMA can efficiently catalyse this prototypical process. Further calculations of CO oxidation on other M–PMA SACs will be reported in another paper.4. Conclusions
In this work, single transition metal atoms (M = Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au) embedded in phosphomolybdic acid were systematically explored by using a DFT method in an effort to gain insights into the metal binding and catalytic potentials. From the calculation results, we found such systems are very stable with each single metal atom coordinated by four oxygen atoms at the 4-H site in a distorted square-planar configuration and slightly protrudes from the oxygen planar surface. The adsorption energies of the single metal atoms at the 4-H site of PMA are significantly larger than those in edge positions of the metal nanoparticles and comparable to those on CeO2 surfaces. The strong binding energies indicating that these single atoms can effectively avoid agglomeration. All the embedded single metal atoms are positively charged as electrons are found to transfer from single metal atoms to PMA, suggesting the potential catalytic applications. Generally, the calculated binding energies of single metal atoms show clear trends as decreasing in magnitude from the left to the right of the period, indicating that metals with less occupied d bands bind more strongly to PMA. Furthermore, our calculation results also predict that Pt–PMA might be a low-cost, stable and efficient SAC for CO oxidation.Acknowledgements
We acknowledge support from National Natural Science Foundation of China (21673040 to S. Lin), Natural Science Foundation of Fujian Province (2016J01052 to S. Lin) and U.S. National Science Foundation (CHE-1462019 to H. Guo).References
- J. Liu, ACS Catal., 2017, 7, 34–59 CrossRef CAS
.
- X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed
.
- B. Qiao, A. Wang, X. Yang, L. F. Allard, Z. Jiang, Y. Cui, J. Liu, J. Li and T. Zhang, Nat. Chem., 2011, 3, 634–641 CrossRef CAS PubMed
.
- J.-X. Liang, X.-F. Yang, A. Wang, T. Zhang and J. Li, Catal. Sci. Technol., 2016, 6, 6886–6892 CAS
.
- R. Lang, T. Li, D. Matsumura, S. Miao, Y. Ren, Y.-T. Cui, Y. Tan, B. Qiao, L. Li, A. Wang, X. Wang and T. Zhang, Angew. Chem., Int. Ed., 2016, 128, 16288–16292 CrossRef
.
- J.-X. Liang, J. Lin, X.-F. Yang, A.-Q. Wang, B.-T. Qiao, J. Liu, T. Zhang and J. Li, J. Phys. Chem. C, 2014, 118, 21945–21951 CAS
.
- G. X. Pei, X. Y. Liu, X. Yang, L. Zhang, A. Wang, L. Li, H. Wang, X. Wang and T. Zhang, ACS Catal., 2017, 7, 1491–1500 CrossRef CAS
.
- J. Lin, A. Wang, B. Qiao, X. Liu, X. Yang, X. Wang, J. Liang, J. Li, J. Liu and T. Zhang, J. Am. Chem. Soc., 2013, 135, 15314–15317 CrossRef CAS PubMed
.
- Y.-G. Wang, D. Mei, V.-A. Glezakou, J. Li and R. Rousseau, Nat. Commun., 2015, 6, 6511 CrossRef CAS PubMed
.
- B. Long, Y. Tang and J. Li, Nano Res., 2016, 9, 3868–3880 CrossRef CAS
.
- M. Moses-DeBusk, M. Yoon, L. F. Allard, D. R. Mullins, Z. Wu, X. Yang, G. Veith, G. M. Stocks and C. K. Narula, J. Am. Chem. Soc., 2013, 135, 12634–12645 CrossRef CAS PubMed
.
- G. Vilé, D. Albani, M. Nachtegaal, Z. Chen, D. Dontsova, M. Antonietti, N. López and J. Pérez-Ramírez, Angew. Chem., Int. Ed., 2015, 54, 11265–11269 CrossRef PubMed
.
- S. Yang, J. Kim, Y. J. Tak, A. Soon and H. Lee, Angew. Chem., Int. Ed., 2016, 55, 2058–2062 CrossRef CAS PubMed
.
- B. Zhang, H. Asakura, J. Zhang, J. Zhang, S. De and N. Yan, Angew. Chem., Int. Ed., 2016, 55, 8319–8323 CrossRef CAS PubMed
.
- J. Jones, H. Xiong, A. T. DeLaRiva, E. J. Peterson, H. Pham, S. R. Challa, G. Qi, S. Oh, M. H. Wiebenga and X. I. P. Hernández, Science, 2016, 353, 150–154 CrossRef CAS PubMed
.
- E. J. Peterson, A. T. DeLaRiva, S. Lin, R. S. Johnson, H. Guo, J. T. Miller, J. Hun Kwak, C. H. F. Peden, B. Kiefer, L. F. Allard, F. H. Ribeiro and A. K. Datye, Nat. Commun., 2014, 5, 4885 CrossRef CAS PubMed
.
- S. Lin, X. Ye, R. S. Johnson and H. Guo, J. Phys. Chem. C, 2013, 117, 17319–17326 CAS
.
- S. Lin, X. Ye and J. Huang, Phys. Chem. Chem. Phys., 2015, 17, 888–895 RSC
.
- C. Huang, X. Ye, C. Chen, S. Lin and D. Xie, Comput. Theor. Chem., 2013, 1011, 5–10 CrossRef CAS
.
- A. Figueroba, G. Kovács, A. Bruix and K. M. Neyman, Catal. Sci. Technol., 2016, 6, 6806–6813 CAS
.
- A. Neitzel, A. Figueroba, Y. Lykhach, T. s. Skála, M. Vorokhta, N. Tsud, S. Mehl, K. r. Ševčíková, K. C. Prince and K. M. Neyman, J. Phys. Chem. C, 2016, 120, 9852–9862 CAS
.
- F. Li, L. Li, X. Liu, X. C. Zeng and Z. Chen, ChemPhysChem, 2016, 17, 3170–3175 CrossRef CAS PubMed
.
- F. Li, Y. Li, X. C. Zeng and Z. Chen, ACS Catal., 2015, 5, 544–552 CrossRef CAS
.
- T. Yang, R. Fukuda, S. Hosokawa, T. Tanaka, S. Sakaki and M. Ehara, ChemCatChem, 2017, 9, 1222–1229 CrossRef CAS
.
- X. Zhang, J. Lei, D. Wu, X. Zhao, Y. Jing and Z. Zhou, J. Mater. Chem. A, 2016, 4, 4871–4876 CAS
.
- X.-K. Gu, B. Qiao, C.-Q. Huang, W.-C. Ding, K. Sun, E. Zhan, T. Zhang, J. Liu and W.-X. Li, ACS Catal., 2014, 4, 3886–3890 CrossRef CAS
.
- W.-C. Ding, X.-K. Gu, H.-Y. Su and W.-X. Li, J. Phys. Chem. C, 2014, 118, 12216–12223 CAS
.
- P. W. N. M. van Leeuwen, Homogeneous catalysis: understanding the art, Kluwer Academic Pubishers, Dordrecht, 2004 Search PubMed
.
- X. Lopez, J. J. Carbo, C. Bo and J. M. Poblet, Chem. Soc. Rev., 2012, 41, 7537–7571 RSC
.
- S. Wen, W. Guan, J. Wang, Z. Lang, L. Yan and Z. Su, Dalton Trans., 2012, 41, 4602–4607 RSC
.
- S. Wen, W. Guan, Y. Kan, G. Yang, N. Ma, L. Yan, Z. Su and G. Chen, Phys. Chem. Chem. Phys., 2013, 15, 9177–9185 RSC
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS
.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter
Mater. Phys., 1976, 13, 5188–5192 CrossRef
.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 254–360 CrossRef
.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653 CrossRef CAS
.
- N. Lopez, T. V. W. Janssens, B. S. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. K. Nørskov, J. Catal., 2004, 223, 232–235 CrossRef CAS
.
- H. Y. Su, M. M. Yang, X. H. Bao and W. X. Li, J. Phys. Chem. C, 2008, 112, 17303–17310 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03490c |
| This journal is © The Royal Society of Chemistry 2017 |