Open Access Article
Open Access ArticleEvaluation of the degree of chitosan deacetylation via induced-electrical properties
Dandan Liab,
Lunan Guoab,
Na Yang *ab,
Yao Zhangab,
Zhengyu Jinabc and
Xueming Xu
*ab,
Yao Zhangab,
Zhengyu Jinabc and
Xueming Xu *abc
*abc
aState Key Laboratory of Food Science and Technology, Jiangnan University, Wuxi 214122, Jiangsu Province, China. E-mail: yangna@jiangnan.edu.cn; xmxu@jiangnan.edu.cn; Fax: +86 510 85917100; Tel: +86 510 85917100
bSchool of Food Science and Technology, Jiangnan University, Wuxi 214122, Jiangsu Province, China
cSynergetic Innovation Center of Food Safety and Nutrition, Jiangnan University, Wuxi 214122, China
First published on 16th May 2017
Abstract
The properties and functionalities of chitosan are closely related to its degree of deacetylation (DD). This study aimed to determine the DD of chitosans, which were of identical molecular weight, by a proposed electro-analytical system based on inductive methodology. Statistically significant differences in electrical parameters, including terminal voltage (U′S) and λ (the ratio of primary voltage to U′S) were observed among chitosans with different DDs. Both U′S and λ were linearly correlated with the DD value, regardless of frequency, suggesting that these electrical parameters can be used to determine the DD of chitosan. More chitosan's coils contributed to higher measurement accuracy, but the change in measurement position showed no improvement. The highest linear coefficient of determination (0.9941) between DD and U′S was obtained by the experimental transformer with 100-turn chitosan's coils at a primary voltage of 10 V and a frequency of 400 Hz. This study explored the potential of an innovative electro-analytical system to determine the DD of chitosan.
1 Introduction
Chitosan is a copolymer of β-1,4-anhydroglucosamine and N-acetyl-β-1,4-anhydroglucosamine. It is produced by an alkaline N-deacetylation of chitin.1 Due to its cationic nature, chitosan is considered one of the most important natural polysaccharides, in environmental and biomedical fields.2 Chitosan performs diverse biological functions, such as antifungal and antimicrobial activities,3 immune-enhancing effects,4 antioxidant activities,5 and wound healing properties.6,7 Thus, it is widely used in food production, agriculture, cosmetics, and biomedicine.1 The above properties and functionalities are closely related to the degree of deacetylation (DD). Therefore, the determination of DD is essential for investigating their chemical structures, physical properties, and structure–properties relationships.Various methods have been applied to determine the DD value of chitosan, including IR spectroscopy,8 NMR spectroscopy,9 UV spectrophotometry,10 elemental analysis,11 chromatography,12 thermal analysis,13 acid titration,14 conductometry,15 and potentiometry.16 Among these methods, conductometry and potentiometry were established based on the cationic nature of chitosan. Chitosan behaves as a cationic polyelectrolyte when dissolved in an acidic aqueous solution, due to the protonation of amino groups on glucosamine units.17 The DD of chitosan is defined as the molar percent of β-1,4-anhydroglucosamine in relation to the total β-1,4-anhydroglucosamine and N-acetyl-β-1,4-anhydroglucosamine,11,17 which means that the DD value is closely related to the amino group content. Changing the amount of amino content, the electrical properties of chitosan acidic solutions change correspondingly. Therefore, the DD of chitosan can be determined through electrical techniques.
Electrical parameters are widely applied for the evaluation of the quality of agro-products and food,18,19 interfacial property of electrolyte solutions,20 and characterization of membranes.21,22 Żywica et al.23 suggested there was a linear correlation between total soluble solids in reconstituted apple juice and electrical parameters, which concluded that it is possible to evaluate the concentrations of apple purées in pulpy juices and beverages by electro-analytical method. Additionally, estimation of the quality of bighead carp (Aristichthys nobilis) during chilling storage24 and determination of the degree of dispersion of fat globules in the homogenization process25 have also been successfully conducted by measuring electrical parameters. However, the electrical properties of agro-product, food, and other materials are usually determined by impedance, resistance, admittance, and conductance measurements via LCR meter, network analyzer, or impedance analyzer.
Therefore, electrical parameters represent quality factors of organic materials, such as fat content,26 fruit maturity,27 moisture content,28 even food adulteration.29 However, sophisticated instruments used in the existing electro-analytic methods is costly. Thus, further studies should assess material characteristics on the basis of measurable electrical properties via a low-cost system. Based on the transformer configuration, induced-electrical detection system was established using liquid sample as a secondary coil. According to Faraday's effect, the varying magnetic flux in the primary coil induces a varying voltage in the secondary coil (sample's coil). When primary voltage (UP) and the ratio of primary coil turn to secondary coil turn (NP/NS) are constant, the induced voltage (US) do not alter according to Ampere's circuital theorem (US/UP = NS/NP). However, the changes in physicochemical properties of materials will affect the terminal voltage (U′S, output voltage) in sample's closed-loop. Therefore, it is possible to use induced-electrical parameter U′S to evaluate material characteristics. Our previous examinations have confirmed that physicochemical properties of liquid food can be estimated by determination of U′S value30,31 and the induced-electrical detection system has a flexible and affordable configuration compared to other electro-detection systems. However, there has been no research on the assessment of physicochemical characteristics of organic materials via measurements of induced-electrical properties by changing turns ratio and using a two-series coil. Therefore, this study aimed to explore the potential of the proposed electroanalytical method as a general technique for the evaluation of chitosan DD. The correlation between DD of chitosans and induced-electrical parameters, including U′S and λ value (the ratio of UP to U′S), was analyzed.
2 Materials and methods
2.1 Materials
Chitosan (DD ≥ 95%) and acetyl-glucosamine were of analytical grade and were purchased from Aladdin Co., Ltd. (Shanghai, China). Acetic anhydride, sodium hydroxide, phosphoric acid, methanol, ethanol, and all other analytical chemicals were manufactured by Sinopharm Chemical Reagent Co., Ltd. (Suzhou, China).2.2 Preparation of chitosans with various DDs
Chitosans with various DDs but the same Mw, were obtained by homogeneous re-acetylation, as reported by Li et al.32 with slight modification. Chitosan (10 g) was first dissolved in 250 mL 2% (w/v) of aqueous acetic acid solution, and then 250 mL of methanol was added and magnetically stirred for 5 min. After acetic anhydride was added slowly to the mixture at molar ratios of 1.05![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1.1
1, 1.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1.2
1, 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4
1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1.6
1, 1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 1.8
1, and 1.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively, acetylation was performed by continuously stirring at 25 °C for 3 h. Since chitosan only dissolves in dilute acid due to its cationic nature, the re-acetylated products were separated by adjusting the solution pH to 10 with 4 mol L−1 NaOH. The obtained white precipitates were collected through filtration under vacuum and washed with 80% ethanol four times (300 mL each time) to remove the residual NaOH, unreacted reagents, and by-products. The filter cake was freeze–dried, and the obtained chitosans were used for further analysis.
1, respectively, acetylation was performed by continuously stirring at 25 °C for 3 h. Since chitosan only dissolves in dilute acid due to its cationic nature, the re-acetylated products were separated by adjusting the solution pH to 10 with 4 mol L−1 NaOH. The obtained white precipitates were collected through filtration under vacuum and washed with 80% ethanol four times (300 mL each time) to remove the residual NaOH, unreacted reagents, and by-products. The filter cake was freeze–dried, and the obtained chitosans were used for further analysis.
2.3 DD measurement
The DDs of native and acetylated chitosans were determined using a first-derivative UV method, in which acetyl-glucosamine was utilized as standard.10 Chitosan (100 mg) was dissolved in 20 mL of 85% phosphoric acid followed by continuous stirring at 60 °C for 40 min. One milliliter of the mixture was then taken into a volumetric flask, and deionized water was added to the solution until a volume of 100 mL was reached. The diluted chitosan solution was then heated at 60 °C for 2 h and scanned using a UV-Vis spectrophotometer (TU-1900, Rayleigh Analytical Instruments, Beijing, China) under the scan mode and in the range from 220 to 190 nm. Acetyl-glucosamine (100, 200, 300, 400, and 500 mg) was weighed and added into the 100 mL 85% phosphoric acid. The solutions were then diluted with deionized water at a ratio of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v, treated at 60 °C for 2 h, and scanned at wavelengths in the range from 220 to 190 nm. As a function of the concentrations of acetyl-glucosamine, a calibration curve was made by plotting the first derivative of the UV values at 203 nm, and the DDs of the chitosans were calculated by using the calibration curve.
1 v/v, treated at 60 °C for 2 h, and scanned at wavelengths in the range from 220 to 190 nm. As a function of the concentrations of acetyl-glucosamine, a calibration curve was made by plotting the first derivative of the UV values at 203 nm, and the DDs of the chitosans were calculated by using the calibration curve.
2.4 Electrical conductivity measurement
Chitosan solutions (0.6% wt) were prepared by slow addition of the chitosans into 1% acetic acid and stirring at 25 °C for 24 h. The electrical conductivity of the obtained solutions was measured using a conductivity meter (Mettler Toledo FE38-Meter, Zürich, Switzerland) equipped with an electrode (Mettler Toledo LE703, Zürich, Switzerland) at 25 °C.2.5 Viscosity measurement
Chitosan (1.8 g) was slowly added into a 1% acetic acid solution (300 mL), and the mixture was magnetically stirred at 25 °C for 4 h. Then, the viscosity of the chitosan-acetic acid solution was determined by a DV-C rotational viscometer (Brookfield, Middleboro, USA) using a spindle s61 at 100 rpm (25 °C).2.6 Molecular weight determination
Molecular weight of chitosans was determined according to the high-pressure size-exclusion chromatography (HPSEC) method. The HPSEC separation was performed by two columns (Shodex OHpak SB-804 HQ and OHpak SB-802 HQ, Showa Denko America, Inc., New York, USA) connected in series with 0.2 mol L−1 CH3COOH/0.1 mol L−1 CH3COONa (pH = 4.5) as the mobile phase at a flow rate of 0.6 mL min−1. The mobile phase was filtered through a 0.45 μm syringe filter (Millipore, Billerica, Massachusetts, USA) and degassed by ultrasonic treatment for 30 min. The column effluent was analyzed using a RI detector (Hitachi RI-5450, Hitachi, Tokyo, Japan). Samples were prepared as follows: chitosan (4 mg mL−1) was dissolved in the mobile phase at 25 °C for 24 h, and then the obtained solution (20 μL) was injected into the system. During the measurement, the temperature of columns was set up to 30 °C. Pullulan standards (Shodex standard P-82) were used to calculate the weight-average molecular weight (Mw).2.7 DD evaluation of chitosans based on inductive methodology
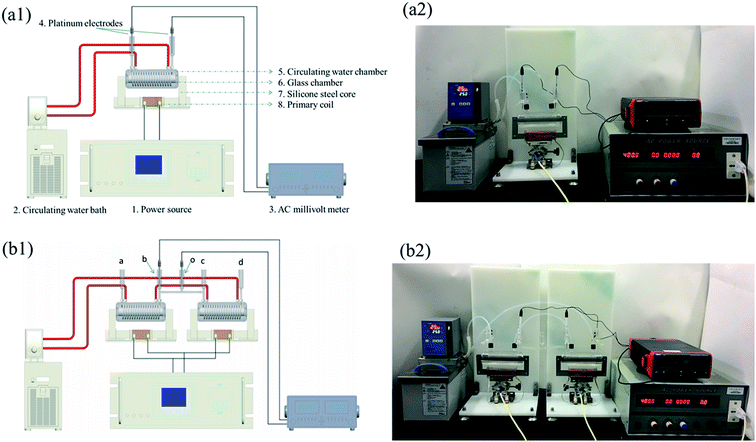
The purpose of this electro-analysis was to determine the induced-electrical properties of chitosans with various DDs via electromagnetic induction. The schematic diagram and a photograph of the system are presented in Fig. 1. The system includes: (1) power source (PS-6105, Taiwan Pusi Electronics Co., Ltd., Taiwan); (2) circulating water bath (MP-10C, Yiheng Technical Co., Ltd., Shanghai, China); (3) AC millivoltmeter (UT631, Uni-Trend Group Limited Co., Ltd., Hong Kong, China); (4) platinum electrodes; (5) circulating water chamber; (6) glass chamber; (7) silicone steel core (no. PC80, cross-sectional area of the magnetic path = 40 mm2, length of the magnetic loop = 220 mm; thickness of the magnetic path = 20 mm); (8) primary coil. Copper conductor was wound on one side of the silicone steel core, acting as the primary coil (NP = 100), whereas the electro-conductive solution was filled in a glass spiral tube (internal diameter of 3 mm; NS = 18) or a polytetrafluoroethylene tube (internal diameter of 3 mm; NS = 100) on the other side, acting as the secondary coil (chitosan's coil: chitosan acetic acid solution in the coil). Primary voltage applied on the primary coil generated an alternating magnetic flux in the core, leading to the induction of a voltage in the chitosan's coil. A pair of platinum electrodes connected to an AC millivoltmeter was employed to measure the U′S value in chitosan's coil. According to the principle of transformer (UP/US = NP/NS), as the UP and NP/NS were fixed, the US was a constant. However, the change of impedance will affect the U′S in the chitosan's circuit (chitosan acetic acid solution in the closed-loop). Therefore, this relationship could be used to characterize the DD value of chitosan by measuring their induced-electrical parameters. In this study, three electro-analytical systems, including an experimental transformer 18 (NS = 18), transformer 100 (NS = 100), and a two-series transformer (NS1 = NS2 = 18) were used. In the two-series system (Fig. 1b), the distance between two experimental transformers (Lbc) was 200 mm.Each chitosan (0.6% (w/v)) was prepared in 1% (w/v) acetic acid at 25 °C for 24 h and injected into the coil with no air bubble. An excitation voltage (5–50 V and 300–700 Hz) generated by an AC power source was imposed on the primary coil. The measurement temperature was 25 °C. The U′S of the chitosan's coil were measured by an AC millivoltmeter. Another induced-electrical parameter λ value was calculated. The regression models between U′S, λ value, and DD of chitosan were established.
2.8 Statistical analysis
Data were analyzed using the DPS package (version 8.0 for Windows, Hangzhou, China), and Fisher's least significant difference (LSD) test was applied to compare the differences between the means at 5% significance level. The correlation between DD of chitosan and measured electrical parameters (U′S and λ value) was determined using SPSS 16.0 software (Pearson's test). Linear regression was performed with Excel (Microsoft, 2011, Redmond, USA). The accuracy of the regression equation was assessed using coefficient of determination (R2) and root mean square error (RMSE).3 Results and discussion
3.1 Physicochemical properties of chitosans with various DDs
The electrical conductivity of an electrolyte solution depends on ion concentration and its migration rate.33 In this study, chitosan samples (1.8 g) were dissolved in a 1% (v/v) acetic acid solution (300 mL) at 25 °C. The ion concentration was determined by the amount of the amino group, whereas ionic migration rate was related to the viscosity of the medium. Chitosans with identical molecular weight but differing DDs had similar viscosities (Table 1) but different amino group contents. Therefore, DD is the key factor that affects the conductivity of chitosan solutions. The increase of DD value from 53.56 to 99.83 resulted in a linear rise of the conductivity from 0.912 to 2.21 mS cm−1 (25 °C). A regression model, y = 37.422x + 15.385, was obtained, indicating relatively high accuracy of the regression equation (R2 = 0.9514 and RMSE = 3.90%).| No. | Chitosan: acetic anhydride (mol mol−1) | DD (%) | Conductivity (mS cm−1) | Viscosity (mPa s) | Mw (×103 g mol−1) |
|---|---|---|---|---|---|
| a Means in the same column with different letter indicate significant difference (P < 0.05); DD: degree of deacetylation; Mw: molecular weight of chitosan. | |||||
| 1 | — | 99.83 ± 0.32a | 2.21 ± 0.102a | 40.68 ± 1.34a | 6.416 ± 0.539a |
| 2 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.05 1.05 |
94.20 ± 0.12b | 1.968 ± 0.073b | 40.14 ± 2.11a | 6.627 ± 0.135a |
| 3 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.1 1.1 |
85.90 ± 0.29c | 1.889 ± 0.042b | 39.44 ± 1.32a | 6.234 ± 0.032a |
| 4 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.2 1.2 |
78.88 ± 0.43d | 1.833 ± 0.056b | 41.21 ± 1.76a | 6.744 ± 0.452a |
| 5 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.4 1.4 |
63.58 ± 0.26e | 1.432 ± 0.034c | 40.33 ± 1.43a | 6.346 ± 0.982a |
| 6 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 1.6 |
55.51 ± 0.31f | 1.08 ± 0.063d | 42.33 ± 2.01a | 6.565 ± 0.262a |
| 7 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.8 1.8 |
53.56 ± 0.34g | 0.912 ± 0.087d | 40.32 ± 2.11a | 6.987 ± 0.463a |
3.2 Using terminal voltage and λ value (UP/U′S) to evaluate DD of chitosan
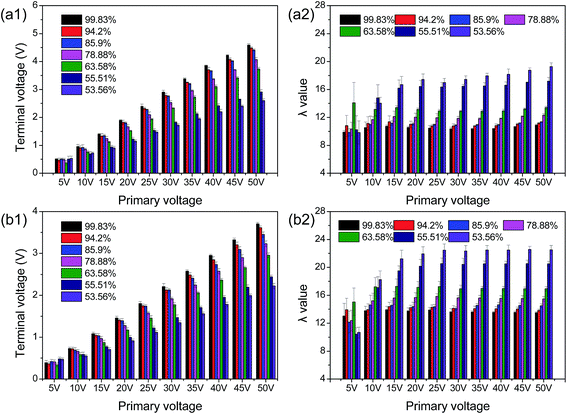
The current system exhibits a flexible configuration as the ratio of primary coil turn to secondary coil turn can be altered. Additionally, induced-electrical properties of organic materials have been investigated at various primary voltages and frequencies.34 These mean that statistical differences among these parameters can be reduced by altering the system configuration and detection conditions.The induced-electrical parameters of the chitosan's circuit, including U′S and λ, were determined by transformer 18 (NS = 18) at a primary voltage of 20 V and a frequency from 300 to 700 Hz. As shown in Fig. 2a, the DD value increased with the rise in U′S but slightly decreased with frequency augmentation for all samples. An opposite variation trend was observed in λ values (Fig. 2b). At 300 Hz, the U′S values of chitosan solutions with different DDs (99.83, 94.20, 85.90, 78.88, 63.58, 55.51, and 53.56) were 2.21, 1.968, 1.889, 1.833, 1.432, 1.08, and 0.912, while the λ values were 9.23, 9.66, 10.16, 10.32, 11.35, and 12.73, respectively. Higher differences were obtained during the measurement performed at 700 Hz. Statistically significant differences among induced-electrical parameters (U′S and λ) of chitosans indicated that these parameters may be used as an indicator of chitosan DD.
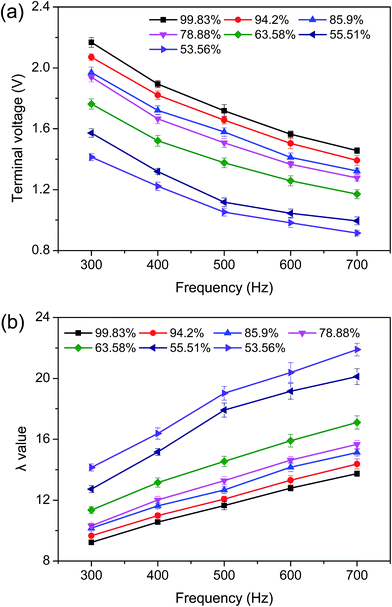 | ||
| Fig. 2 Effects of frequency and DD on induced-electrical parameters determined by transformer 18 at 20 V primary voltage (UP): (a) terminal voltage (U′S); (b) λ value (UP/U′S). | ||
As described before (Section 2.6), the induced voltage did not change (UP/US = NP/NS) as primary voltage and coil turns remained constants. However, the increase in the DD of chitosan elevated the amino group content, resulting in an increase of ion concentration and a decrease of the impedance in the chitosan's coil. The reduced total impedance boosted the induced current in the chitosan's coil according to Ohm's law, in which the induced current was equal to the ratio of the induced voltage to the equivalent impedance of the chitosan's circuit. As a result, the change in DD caused variations in the U′S and λ of the chitosan solution. However, it is important to note that the U′S values of eggs30 and pickled cucumbers31 slightly increased with frequency elevation. This difference might have been caused by specific physicochemical properties of the samples.
The effects of the UP on the U′S and λ value determined by the experimental transformer 18 (NS = 18) at 400 Hz are presented in Fig. 3. The rise in UP from 5 to 50 V, led to a significantly increase in the U′S of all samples. In contrast, λ value was reduced as the UP increased. This result can be explained by Ampere's circuital theorem, in which induced voltage in the chitosan's coil is positively proportional to the UP. A similar result was observed in our previous study.30,31,34
These results demonstrated the potential of U′S and λ as indexes for the evaluation of the DD of chitosan. The correlations between U′S, λ value, and DD were subsequently determined (Tables 2–5).
3.3 Relationships between DD and terminal voltage and λ determined by transformer 18 system
As shown in Tables 2 and 3, correlation and linear regression analysis of DD as a function of changes in U′S and λ of chitosans showed that mathematical relationships described by the equation Y = A ± BX were observed within the range of UP from 10 to 50 V and frequencies of 400 and 700 Hz. As the UP increased from 10 to 50 V, correlation coefficient ranged from 0.911 to 0.985 at α < 0.01, 400 and 700 Hz, revealing that the DD value can be determined based on the measurements of U′S and λ at the tested frequencies. However, no correlation was observed between induced-electrical parameters and DD value of chitosan at a primary voltage of 5 V. Additionally, at higher UP (40 V and 50 V), correlation coefficient between the induced-electrical parameters and DD was lower than that at lower UP, especially at 400 Hz. The reason might be the measurement error of the voltmeter and electromagnetic interference produced by the power source, affected the accuracy. When the electro-analysis was performed at low excitation voltage (5 V), induced voltage in the chitosan's coil was low (<0.6 V), and thus the effect of measurement error was obvious. At high excitation voltage (50 V), however, the electromagnetic interference was significant. As a result, the most effective prediction model (DD = 259.12U′S − 91.546, R2 = 0.9701, RSME = 2.98) for DD was obtained at a primary voltage of 10 V and a frequency of 700 Hz.| Frequency (Hz) | Primary voltage (V) | r | α | Regression equations | R2 | RMSE (%) |
|---|---|---|---|---|---|---|
| a r, correlation coefficient; α, significance level; ** significance of correlation (α ≤ 0.01); R2, determination coefficient; RMSE represents root mean square error. | ||||||
| 400 | 5 | 0.832 | 0.1 | — | — | — |
| 10 | 0.977** | 0.000 | DD = 170.59U′S − 65.591 | 0.9537 | 3.71 | |
| 15 | 0.967** | 0.000 | DD = 89.759U′S − 30.044 | 0.9359 | 4.37 | |
| 20 | 0.964** | 0.000 | DD = 60.317U′S − 19.525 | 0.929 | 4.60 | |
| 25 | 0.964** | 0.000 | DD = 47.913U′S − 20.108 | 0.9299 | 4.57 | |
| 30 | 0.961** | 0.000 | DD = 37.831U′S − 15.211 | 0.9227 | 4.8 | |
| 35 | 0.956** | 0.001 | DD = 31.578U′S − 12.463 | 0.9144 | 5.05 | |
| 40 | 0.955** | 0.001 | DD = 27.357U′S − 11.231 | 0.9127 | 5.1 | |
| 45 | 0.953** | 0.001 | DD = 24.675U′S − 10.362 | 0.9078 | 5.24 | |
| 50 | 0.949** | 0.001 | DD = 22.303U′S − 9.4322 | 0.9001 | 5.45 | |
| 700 | 5 | −0.538 | 0.213 | — | — | — |
| 10 | 0.985** | 0.000 | DD = 259.12U′S − 91.546 | 0.9701 | 2.98 | |
| 15 | 0.974** | 0.000 | DD = 126.04U′S − 40.665 | 0.9492 | 3.89 | |
| 20 | 0.970** | 0.000 | DD = 89.654U′S − 33.276 | 0.948 | 3.93 | |
| 25 | 0.966** | 0.000 | DD = 66.11U′S − 24.753 | 0.9324 | 4.49 | |
| 30 | 0.963** | 0.000 | DD = 53.005U′S − 22.251 | 0.9278 | 4.63 | |
| 35 | 0.969** | 0.000 | DD = 46.03U′S − 22.976 | 0.9387 | 4.27 | |
| 40 | 0.970** | 0.000 | DD = 40.23U′S − 22.951 | 0.9409 | 4.19 | |
| 45 | 0.969** | 0.000 | DD = 35.328U′S − 21.835 | 0.9386 | 4.23 | |
| 50 | 0.971** | 0.000 | DD = 31.35U′S − 20.904 | 0.9428 | 4.13 | |
| Frequency (Hz) | Primary voltage (V) | r | α | Regression equations | R2 | RMSE (%) |
|---|---|---|---|---|---|---|
| a r, correlation coefficient; α, significance level; ** significance of correlation (α ≤ 0.01); R2, determination coefficient; RMSE represents root mean square error. | ||||||
| 400 | 5 | −0.234 | 0.614 | — | — | — |
| 10 | −0.962** | 0.001 | DD = −10.795λ + 208.97 | 0.9257 | 4.7 | |
| 15 | −0.942** | 0.001 | DD = −7.1852λ + 170.04 | 0.8883 | 5.77 | |
| 20 | −0.931** | 0.002 | DD = −6.2716λ + 158.08 | 0.866 | 6.32 | |
| 25 | −0.933** | 0.002 | DD = −6.4468λ + 159.19 | 0.8696 | 6.23 | |
| 30 | −0.925** | 0.003 | DD = −6.0117λ + 153.71 | 0.8561 | 6.56 | |
| 35 | −0.917** | 0.004 | DD = −5.6772λ + 149.86 | 0.84 | 6.9 | |
| 40 | −0.914** | 0.004 | DD = −5.5325λ + 148.38 | 0.8362 | 6.98 | |
| 45 | −0.911** | 0.004 | DD = −5.3162λ + 147.31 | 0.8291 | 7.13 | |
| 50 | −0.904** | 0.005 | DD = −5.1106λ + 145.68 | 0.8178 | 7.36 | |
| 700 | 5 | 0.466 | 0.292 | — | — | — |
| 10 | −0.980** | 0.000 | DD = −10.321λ + 238.22 | 0.9608 | 3.42 | |
| 15 | −0.949** | 0.001 | DD = −6.2893λ + 180.52 | 0.9011 | 5.52 | |
| 20 | −0.941** | 0.002 | DD = −5.5234λ + 168.46 | 0.8864 | 5.81 | |
| 25 | −0.935** | 0.002 | DD = −5.1862λ + 163.8 | 0.874 | 6.12 | |
| 30 | −0.931** | 0.002 | DD = −5.0901λ + 161.14 | 0.8667 | 6.3 | |
| 35 | −0.933** | 0.002 | DD = −5.0772λ + 161.37 | 0.8708 | 6.2 | |
| 40 | −0.934** | 0.002 | DD = −5.0787λ + 161.33 | 0.8721 | 6.17 | |
| 45 | −0.932** | 0.002 | DD = −5.0055λ + 160.09 | 0.8688 | 6.25 | |
| 50 | −0.935** | 0.002 | DD = −4.9861λ + 159.44 | 0.8738 | 6.13 | |
Higher R2 values (0.9001 < R2 < 0.9701) and lower RMSE values (2.98% < RMSE < 5.45%) were obtained for the negative linear regressions of DD on U′S value when compared to those for the λ value (0.8178 < R2 < 0.9608; 3.42% < RMSE < 7.36%), suggesting that U′S value may be more effective than λ value for the estimation of chitosan DD. Our previous study indicated that λ value fits better for the evaluation of moisture content in eggs,30 might have been caused by the different chemical compositions of the materials.
3.4 Relationship between DD and terminal voltage determined by transformer 100 system
With the increase in chitosan's coil turns, induced voltage in chitosan's coil increased. As a result, statistical differences among the determined induced-electrical parameters of chitosan might be increased. Therefore, a system with 100-turn coil (transformer 100) was developed to determine the DD of chitosan.At excitation voltage from 5 to 50 V and frequency ranging from 300 to 700 Hz, the analysis between DD and U′S of chitosans demonstrated the presence of a correlation at a significance level of α < 0.01, with correlation coefficients ranging from 0.941 to 0.995 (Table 4). This suggested that relationships between DD and U′S in the tested ranges of UP and frequency can be expressed by the equation Y = A ± BX. Values of R2 from 0.9334 to 0.9941 and of RMSE from 1.09% to 3.28% were established by evaluating mathematical correlations between DD and U′S of the tested samples. The optimal model DD = 123.44U′S − 83.147 with R2 = 0.9941 and RMSE = 1.09% was obtained at 10 V and 400 Hz. These R2 values were higher, whereas RMSE values were much lower, than those obtained by transformer 18 (Table 2). The reason might be the effects of electro-magnetic interference induced by the power source on induced-electrical parameters determination decreased as chitosan's coil turns increased. Therefore, U′S values measured by transformer 100 system were more precise to estimate the DD of chitosan because the utilization of magnetic flux was improved.35
| Frequency (Hz) | Primary voltage (V) | r | α | Regression equations | R2 | RMSE (%) |
|---|---|---|---|---|---|---|
| a r, correlation coefficient; α, significance level; * significance of correlation (α ≤ 0.05); ** significance of correlation (α ≤ 0.01); R2, determination coefficient; RMSE represents root mean square error. | ||||||
| 400 | 5 | 0.995** | 0.000 | DD = 252.01U′S − 128.29 | 0.9771 | 1.41 |
| 10 | 0.987** | 0.002 | DD = 123.44U′S − 83.147 | 0.9941 | 1.09 | |
| 15 | 0.981** | 0.003 | DD = 36.756U′S + 2.8066 | 0.9625 | 2.17 | |
| 20 | 0.978** | 0.004 | DD = 21.23U′S + 15.974 | 0.9556 | 2.48 | |
| 25 | 0.979** | 0.004 | DD = 16.698U′S + 16.48 | 0.959 | 2.46 | |
| 30 | 0.975** | 0.005 | DD = 13.798U′S + 17.151 | 0.9512 | 2.79 | |
| 35 | 0.975** | 0.005 | DD = 12.07U′S + 16.691 | 0.9504 | 2.82 | |
| 40 | 0.966** | 0.007 | DD = 10.44U′S + 18.39 | 0.9334 | 3.28 | |
| 45 | 0.968** | 0.007 | DD = 9.5051U′S + 18.567 | 0.9369 | 3.09 | |
| 50 | 0.981** | 0.003 | DD = 9.2735U′S + 16.373 | 0.962 | 2.58 | |
| 700 | 5 | 0.989* | 0.011 | DD = 101.21U′S − 25.183 | 0.9111 | 2.55 |
| 10 | 0.941* | 0.017 | DD = 109.9U′S − 31.65 | 0.9853 | 2.15 | |
| 15 | 0.964 | 0.008 | DD = 55.826U′S − 1.3197 | 0.9674 | 2.08 | |
| 20 | 0.958* | 0.01 | DD = 38.737U′S + 5.0861 | 0.9587 | 1.93 | |
| 25 | 0.964** | 0.008 | DD = 29.374U′S + 9.2074 | 0.9574 | 2.23 | |
| 30 | 0.962** | 0.009 | DD = 23.993U′S + 9.8468 | 0.9499 | 2.17 | |
| 35 | 0.961** | 0.009 | DD = 20.432U′S + 10.638 | 0.9456 | 2.13 | |
| 40 | 0.962** | 0.009 | DD = 17.36U′S + 12.122 | 0.9447 | 2.37 | |
| 45 | 0.960** | 0.010 | DD = 15.934U′S + 10.819 | 0.9392 | 1.97 | |
| 50 | 0.964** | 0.008 | DD = 14.07U′S + 11.76 | 0.9519 | 2.28 | |
3.5 Relationship between DD and terminal voltage determined by a two-series system
As shown in Fig. 1a, U′S and λ obtained in parts 3.3 and 3.4 were determined by a pair of platinum electrodes connected to an AC millivoltmeter. During the measurement, electrodes were inserted into the chitosan's circuit under an alternating magnetic flux. To increase measurement accuracy, the determination position was changed. As can be seen in Fig. 1b, a detection system based on a two-series coil was developed, and induced-electrical parameter U′bo was determined (Table 5). Since the mutual induction exerted less pronounced effects on the measurement point “o”, correlation coefficient between U′bo and DD was expected to be higher. However, the R2 values (0.8429 < R2 < 0.9642) were lower than the values obtained in parts 3.3 and 3.4 (Tables 2 and 3). U′bo values showed a trend that was opposite to that of U′S values, as determined by using the single-coil system (parts 3.3 and 3.4). The reduced R2 values might be explained by the fact U′bo values were much lower than the U′S values, caused by errors in voltmeter measurement. Therefore, the accuracy of the voltmeter had to be increased, or the electrical potential between position “b” and “o” needed to be amplified. Theoretically, the voltage of the U′bo should be augmented with the increase of the distance between position “b” and “o”. In future, the influence of the length between position “b” and “o” (Lbo) on the correlation will be explored.| Frequency (Hz) | Primary voltage (V) | r | α | Regression equations | R2 | RMSM (%) |
|---|---|---|---|---|---|---|
| a r, correlation coefficient; α, significance level; * significance of correlation (α ≤ 0.05); ** significance of correlation (α ≤ 0.01); R2, determination coefficient; RMSE represents root mean square error. | ||||||
| 400 | 5 | −0.956** | 0.003 | DD = −1308.8U′bo + 138 | 0.9136 | 5.32 |
| 10 | −0.951** | 0.003 | DD = −999.6U′bo + 126.62 | 0.9053 | 5.57 | |
| 15 | −0.955** | 0.003 | DD = −964.67 U′bo + 132.85 | 0.9127 | 5.35 | |
| 20 | −0.956** | 0.003 | DD = −823.87U′bo + 130.69 | 0.9141 | 5.31 | |
| 25 | −0.953** | 0.003 | DD = −691.37U′bo + 127.85 | 0.9076 | 5.5 | |
| 30 | −0.950** | 0.004 | DD = −581.54U′bo + 125.2 | 0.9016 | 5.68 | |
| 35 | −0.948** | 0.004 | DD = −503.5U′bo + 123.5 | 0.8997 | 5.74 | |
| 40 | −0.949** | 0.004 | DD = −441.42U′bo + 122.35 | 0.9012 | 5.69 | |
| 45 | −0.946** | 0.004 | DD = −399.92U′bo + 121.25 | 0.8954 | 5.86 | |
| 50 | −0.982** | 0.003 | DD = −337.5U′bo + 122.03 | 0.9642 | 3.62 | |
| 700 | 5 | −0.937* | 0.019 | DD = −1220.5U′bo + 133.54 | 0.8777 | 6.04 |
| 10 | −0.935* | 0.02 | DD = −945.47U′bo + 128.85 | 0.8735 | 6.14 | |
| 15 | −0.932* | 0.021 | DD = −699.18U′bo + 123.41 | 0.8692 | 6.24 | |
| 20 | −0.931* | 0.022 | DD = −533.42U′bo + 120.18 | 0.8667 | 6.3 | |
| 25 | −0.929* | 0.023 | DD = −425.61U′bo + 117.75 | 0.8623 | 6.41 | |
| 30 | −0.93* | 0.022 | DD = −347.68U′bo + 116.21 | 0.8656 | 6.33 | |
| 35 | −0.927* | 0.024 | DD = −296.12U′bo + 115.23 | 0.8585 | 6.49 | |
| 40 | −0.927* | 0.023 | DD = −255.17U′bo + 114.4 | 0.8594 | 6.47 | |
| 45 | −0.93* | 0.022 | DD = −227.02U′bo + 114.23 | 0.8648 | 6.35 | |
| 50 | −0.918* | 0.028 | DD = −192.35U′bo + 111.95 | 0.8429 | 6.84 | |
3.6 Calibration of regression model
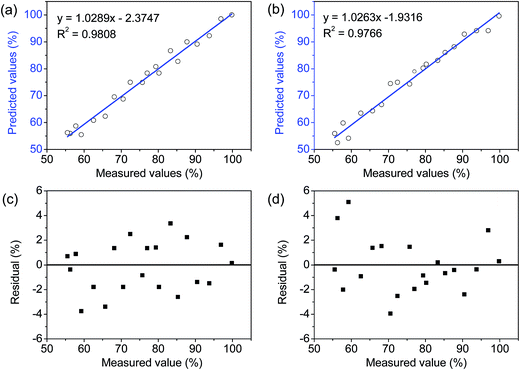
According to the results obtained in parts 3.3, 3.4, and 3.5, regression models DD = 259.12U′S – 91.546 and DD = 123.44U′S – 83.147 were superior. These results were further assessed using a regression analysis of 20 samples which had DDs ranging from 55.55 to 99.83%. The correlations between reference measurements (the first-derivative UV method) and predictions, which were obtained from optimal models, are shown in Fig. 4. All data points have clustered closely to the blue lines along the entire range of DD-values, which means that there is no systematic error present during the predictions.36 To better evaluate the models, residual values and RMSE were calculated. A homoscedasticity of the residual values was observed (Fig. 4c and d) and the RMSE had values as low as 1.99% and 2.18% for the two models, respectively. Thus, the optimized regression models were suitable to predict DD of chitosan. The proposed electro-analytical method has the potential to determine physicochemical properties of organic material.4 Conclusion
In this study, we evaluated the DD of chitosan with identical Mw by using inductive methodology. Induced-electrical parameters, such as U′S and λ, were sensitive to the changes in the DD values because of changed amino group content. At constant of coil turn ratio (NP/NS) and primary voltage, U′S continuously increased in linearly depending on the increase in DD values, regardless of frequency. The highest correlation coefficient (0.9941) was obtained at a UP of 10 V and 400 Hz. Although the change in the measurement position slightly decreased correlation coefficient between the induced-electrical parameter and DD values, coil turn ratio increased which was conducive to the measurement accuracy. The regression model suggests the feasibility of the electro-analytical method based on magneto-electric coupling effect for evaluation of chitosan DD.Acknowledgements
This work was financially supported by the Prospective Joint Research Project of Jiangsu Province (No. BY2016022-06) and the Graduate Student Innovation Project of Jiangsu Province (No. KYLX16_0820).References
- S. T. Koev, P. H. Dykstra, X. Luo, G. W. Rubloff, W. E. Bentley, G. F. Payne and R. Ghodssi, Lab Chip, 2010, 10, 3026–3042 RSC.
- V. K. Thakur and M. K. Thakur, ACS Sustainable Chem. Eng., 2014, 2, 2637–2652 CrossRef CAS.
- A. Munoz-Bonilla, M. L. Cerrada and M. Fernandez-Garcia, in Polymeric Materials with Antimicrobial Activity: From Synthesis to Applications, The Royal Society of Chemistry, 2014, pp. 22–53, 10.1039/9781782624998-00022.
- A. Smith, M. Perelman and M. Hinchcliffe, Hum. Vaccines Immunother., 2013, 10, 797–807 CrossRef.
- T. Feng, Y. Du, J. Li, Y. Hu and J. F. Kennedy, Carbohydr. Polym., 2008, 73, 126–132 CrossRef CAS.
- S. K. L. Levengood and M. Zhang, J. Mater. Chem. B, 2014, 2, 3161–3184 RSC.
- B. Moghadas, E. Dashtimoghadam, H. Mirzadeh, F. Seidi and M. M. Hasani-Sadrabadi, RSC Adv., 2016, 6, 7701–7711 RSC.
- M. R. Kasaai, Carbohydr. Polym., 2008, 71, 497–508 CrossRef CAS.
- M. R. Kasaai, Carbohydr. Polym., 2010, 79, 801–810 CrossRef CAS.
- S. C. Tan, E. Khor, T. K. Tan and S. M. Wong, Talanta, 1998, 45, 713–719 CrossRef CAS PubMed.
- Z. M. dos Santos, A. L. P. F. Caroni, M. R. Pereira, D. R. da Silva and J. L. C. Fonseca, Carbohydr. Res., 2009, 344, 2591–2595 CrossRef CAS PubMed.
- Z. Han, Y. Zeng, H. Lu and L. Zhang, Carbohydr. Res., 2015, 413, 75–84 CrossRef CAS PubMed.
- L. S. Guinesi and É. T. G. Cavalheiro, Thermochim. Acta, 2006, 444, 128–133 CrossRef CAS.
- T. Sannan, K. Kurita and Y. Iwakura, Makromol. Chem., 1976, 177, 3589–3600 CrossRef CAS.
- L. Raymond, F. G. Morin and R. H. Marchessault, Carbohydr. Res., 1993, 246, 331–336 CrossRef CAS.
- X. Jiang, L. Chen and W. Zhong, Carbohydr. Polym., 2003, 54, 457–463 CrossRef CAS.
- C. Wu, C. Y. Kao, S. Y. Tseng, K. C. Chen and S. F. Chen, Carbohydr. Polym., 2014, 111, 236–244 CrossRef CAS PubMed.
- M. Xu, R. Wang and Y. Li, Talanta, 2016, 148, 200–208 CrossRef CAS PubMed.
- N. A. Karaseva and T. N. Ermolaeva, Talanta, 2012, 93, 44–48 CrossRef CAS PubMed.
- A. Trojánek, V. Mareček and Z. Samec, Electrochim. Acta, 2015, 179, 3–8 CrossRef.
- K. Zhao, Q. Lu and W. Su, RSC Adv., 2014, 4, 63085–63099 RSC.
- J. M. Spurgeon, M. G. Walter, J. Zhou, P. A. Kohl and N. S. Lewis, Energy Environ. Sci., 2011, 4, 1772–1780 CAS.
- R. Żywica and J. K. Banach, J. Food Eng., 2015, 158, 8–12 CrossRef.
- S. Zhu, Y. Luo, H. Hong, L. Feng and H. Shen, Food Bioprocess Technol., 2013, 6, 3068–3075 CrossRef.
- M.-C. Michalski, F. Michel, D. Sainmont and V. Briard, Colloids Surf., B, 2002, 23, 23–30 CrossRef CAS.
- B. A. Lawton and R. Pethig, Meas. Sci. Technol., 1993, 4, 38 CrossRef.
- S. O. Nelson, W. Guo and S. Trabelsi, 2008.
- Z. Abbas, Y. You Kok, A. H. Shaari, K. Khalid, J. Hassan and E. Saion, IEEE Sens. J., 2005, 5, 1281–1287 CrossRef.
- H. Lizhi, K. Toyoda and I. Ihara, J. Food Eng., 2010, 96, 167–171 CrossRef.
- N. Yang, Y. Jin, H. Wang, X. Duan, B. Xu, Z. Jin and X. Xu, J. Food Eng., 2015, 155, 45–52 CrossRef.
- Y. M. Jin, N. Yang, Q. Ma, F. F. Wu, X. M. Xu and Q. Tong, Food Bioprocess Technol., 2015, 8, 749–757 CrossRef CAS.
- X. Li and W. Xia, Carbohydr. Polym., 2010, 82, 958–964 CrossRef CAS.
- R. A. Robinson and R. H. Stokes, Electrolyte solutions, Courier Corporation, 2002 Search PubMed.
- Y. Jin, N. Yang, X. Duan, F. Wu, Q. Tong and X. Xu, Biosystems Eng., 2015, 129, 70–77 CrossRef.
- N. Yang, Y. Jin, D. Li, Z. Jin and X. Xu, Chem. Eng. J., 2017, 313, 599–609 CrossRef CAS.
- Z. Wu, E. Xu, J. Long, Y. Zhang, F. Wang, X. Xu, Z. Jin and A. Jiao, Food Control, 2015, 50, 405–412 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |