Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Self-assembled chiral phosphorus nanotubes from phosphorene: a molecular dynamics study†
Douxing Pan abc,
Tzu-Chiang Wang*b,
Chao Wangb,
Wei Guoa and
Yugui Yao*a
abc,
Tzu-Chiang Wang*b,
Chao Wangb,
Wei Guoa and
Yugui Yao*a
aLaboratory of Quantum Functional Material Design and Application, School of Physics, Beijing Institute of Technology, Beijing 100081, China. E-mail: ygyao@bit.edu.cn.
bState Key Laboratory of Nonlinear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: tcwang@imech.ac.cn
cUniversity of Chinese Academy of Sciences, Beijing 100190, China
First published on 8th May 2017
Abstract
Controlled syntheses in nanoscale structures should be expected and phosphorous nanotubes with predefined chiralities are important in electronic devices with tunable bandgap. Here, incorporating molecular dynamics simulations with theoretical analyses, we show that a zigzag phosphorene nanoribbon can self-assemble and form a corresponding chiral phosphorous nanotube surrounding a template armchair phosphorous nanotube. The van der Waals potential between the nanoribbon and the nanotube is transformed to the intrinsic deformed and chemical bonding energies of the synthesized tube together with partial kinetic energy. The self-assembly process has an apparent temperature dependence and size effect and the formed chiral tube is thermodynamically stable. Also, the chirality and measurement can be tuned by the radius of template tube and the aspect ratio of raw ribbon. The study suggests a novel and feasible approach for controlled synthesis of phosphorous nanotubes and thus is of great interest for semiconductor device applications.
The mechanical behaviors of two-dimensional (2D) materials are crucial to a variety of applications ranging from ultrafast electronics to multifunctional nanocomposites.1,2 Phosphorene, as a fire-new graphene-like single-element 2D material, is promising for thin-film electronics, infrared optoelectronics and novel devices where anisotropic properties are desirable.3–5 The corrugated crystal structure of phosphorene not only leads to novel physical properties, but also produces anisotropic mechanical behaviors,4–6 for example, apparent nonlinear Young's modulus and ultimate strain,6 prominent anisotropic elasticity,7 negative Poisson's ratio8 and highly anisotropic ripple pattern4 as well as bending-induced extension.5 Recently, the fracture behaviors of phosphorene at finite temperatures are explored and the failure crack propagates preferably along the groove in the corrugated structure when uniaxial tension is applied in its armchair direction.9 Moreover, as typical phosphorene allotropes, the structural stability and mechanical properties of phosphorus nanotubes (PNTs), and Young's modulus and fracture strength are found to be strongly dependent on the diameter and length of the nanotube.10
Due to the tremendous needs for functional nanomaterials,2,11,12 controlled synthesis should be crucial in nanoscale structures, and PNTs with predefined chiralities are desired for electronic devices with tunable bandgap. On the other hand, due to the realization of graphene with tailored properties using different techniques,13–16 self-assemblies of graphene ribbons (GNRs) have been extensively investigated, theoretically and experimentally.2,11–13 Also, with the ever-increasing controllabilities in supramolecular organizations,2,12,14,15 GNRs have been proposed for the novel generation of nanostructures including carbon nanoscrolls (CNSs),2,17,18 twisted GNRs and chiral CNTs,12,15 as well as versatile configurations assembled by fullerenes and graphene flakes including disordered, parallel and vertical wrappings.19 However, can the self-assembly happen for double-atomically thin phosphorene? If yes, can chiral phosphorus nanotubes (cPNTs)20 be assembled from phosphorene with tailored shapes and sizes, and how?
In this work, we demonstrate by classic molecular dynamics (MD) simulations the self-assembly mechanical behaviors of phosphorene nanoribbons (PNRs) on the surface of PNTs. The study shows that an armchair phosphorous nanotube (aPNT) can induce a zigzag phosphorene nanoribbon (zPNR) to self-assemble into a corresponding cPNT. The van der Waals (vdW) interaction between the aPNT and zPNR is the driving force of self-assembly behavior. The self-assembly is not only dependent on the radius of template tube and the size of raw ribbon, but also on the temperature. The formed chiral tube is thermodynamically stable and its chirality can be well controlled theoretically. Our study provides a novel and feasible approach for the fine controlled synthesis of phosphorene allotropes and novel phosphorene-based composite functional nanostructures, and should be of great importance to developments of electronic devices with tunable bandgap.
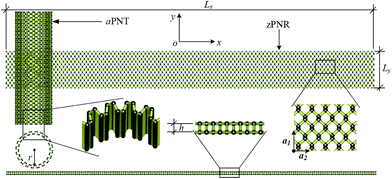
The computational model is shown in Fig. 1, consisting of a zigzag phosphorene nanoribbon with a length Lx, width Ly and thickness h and a template armchair phosphorus nanotube with an equivalent radius r. The aPNT with a length at least 2Ly, is initially fixed at a distance of 1.5r away from left side of the zPNR and around 0.35 nm above the zPNR along z-direction which is the equilibrium distance between the aPNT and zPNR. Three different aPNTs with radii r = 1.10, 1.47 and 1.84 nm, are used to explore the curvature of the template aPNT on the self-assembly behavior of the zPNR. Similar to the slenderness ratio of the column for characterization of size effect in mechanics of materials,21 an aspect ratio of the zPNR is introduced as
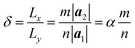 | (1) |
All simulations were carried out within the framework of classic MD-based method, implemented in the large-scale atomic/molecular massively parallel simulator (LAMMPS) code.22 The interatomic interactions in aPNT or zPNR are characterized by the Stillinger–Weber (SW) potential,23 which has been previously parameterized to correctly describe the mechanical and thermal properties of phosphorene by Jiang et al.24 and Xu et al.,25 and cited by the literatures mentioned in the introduction.6,9,10 The interaction between aPNT and zPNR is described by the Lennard-Jones (LJ) potential
| VLJ(r) = 4ε[(σ/r)12 − (σ/r)6] | (2) |
Prior to simulations, the initial aPNT and zPNR equilibrium configurations were both achieved via the conjugate-gradient (CG) algorithm. Then, the aPNT–zPNR system under free boundary conditions was relaxed to reach a stable thermodynamic state in a canonical (NVT) ensemble with a time step of 1 fs for ∼0.5 ns in Nose–Hoover thermostat. As done in other works,2,6,9,10,14 for facilitating the discussion, particularly, for focusing on the physical and mechanical nature of the “chiral” self-assembly itself, we presuppose that experiments are performed in vacuum or inert atmosphere to avoid terminating the edges of zPNR due to ambient oxygen or humidity in practice.27
Fig. 2 shows snapshots at four successive stages of the self-assembly process of a zPNR with aspect ratio δ = 13.86 on a fixed aPNT at a constant environmental temperature 30 K. Initially, the whole zPNR is at an activated state accompanying slightly bending, twisting, shrinking and expanding due to the thermal motion at a finite environmental temperature as shown in Fig. 2a. As the ribbon sticking the fixed tube, its left side starts to slide and rolls on the outside of the nanotube due to the vdW interaction from the aPNT with the remaining part keeping swinging as shown in Fig. 2b. Interestingly, the nano-ribbon can rearrange itself from the initial state with the longitudinal direction perpendicular to the axis of aPNT as shown in Fig. 1 to form a spiral helix angle and starts to roll around the nano-tube, which is much different from the self-assembly of GNR.12,14,15 At the same time, the partly-rolled phosphorene ribbon slides much quickly and reciprocally along the tube as the rolling process. A new perfect PNT with certain chirality (which has been actually formed at the second stage shown in Fig. 2b under the given condition) is formed gradually due to the coalescence of connectors as more part of the ribbon is rolled on the aPNT as shown in Fig. 2c and d. The whole process has been videotaped as Movie1.avi in our ESI,† which illustrates the dynamics better than structural snap shots.
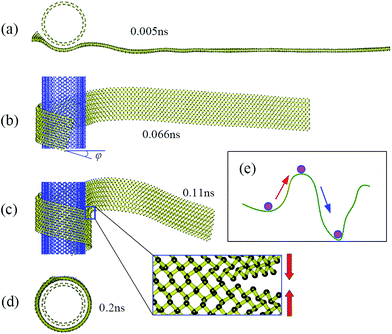 | ||
| Fig. 2 Thermodynamic process. Snapshots of self-assembly process of zPNR(δ = 13.86) on aPNT(n = 25) at four different moments from (a) to (d) (see also Movie1.avi†). Chiral angle φ in (b) is formed gradually at this stage. The enlarged part in (c) displays bonding process in zPNR edges squeezed each other. (e) Schematic diagram for van der Waals (vdW) force induced local thermal energy overcoming energy barriers from (intrinsic) Stillinger–Weber(SW) potential. | ||
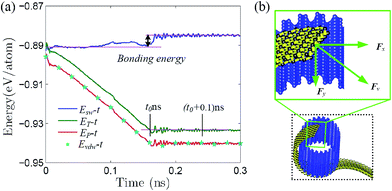
The above thermodynamic self-assembly is driven by the minimization of free energy as shown in Fig. 3a, where the (external) total, potential and vdW energy are depicted against simulation time. All these energies decrease gradually with respect to time and reach a stable minimum (at t0 ∼ 0.16 ns as denoted in the figure for the total energy), which is similar to that of GNR.2,12,14,15 The free energy of zPNR self-assembly after equilibrium is much larger than that of GNR,14–16 since the configuration energy of graphene is −9.214 eV per atom, much smaller than that of phosphorene, −5.365 eV per atom, according to density functional theory (DFT) calculations.3,5,22 The potential curve is coincided with that of the vdW interaction indicating that the self-assembly process is actually driven by the vdW force. Fig. 3b presents a free-body diagram for the part of raw ribbon rolled on the surface of template tube and the traction force Fv acting on the nano-ribbon from vdW interaction, which can be decomposed into the component Fx at the tangent of nano-tube pulling the ribbon to roll around the ring, and the component Fy along the axis of nano-tube pulling the ribbon to slide along the groove of corrugated crystal.
The chiral vector of the chiral phosphorus nanotube generated can be described theoretically as
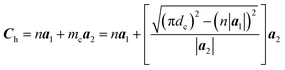 | (3) |
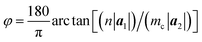 | (4) |
We conducted a series of simulations using zPNRs with varied aspect ratios δ and aPNTs with different radii r or chiral indexes n to compare the theoretical predictions with MD simulations in which stable chiral tubes can be extracted from the simulating system at (t0 + 0.1) ns. It is shown from Table 1 that the predictions of chiralities for the produced phosphorus nanotubes by eqn (3) and (4) are well consistent with the results of MD simulations, meaning that the chirality of the self-assembled cPNT is dependent on the width Ly = n|a1| of zPNR and the radius r of aPNT.
| zPNR (Ly/nm) [h = 0.21 nm] | cPNT [(n, mc)|(φ/°)] | aPNT (r/nm) [σ = 0.35 nm] | |
|---|---|---|---|
| Formula (3)|(4) | MD-simulation | ||
| a Note that: σ = 0.35 nm is an average relaxed distance between phosphorene ribbon and phosphorus nanotube, slightly different from that for bilayer phosphorene. | |||
| 1.84 (δ = 24.25) | (4, 31)|10.24 | (4, 30)|10.58 | 1.10 (NL = 30) |
| 1.84 (δ = 48.25) | (4, 45)|7.10 | (4, 45)|7.10 | 1.84 (NL = 30) |
| 3.23 (δ = 20.71) | (7, 37)|14.84 | (7, 37)|14.84 | 1.47 (NL = 30) |
| 3.23 (δ = 20.71) | (7, 44)|12.56 | (7, 44)|12.56 | 1.84 (NL = 20) |
| 3.23 (δ = 13.86) | (7, 44)|12.56 | (7, 44)|12.56 | 1.84 (NL = 30) |
Fig. 4 presents three typical cPNTs with front and top views, whose radii rc are 1.66, 2.02, 2.39 nm, respectively. The enlarged part in Fig. 4a as an example displays the perfect bonding structure in cPNT(4, 30). Such a mutual bonding was also discussed by Czerwinski, et al. based on classic AIREBO force field28 and so was it for Tersoff potential in some specific conditions (such as high pressure).21,22,29 But in current case, it is not only attributed to the dangling chemical bonds in zPNR edges, but also due to the strong constraining force from vdW interaction overcoming the activation energy barriers from intrinsic SW potential.21,23 Fig. 3e presents a schematic diagram, where vdW force induced local thermal energy makes the bonding edges (interaction) climb to a high energy barrier of SW potential, and then drop to a lower energy well. Therefore, as just shown in the detailed illustration of Fig. 2c, the helical pitch becomes so small that the zPNR edges can squeeze and bond with each other. It should be noted that, the strong impact can be, essentially, attributed to an extremely high pressure, and the bonding just forms by means of the mathematical form of non-mechanical (SW) potential functions consisting of two- and three-body interactions.21–23,29 It is also noted that some mechanical classical force fields such as CHARMM, can not arrive at bond breaking or forming even in current case, where bonds, angles and dihedrals are all assigned according to the (phosphorene) crystal configuration.14,21,22 Moreover, Fig. 3a presents a variation of SW energy against the simulation time. It can be seen that the energy curve almost hold a level value before the third stage and after the forth stage of the winding process except tiny fluctuations due to small local distortions of the zPNR. A general increasing energy is observed from ∼0.09 to ∼0.16 ns with evident fluctuations. It shows that an average bonding energy is saved in the new tube as an intrinsic SW potential during the bonding process, accompanying by large local distortions. The single bond forming can be roughly estimated as a local thermal energy at extremely high temperature of 29158 K (kBT = 0.005 eV per atom in Fig. 3a with total 5025 atoms in the system and assuming that 10 atoms form chemical bonds at the same time). This further demonstrates a fully admissible bonding condition. Comparing cPNT(4, 30) in Fig. 4a with cPNT(4, 45) in Fig. 4c for the same chirality index n = 4, it is known that the chirality of son-tube is independent on the length La (also, NL = La/|a2| as an integer indicator listed in Table 1) of parent-tube and/or the length Lx of raw-ribbon, but its length can be measured by them fully, and could approximately conform to the theoretical formula
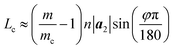 | (5) |
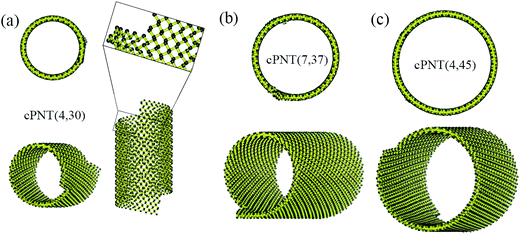 | ||
| Fig. 4 Three typical cPNTs with isometric and top views: (a) cPNT(4, 30), (b) cPNT(7, 37) with a Movie2.avi presented in the ESI,† (c) cPNT(4, 45), whose self-assemblies are induced by the aPNTs with n = 15, 20 and 25, respectively. The enlarged part in (a) displays the bonding structure in cPNT(4, 30). | ||
For the simulated cPNT(7, 44) in Table 1 with the same width Ly = 3.23 nm of zPNRs and the same radius r = 1.84 nm of the aPNT, according to eqn (5) the effective lengths Lc are calculated as 0.60 nm and 1.15 nm, respectively, both in good agreement with the results of MD simulations.
Due to the anisotropic nature of phosphorene and the bending instability along its zigzag direction,5,10 the zPNRs prefer moving forward in a spiral way outside the aPNTs to bend themselves directly, and finally form chiral tubes with different radii, as shown in Fig. 4a–c. Recently, Fernández-Escamilla et al. pointed out based on their DFT calculations that cPNTs hold larger binding energy than zPNTs and the values are comparable to aPNTs.20 For checking the stability of assembled cPNT, the ESI Movie2.avi† presented the thermodynamic process of cPNT(7, 37) shown in Fig. 4b at 100 K and the asymmetric ends was directly chopped off (e.g., a recent controlled sculpture method of phosphorene nanoribbons developed by Das et al.30) to eliminate the sway induced the stress concentration. The result shows that the chiral tube can hold at least 0.4 ns at 100 K in a canonical ensemble, much more stable than the zPNT.10 Also, the large thermal motion of the cPNT(7, 37) is constrained by the SW potential to be a corresponding thermal deformation and partially heat-driven oscillations.
In order to further study the temperature dependence and size effect, it is necessary to introduce a self-assembly energy Ees and velocity Ves as
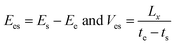 | (6) |
Fig. 5a shows that the self-assembly energy and velocity change with aspect ratio for the self-assemblies induced by the aPNT(n = 25) and the self-assembly energy increases while the self-assembly velocity decreases with aspect ratio, regardless of the temperature being at 10 or 30 K. Moreover, for the aPNT(n = 25) induced the self-assembly of the zPNR(δ = 13.86), as presented in Fig. 5b, the self-assembly energy decreases while the self-assembly velocity increases with temperature. This is because the higher temperature mainly contributes the kinetic energy and makes the average atom velocity quicker to speed up the self-assembly process. Under given temperature and length of one side, the smaller aspect ratio mainly lowers the potential energy difference shortening the self-assembly time and makes the rolling easier on the outside surface of aPNT.14,21 At the temperature of 70 K or higher, the self-assembly process becomes so fierce that a fracture behavior happens, as shown in the inset of Fig. 5b for details, and this further demonstrates the controlled temperature should be kept at T < 100 K.
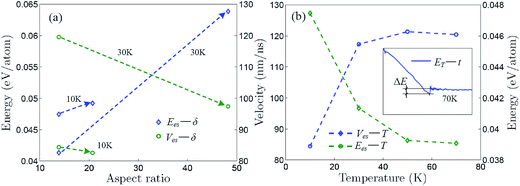 | ||
| Fig. 5 Self-assembly energy and velocity curves. Self-assembly energy and velocity change with (a) aspect ratio for self-assembly induced by aPNT(n = 25) and (b) Kelvin temperature for self-assembly of zPNT(δ = 13.86) induced by aPNT(n = 25). The inset in (b) shows variation of total energy with respect to time at 70 K, in which a fracture energy ΔE is defined approximately, being the same as the average bonding forming energy presented in Fig. 3a. | ||
In summary, a self-assembly mechanical behavior from phosphorene nanoribbon to chiral phosphorous nanotube was studied systematically for the first time, based on classic molecular dynamics simulations incorporating theoretical analysis. We predicted that a template armchair phosphorus nanotube can induce a zigzag phosphorene nanoribbon to form a corresponding chiral phosphorous nanotube. The van der Waals interaction between the template nanotube and raw nanoribbon is the driving force of self-assembly process, which leads to the bending, twisting and shrinking of the raw ribbon in vacuum and sticking, sliding and rolling outside the template tube. Particularly, the interaction is transformed to the intrinsic deformed and chemical bonding energies of the synthesized tube after overcoming the energy barriers from Stillinger–Weber potential. A positive correlation was found between the self-assembly energy and aspect ratio or between the self-assembly velocity and temperature, while a negative correlation was found between the self-assembly energy and temperature or between the self-assembly velocity and aspect ratio. The formed chiral tube is thermodynamically stable and its chiralities and sizes can be controlled pretty well.
Acknowledgements
The work reported here is supported by the NSFC of China (Grant No. 11602270, 11574029, and 11532013), the MOST of China (Grant No. 2014CB920903, 2016YFA0300600), and the National Basic Research Program of China (“973” Project, Grant No. 2012CB937500). The first author thanks Dr Dongmei Hu in Jilin University for helpful discussions and the reviewer from ACS Nano for his/her constructive suggestions on classic bonding mechanism.References
- J. A. Rogers, M. G. Lagally and R. G. Nuzzo, Nature, 2011, 477, 45 CrossRef CAS PubMed.
- X. H. Shi, N. M. Pugno and H. J. Gao, J. Comput. Theor. Nanosci., 2010, 7, 1 CrossRef.
- L. Li, et al., Nat. Nanotechnol., 2014, 9, 372 CrossRef CAS PubMed.
- A. A. Kistanov, Y. Q. Cai, K. Zhou, S. V. Dmitriev and Y.-W. Zhang, J. Phys. Chem. C, 2016, 120, 6876 CAS.
- D. X. Pan, Y. Li, T.-C. Wang and W. Guo, Acta Mech. Sin., 2017, 33, 71 CrossRef CAS.
- Z. Y. Yang, J. H. Zhao and N. Wei, Appl. Phys. Lett., 2015, 107, 023107 CrossRef.
- Y. Ding, Y. Wang, L. Shi, Z. Xu and J. Ni, Phys. Status Solidi RRL, 2014, 8, 939 CrossRef CAS.
- J.-W. Jiang and H. S. Park, Nat. Commun., 2014, 5, 4727 CAS.
- Z.-D. Sha, Q.-X. Pei, Z. W. Ding, J.-W. Jiang and Y.-W. Zhang, J. Phys. D: Appl. Phys., 2015, 48, 395303 CrossRef.
- X. B. Liao, F. Hao, H. Xiao and X. Chen, Nanotechnology, 2016, 27, 215701 CrossRef PubMed.
- A. V. Talyzin, I. V. Anoshkin, A. V. Krasheninnikov, R. M. Nieminen, A. G. Nasibulin, H. Jiang and E. I. Kauppinen, Nano Lett., 2011, 11, 4352 CrossRef CAS PubMed.
- O. O. Kit, T. Tallinen, L. Mahadevan, J. Timonen and P. Koskinen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085428 CrossRef.
- H. E. Lim, Y. Miyata, R. Kitaura, Y. Nishimura, Y. Nishimoto, S. Irle, J. H. Warner, H. Kataura and H. Shinohara, Nat. Commun., 2013, 4, 2548 Search PubMed.
- T.-C. Wang, C. Zhang and S. H. Chen, J. Nanosci. Nanotechnol., 2013, 13, 1136 CrossRef CAS PubMed.
- C. Zhang, Z. L. Peng and S. H. Chen, J. Phys. Chem. C, 2014, 118, 19477 CAS.
- Y. Wang, H. F. Zhan, C. Yang, Y. Xiang and Y. Y. Zhang, Comput. Mater. Sci., 2015, 96, 300 CrossRef CAS.
- D. Yu and F. Liu, Nano Lett., 2007, 7, 3046 CrossRef CAS PubMed.
- L. He, J.-Q. Lu and H. Jiang, Small, 2009, 5, 2802 CrossRef CAS PubMed.
- J.-W. Feng, H.-M. Ding and Y.-Q. Ma, Carbon, 2015, 90, 34 CrossRef CAS.
- H. N. Fernández-Escamilla, J. J. Quijano-Briones and A. Tlahuice-Flores, Phys. Chem. Chem. Phys., 2016, 18, 12414 RSC.
- J. Morrison, Modern Physics for Scientists and Engineers, Academic Press, 2nd edn, 2015 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1996, 117, 1 CrossRef.
- F. H. Stillinger and T. A. Weber, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 5262 CrossRef CAS.
- J.-W. Jiang, T. Rabczuk and H. S. Park, Nanoscale, 2015, 7, 6059 RSC.
- W. Xu, L. Y. Zhu, Y. Q. Cai, G. Zhang and B. W. Li, J. Appl. Phys., 2015, 117, 214308 CrossRef.
- J.-W. Jiang and H. S. Park, J. Appl. Phys., 2015, 117, 124304 CrossRef.
- R. A. Doganov, et al., Nat. Commun., 2015, 6, 6647 CrossRef CAS PubMed.
- B. Czerwinski, Z. Postawa, B. J. Garrison and A. Delcorte, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 303, 22 CrossRef.
- J. Tersoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 37, 6991 CrossRef.
- P. M. Das, et al., ACS Nano, 2016, 10, 5687 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03807k |
| This journal is © The Royal Society of Chemistry 2017 |