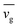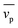Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Low thermal conductivity in Si/Ge hetero-twinned superlattices†
Huicong Donga,
Bin Wen *a,
Yuwen Zhangb and
Roderick Melnikc
*a,
Yuwen Zhangb and
Roderick Melnikc
aState Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China. E-mail: wenbin@ysu.edu.cn
bDepartment of Mechanical and Aerospace Engineering, University of Missouri-Columbia, Columbia, Missouri, USA
cThe MS2Discovery Interdisciplinary Research Institute, Wilfrid Laurier University, 75 University Ave. West, Waterloo, Ontario, Canada N2L 3C5
First published on 9th June 2017
Abstract
The thermophysical properties of Si/Ge hetero-twinned superlattices (SLs) are investigated by nonequilibrium molecular dynamic simulations. The results indicate that the Si/Ge hetero-twinned SLs show low thermal conductivity, which is similar to that of conventional Si/Ge SLs. Analysis with phonon kinetic theory shows that low thermal conductivity in the Si/Ge hetero-twinned SLs is caused by the combined actions of reduced phonon group velocity and reduced relaxation time. Moreover, despite similar thermal conductivity in Si/Ge hetero-twinned SLs and conventional Si/Ge SLs, the phonon group velocity and relaxation time in the two structures are totally different. Our results demonstrate the potential of a new kind of SLs with strong phonon scattering.
Introduction
Superlattices (SLs), consisting of periodically alternating nanolayers, are of great interest due to their wide applications in many fields, such as in developing high-performance thermoelectric devices, thermal management in semiconductor lasers,1–5 etc. The previous simulated and experimental results indicated that the thermal transport properties in SLs can be adjusted by regulating the lattice period6,7 and the structures of interfaces.8,9According to the structures of the interfaces, SLs can be divided into two kinds: (1) heterostructure SLs (SLs consist of two components10), and (2) homo-coherent twinned SLs (SLs consist of nanotwinned layers from one component9). It has been demonstrated that the cross-plane thermal conductivity of crystalline heterostructure SLs is much lower than that of bulk materials with a single component, and, sometimes even lower than those of their corresponding alloys.11–13 The significant reduction of thermal conductivity in heterostructure SLs is caused by numerous strong scatterings at the heterogeneous interfaces.14 As for the homo-coherent twinned SLs, the results are rather different that their thermal conductivity is only slightly reduced when compared with that of the corresponding single bulk crystalline, because homo-coherent twin interfaces show weak effect on thermal transmission.9,15
By combining the structure properties of heterostructure and homo-coherent twinned SLs, a new type of SLs, hetero-twinned SLs, with hetero-coherent twin interfaces periodically arranged in, has been proposed and observed in experimentally, which has been reported can be deposited via DC magnetron sputtering at room temperature.16,17 Although the mechanisms responsible for mechanical properties of the hetero-twinned SLs have been studied,18 their thermal properties are still puzzled. To clear this issue, Si/Ge hetero-twinned SLs are chosen as the object of study, and their thermal properties have been investigated. The results indicate that Si/Ge hetero-twinned SLs show low thermal conductivity due to the reduced average phonon group velocity and relaxation time.
Simulation section
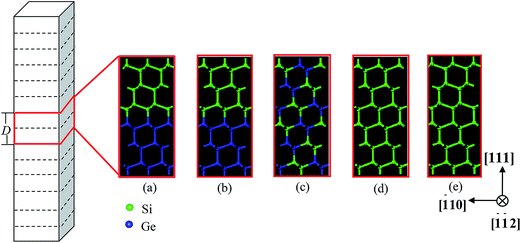
To build Si/Ge hetero-twinned SLs, the X, Y, Z axes of Si layers correspond to the lattice orientations of [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10], [
10], [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 2], [111], and [
2], [111], and [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 10], [11
10], [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ], [111] for Ge layers. The lattice constant of single crystal Si (aSi) at 0 K is 5.43 Å, and that of single crystal Ge (aGe) is 5.66 Å; thus, the lattice misfit between Si and Ge single crystal is 4%. To build Si/Ge hetero-twinned superlattice samples, an average lattice constant of Si and Ge, [111], is used to arrange atoms. Fig. 1 shows a typical model of Si/Ge hetero-twinned SLs, which is created by periodically stacking Si/Ge thin slices on upon the other along the [111] direction. The unit cell (the periodic thickness D is 1.93 nm) for the periodic slice of Si/Ge hetero-twinned SLs has been placed in Fig. 1(a), as well as that of conventional Si/Ge SLs in Fig. 1(b), Si0.5Ge0.5 alloys in Fig. 1(c), single crystal Si in Fig. 1(d), and twinned Si in Fig. 1(e). In simulation, the periodic thickness D of Si/Ge hetero-twinned SLs, conventional Si/Ge SLs and twinned Si varies from 1.93 to 57.83 nm. The cross sections of the five models are all 2.05 nm × 1.97 nm, and model lengths along [111] direction range from 81 to 230 nm.
], [111] for Ge layers. The lattice constant of single crystal Si (aSi) at 0 K is 5.43 Å, and that of single crystal Ge (aGe) is 5.66 Å; thus, the lattice misfit between Si and Ge single crystal is 4%. To build Si/Ge hetero-twinned superlattice samples, an average lattice constant of Si and Ge, [111], is used to arrange atoms. Fig. 1 shows a typical model of Si/Ge hetero-twinned SLs, which is created by periodically stacking Si/Ge thin slices on upon the other along the [111] direction. The unit cell (the periodic thickness D is 1.93 nm) for the periodic slice of Si/Ge hetero-twinned SLs has been placed in Fig. 1(a), as well as that of conventional Si/Ge SLs in Fig. 1(b), Si0.5Ge0.5 alloys in Fig. 1(c), single crystal Si in Fig. 1(d), and twinned Si in Fig. 1(e). In simulation, the periodic thickness D of Si/Ge hetero-twinned SLs, conventional Si/Ge SLs and twinned Si varies from 1.93 to 57.83 nm. The cross sections of the five models are all 2.05 nm × 1.97 nm, and model lengths along [111] direction range from 81 to 230 nm.
In this work, molecular dynamic (MD) simulations19,20 have been applied to study the thermal transmission in Si/Ge hetero-twinned SLs by using LAMMPS package.21 In all MD simulations here, the Tersoff potential8 is used to describe the covalent interactions between Si and Ge atoms. Periodic boundaries are used in all three directions. Time step in all MD simulations are 1 fs. The atomic structures of Si/Ge hetero-twinned SLs are first equilibrated at a constant temperature of T = 300 K for 500 ps using a NVT ensemble. After that, the non-equilibrium MD simulations (refer to ESI†) are conducted on the relaxed structures for thermal conductivity calculation by using Fourier's law.22
Results and discussion
Thermal conductivities of Si/Ge hetero-twinned SLs with different model lengths are calculated along [111], so as to eliminate the effect of model length on thermal conductivity of bulk Si/Ge hetero-twinned SLs. As suggested by Schelling et al.,23 the inverse of thermal conductivity (1/K) is linearly related to the inverse of model length (1/L), which can be expressed by the following relationship:
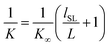 | (1) |
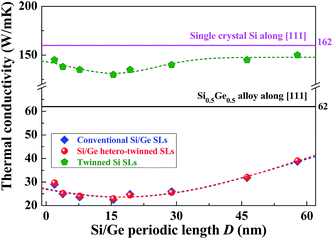 | ||
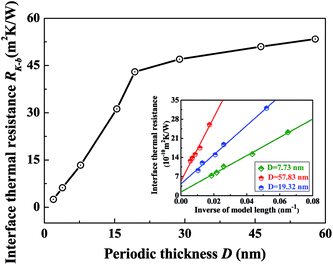
| Fig. 2 Periodic thickness dependence of thermal conductivity for Si/Ge hetero-twinned SLs, in comparison with that of single crystal Si, twinned Si, Si/Ge alloy and conventional Si/Ge SLs. | ||
It should also be noticed in Fig. 2 that thermal conductivity of bulk Si/Ge hetero-twinned SLs doesn't vary monotonously with the increase of periodic thickness, which has also been observed by many other researchers in superlattice systems.2,7,8 To explore the origin of this phenomenon, the total thermal resistance of SLs RSLs has been described by the summation of thermal resistance for individual layers as well as that for interfaces, as shown in eqn (2)
| RSLs = RSi,N + RGe,N + Rinterface | (2) |
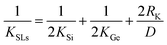 | (3) |
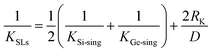 | (4) |
While when the periodic thickness is sufficiently smaller than the phonon mean free path, phonon scattering within the individual layer will be ballistically25 (no thermal resistance in individual layers), thus, the total thermal resistance of the superlattice equals to the total interface thermal resistance, and in this situation, eqn (3) can be expressed as
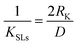 | (5) |
For periodic thickness comparable to phonon mean free path, combination of diffusive and ballistic phonon scattering will occur within the individual layer. By combining eqn (4) and (5), we can obtain that
 | (6) |
To obtain interface thermal resistance in bulk SLs RK-b, NEMD simulations (refer to ESI 2†) are carried out on Si/Ge hetero-twinned SLs with different model length for different periodic thickness. Inset in Fig. 3 shows the model length dependent interface thermal resistance in Si/Ge hetero-twinned SLs with D = 7.73 nm, 19.32 nm and 57.83 nm, it can be seen that with the increase of periodic thickness, the interface thermal resistance is decreased, and the relationship between RK and 1/L is indeed linear, which can also be observed in other periodic thickness. By using extrapolation method, interface thermal resistance in the bulk SLs with different periodic thickness can be obtained, and results have been plotted in Fig. 3. It can be seen that with the periodic thickness decreases from 57.83 nm to 1.932 nm, interface thermal resistance in the bulk SLs RK-b decreases from 5.34 × 10−10 m2 K W−1 to 2.5 × 10−11 m2 K W−1, especially when the periodic thickness decreases from 15.47 nm to 1.932 nm, RK-b decreases rapidly and almost linearly. When the periodic thickness ranges from 1.932 nm to 15.47 nm, coherent phonons exist. With the decrease of periodic thickness, the action of coherent becomes stronger. Such coherent phonon behavior will eliminate the effect of interface phonon scattering,26 thus, leading to rapid decrease of interface thermal resistance, and further causing the decrease of Si/Ge hetero-twinned SLs thermal conductivity with periodic thickness increases from 1.932 nm to 15.47 nm. While when the periodic thickness ranges from 19.32 nm to 57.83 nm, coherent phonons almost don't exist, and as a result, the interface thermal resistance becomes more and more close to a fixed value, and further, the thermal conductivity of Si/Ge hetero-twinned SLs increases with increased periodic thickness. The nonmonotonic dependence of Si/Ge hetero-twinned SLs on periodic thickness is caused by the combined action of phonon coherent and interface phonon scattering.26 Our results also support a hypothesis that in SLs with a short periodic thickness, there are almost no interfaces and the whole SLs should be considered as a giant lattice.27
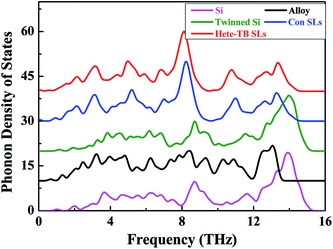
To explore the strong phonon scattering in Si/Ge hetero-twinned SLs, phonon density of states (PDOS) for Si/Ge hetero-twinned SLs with a periodic thickness of 1.93 nm, as well PDOS that for single crystal Si, twinned Si, Si0.5Ge0.5 alloy, and conventional Si/Ge SLs with similar structures and the same atom number, are calculated by using PHONOPY.28 As can be seen from Fig. 4, the PDOS of Si/Ge hetero-twinned SLs is similar to that of the conventional Si/Ge SLs, and the high frequency peaks in the PDOS of the two structures are both approximately at 8.1 THz, thus resulting in the similar thermal conductivity for them. At the same time, when compared with single crystal Si, twinned Si and Si0.5Ge0.5 alloy, there is a distinct redshift for the PDOS in Si/Ge hetero-twinned SLs, which indicates the possibility of increased phonon scattering in Si/Ge hetero-twinned SLs, under the condition that the total number of phonon modes is exactly the same for the above five structures. Thus, it can be concluded that the redshift of the phonons with high frequency results in the low thermal conductivity of Si/Ge hetero-twinned SLs.29 Besides, the similar PDOS of bulk twinned Si and the single crystal Si can also be observed, which indicates the weak phonon scattering at twin boundaries.
Since it is well known that phonons are primary heat carriers in semiconductors,30 low thermal conductivity of bulk Si/Ge hetero-twinned SLs has also been studied by phonon kinetic theory, in which thermal conductivity K can be described by31
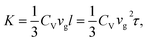 | (7) |
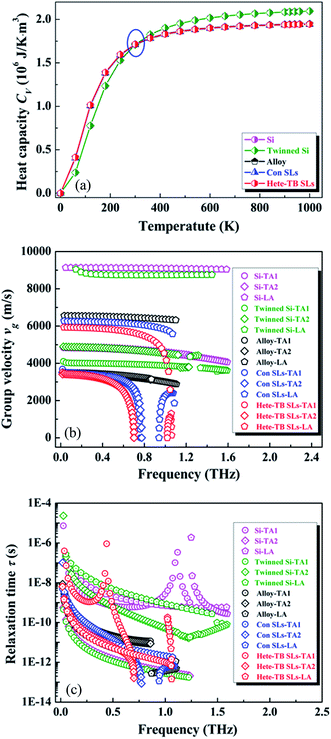
In comparison with thermal transmission in bulk Si/Ge hetero-twinned SLs (DP = 1.93 nm), this characteristic has also been analyzed for single crystal Si, twinned Si, Si0.5Ge0.5 alloy and conventional Si/Ge SLs with similar structures and the same atom number by phonon kinetic theory. Specific heat capacities of these structures at room temperature are calculated by using PHONOPY firstly (details can be found in ESI 3†), and results are summarized in Fig. 5(a). It can be seen that with the increase in temperature, the specific heat capacity is increased, and finally it reaches a constant value when the temperature is between 800 and 1000 K. For single crystal Si and twinned Si, the value32 is 2.1 × 106 J K−1 m3, and for bulk Si/Ge hetero-twinned SLs, Si0.5Ge0.5 alloy and conventional Si/Ge SLs, the value is 1.95 × 106 J K−1 m3. A crossover of specific heat capacities for the five structures occurs at 300 K, and this distinct value32 is 1.71 × 106 J K−1 m3. Thus, it can be concluded that when compared with the other four structures, low thermal conductivity in Si/Ge hetero-twinned SLs is not related to the specific heat capacity at room temperature.
The phonon group velocity can be obtained from the following relationship33
| vg = (∂ω/∂q), | (8) |
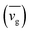 , phase velocity
, phase velocity 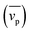 , Grüneisen parameter (
, Grüneisen parameter (![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ), relaxation time (
), relaxation time (![[small tau, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d4.gif) ), thermal conductivity from phonon kinetic theory (KPH) and in MD simulation (KMD) for Si/Ge hetero-twinned SLs (Hete-TB SLs), single crystal Si (Si), twinned Si, Si0.5Ge0.5 alloy (Alloy) and conventional Si/Ge SLs (Con SLs)
), thermal conductivity from phonon kinetic theory (KPH) and in MD simulation (KMD) for Si/Ge hetero-twinned SLs (Hete-TB SLs), single crystal Si (Si), twinned Si, Si0.5Ge0.5 alloy (Alloy) and conventional Si/Ge SLs (Con SLs)
In addition to the volume heat capacity and phonon group velocity, relaxation time τ is also a significant factor that affects thermal transmission in Si/Ge hetero-twinned SLs. The relaxation time τ can be obtained by applying a semi-empirical theory, in which τ strongly depends on the anharmonicity of the bonding, and it can be expressed by34,35
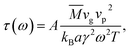 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ω/d
ω/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V|j.
V|j.
To calculate the relaxation time of Si/Ge hetero-twinned SLs, both frequency-dependent phase velocities and Grüneisen parameters have been calculated. The same has been done for bulk single crystal Si, twinned Si and Si0.5Ge0.5 alloy and conventional Si/Ge SLs. As shown in Fig. S5,† when compared with single Si crystal, the existence of twin boundaries almost has no effect on phase velocity, while the phase velocity of Si/Ge hetero-twinned SLs is largely reduced, and it is even lower than that of conventional Si/Ge SLs. Consequently, the average phase velocity of Si/Ge hetero-twinned SLs is the lowest among the five structures, as shown in Table 1. As for Grüneisen parameters, which have been plotted in Fig. S6,† compared with the other four structures, the existence of Si/Ge hetero-twinned boundaries has strong effect on it at different frequencies. The average values of Grüneisen parameters for the five structures can also be found in Table 1. It can be seen that compared with single crystal Si, Grüneisen parameters of Si/Ge hetero-twinned SLs, the conventional Si/Ge SLs and Si/Ge alloy are increased, while this parameter for the twinned Si is only slightly reduced. After calculation of phase velocity and Grüneisen parameters, according to eqn (9), A is the only parameter needed to be determined. To this end, the average values of group velocity, phase velocity and Grüneisen parameters of single crystal Si in Table 1 are used, and the value of A is determined as 9.1 × 10−5. Assuming that for all the five structures, value of A is the same, thus eqn (9) leads to
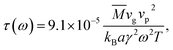 | (10) |
Fig. 5(c) shows the frequency-dependent relaxation time τ for the five structures. It can be seen that relaxation time differs largely with the variation of phonon frequency. Especially, when the frequency is low, the relaxation time can amount to more than 10 ns, which is consistent with the previous results for LA branch in single crystal Si.37 For one branch of acoustic transverse modes in twinned Si, τSi-TB, is almost the same with that of the single Si crystal τSi, while τSi-TB differs from τSi for the left branch of acoustic transverse mode and longitudinal mode; τSi-TB is lower than τSi, especially at the frequency between 1 to 1.3 THz. The Moreover, different relaxation times of Si/Ge hetero-twinned τSi/Ge-TB and conventional Si/Ge SLs τSi/Ge can also be observed. For one acoustic transverse branch, τSi/Ge-TB is higher than τSi/Ge at the frequency between 0 to about 0.5 THz. The same is true for the acoustic longitudinal branch at the frequency close to 1 THz. Considering the combined actions of phonons in the entire frequency range, the integrated relaxation time was calculated by inserting average values of parameters in eqn (10). As shown in Table 1, when compared with single Si crystal, the relaxation time of twinned Si is only slightly reduced, indicating the weak effect of twin boundaries on relaxation time. The relaxation time of Si/Ge hetero-twinned SLs is largely reduced, and it makes a significant contribution to the low thermal conductivity in Si/Ge hetero-twinned SLs. Moreover, it can also be observed that the relaxation time of Si/Ge hetero-twinned SLs is larger than that of conventional Si/Ge SLs, which demonstrates the different effects of the two structures on relaxation time.
According to eqn (7), the thermal conductivity can be obtained by a relationship connecting the heat capacity, group velocity, and relaxation time. Calculated results for the five structures by phonon kinetic theory have also been presented in Table 1. It can be seen that compared with single crystal Si, twinned Si and Si0.5Ge0.5 alloy, thermal conductivity of Si/Ge hetero-twinned SLs is much lower, while it's close to that of conventional Si/Ge SLs, which is consistent with the results obtained by NEMD simulations. By combining the calculated group velocity and relaxation time in Table 1, it can be deduced that the low thermal conductivity in Si/Ge hetero-twinned SLs is caused by the combined actions of reduced phonon group velocity and reduced relaxation time. Furthermore, it can also be observed that despite of similar thermal conductivities in Si/Ge hetero-twinned SLs and conventional Si/Ge SLs, the average phonon group velocity in Si/Ge hetero-twinned SLs is lower, while the relaxation time in it is larger, which makes up the smaller group velocity.
Conclusion
In conclusion, by employing nonequilibrium molecular dynamic simulations, thermal transport in Si/Ge hetero-twinned SLs have been studied. The results indicate that compared with single crystal Si, twinned Si and Si0.5Ge0.5 alloy, Si/Ge hetero-twinned SLs show low thermal conductivity, which is similar to that of conventional Si/Ge SLs. Phonon kinetic theory has also been applied to analyze the low thermal conductivity, and results show that low thermal conductivity in Si/Ge hetero-twinned SLs is caused by the combined actions of reduced phonon group velocity and reduced relaxation time. Moreover, despite of similar thermal conductivities in Si/Ge hetero-twinned SLs and conventional Si/Ge SLs, which is caused by the combined action of umklapp phonon scattering and interface scattering, phonon group velocity and relaxation time in the two structures are fundamentally different that the average phonon group velocity in Si/Ge hetero-twinned SLs is lower, while the larger average relaxation time in Si/Ge hetero-twinned SLs makes up the lower group velocity exactly. Our results demonstrate a new kind of SLs with strong phonon scattering.Acknowledgements
This work was supported by the National Natural Science Foundation of China under grant numbers 51372215. Y. Z. acknowledges the support from the U.S. National Science Foundation under grant number CBET-1404482. R. M. acknowledges the support from the NSERC and CRC programs, Canada.References
- Y. Chen, D. Li, J. Yang, Y. Wu, J. R. Lukes and A. Majumdar, Phys. B, 2004, 349, 270–280 CrossRef CAS.
- Y. Chen, D. Li, J. R. Lukes, Z. Ni and M. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174302 CrossRef.
- Y. K. Koh, Y. Cao, D. G. Cahill and D. Jena, Adv. Funct. Mater., 2009, 19, 610–615 CrossRef CAS.
- Y. Chalopin, K. Esfarjani, A. Henry, S. Volz and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195302 CrossRef.
- Z. Tian, K. Esfarjani and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 235304 CrossRef.
- V. Samvedi and V. Tomar, Nanotechnology, 2009, 20, 365701 CrossRef PubMed.
- J. Garg and G. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 140302 CrossRef.
- M. Hu and D. Poulikakos, Nano Lett., 2012, 12, 5487–5494 CrossRef CAS PubMed.
- A. Porter, C. Tran and F. Sansoz, Phys. Rev. B, 2016, 93, 195431 CrossRef.
- M. I. H. E. S. Landry and A. J. H. McGaughey, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 184302 CrossRef.
- T. Borca-Tasciuc, W. Liu, J. Liu, T. Zeng, D. W. Song, C. D. Moore, G. Chen, K. L. Wang, M. S. Goorsky, T. Radetic, R. Gronsky, T. Koga and M. S. Dresselhaus, Superlattices Microstruct., 2000, 28, 199–206 CrossRef CAS.
- S. Xiong, Y. A. Kosevich, K. Sääskilahti, Y. Ni and S. Volz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195439 CrossRef.
- S. M. Lee, D. G. Cahill and R. Venkatasubramanian, Appl. Phys. Lett., 1997, 70, 2957 CrossRef CAS.
- Y. T. Shin-ichiro Tamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2627–2630 CrossRef.
- H. Dong, J. Xiao, R. Melnik and B. Wen, Sci. Rep., 2016, 6, 19575 CrossRef CAS PubMed.
- Y. Liu, D. Bufford and H. Wang, et al., Acta Mater., 2011, 59, 1924 CrossRef CAS.
- J. Li, Y. Chen and S. Xue, et al., Acta Mater., 2016, 114, 154 CrossRef CAS.
- T. Fu, X. Peng, X. Chen, S. Weng, N. Hu, Q. Li and Z. Wang, Sci. Rep., 2016, 6, 35665 CrossRef CAS PubMed.
- D. R. F. Müller-Plathe, Comput. Theor. Polym. Sci., 1999, 9, 203–209 CrossRef.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082 CrossRef.
- S. Plimpton, J. Chem. Phys., 1995, 117, 1–19 CAS.
- A. Bagri, S.-P. Kim, R. S. Ruoff and V. B. Shenoy, Nano Lett., 2011, 11, 3917–3921 CrossRef CAS PubMed.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 144306 CrossRef.
- H. R. Shanks, P. D. Maycock and P. H. Sidles, et al., Phys. Rev., 1963, 130, 1743 CrossRef CAS.
- B. Saha, Y. R. Koh, J. Comparan, S. Sadasivam, J. L. Schroeder, M. Garbrecht, A. Mohammed, J. Birch, T. Fisher, A. Shakouri and T. D. Sands, Phys. Rev. B, 2016, 93, 045311 CrossRef.
- M. Hu and D. Poulikakos, Nano Lett., 2012, 12, 5487 CrossRef CAS PubMed.
- M. Kazan and P. Masri, Surf. Sci. Rep., 2014, 69, 1–37 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- Y. Gao, X. Zhang, Y. Jing and M. Hu, Nanoscale, 2015, 7, 7143–7150 RSC.
- J. Zou and A. Balandin, J. Appl. Phys., 2001, 89, 2932–2938 CrossRef CAS.
- Z. Wang, J. E. Alaniz, W. Jang, J. E. Garay and C. Dames, Nano Lett., 2011, 11, 2206–2213 CrossRef CAS PubMed.
- M. Maldovan, J. Appl. Phys., 2011, 110, 114310 CrossRef.
- X. Feng, J. Xiao, R. Melnik, Y. Kawazoe and B. Wen, J. Chem. Phys., 2015, 143, 104503 CrossRef PubMed.
- Y. Ding, B. Xiao, G. Tang and J. Hong, J. Phys. Chem. C, 2016, 121, 225–236 Search PubMed.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, J. Mater. Chem., 2011, 21, 15843 RSC.
- H. Jin, O. D. Restrepo, N. Antolin, S. R. Boona, W. Windl, R. C. Myers and J. P. Heremans, Nat. Mater., 2015, 14, 601–606 CrossRef CAS PubMed.
- A. Ward and D. A. Broido, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085205 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03833j |
| This journal is © The Royal Society of Chemistry 2017 |