Unidirectional anisotropy mediated giant memory effect in antiferromagnetic Cr₂O₃ nanorods

Abstract

Understanding the magnetic anisotropy of antiferromagnetic (AF) transition metal oxides is a matter of importance for its future application in spintronics. In this study we have carried out temperature and field-dependent magnetization measurements to investigate the magnetic anisotropy of AF Cr₂O₃ nanorods (NRs) with 〈d〉_XRD = 24 nm diameter. Our experimental findings suggest that the observed field-cooled memory effect from exchange-coupled Cr₂O₃ NRs is mediated by unidirectional anisotropy. This finding opens an opportunity for devices utilizing the anisotropy field of bare AF Cr₂O₃ nano-crystalline structures.

---

1. Introduction

In recent years one dimensional (1D) nanostructures with varied geometry such as nanowires, nanorods (NRs), nanotubes, and nanobelts have attracted much attention because of their promising technological applications in spintronics, lasers, generators, etc.^1–3 The 1D nanostructured materials of antiferromagnetic (AF) transition metal oxides (TMOs),^4,5 which show entirely different magnetic, optical and electrical properties from those of their bulk counterparts, have been used in the field of data storage⁶ and spin-valve devices.⁷ Depending on the finite size effect, the density of point defects (anionic and/or cationic vacancies) and surface effects, the magnetic properties of TMOs vary from spin-glass (SG), superparamagnetic (SPM) to ferromagnetic (FM).^8–10 Among different TMOs, Cr₂O₃ is a low-anisotropy easy-axis AF with a Neel temperature around ∼307 K.¹¹ This material displays piezo magnetic, magneto electric effect, and also used in devices involving exchange bias (EB) effect make it promising material for future spintronic based applications.^12–14 At nanoscale due to enhanced surface to volume ratio the interface interaction between surface spins and uncompensated core become more pronounced which has impulsed the fabrication and study of nano-systems looking for new properties and applications.^10,15–18

The memory effect has been studied in superparamagnetic (SPM)¹⁹ and SG²⁰ system, in which formal shows weak field-cooled (FC) aging and later shows aging with both FC and zero-field-cooled (ZFC). Recently, we have also reported memory effect from weakly interaction Fe₃O₄ nanoparticles.²¹ Using Monte Carlo simulation, it has been proved that interface exchange interaction in FM-core/AF-shell nanoparticles (NPs) provides an additive source for the frustration of the system resulting in an enhancement of the memory effect.²² However, unlike FM-core/AF-shell system, the interface interaction in bare AF nanostructures is much more complex. Very recently, we have reported spontaneous EB (SEB) from AF oxide NPs during the first field of hysteresis loop measurement.²³ SEB in AF NPs is governed by the unidirectional anisotropy (UA) across frustrated surface spins and the uncompensated AF core mediated by interfacial strongly pinned spins. Such bare AF NPs exhibits field-cooled (FC) memory effect strength of which varies with the concentration of point defects resulting in disappearance in big size particles.⁸ In this work, we present detailed structural and magnetic characterization of 1D Cr₂O₃ NRs. The aim is to study the effect of UA on the memory effect within the blocking state.

2. Experimental details

The as-received CrO₂ NRs utilized in this study are commercially available NRs used in magnetic recording are annealed in an ambient atmosphere at 650 °C for 1 hour using a chemical vapor deposition (CVD) method, which resulted in formation of pure Cr₂O₃ NRs. The annealing of the sample is carried out in a tube furnace with heating rate of 5 K min⁻¹ and allowed to cool down naturally. In general, CrO₂ is a metastable oxide that readily decomposes into thermal dynamically stable chromia (Cr₂O₃) as annealing temperature above 400 °C.^24,25 In the present work, the chemical reaction for the formation of chromia nanorods can be represented as 4CrO₂ → 2Cr₂O₃ + O₂, which is an antiferromagnetic insulator with a Néel temperature of 307 K.²⁶ And the small amount of x indicates the existence of oxygen vacancies. The morphology and size distribution analysis was carried out by using field-emission scanning electron microscopy (FE-SEM, JEOL JSM-6500F) microscope. Structural properties were studied by using a high-resolution transmission electron microscopy (HR-TEM) and selective area diffraction pattern (SAED) using JEOL 2010 TEM working at 200 kV. Further analysis of structural property was carried out by synchrotron radiation X-ray diffraction (SRXRD) (λ = 0.7749 Å) at National Synchrotron Radiation Research Center (NSRRC) beam line BL01C2 in Taiwan. The ZFC and FC temperature and field dependences of magnetization of the NRs were measured using a quantum design MPMS-SQUID-VSM magnetometer. The magnetic memory effect on thermal variation of magnetization using FC-protocol with 100 Oe field is also investigated.

3. Results and discussion

3.1. Morphological and stoichiometric analysis

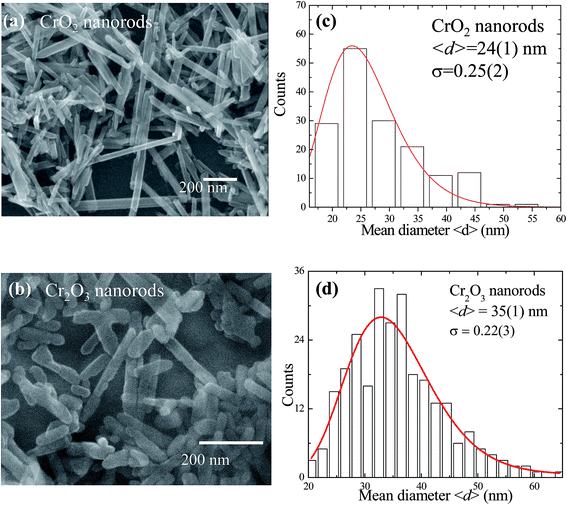
The SEM images of as-received CrO₂ and Cr₂O₃ nanorods illustrated in Fig. 1(a) and (b) shows NRs like geometry having mean length around 100–200 nm, respectively. Fig. 1(c) and (d) depict the histogram of mean diameter distribution of NRs calculated from SEM images. The solid red line in Fig. 1(c) and (d) describes the asymmetric distribution of diameter fitted with log-normal distribution function: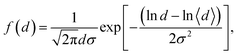 where 〈d〉 is the mean diameter and σ standard deviation of the function. The fitted value of diameters and standard deviation are 24(1) nm and 0.25(2) for CrO₂ NRs and 35(1) nm and 0.22(3) for Cr₂O₃ NRs, respectively. The observed wide distribution and agglomeration behavior of the nanorods can significantly affect the magnetization properties. Fig. 2(a) and (b) show the TEM image of single CrO₂ and Cr₂O₃ nanorod retaining crystalline structure. The inter-planar distance d = 0.3037 and 0.3722 nm obtained from HR-TEM image for CrO₂ and Cr₂O₃ nanorod, respectively, as shown in Fig. 2(c) and (d), corresponding to the (110) plane of CrO₂ with P4₂/mnm space group and the (200) plane of Cr₂O₃ with R3̄c space group, respectively. The SAED patterns of NRs displayed in Fig. 2(e) and (f) can be ascribed to the existence of tetragonal-CrO₂ oriented along the [100] zone axis and hexagonal-Cr₂O₃ oriented along the [−101] zone axis, respectively, revealing a single crystallinity.

Fig. 1 (a) and (b) SEM images of CrO₂ and Cr₂O₃ NRs. (c) and (d) Histogram of the mean diameter distribution of NRs where the solid line represents the fitting curve using log-normal distribution function.

Fig. 2 (a) and (b) TEM, (c) and (d) HR-TEM, and (e) and (f) SAED patterns for CrO₂ and Cr₂O₃ NRs, respectively.

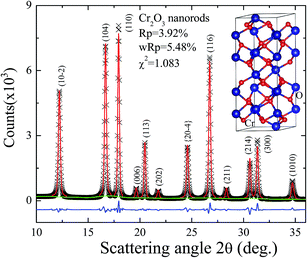
The SR-XRD spectrum of NRs shown in Fig. 3 confirms the formation of pure Cr₂O₃ without any trace of CrO₂ impurity. The observed broad SR-XRD peak of NRs could be fitted well with Gaussian function. The fitted value of full-width at half-maximum (FWHM) of most intense (110) peak, indexed based on the space group R3̄c is 0.1566 ± 0.0012°, corresponding to the grain size of ∼27 nm (calculated by using Scherrer formula).²⁷ The effect of crystalline size and the strain on XRD peak broadening was further investigated by using Williamson–Hall (W–H) plot.²⁸ The intercept of the linear fit gives the inverse of the crystalline size 〈d〉_XRD ∼ 24 nm and slope of the curve gives strain η ∼ 8.341 × 10⁻⁵. The obtained low value of crystalline size as compared to mean diameter indicates effect of annealing resulted in the formation of multi granular Cr₂O₃ nanorod. During annealing process, in the initial stage surface of CrO₂ nanorod oxidized to Cr₂O₃, resulting in the formation of nanoscale layer of Cr₂O₃ grains at the surface. Diffusion of oxygen into the CrO₂ voids takes place through these microcracks, resulting in the growth of Cr₂O₃ at the grain boundaries which leads to the formation of multi-granular nanorod and hence size estimated from W–H plot will be use in the further discussions. For estimating lattice parameters SR-XRD pattern was analyzed by refining spectra using Rietveld analysis²⁹ with general structural analysis system (GSAS) software package.³⁰ As shown in Fig. 3, the red solid line is the fitted curve to the diffraction pattern indicated by crosses. The green curve is fit to the background and blue curve in the bottom of figure gives the difference between observed and fitted pattern. The fitted values of lattice constant a = b = 4.9667 Å, and c = 13.6172 Å confirm the R3̄c hexagonal Cr₂O₃ phase, as shown in the inset. The value of lattice constant and strain is very close to the value reported from 18 nm Cr₂O₃ NPs.¹⁷ As compared to reported values from bulk Cr₂O₃ (a = b = 4.9590 Å, and c = 13.5890 Å), the observed lattice expansion from Cr₂O₃ NRs is ascribed to finite size effect.

Fig. 3 X-ray diffraction and Rietveld refinement of Cr₂O₃ NRs.

3.2. Magnetic properties

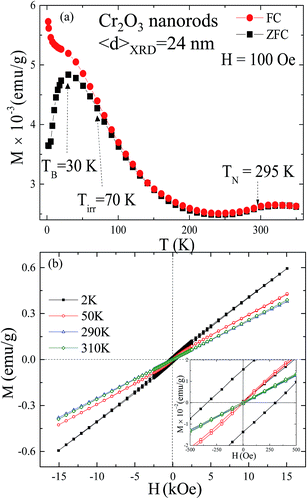
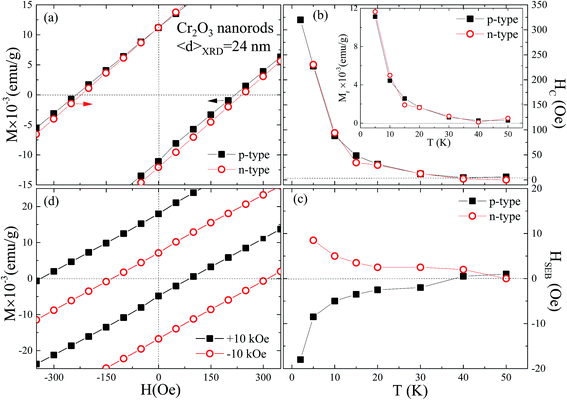
Fig. 4(a) shows the temperature (T) dependence of magnetization M(T) curve measured with ZFC–FC mode from 2 to 350 K with an applied magnetic field of H_a = 100 Oe. From M(T) curves, with the increase of T four clear features are seen. First, in low T region an abrupt drop in the FC magnetization below 15 K assigned to surface frozen spins. Second, a blocking temperature T_B = 30 K is defined as the maximum value of ZFC curve and could be related to a superparamagnetic (SPM) property of NRs. According to the Neel–Brown model³¹ the T_B for Cr₂O₃ NRs can be defined as T_B ≈ KV/22k_B, where K is the magnetocrystalline anisotropy energy density. Using T_B = 30 K, above equation yields K = 1.259 × 10⁴ erg cm⁻³ for 24 nm Cr₂O₃, which is one order smaller than the value reported from 24 nm Cr₂O₃ NPs.¹⁷ Third, an irreversible temperature T_irr ∼ 70 K is defined as the temperature at which (M_FC − M_ZFC)/M_FC(2K) ≈ 0.02, relating to SG like behavior i.e. short-range spin-correlation. Fourth, above T_irr, SPM signals dominate, magnetization decreases with increase of T and a plateau region around T_N ∼ 295 K is observed. This value is very close to the bulk AF transition temperature ∼307 K and therefore corresponds to Neel temperature of Cr₂O₃ NRs. Fig. 4(b) shows the isothermal magnetization loop M(H) at selective temperatures 2, 50, 290 and 310 K measured with ZFC protocol over ±15 kOe field. The applied magnetic field dependence of the magnetization reveals different behaviors at various temperatures. At T = 310 K, the magnetization presents a lineal dependence with the applied magnetic field in agreement with the paramagnetic (PM) state of the Cr³⁺ ions. At intermediate temperature of plateau region, T_B < T < T_N, as shown in Fig. 4(a), the M(H_a) curves are reversible and reveal a curvature characteristic behavior of a superparamagnetic assembly of nanorods. At 2 K, M(H) loop exhibit a weak FM behavior, with linear and non-linear curve in high- and low-field region having a coercivity of H_C = (H_C⁺ − H_C⁻)/2 = 320 Oe, as shown in the inset of Fig. 4(b). H_C⁺ and H_C⁻ are the field corresponding to the points in the forward and reverse branches of the M(H) loop at which magnetization is zero. No noticeable difference in the M(H) loop of 50, 290 and 310 K were found between the measurements made with a field-increasing and -decreasing loop suggesting PM/AF property above T_B. Furthermore, value of magnetization at 310 K is slightly higher than at 290 K consistent with the observed plateau region around T_N ∼ 295 K from M(T) curve. The observed weak ferromagnetism at 2 K is could be due to uncompensated surface spins at the interface of crystalline domains.

Fig. 4 (a) ZFC–FC magnetization curve of Cr₂O₃ NRs measured in a field of 100 Oe. (b) Magnetic hysteresis loop measured at 2, 50, 290 and 310 K. Inset of (b) shows the near zero-field region of hysteresis loop.

Spontaneous exchange bias (SEB) results from a break in the symmetry across the FM–AFM interface and setting up of the UA during the first field of hysteresis loop measurement.²¹ To study the SEB phenomenon magnetization versus applied magnetic field, M(H_a) was measured using a p-type (0 → +H_max → −H_max → +H_max) protocol and n-type (0 → −H_max → +H_max → −H_max) protocol in ZFC mode at 5 K, as shown in Fig. 5(a). The non-zero value of H_C (H_C = (|H_C⁺| + |H_C⁻|)/2) and remanence M_r (M_r = (|M_r⁺| + |M_r⁻|)/2) clearly point to the existence of a weak-FM component at 5 K. M_r⁺ and M_r⁻ are the remanent magnetization corresponding to the points in the forward and reverse branches of the M(H) loop at zero applied field. However, p- and n-type M(H) loops at 40 K (above T_B) are symmetric and exhibits PM property having zero value of H_C and M_r, consistent with M(T) curve. The obtained values of H_C with both p- and n-type protocol at different T exhibits similar temperature dependencies and vanishes above T_B as depicted in Fig. 5(b). Similar temperature dependency was also observed for M_r as shown in the inset of Fig. 5(b). Furthermore, M(H) loops in Fig. 5(a) are highly asymmetric and p-type (n-type) is shifted toward the negative (positive) magnetic axis. The M(H) loop asymmetry along the applied magnetic field axis can be quantified as SEB, H_SEB = (|H_C⁺| − |H_C⁻|)/2. The estimated values of H_SEB with p- and n-type M(H) at 5 K shows similar value of −18 and 8.5 Oe, respectively. Slightly lower values of H_SEB are obtained after the n-type measurements than those of the p-type. Maity et al.^32,33 reported H_SEB of −850 Oe and +615 Oe after p- and n-type hysteresis loop measurements from the Bi₂Fe₄O₉–BiFeO₃ FM/AFM system, respectively. The slight difference observed in the behavior of SEB field obtained using the p- and n-type protocols is a common phenomenon. The reported high value of SEB from Bi₂Fe₄O₉–BiFeO₃ as compared to Cr₂O₃ NRs is due to the inter-coupling between the log-range ordered FM and AFM spins at the interface.^32,33 Furthermore, the p-type and n-type M(H_a) loops measured in the ZFC mode are almost symmetric in nature and exhibit a similar value for SEB, which is within the experimental measurement error.

Fig. 5 (a) Near zero-field region of magnetic hysteresis loop measured at 5 K with p- and n-type protocols after zero-field cooling. Temperature dependency of (b) coercivity and (c) SEB field obtained from p- and n-type of hysteresis loops. Inset of (b) shows the temperature dependency of remenance. (d) Near zero-field region of magnetic hysteresis loop measured at 5 K with field cooling in ±10 kOe.

The observed similar value of H_SEB in both field direction indicate shifts in M(H) loops are not experimental artifacts, but rather an intrinsic property of Cr₂O₃ NRs. The temperature dependency of H_SEB obtained from both p- and n-type M(H) loops vanishes at and above T_B as shown in Fig. 5(c). To further confirm the SEB loop shift, FC M(H) loops were measured with a cooling field of ±10 kOe at 5 K shown in Fig. 5(d) reveals an enhanced asymmetric behavior with loop shift in opposite field directions. The estimated values of H_C, M_r and H_EB for cooling field of +10 kOe (−10 kOe) are 213 Oe (225 Oe), 0.011 emu g⁻¹ (0.012 emu g⁻¹) and −125 Oe (89 Oe), respectively. The above observed results confirm the existence of UA below T_B at the interface of frustrated surface spins and the uncompensated AF core. Furthermore, this is first report to observe SEB in an AF Cr₂O₃ NRs. The observed non-zero values of M_r and H_C confirm the FM behavior of the 24 nm Cr₂O₃ nanorods originating from finite size effect. It is worthy to note that the observed minor loop of the magnetization at low temperature may originate from the non-saturated magnetization at higher applied magnetic field, causing the vertical/horizontal shift of magnetization. In the present study, such weak magnetic properties can be explained by the presence of uncompensated spins at the surface of Cr₂O₃ nanorods, as has been discussed in previous reports for Cr₂O₃ nanoparticles.^34–37 In nanoscale materials, the uncompensated surface spins show a lower coordination number, resulting a net magnetic moment can be induced on the surface.^38,39 The observed SEB effect arises from intercoupling between the short-range ordered clusters of frustrated surface spins and uncompensated antiferromagnetic cores at the interface during the first field of hysteresis loop measurement. Such inter-coupling sets up unidirectional anisotropy at the interface; for a detailed description was discussed in our previous work.²³

3.3. Memory effect

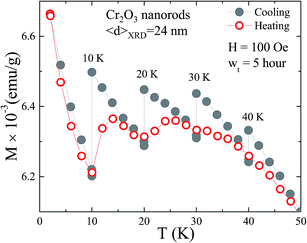
The magnetic anisotropy plays an important role in shaping the magnetic properties of nanoscale material which can be altered by the random size distribution, strong inter particle interactions and unidirectional anisotropy in the core/shell magnetic nanoparticles.^21,40 The effect of enhanced magnetic anisotropy on the magnetic properties of nanoparticles can be studied effectively by measuring the thermoremanent spin dynamics,⁴¹ the memory effect⁴² and the effect of aging⁴³ using field cooling and zero field cooling processes. The field cooling and zero field cooling memory effects have been used for the characterization of superparamagnetic⁴⁴ and spin-glass⁴² systems. To characterize magnetic properties, the memory effect in FC magnetization with FC protocol is investigated. The results for FC memory effect within 2 to 50 K temperature range are depicted in Fig. 6. Initially NRs were cool down from 300 K down to 2 K with a cooling rate of 2 K min⁻¹ in a static magnetic field of 100 Oe and magnetization recorded as a function of temperature. During recording, temperature of the sample was “held” at 40, 30, 20, and 10 K for a time period of 5 h each and magnetic moments were allowed to relax by switching off the magnetic field. After 5 h relaxation, magnetic field turn on and measurement was subsequently resumed with the same cooling rate. The above magnetization curve is designated as “cooling curve” shown in Fig. 6. After reaching the desired low temperature of 2 K, NRs were warmed and magnetization recorded at rate of 2 K min⁻¹ in 100 Oe field without any stop, designated as “warming” curve, also called as “memory curve” as shown in Fig. 6. Discernible evidence of steps is clearly visible in the memory curve around 10, 20 and 30 K below T_B. The observed step-like behavior indicates that the spin configuration imprinted in the blocking state (below T_B) of NRs is retrieved by the memory curve. This step like behavior is the signature of the magnetic memory effect which can be used as a good measure for understanding SPM or SG system. The unique part in Fig. 6 is the increasing behavior of magnetization with the decrease of temperature which has been used as a fingerprint test to distinguish SG and blocked SPM system. In non-interacting SPM nanostructure moments prefer to stay blocked along the easy axis direction which is along the field direction resulting in increase of magnetization with the decrease of temperature. On the other hand, an interacting SG system shows decrease in the magnetization with the decrease of temperature. Therefore, observed FC memory effect is could be either because of wide distribution in length of NRs as observed from SEM images causing distribution in magnetocrystalline anisotropy or because of setup of UA in blocked state. In a spin glassy system, the length of the spin–spin correlation grows during the stop, even in a zero field, and a memory dip typically shows up upon reheating. This is not possible in a non/weak-interacting nanoparticle system which does not show the memory dip in the ZFC mode. The above finding indicates that the FC memory effect in strongly-interacting 24 nm Cr₂O₃ NRs could be induced either by the size distribution (which resulted in the broad distribution of blocking temperatures) or the strongly pinned interfacial spin mediated UA. However, the observed decreasing behavior of both the FC memory effect and the SEB field with the increase of temperature indicates that the memory effect in Cr₂O₃ NRs is mediated by strongly pinned interfacial spins. However, size distribution leads to broad distribution of T_B, which is not consistent with M(T). Furthermore, observed non-zero coercivity in blocked state indicate weak ferromagnetic behavior which differs significantly from SPM system. Therefore, we confirmed that observed memory effect from AF NRs could be manifested by UA of Cr₂O₃.

Fig. 6 FC memory effect in the 100 Oe field with a halt of 5 h at 10, 20, 30 and 40 K.

4. Conclusion

The AF Cr₂O₃ nanorods (NRs) with diameter of 〈d〉_XRD = 24 nm are investigated by means of DC magnetometer in order to study the unidirectional anisotropy (UA) properties. Temperature dependent magnetization M(T) reveal T_B = 30 K below which system is in blocked state. A SEB field of 18 Oe is reported at 2 K attributed to setting up of UA during the first field of hysteresis loop measurement. The field-cooled (FC) magnetization relaxation measured at different temperature shows the presence of multimagnetic anisotropy. However, disappearance of FC memory effect, coercivity and SEB field above T_B and observed narrow distribution of M(T) curve rule out the possibility of interacting SPM system. Hence, we conclude that FC memory effect from AF Cr₂O₃ NRs is mediated by UA.

Acknowledgements

We would like to thank the Ministry of Science and Technology (MOST) of the Republic of China for their financial support of this research through project number MOST-105-2112-M-259-003.

References

1. A. Asenjo-Garcia, J. D. Hood, D. E. Chang and H. J. Kimble, Atom-light interactions in quasi-one-dimensional nanostructures: a Green's-function perspective, Phys. Rev. A, 2017, 95(3), 033818.
2. Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, One-Dimensional Nanostructures: Synthesis, Characterization, and Applications, Adv. Mater., 2003, 15(5), 353–389.
3. A. C. Gandhi, H.-J. Hung, P.-H. Shih, C.-L. Cheng, Y.-R. Ma and S. Y. Wu, In Situ Confocal Raman Mapping Study of a Single Ti-Assisted ZnO Nanowire, Nanoscale Res. Lett., 2009, 5(3), 581–586.
4. R. S. Devan, R. A. Patil, J.-H. Lin and Y.-R. Ma, One-Dimensional Metal-Oxide Nanostructures: Recent Developments in Synthesis, Characterization, and Applications, Adv. Funct. Mater., 2012, 22(16), 3326–3370.
5. S. Yang, S. Liu, C. Lan and S. Yang, Single crystalline Cr₂O₃ nanowires/nanobelts: CrCl₃ assistant synthesis and novel magnetic properties, Appl. Surf. Sci., 2012, 258(22), 8965–8969.
6. J. L. Xie, C. X. Guo and C. M. Li, Construction of one-dimensional nanostructures on graphene for efficient energy conversion and storage, Energy Environ. Sci., 2014, 7(8), 2559–2579.
7. T. Zhai and J. Yao, One-Dimensional Nanostructures, Principles and Applications, John Wiley & Sons, Inc., 2012.
8. A. C. Gandhi, T. S. Chan, J. Pant and S. Y. Wu, Strong Pinned-Spin-Mediated Memory Effect in NiO Nanoparticles, Nanoscale Res. Lett., 2017, 12(1), 207.
9. D. Tobia, E. L. Winkler, R. D. Zysler, M. Granada and H. E. Troiani, Superparamagnetism in AFM Cr₂O₃ nanoparticles, J. Alloys Compd., 2010, 495(2), 520–523.
10. D. Tobia, E. De Biasi, M. Granada, H. E. Troiani, G. Zampieri, E. Winkler and R. D. Zysler, Evolution of the magnetic anisotropy with particle size in antiferromagnetic Cr₂O₃ nanoparticles, J. Appl. Phys., 2010, 108(10), 104303.
11. (a) L. M. Corliss, J. M. Hastings, R. Nathans and G. Shirane, Magnetic Structure of Cr₂O₃, J. Appl. Phys., 1965, 36(3), 1099–1100; (b) P. J. Brown, J. B. Forsyth, E. Lelièvre-Berna and F. Tasset, Determination of the magnetization distribution in Cr₂O₃ using spherical neutron polarimetry, J. Phys.: Condens. Matter, 2002, 14(8), 1957.
12. S. A. Makhlouf, Z. H. Bakr, H. Al-Attar and M. S. Moustafa, Structural, morphological and electrical properties of Cr₂O₃ nanoparticles, J. Mater. Sci. Eng. B, 2013, 178(6), 337–343.
13. S. Sahoo and C. Binek, Piezomagnetism in epitaxial Cr₂O₃ thin films and spintronic applications, Philos. Mag. Lett., 2007, 87(3–4), 259–268.
14. T. R. McGuire, E. J. Scott and F. H. Grannis, Antiferromagnetism in a Cr₂O₃ Crystal, Phys. Rev., 1956, 102(4), 1000–1003.
15. D. Tobia, E. Winkler, R. D. Zysler, M. Granada and H. E. Troiani, Size dependence of the magnetic properties of antiferromagnetic Cr₂O₃ nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78(10), 104412.
16. D. Li, Z. Han, J. G. Zheng, X. L. Wang, D. Y. Geng, J. Li and Z. D. Zhang, Spin canting and spin-flop transition in antiferromagnetic Cr₂O₃ nanocrystals, J. Appl. Phys., 2009, 106, 053913.
17. P. Hajra, P. Brahma, S. Dutta, S. Banerjee and D. Chakravorty, Enhancement of magnetic anisotropy in mechanically attrited Cr₂O₃ nanoparticles, J. Magn. Magn. Mater., 2012, 324(7), 1425–1430.
18. O. Gomonay, S. Kondovych and V. Loktev, Shape-induced anisotropy in antiferromagnetic nanoparticles, J. Magn. Magn. Mater., 2014, 354, 125–135.
19. M. Sasaki, P. E. Jönsson, H. Takayama and H. Mamiya, Aging and memory effects in superparamagnets and superspin glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(10), 104405.
20. K. Jonason, E. Vincent, J. Hammann, J. P. Bouchaud and P. Nordblad, Memory and Chaos Effects in Spin Glasses, Phys. Rev. Lett., 1998, 81(15), 3243–3246.
21. A. C. Gandhi, P. M. Reddy, T.-S. Chan, Y.-P. Ho and S. Y. Wu, Memory effect in weakly-interacting Fe₃O₄ nanoparticles, RSC Adv., 2015, 5(103), 84782–84789.
22. M. Vasilakaki, K. N. Trohidou, D. Peddis, D. Fiorani, R. Mathieu, M. Hudl, P. Nordblad, C. Binns and S. Baker, Memory effects on the magnetic behavior of assemblies of nanoparticles with ferromagnetic core/antiferromagnetic shell morphology, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(14), 140402.
23. A. C. Gandhi, J. Pant and S. Y. Wu, Dense inter-particle interaction mediated spontaneous exchange bias in NiO nanoparticles, RSC Adv., 2016, 6(3), 2079–2086.
24. T. P. Kobylinski and B. W. Taylor, The catalytic chemistry of nitric oxide: I. The effect of water on the reduction of nitric oxide over supported chromium and iron oxides, J. Catal., 1973, 31, 450.
25. M. Audier, M. Salaün, H. Roussel, F. Delyon and M. Duneau, CrO2-to-Cr2O3 Transformation in a Three-Dimensional Interference Field of Ultraviolet Laser Light, Cryst. Growth Des., 2010, 10, 1923–1928.
26. W.-Q. Han, L. Wu, A. Stein, Y. Zhu, J. Misewich and J. Warren, Oxygen-Deficiency-Induced Superlattice Structures of Chromia Nanobelts, Angew. Chem., Int. Ed., 2006, 45, 6554.
27. B. E. Warren, X-ray Diffraction, Addsion-Wesley, Reading, MA, 1969.
28. A. C. Gandhi, J. Pant, S. D. Pandit, S. K. Dalimbkar, T.-S. Chan, C.-L. Cheng, Y.-R. Ma and S. Y. Wu, Short-Range Magnon Excitation in NiO Nanoparticles, J. Phys. Chem. C, 2013, 117(36), 18666–18674.
29. H. Rietveld, A profile refinement method for nuclear and magnetic structures, J. Appl. Crystallogr., 1969, 2(2), 65–71.
30. A. C. Larson and R. B. Von Dreele Los, Alamos National Laboratory Report LA-UR-86-748 Los Alamos, Los Alamos National Laboratory, 1987.
31. (a) L. Neel, Théorie du traînage magnétique des ferromagnétiques en grains fins avec application aux terres 5 cuites, Ann. Geophys., 1949, 5(37), 99–136; (b) W. F. Brown, Thermal Fluctuations of a Single-Domain Particle, Phys. Rev., 1963, 130(5), 1677–1686.
32. T. Maity, S. Goswami, D. Bhattacharya, G. C. Das and S. Roy, Spontaneous exchange bias in a nanocomposite of BiFeO₃-Bi₂Fe₄O₉, J. Appl. Phys., 2013, 113, 17D916.
33. T. Maity, S. Goswami, D. Bhattacharya and S. Roy, Superspin Glass Mediated Giant Spontaneous Exchange Bias in a Nanocomposite of BiFeO₃–Bi₂Fe₄O₉, Phys. Rev. Lett., 2013, 110, 107201.
34. M. Bañobre-López, C. Vázquez-Vázquez, J. Rivas and M. A. López-Quintela, Magnetic properties of chromium (III) oxide nanoparticles, Nanotechnology, 2003, 14, 318–322.
35. W. S. Zhang, E. Brueck, Z. D. Zhang, O. Tegus, W. F. Li, P. Z. Si, D. Y. Geng and K. H. J. Buschow, Structure and magnetic properties of Cr nanoparticles and Cr₂O₃ nanoparticles, J. Phys. B: At., Mol. Opt. Phys., 2005, 358, 332–338.
36. C. Vázquez-Vázquez, M. Bañobre-López, M. A. López-Quintela, L. E. Hueso and J. Rivas, Evidence of weak ferromagnetism in chromium(III) oxide particles, J. Magn. Magn. Mater., 2004, 272–276, 1547–1548.
37. S. A. Makhlouf, Magnetic properties of Cr₂O₃ Nanoparticles, J. Magn. Magn. Mater., 2004, 272–276, 1530–1532.
38. M. Feygenson, A. Kou, L. E. Kreno, A. L. Tiano, J. M. Patete, F. Zhang, M. S. Kim, V. Solovyov, S. S. Wong and M. C. Aronson, Properties of highly crystalline NiO and Ni nanoparticles prepared by high-temperature oxidation and reduction, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 014420.
39. A. C. Santulli, M. Feygenson, F. E. Camino, M. C. Aronson and S. S. Wong, Synthesis and Characterization of One-Dimensional Cr2O3 Nanostructures, Chem. Mater., 2011, 23, 1000–1008.
40. G. Zhang, K. Potzger, S. Zhou, A. Mücklich, Y. Ma and J. Fassbender, Memory effect of magnetic nanoparticle systems originating from particle size distribution, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267(8–9), 1596–1599.
41. M. Ulrich, J. García-Otero, J. Rivas and A. Bunde, Slow relaxation in ferromagnetic nanoparticles: indication of spin-glass behavior, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(2), 024416.
42. K. Jonason, E. Vincent, J. Hammann, J. P. Bouchaud and P. Nordblad, Memory and chaos effects in spin glasses, Phys. Rev. Lett., 1998, 81(15), 3243–3246.
43. T. Jonsson, J. Mattsson, C. Djurberg, F. A. Khan, P. Nordblad and P. Svedlindh, Aging in a magnetic particle system, Phys. Rev. Lett., 1995, 75(22), 4138–4141.
44. M. Sasaki, P. E. Jönsson, H. Takayama and H. Mamiya, Aging and memory effects in superparamagnets and superspin glasses, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71(10), 104405.

---