Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Linear magnetoresistance in gold foams
Zhaoguo Li *,
Jiangshan Luo,
Xiulan Tan,
Qi Fang,
Yong Zeng,
Lingbiao Meng,
Minjie Zhou,
Weidong Wu and
Jicheng Zhang*
*,
Jiangshan Luo,
Xiulan Tan,
Qi Fang,
Yong Zeng,
Lingbiao Meng,
Minjie Zhou,
Weidong Wu and
Jicheng Zhang*
Research Center of Laser Fusion, China Academy of Engineering Physics, Mianyang 621900, P. R. China. E-mail: lizhaoguoabc@163.com; zhangjccaep@126.com
First published on 17th May 2017
Abstract
The electrical transport properties of metal foams may not only be of fundamental research interest but can also lead to wide application in sensors. We report the magnetotransport properties of gold foams prepared by a chemical template–dealloying method. The temperature dependence of the resistivity of gold foams represents a metallic behavior with zero magnetic field. With increasing magnetic field, a crossover from quadratic to linear dependence of the magnetoresistance in gold foams is observed in the studied temperature range (2–50 K). The physical mechanisms resulting in this observation may be ascribed to the classical linear magnetoresistance theory based on the spatial mobility fluctuations or current distribution effect. However, further evidence is required to determine the exact mechanism.
I. Introduction
The electrical transport study of nanostructures has attracted substantial research interest in the past decades. Various novel physical phenomena have been discovered, such as the quantum Hall effect in quantum wells,1 the single-electron tunneling in quantum dots,2 the quantum interference effect in disordered systems,3 the giant magnetoresistance (MR) effect in alternating ferromagnetic and non-magnetic layered films,4 and so forth. The newly discovered artificial nanostructures have also promoted quantum transport studies, such as carbon nanotubes,5 graphene,6 topological insulators,7 transition metal dichalcogenides,8 and so forth. Overall, the transport study of nanostructures will remain a very active research area in the future owing to its importance in fundamental physics and for practical applications.The low-density gold foam is a typical nanostructured material, which exhibits numerous potential applications in catalysts, sensors, plasmonics, and so forth, owing to the high surface-volume ratio and low electrical resistivity.9 The electrical transport study of gold foams is a critical issue for exploring the effect of the three-dimensional (3D) interior topology of nanostructures on their electrical transport properties.10–14 Fujita et al.10 reported extremely low MR values for nanoporous gold films. Their work underscored the importance of the 3D topology of a nanostructure on the electronic transport properties. Xia et al.11 observed that the thermal and electrical conductivities of nanoporous gold films were significantly lower than those of bulk gold, but the corresponding Lorenz number was strikingly similar to that of bulk gold. Their work reveals the anomalous electrical transport properties in nanoporous gold materials; however, the physical mechanisms of the above experimental phenomena remain unknown. Therefore, further experimental and theoretical efforts are required in this direction.
Here, we report on the magnetotransport behavior of gold foams. The temperature dependence of the resistivity of gold foams represents a metallic behavior with zero magnetic field. The MR curves between −9 T and 9 T for gold foams are measured in the low temperature regime (2–50 K). A crossover from a quadratic to a linear dependence of the MR in gold foams is observed with an increase of the magnetic field. The physical mechanisms behind this observation are discussed.
II. Methods
The gold foams studied in this work were prepared by a chemical template–dealloying method. First, Au and Ag nanoparticles were electroless deposited onto polystyrene (PS) microspheres which were employed as the sacrificial template. Next, the cylindrical PS/(Au–Ag) monolith was formed by filter-casting of the nanoparticle coated PS suspension. Then, the self-supported Au–Ag foams were produced by removing the polystyrene template. The self-supported gold foams with bimodal porous structure were finally obtained after dealloying of Ag. The details of the preparation technology can be found in ref. 15. The structure of gold foams was characterized by X-ray diffraction (XRD), scanning electron microscopy (SEM) and X-ray computed tomography (CT). To measure the resistivity, the Hall-type electrodes were attached onto the gold foams by using silver paint. The magnetotransport measurements of the gold foams were performed on a Quantum Design physical property measurement system, which can provide a low temperature condition of T = 2 K in magnetic fields up to B = 9 T.III. Results
We investigated three gold foams that were cleaved from a monolith. For comparison, a gold film prepared by electron-beam evaporation was also studied. The parameters of these samples are listed in Table 1.| Sample | l (mm) | w (mm) | t (mm) | ρ0 (μΩ m) | μ (cm2 V−1 s−1) | n (cm−3) | Δρ(9 T)/ρ(0) (%) |
|---|---|---|---|---|---|---|---|
| S1 | 1.0 | 0.5 | 0.3 | 1.41 | 6.2 | 4.13 × 1021 | 1.35 |
| S2 | 0.8 | 0.9 | 0.4 | 2.45 | 10.8 | 4.11 × 1021 | 1.87 |
| S3 | 1.1 | 0.8 | 0.6 | 2.01 | 9.7 | 3.21 × 1021 | 1.50 |
| Au film | 0.05 | 0.01 | 3 × 10−5 | 0.012 | 69 | 7.45 × 1022 | 0.39 |
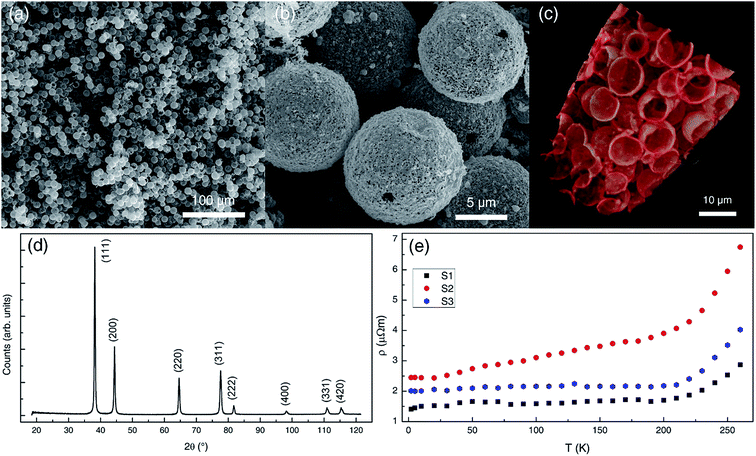
Fig. 1(a) shows the SEM image of the gold foams. We observed that the foam consists of gold microspherical shells. The details of the single microspherical shell are shown in Fig. 1(b), where the diameter of the shells was approximately 10 μm. The hollow structure of the gold microspherical shells can be identified by nano-CT measurements, as shown in Fig. 1(c), and the thickness of the shells was obtained as ∼400 nm. The XRD measurements show the polycrystalline structure of the gold foams [Fig. 1(d)]. Fig. 1(e) shows the temperature dependence of the resistivity ρ(T) for the three gold foam samples (named as S1, S2 and S3) at zero magnetic field. The electrical resistivity decreased with a decreasing temperature, which is a typical metallic behavior. The values of the gold foams' resistivity at low temperatures were in the order of 1 μΩ m, which is 100 times larger than the resistivity of the gold film (Table 1). The large difference in resistivity between gold foams and films originated from the high porosity of the foams. The calculated resistivity of the gold foams, as indicated in Table 1, did not exclude the voids in the foams. This issue will be discussed further below.
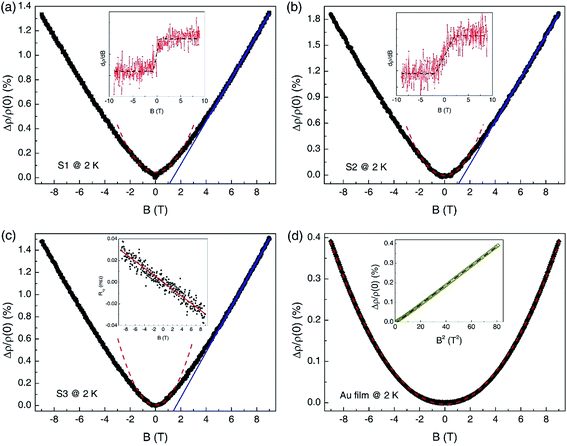
Fig. 2(a–c) display the MR curves at T = 2 K for S1 to S3, respectively, where the MR value is defined as Δρ(B)/ρ(0) = [ρ(B) − ρ(0)]/ρ(0) × 100%. A nonsaturating of the MR values at a very high magnetic field can be observed. The insets of Fig. 2(a) and (b) show the field derivative of MR, that is, dρ(B)/dB of S1 and S2, respectively. We can see that dρ/dB initially increased linearly with an increase in the field, which indicates the B2 dependence of ρ(B). Then, dρ/dB was saturated for B above the critical field [the dashed curves in the insets of Fig. 2(a) and (b)], which corresponds to a linear MR. The solid lines in Fig. 2(a–c) indicate the linear MR curves of the gold foams. Fig. 2(d) shows the MR curve of a homogeneous Au film at T = 2 K. The Δρ(B)/ρ(0) plotted as a function of B2 for the gold film is shown in the inset of Fig. 2(d). The linear dependence of Δρ(B)/ρ(0) − B2 revealed the classical magnetotransport in the gold films. The classical diffusion of electrons in materials arising from the Lorentz force will lead to a B2 dependence of MR, that is, Kohler's rule:16 Δρ(B)/ρ(0) ≃ (μB)2, where μ is the electron mobility. The dashed curve in Fig. 2(d) is the Kohler fitting result. A good fitting result is obtained over the whole magnetic field range of the gold film. For the gold foams, we can see that Kohler's rule was valid only in the low-field regime (|B| ≲ 2 T), and the high-field regime (|B| ≳ 3 T) was dominated by a linear MR behavior [Fig. 2(a–c)].
The inset of Fig. 2(c) shows the Hall resistance of sample S3. The linear fitting of the Rxy–B curve gives the electron concentration of the gold foams nfoam ≈ 3.21 × 1021 cm−3 for S3. By using the free electron gas model, we could estimate the electron mobility in gold foams as μ = 1/(neρ) ≈ 9.7 cm2 V−1 s−1 for S3. Additionally, nfilm ≈ 7.45 × 1022 cm−3 was also obtained, which is consistent with the values of bulk gold.17 The electron concentration n and mobility μ of all samples are listed in Table 1. We observe that the value of nfilm was ∼20 times larger than that of nfoam. Intuitively, the reason for this could be ascribed to the voids in the foams as the calculated ρ did not exclude the void volumes in the gold foams. If we consider the porosity of the gold foams [∼80% (ref. 15)], the revised nfoam was in the order of 1022 cm−3. This value is consistent with the values of the gold films and bulk.
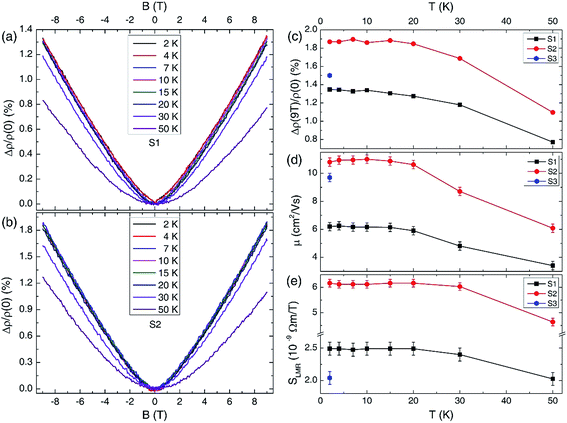
Fig. 3(a) and (b) represent the MR curves of gold foam samples S1 and S2, respectively, from 2 K to 50 K. Several features of these MR curves were distinguishable, such as, the MR is (i) positive; (ii) relatively large (∼1.9% at B = 9 T and T = 2 K); (iii) unsaturated in the high-field regime that is directly proportional to the magnetic field over the whole temperature range. Moreover, the MR curves with T ≲ 20 K were nearly coincident with each other. For temperatures exceeding ∼20 K, the MR values were weakened, and the magnetic field range where Kohler's rule was dominant was widened. For example, at T = 50 K, Kohler's rule was valid in the low-field regime for |B| ≲ 5 T, and a linear MR behavior could be observed in the high-field regime (|B| ≳ 5 T). Fig. 3(c) shows the MR values at B = 9 T plotted as a function of the temperature for the gold foam samples. Fig. 3(d) displays the temperature dependence of the electron mobility μ that was extracted from the Hall fitting of the Rxy–B data of the gold foams. We can see that Δρ(9 T)/ρ(0) and μ were nearly constant at T ≲ 20 K, and they were decreased when the temperature exceeds ∼20 K owing to the enhancement of the thermal phonon scattering in the gold foams. These tendencies are consistent with the results from nanoporous gold.10
Fig. 4 compares the MR values at a high magnetic field (B = 9 T) for different forms of gold material. The MR values of the homogeneous gold films and the gold foams are shown (see Table 1 and Fig. 2). The MR values of the nanoporous gold at B = 18 T and T = 4.2 K were adapted from the report by Fujita et al.10 The typical value of Δρ(18 T)/ρ(0) for nanoporous gold is 0.6%, which is larger than that of gold films but smaller than the Δρ(9 T)/ρ(0) values for our gold foams. The large difference of the MR values between the different gold forms further demonstrated that the electrical transport properties were affected by the 3D topology of the nanostructures.
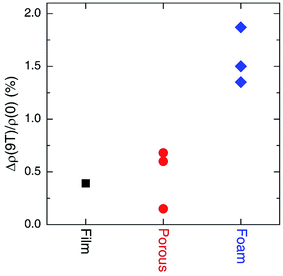 | ||
| Fig. 4 Magnetoresistance values Δρ(9 T)/ρ(0) of the homogeneous gold films, the nanoporous gold films and the gold foams. The results of the nanoporous gold films are adapted from ref. 10. | ||
IV. Discussions
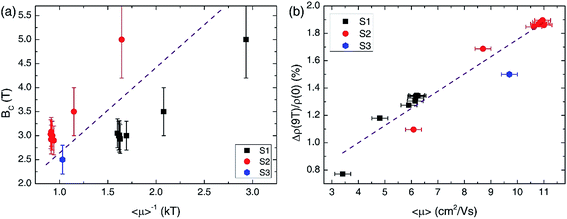
Now, we discuss the physical mechanisms behind the linear MR behavior in our gold foams. The linear MR phenomenon has been widely studied in several materials, such as Ag2±δSe,18 Ag2±δTe,19 Bi films,20 InSb,21 Bi2Te3,22 Bi2Se3,23 Cd3As2,24 WTe2,25 TaAs,26 β-RhSn4,27 GaAs quantum wells,28 graphene29 and carbon foams.30–32 To the best of our knowledge, two types of theoretical models have been proposed to explain the linear MR phenomena: the classical model and the quantum model. One of the classical linear MR models was suggested by Parish and Littlewood (PL).33,34 They argued that the magnetotransport properties of the inhomogeneous materials were governed by the spatial mobility fluctuations rather than the mobility itself. The large mobility fluctuations would lead to a linear MR behavior in the strong disordered systems. Another classical model was proposed by Sampsell and Garland,35 and Stroud and Pan36 (SGSP). They exactly calculated the electrical current distributions in the free-electron conductors with non-conducting spherical and cylindrical inclusions. The calculated results revealed that the current distortions occurred while the magnetic field was present. A larger field resulted in a larger current distortion. This effect led to a linear MR behavior in the high field regime. In contrast, a quantum model was developed by Abrikosov37 in 1969. According to Abrikosov's theory, a linear MR appeared in gapless semiconductors with a linear energy dispersion under the quantum limit condition, that is, the applied magnetic field must be so strong that only the lowest Landau level is populated. Recently, several quantum models have been proposed38,39 to interpret the linear MR properties in topological insulators22,23 and topological semimetals24–26 that lie outside of the Abrikosov paradigm. These progresses were not discussed here as they are inappropriate for our foam materials.In our samples, first we excluded Abrikosov's mechanism owing to the breaking of the quantum limit condition at such a low magnetic field (EF/ℏωC ∼ 2500 ≫ 1 at B = 9 T, where EF is the Fermi level and ℏωC is the first Landau level) in our gold foams. Next, we attempt to determine the applicability of the classical PL model in our gold foams. Obviously, the strong structure inhomogeneity of gold foams will leads to the spatial inhomogeneity of electron mobility. According to the PL theory, in the case of Δμ/<μ> < 1 (where <μ> is the average mobility and Δμ is the mobility fluctuation), we could expect (i) BC ∝ <μ>−1 (BC is the critical field above which the MR becomes linear) and (ii) Δρ/ρ(0) ∝ <μ>. Fig. 5(a) and (b) show the dependence of BC on <μ>−1 and the dependence of MR at B = 9 T on <μ>, respectively. These experimental results were consistent with the predictions from PL theory. However, the precondition of Δμ/<μ> < 1 deserves the experimental confirmation in the future. Finally, we considered the classical SGSP theory. This predicted a theoretical expression for the linear MR for samples containing spherical and cylindrical voids:35,36,40
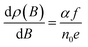 | (1) |
V. Conclusions
We experimentally studied the magnetotransport properties of the gold foams that were prepared by a chemical template–dealloying method. The temperature dependence of the resistivity of the gold foams represents a metallic behavior with zero magnetic field. With an increasing magnetic field, a crossover from a quadratic to linear dependence of the magnetoresistance and the nonsaturating linear magnetoresistance in gold foams are observed. The physical mechanisms of the linear magnetoresistance in the gold foams are discussed within the frameworks of the classical PL and SGSP theories, but further investigations are required to determine the exact mechanism. Our work reveals a linear magnetoresistance phenomenon in the gold foams, which may be useful for future applications.Acknowledgements
This work is financially supported by the National Natural Science Foundation of China (Grant No. 11604310, 11404304, 60908023), the National Key Scientific Instrument and Equipment Development Project of China (Grant No. 2014YQ090709) and the Key Laboratory of Ultra-Precision Machining Technology Foundation of CAEP (Grant No. ZZ15003).References
- H. L. Stormer, Rev. Mod. Phys., 1999, 71(4), 875 CrossRef CAS.
- F. A. Zwanenburg, A. S. Dzurak and A. Morello, et al., Rev. Mod. Phys., 2013, 85(3), 961 CrossRef CAS.
- A. G. Aronov and Y. V. Sharvin, Rev. Mod. Phys., 1987, 59(3), 755 CrossRef.
- I. Zutic, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76(2), 323 CrossRef CAS.
- J.-C. Charlier, X. Blase and S. Roche, Rev. Mod. Phys., 2007, 79(2), 677 CrossRef CAS.
- S. D. Sarma, S. Adam, E. H. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83(2), 407 CrossRef.
- M. Z. Hasan and C. L. Kane, Rev. Mod. Phys., 2010, 82(4), 3045 CrossRef CAS.
- H. Yu, X. Cui, X. Xu and W. Yao, Natl. Sci. Rev., 2015, 2(1), 57 CrossRef.
- B. C. Tappan, S. A. Steiner-III and E. P. Luther, Angew. Chem., Int. Ed., 2010, 49(27), 4544 CrossRef CAS PubMed.
- T. Fujita, H. Okada, K. Koyama, K. Watanabe, S. Maekawa and M. W. Chen, Phys. Rev. Lett., 2008, 101(16), 166601 CrossRef CAS PubMed.
- R. Xia, J. L. Wang and R. Wang, et al., Nanotechnology, 2010, 21(8), 085703 CrossRef PubMed.
- A. K. Mishra, C. Bansal and H. Hahn, J. Appl. Phys., 2008, 103(9), 094308 CrossRef.
- P. Wahl, T. Traußnig, S. Landgraf, H.-J. Jin, J. Weissmuller and R. Wurschum, J. Appl. Phys., 2010, 108(7), 073706 CrossRef.
- M. Hakamada, N. Kato and M. Mabuchi, Appl. Surf. Sci., 2016, 387, 1088 CrossRef CAS.
- K. Zhang, X. Tan, J. Zhang, W. Wu and Y. Tang, RSC Adv., 2014, 4(14), 7196 RSC.
- J. S. Dugdale, The electrical properties of disordered metals, New York, Cambridge University Press, 1995 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, New Jersey, John Wiley & Sons Inc, 2005 Search PubMed.
- R. Xu, A. Husmann, T. F. Rosenbaum, M. L. Saboungi, J. E. Enderby and P. B. Littlewood, Nature, 1997, 390(6655), 57–60, DOI:10.1038/36306.
- M. Lee, T. F. Rosenbaum, M.-L. Saboungi and H. S. Schnyders, Phys. Rev. Lett., 2002, 88(6), 066602 CrossRef CAS PubMed.
- F. Y. Yang, K. Liu, K. Hong, D. H. Reich, P. C. Searson and C. L. Chien, Science, 1999, 284, 1335 CrossRef CAS PubMed.
- J. Hu and T. F. Rosenbaum, Nat. Mater., 2008, 7(9), 697–700, DOI:10.1038/nmat2259.
- X. Wang, Y. Du, S. Dou and C. Zhang, Phys. Rev. Lett., 2012, 108(26), 266806 CrossRef PubMed.
- H. T. He, H. C. Liu and B. K. Li, et al., Appl. Phys. Lett., 2013, 103(3), 031606 CrossRef.
- T. Liang, Q. Gibson, M. N. Ali, M. Liu, R. J. Cava and N. P. Ong, Nat. Mater., 2015, 14, 280 CrossRef CAS PubMed.
- M. N. Ali, J. Xiong and S. Flynn, et al., Nature, 2014, 514, 205 CAS.
- X. Huang, L. Zhao and Y. Long, et al., Phys. Rev. X, 2015, 5(3), 031023 Search PubMed.
- X. Z. Xing, C. Q. Xu and N. Zhou, et al., Appl. Phys. Lett., 2016, 109(12), 122403 CrossRef.
- T. Khouri, U. Zeitler and C. Reichl, et al., Phys. Rev. Lett., 2016, 117(25), 256601 CrossRef CAS PubMed.
- F. Kisslinger, C. Ott and C. Heide, et al., Nat. Phys., 2015, 11(8), 650 CrossRef CAS.
- L. Wang, M. Yin, M. Abdi and T. Datta, Appl. Phys. Lett., 2015, 107(2), 023103 CrossRef.
- P. Li, Q. Zhang, X. He, W. Ren, H.-M. Cheng and X.-X. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94(4), 045402 CrossRef.
- Y. Tanabe, Y. Ito and K. Sugawara, et al., Adv. Mater., 2016, 28(46), 10304 CrossRef CAS PubMed.
- M. M. Parish and P. B. Littlewood, Nature, 2003, 426, 162 CrossRef CAS PubMed.
- M. M. Parish and P. B. Littlewood, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(9), 094417 CrossRef.
- J. B. Sampsell and J. C. Garland, Phys. Rev. B: Solid State, 1976, 13(2), 583 CrossRef CAS.
- D. Stroud and F. P. Pan, Phys. Rev. B: Solid State, 1976, 13(4), 1434 CrossRef CAS.
- A. A. Abrikosov, Soviet Physics - JETP, 1969, 29(4), 746 Search PubMed.
- C. M. Wang and X. L. Lei, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(3), 035442 CrossRef.
- J. C. W. Song, G. Refael and P. A. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(18), 180204 CrossRef.
- C. J. Beers, J. C. M. V. Dongen, H. V. Kempen and P. Wyder, Phys. Rev. Lett., 1978, 40(18), 1194 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |