Open Access Article
Open Access ArticleBehavior of interactions between hydrogen chalcogenides and an anthracene π-system elucidated by QTAIM dual functional analysis with QC calculations†‡
Satoko Hayashi*,
Yuji Sugibayashi and
Waro Nakanishi *
*
Department of Material Science and Chemistry, Faculty of Systems Engineering, Wakayama University, 930 Sakaedani, Wakayama, 640-8510 Japan. E-mail: hayashi3@sys.wakayama-u.ac.jp; nakanisi@sys.wakayama-u.ac.jp; Fax: +81 73 457 8353; Tel: +81 73 457 8252
First published on 22nd June 2017
Abstract
The nature of EH2-*-π(C14H10) interactions (E = O, S, Se and Te) of an anthracene system was elucidated by applying QTAIM dual functional analysis (QTAIM-DFA) after clarification of the structural features with quantum chemical (QC) calculations. π-HB (hydrogen bond) interactions were detected for E = O, S, Se and Te, whereas π-EB (chalcogen bond) interactions were observed for E = O in (EH2)-*-π(C14H10), where the bond paths connected H in EH2 to C14H10 in π-HB, and they connected E in EH2 to C10H8 in π-EB. The QTAIM-DFA parameters of (R, θ) and (θp, κp) were evaluated for the interactions via analysing the plots of Hb(rc) versus Hb(rc) − Vb(rc)/2 for the interactions at the bond critical points. Data obtained from the perturbed structures around the fully optimized structures were employed for the plots, in addition to the fully optimized structures. Data obtained from the fully optimized structures were analysed using (R, θ), which corresponded to the static nature, and those obtained from the perturbed structures were analysed using (θp, κp), which represented the dynamic nature of the interactions, where θp corresponds to the tangent line of the plot and κp is the curvature. The θ and θp values are less than 90° for all the interactions examined, except for the iH-*-11C(π) interaction in TeH2-*-C14H10 (C1: IIBAtc), where iH is located closer to the centre of C14H10. Therefore, the interactions examined were predicted to have vdW nature, appeared in the pure-CS (closed shell) interaction region, although iH-*-11C(π) was predicted to have the pure-CS/typical-HB nature without covalency. Additionally, the π-HB interaction seems to be slightly stronger than π-EB in (OH2)-*-π(C14H10).
Introduction
Significant attention has been paid to the interactions between hydrogen chalcogenides (EH2: E = O, S, Se and Te) and aromatic π-systems, and some structures have been reported for benzene adducts formed through π-interactions.1–8 The interactions in benzene π-systems are mainly characterized by the hydrogen bonds formed between EH2 and the benzene π-system, which act as a proton donor and proton acceptor, respectively, and have been called hydrogen bonds of the π-type (π-HBs) herein.1–8 The π-HB (hydrogen bond) interactions were also investigated for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts between EH2 (E = O and S) and the naphthalene π-system.9–20 Indeed, there have been many investigations on π-adducts, which are mainly based on a theoretical background; however, these investigations seem to be rather limited to structural features. The nature of the π-HB interactions has seldom been reported, especially for the anthracene π-system, π(C14H10), to the best of our knowledge.
1 adducts between EH2 (E = O and S) and the naphthalene π-system.9–20 Indeed, there have been many investigations on π-adducts, which are mainly based on a theoretical background; however, these investigations seem to be rather limited to structural features. The nature of the π-HB interactions has seldom been reported, especially for the anthracene π-system, π(C14H10), to the best of our knowledge.
Very recently, we reported the nature of the EH2⋯π interactions for benzene and naphthalene π-systems, together with their structural features.1,2,10,11 The H atom(s) in EH2 is (are) connected to the benzene π-system, EH2⋯π(C6H6), via bond paths (BPs). Through careful examination of the BPs in the adducts, another type of interaction was also detected in H2E⋯π(C6H6), where E in EH2 is joined to the benzene π-system via a BP. Such interaction was called a chalcogen π-type (π-EB) bond. EH2 is connected to the C atoms or BCPs (bond critical points: rc: *)21 on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds of C6H6 by BPs. In the case of the benzene π-system, π-EBs seem more important relative to π-HBs, although the predicted importance may change depending on the calculation system.2
C bonds of C6H6 by BPs. In the case of the benzene π-system, π-EBs seem more important relative to π-HBs, although the predicted importance may change depending on the calculation system.2
What happens if EH2 (E = O, S, Se and Te) interacts with the anthracene π-system? The anthracene π-system contains two types of (three) benzene π-systems and one type of (two) naphthalene π-system, in addition to the original anthracene π-system. What are the differences and similarities in the EH2⋯π interactions between the anthracene π-system and the π-systems of naphthalene and benzene? The nature of the interactions in (EH2)⋯π(C14H10) (E = O, S, Se and Te) is elucidated together with its structural feature. Scheme 1 illustrates some of the structures expected for (EH2)-*-π(C14H10) of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts, which are inferred from the structures of (EH2)-*-π(C10H8) and (EH2)-*-π(C6H6). Type IIAAtc and type IICAtc in (EH2)⋯π(C14H10) are defined for the adduct, where EH2 locates on the central and outer benzene rings of anthracene, respectively, whereas it is above the 11C–12C (or 13C–14C) bond in type IIBAtc. The structures for the 1
1 adducts, which are inferred from the structures of (EH2)-*-π(C10H8) and (EH2)-*-π(C6H6). Type IIAAtc and type IICAtc in (EH2)⋯π(C14H10) are defined for the adduct, where EH2 locates on the central and outer benzene rings of anthracene, respectively, whereas it is above the 11C–12C (or 13C–14C) bond in type IIBAtc. The structures for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct of (EH2)-*-π(C6H6) and (EH2)-*-π(C10H8) are also shown in Scheme 1 for convenience of discussion. The optimized structures are called type IaBzn, IbBzn and type IIBzn for (EH2)-*-π(C6H6) and type INap and type IINap for (EH2)-*-π(C10H8).
1 adduct of (EH2)-*-π(C6H6) and (EH2)-*-π(C10H8) are also shown in Scheme 1 for convenience of discussion. The optimized structures are called type IaBzn, IbBzn and type IIBzn for (EH2)-*-π(C6H6) and type INap and type IINap for (EH2)-*-π(C10H8).
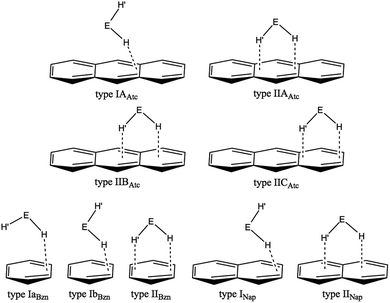 | ||
| Scheme 1 Structures expected for (EH2)⋯π(C14H10) (E = O, S, Se and Te), based on that optimized for (EH2)⋯π(C6H6) and (EH2)⋯π(C10H8). | ||
The QTAIM (quantum theory of atoms-in-molecules) approach, introduced by Bader22,23 enables the analysis of the nature of chemical bonds and interactions.24–30 Interactions seem to be defined by the corresponding BPs, but we must be careful to use the correct terminology with the concept.31 BCP is an important concept in QTAIM, which is a point along the BP at the interatomic surface, where charge density, ρ(r), reaches a minimum.32 It is denoted by ρb(rc), in addition to other QTAIM functions at BCPs, such as Laplacians of ρ(r) (∇2ρb(rc)), total electron energy densities Hb(rc), potential energy densities Vb(rc) and kinetic energy densities Gb(rc), together with kb(rc) (= Vb(rc)/Gb(rc)).
Recently, we proposed QTAIM dual functional analysis (QTAIM-DFA),33–36 according to QTAIM.22–30,37 QTAIM-DFA enables experimental chemists to analyse their own results concerning chemical bonds and interactions with their own image.38 QTAIM-DFA provides an excellent possibility for evaluating, classifying and understanding weak to strong interactions in a unified form.33–36 To elucidate the nature of the interactions in question with QTAIM-DFA, Hb(rc) is plotted versus Hb(rc) − Vb(rc)/2 [= (ħ2/8m)∇2ρb(rc)], where both the x and y axes are given units of energy. In our treatment, data for perturbed structures around fully optimized structures are employed for the plots, in addition to the fully optimized structures.33–36 We propose the concept of “the dynamic nature of interactions” which originated from the data containing the perturbed structures.33a,34–36,39
Data from the fully optimized structures correspond to the static nature of interactions. QTAIM-DFA is applied to typical chemical bonds and interactions and rough criteria are established. The rough criteria can distinguish the chemical bonds and interactions in question from others. QTAIM-DFA and the criteria are explained in the ESI with Schemes S1 and S2, Fig. S1 and eqn (S1)–(S7).‡ The basic concept of the QTAIM approach is also surveyed.
QTAIM-DFA is applied to elucidate the dynamic and static nature of the interactions in (EH2)-*-π(C14H10) (E = O, S, Se and Te). The discussion is limited to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts of (EH2)-*-π(C14H10) for simplicity. Herein, we present the results of the investigations on the nature of the interactions in question. The interactions are classified and characterized as a reference by employing the criteria.
1 adducts of (EH2)-*-π(C14H10) for simplicity. Herein, we present the results of the investigations on the nature of the interactions in question. The interactions are classified and characterized as a reference by employing the criteria.
Methodological details in calculations
Structures were optimized using the Gaussian 09 programs.40 The 6-311+G(3df) basis set41 was employed for O, S and Se and the basis set of the (7433111/743111/7411/2 + 1s1p1d1f) type from Sapporo Basis Set Factory42 was used for Te with the 6-311++G(d, p) basis set41 for C and H. The basis set system (BSS) is called BSS-F according to examinations of the BSSs in a previous study. The Møller–Plesset second order energy correlation (MP2) level43 was applied to the calculations. Optimized structures were confirmed by the frequency analysis.QTAIM functions were calculated by employing the wfn files using the Gaussian 09 program package40 with the same method for optimizations, and the data were analysed with the AIM2000 program.44 The normal coordinates of internal vibrations (NIV) obtained by the frequency analysis were employed to generate the perturbed structures,35,36 which is explained in eqn (1). The k-th perturbed structure in question (Skw) was generated by the addition of the normal coordinates of the k-th internal vibration (Nk) to the standard orientation of a fully optimized structure (S0) in the matrix representation.35 The coefficient fkw in eqn (1) controls the difference in the structures between Skw and S0: fkw is determined to satisfy eqn (2) for the interaction in question, where, r and r0 stand for the distances in question in the perturbed and fully optimized structures, respectively, with a0 of Bohr radius (0.52918 Å). The perturbed structures with NIV correspond to that with r being elongated or shortened by 0.05a0 or 0.1a0, relative to r0, as shown in eqn (2). Nk of five digits are used to predict Skw. The selected vibration must contain the motion of the interaction in question most effectively among all the zero-point internal vibrations.
| Skw = S0 + fkwNk | (1) |
| r = r0 + wa0 (w = (0), ±0.05 and ±0.1; a0 = 0.52918 Å) | (2) |
| y = co + c1x + c2x2 + c3x3 | (3) |
(Rc2: square of correlation coefficient).
In the QTAIM-DFA treatment, Hb(rc) is plotted versus Hb(rc) − Vb(rc)/2 for data of five points of w = 0, ±0.05 and ±0.1, as shown in eqn (2). Each plot is analysed using a regression curve of the cubic function, as shown in eqn (3), where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)) (Rc2 > 0.99999 usually).45
Results and discussion
Structural feature of (EH2)⋯π(C14H10) (E = O, S, Se and Te)
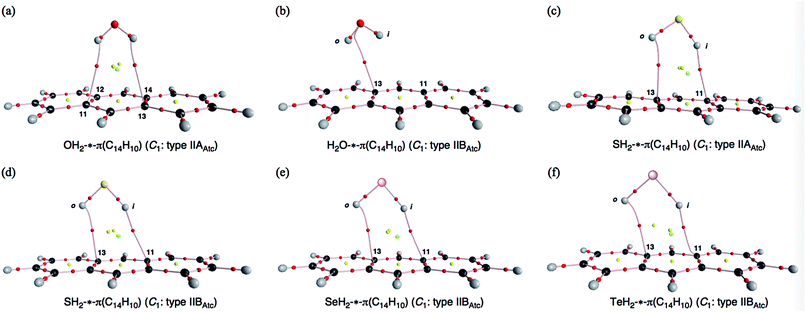
Before the final structural optimizations for (EH2)-*-π(C14H10) (E = O, S, Se and Te), the minima were searched for systematically with MP2/BSS-F. The search was started assuming typically type IIAAtc, type IIBAtc and type IICAtc structures of the C1 symmetry. The type IIAAtc and type IIBAtc structures of (EH2)-*-π(C14H10) were optimized for E = O and S, whereas only type IIBAtc was optimized for E = Se and Te. The processes of the convergence are summarized in Table S1 of the ESI.‡The type IIAAtc structure optimized for (OH2)-*-π(C14H10) with MP2/BSS-F was apparently different from type IIBAtc, as confirmed by the r1 values. In the case of (SH2)⋯π(C14H10), one structure was optimized, which was close to the type IIAAtc structure if initially assuming a typical type IIAAtc structure. The type IIAAtc structure optimized for (SH2)⋯π(C14H10) [SH2⋯π(C14H10) (C1: IIAAtc)] seems somewhat distorted from the Cs symmetry.46 The search converged to another one, if started assuming typical type IIBAtc and type IICAtc structures, which are close to type IIAAtc. Indeed, their r1 values are very close to each other, but the ϕ2 and ϕ3 values seem meaningfully different for the two types (Fig. 1c and d, respectively). Therefore, the second structure is (tentatively) called type IIBAtc, herein. No type IAtc structures were detected after similar treatment, even if optimizations started from those very close to type IAAtc.
Table 1 collects the structural parameters selected for the optimized structures of (EH2)-*-π(C14H10) (E = O, S, Se and Te), r1, r2, r3, θ1, θ2, θ3, ϕ1, ϕ2 and ϕ3, which are defined in Scheme 2. The optimized structures are not shown in the figures, but they can be found in molecular graphs, which are drawn on the optimized structures (see Fig. 1). What factors appear to control the optimized structures? We compared the H⋯H distance in EH2, r(H, H: EH2), with the 11C⋯13C distance in C14H10, r(11C, 13C: C14H10). Indeed, r(H, H: EH2) for E = O (1.522 Å), S (1.931 Å), Se (2.088 Å) and Te (2.361 Å) is shorter than r(11C, 13C: C14H10) (2.452 Å for the central benzene ring), but the differences in r (Δr = r(C, C: C14H10) − r(H, H: EH2)) are larger than 0.5 Å for O (Δr = 0.9303 Å) and S (0.5215 Å), whereas they are smaller than 0.4 Å for Se (0.3644 Å) and Te (0.0913 Å) (see Table S2 of the ESI‡). The type IIBAtc structures of (EH2)-*-π(C14H10) (E = O, S, Se and Te) would form with no limitations of Δr, whereas it may be necessary for Δr larger than around 0.5 Å to give the type IIAAtc structures (E = O and S). In the case of type IIBAtc, one H in EH2 seems to be slightly above the 11C⋯13C bond for E = S, Se and Te, but OH2 seems to exist almost right above the 11C⋯13C bond, which may also be controlled by Δr. Indeed, the difference in Δr between E = S and Se seems small, at a first glance, but the small difference would play an important role in the appearance of the type IIAAtc structure.
| Species (X–Y) (symmetry: type) | r1 (Å) | r2 (Å) | r3 (Å) | θ1 (°) | θ2 (°) | θ3 (°) | ϕ1 (°) | ϕ2 (°) | ϕ3 (°) | ΔEESd (kJ mol−1) | ΔEEnte (kJ mol−1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a BSS-F: the 6-311+G(3df) basis set was employed for O, S and Se and the basis set of the (7433111/743111/7411/2 + 1s1p1d1f) type for Te with the 6-311++G(d,p) basis set for C and H.b See Scheme 2 for the structural parameters.c Optimized structures are not given in the figures but can be found in the molecular graphs drawn on the optimized structures (see Fig. 1).d ΔEES = EES((EH2)-*-π(C14H10)) − (EES(EH2) + EES(C14H10)) on the energy surface.e ΔEEnt = EEnt((EH2)-*-π(C14H10)) − (EEnt(EH2) + EEnt(C14H10)) with the thermal corrections to enthalpies.f Very close to Cs.g The structures are very close to each other; however, they are analysed as two different structures here since the differences in ϕ2 and ϕ3 seem meaningful. They are called IIAAtc and IIBAtc. | |||||||||||
| OH2⋯π(C14H10) (C1:f IIAAtc) | 3.2865 | 0.9629 | 0.9629 | 89.9 | 51.8 | 103.5 | −92.5 | −1.7 | 2.8 | −22.7 | −18.1 |
| H2O⋯π(C14H10) (C1: IIBAtc) | 3.6682 | 0.9631 | 0.9624 | 63.4 | 69.6 | 103.6 | −93.8 | −14.3 | 3.5 | −21.9 | −17.6 |
| SH2⋯π(C14H10) (C1: IIAAtc)g | 3.6162 | 1.3389 | 1.3400 | 80.5 | 60.6 | 92.2 | −92.1 | −6.4 | −3.3 | −28.7 | −25.0 |
| SH2⋯π(C14H10) (C1: IIBAtc)g | 3.6165 | 1.3389 | 1.3400 | 80.5 | 60.6 | 92.2 | −91.8 | −2.1 | −1.9 | −28.7 | −25.0 |
| SeH2⋯π(C14H10) (C1: IIBAtc) | 3.6959 | 1.4597 | 1.4603 | 78.9 | 61.5 | 91.3 | −91.5 | 3.0 | −0.2 | −31.7 | −28.3 |
| TeH2⋯π(C14H10) (C1: IIBAtc) | 3.7703 | 1.6576 | 1.6578 | 78.1 | 64.2 | 91.5 | −89.9 | −11.4 | −17.5 | −40.5 | −36.8 |
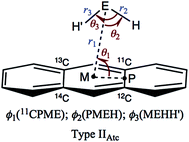 | ||
| Scheme 2 Structural Parameters Illustrated for Type IIAtc of (EH2)-*-π(C14H10) (E = O, S, Se and Te). | ||
What are the stabilization energies in the formation of the adducts? Table 1 contains the ΔE (ΔEES and ΔEEnt) values for (EH2)⋯π(C14H10), where, ΔEES and ΔEEnt are the ΔE values on the energy surfaces and those with the thermal corrections to enthalpies, respectively [ΔE = (E((EH2)⋯π(C14H10)) − (E(EH2) + E(C14H10))]. An excellent correlation was obtained in the plot of ΔEEnt versus ΔEES (y = 5.262 + 1.047x; Rc2 = 0.998 (n = 6: number of data points)), although is not shown in the figure. Therefore, the ΔEES values will be employed for the discussion of ΔE. A good correlation was also obtained in the plot of ΔEES versus r1, if the data for H2O⋯π(C14H10) (C1: IIBAtc) are neglected (y = −1410.42 + 820.87x – 121.30x2; Rc2 = 0.975 (n = 5)), where the structure of H2O⋯π(C14H10) (C1: IIBAtc) seems different from the others.
What are the relations between ΔEAtc, ΔENap and ΔEBzn? The ΔENap values are linearly proportional to ΔEBzn in type II. The ratio of ΔENap/ΔEBzn becomes larger in the order of E = O (ΔENap/ΔEBzn = 1.34) < S (1.60) < Se (1.68) < Te (1.75), which shows a substantial chalcogen dependence. On the other hand, the ΔEAtc/ΔENap ratio seems almost constant for E = O (ΔEAtc/ΔENap = 1.01) < S (1.07) < Se (1.09) < Te (1.11). The different basis sets for Te may somewhat affect the evaluated values for E = Te, which are from the Sapporo Basis Set Factory, whereas the others are from the Gaussian09 program. What mechanisms operate to control the ratios? It is difficult to clarify this, however, we examined the ratios of r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bzn/r1
Bzn/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap and r1
Nap and r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Atc/r1
Atc/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap. The r1
Nap. The r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bzn/r1
Bzn/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap ratios become larger in the order of 1.01 (E = O) < 1.13 (S) < 1.15 (Se) < 1.19 (Te) and the r1
Nap ratios become larger in the order of 1.01 (E = O) < 1.13 (S) < 1.15 (Se) < 1.19 (Te) and the r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Atc/r1
Atc/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap ratios increase similarly in the order of 1.00 (E = O) < 1.09 (S) < 1.11 (Se) < 1.13 (Te). However, the chalcogen dependence of the ratios seems somewhat smaller for r1
Nap ratios increase similarly in the order of 1.00 (E = O) < 1.09 (S) < 1.11 (Se) < 1.13 (Te). However, the chalcogen dependence of the ratios seems somewhat smaller for r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Atc/r1
Atc/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap, relative to the case for r1
Nap, relative to the case for r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Bzn/r1
Bzn/r1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Nap. These results would be responsible for the observed ΔE/ΔE ratios, although the vdW and/or covalent radii of chalcogens must also be carefully examined for the discussion.
Nap. These results would be responsible for the observed ΔE/ΔE ratios, although the vdW and/or covalent radii of chalcogens must also be carefully examined for the discussion.
Before the application of QTAIM-DFA to (EH2)⋯π(C14H10), the molecular graphs and contour plots are examined next.
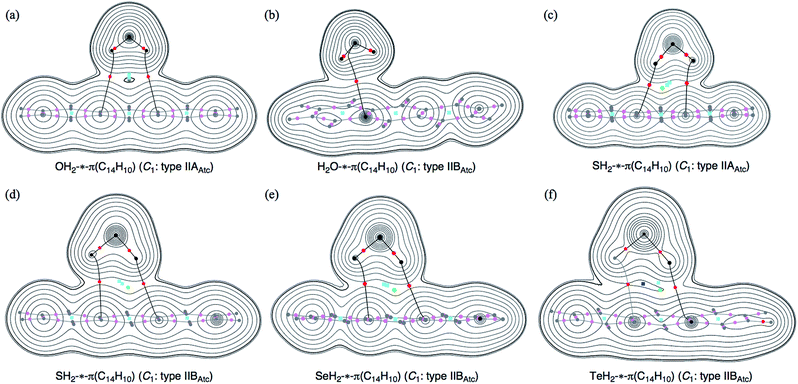
Molecular graphs and contour plots of ρ(r) for (EH2)⋯π(C14H10)
Fig. 1 illustrates the molecular graphs for (EH2)-*-π(C14H10) (E = O, S, Se and Te), which were calculated with MP2/BSS-F. The BCPs are clearly detected, which contain that expected between EH2 and C14H10. Each BP with a BCP connects each H in EH2 and the carbon atom of 11C or 13C in C14H10 for all optimized structures in Table 2, except for the type IIBAtc of H2O-*-π(C14H10). The BP with BCP joins O in OH2 and a carbon atom of 11C or 13C in C14H10 of OH2-*-π(C14H10). Therefore, the interactions between EH2 and C14H10 are classified by π-HBs for all the adducts in Table 2, except for the type IIBAtc of H2O-*-π(C14H10), the interaction of which should be classified by the π-EB type. Ring critical points (RCPs) and cage critical points (CCPs) are also detected in Fig. 1. Fig. 2 shows the contour plots of ρ(r) for (EH2)⋯π(C14H10) (E = O, S, Se and Te) calculated with MP2/BSS-F. The contour plots of ρ(r) are drawn on a plane containing E, BCP (*) of the (EH2)-*-π type and an atom or BCP suitable for the contour plots of (EH2)-*-π(C14H10). The BCPs are well located at the (three dimensional) saddle points of ρ(r) in the species. Negative Laplacians and trajectory plots are drawn in Fig. S2 and S3 of the ESI.‡ It is well visualized how the BCPs are classified through ∇2ρ(r) and the space around the species is well divided by the atoms in it.| Interaction (X-*-Y)e | Typeb | ρb(rc) (eao−3) | c∇2ρb(rc)c (au) | Hb(rc) (au) | kb(rc)d | R (au) | θ (°) | Freq (cm−1) | kf (unitf) | θp (°) | κp (au−1) | Classification characterization |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a BSS-F: the 6-311+G(3df) basis set employed for O, S and Se and the basis set of the (7433111/743111/7411/2 + 1s1p1d1f) type for Te with the 6-311++G(d, p) basis set for C and H.b See Scheme 1 and Fig. 1.c c∇2ρb(rc) = Hb(rc) − Vb(rc)/2, where c = ħ2/8m.d kb(rc) = Vb(rc)/Gb(rc).e The optimized structure has C1 symmetry and atoms taking part in the interaction are shown in bold with BCP denoted by *.f mDyne Å−1.g Very close to Cs symmetry.h iH and oH in EH2 stand for the atoms taking part in the interactions, which are placed more inside and more outside, respectively, in relation to the centre of C14H10.i Vary large value of 1259 au−1. | ||||||||||||
| OHH-*-11(13)C(π) | IIAAtcg | 0.0060 | 0.0024 | 0.0007 | −0.814 | 0.0025 | 72.6 | 108.7 | 0.0411 | 74.5 | 8.0 | p-CS/vdW |
| H2O-*-13C(π) | IIBAtc | 0.0069 | 0.0029 | 0.0009 | −0.831 | 0.0031 | 73.9 | 104.5 | 0.0346 | 79.3 | 18.1 | p-CS/vdW |
| SoHiH-*-11C(π)h | IIAAtc | 0.0072 | 0.0027 | 0.0009 | −0.807 | 0.0029 | 72.1 | 65.9 | 0.0151 | 72.2 | 1.1 | p-CS/vdW |
| SiHoH-*-13C(π)h | IIAAtc | 0.0065 | 0.0024 | 0.0007 | −0.835 | 0.0025 | 74.2 | 65.9 | 0.0151 | 74.3 | 145.7 | p-CS/vdW |
| SoHiH-*-11C(π)h | IIBAtc | 0.0070 | 0.0027 | 0.0009 | −0.799 | 0.0029 | 71.5 | 65.8 | 0.0161 | 73.6 | 37.3 | p-CS/vdW |
| SiHoH-*-13C(π)h | IIBAtc | 0.0065 | 0.0024 | 0.0007 | −0.836 | 0.0025 | 74.2 | 65.8 | 0.0161 | 73.4 | 61.8 | p-CS/vdW |
| SeoHiH-*-11C(π)h | IIBAtc | 0.0072 | 0.0028 | 0.0010 | −0.789 | 0.0029 | 70.8 | 54.6 | 0.0158 | 72.7 | 30.4 | p-CS/vdW |
| SeiHoH-*-13C(π)h | IIBAtc | 0.0070 | 0.0025 | 0.0007 | −0.846 | 0.0026 | 75.0 | 54.6 | 0.0158 | 74.2 | 37.1 | p-CS/vdW |
| TeoHiH-*-11C(π)h | IIBAtc | 0.0077 | 0.0028 | 0.0008 | −0.829 | 0.0029 | 73.7 | 50.5 | 0.0086 | 93.8 | i | p-CS/t-HBnc |
| TeiHoH-*-13C(π)h | IIBAtc | 0.0088 | 0.0031 | 0.0008 | −0.849 | 0.0032 | 75.3 | 23.9 | 0.0028 | 82.9 | 299.8 | p-CS/vdW |
Survey of the interactions in (EH2)-*-π(C14H10) (E = O, S, Se and Te)
As shown in Fig. 1 and 2, some BPs are apparently curved. Therefore, the lengths of the BPs (rBP) will be substantially different from the straight-line distances (RSL) in some cases. The rBP and RSL values are collected in Table S2 of the ESI‡ for (EH2)-*-π(C14H10) (E = O, S, Se and Te), which were evaluated with MP2/BSS-F, together with the differences between rBP and RSL (ΔrBP = rBP − RSL). There are two types of BPs in each adduct since each adduct has C1 symmetry. Therefore, it is necessary to define the BPs to distinguish the two. Letting iH and oH in EH2 connect to π(C14H10) through BPs, which are placed more inside and more outside, respectively, in relation to the centre of C14H10, then iBP and oBP can be defined as iBP (iH-*-π) and oBP (oH-*-π), respectively.The ΔrBP values are small (ca. 0.03 Å) for iBP (SoHiH-*-11C(π)) and iBP (SeoHiH-*-11C(π)) in (EH2-*-π(C14H10)) (C1: IIBAtc). Thus, the iBPs can be approximated as straight lines. However, the ΔrBP value is large (0.41 Å) for oBP (SeiHoH-*-11C(π)), which seems difficult to be approximated by a straight line. The values seem moderate (0.09–0.17 Å) for most of the π-HB and π-EB interactions in EH2-*-π(C14H10) for E = O, S, Se and Te, other than three cases. The BPs could be approximated as almost straight lines to gentle curves. The rBP values are plotted versus RSL in Fig. 3. A very good correlation was obtained for the case of 0.09 ≤ ΔrBP ≤ 0.17 Å, which is shown in the figure. The data for three BPs deviate from the correlation, although two of them can be approximated as straight lines, as mentioned above.
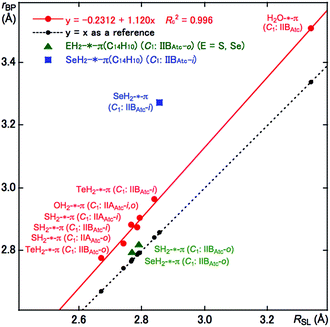 | ||
| Fig. 3 Plots of rBP versus RSL for (EH2)-*-π(C14H10) (E = O, S, Se and Te), evaluated with BSS-F at the MP2 level. | ||
QTAIM-DFA was applied to the interactions between EH2 and C14H10 in EH2-*-π(C14H10) (E = O, S, Se and Te) and the QTAIM functions were calculated for the interactions at BCP. The results are given in Table 2. Fig. 4 shows the plot of Hb(rc) versus Hb(rc) − Vb(rc)/2 for EH2-*-π(C14H10) (E = O, S, Se and Te), which contains the data for the perturbed structures evaluated with MP2/BSS-F. All the data in Fig. 4 appear in the area of Hb(rc) − Vb(rc)/2 > 0 and Hb(rc) > 0, which belongs to the pure-CS (closed shell: p-CS) region. The plots were analysed according to eqn (S3)–(S6) of the ESI‡ by applying QTAIM-DFA. These results are discussed next.
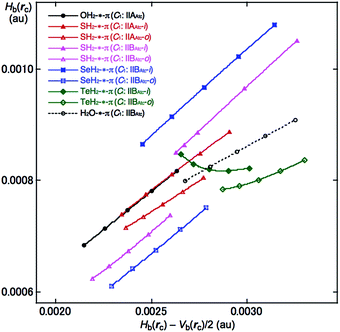 | ||
| Fig. 4 Plots of Hb(rc) versus Hb(rc) − Vb(rc)/2 for (EH2)-*-π(C14H10), evaluated with MP2/BSS-F. Compounds with marks are shown in the figure. | ||
Nature of π-HBs and π-EBs in EH2-*-π(C14H10) (E = O, S, Se and Te)
Table 2 collects the QTAIM-DFA parameters of (R, θ) and (θp, κp) for the π-HB and π-EB interactions, together with the frequencies and the force constants (kf) correlated to NIV, which are employed to generate the perturbed structures. The nature of π-HBs and π-EBs in EH2-*-π(C14H10) is discussed based on the (R, θ, θp) values employing the standard values as a reference (see Scheme S2 of the ESI‡). It should be instructive to survey the criteria related to that herein before a detailed discussion. The criteria tell us that 45° < θ < 90° for pure-CS interactions. The θp value predicts the character of the interactions. In the p-CS region, the character of the interactions will be the vdW type for 45° < θp < 90°, whereas it will be the t-HB (typical hydrogen bonds) type with no covalency (t-HBnc) for 90° < θp ≤ 125°, where θp = 125° tentatively corresponds to θ = 90°.The θ and θp values are less than 90° for all the π-HBs and π-EB in EH2-*-π(C14H10) examined herein, except for the TeiHoH-*-11C(π) interaction in TeH2-*-π(C14H10). Therefore, the π-HBs and π-EB interactions in EH2-*-π(C14H10) in Table 2 are all classified by the pure-CS interactions and characterized as the vdW type (p-CS/vdW), except for TeiHoH-*-11C(π) in TeH2-*-π(C14H10). Although oBP (TeiHoH-*-13C(π)) is predicted to have the nature of (p-CS/vdW), iBP (TeiHoH-*-11C(π)) is predicted to have the nature of (p-CS/t-HBnc). The π-EB interaction in the H2O-*-11C(π) type [(θ, θp) = (73.9°, 79.3°)] is predicted to be somewhat stronger than the π–HB interaction of the OHH-*-11C(π) type [(θ, θp) = (72.6°, 74.5°)] for OH2-*-π(C14H10). The π-HB interactions in the anthracene system are predicted to be very similar to that in the naphthalene system, which seem slightly stronger than that in the benzene system. The results are in accordance with that derived from the energies for the formation of the adducts.
The delocalization indexes and ellipticity are the important parameters to clarify and understand the nature of the (EH2)⋯π interactions.47 The nature of the (EH2)⋯π interactions will be discussed elsewhere based on these parameters for the series of (EH2)⋯π(C6H6), (EH2)⋯π(C10H8), and (EH2)⋯π(C14H10) (E = O, S, Se and Te).
Conclusions
The behaviour of the interactions for EH2 adducts with the anthracene π-system (E = O, S, Se and Te) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio is elucidated by applying QTAIM-DFA. The structures were optimized with MP2/BSS-F. Two types of structures were optimized for E = O and S, whereas one was optimized for E = Se and Te. The BCPs are clearly detected in the molecular graphs. The interactions are the π-HB type for EH2-*-π(C14H10) (C1: IIAAtc) (E = O and S) and EH2-*-π(C14H10) (C1: IIBAtc) (E = S, Se and Te), whereas they are the π-EB type for H2O-*-π(C14H10) (C1: IIBAtc). The QTAIM-DFA parameters of (R, θ) and (θp, κp) are calculated for the species, according to eqn (S3)–(S6).‡ The θ values are less than 90° for all interactions examined in this work. The θp values are also less than 90° for all the interactions in question, except for iH-*-11C(π) in TeH2-*-C14H10 (C1: IIBAtc). Therefore, all the π-HB and π-EB interactions examined in this work are classified by pure-CS interactions and characterized as vdW in nature (p-CS/vdW), although iH-*-11C(π) in TeH2-*-C14H10 (C1: IIBAtc) is predicted to have the p-CS/t-HB nature without covalency. The π-EB interaction is predicted to be somewhat stronger than π-HB in (OH2)-*-π(C14H10). It is demonstrated that the predicted nature of EH2-*-π(C14H10) is closer to that of EH2-*-π(C10H8) rather than that of EH2-*-π(C6H6). The π-HB and π-EB interactions in the anthracene π-system are well elucidated by applying QTAIM-DFA.
1 ratio is elucidated by applying QTAIM-DFA. The structures were optimized with MP2/BSS-F. Two types of structures were optimized for E = O and S, whereas one was optimized for E = Se and Te. The BCPs are clearly detected in the molecular graphs. The interactions are the π-HB type for EH2-*-π(C14H10) (C1: IIAAtc) (E = O and S) and EH2-*-π(C14H10) (C1: IIBAtc) (E = S, Se and Te), whereas they are the π-EB type for H2O-*-π(C14H10) (C1: IIBAtc). The QTAIM-DFA parameters of (R, θ) and (θp, κp) are calculated for the species, according to eqn (S3)–(S6).‡ The θ values are less than 90° for all interactions examined in this work. The θp values are also less than 90° for all the interactions in question, except for iH-*-11C(π) in TeH2-*-C14H10 (C1: IIBAtc). Therefore, all the π-HB and π-EB interactions examined in this work are classified by pure-CS interactions and characterized as vdW in nature (p-CS/vdW), although iH-*-11C(π) in TeH2-*-C14H10 (C1: IIBAtc) is predicted to have the p-CS/t-HB nature without covalency. The π-EB interaction is predicted to be somewhat stronger than π-HB in (OH2)-*-π(C14H10). It is demonstrated that the predicted nature of EH2-*-π(C14H10) is closer to that of EH2-*-π(C10H8) rather than that of EH2-*-π(C6H6). The π-HB and π-EB interactions in the anthracene π-system are well elucidated by applying QTAIM-DFA.
Acknowledgements
This work was partially supported by a Grant-in-Aid for Scientific Research (No. 26410050) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. The support of the Wakayama University Original Research Support Project Grant and the Wakayama University Graduate School Project Research Grant is also acknowledged.Notes and references
- Y. Sugibayashi, S. Hayashi and W. Nakanishi, ChemPhysChem, 2016, 17, 2579–2589 CrossRef CAS PubMed.
- S. Hayashi, Y. Sugibayashi and W. Nakanishi, Phys. Chem. Chem. Phys., 2016, 18, 9948–9960 RSC.
- S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard III and G. A. Blake, Science, 1992, 257, 942–945 Search PubMed . See also; R. N. Pribble and T. S. Zwier, Science, 1994, 265, 75–79 Search PubMed; X. Wang and P. P. Power, Angew. Chem., Int. Ed., 2011, 50, 10965–10968 CrossRef CAS PubMed.
- K. P. Gierszal, J. G. Davis, M. D. Hands, D. S. Wilcox, L. V. Slipchenko and D. Ben-Amotz, J. Phys. Chem. Lett., 2011, 2, 2930–2933 CrossRef CAS.
- J. Ma, D. Alfe, A. Michaelides and E. Wang, J. Chem. Phys., 2009, 130, 154303–154304 CrossRef PubMed.
- S. Li, V. R. Cooper, T. Thonhauser, A. Puzder and D. C. Langreth, J. Phys. Chem. A, 2008, 112, 9031–9036 CrossRef CAS PubMed.
- T. P. Tauer, M. E. Derrick and C. D. Sherrill, J. Phys. Chem. A, 2005, 109, 191–196 CrossRef CAS PubMed.
- T. Takatani and C. D. Sherrill, Phys. Chem. Chem. Phys., 2007, 9, 6106–6114 RSC.
- E. M. Cabaleiro-Lago, J. Rodriguez-Otero and A. Pena-Gallego, J. Phys. Chem. A, 2008, 112, 6344–6350 CrossRef CAS PubMed.
- H. S. Biswal and S. Wategaonkar, J. Phys. Chem. A, 2009, 113, 12774–12782 CrossRef CAS PubMed.
- S. Hayashi, Y. Sugibayashi and W. Nakanishi, RSC Adv., 2016, 6, 49651–49660 RSC.
- L. Pauling, The Nature of the Chemical Bond, ed. L. Pauling, Cornell University Press, Ithaca, NY, 3rd edn, 1960 Search PubMed.
- S. Kozmon, R. Matuška, V. Spiwok and J. Koča, Phys. Chem. Chem. Phys., 2011, 13, 14215–14222 RSC.
- J. M. Hermida-Ramon and A. M. Grana, J. Comput. Chem., 2007, 28, 540–546 CrossRef CAS PubMed.
- C. D. Zeinalipour-Yazdi and D. P. Pullman, J. Phys. Chem. B, 2006, 110, 24260–24265 CrossRef CAS PubMed.
- T. Sato, T. Tsuneda and K. Hirao, J. Chem. Phys., 2005, 123, 104307 CrossRef PubMed.
- S. Tsuzuki, K. Honda, T. Uchimaru and M. Mikami, J. Chem. Phys., 2004, 120, 647–659 CrossRef CAS PubMed.
- A. Reyes, M. A. Tlenkopatchev, L. Fomina, P. Guadarrama and S. Fomine, J. Phys. Chem. A, 2003, 107, 7027–7031 CrossRef CAS.
- T. R. Walsh, Chem. Phys. Lett., 2002, 363, 45–51 CrossRef CAS.
- B. Collignon, P. N. M. Hoang, S. Picaud, D. Liotard, M. T. Rayez and J. C. Rayez, J. Mol. Struct.: THEOCHEM, 2006, 772, 1–12 CrossRef CAS.
- A chemical bond or an interaction between A and B is denoted by A–B, which corresponds to BPs between A and B in QTAIM. A-*-B is employed here to emphasize the presence of BCP on A–B, although A-•-B would be more suitable since dots are usually used to represent BCPs on BPs.
- Atoms in Molecules. A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, Oxford, UK, 1990 Search PubMed.
- C. F. Matta and R. J. Boyd, An Introduction to the Quantum Theory of Atoms in Molecules In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, Germany, 2007, ch. 1 Search PubMed.
- (a) R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068 CrossRef CAS; (b) R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS; (c) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS; (d) F. W. Biegler-König, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317–328 CrossRef; (e) R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9–15 CrossRef CAS; (f) T. H. Tang, R. F. W. Bader and P. MacDougall, Inorg. Chem., 1985, 24, 2047–2053 CrossRef CAS; (g) F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545–559 CrossRef; (h) F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489–1494 CrossRef PubMed.
- J. A. Dobado, H. Martînez-Garcîa, J. Molina and M. R. Sundberg, J. Am. Chem. Soc., 2000, 122, 1144–1149 CrossRef CAS.
- J. Molina and J. A. Dobado, Theor. Chem. Acc., 2001, 105, 328–337 CrossRef CAS.
- S. K. Ignatov, N. H. Rees, B. R. Tyrrell, S. R. Dubberley, A. G. Razuvaev, P. Mountford and G. I. Nikonov, Chem.–Eur. J., 2004, 10, 4991–4999 CrossRef CAS PubMed.
- S. K. Tripathi, U. Patel, D. Roy, R. B. Sunoj, H. B. Singh, G. Wolmershäuser and R. J. Butcher, J. Org. Chem., 2005, 70, 9237–9247 CrossRef CAS PubMed.
- (a) M. Yamashita, Y. Yamamoto, K.-Y. Akiba, D. Hashizume, F. Iwasaki, N. Takagi and S. Nagase, J. Am. Chem. Soc., 2005, 127, 4354–4371 CrossRef CAS PubMed; (b) Y. Yamamoto and K.-Y. Akiba, J. Synth. Org. Chem., Jpn., 2004, 62, 1128–1137 CrossRef CAS.
- W. Nakanishi, T. Nakamoto, S. Hayashi, T. Sasamori and N. Tokitoh, Chem.–Eur. J., 2007, 13, 255–268 CrossRef CAS PubMed.
- Interactions would be easily imaged by means of QTAIM if they can be defined as the corresponding bond paths (BPs), especially for experimental chemists. However, it is demonstrated that the detection of the BPs between two atoms in a molecule emerging from natural alignment of the gradient vector field of the one-electron density of a molecule is neither necessary nor a sufficient condition for the presence of a chemical bond between those atoms.48 In this connection, it is pointed out that the terms line paths (LPs) and line critical points (LCPs) should be used in place of BPs and BCPs, respectively.48b Consequently, the dynamic and static nature in this work should be regarded as the investigation performed at LCPs on LPs corresponding to the EH2-π interactions in the anthracene-π system. Nevertheless, BPs and BCPs are used in this paper for the discussion of the EH2-π(C14H10) interactions, similarly to the case of the previous discussion for the EH2-π(C6H6) and EH2-π(C10H8) interactions. The interactions expected between EH2 and π(C14H10) are clearly detected by BPs with BCPs which is another reason to use BPs and BCPs in this work.
- Critical points (CPs) are characterized by the rank (ω) and the signature (σ). The CPs of the species in the three-dimensional space are classified by ω = 3, which generally corresponds to all species. On the other hand, σ is defined by the simple algebraic sum of the signs of ∂2ρb(rc)/∂ri2 (ri = x, y and z for i = 1, 2 and 3, respectively), where the + and − signs of ∂2ρb(rc)/∂ri2 are counted as +1 and −1, respectively. Therefore, σ = −3, −1, 1 and 3 correspond to attractors (nuclei), bond critical points (BCPs), ring critical points (RCPs) and cage critical points (CCPs), respectively. Namely, BCP is characterized by (ω, σ) = (3, −1).17,18.
- (a) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050–10057 CrossRef CAS PubMed; (b) W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2008, 112, 13593–13599 CrossRef CAS PubMed.
- W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181–197 CrossRef CAS.
- W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423–7430 CrossRef CAS PubMed.
- W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293–1305 CrossRef CAS.
- See also, D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628 CrossRef.
- QTAIM-DFA is successfully applied to analyse weak to strong interactions in the gas phase. It could also be applied to the interactions in crystals and that in larger systems containing bioactive materials. The methodological improvement is inevitable to generate perturbed structures suitable for the systems.
- The concept of a dynamic molecular graph was recently proposed by Corte's-Guzma'n and co-workers through the investigation of the Born–Oppenheimer molecular dynamics (BOMD), which was exemplified by [Fe{C-(CH2)3}(CO)3]. The investigation illustrates the change in the behaviour of the molecular graph.49 The concept of the dynamic molecular graph would be closely related to that of the dynamic nature of interactions predicted by employing the perturbed structures generated with the normal coordinate of internal vibrations (NIV). In this treatment, the selected vibration for NIV must contain the motion of the interaction in question most effectively among all the zero-point internal vibrations. A structural catastrophe is confirmed not to occur for the perturbed and fully optimized structures for the elucidation of the dynamic nature of the interaction in question with NIV.35.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- For the 6-311G basis sets, see: (a) R. C. Binning Jr and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216 CrossRef; (b) L. A. Curtiss, M. P. McGrath, J.-P. Blaudeau, N. E. Davis, R. C. Binning Jr and L. Radom, J. Chem. Phys., 1995, 103, 6104–6113 CrossRef CAS; (c) M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511–516 CrossRef CAS For the diffuse functions (+ and ++), see: T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124 CrossRef.
- (a) C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef; (b) J. Gauss, J. Chem. Phys., 1993, 99, 3629–3643 CrossRef CAS; (c) J. Gauss, Ber. Bunsen-Ges. Phys. Chem., 1995, 99, 1001–1008 CrossRef CAS.
- The AIM2000 program (Version 2.04) is employed to analyze and visualize atoms-in-molecules: F. Biegler-König, J. Comput. Chem., 2000, 21, 1040–1048 CrossRef . See also ref. 24g.
- S. Hayashi, K. Matsuiwa, M. Kitamoto and W. Nakanishi, J. Phys. Chem. A, 2013, 117, 1804–1816 CrossRef CAS PubMed.
- The Cs structure of SH2–π(C14H10) (IIAAtc) was also obtained if optimized with MP2/BSS-F′, where 6-311+G(d,p) was employed for C and H in place of 6-311++G(d,p) in BSS-F′. However, the optimized structures with MP2/BSS-F′, which all had positive frequencies, were also C1, although they seem slightly closer to Cs.
- G. V. Baryshnikov, B. F. Minaev, V. A. Minaeva, A. T. Baryshnikova and M. Pittelkow, J. Mol. Struct., 2012, 1026, 127–132 CrossRef CAS; G. V. Baryshnikov, B. F. Minaev, V. A. Minaeva and V. G. Nenajdenko, J. Mol. Model., 2013, 19, 4511–4519 CrossRef PubMed; N. N. Karaush, G. V. Baryshnikov, V. A. Minaeva and B. F. Minaev, New J. Chem., 2015, 39, 7815–7821 RSC; N. N. Karaush, G. V. Baryshnikov and B. F. Minaev, RSC Adv., 2015, 5, 24299–24305 RSC.
- (a) R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396 CrossRef CAS PubMed; (b) C. Foroutan-Nejad, S. Shahbazian and R. Marek, Chem.–Eur. J., 2012, 18, 4982–4993 CrossRef PubMed; (c) M. García-Revilla, E. Francisco, P. L. A. Popelier and A. M. Pendás, ChemPhysChem, 2013, 14, 1211–1218 CrossRef PubMed; (d) Z. A. Keyvani, S. Shahbazian and M. Zahedi, Chem.–Eur. J., 2016, 22, 5003–5009 CrossRef CAS PubMed.
- F. Cortés-Guzmán, T. Rocha-Rinza, J. M. Guevara-Vela, G. Cuevas and R. M. Gómez, Chem.–Eur. J., 2014, 20, 5665–5672 CrossRef PubMed.
Footnotes |
| † Dedicated to Professor Marian Mikołajczyk (Professor at the Centre of Molecular and Macromolecular Studies, Polish Academy of Sciences in Lodz, Poland) on the occasion of his 80th birthday. |
| ‡ Electronic supplementary information (ESI) available: QTAIM-DFA approach, Cartesian coordinates for optimized structures of (EH2)⋯π(C14H10) (E = O, S, Se and Te). See DOI: 10.1039/c7ra04224h |
| This journal is © The Royal Society of Chemistry 2017 |