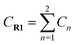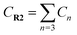A theoretical study of an electronically mismatched Diels–Alder cycloaddition

Abstract

Both (E)-1-methoxy-4-(prop-1-en-1-yl) benzene and isoprene exhibit electron-rich properties. However, a recent [4 + 2] cycloaddition between them shows quite high selectivity and productivity with low loading of the ruthenium photosensitizer ([Ru(bpz)₃²⁺]) under visible light. It is an interesting and untraditional D–A reaction because of the electronic mismatch between the diene and dienophile, which are impossible to react with each other theoretically. Presently, under the theoretical level of M062X/cc-pVTZ/LANL2DZ with the solvent effect of CH₂Cl₂, we design all the possible sixteen pathways in order to understand the most appropriate mechanism of this novel D–A cyclization. The results suggest that the triplet state ruthenium transfers the electrons of dienes to the catalyst by cycloaddition as a stepwise pathway. The analysis of substituent effects indicates that the necessary precondition for the D–A reaction is the electric matching. Finally, we obtain the approximate function between kinetic property and electronic structures. The reactivity can be controlled by tuning electronic structure and the molecular polarization through different substituents.

---

1. Introduction

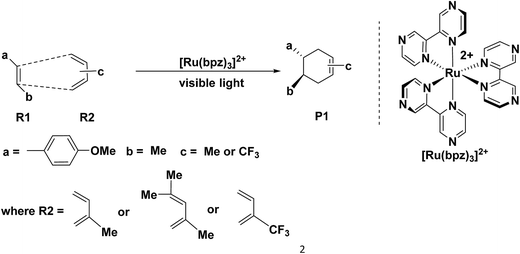
The Diels–Alder (D–A) reaction^1–4 is an effective method to synthesis six-membered rings with high selectivity,⁵ where the dominant interaction is the donation of electron density from the HOMO of diene to the LUMO of dienophile.^6,7 Therefore, it is common to apply [4 + 2] cycloaddition in the drug synthesis, such as those of the chalconoid natural products and the prenylflavonoid D–A natural products.^8–15 Generally, the classic D–A cycloadditions are reacted by electronic-deficient diene and electronic-rich dienophile synergetically.^16–19 However, there are a series of untraditional D–A reactions^20–31 between electronically mismatched components, such as the addition between 1,3-butadiene and ethylene (both electron-deficient components) or trans-1,3-butadiene and C60 or C70 (both electron-rich components). This novel D–A reaction always exhibits excellent selectivity but also requires stricter conditions than those of the traditional D–A reaction, where the components of dienes and dienophiles generally experience different transformations in order to satisfy the requirement of D–A reaction through the formation of free radical ions,^20,21 molecular electrical reversal^22–25 and polarity reversal.^26,27 In addition, synergetic^28,29 or stepwise pathways^30,31 are the two possible mechanisms of the electronically mismatched D–A reaction. The synergetic pathway is similar with that of the traditional D–A cycloaddition, where the dienes and the dienophiles are cyclized synergetically after the corresponding transformations, such as synchronical mechanism,²⁸ biradicaloidal one step-mechanism²⁹ and stepwise biradical mechanism.³⁰ However, in the stepwise pathway, there are one step-two stage mechanism, stepwise zwitterionic mechanism³¹ pointed out by Radomir Jasiński, where the products are formed through the chain-like ions^32–34 as intermediates, such as the combinations between the cation of penta-1,3-diene radical and ethylene.³⁵

Recently, Yoon's group³⁶ reported a special [4 + 2] cycloaddition between two electron-rich components for the synthesis of P1 through the formation of a free radical cation (Scheme 1). The free radical cation is generated from the charge transfer of the dienes (R1, (E)-1-(tert-butoxy)-4-(3,3-dimethylbut-1-en-1-yl) benzene), which is reacted with the catalyst of the ruthenium photosensitizer ([Ru(bpz)₃²⁺] showed in Scheme 1) under the visible light. Then, the cycloaddition exhibits ultra-high selectivity and yields (98%) under mild conditions. This is an untraditional D–A reaction between two electron-rich components under considerably mild conditions.

Scheme 1 The reported D–A reaction catalyzed by the visible-light photocatalyst.

Our study is focused on the kinetic properties of the electronically mismatched reaction based on Yoon's experiment. This issue mainly arises from the following three aspects. First of all, the electronic state of Ru in the ruthenium photosensitizer is confirmed by the comparison of the energies of the transformation among different valence states. The oxidation quenching and the reduction quenching are also compared to confirm the most possible pathway of the formation of free radical cations. Second, we design eight groups of reagents including the different isomers of dienes and dienophiles with the consideration of all the possible different optical activities and the steric effects. Then, the corresponding eight pathways, including synergetic and stepwise mechanisms, are designed and compared for further confirmation of the most possible mechanisms. Finally, we discuss the substituent effect in order to obtain the relationship between reactivity and the electronic properties of the reagents.

2. Methods

All the calculations are performed with Gaussian09 package.³⁷ The geometry optimizations of all species in this study are performed using M062X method with the basis set of cc-pVTZ³⁸ except ruthenium, for which the LANL2DZ basis set^39,40 is applied. We should note that the results including the energy barriers are underestimated slightly, which is proven using the DFT method.³¹ We obtain all the frequencies at the same theoretical level in order to calculate the thermodynamic properties. We confirm all the transition states by applying the intrinsic reaction coordinate (IRC)^41,42 method. The solvent effect (CH₂Cl₂) with SMD model⁴³ is considered on the basis of gas-phase optimized geometries.

3. Results and discussion

3.1 The charge transfer by ruthenium photosensitizer

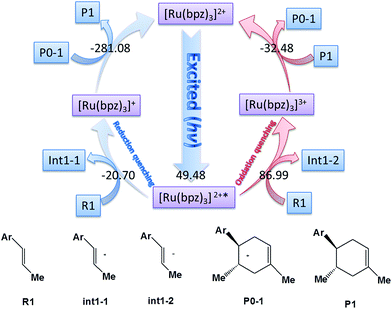
The catalyst [Ru(bpz)₃]²⁺ is the photosensitizer (See Scheme 1), where the center atom ruthenium can be excited by visible light in order to transfer the electrons before the cycloaddition. However, for ruthenium itself, there are different valence states (ruthenium 4d⁷/4d⁶/4d⁵) with different catalytic activities.

Yoon's study³⁸ provides fundamental understanding on the overall catalytic cycle and reasonable explanation of the transformation of the Ru catalysts. The structure of [Ru(bpz)₃]²⁺ is shown in Scheme 1, where the center atom is clearly in an octahedral field. We list and calculate the energies between all the different possible electronic valence states of ruthenium in Table 1. As for the valence state of 4d⁶ of ruthenium (Ru²⁺), the excitation of Ru²⁺ in [Ru(bpz)₃]²⁺ from a singlet ground state to the excited triplet state requires lower energy (49.48 kcal mol⁻¹). Furthermore, the exited triplet state of [Ru(bpz)₃]²⁺* appears to have the highest chemical potential in the transformations, which suggests its highest activity of catalysis. Therefore, with visible light radiation, the catalyst [Ru(bpz)₃]²⁺ should be excited to be [Ru(bpz)₃]²⁺* to transfer electrons from the reactants in quenching. This is consistent with the experiment that [Ru(bpz)₃]²⁺* plays an important role in transferring the electrons of the reagents to form the free radical ions for the electronically mismatched D–A reaction.

Table 1 The possible transformations of the electronic states of ruthenium in the octahedral field^a

Valence state	Excitation	Transformation of electronic states	ΔG (kcal mol^−1)
a *Means the excited states of the atom.
4d^7	Ru^+ → Ru^+*	(t2g)^6(eg)^1 → (t2g)^5(eg)^2	44.90
4d^6	Ru^2+ → Ru^2+*	(t2g)^6(eg)^0 → (t2g)^5(eg)^1	49.48
		(t2g)^6(eg)^0 → (t2g)^4(eg)^2	106.84
4d^5	Ru^3+ → Ru^3+*	(t2g)^5(eg)^0 → (t2g)^4(eg)^1	57.00
		(t2g)^5(eg)^0 → (t2g)^3(eg)^2	114.14

---

The charge transfer between different electronic states
Ru^2+ → Ru^+	(t2g)^6(eg)^1 → (t2g)^6(eg)^0	−90.17
Ru^2+* → Ru^+	(t2g)^6(eg)^1 → (t2g)^5(eg)^1	−139.65
Ru^2+* → Ru^3+	(t2g)^5(eg)^1 → (t2g)^5(eg)^0	−107.34

---

There are two different pathways to quench [Ru(bpz)₃]²⁺* in order to transfer the charge of reagents and accomplish the cyclization of the catalysis to regenerate the ground state [Ru(bpz)₃]²⁺. We compare the Gibbs free energies of the two possible ways of quenching of the excited [Ru(bpz)₃]²⁺* in Fig. 1. One is the oxidation quenching when it reacts with H–L (for example) to form the anion of int1-2 with the change of Gibbs free energy of 86.99 kcal mol⁻¹. The other one between [Ru(bpz)₃]²⁺* and R1 is the reduction quenching that requires a free energy of −20.70 kcal mol⁻¹ to generate the cation [Ru(bpz)₃]⁺. The continuous D–A reaction releases an energy of −281.08 kcal mol⁻¹ to form the product P1, suggesting that the reduction quenching with the formation of free radical cation is advantageous to the electronic migration.

Fig. 1 The possible pathways of the quenching of [Ru(bpz)₃]²⁺*with different valence states. The values in the figure are the Gibbs Free energies of the corresponding reactions with the units of kcal mol⁻¹. The [Ru(bpz)₃]²⁺* means the triplet state of the center atom of ruthenium.

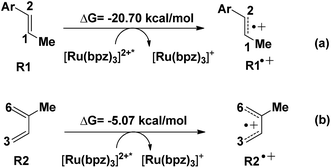
Another aspect is that both R1 (dienophile) and R2 (diene) are possibly transformed to the corresponding free radical cations R1˙⁺ and R2˙⁺ in the quenching of [Ru(bpz)₃]²⁺* (see Scheme 2), where the molar Gibbs free energies of the two reactions are −20.7 and −5.07 kcal mol⁻¹, respectively. Thus, we can conclude that R1˙⁺ is easier to be generated than R2˙⁺ thermodynamically.

Scheme 2 The ionization of the R1 (dienophiles) and R2 (dienes).

The NBO atomic charges of the reactive sites (C1/C2 of dienophile and C3/C6 of diene) have been listed in Table 2. R1 and R2 both appear to have electron-rich properties from the results. This electronically mismatched characters are changed after the charge transferring with [Ru(bpz)₃]²⁺*. The charges on C2 increased from −0.26 to −0.01 a.u. after the transformation, where the polarization drops the electronic density of the electron-acceptor. Clearly, R1˙⁺ is more susceptible to a nucleophilic attack from R2, which is more electronegative than R2˙⁺. This is also consistent with the results of the HOMO–LUMO gaps, where the lowest gap of 0.14 eV (just corresponding to the reaction between R1˙⁺ and R2) suggests the most reactivity. Our story of this untraditional [4 + 2] cycloaddition starts from R1˙⁺ (int1-1 below) combined with R2.

Table 2 The NBO charge, HOMO–LUMO gap of R1, R1˙⁺, R2 and R2˙⁺

Reagents	NBO charge (a.u)	Reaction under the catalyst	HOMO–LUMO gap (eV)
	C1/C2(R1) or C3/C6(R2)
R1	−0.20/−0.26	R1 + R2	0.20
R1˙^+	−0.21/−0.01	R1 + R2˙^+	0.29
R2	−0.41/−0.43	R1˙^+ + R2	0.14
R2˙^+	−0.16/−0.13	R1˙^+ + R2˙^+	0.23

---

3.2 The mechanism of the cyclization

The theoretical study is based on the experimental results, where the reagents are (1R,2S)-R1˙⁺ (denoted as int1-1 below) and R2 to generate the product (1R,2S)-P1. Due to the optical activities of the dienophile and the different substitution sites of –CH₃ on the diene, there are two possible structures for R1˙⁺ (cis/trans conformation of R1˙⁺) and four combination ways between each R1˙⁺and R2, which results in eight possible conformations of the products in total (Fig. S1† and Table 3). We point out and compare the stepwise and synergetic mechanisms for all the eight possible pathways (showed in Fig. 2a and S2–S8†) to confirm the most possible mechanism among them. All the optimized structures in Fig. 2a are shown in Fig. 2b.

Table 3 The energy barriers of the stepwise and synergetic pathways, the Gibbs free energies of the transformations from [P0–n]˙⁺ to Pn (n = 1–8) for all the eight possible pathways

Product (Pn)	Reactants	Stepwise		Synergetic	[P0–n]˙^+ → Pn
		Step 1	Step 2		R1˙^+^c	[Ru(bpy)3]^+
a Means the methyl connects with C5 atom of the diene.b Means the methyl connects with C4 atom of the diene.c R1˙^+ represents the corresponding free radical cations in 2nd row.
P1	(1R,2S)-R1˙^+ + R2 (5-Me)^a	6.26	1.60	18.93	−30.14	−53.62
P2	(1S,2R)-R1˙^+ + R2 (5-Me)	7.30	0.75	16.89	−28.80	−57.58
P3	(1S,2S)-R1˙^+ + R2 (5-Me)	7.19	1.15	17.58	−31.55	−60.33
P4	(1R,2R)-R1˙^+ + R2 (5-Me)	7.70	2.82	18.10	−28.16	−56.94
P5	(1S,2S)-R1˙^+ + R2 (4-Me)^b	11.59	5.54	13.75	−32.85	−61.62
P6	(1S,2R)-R1˙^+ + R2 (4-Me)	6.86	2.87	16.55	−29.14	−57.92
P7	(1R,2S)-R1˙^+ + R2 (4-Me)	6.76	2.26	16.85	−28.06	−56.84
P8	(1R,2R)-R1˙^+ + R2 (4-Me)	7.67	3.88	16.81	−29.31	−58.08

---

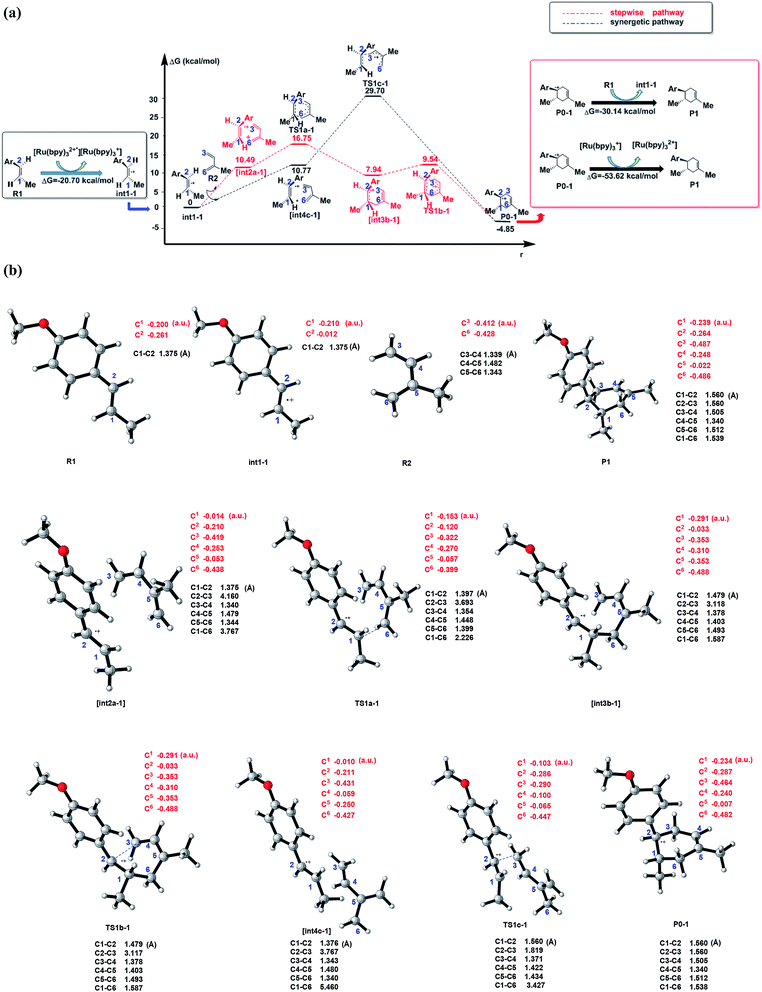Fig. 2 (a) Schematic energy profiles of the C–C cycloaddition reaction between R1˙⁺(dienophile) and R2 (diene). The red line is designed as the stepwise pathway and the black line is regarded as the synergetic pathway. The charge transformation to match the electronic properties is showed in the black box (start of cyclization) and red box (termination of the cyclization). [int2a-1] and [int4c-1] are the pre-reaction compounds after the molecular orientation in the corresponding pathways, which are stationary points on the potential energy surface. (b) The optimized structures, typical bond lengths(black) and NBO atomic charges (red) of all the stable states in (a) and transition states (by using CYLview⁴⁴).

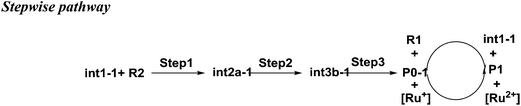
As shown in Scheme 3, there are three steps and two intermediates from the cation of int1-1 to the product of P0–1 in the stepwise pathway. It requires 10.49 kcal mol⁻¹ for the molecular orientation from int1-1 + R2 to int2a-1 in step 1. The atomic charges on C1 and C6 are −0.01 and 0.44 a.u. with the distance of 3.77 Å in the molecule of int2a-1. The first nucleophilic attack is triggered between C1 and C6 to form the intermediate int3a-1 through the transition state of TS1a-1 in step 2, wherein, the atom of C6 (a stronger nucleophile than C3 in the dienes) connects with the electropositive atom of C1 first (Fig. 2a). It is an exothermic step with the reaction enthalpy of 8.81 kcal mol⁻¹. The energy barrier from int2a-1 to TS1a-1 is 6.26 kcal mol⁻¹, which is the rate-determining step in the entire stepwise pathway. The rate constant can be given by 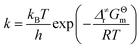on the basis of the transition state theory (TST), which is about 1.6 × 10⁸ s⁻¹ at the temperature of 298.15 K. The NBO charges of C1/C6/C2/C3 in int2a-1 are −0.01/−0.43/−0.21/−0.41 a.u. respectively. The atomic charge polarizes from −0.01 a.u. to −0.29 a.u. on C1 and slightly drops from −0.43 a.u. to −0.48 a.u. on C6 from int2a-1 to int3b-1 with the hybridization transformations from sp² to sp³ for both C1 and C6. The polarized bond of C1=C2 affects the continuous connection between C2 and C3, where the atomic charges on C2 and C3 are 0.03 a.u. and −0.35 a.u., respectively. Then, the product of P0–1 cation is formed through the transition state of TS1b-1 from the intermediate int3b-1. The energy barrier is only 1.60 kcal mol⁻¹ with the reaction potential energy of 12.79 kcal mol⁻¹ in step3, which means the cyclization is highly spontaneous and irreversible. Similar to TS1a-1, the hybridization of both C2 and C3 transforms from sp² to sp³ in TS1b-1 to form P0–1, where both the bond angles of C3–C2–C1 and C2–C1–C6 are 110° as per our calculation. The bond lengths and charges are averaged on the ring in P0–1. The charges of C1/C6/C2/C3 in P0–1 are averaged as −0.23/−0.43/−0.28/−0.46 a.u. respectively.

Scheme 3 The stepwise pathway from int1-1 to P1.

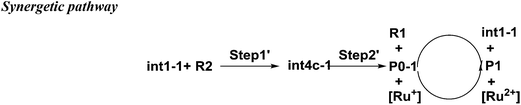
There is another pathway from int1-1 to the cation of P0–1 as shown in Scheme 4. The schematic energy surface of synergetic mechanism is shown as the black dashed line in Fig. 2a. Similar to the stepwise pathway, there is a molecular orientation to form int4c-1 with the energy of 10.77 kcal mol⁻¹ in step 1, where C2 atom gets closer to C3 atom. The distance between C2 and C3 is 3.76 Å. The NBO charges of C1/C6/C2/C3 in int4-1 are 0/−0.43/−0.21/−0.43 a.u., respectively, which is similar to that of int2a-1. Then, the nucleophilic attack by the diene directly (step 2′) results in the product P0–1. Both C3 and C6 attack C1 and C2 at the same time to perform the cyclization through the transition state of TS1c-1 with the barrier of 18.93 kcal mol⁻¹, which is almost three times higher than the barrier of the key step of the stepwise pathway. Therefore, the rate constant at 298.15 K is 0.08 s⁻¹ based on the TST, which is much slower than that of the stepwise pathway. Step 2′ is an exothermic reaction with the enthalpy of −15.62 kcal mol⁻¹. Compared with the two energy barriers, the stepwise pathway should be the advantageous mechanism of this untraditional D–A cyclization.

Scheme 4 The synergetic pathway from int1-1 to P0.

There are two pathways for the cation of P0–1 to obtain an electron by reacting with the dienophiles (R1) or [Ru(bpy)₃]⁺ to transform to an electroneutral product as the red box shown in the Fig. 2a. The Gibbs free energies of the transformations are −30.14 kcal mol⁻¹ for the reaction P0–1/R1 and −53.62 kcal mol⁻¹ for P0–1/[Ru(bpy)₃]⁺. Both the reactions are the exothermic and irreversible. The lower Gibbs free energy of the reaction between P0–1 and [Ru(bpy)₃]⁺ suggests that P0–1 prefers reacting with the Ru catalyst rather than int1-1 in the transformation. Therefore, there are two roles of the photosensitizer [Ru(bpz)₃]²⁺ in the D–A reaction. One is as the electron-acceptor to obtain the electron from R1 to prepare an electron-deficient component. The other one is as the electron-donor to give an electron to P0–1 to accomplish the cyclization and the catalysis.

We also carried out a similar calculation for the other seven pathways, and all the energy barriers are listed in Table 3. The schematic energy profiles are listed in the ESI.† All the sixteen pathways suggest that the stepwise pathway is more advantageous than the synergetic pathway in the electronically mismatched [4 + 2] cycloaddition, and the rate-determining step is always the first step in the stepwise pathway. The different energy barriers are caused by the steric effects of the reagents. Based on the calculations of the Gibbs free energies, the catalyst [Ru(bpz)₃]²⁺ accelerates the entire cyclization as the charge carrier.

In addition, Yoon's group reported that the productivity of this cycloaddition is greatly improved from 46% to 98% after the introduction of the ruthenium photosensitizer and oxygen.³⁶ We consider different combinations between O₂-R1⁺ (A1–A3 in Scheme S1†), O₂-P0–1 (B1–B3 in Scheme S1†) and O₂-[Ru(bpz)₃]⁺ (C1–C2 in Scheme S1†) in order to study the effects of oxygen (in ESI†). The thermodynamic results show that all the reactions between the oxygen and the free radical of reactant (R1⁺) or product (P0–1) of the cycloaddition are endothermic and non-spontaneous processes, which means that oxygen is not necessary for the reaction. This is consistent with the experiment indicating that this D–A cycloaddition can proceed without oxygen. However, both the negative enthalpies and Gibbs free energies of the reaction C1 and C2 (see Scheme S1 in ESI†) suggest that oxygen is easy to combine with the ruthenium catalyst as the charge carrier. Hence, oxygen is a catalyst in the charge transferring of the transformation from Ru⁺ to Ru²⁺, which affects the selectivity and the productivity of the cycloaddition.

3.3 The substituent effect of electronically mismatched [4 + 2] cycloaddition

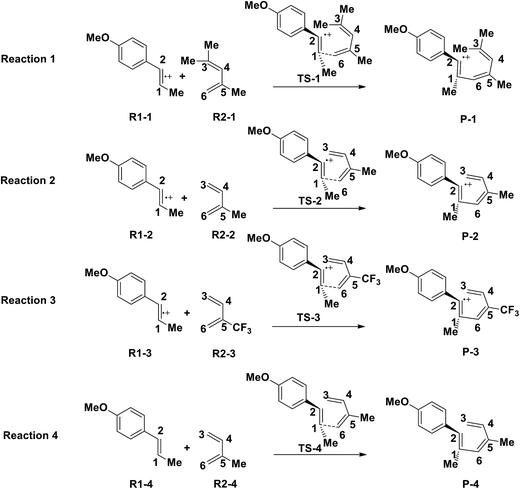
Yoon's D–A reaction is cyclized by the formation of the free radical cations of dienophile with the catalyst of the photosensitizer [Ru(bpz)₃]²⁺. From the results above, it can be deduced that the electronic properties of the diene and the dienophile affect the cyclization directly. We design and compare four D–A reactions to obtain the different reactivities affected by substituents. The reactions (reaction (1)–(3) in Scheme 5) are between the free radical cations of dienophiles (R1, similar int1-1 before) and dienes (R2) with different substituents. Compared with the experimental reaction (reaction (2)), we introduce the other two methyls as electron donors in R2-1 and a trifluoromethyl as the electron acceptor in R2-3. In addition, we hypothesize that the reaction proceeds between the dienophiles (R1) and dienes (R2) directly without any charge-transferring as in reaction (4). For convenience, we choose the rate-determining steps in the corresponding stepwise pathways, where the cyclization starts from the combination between C1 and C6 in all the four simulations. The relative results are listed in Table 4. All the optimized structures including the atomic charges are listed in Fig. S9.†

Scheme 5 The rate-determining steps of proposed D–A reactions with substituent effects.

Table 4 The NBO analysis of the reagents, reaction enthalpies and energy barriers

Reaction	NBO atomic charge^a (a.u.)			Wiberg bond index		H–L gap^c (G, eV)	ΔrHm (kcal mol^−1)	Barrier (E) (kcal mol^−1)
			Dchar^b	C1–C2 (R1)	C6–C5 (R2)
a 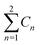means the summary of the NBO charge of C1 and C2 in R1. means the summary of the NBO charge of all the atoms except hydrogen's in R2.b Dchar means the NBO atomic charge difference of 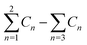.c H–L gap means HOMO–LUMO gap of the corresponding reaction.
1	−0.22	−2.86	2.64	1.54	1.86	0.13	−3.05	15.53
2 (exp)	−0.22	−1.86	1.64	1.54	1.85	0.14	−4.09	16.76
3	−0.22	−1.19	0.97	1.54	1.84	0.16	−4.45	20.52
4	−0.46	−1.86	1.4	1.84	1.85	0.20	−55.72	41.52
Fitting equation based on E = E(G, Dchar):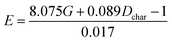

---

Comparing reaction (4) with the other three reactions, there are two electron-rich reagents (−0.46 a.u. of C_R1 and −1.86 a.u. of C_R2) in reaction (4) with the highest energy barrier of 41.5 kcal mol⁻¹. Essentially, there should be no reaction between R1-4 and R2-4 in the experiment. Therefore, first of all, electrical matching between the two components is a necessary precondition for the D–A reaction. Furthermore, we decrease the electron density of dienophiles to satisfy the requirement of electrical matching. As for reactions (1)–(3), the differences between dienes and dienophiles affect the kinetic properties, where larger the charge differences, lower the energy barriers. Third, the strong electro-negativities of the reactive positions suggest the abilities of the nucleophilic attack, which can be reflected from the covalent properties. From the analysis of covalent properties, the Wiberg bond index of C1–C2 is reduced from 1.84 in R1-4 to 1.54 after the charge transferring from R1-1 to R1-3, which corresponds to a polarization of C1–C2 for an easier nucleophilic attack. However, the covalent component of C6–C5 bond gradually decreases with the reduction of the substituents of the electron-donor. The HOMO–LUMO gaps, reaction enthalpies and energy barriers of the four compounds all follow similar regulations with the different substituents. The reaction enthalpies indicate that the reactions with lower activation energies are reversible. Considering the possible influencing factors of energy barriers, we approximately fit the equation among the barriers (E), HOMO–LUMO gaps (G) and the charge differences (D_char) in Table 4. Based on the equation and experimental results, a possible electrical matching D–A reaction proceeds under mild conditions (approximately with the barrier of 25 kcal mol⁻¹), which requires the charge difference at least 3.31 a.u. with the HOMO–LUMO gap around 0.14 eV. The [4 + 2] cycloaddition is possibly controlled in a mild condition by tuning the difference of density for the dienes and dienophiles by introducing different substituents into the reagents.

4. Conclusion

The reaction between (E)-1-methoxy-4-(prop-1-en-1-yl)benzene and isoprene is an electronically mismatched D–A reaction but still exhibits quite high selectivity and productivity catalyzed by the ruthenium photosensitizer [Ru(bpz)₃²⁺] to form the product (1R,2R)-4′-(tert-butoxy)-4-(tert-butyl)-2-methyl-1,2,3,6-tetrahydro-1,1′-biphenyl.

With the participation of oxygen, there is a charge transfer process first in the transformation from [Ru(bpz)₃]⁺ to [Ru(bpz)₃]²⁺. Then, the catalyst of the ruthenium photosensitizer, as the charge carrier, triggers and terminates the cyclization by tuning the electrical properties of the components. The most advantageous mechanism should be the stepwise mechanism on the basis of our calculations. Based on the results, the first step in the stepwise pathway is the rate-determining step with the energy barrier of 6.26 kcal mol⁻¹ and with the transformation rate of 1.6 × 10⁸ s⁻¹ theoretically, which is consistent with the experiment.

From the analysis of substituent effects, we conclude that the necessary precondition for [4 + 2] cycloaddition is electric matching. Then, the reactivity is determined by both the electronic densities of the reactive sites and the charge differences between dienes and dienophiles. Moreover, D–A reaction could be controlled by the substituent effects to exhibit excellent reactivity kinetically (low energy barrier) and thermodynamically (reversibility). We hope our study will be helpful to understand the mechanism of such untraditional [4 + 2] cycloaddition and its future application.

Acknowledgements

This study is supported by the Natural Science Foundation of Anhui Province, the Natural science research project of Anhui Province (KJ2016A032) and the opening project of State Key Laboratory of Science and Technology (Beijing Institute of Technology, KFJJ16-11M).

References

1. H. Pellissier, Tetrahedron Lett., 2015, 71, 8855–8869.
2. W. Carruthers, Cycloaddition Reactions in Organic Synthesis, PERGAMON edu., BPPC wheatons Ltd., Exeter Great Britain, 1990.
3. H. P. Hu, Y. B. Liu, J. Guo, L. L. Lin, Y. L. Xu, X. H. Liu and X. M. Feng, Chem. Commun., 2015, 51, 3835–3837.
4. O. Diels and K. Alder, Justus Liebigs Ann. Chem., 1928, 460, 98–122.
5. S. Kotha, A. S. Chavan and D. Goyal, ACS Comb. Sci., 2015, 17, 253–302.
6. K. Juhl and K. A. J. ørgensen, Angew. Chem., 2003, 42, 1498–1501.
7. L. R. Domingo, J. A. Sáez and S. R. Emamian, Org. Biomol. Chem., 2015, 13, 2034–2038.
8. R. Mose, M. E. Jensen, G. Preegel and K. A. Jørgensen, Angew. Chem., 2015, 127, 13834–13838.
9. J. Q. Gu, E. J. Park, J. S. Vigo, J. G. Graham, H. H. Fong, J. M. Pezzuto and A. D. Kinghorn, J. Nat. Prod., 2002, 65, 1616–1620.
10. P. Tuntiwachwuttikul, O. Pancharoen, L. Reutrakul, T. Aust and V. Byrne, J. Chem., 2010, 132, 7514–7518.
11. C. S. Sevov and O. Wiest, J. Org. Chem., 2008, 73, 7909–7915.
12. S. Ueda, T. Nomura, T. Fukai and J. Massumoto, Chem. Pharm. Bull., 1982, 30, 329–388.
13. F. Ferrari, F. D. Monache and R. A. D. Lima, Tetrahedron Lett., 1998, 47, 1165–1166.
14. C. Qi, H. Cong, K. J. Cahill, P. Müller, R. P. Johnson and J. A. Porcojr, Heterocycles, 2013, 52, 8345–8348.
15. T. Nomura and T. Fukai, Chem. Pharm. Bull., 1980, 28, 2809–2812.
16. R. Chopra, K. Sharma, M. Kumar and V. Bhalla, J. Org. Chem., 2016, 81, 1039–1046.
17. J. Luo, M. F. Xu, R. Z. Li, K. W. Huang, C. Y. Jiang, Q. B. Qi, W. D. Zeng, J. Zhang, C. Y. Chi, P. Wang and J. S. Wu, Chem. Rev., 2013, 136, 265–272.
18. S. Gupta, M. I. Alam, T. S. Khan, N. Sinhaand and M. A. Haider, RSC Adv., 2016, 6, 60433–60445.
19. S. Sato, Y. Maeda, J. D. Guo, M. Yamada, N. Mizorogi, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2013, 135, 5582–5587.
20. C. X. Cui and Y. J. Liu, J. Phys. Org. Chem., 2015, 28, 281–289.
21. U. Haberl, O. Wiest and E. Steckhan, J. Am. Chem. Soc., 1999, 5, 2859–2865.
22. C. X. Cui and Y. J. Liu, J. Phys. Org. Chem., 2014, 27, 652–660.
23. W. J. Wever, J. W. Bogart, J. A. Baccile, A. N. Chan, F. C. Schroeder and A. A. Bowers, J. Am. Chem. Soc., 2015, 137, 3494–3497.
24. D. L. A. Scarborough, R. Kobayashi, C. D. Thompson and E. I. Izgorodina, Int. J. Quantum Chem., 2015, 115, 989–1001.
25. H. Kawakami, H. Okada and Y. Matsuo, Org. Lett., 2013, 15, 4466–4469.
26. N. A. Valley and O. Wiest, J. Org. Chem., 2006, 72, 559–566.
27. S. Q. Zhu and M. Rueping, Chem. Commun., 2012, 48, 11960–11962.
28. R. Jasiński, React. Kinet., Mech. Catal., 2016, 119, 49–57.
29. D. A. Singleton, B. E. Schulneier, C. Hang, A. A. Thomas, S. W. Leung and S. R. Merrigan, Tetrahedron, 2001, 57, 5149–5160.
30. R. Jasiński, Comput. Theor. Chem., 2014, 1046, 93–98.
31. R. Jasiński, M. Kubik, A. Łapczuk-Krygier, A. Kácka, E. Dresler and A. Boguszewska-Czubara, React. Kinet., Mech. Catal., 2014, 113, 333–345.
32. D. Seebach, X. Y. Sun, C. Sparr, M. O. Ebert, W. B. Schweizer and A. K. Beck, Helv. Chim. Acta, 2012, 95, 1064–1078.
33. C. S. Sevov and O. Wiest, J. Org. Chem., 2008, 73, 7909–7915.
34. J. J. Murphy, R. B. Driver, R. Walsh and J. C. Stephens, J. Chem., 2016, 93, 1626–1630.
35. J. W. Ren, Z. F. Zhou, J. A. Xiao, X. Q. Chen and H. Yang, Eur. J. Org. Chem., 2016, 2016, 1264–1268.
36. S. Lin, M. A. Ischay, C. G. Fry and T. P. Yoon, J. Am. Chem. Soc., 2011, 133, 19350–19353.
37. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision A, Gaussian, Inc., Wallingford CT, 2009.
38. A. S. B. Miehlich, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206.
39. C. T. Lee, W. Yang and R. G. T. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
40. C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert and L. S. Sunderlin, J. Phys. Chem. A., 2001, 105, 8111–8116.
41. S. M. Stevenson and E. M. Ferreira, Angew. Chem., 2015, 54, 6506–6510.
42. K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
43. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem., 2009, 113, 6378–6396.
44. C. Y. Legault, CYLview, Université de Sherbrooke Quebec, Canada, 2009.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04480a

---