Open Access Article
Open Access ArticleComplications in complexation kinetics for lanthanides with DTPA using dye probe molecules in aqueous solution†
K. Larsson *a,
T. D. Cullena,
S. P. Mezyk
*a,
T. D. Cullena,
S. P. Mezyk a,
R. G. McDowell
a,
R. G. McDowell b and
L. R. Martin‡
b and
L. R. Martin‡
 b
b
aDepartment of Chemistry and Biochemistry, California State University Long Beach, 1250 Bellflower Blvd., Long Beach, CA 90840, USA. E-mail: Stephen.Mezyk@csulb.edu; larsson.kristian@gmail.com; Tel: +1-562-985-4649
bAqueous Separations and Radiochemistry Department, Idaho National Laboratory, Idaho Falls, ID 83415, USA. E-mail: martinlr@ornl.gov; Rocklan.McDowell@inl.gov
First published on 17th May 2017
Abstract
The complexation kinetics for the polyaminopolycarboxylic ligand DTPA to lanthanides in acidic aqueous solution were investigated using the dye ligand displacement technique and stopped-flow spectroscopy. Significant rate differences were obtained for different dye probes used, indicating that the kinetics of the dissociation of the dye molecule significantly impacts the overall measured kinetics when using this common methodology. The conditions of the solution also influenced the dye-lanthanide-DTPA interactions, which reconciled previously disparate data in the literature.
Introduction
The solution complexation chemistry of the polyaminopolycarboxylic acid DTPA1–4 (di-2-ethylenetriamine-N,N,N′,N′′,N′′-pentaacetic acid) with the 4f lanthanide and 5f actinide elements is of interest to a variety of research communities, including used nuclear fuel reprocessing by the TALSPEAK (Trivalent Actinide Lanthanide Separations by Phosphorus-reagent Extraction from Aqueous Komplexes) process,5–9 chelation therapy10,11 various electronic and magnetic applications,12 and for research of contrast agents in magnetic resonance imaging (MRI).13–16 As such, research has been continued to the present day to determine reliable thermodynamic stability constants for lanthanide (Ln) and actinide (An) DTPA complexes.17–24 However, there still remains considerable uncertainty about the kinetics involved in the DTPA complexation of the 4f series ions, with the multiple species present (DTPAH5−xx− and buffer species) having a significant effect on the rate of complexation. This can considerably complicate the chemistry at a large-scale, particularly in the TALSPEAK extraction system. TALSPEAK utilizes DTPA in an aqueous phase containing 0.5–2.0 M lactic acid buffer to “hold back” actinide elements, while the lanthanide elements are extracted by the ion-exchanging extractant HDEHP (bis-(2-ethylhexyl) phosphoric acid) into an organic diluent. However, even after many decades of investigation recent reports addressing fundamental aspects of TALSPEAK chemistry have found that metal distribution data are not always reliably modelled by the established mono- and biphasic thermodynamic equilibria.7,9 Moreover, the TALSPEAK separation suffers from poor phase transfer kinetics, which has been associated with the slow rate of the Ln-DTPA complex dissociation in the aqueous phase at the liquid–liquid interface.9,25To date there have been few studies that investigated the kinetics for DTPA complexation and decomplexation reactions with the lanthanides.3,26,27 Each of these used dye probe molecules. The complexation of Gd(III) with DTPA was investigated27 using a high-pressure stopped-flow spectrophotometer. Kinetic measurements were made based upon DTPA ligand substitution reactions for Gd(III) ions pre-complexed with the dye arsenazo III (3,6-bis(o-arsonophenylazo)-4,5-dihydroxyl-naphthalene-2,7-disulfonic acid). Under these conditions it was proposed there were two metal-dye complexes present, with the Gd(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsenazo III stoichiometry of 1
arsenazo III stoichiometry of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The observed kinetics were dual-exponential, which was attributed to the separate DTPA substitution kinetics for these two complexes. However, these observed kinetics were also found to be independent of DTPA concentration, which the researchers attributed this to the rate-limiting step being the intramolecular decomplexation of Gd(III)
2. The observed kinetics were dual-exponential, which was attributed to the separate DTPA substitution kinetics for these two complexes. However, these observed kinetics were also found to be independent of DTPA concentration, which the researchers attributed this to the rate-limiting step being the intramolecular decomplexation of Gd(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsenazo III complex to produce the free arsenazo III dye by an acid-catalyzed mechanism. Their rate constant for DTPA complexation at pH 3.6 and 25 °C ([DTPA] = 10 mM, I = 0.3 M) was k = 0.33 s−1 for the 1
arsenazo III complex to produce the free arsenazo III dye by an acid-catalyzed mechanism. Their rate constant for DTPA complexation at pH 3.6 and 25 °C ([DTPA] = 10 mM, I = 0.3 M) was k = 0.33 s−1 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, and k = 0.04 s−1 for the 1
1 complex, and k = 0.04 s−1 for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex in an acetate buffer solution.
2 complex in an acetate buffer solution.
A subsequent investigation26 for Eu(III)-DTPA complexation found analogous dual-exponential reaction kinetics, even though the reported experimental conditions ensured almost all (>99%) the complexes were of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Eu(III)
2 Eu(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsenazo III stoichiometry. The temperature-dependent Eu(III) kinetics were again found to be acid-catalyzed, the Eu(III)-DTPA complexation was not strongly dependent upon external ionic strength over the range 0.05–0.25 M, and for this metal ion the faster component was dependent upon the DTPA concentration. The complexation rate constant for this reaction was described by the expression:
arsenazo III stoichiometry. The temperature-dependent Eu(III) kinetics were again found to be acid-catalyzed, the Eu(III)-DTPA complexation was not strongly dependent upon external ionic strength over the range 0.05–0.25 M, and for this metal ion the faster component was dependent upon the DTPA concentration. The complexation rate constant for this reaction was described by the expression:
| k1/s−1 = 7.08 + 1.44 × 105*[H+] | (1) |
This corresponds to an observed rate constant of k1 ≈ 43 s−1 for the Eu(III) complexation at pH 3.6. The overall DTPA complexation mechanism was proposed to be a combination of a rate-limiting, acid-catalyzed, loss of the first arsenazo III ligand followed by fast binding of the DTPA ligand, occurring simultaneously with the direct reaction of the DTPA with the Eu(III)-protonated arsenazo III species. The much faster kinetics for both pathways for Eu(III) as compared to Gd(III) was attributed to the much higher lability28 of the Eu(III) system.
A more recent kinetic study was performed by Nash et al.,3 where the arsenazo III ligand system was used to probe lanthanide complexation kinetics under TALSPEAK conditions with an aqueous phase containing 0.30 M lactate, and at a pH of 3.6. In contrast to the original two studies26,27 performed in the absence of lactate, this work reported only single exponential decay kinetics. These data were consistent with the assumption that the arsenazo III decomplexation was not the rate determining step of the measured reaction. Their comparative value for Eu(III) was k = 2.10 × 104 M−1 s−1, approximately five times faster than the equivalent second-order rate constant value determined by Shi et al.26 Varying the La(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsenazo III concentrations in the 50–100 μM range did not change the observed kinetics, and increasing the lactate concentration from 0.1 to 0.3 M gave no effect on the formation constant but a large change in dissociation rate constant.
arsenazo III concentrations in the 50–100 μM range did not change the observed kinetics, and increasing the lactate concentration from 0.1 to 0.3 M gave no effect on the formation constant but a large change in dissociation rate constant.
In order to further investigate the discrepancies between the three DTPA-lanthanide kinetic studies, and to verify the viability of the ligand-displacement methodology for measuring DTPA complexation and de-complexation rate constants, this study used stopped-flow spectrophotometry with multiple dye probe molecules to investigate lanthanide complexation under various aqueous solution conditions.
The primary data of this work were gathered for the dye molecule xylenol orange (2,2′,2′′,2′′′-((1,1-dioxido-3H-2,1-benzoxathiole-3,3-diyl)bis((6-hydroxy-5-methyl-3,1-phenylene) methylenenitrilo))tetraacetic acid) with DTPA for a range of the lanthanide(III) elements in a slightly acidic (pH 3.6) aqueous phase in order to be directly comparable to previous literature values. Xylenol orange was chosen as the main probe dye in this study due to its lower stability constant with europium than arsenazo III,29,30 which would be expected to minimize any potential impact on the dye decomplexation reaction kinetics.
Experimental
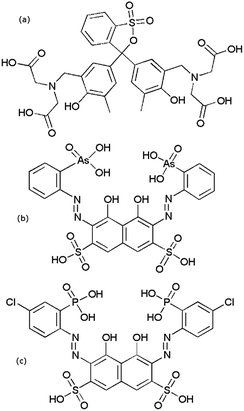
All commercial reagents were used as obtained. Lanthanide nitrate salts were prepared by reacting the relevant lanthanide oxide (99.999% Rare Earth Products) with 5.9 equivalents of nitric acid (Sigma Aldrich 99+%). The reaction mixture was filtered through a 0.2 μm syringe filter to remove any remaining solid. This solution was then diluted with 1 mM nitric acid solution. Solution concentrations were determined by ICP-MS. Working solutions were prepared by diluting these stock solutions to the appropriate concentration. Lanthanum and europium nitrate salts from Sigma-Aldrich (99.9%) were used for arsenazo III experiments. Arsenazo III disodium salt (Alfa Aesar), chlorophosphonazo III (bis(4-chloro-2-phosphonobenzolazo) chromotropic acid) (Sigma-Aldrich), xylenol orange tetrasodium salt (Alfa Aesar), and lactic acid 1.0 N (Alfa Aesar) were used as received. All solutions were made using ≥18 MΩ cm−1 water from a Millipore Milli-Q system. Stock solutions of DTPA (Strem Chemicals, 97%) were made and diluted as required. A DCTA (Fluka, monohydrate, 98.5%), 1,2-diaminocyclohexanetetraacetic acid, stock solution was prepared for a dye comparison experiment. Structures of the dyes are shown in Fig. 1.Solutions of dye-complexed lanthanide ions were made at a typical concentration of 50–60 μM for both the metal ion and the dye immediately before use. All solutions were pH adjusted to 3.6 using HClO4 or NaOH, unless otherwise stated. The change in pH upon solution mixing in the stopped flow spectrophotometer was negligible as confirmed by benchtop tests. UV-visible spectra were determined using either an Ocean Optics Red Tide USB650 Fiber Optic Spectrometer or a Shimadzu 1800 spectrophotometer over the range 200–900 nm. Spectra were collected using a 1.00 cm pathlength quartz cuvette at room temperature (23 ± 2 °C). Individual UV-visible absorption spectra for separate solutions of DTPA, metal ions, and the metal–xylenol orange complex measured at multiple metal ion concentrations showed that both free DTPA and metal–DTPA complexes had no significant absorbance over the studied wavelength range. The maximum absorption difference between the free dye and the metal-complexed dye was established before the kinetic measurements (see data in ESI†).
The lanthanide ion to xylenol orange stoichiometry is known to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at equivalent concentrations of dye and metal or in metal excess conditions.31,32 This was verified for Eu(III) at pH 3.6 by investigating the absorbance at 568 nm (see ESI†). Kinetic measurements were done using a Hi-Tech Scientific SF-61DX2 Stopped-Flow System using a high-pressure xenon lamp. The observed kinetics were analysed using Origin™ 6.0 software.
1 at equivalent concentrations of dye and metal or in metal excess conditions.31,32 This was verified for Eu(III) at pH 3.6 by investigating the absorbance at 568 nm (see ESI†). Kinetic measurements were done using a Hi-Tech Scientific SF-61DX2 Stopped-Flow System using a high-pressure xenon lamp. The observed kinetics were analysed using Origin™ 6.0 software.
Results and discussion
The kinetics of lanthanide ion complexation by DTPA were measured by monitoring the change in absorbance at 568 nm with time, as free DTPA was rapidly (deadtime ≤ 1.5 ms) mixed with the dye-complexed metal solution from two separate syringes. These kinetic experiments were conducted under pseudo-first-order conditions, where the initial DTPA concentration was kept in excess (approximately 10 fold or more) relative to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 dye-metal complex concentration. As the DTPA complexes the metal, the dye-metal complex releases the dye according to eqn (2) (omitting speciation and specific charges), allowing DTPA complexation of the free metal ion (eqn (3)). De-complexing the dye causes a decrease in the absorbance at the monitoring wavelength.
1 dye-metal complex concentration. As the DTPA complexes the metal, the dye-metal complex releases the dye according to eqn (2) (omitting speciation and specific charges), allowing DTPA complexation of the free metal ion (eqn (3)). De-complexing the dye causes a decrease in the absorbance at the monitoring wavelength.
 | (2) |
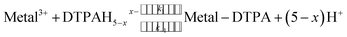 | (3) |
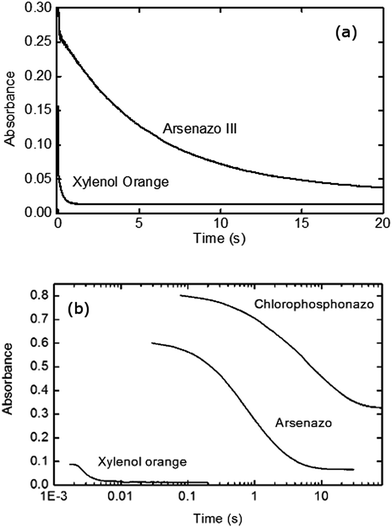
Initial stopped-flow experiments were performed to compare the influence of the dye choice. Fig. 2a shows the measured kinetics for xylenol orange and arsenazo III for Eu(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dye complexation kinetics with DTPA. Under these identical conditions it can readily be seen that the dye choice strongly influences the measured kinetic data, with significantly faster decay obtained for the less strongly complexed xylenol orange dye. To further investigate this finding an additional dye was investigated, chlorophosphonazo III, using a slower complexant (DCTA) to accentuate the difference between the dyes. The chlorophosphonazo III was, however, not stable at pH 3.6 so pH 4.25 was used (Fig. 2b). The large difference between the three dyes show that the dye decomplexation is the rate determining step, and not the rate of reaction of the complexant binding to the lanthanide.
dye complexation kinetics with DTPA. Under these identical conditions it can readily be seen that the dye choice strongly influences the measured kinetic data, with significantly faster decay obtained for the less strongly complexed xylenol orange dye. To further investigate this finding an additional dye was investigated, chlorophosphonazo III, using a slower complexant (DCTA) to accentuate the difference between the dyes. The chlorophosphonazo III was, however, not stable at pH 3.6 so pH 4.25 was used (Fig. 2b). The large difference between the three dyes show that the dye decomplexation is the rate determining step, and not the rate of reaction of the complexant binding to the lanthanide.
The impact of ionic strength on the metal–xylenol orange complex was also investigated. Increasing the ionic strength to I = 0.1 M impacted the absorption for the metal–xylenol orange complex, and reduced the absorbed light level to the point that kinetic measurements were unreliable at these low concentrations. These findings are consistent with previously reported data for xylenol orange complexed with zinc ions.33 Therefore, all xylenol orange data in this study were collected at lowest possible ionic strength values, i.e. no additional ionic strength matrix. Under the experimental conditions, I was dominated by the DTPA concentration and ranged up to I = 0.016 M. The data for xylenol orange showed an initial fast decay, k1, complete in approximately 100–200 ms, and then a much smaller (A2 < A1), slower decay, with rate constant k2. These kinetics were found to be described well by a dual-exponential decay function (eqn (4)).
| y = A1e−k1t + A2e−k2t + B | (4) |
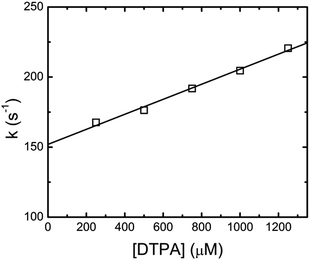
This kinetic analysis is in good agreement with the earlier study by Shi et al., but different to the first order kinetics reported by Nash et al.3 By fitting eqn (4) to the xylenol orange data, it was found that the faster component was dependent upon DTPA concentration. Plotting the fitted fast-component as pseudo-first-order rate constants as a function of DTPA concentration gave straight line plots. These data are shown in Fig. 3 for Eu(III). The slope of this plot gives a value of k1 = (5.48 ± 0.64) × 104 M−1 s−1 at 26.1 °C. The intercept of this pseudo first order kinetics plot corresponds to the assumed decomplexation rate k−1 of eqn (2). Under these conditions a value for the Eu(III)-dye-DTPA decomplexation rate constant of k−1 = 154.0 ± 5.4 s−1 was determined. The k1 and k−1 values for the lanthanides of this study are summarized in Table 1.
| Metal | Temp. (K) | k1103 (M−1 s−1) | k−1 (s−1) |
|---|---|---|---|
| Lu | 300.3 | 13.3 ± 0.5 | 9.0 ± 0.5 |
| Er | 296.2 | 10.2 ± 0.4 | 9.2 ± 2.6 |
| Ho | 296.2 | 11.6 ± 0.5 | 12.9 ± 2.9 |
| Tb | 296.3 | 28.3 ± 3.4 | 31.4 ± 2.3 |
| Eu | 299.2 | 54.8 ± 6.4 | 154.0 ± 5.4 |
Rate constants for the slower exponential decay component, with rate constant k2, were also calculated (see ESI†). These values showed a continuous decrease across the lanthanide series. In terms of assigning a specific reaction mechanism for the second, slower, rate constant (k2) we follow the previous literature for arsenazo III, where this component was attributed to a species containing an additionally chelated dye ligand.26 The kinetic trace of the second ligand was less than 5% of the total reactivity, consistent with the expected small percentage of higher order complexes (see ESI†) for conditions of excess dye to lanthanide concentrations.
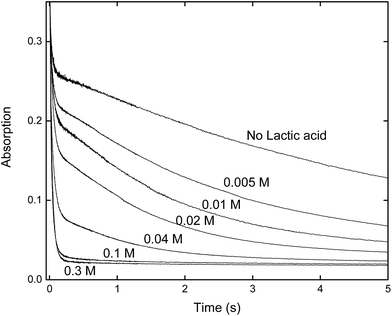
The rate constants given in Table 1, are plotted in comparison to literature data in Fig. 4 and 5, diverge considerably to the data reported previously, especially for europium. The discrepancy in the measured DTPA–metal complexation rate constants, in Fig. 4, for arsenazo III between the values of Nash et al.3 and Shi et al.26 is attributable to how their probe molecule is influenced by the presence of lactic acid.3 Fig. 6 demonstrates how the lactic acid concentration influences the kinetics of the Eu(III)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arsenazo III complex reaction with DTPA, where increasing the lactic acid concentration gives far faster kinetics.
arsenazo III complex reaction with DTPA, where increasing the lactic acid concentration gives far faster kinetics.
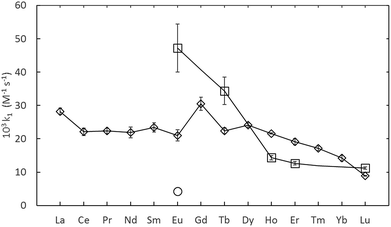 | ||
| Fig. 4 Summary of measured lanthanide-dye-DTPA complexation kinetics from Shi et al.26 (O, converted to second-order) Nash et al.3 (⋄) and this study (□, adjusted to 25 °C). All data at pH 3.6. | ||
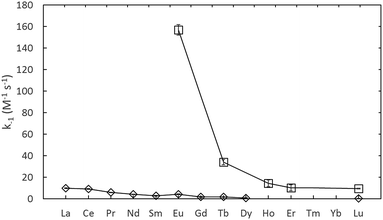 | ||
| Fig. 5 Assumed decomplexation rate constants using arsenazo III, from Nash et al.3 (⋄, in 0.3 M lactic acid) and using xylenol orange from this study (□, adjusted to 25 °C). | ||
It is likely that the lactic acid prevents the formation of a the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (dye
1 (dye![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) metal) complex being measured by Shi et. al., thereby making the measured kinetics of DTPA complexation faster.3,26
metal) complex being measured by Shi et. al., thereby making the measured kinetics of DTPA complexation faster.3,26
The differences in the measured second order rate constants for DTPA complexation of europium using xylenol orange and arsenazo III are shown in Fig. 4 and 5. The large difference in kinetic traces (Fig. 2) for the dye complexation kinetics supports our conclusion that the choice of probe dye has a large impact on the results obtained. Xylenol orange is the most weakly bound dye (lowest stability constant) and gives a highest measured rate constant of all the dyes for europium, indicating that de-complexing the dye probe molecule is the rate limiting step regardless of the strength of the binding complexant. The comparison with the chlorophosphonazo III dye showed that there can be more than a factor of 1000 times in the time required to reach equilibrium (Fig. 2). In addition, since the rate constants obtained for europium with xylenol orange were faster than even the fastest arsenazo III kinetics in the presence of lactate this indicates that the Eu-arsenazo(III)-DTPA complexation variations are actually due to the dye probe behaviour, and the change is therefore not necessarily representative of europium's reaction with DTPA. This suggests that the difference in kinetics due to a change in solution parameters when using a dye does not necessarily reflect an equivalent change in the complexation reaction of interest.
Conclusions
Using the dye ligand displacement technique and stopped-flow spectrometry showed a difference in the measured kinetic constants for xylenol orange and arsenazo III. This difference was determined to be due to the strong influence of the dye-decomplexation kinetics, which makes the obtained results dependent on the chosen dye. This implies that the assumption that the decomplexation of dye probe molecules from lanthanides is fast enough to be ignored likely leads to a significant underestimation of the true rate constants for DTPA complexation with lanthanides. The results for the reactions involving dyes were also shown to vary with the chemical solution conditions, such as the concentration of lactate. A study into how to remove the influence of the dye decomplexation kinetics when measuring DTPA-lanthanide kinetics is currently underway.Acknowledgements
This research was funded by the U.S. DOE Office of Nuclear Energy as part of the FCR&D Thermodynamics and Kinetics program, under DOE Idaho Operations Office contract DE-AC07-05ID14517. Partial funding for this work was also provided by Nuclear Energy Universities Program, under DOE-NEUP program DE-NE0008410.References
- V. Alexander, Chem. Rev., 1995, 95, 273–342 CrossRef CAS.
- C. A. Chang, P. H. L. Chang, V. K. Manchanda and S. Kasprzyk, Inorg. Chem., 1988, 27, 3786–3789 CrossRef CAS.
- K. L. Nash, D. Brigham, T. C. Shehee and A. Martin, Dalton Trans., 2012, 41, 14547–14556 RSC.
- X. Y. Chen, G. S. Goff, W. C. Ewing, B. L. Scott and W. Runde, Inorg. Chem., 2012, 51, 13254–13263 CrossRef CAS PubMed.
- B. Weaver and F. A. Kappelmann, J. Inorg. Nucl. Chem., 1968, 30, 263–272 CrossRef CAS.
- M. Nilsson and K. L. Nash, Solvent Extr. Ion Exch., 2007, 25, 665–701 CrossRef CAS.
- K. L. Nash, Solvent Extr. Ion Exch., 2015, 33, 1–55 CrossRef CAS.
- T. S. Grimes, R. T. Tillotson and L. R. Martin, Solvent Extr. Ion Exch., 2014, 32, 378–390 CrossRef CAS.
- M. Nilsson and K. L. Nash, Solvent Extr. Ion Exch., 2009, 27, 354–377 CrossRef CAS.
- A. L. Serandour, O. Gremy, M. Frechou, D. Renault, J. L. Poncy and P. Fritsch, Radiat. Res., 2008, 170, 208–215 CrossRef CAS PubMed.
- G. N. Stradling, J. Alloys Compd., 1998, 271–273, 72–77 CrossRef CAS.
- L. K. Aminov, B. Z. Malkin and M. A. Teplov, Magnetic Properties of nonmetallic Lanthanide Compounds, in Handbook on the Physics and Chemistry of Rare Earths, ed. Karl A. Gschneidner Jr and Eyring LeRoy, 1996, vol. 22, pp. 295–506 Search PubMed.
- K. Micskei, L. Helm, E. Brücher and A. E. Merbach, Inorg. Chem., 1993, 32, 3844–3850 CrossRef CAS.
- C. J. Chang and K. N. Raymond, Inorg. Chem., 2014, 53(4), 1791–1793 CrossRef CAS PubMed.
- S. Comby, R. M. Surender, O. Kotova, L. K. Truman, J. K. Molloy and T. Gunnlangsson, Inorg. Chem., 2014, 53(4), 1867–1879 CrossRef CAS PubMed.
- S. Sung, H. Holmes, L. Wainwright, A. Toscani, G. J. Stansiuk, A. J. P. White, J. D. Bell and J. D. E. T. Wilton-Ely, Inorg. Chem., 2014, 53(4), 1989–2005 CrossRef CAS PubMed.
- G. Tian, L. R. Martin, Z. Zhang and L. Rao, Inorg. Chem., 2011, 50, 3087–3096 CrossRef CAS PubMed.
- T. S. Grimes, G. Tian, L. Rao and K. L. Nash, Inorg. Chem., 2012, 51, 6299–6307 CrossRef CAS PubMed.
- J. C. Braley, T. S. Grimes and K. L. Nash, Ind. Eng. Chem. Res., 2012, 51, 629–638 CrossRef.
- S. Leguay, T. Vercouter, S. Topin, J. Aupiais, D. Guillaumont, M. Miguirditchian, P. Moisy and C. Le Naour, Inorg. Chem., 2012, 51, 12638–12649 CrossRef CAS PubMed.
- M. A. Brown, A. Paulenova and A. V. Gelis, Inorg. Chem., 2012, 51, 7741–7748 CrossRef CAS PubMed.
- A. E. V. Gorden, M. A. DeVore II and B. A. Maynard, Inorg. Chem., 2013, 52, 3445–3458 CrossRef CAS PubMed.
- G. Tian, Z. Zhang, L. R. Martin and L. Rao, Inorg. Chem., 2015, 54, 1232–1239 CrossRef CAS PubMed.
- R. D. Baybarz, J. Inorg. Nucl. Chem., 1965, 27(8), 1831–1839 CrossRef CAS.
- Z. Kolarik and W. Kuhn, Proc. Int. Solvent Extr. Conf., ISEC 74, Lyon, 8–14th September, 1974, vol. 3pp. 2593–2606 Search PubMed.
- Y. Shi, Q. Ji, E. M. Eyring and R. van Eldik, Dalton Trans., 1996, 2127–2134 RSC.
- K. B. Reddy, S. Cao, E. C. Orr, I. Fabian, R. van Eldik and E. M. Eyring, Dalton Trans., 1994, 2497–2501 RSC.
- C. Cossy, L. Helm and A. E. Merbach, Inorg. Chem., 1989, 28, 2699–2703 CrossRef CAS.
- V. I. Kornev and G. I. Manasheva, Soviet Journal of Coordination Chemistry, 1978, 4, 1169–1172 Search PubMed.
- P. K. Spitsyn, V. S. Shvarev and T. P. Popyvanova, Russ. J. Inorg. Chem., 1972, 17, 502–504 Search PubMed.
- V. B. Kumok and V. S. Serebrennikov, Russ. J. Inorg. Chem., 1966, 11, 47–49 Search PubMed.
- K. Tonosaki and M. Otomo, Bull. Chem. Soc. Jpn., 1962, 35, 1683–1686 CrossRef CAS.
- B. J. Colston and V. J. Robinson, Analyst, 1997, 122, 1451–1455 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04755J |
| ‡ Present address: Oak Ridge National Laboratory, P.O. Box 2008, Oak Ridge, TN, 37831, USA. |
| This journal is © The Royal Society of Chemistry 2017 |