Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanistic investigations and molecular properties of 1,2-bis(ferrocenyl)dimetallenes including group 14 elements†
Hsu-Cheng Huaa and
Ming-Der Su *ab
*ab
aDepartment of Applied Chemistry, National Chiayi University, Chiayi 60004, Taiwan. E-mail: midesu@mail.ncyu.edu.tw
bDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 80708, Taiwan
First published on 19th September 2017
Abstract
The molecular properties and reactive activities of the d-π conjugated (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) systems possessing the E14
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) systems possessing the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 unit were explored using density functional theory (M06-2X/Def2-SVPD). The theoretical investigations on the basis of several physical properties (the bonding analysis, UV-vis and Raman spectra) indicate that a coupling occurs between the double bonded moiety, E14
E14 unit were explored using density functional theory (M06-2X/Def2-SVPD). The theoretical investigations on the basis of several physical properties (the bonding analysis, UV-vis and Raman spectra) indicate that a coupling occurs between the double bonded moiety, E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14, and the ferrocenyl groups. Moreover, the present theoretical findings strongly suggest that the chemical reactivity of such d-π conjugated molecules increase in the order as follows: 1-C ≪ 1-Si < 1-Ge < 1-Sn < 1-Pb. Specifically, the larger the atomic radius of the group 14 element involved in such d-π conjugated compounds, the smaller its π bond strength and more facile its [1 + 4] or [1 + 2] cycloaddition with either a butadiene or a selenium atom, respectively. The singlet–triplet energy splittings, based on the VBSCD model, have been used as a guide to interpret the reactivity.
E14, and the ferrocenyl groups. Moreover, the present theoretical findings strongly suggest that the chemical reactivity of such d-π conjugated molecules increase in the order as follows: 1-C ≪ 1-Si < 1-Ge < 1-Sn < 1-Pb. Specifically, the larger the atomic radius of the group 14 element involved in such d-π conjugated compounds, the smaller its π bond strength and more facile its [1 + 4] or [1 + 2] cycloaddition with either a butadiene or a selenium atom, respectively. The singlet–triplet energy splittings, based on the VBSCD model, have been used as a guide to interpret the reactivity.
I. Introduction
Recently, Sasamori, Tokitoh, and co-workers1 reported the synthesis and characterization of the first stable tetrelenes containing ferrocenyl (Fc) functional groups: (E)-Tip(Fc)Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si(Fc)Tip (Tip = 2,4,6-triisopropylphenyl, Fc = ferrocenyl), (E)-Tip(Rc)Si
Si(Fc)Tip (Tip = 2,4,6-triisopropylphenyl, Fc = ferrocenyl), (E)-Tip(Rc)Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si(Rc)Tip (Rc = ruthenocenyl) 1-Si, and (E)-Tip(Fc)Ge
Si(Rc)Tip (Rc = ruthenocenyl) 1-Si, and (E)-Tip(Fc)Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge(Fc)Tip 1-Ge, revealing highly unusual d-π interactions2 between the Si
Ge(Fc)Tip 1-Ge, revealing highly unusual d-π interactions2 between the Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si and the Ge
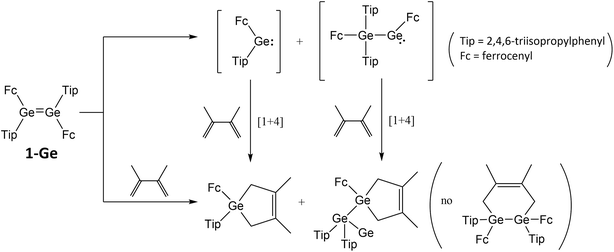
Si and the Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π bond and the metallocenyl units, based on X-ray crystallographic, spectroscopic, and electrochemical analysis. They are the first disilenes and digermene containing functionality afforded by metallocenyl moieties. In particular, experimental studies show that the thermal reactions of (E)-Tip(Fc)Ge
Ge π bond and the metallocenyl units, based on X-ray crystallographic, spectroscopic, and electrochemical analysis. They are the first disilenes and digermene containing functionality afforded by metallocenyl moieties. In particular, experimental studies show that the thermal reactions of (E)-Tip(Fc)Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge(Fc)Tip and 2,3-dimethyl-1,3-butadiene result in the corresponding [1 + 4] cycloaddition products with the cleavage of the Ge
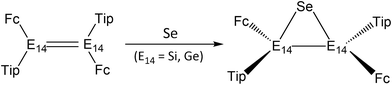
Ge(Fc)Tip and 2,3-dimethyl-1,3-butadiene result in the corresponding [1 + 4] cycloaddition products with the cleavage of the Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge double bond, rather than producing a [2 + 4] cycloproduct (Scheme 1).1c On the other hand, the reactions of 1-Si and 1-Ge with elemental selenium afforded three-membered selenadisilirane and selenadigermirane,1b respectively (Scheme 2). However, to the authors' knowledge, no definite mechanisms for the above reactions have been reported, either experimentally or theoretically. In addition to these, since experimental data and trends are not easily available for such d-π-conjugated systems, in particular for heavier d-π-conjugated analogues, a computational study plays an efficient role in the investigation of both their physical and chemical properties.
Ge double bond, rather than producing a [2 + 4] cycloproduct (Scheme 1).1c On the other hand, the reactions of 1-Si and 1-Ge with elemental selenium afforded three-membered selenadisilirane and selenadigermirane,1b respectively (Scheme 2). However, to the authors' knowledge, no definite mechanisms for the above reactions have been reported, either experimentally or theoretically. In addition to these, since experimental data and trends are not easily available for such d-π-conjugated systems, in particular for heavier d-π-conjugated analogues, a computational study plays an efficient role in the investigation of both their physical and chemical properties.
This study, therefore, pursues the first systematic theoretical inspection of the d-π-conjugated molecules, (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb), using density functional theory (DFT). From the present work, it is hoped that the computed molecular properties, as well as the chemical reactivity, can provide a guide for any future experimental studies of unknown d-π-conjugated compounds possessing a E14
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb), using density functional theory (DFT). From the present work, it is hoped that the computed molecular properties, as well as the chemical reactivity, can provide a guide for any future experimental studies of unknown d-π-conjugated compounds possessing a E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 unit.
E14 unit.
II. Results and discussion
1 The geometries and electronic structures of (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) E14(Fc)Tip species
E14(Fc)Tip species
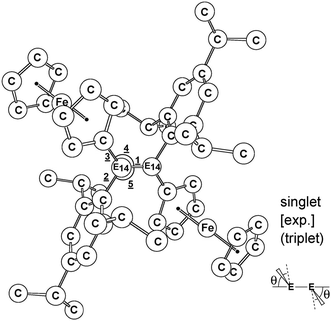
DFT calculations (M06-2X/Def2-SVPD)3,4 were performed to check the molecular parameters of 1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb and to provide a significant insight into the factors influencing their chemical reactivity. All computations were executed using the Gaussian 09 suite of programs (ESI†).5 The selected geometrical parameters of (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip, computed both as singlet and as triplet species, are collected in Table 1. Cartesian coordinates calculated for the stationary points at the M06-2X level are available in ESI.†
E14(Fc)Tip, computed both as singlet and as triplet species, are collected in Table 1. Cartesian coordinates calculated for the stationary points at the M06-2X level are available in ESI.†
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) at both singlet and triplet states calculated at the M06-2X/Def2-SVPD level of theory. The available experimental data are taken from ref. 1. Hydrogen is omitted for clarity
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) at both singlet and triplet states calculated at the M06-2X/Def2-SVPD level of theory. The available experimental data are taken from ref. 1. Hydrogen is omitted for clarity
| 1-C | 1-Si | 1-Ge | 1-Sn | 1-Pb | |
|---|---|---|---|---|---|
| 1 | 1.364 | 2.166 | 2.251 | 2.635 | 2.863 |
| [2.173] | [2.332] | ||||
| (1.500) | (2.323) | (2.416) | (2.743) | (2.906) | |
| 2 | 1.503 | 1.824 | 1.934 | 2.142 | 2.262 |
| [1.880] | [1.981] | ||||
| (1.545) | (1.893) | (1.958) | (2.156) | (2.273) | |
| 3 | 1.492 | 1.824 | 1.903 | 2.090 | 2.204 |
| [1.848] | [1.935] | ||||
| (1.501) | (1.851) | (1.928) | (2.121) | (2.229) | |
| 4 | 125.9° | 121.8° | 119.7° | 113.9° | 114.0° |
| [116.3°] | [114.6°] | ||||
| (125.8°) | (115.9°) | (116.5°) | (115.0°) | (114.6°) | |
| 5 | 120° | 118.9° | 105.6° | 96.48° | 95.31° |
| [117.0°] | [116.5°] | ||||
| (117.3°) | (115.9°) | (116.5°) | (115.0°) | (114.6°) | |
| θ | 6.8° | 29.3° | 46.5° | 64.2° | 68.4° |
| [27.9°] | [43.7°] | ||||
| (7.4°) | (49.1°) | (52.0°) | (61.9°) | (63.4°) | |
Firstly, we compared the geometries of 1-Si and 1-Ge with the M06-2X computational results, since only these structures have been determined by X-ray crystal analyses.1 The calculated Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si and Ge
Si and Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge bond lengths of 1-Si and 1-Ge are 2.166 and 2.251 Å, which are somewhat shorter than the experimental data, 2.173 (ref. 1 and 6) and 2.332 Å,1b respectively, as shown in Table 1. Moreover, it is found that the calculated Si–C and Ge–C (ipso-ferrocenyl) bond distance of 1-Si (1.824 Å) and 1-Ge (1.903 Å) are shorter than those of the Si–C and Ge–C (ipso-Tip) bonds (1.885 Å for 1-Si and 1.934 Å for 1-Ge), whose trend is similar to the experimental observations.1 The reasons for such short values are probably due to conjugative interactions between the π-electrons of the Si
Ge bond lengths of 1-Si and 1-Ge are 2.166 and 2.251 Å, which are somewhat shorter than the experimental data, 2.173 (ref. 1 and 6) and 2.332 Å,1b respectively, as shown in Table 1. Moreover, it is found that the calculated Si–C and Ge–C (ipso-ferrocenyl) bond distance of 1-Si (1.824 Å) and 1-Ge (1.903 Å) are shorter than those of the Si–C and Ge–C (ipso-Tip) bonds (1.885 Å for 1-Si and 1.934 Å for 1-Ge), whose trend is similar to the experimental observations.1 The reasons for such short values are probably due to conjugative interactions between the π-electrons of the Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si and Ge
Si and Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge units and those of the ferrocenyl units in both 1-Si and 1-Ge, respectively.1 Additionally, the M06-2X results shown in Table 1 indicate that 1-Si and 1-Ge exhibit a characteristic trans-bent structure with a trans-bent angle (θ) of 29.4° and 46.5°, which are analogous to the reported X-ray analyses, 27.9° (ref. 1a) and 43.7°,1b respectively.7 From the above comparisons, the reasonably good agreement between the experimental data and the computational results is quite encouraging.8,9 It is, therefore, certain that the theoretical method (M06-2X/Def2-SVPD) used in this work should be reliable for any further investigations of their molecular properties as well as energetic features of the chemical reactions, for which experimental values are not attainable.
Ge units and those of the ferrocenyl units in both 1-Si and 1-Ge, respectively.1 Additionally, the M06-2X results shown in Table 1 indicate that 1-Si and 1-Ge exhibit a characteristic trans-bent structure with a trans-bent angle (θ) of 29.4° and 46.5°, which are analogous to the reported X-ray analyses, 27.9° (ref. 1a) and 43.7°,1b respectively.7 From the above comparisons, the reasonably good agreement between the experimental data and the computational results is quite encouraging.8,9 It is, therefore, certain that the theoretical method (M06-2X/Def2-SVPD) used in this work should be reliable for any further investigations of their molecular properties as well as energetic features of the chemical reactions, for which experimental values are not attainable.
The electronic structures of (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip were analyzed using the natural bond orbital (NBO)10 partitioning scheme in combination with the Wiberg bond indices (WBI),11 which are summarized in Table 2. It is apparent that the order of WBI for the E14
E14(Fc)Tip were analyzed using the natural bond orbital (NBO)10 partitioning scheme in combination with the Wiberg bond indices (WBI),11 which are summarized in Table 2. It is apparent that the order of WBI for the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 doubly bonded species decreases from carbon to lead. In particular, only the WBI of 1-Pb is 0.77, being less than 1.0, implying that the bonding between the two lead atoms is best described as a single bond. About the NBO10 analysis given in Table 2, our theoretical findings indicate that there exists a 1
E14 doubly bonded species decreases from carbon to lead. In particular, only the WBI of 1-Pb is 0.77, being less than 1.0, implying that the bonding between the two lead atoms is best described as a single bond. About the NBO10 analysis given in Table 2, our theoretical findings indicate that there exists a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 p orbital contribution to the π bond in the case of 1-C. On the other hand, the heavier the group 14 element (E14) involved, the higher the asymmetric contributions to the π bond. However, since the 1-C, 1-Sn, and 1-Pb molecules have not been experimentally reported yet and the study of the bonding characters is beyond the scope of the present work, we thus consider the theoretical results collected in Table 2 is a prediction.
1 p orbital contribution to the π bond in the case of 1-C. On the other hand, the heavier the group 14 element (E14) involved, the higher the asymmetric contributions to the π bond. However, since the 1-C, 1-Sn, and 1-Pb molecules have not been experimentally reported yet and the study of the bonding characters is beyond the scope of the present work, we thus consider the theoretical results collected in Table 2 is a prediction.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond length (Å), the natural bond orbital (NBO) and natural resonance theory (NRT) analyses of the compounds (E)-Tip(Fc)E14
E14 double bond length (Å), the natural bond orbital (NBO) and natural resonance theory (NRT) analyses of the compounds (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a,b,c,d
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a,b,c,d
E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 E14 |
Bond length (Å) | WBI | Occupancy | NBO analysis | BDE (kcal mol−1) |
|---|---|---|---|---|---|
a All are computed at the M06-2X/Def2-SVPD level of theory.b Wiberg bond index (WBI).c Occupancy of the corresponding σ and π bonding NBO.d Bonding dissociation energy (BDE), units: kcal mol−1. BDE = 2E[(E)-Tip(Fc)E14:] − E[(E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip]. E14(Fc)Tip]. |
|||||
| 1-C | 1.364 | 1.71 | σ = 1.96 | 0.707 C(sp1.61) + 0.707 C(sp1.61), where C = 50.00%, C = 50.00% | 132.7 |
| π = 1.88 | 0.707 C(sp99.99) + 0.707 C(sp99.99), where C = 49.99%, C = 50.01% | ||||
| 1-Si | 2.116 | 1.62 | σ = 1.93 | 0.707 Si(sp1.83) + 0.707 Si(sp1.83), where Si = 50.01%, Si = 49.99% | 13.64 |
| π = 1.85 | 0.706 Si(sp17.25) + 0.708 Si(sp17.67), where Si = 49.86%, Si = 50.14% | ||||
| 1-Ge | 2.251 | 1.53 | σ = 1.89 | 0.707 Ge(sp2.02) + 0.707 Ge(sp2.03), where Ge = 49.99%, Ge = 50.01% | −3.08 |
| π = 1.83 | 0.708 Ge(sp9.56) + 0.706 Ge(sp9.56), where Ge = 50.17%, Ge = 49.83% | ||||
| 1-Sn | 2.635 | 1.21 | σ = 1.77 | 0.708 Sn(sp2.20) + 0.706 Sn(sp2.24), where Sn = 50.16%, Sn = 49.84% | −30.23 |
| π = 1.73 | 0.709 Sn(sp4.26) + 0.705 Sn(sp4.22), where Sn = 50.26%, Sn = 49.74% | ||||
| 1-Pb | 2.863 | 0.77 | σ = 1.97 | 0.699 Pb(sp1.66) + 0.715 Pb(sp1.81), where Pb = 48.82%, Pb = 51.18% | −30.45 |
| π = 1.64 | 0.716 Pb(sp99.99) + 0.699 Pb(sp1.00), where Pb = 51.20%, Pb = 48.80% | ||||
Specifically, the larger the atomic radius of E14 involved in the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip species, the longer the E14
E14(Fc)Tip species, the longer the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond length, and the smaller the bond order of the E14
E14 double bond length, and the smaller the bond order of the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 bond, the weaker the E14
E14 bond, the weaker the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond strength. Indeed, from the viewpoint of the bond dissociation energy (BDE; kcal mol−1) of the E14
E14 double bond strength. Indeed, from the viewpoint of the bond dissociation energy (BDE; kcal mol−1) of the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond, i.e., (E)-Tip(Fc)E14
E14 double bond, i.e., (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip → 2 × Tip(Fc)E14 (BDE = 2E(Tip(Fc)E14:) − E((E)-Tip(Fc)E14
E14(Fc)Tip → 2 × Tip(Fc)E14 (BDE = 2E(Tip(Fc)E14:) − E((E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip)), the M06-2X calculations shown in Table 2 reveal that the BDE decreases in the order: C
E14(Fc)Tip)), the M06-2X calculations shown in Table 2 reveal that the BDE decreases in the order: C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (133) > Si
C (133) > Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si (14) > Ge
Si (14) > Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge (−3.1) > Sn
Ge (−3.1) > Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn (−30) > Pb
Sn (−30) > Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb (−31). From these results, one may readily anticipate that the double bonds for both 1-Sn and 1-Pb can be relatively easily broken, whereas the 1-C π-bonded compound is quite stable in both the solution phase and the solid phase. However, the M06-2X studies show that the BDEs of 1-Si and 1-Ge are roughly equal to zero, demonstrating that the two species can dissociate in solution. These predictions are in good agreement with the available experimental evidence (vide infra).1
Pb (−31). From these results, one may readily anticipate that the double bonds for both 1-Sn and 1-Pb can be relatively easily broken, whereas the 1-C π-bonded compound is quite stable in both the solution phase and the solid phase. However, the M06-2X studies show that the BDEs of 1-Si and 1-Ge are roughly equal to zero, demonstrating that the two species can dissociate in solution. These predictions are in good agreement with the available experimental evidence (vide infra).1
Besides these, the M06-2X computational data given in Table 2 reveal that there exists substantially more σ-character within the π bond of the diplumbylene in relation to the other dimetallenes. As a result, this feature should relate to the presence of a weak slipped π-interaction in the 1-Pb species.12
In order to gain a better understanding of the chemical bonding of the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip compounds, their frontier molecular orbitals (MOs) based on the M06-2X/Def2-SVPD method are schematically illustrated in Fig. 1. In principle, the HOMO and LUMO of these double bonded species predominantly consist of E14
E14(Fc)Tip compounds, their frontier molecular orbitals (MOs) based on the M06-2X/Def2-SVPD method are schematically illustrated in Fig. 1. In principle, the HOMO and LUMO of these double bonded species predominantly consist of E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 p-π and p-π* orbitals, respectively. As shown in Fig. 1, after the replacement of two E14 atoms at the (E)-Tip(Fc)E14
E14 p-π and p-π* orbitals, respectively. As shown in Fig. 1, after the replacement of two E14 atoms at the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip center, the energy of LUMO (the π* orbital) decreases from 1-C to 1-Pb, whereas the energy of HOMO increases in the order: Eπ(1-C) < Eπ(1-Pb) < Eπ(1-Sn) < Eπ(1-Ge) < Eπ(1-Si). As a result, on the basis of M06-2X calculations, the energy gaps (kcal mol−1) between HOMO and LUMO for the (E)-Tip(Fc)E14
E14(Fc)Tip center, the energy of LUMO (the π* orbital) decreases from 1-C to 1-Pb, whereas the energy of HOMO increases in the order: Eπ(1-C) < Eπ(1-Pb) < Eπ(1-Sn) < Eπ(1-Ge) < Eπ(1-Si). As a result, on the basis of M06-2X calculations, the energy gaps (kcal mol−1) between HOMO and LUMO for the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip molecules are estimated to be 154 (1-C) > 109 (1-Si) > 107 (1-Ge) > 99 (1-Sn) > 98 (1-Pb), whose trend is consistent with that of its singlet–triplet energy splitting (ΔEst = Etriplet − Esinglet),13 i.e., 46 (1-C) > 36 (1-Si) > 34 (1-Ge) > 24 (1-Sn) > 21 (1-Pb). That is to say, the heavier the group 14 atoms (E14
E14(Fc)Tip molecules are estimated to be 154 (1-C) > 109 (1-Si) > 107 (1-Ge) > 99 (1-Sn) > 98 (1-Pb), whose trend is consistent with that of its singlet–triplet energy splitting (ΔEst = Etriplet − Esinglet),13 i.e., 46 (1-C) > 36 (1-Si) > 34 (1-Ge) > 24 (1-Sn) > 21 (1-Pb). That is to say, the heavier the group 14 atoms (E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14) involved, the smaller the ΔEst of E14
E14) involved, the smaller the ΔEst of E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 appears to be. Supposing the chemical reactions are “frontier-controlled”, then the ΔEst of the E14
E14 appears to be. Supposing the chemical reactions are “frontier-controlled”, then the ΔEst of the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 systems can be considered as a criterion regarding their reactivity. From the calculations shown above, the M06-2X data indicate that the ΔEst of the 1-Sn and 1-Pb are smaller than those of the other three compounds (1-C, 1-Si, and 1-Ge). This theoretical evidence strongly suggests that the (E)-Tip(Fc)E14
E14 systems can be considered as a criterion regarding their reactivity. From the calculations shown above, the M06-2X data indicate that the ΔEst of the 1-Sn and 1-Pb are smaller than those of the other three compounds (1-C, 1-Si, and 1-Ge). This theoretical evidence strongly suggests that the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (E14 = C, Si, and Ge) compounds are stable enough to be detected, while 1-Sn and 1-Pb molecules are kinetically unstable and easily react with the other species (such as the solvent molecules). Again, these findings agree well with the theoretical data given in Table 2 as well as the available experimental observations.1
E14(Fc)Tip (E14 = C, Si, and Ge) compounds are stable enough to be detected, while 1-Sn and 1-Pb molecules are kinetically unstable and easily react with the other species (such as the solvent molecules). Again, these findings agree well with the theoretical data given in Table 2 as well as the available experimental observations.1
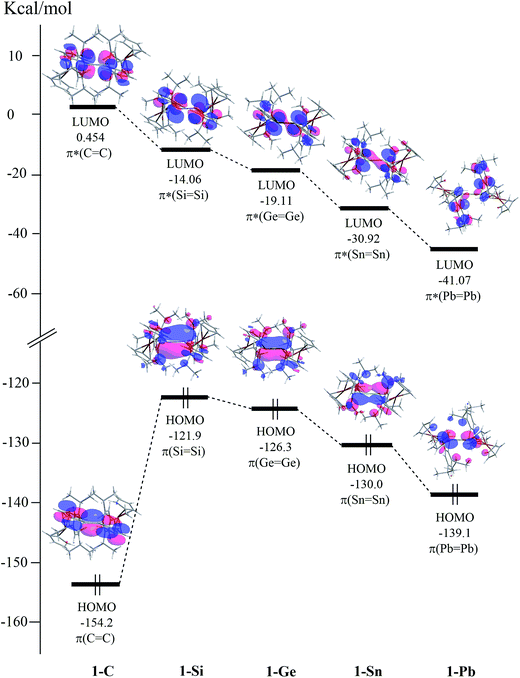 | ||
Fig. 1 Calculated frontier molecular orbitals for the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) species at the M06-2X/Def2-SVPD level of theory. For more information see the text. E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) species at the M06-2X/Def2-SVPD level of theory. For more information see the text. | ||
UV spectroscopy may be one of the most valuable methods for detecting the double-bond character of dimetallenes.14 The UV-vis spectra of E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb), investigated by using the M06-2X/Def2-SVPD level of theory, are summarized in Table 3, accompanied by available experimental findings.1 In the case of 1-Si, the M06-2X spectrum contains two intense absorption peaks at 427 nm (ε = 14
E14 (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb), investigated by using the M06-2X/Def2-SVPD level of theory, are summarized in Table 3, accompanied by available experimental findings.1 In the case of 1-Si, the M06-2X spectrum contains two intense absorption peaks at 427 nm (ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312, Si
312, Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → Si
Si π(HOMO) → Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π*(LUMO)) and 227 nm (ε = 31
Si π*(LUMO)) and 227 nm (ε = 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720, Si
720, Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → d-π* orbitals of metallocenyl moiety). In addition, a weak and broadened absorption peak is seen at 308 nm (ε = 2531, Si
Si π(HOMO) → d-π* orbitals of metallocenyl moiety). In addition, a weak and broadened absorption peak is seen at 308 nm (ε = 2531, Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → d-π*orbitals of metallocenyl moiety and d-π orbitals of metallocenyl unit → Si
Si π(HOMO) → d-π*orbitals of metallocenyl moiety and d-π orbitals of metallocenyl unit → Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π*(LUMO)). In the case of 1-Ge, the same level computations show that there are two strong absorption peaks at 449 nm (ε = 14
Si π*(LUMO)). In the case of 1-Ge, the same level computations show that there are two strong absorption peaks at 449 nm (ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 692, Ge
692, Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π(HOMO) → Ge
Ge π(HOMO) → Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π*(LUMO)) and 223 nm (ε = 33
Ge π*(LUMO)) and 223 nm (ε = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570, d-π orbitals of metallocenyl moiety → Ge
570, d-π orbitals of metallocenyl moiety → Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π*(LUMO)). As there are no relevant experimental or theoretical data for the UV-vis absorption spectra regarding the (E)-Tip(Fc)E14
Ge π*(LUMO)). As there are no relevant experimental or theoretical data for the UV-vis absorption spectra regarding the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (E14 = C, Sn, and Pb) systems, the data given in Table 3 are predictions.
E14(Fc)Tip (E14 = C, Sn, and Pb) systems, the data given in Table 3 are predictions.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a
| Molecular | Wavelength (nm) molar absorptivity (M−1 cm−1) | Transition |
|---|---|---|
| a All are computed at the M06-2X/Def2-SVPD level of theory.b Experimental data are shown in the square bracket. Experimental data see: ref. 1b.c Experimental data are shown in the square bracket. Experimental data see: ref. 1b. | ||
| 1-C | 276.4 (ε = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 617) 617) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π(HOMO) → C C π(HOMO) → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C π*(LUMO) C π*(LUMO) |
191.1 (ε = 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353) 353) |
d(Fe) + π(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) → d(Fe) + π*(C C) → d(Fe) + π*(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) C) |
|
| 1-Si | 427.3 (ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312) 312) |
Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → Si Si π(HOMO) → Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π*(LUMO) Si π*(LUMO) |
[427 (ε = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)]b 000)]b |
||
| 308.2 (ε = 2531)b | d(Fe) + π(Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si) → Si Si) → Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π*(LUMO) Si π*(LUMO) |
|
| [332 (ε = 5900)] | Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → d(Fe) + π*(Si Si π(HOMO) → d(Fe) + π*(Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si) Si) |
|
227.1 (ε = 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720) 720) |
Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si π(HOMO) → d(Fe) + π*(Si Si π(HOMO) → d(Fe) + π*(Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si) Si) |
|
| 1-Ge | 449.0 (ε = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 692) 692) |
Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π(HOMO) → Ge Ge π(HOMO) → Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π*(LUMO) Ge π*(LUMO) |
[430 (ε = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000)]c 000)]c |
||
| [500 (sh)]c | ||
222.5 (ε = 33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570) 570) |
d(Fe) + π(Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge) → Ge Ge) → Ge![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Ge π*(LUMO) Ge π*(LUMO) |
|
| 1-Sn | 508.4 (ε = 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 437) 437) |
Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn π(HOMO) → Sn Sn π(HOMO) → Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn π*(LUMO) Sn π*(LUMO) |
232.9 (ε = 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 889) 889) |
Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn π(HOMO) → d(Fe) + π*(Sn Sn π(HOMO) → d(Fe) + π*(Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn) Sn) |
|
d(Fe) + π(Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn) → Sn Sn) → Sn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Sn π*(LUMO) Sn π*(LUMO) |
||
| 1-Pb | 465.2 (ε = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231) 231) |
Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb π(HOMO) → Pb Pb π(HOMO) → Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb π*(LUMO) Pb π*(LUMO) |
208.2 (ε = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592) 592) |
d(Fe) + π(Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb) → d(Fe) + π*(Pb Pb) → d(Fe) + π*(Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb) Pb) |
|
Table 4 displays the computed Raman spectra of E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) using the M06-2X/Def2-SVPD method, compared with the reported experimental Raman data. However, the M06-2X calculations indicate that the νSiSi vibrational frequencies of 1-Si are estimated to be 648 and 724 cm−1, which are slightly higher than the experimentally observed νSi
E14 (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb) using the M06-2X/Def2-SVPD method, compared with the reported experimental Raman data. However, the M06-2X calculations indicate that the νSiSi vibrational frequencies of 1-Si are estimated to be 648 and 724 cm−1, which are slightly higher than the experimentally observed νSi![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si value (595 and 665 cm−1).1,15 Their vibrational motions are given in Fig. A and B (ESI†), respectively. Again, since to date no Raman spectra of other species (1-C, 1-Ge, 1-Sn, and 1-Pb) have been evaluated and reported, the theoretical data given in Table 4 can be a guide for further experimental studies.
Si value (595 and 665 cm−1).1,15 Their vibrational motions are given in Fig. A and B (ESI†), respectively. Again, since to date no Raman spectra of other species (1-C, 1-Ge, 1-Sn, and 1-Pb) have been evaluated and reported, the theoretical data given in Table 4 can be a guide for further experimental studies.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a,b
E14(Fc)Tip (1-C, 1-Si, 1-Ge, 1-Sn, and 1-Pb)a,b
| Molecular | Frequency (cm−1) |
|---|---|
| a All are computed at the M06-2X/Def2-SVPD level of theory.b Experimental data are shown in the square bracket. Experimental data see: ref. 1b. | |
| 1-C | 1513.1 (C–C stretch) |
1681.2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch) C stretch) |
|
| 3043.8 (C–H stretch) | |
| 3130.5 (C–H stretch) | |
| 3031.8 (C–H stretch) | |
| 1-Si | 648.4 (Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si stretch) Si stretch) |
| [595]1d | |
723.7 (Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si stretch) Si stretch) |
|
| [665]1d | |
| 1248.6 (C–C stretch) | |
| 2950.7 (C–H stretch) | |
| 3046.5 (C–H stretch) | |
| 1-Ge | 1231.4 (C–C stretch) |
| 2977.5 (C–H stretch) | |
| 3045.1 (C–H stretch) | |
| 3141.3 (C–H stretch) | |
| 3272.6 (C–H stretch) | |
| 1-Sn | 1413.7 (C–H band) |
| 2951.5 (C–H stretch) | |
| 3043.9 (C–H stretch) | |
| 3138.3 (C–H stretch) | |
| 3275.0 (C–H stretch) | |
| 1-Pb | 1688.2 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretch) C stretch) |
| 3019.9 (C–H stretch) | |
| 3044.1 (C–H stretch) | |
| 3131.3 (C–H stretch) | |
| 3266.1 (C–H stretch) | |
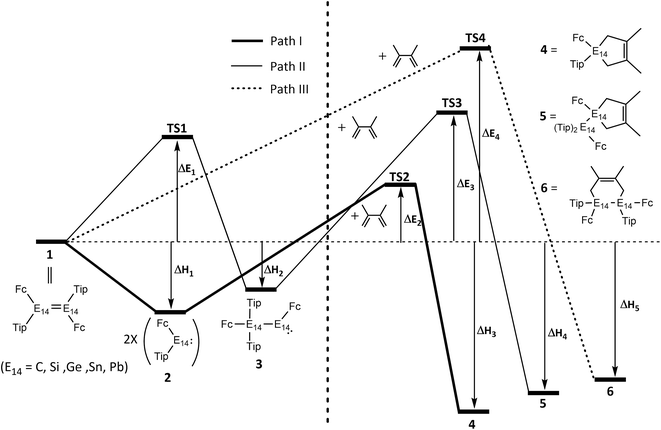
The cycloaddition addition of 2,3-dimethyl-1,3-butadiene with 1 studied in this work follows the general reaction paths (path I, path II, and path III) as represented in Scheme 3. That is to say, 1 would first produce both two equivalent heavy carbene analogues ((Tip)(Fc)E14:, 2)16 and one corresponding 1,2-migration intermediate ((Tip)2(Fc)E14–E14(Fc), 3). Subsequently, these then react with butadiene to yield two types of [1 + 4] cycloproducts (4 and 5), instead of the [2 + 4] cycloformation (6). Theoretical studies regarding the potential energy surfaces for the d-π electron systems containing the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond are shown in the following sections.
E14 double bond are shown in the following sections.
2 The mechanism of path I for the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) E14(Fc)Tip molecules
E14(Fc)Tip molecules
According to the reaction mechanisms given in Scheme 3, reaction path I should proceed as follows: 1 (E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14) + 2,3-dimethyl-1,3-butadiene → 2 × 2 + 2,3-dimethyl-1,3-butadiene → TS2 → 4. The relative energies obtained at the M06-2X/Def2-SVPD level of theory are collected in Table 5. Three points are noteworthy.
E14) + 2,3-dimethyl-1,3-butadiene → 2 × 2 + 2,3-dimethyl-1,3-butadiene → TS2 → 4. The relative energies obtained at the M06-2X/Def2-SVPD level of theory are collected in Table 5. Three points are noteworthy.
| Reaction | 1-C | 1-Si | 1-Ge | 1-Sn | 1-Pb |
|---|---|---|---|---|---|
| a The Gibbs free energies.b ΔEst = Etriplet − Esinglet; see ref. 13 and 17. | |||||
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 2 (ΔH1) | +132.7 | +13.6 | −3.1 | −30.2 | −30.5 |
| 2 (ΔEst)b | −11.2 | +27.2 | +29.0 | +32.7 | +39.6 |
| TS2 (ΔE2) | +10.1 | +16.5 | +17.1 | +19.0 | +25.7 |
| 4 (ΔH3) | −72.2 | −56.1 | −39.6 | −12.6 | +20.6 |
(i) As discussed earlier, due to the relative weakness of the heavier E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond, the 1 d-π electron species should, presumably, produce the heavy carbene analogue (Tip(Fc)E14:; 2). As discussed earlier, from a chemical bonding viewpoint where the π bond strength of a double bond decreases from C
E14 double bond, the 1 d-π electron species should, presumably, produce the heavy carbene analogue (Tip(Fc)E14:; 2). As discussed earlier, from a chemical bonding viewpoint where the π bond strength of a double bond decreases from C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C to
C to ![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) Pb
Pb![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Pb
Pb![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) , the reason is that when heavier group 14 elements (E14) are involved, it can lead to longer double bond distances.18 As a result, the greater the atomic mass of E14 involved in the double bond of a 1 compound, the weaker its π bond and the smaller the singlet–triplet energy splitting (ΔEst). In fact, as shown earlier, on the basis of both BDE (Table 1 and ΔH1 in Table 5) and ΔEst (Table 1)13,17 analysis of the reactant molecule, one may readily obtain the conclusion that the ease of breaking the E14
, the reason is that when heavier group 14 elements (E14) are involved, it can lead to longer double bond distances.18 As a result, the greater the atomic mass of E14 involved in the double bond of a 1 compound, the weaker its π bond and the smaller the singlet–triplet energy splitting (ΔEst). In fact, as shown earlier, on the basis of both BDE (Table 1 and ΔH1 in Table 5) and ΔEst (Table 1)13,17 analysis of the reactant molecule, one may readily obtain the conclusion that the ease of breaking the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond of 1 should decrease in the order: 1-Pb > 1-Sn > 1-Ge > 1-Si > 1-C.
E14 double bond of 1 should decrease in the order: 1-Pb > 1-Sn > 1-Ge > 1-Si > 1-C.
(ii) Fig. 2 presents the relative energies of the valence molecular orbitals in the series of the 2 molecules (2-C, 2-Si, 2-Ge, 2-Sn, and 2-Pb) based on the M06-2X/Def2-SVPD calculations. As seen in Fig. 2, the replacement of a single E14 atom at the center of 2 greatly decreases the energy of the HOMO (sp-σ orbital) when going from 2-C to 2-Pb for the sake of the relativistic effect.9 However, this substitution keeps the energy of the LUMO (p-π orbital) roughly constant along the group 14 elements. It is, therefore, anticipated that the energy gap between the HOMO and LUMO of 2 should increase from 2-C to 2-Pb. Indeed, this prediction is consistent with the trend of the calculated ΔEst (kcal mol−1) for the 2 species, as already shown in Table 4.
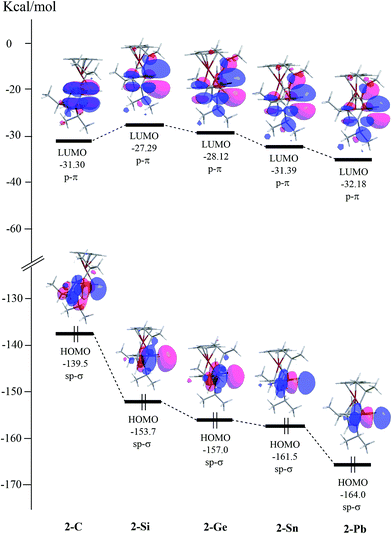 | ||
| Fig. 2 Calculated frontier molecular orbitals for the 2 (Tip(Fc)E14:; 2-C, 2-Si, 2-Ge, 2-Sn, and 2-Pb) species at the M06-2X/Def2-SVPD level of theory. For more information see the text. | ||
(iii) Considering both the calculated activation energies and the reaction enthalpies based on the M06-2X computational results given in Table 5, it is concluded that, for the [1 + 4] cycloaddition reaction of 2, the reactivity decreases in the order: 2-C > 2-Si > 2-Ge > 2-Sn ≫ 2-Pb. In order to verify the important factor that determines the general feature of path I, a valence bond state correlation diagram (VBSCD) model13,16 was used to obtain a deeper understanding of the reactivity of 2. From Table 5, it is apparent that the smaller the value of ΔEst of 2, the lower its barrier height the more exothermic the reaction, and thus the faster the [1 + 4] reaction with a butadiene.
3 The mechanism of path II for the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) E14(Fc)Tip molecules
E14(Fc)Tip molecules
Again, on the basis of mechanisms shown in Scheme 3, the path II mechanism of the [1 + 4] cycloaddition reaction of 1 can be represented as follows: 1 + 2,3-dimethyl-1,3-butadiene → TS1 + 2,3-dimethyl-1,3-butadiene → 3 + 2,3-dimethyl-1,3-butadiene → TS3 → 5. Table 6 displays the relative energies on the singlet potential energy surface along the assumed thermal reaction pathway from Rea to final product (5) at the M06-2X/Def2-SVPD level of theory. Attention should be paid to four important conclusions from these results.
| Reaction | 1-C | 1-Si | 1-Ge | 1-Sn | 1-Pb |
|---|---|---|---|---|---|
| a The Gibbs free energies.b ΔEst = Etriplet − Esinglet; see ref. 13 and 17. | |||||
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| TS1 (ΔE1) | +234.1 | +44.6 | +33.4 | +7.1 | −8.0 |
| 3 (ΔH2) | +110.3 | −10.3 | −18.8 | −25.9 | −38.4 |
| 3 (ΔEst)b | −13.5 | −6.1 | +2.3 | +13.1 | +14.7 |
| TS3 (ΔE3) | +39.1 | +45.6 | +52.5 | +61.9 | +63.7 |
| 5 (ΔH4) | −59.5 | −43.8 | −18.9 | +2.1 | +19.8 |
(i) In path II, the first step of reaction (1 → TS1 → 3) is that 1 undergoes a 1,2-Tip migration before it reacts with 2,3-dimethyl-1,3-butadiene, in which the Tip substituent migrates from one E14 atom to the other E14 atom. From Table 6, taking activation energy and reaction enthalpy into consideration, it can be readily seen that the greater the atomic mass of the group 14 element (E14) involved in the 1 species, the smaller the migration barrier and the larger the exothermicity of the 1,2-shift. The reason for such a phenomenon can be attributed to the bond strength of the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond. As mentioned earlier, due to the examination of both BDE (Table 2 and ΔH1 in Table 5) and ΔEst (Table 1) for the 1 systems,13,17 one can easily obtain the conclusion that the E14
E14 double bond. As mentioned earlier, due to the examination of both BDE (Table 2 and ΔH1 in Table 5) and ΔEst (Table 1) for the 1 systems,13,17 one can easily obtain the conclusion that the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 π bond strength of 1 decreases in the order: 1-C > 1-Si > 1-Ge > 1-Sn > 1-Pb. It is therefore expected that 1 ((E)-Tip(Fc)E14
E14 π bond strength of 1 decreases in the order: 1-C > 1-Si > 1-Ge > 1-Sn > 1-Pb. It is therefore expected that 1 ((E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip) with two heavier E14 centers greatly favors the 1,2-Tip shift to form carbene analogue 3 ((Tip)2(Fc)E14–E14(Fc)). This prediction has been confirmed by examining the migration barriers (ΔE1) as well as the corresponding enthalpies (ΔH2), as already shown in Table 5.
E14(Fc)Tip) with two heavier E14 centers greatly favors the 1,2-Tip shift to form carbene analogue 3 ((Tip)2(Fc)E14–E14(Fc)). This prediction has been confirmed by examining the migration barriers (ΔE1) as well as the corresponding enthalpies (ΔH2), as already shown in Table 5.
(ii) Fig. 3 shows the relative energies of HOMO and LUMO in the series of the 3 molecules (3-C, 3-Si, 3-Ge, 3-Sn, and 3-Pb) at the M06-2X/Def2-SVPD level of theory. Again, it can be readily seen that the substitution of two E14 atoms in 3 can result in the decrease of both HOMO and LUMO energies owing to the relativistic effect,9 as already stated earlier. The M06-2X/Def2-SVPD computations given in Table 6 indicate that the ΔEst (kcal mol−1) for the 3 compounds increases rapidly from 3-C down to 3-Pb.
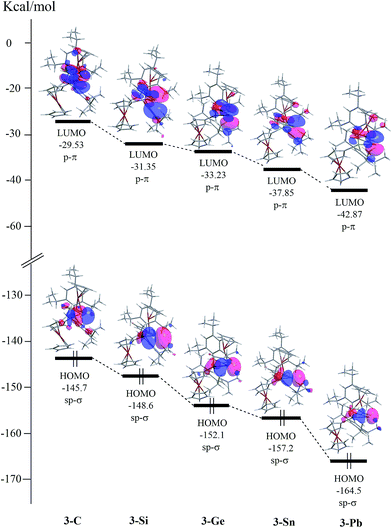 | ||
| Fig. 3 Calculated frontier molecular orbitals for the 3 ((Tip)2(Fc)E14–E14(Fc); 3-C, 3-Si, 3-Ge, 3-Sn, and 3-Pb) species at the M06-2X/Def2-SVPD level of theory. For more information see the text. | ||
(iii) As seen in Scheme 3, the next step of path II is that 3 reacts with 2,3-dimethyl-1,3-butadiene to encounter the [1 + 4] cycloaddition reaction to produce another cycloproduct 5. Again, from Table 6, taking both the activation barrier and reaction enthalpy into account, it is obvious that the larger the atomic number of the group 14 element (E14) contained in the 3 species, the higher the [1 + 4] barrier height (ΔE3), the less exothermicity (ΔH4), and a higher barrier [1 + 4] cycloaddition is obtained. In fact, these phenomena can be interpreted by using the VBSCD model,13,17 as shown earlier. In other words, the present theoretical investigations demonstrate that the heavier the group 14 elements occupying the heavy 3 system, the larger its singlet–triplet energy splitting (ΔEst), the larger its activation energy (ΔE3), and the smaller its reaction enthalpy (ΔH4), which, in turn, results in a slower [1 + 4] cycloaddition reaction with a butadiene.
(iv) When comparing the computational data for the mechanisms of path I and path II (Scheme 3, Tables 5 and 6), it is evident to see that both the activation energies and exothermicities for path I (ΔE2 and ΔH3) are smaller and larger, respectively, than those for path II (ΔE3 and ΔH4). It is thus predicted that the cycloproduct (4) produced by path I should be in a larger yield than the other cycloproduct (5) formed by path II. This anticipation is in good agreement with the experimental evidence for the 1-Ge system.1b
4 The mechanism of path III for the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) E14(Fc)Tip molecules
E14(Fc)Tip molecules
Finally, the [2 + 4] cycloaddition reactions for 1 and 2,3-dimethyl-1,3-butadiene are also examined in the present work. However, from the obtainable experimental reports so far,1b it has been found that the six-membered cyclic product through the Diels–Alder reaction mechanism could not be observed (Scheme 1). In order to explain the reasons, the M06-2X/Def2-SVPD computations were also used in this reaction to investigate the [2 + 4] cycloaddition mechanisms for all the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip molecules. As seen in Scheme 3, the [2 + 4] cycloaddition mechanism (path III) can be represented as follows: 1 + 2,3-dimethyl-1,3-butadiene → TS4 → 6 ([2 + 4] cyclic product). The relative energies for these stationary points are summarized in Table 7. Two noteworthy features from Table 7 are revealed.
E14(Fc)Tip molecules. As seen in Scheme 3, the [2 + 4] cycloaddition mechanism (path III) can be represented as follows: 1 + 2,3-dimethyl-1,3-butadiene → TS4 → 6 ([2 + 4] cyclic product). The relative energies for these stationary points are summarized in Table 7. Two noteworthy features from Table 7 are revealed.
| Reaction | 1-C | 1-Si | 1-Ge | 1-Sn | 1-Pb |
|---|---|---|---|---|---|
| a The Gibbs free energies.b ΔEst = Etriplet − Esinglet; see ref. 13 and 17. | |||||
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 (ΔEst)b | +43.0 | +32.9 | +30.3 | +18.2 | +15.5 |
| TS4 (ΔE4) | +193.4 | +44.6 | +39.9 | +17.5 | −6.5 |
| 6 (ΔH5) | +122.3 | +40.1 | −18.5 | −45.3 | −51.7 |
(i) As illustrated in Table 7, considering both the activation energies and reaction enthalpies for the path III mechanism, it is convenient to see that the reactivity of 1 increases in the order: 1-C ≪ 1-Si < 1-Ge ≪ 1-Sn < 1-Pb. In particular, it is interesting to find that the activation barrier (193 kcal mol−1) for path III of the 1-C molecule is the highest. The subsequent higher barrier heights are the 1-Si (45 kcal mol−1) and 1-Ge (40 kcal mol−1) compounds, which are still higher than the 1-Sn (18 kcal mol−1) and 1-Pb (−6.5 kcal mol−1) species. Consequently, one can easily foresee that the [2 + 4] cycloaddition reactions for the 1-C, 1-Si, 1-Ge with a butadiene are unlikely to occur, whereas the [2 + 4] cycloproducts through the reactions of 1-Sn and 1-Pb with a butadiene should be effortlessly observable. This prediction agrees with the experimental findings for the 1-Ge case.7c
(ii) According to the VBSCD model13,16 mentioned earlier, from Fig. 1 and Table 7, it is simple to see that the greater the atomic number of E14 atoms contained in 1, the smaller the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 π bond strength, the smaller the HOMO–LUMO energy gap, the smaller the value of ΔEst of 1, the lower its barrier height, the greater its exothermicity, and the faster the [2 + 4] reaction with a butadiene.
E14 π bond strength, the smaller the HOMO–LUMO energy gap, the smaller the value of ΔEst of 1, the lower its barrier height, the greater its exothermicity, and the faster the [2 + 4] reaction with a butadiene.
(iii) One may ask why the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (1) species undergoes the [1 + 4] addition reaction rather than the [2 + 4] cycloaddition reaction as shown in Scheme 1 (ref. 1) and Scheme 3. The reason for this can be attributed to the steric effects between the 2,3-dimethyl-1,3-butadiene and the d-π conjugated systems ((E)-Tip(Fc)E14
E14(Fc)Tip (1) species undergoes the [1 + 4] addition reaction rather than the [2 + 4] cycloaddition reaction as shown in Scheme 1 (ref. 1) and Scheme 3. The reason for this can be attributed to the steric effects between the 2,3-dimethyl-1,3-butadiene and the d-π conjugated systems ((E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip) bearing an E14
E14(Fc)Tip) bearing an E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond (Scheme 4). Since 2,3-dimethyl-1,3-butadiene contains two methyl groups, which can lead to steric overcrowding with the Fc and Tip bulky substituents of 1, this would thus result in large barrier heights (Table 7) when 1 and 2,3-dimethyl-1,3-butadiene undergo the [2 + 4] cycloaddition. In addition, as discussed earlier, the bonding strength of E14
E14 double bond (Scheme 4). Since 2,3-dimethyl-1,3-butadiene contains two methyl groups, which can lead to steric overcrowding with the Fc and Tip bulky substituents of 1, this would thus result in large barrier heights (Table 7) when 1 and 2,3-dimethyl-1,3-butadiene undergo the [2 + 4] cycloaddition. In addition, as discussed earlier, the bonding strength of E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 for the heavier group 14 elements are rather weak. Consequently, 1 and 2,3-dimethyl-1,3-butadiene prefer to undergo a [1 + 4] addition rather than to proceed to a [2 + 4] cycloaddition.
E14 for the heavier group 14 elements are rather weak. Consequently, 1 and 2,3-dimethyl-1,3-butadiene prefer to undergo a [1 + 4] addition rather than to proceed to a [2 + 4] cycloaddition.
5 The cycloaddition reactions of (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) E14(Fc)Tip molecules with a selenium atom
E14(Fc)Tip molecules with a selenium atom
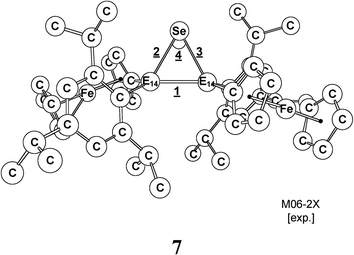
As remarked in the introduction (Scheme 2), when 1-Si and 1-Ge react with a selenium atom, they are found to proceed readily and produce three-membered cyclic products.1,19 Thus, we extended these studies to the other heavier (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip systems by using the theoretical method (M06-2X/Def2-SVPD). A thermally concerted mechanism for such a [1 + 2] cycloaddition reaction is thus suggested as follows: 1 + Se → TS5 → 7 (three-membered ring product). The relative energies, calculated at the M06-2X/Def2-SVPD level of theory, for the stationary points shown above are collected in Table 8. The computationally and experimentally selected geometrical parameters are collected and given in Table 9. Three interesting conclusions drawn from the theoretical study can be summarized as follows.
E14(Fc)Tip systems by using the theoretical method (M06-2X/Def2-SVPD). A thermally concerted mechanism for such a [1 + 2] cycloaddition reaction is thus suggested as follows: 1 + Se → TS5 → 7 (three-membered ring product). The relative energies, calculated at the M06-2X/Def2-SVPD level of theory, for the stationary points shown above are collected in Table 8. The computationally and experimentally selected geometrical parameters are collected and given in Table 9. Three interesting conclusions drawn from the theoretical study can be summarized as follows.
| Reaction | 1-C | 1-Si | 1-Ge | 1-Sn | 1-Pb |
|---|---|---|---|---|---|
| a The Gibbs free energies.b ΔEst = Etriplet − Esinglet; see ref. 13 and 17. | |||||
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 (ΔEst)b | +43.0 | +32.9 | +30.3 | +18.2 | +15.5 |
| 7 (ΔH6) | −20.2 | −61.3 | −76.4 | −129.2 | −145.0 |
(i) As seen in Table 9, the optimized geometrical parameters of 7-Si and 7-Ge are reasonably in agreement with those observed experimentally,1 strongly suggesting that the method (M06-2X/Def2-SVPD) used in this work should give meaningful information on the bonding properties of 7 (vide infra). Moreover, it is obvious from Table 9 that both the Si–Si and Ge–Ge bond distances of 7-Si and 7-Ge are 2.286 (exp. 2.288)1a and 2.385 (exp. 2.370)1b Å, which are slightly shorter than the traditional Si–Si and Ge–Ge single bond lengths (2.33–2.37 Å)20 and (2.43–2.52 Å),21 respectively. The reason for such shorter bond distances is due to the π-complex characters of selenadisilirane and selenadigermirane.1 As a result, the two three-membered cyclic products (7-Si and 7-Ge) were thought to exhibit considerable π-coupling characteristics between E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 π bonds and ferrocenyl groups. Nevertheless, repeated attempts to find the transition state for the cycloaddition reaction of 1 with a selenium atom using the M06-2X method were always unsuccessful. Accordingly, the present theoretical investigations indicate that no transition states exist on the M06-2X/Def2-SVPD surface for the [1 + 2] cycloaddition reaction of 1 with a selenium atom.
E14 π bonds and ferrocenyl groups. Nevertheless, repeated attempts to find the transition state for the cycloaddition reaction of 1 with a selenium atom using the M06-2X method were always unsuccessful. Accordingly, the present theoretical investigations indicate that no transition states exist on the M06-2X/Def2-SVPD surface for the [1 + 2] cycloaddition reaction of 1 with a selenium atom.
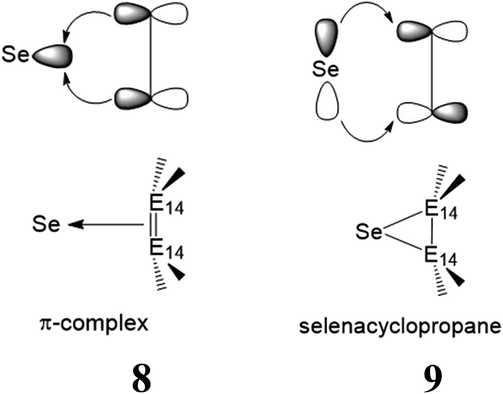
(ii) The chemical bonding properties of the [1 + 2] products (7) can be readily explained in terms of the Dewar–Chatt–Duncanson model.22 On the basis of this model, their bonding schemes are categorized into two representations: one is a π-complex (8), with the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14-to-selenium σ-donation making the greater contribution, and the other is a selenacyclopropane (9), with major selenium-to-E14
E14-to-selenium σ-donation making the greater contribution, and the other is a selenacyclopropane (9), with major selenium-to-E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 π-back-donation, as shown in 8 and 9, respectively. In order to identify which pattern is predominant in such three-membered ring products (7), it is better to examine the molecular orbital pictures of their HOMO and LUMO. As seen in Fig. 4, all the computed HOMOs of the 7 species are composed of the σ-orbital of the selenium atom and the p-π orbitals of the E14
E14 π-back-donation, as shown in 8 and 9, respectively. In order to identify which pattern is predominant in such three-membered ring products (7), it is better to examine the molecular orbital pictures of their HOMO and LUMO. As seen in Fig. 4, all the computed HOMOs of the 7 species are composed of the σ-orbital of the selenium atom and the p-π orbitals of the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 unit, presenting the π-complex in character. In consequence, the bonding schemes in such [1 + 2] molecules (7) are better characterized as the π-complex bonding (8), rather than the three-membered ring bonding (9). This theoretical finding is consistent with the earlier theoretical examinations by Tokitoh and co-workers.1
E14 unit, presenting the π-complex in character. In consequence, the bonding schemes in such [1 + 2] molecules (7) are better characterized as the π-complex bonding (8), rather than the three-membered ring bonding (9). This theoretical finding is consistent with the earlier theoretical examinations by Tokitoh and co-workers.1
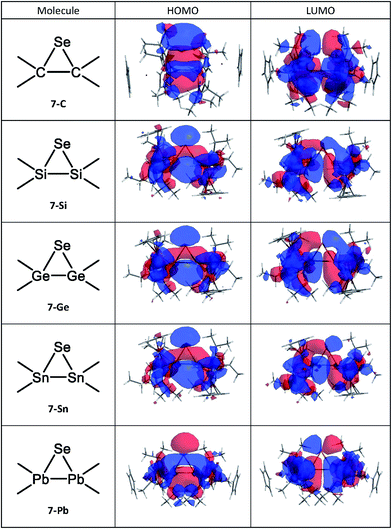 | ||
| Fig. 4 Calculated HOMO and LUMO for the 7 (three-membered cyclic product) molecules at the M06-2X/Def2-SVPD level of theory. For more information see the text. | ||
(iii) The M06-2X computational results shown in Table 8 reveal that the order of the reactivity for producing cyclic products (7) increases as follows: 1-C ≪ 1-Si < 1-Ge < 1-Sn < 1-Pb. Again, this trend is quite similar to those species shown in Scheme 3 discussed earlier. That is to say, using the VBSCD model,13,17 it is easy to anticipate that the longer the atomic radius of group 14 element (E14) involved in the 1 molecule, the smaller its singlet–triplet energy splitting ΔEst, and the easier the formation of a [1 + 2] three-membered ring product with a selenium atom.
III. Conclusion
In this work, we have theoretically studied the molecular properties as well as the reactive activities of the novel d-π conjugated systems ((E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip; 1) featuring an E14
E14(Fc)Tip; 1) featuring an E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond using the M06-2X/Def2-SVPD level of theory. The important conclusions that can be drawn from the above studies are as follows:
E14 double bond using the M06-2X/Def2-SVPD level of theory. The important conclusions that can be drawn from the above studies are as follows:
(1) The present computed UV-vis and Raman spectra, as well as several molecular properties, reveal that there exist coupling interactions between the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond and the ferrocenyl groups in the d-π conjugated (E)-Tip(Fc)E14
E14 double bond and the ferrocenyl groups in the d-π conjugated (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip molecules.
E14(Fc)Tip molecules.
(2) The theoretical findings demonstrate that the greater the atomic radius of the group 14 element E14 contained in such d-π conjugated systems, the longer the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 double bond distance, the weaker its π bond strength, the smaller its WBI bond order, the smaller its BDE to produce two equivalent carbene analogues (Tip(Fc)E14:), and the larger the yields of the formations of either [1 + 4] or [1 + 2] cyclo adducts. That is to say, the heavier the atomic mass of the group 14 element involved in the d-π conjugated compounds studied in this work, the smaller its π bond strength and more facile its [1 + 4] or [1 + 2] cycloadditions with either a butadiene or a selenium atom, respectively. In short, the order of the chemical reactivity increases as follows: 1-C ≪ 1-Si < 1-Ge < 1-Sn < 1-Pb.
E14 double bond distance, the weaker its π bond strength, the smaller its WBI bond order, the smaller its BDE to produce two equivalent carbene analogues (Tip(Fc)E14:), and the larger the yields of the formations of either [1 + 4] or [1 + 2] cyclo adducts. That is to say, the heavier the atomic mass of the group 14 element involved in the d-π conjugated compounds studied in this work, the smaller its π bond strength and more facile its [1 + 4] or [1 + 2] cycloadditions with either a butadiene or a selenium atom, respectively. In short, the order of the chemical reactivity increases as follows: 1-C ≪ 1-Si < 1-Ge < 1-Sn < 1-Pb.
(3) The theoretical evidence reveals that the steric congestions between (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip and 2,3-dimethyl-1,3-butadiene would make these reactants undergo the [1 + 4] addition reactions rather than the [2 + 4] cycloaddition reactions.
E14(Fc)Tip and 2,3-dimethyl-1,3-butadiene would make these reactants undergo the [1 + 4] addition reactions rather than the [2 + 4] cycloaddition reactions.
(4) On the basis of the VBSCD model,13,17 one can use the singlet–triplet energy gap (ΔEst) of the (E)-Tip(Fc)E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip compound as a diagnostic tool to anticipate its chemical reactivity.
E14(Fc)Tip compound as a diagnostic tool to anticipate its chemical reactivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the National Center for High-Performance Computing of Taiwan for generous amounts of computing time. They also thank the Ministry of Science and Technology of Taiwan for the financial support. Special thanks are also due to reviewers 1 and 2 for very help suggestions and comments.References
- (a) T. Sasamori, A. Yuasa, Y. Hosoi, Y. Furukawa and N. Tokitoh, Organometallics, 2008, 27, 3325 CrossRef CAS; (b) N. Tokitoh, A. Yuasa and T. Sasamori, Phosphorus, Sulfur Silicon Relat. Elem., 2010, 185, 824 CrossRef; (c) N. Tokitoh, A. Yuasa and T. Sasamori, Phosphorus, Sulfur Silicon Relat. Elem., 2011, 186, 1217 CrossRef CAS; (d) T. Sasamori, H. Miyamoto, H. Sakai, Y. Furukawa and N. Tokitoh, Organometallics, 2012, 31, 3904 CrossRef CAS.
- The d-π-conjugated systems indicate the multinuclear transition-metal complexes are bridged by organic π-conjugated systems. See: A. Yuasa, T. Sasamori, Y. Hosoi, Y. Furukawa and N. Tokitoh, Bull. Chem. Soc. Jpn., 2009, 82, 793 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157 CrossRef CAS PubMed.
- The Def2-SVPD basis sets see: (a) D. Andrae, U. Haeussermann, M. H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123 CrossRef CAS; (b) B. Metz, H. Stoll and M. Dolg, J. Chem. Phys., 2000, 113, 2563 CrossRef CAS; (c) K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- M. J. Frisch, et al., Gaussian, Inc., Wallingford CT, 2013.
- The Si
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si bond distance of (E)-Tip(Rc)Si
Si bond distance of (E)-Tip(Rc)Si![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Si(Rc)Tip (Rc = ruthenocenyl), 1-Si, is 2.185 Å. The Si–C (ipso-ruthenocenyl) and Si–C (ipso-Tip) bond distances of 2 are 1.845 and 1.887 Å, respectively. See ref. 1b.
Si(Rc)Tip (Rc = ruthenocenyl), 1-Si, is 2.185 Å. The Si–C (ipso-ruthenocenyl) and Si–C (ipso-Tip) bond distances of 2 are 1.845 and 1.887 Å, respectively. See ref. 1b. - In fact, these molecules, bearing so-called “non-classical double bonds”, have already been verified as the preferred organizations for disilenes and digermenes, and are global minima on the potential energy surfaces for all the similar heavier analogues of ethylene. For recent reviews, see: (a) T. Tsumuraya, S. A. Batcheller and S. Masamune, Angew. Chem., Int. Ed. Engl., 1991, 30, 902 CrossRef; (b) R. S. Grev, Adv. Organomet. Chem., 1991, 33, 125 CrossRef CAS; (c) M. Weidenbruch, Coord. Chem. Rev., 1994, 130, 275 CrossRef CAS; (d) T. Iwamoto, H. Sakurai and M. Kira, Bull. Chem. Soc. Jpn., 1998, 71, 2741 CrossRef CAS; (e) P. P. Power, J. Chem. Soc., Dalton Trans., 1998, 2939 RSC; (f) M. Kira and T. Iwamoto, J. Organomet. Chem., 2000, 610, 236 CrossRef.
- Moreover, several other interesting points can also be found in Fig. 1. Firstly, it is apparent that no matter what multiplicity the group 14 (E)-Tip(Fc)E14
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14(Fc)Tip (abbreviation: E14
E14(Fc)Tip (abbreviation: E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14) chooses, the M06-2X computations indicate that both the E14
E14) chooses, the M06-2X computations indicate that both the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 and the E14–C bond lengths all present a monotonic increase down the group from carbon to lead, due to the increase in the atomic radius of E from C to Pb. In addition, these bond distances are larger in the triplet state than those in the corresponding singlet state. Secondly, the ∠(ipso-ferrocenyl)C–E14–E14 and ∠(ipso-Tip)C–E14–E14 bond angles decrease from C to Pb, The reasons for such phenomena are, basically, attributed to the relativistic effect (see ref. 8). However, these bond angles are smaller in the triplet state than those in the corresponding singlet state. Thirdly, the computational results show that regardless of whether a singlet or triplet state, the trans-bent angle (θ) in the E14
E14 and the E14–C bond lengths all present a monotonic increase down the group from carbon to lead, due to the increase in the atomic radius of E from C to Pb. In addition, these bond distances are larger in the triplet state than those in the corresponding singlet state. Secondly, the ∠(ipso-ferrocenyl)C–E14–E14 and ∠(ipso-Tip)C–E14–E14 bond angles decrease from C to Pb, The reasons for such phenomena are, basically, attributed to the relativistic effect (see ref. 8). However, these bond angles are smaller in the triplet state than those in the corresponding singlet state. Thirdly, the computational results show that regardless of whether a singlet or triplet state, the trans-bent angle (θ) in the E14![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) E14 compounds reveals a monotonic increase from carbon to lead, again due to the relativistic effect (ref. 8).
E14 compounds reveals a monotonic increase from carbon to lead, again due to the relativistic effect (ref. 8). - The “orbital non-hybridization effect”, also known as the “inert s-pair effect”, see: (a) P. Pyykk and J.-P. Desclaux, Acc. Chem. Res., 1979, 12, 276 CrossRef; (b) W. Kutzelnigg, Angew. Chem., Int. Ed. Engl., 1984, 23, 272 CrossRef; (c) P. Pyykk, Chem. Rev., 1988, 88, 563 CrossRef; (d) P. Pyykk, Chem. Rev., 1997, 97, 597 CrossRef.
- E. D. Glendening, A. E. Reed, J. Carpenter and F. Weinhold, NBO Version 3.1 Search PubMed.
- K. B. Wiberg, Tetrahedron, 1968, 1083 CrossRef CAS.
- (a) M. Stürmann, M. Weidenbruch, K. W. Klinkhammer, F. Lissner and H. Marsmann, Organometallics, 1998, 17, 4425 CrossRef; (b) M. Stürmann, W. Saak, M. Weidenbruch and K. W. Klinkhammer, Eur. J. Inorg. Chem., 1999, 579 CrossRef; (c) M. Stürmann, W. Saak, H. Marsmann and M. Weidenbruch, Angew. Chem., Int. Ed., 1999, 38, 187 CrossRef.
- For details, see: (a) S. Shaik, H. B. Schlegel and S. Wolfe in Theoretical Aspects of Physical Organic Chemistry, John Wiley & Sons Inc., USA, 1992 Search PubMed; (b) A. Pross, in Theoretical and Physical principles of Organic Reactivity, John Wiley & Sons Inc., USA, 1995 Search PubMed; (c) S. Shaik, Prog. Phys. Org. Chem., 1985, 15, 197 CAS; (d) S. Shaik and P. C. Hiberty, in A Chemist's Guide to Valence Bond Theory, Wiley, Interscience, USA, 2008 Search PubMed.
- For instance: M. Kira and N. Iwamoto, Adv. Organomet. Chem., 2006, 54, 73 CrossRef CAS.
- The reason for such differences could be due to the anharmonic nuclear motions (internal rotation, inversion and pseudorotation) on Raman frequencies. For instance, see: G. Katzer and A. F. Sax, J. Phys. Chem. A, 2002, 106, 7204 CrossRef CAS.
- For instance: (a) N. Tokitoh, H. Suzuki and R. Okazaki, J. Am. Chem. Soc., 1993, 115, 1042 Search PubMed; (b) H. Suzuki, N. Tokitoh and R. Okazaki, Bull. Chem. Soc. Jpn., 1995, 68, 2471 CrossRef CAS; (c) K. L. Hurni, P. A. Rupar, N. C. Payne and K. M. Baines, Organometallics, 2007, 26, 5569 CrossRef CAS; (d) R. Sedlak, O. A. Stasyuk, C. F. Guerra, J. Řezáč, A. Růžička and P. Hobza, J. Chem. Theory Comput., 2016, 12, 1696 CrossRef CAS PubMed; (e) Y. Sugiyama, T. Sasamori, Y. Hosoi, Y. Furukawa, N. Takagi, S. Nagase and N. Tokitoh, J. Am. Chem. Soc., 2006, 128, 1023 CrossRef CAS PubMed.
- (a) The first paper that originated the VBSCD model see: S. Shaik, J. Am. Chem. Soc., 1981, 103, 3692 CrossRef CAS; (b) About the most updated review of the VBSCD model, one can see: S. Shaik and A. Shurki, Angew. Chem., Int. Ed., 1999, 38, 586 CrossRef; (c) R. Hoffmann, S. Shaik and P. C. Hiberty, Acc. Chem. Res., 2003, 36, 750 CrossRef CAS PubMed.
- (a) M. Kira, T. Iwamoto and S. Ishida, Bull. Chem. Soc. Jpn., 2007, 80, 258 CrossRef CAS; (b) M. Kira, Chem. Commun., 2010, 46, 2893 RSC.
- For instance, see: (a) T. Kudo, S. Akiba, Y. Kondo, H. Watanabe, K. Morokuma and T. Vreven, Organometallics, 2003, 22, 4721 CrossRef CAS; (b) J. A. Boatz and M. S. Gordon, J. Phys. Chem., 1989, 93, 3025 CrossRef CAS.
- W. S. Sheldrick, in The Chemistry of Organic Silicon Compounds, ed. S. Patai and Z. Rappoport, John Wiley & Sons, Chichester, New York, 1989, Part 1, p. 249 Search PubMed.
- E. I. Solomon, R. A. Scott and R. B. King, in Computational Inorganic and Bioinorganic Chemistry, John Wiley & Sons, Chichester, New York, 2013, p. 323 Search PubMed.
- (a) M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C71 Search PubMed; (b) J. Chatt and L. A. Duncanson, J. Chem. Soc., 1953, 2939 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra04935h |
| This journal is © The Royal Society of Chemistry 2017 |