Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A new method for fast statistical measurement of interfacial misfit strain around nano-scale semi-coherent particles
Liang Liang Songab,
Shaojun Liua and
Xiaodong Mao *a
*a
aKey Laboratory of Neutronics and Radiation Safety, Institute of Nuclear Energy Safety Technology, Chinese Academy of Sciences, Hefei, Anhui 230031, China. E-mail: xiaodong.mao@fds.org.cn
bUniversity of Science and Technology of China, Hefei, Anhui, China
First published on 31st May 2017
Abstract
An innovative diffraction contrast imaging method derived from Ashby–Brown contrast is presented for fast and statistical measurement of interfacial misfit strain around nano-sized semi-coherent particles. A correlation between nano-scale interfacial misfit strain and the fringe-like transmission electron microscopy (TEM) contrast lines was set up, by which interfacial misfit strain could be obtained by measuring the inter-spacings between the so-called “no-contrast” lines. The mechanism of the measurement lies on the symmetry of the strain field at specific orientations around semi-coherent particles due to the presence of misfit dislocations, which induces “no-contrast” lines on TEM images under proper two-beam conditions. A much lower average lattice misfit strain of 4%, rather than 9.45% expected from lattice misfit between matrix and precipitate crystals, was revealed along (02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )Matrix in austenitic oxide dispersion strengthened steel by this method, and was confirmed by geometric phase analysis (GPA) on high resolution transmission electron microscopy (HRTEM) images. This diffraction contrast imaging method is especially suitable for measuring misfit strain around particles that are smaller than 10 nm, and is expected to bridge the gap between nano-scale interfacial structure and mechanical properties of materials that are strengthened by semi-coherent nano-particles.
)Matrix in austenitic oxide dispersion strengthened steel by this method, and was confirmed by geometric phase analysis (GPA) on high resolution transmission electron microscopy (HRTEM) images. This diffraction contrast imaging method is especially suitable for measuring misfit strain around particles that are smaller than 10 nm, and is expected to bridge the gap between nano-scale interfacial structure and mechanical properties of materials that are strengthened by semi-coherent nano-particles.
1. Introduction
It is a long-lasting challenge to correlate microstructure with physical and mechanical properties for multi-phase materials, such as complex oxide systems, multilayered materials, dispersion strengthened composites, etc. Interfaces often determine macroscopic mechanical, physical, and chemical properties of these materials.1–5 It is widely recognized that, to design and to control macroscopic materials properties successfully, a fundamental understanding of the structure and chemistry of the interfaces is necessary. For engineering materials such as oxide dispersion strengthened alloys, the structure and interfacial misfit strain of the ceramic/metal (C/M) interface are of great importance to understand and predict the mechanical behaviors, owing to the extraordinary influence of the misfit strain on dislocation motion.6–8 Lack of a fast and statistical quantitative measurement method has been a major obstacle to analyze the complex strain field at the nano-scale C/M interface. While the theories of metal and ceramic homophase interfaces (grain boundaries) are fairly well developed, heterophase C/M interfaces are a relatively less well-studied subject. Experimentally the nano-scale C/M interfaces have been exclusively studied by HRTEM.9–15 However, statistical data on a large number of interfaces are needed for predicting the mechanical properties, which can hardly be accomplished. A fast and statistical method for data acquisition on a large number of interfaces is keenly needed. In this paper, such a method is presented that fast and statistical measurement on interfacial strain around semi-coherent particle could be achieved.A misfit contrast of a coherent, spherical particle under a two-beam condition in TEM was quantified by Ashby and Brown.16 It indicates an undistorted vertical plane that runs right through the center of the particle. This absence of distortion causes a “line of no contrast” that runs through the image of the particle perpendicular to the active g vector. A simplified explanation is that, according to the Howie–Whelan equations, the amplitude Ag of a diffracted beam by a column of the matrix around the coherent particle is
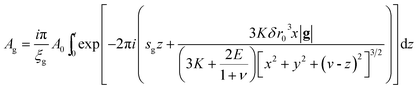 | (1) |
An Ashby–Brown contrast does not apply to semi-coherent particles, where the elastic distortion around semi-coherent particles has no spherical symmetry. Fringes observed on semi-coherent and incoherent particles were normally explained by moiré fringes which are formed due to the overlapped images by two perfect crystals.17–22 However, as a semi-coherent particle becomes smaller in size to several nanometers, the volume of a transitional zone of a distorted interface cannot be ignored, which may dominate the TEM image contrast. For instance, a 64 Å-thick transitional zone was detected across a Fe/Y2O3 interface.23 Therefore, the TEM image contrast of spherical precipitates with a size of around 10 nm or smaller should be preferably illustrated by an elastic strain field rather than moiré fringes. Precipitates of this size are of particular interest as they exhibit a high dispersion strengthening effect.24–26 For instance, Co-rich particles in Cu–Co alloys,17 a GP-zone in Al base alloys,24 NbC nano-particles in Nb-containing austenitic steel,25 and δ-Ni2Si precipitates in Cu–Ni–Si alloys.22 Recently, to meet the requirements of cladding tubes and other structural components of Gen. IV fission reactors, oxide dispersion strengthened (ODS) steel has attracted much attention.20,21,26–32 Oxide particles with sizes smaller than 10 nm are uniformly distributed in a steel matrix to impede the dislocation motion and attract irradiation induced point defects, reaching a high creep strength and good irradiation resistance.26,31,33 Due to a large difference in lattice parameters between oxides and metals or different crystal structures, interfaces between oxide particles and alloy matrix tend to be semi-coherent, which was frequently observed in oxide dispersion strengthened steel.20,21,33–38 Fringes observed in these studies were explained as moiré fringes, and the oxide particles were identified to be Y2O3, Y2Ti2O7, YAlO3, and Y4Zr3O12 of around 5 nm in diameter and have certain orientation relationships (ORs) with the matrix.20,21,33,35,36 Considering a 64 Å-thick transitional zone across a Fe/Y2O3 interface, the whole particle with a diameter of 5 nm and a matrix shell around the particle with a thickness of around 3 nm is within the transitional zone. Explanation by moiré fringes might be misleading because the whole image formation volume is distorted. The Ashby–Brown theory could be expanded to semi-coherent spherical precipitates by introducing stacked misfit dislocation loops on the precipitate/matrix interfaces. An elastic strain field around coherent and semi-coherent precipitates in a matrix has been intensively studied by experimental measurements and theoretical calculations and simulations.39–45 Previous study has shown that the elasticity problem of a transformed inclusion constrained in an infinite matrix could be solved by considering a dislocation cage made of uniformly stacked dislocation loops.46 If we consider that misfit dislocations are formed at the semi-coherent interface, the diffraction contrast of semi-coherent particles can be illustrated by a simple schematic configuration of the lattice displacement around the particles. The selection and valid property prediction of structural materials is very important to the safety of the reactors, and have great influence on thermal efficiency.47,48 Understanding the correlation between microstructure and mechanical properties of materials such as ODS steel will be of great significance for nuclear energy development.
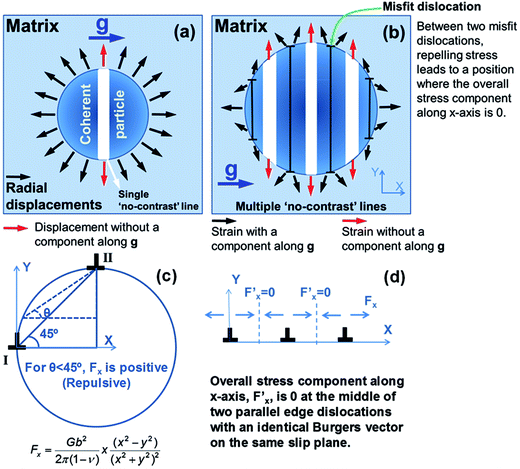
The concepts of a fully coherent particle with a single ‘no-contrast’ line with a spherically symmetrical strain field in Ashby and Brown's paper and a semi-coherent particle with misfit dislocation loops showing multiple ‘no-contrast’ lines are illustrated in Fig. 1a and b. Misfit dislocations at the interfaces are edge dislocations with an identical Burgers vector, and are parallel to each other (Fig. 1b). The strain field around an edge dislocation is symmetrical about the extra half-plane of atoms. Therefore, the repelling stress is offset at the middle of two neighboring parallel edge dislocations with the same Burgers vector (Fig. 1c). Because the angle (θ) between two misfit dislocations on a spherical precipitate is always smaller than 45° (as indicated in Fig. 1d), they repel each other. Thus, we can find a plane between the two parallel misfit dislocations where the overall strain component (Rx) along g is zero (thus g·Rx = 0). Since such a pair of perfectly matched planes exists between every two misfit dislocations, there will be n − 1 ‘no-contrast’ lines (n is the number of misfit dislocations), as illustrated in Fig. 1b. This concept is applied to investigate Y2Ti2O7 particles in an austenitic matrix. It will be shown that a strain field can ideally explain the contrast of semi-coherent Y2Ti2O7 particles, and moiré fringe explanation will not stand for this particular case.
2. Experiment
The austenitic ODS steel in this study has a nominal composition of Fe(bal.)–17Cr–12Ni–2.5Mo–0.3Ti–0.3Y2O3 in wt%. The fabrication processes include mechanical alloying (MA) of pre-alloyed powder with 0.3% Y2O3, consolidation of MA powder by hot isostatic pressing (HIP) at 1150 °C for 4 h, hot rolling of the HIP sample at 1200 °C with a total reduction ratio of 50%, and finally solution heat treated at 1150 °C for 1 hour, followed by air cooling.TEM analyses were conducted at 200 kV by JEOL FE2100F HRTEM equipped with a Si-floating EDS. Electron beam transparent thin foil samples were prepared by standard procedures including slicing, grinding and polishing. The final thinning was performed by jet-polishing at 20 V and 253 K with the a solution of 5 vol% perchloric acid and 95 vol% methanol. Carbon extraction replica samples of the nano-sized oxide particles in the ODS steel sample were also prepared and observed under TEM to obtain more accurate EDS analyses on particle composition and statistical analysis of the particle size distribution by excluding the contrast deterioration due to the matrix. Carbon extraction replica samples were prepared from the electro-polished and etched ODS steel sample surface. The surface was etched by a solution of 2% HF–2% HNO3–96% H2O.
3. Results and discussion
The austenitic ODS steel sample shows ultrafine-grained microstructure, with an average grain size of around 300 nm, as shown in Fig. 2a. Annealing twins account for a high fraction of high angle grain boundaries. Nano-sized particles with a very high number density are uniformly distributed in the steel matrix, as shown in Fig. 2b. Fig. 2c shows images of nano-particles taken from the carbon extraction replica sample. Particles are spherical in shape, and have relatively uniform sizes, ranging from around 3 nm to 30 nm. The average size of particles is around 5 nm. EDS analyses indicated that these particles are Y–Ti–O particles. Selected area diffraction (SAD) and nano-beam electron diffraction (NBED) have demonstrated that these Y–Ti–O particles are Y2Ti2O7 with a FCC crystal structure, and the orientation relationship (OR) between Y2Ti2O7 particles and the austenitic matrix was(![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 20)Y2Ti2O7//(200)Matrix, and (
20)Y2Ti2O7//(200)Matrix, and (![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) 1)Y2Ti2O7//(0
1)Y2Ti2O7//(0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 2)Matrix.49 The Y2Ti2O7 particles are semi-coherent with the matrix, with undistorted misfits of 0.86% along (200)Matrix and 9.45% along (0
2)Matrix.49 The Y2Ti2O7 particles are semi-coherent with the matrix, with undistorted misfits of 0.86% along (200)Matrix and 9.45% along (0![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) 2)Matrix. It was also demonstrated that parallel planes could only be obtained in these two directions. All other lattice planes between the oxide and matrix were tilted by small angles.
2)Matrix. It was also demonstrated that parallel planes could only be obtained in these two directions. All other lattice planes between the oxide and matrix were tilted by small angles.
 | ||
| Fig. 2 (a) Microstructure of the austenitic ODS steel, (b) nano-sized particles in the matrix, and (c) image of nano-sized particles from a carbon extraction replica sample. | ||
Fig. 3a shows a typical image of particles with single no-contrast lines running through particle centers perpendicular to the active g vector, g200, and Fig. 3b shows the same area under g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) . Mostly, 2 or 3 no-contrast lines perpendicular to g02
. Mostly, 2 or 3 no-contrast lines perpendicular to g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) can be seen in a particle image, showing a lobe–lobe morphology. This contrast difference can be understood by considering that misfits along {200} and {022} planes are different. A misfit of 0.86% along (200)Matrix requires 116 planes of (200)Matrix to accommodate a misfit dislocation, which corresponds to a distance of 20.9 nm (116 times 0.18 nm). This distance is larger than the size of the Y2Ti2O7 oxide particles in the image. No misfit dislocation can be formed at the interface along the (200) planes of the matrix, and the diffraction condition under g200 is identical with that of a coherent spherical particle. For (02
can be seen in a particle image, showing a lobe–lobe morphology. This contrast difference can be understood by considering that misfits along {200} and {022} planes are different. A misfit of 0.86% along (200)Matrix requires 116 planes of (200)Matrix to accommodate a misfit dislocation, which corresponds to a distance of 20.9 nm (116 times 0.18 nm). This distance is larger than the size of the Y2Ti2O7 oxide particles in the image. No misfit dislocation can be formed at the interface along the (200) planes of the matrix, and the diffraction condition under g200 is identical with that of a coherent spherical particle. For (02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )Matrix planes, however, a lattice misfit of 9.45% means that a misfit dislocation should be formed for every 10 or 11 planes of (02
)Matrix planes, however, a lattice misfit of 9.45% means that a misfit dislocation should be formed for every 10 or 11 planes of (02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )Matrix, which corresponds to a distance between misfit dislocations of 11 × 1.2728 = 14 Å (d022 = 1.2728 Å). For particles with sizes of 3 nm, 4 nm, and 5 nm, there will be 2, 2, and 3 misfit dislocations, respectively, which are evident in Fig. 3b. Therefore, semi-coherent Y2Ti2O7 particles exhibit different numbers of no-contrast lines under different two-beam conditions owing to the lattice misfit variations along different planes.
)Matrix, which corresponds to a distance between misfit dislocations of 11 × 1.2728 = 14 Å (d022 = 1.2728 Å). For particles with sizes of 3 nm, 4 nm, and 5 nm, there will be 2, 2, and 3 misfit dislocations, respectively, which are evident in Fig. 3b. Therefore, semi-coherent Y2Ti2O7 particles exhibit different numbers of no-contrast lines under different two-beam conditions owing to the lattice misfit variations along different planes.
 | ||
Fig. 3 Ashby–Brown contrast of Y2Ti2O7 particles under different two-beam conditions, (a) g200, (b) g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) . . | ||
However, the fringes shown Fig. 3b indicate that inter-spacings between no-contrast lines are mostly larger than the calculated value of 1.4 nm, and show different values for different particles. Since all of these particles are identified to be the same Y2Ti2O7 particles with the same orientation, this phenomenon cannot be explained by the moiré fringes. Considering that a lattice distortion occurs to reduce the interface stress, the actual d(02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) of the austenite matrix can increase, leading to a smaller lattice misfit at the interface and thus a larger misfit dislocation gap. The relaxation of the interfacial misfit strain and the corresponding broadening of inter-spacing between misfit dislocations can be seen in Fig. 4. Fig. 4a shows diffraction contrast images of particles under g02
) of the austenite matrix can increase, leading to a smaller lattice misfit at the interface and thus a larger misfit dislocation gap. The relaxation of the interfacial misfit strain and the corresponding broadening of inter-spacing between misfit dislocations can be seen in Fig. 4. Fig. 4a shows diffraction contrast images of particles under g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) , while Fig. 4b exhibits misfit dislocations at the interfaces of a typical particle. It can be seen that the inter-spacing between two neighboring misfit dislocations is around 2.8 nm, being far larger than the calculated value of 1.4 nm, indicating large extent of relaxation of the misfit strain at the interface. An inter-spacing of 2.8 nm between no-contrast lines corresponds to a distance of 22 × d{022}Matrix (without lattice distortion). The inter-planar spacing between (02
, while Fig. 4b exhibits misfit dislocations at the interfaces of a typical particle. It can be seen that the inter-spacing between two neighboring misfit dislocations is around 2.8 nm, being far larger than the calculated value of 1.4 nm, indicating large extent of relaxation of the misfit strain at the interface. An inter-spacing of 2.8 nm between no-contrast lines corresponds to a distance of 22 × d{022}Matrix (without lattice distortion). The inter-planar spacing between (02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) )Matrix planes at the oxide/matrix interface after a lattice distortion by a misfit strain comes to be 0.1217 nm (2.8 nm/23). The lattice misfit at the interface thus becomes 4.54%, compared to 9.45% without a lattice distortion, showing a reduction of the lattice misfit at the interface by up to 51.9% due to the lattice distortion. It indicates that the lattice misfit relaxation around semi-coherent interface may play a dominant role in determining the mechanical behaviors.
)Matrix planes at the oxide/matrix interface after a lattice distortion by a misfit strain comes to be 0.1217 nm (2.8 nm/23). The lattice misfit at the interface thus becomes 4.54%, compared to 9.45% without a lattice distortion, showing a reduction of the lattice misfit at the interface by up to 51.9% due to the lattice distortion. It indicates that the lattice misfit relaxation around semi-coherent interface may play a dominant role in determining the mechanical behaviors.
 | ||
Fig. 4 (a) Multiple no-contrast lines on semi-coherent Y2Ti2O7 particles under g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) , (b) HRTEM image of the misfit dislocations at the oxide/matrix interface. , (b) HRTEM image of the misfit dislocations at the oxide/matrix interface. | ||
Above measurement on interfacial misfit strain is consistent with the HRTEM image measurement. Quantitative measurement of lattice displacement and strain map around a semi-coherent Y2Ti2O7 particle was generated by the GPA method on a HRTEM image, as shown in Fig. 5. An introduction to the GPA method can be found in ref. 50. It can be seen that an average lattice displacement of around 4% along [02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] direction is present in the matrix surrounding the particle, being consistent with the results from the diffraction contrast measurement on the inter-spacings between no-contrast lines. It shall be noted that the strain field was affected by the amorphous edge so that the strain was smaller as the particle was near to the sample edge. The volume of the matrix around the Y2Ti2O7 particle with obvious lattice displacement is comparable or larger than the particle volume itself, indicating a strong interfacial strain, which may contribute to the mechanical strength by strain hardening. It also indicates that a lattice distortion exclusively occurred in the matrix, while distortion in the particle is rather small or even ignorable. This occurs due to the fact that Young's modulus of Y2Ti2O7 is much larger than the Fe base matrix.51
] direction is present in the matrix surrounding the particle, being consistent with the results from the diffraction contrast measurement on the inter-spacings between no-contrast lines. It shall be noted that the strain field was affected by the amorphous edge so that the strain was smaller as the particle was near to the sample edge. The volume of the matrix around the Y2Ti2O7 particle with obvious lattice displacement is comparable or larger than the particle volume itself, indicating a strong interfacial strain, which may contribute to the mechanical strength by strain hardening. It also indicates that a lattice distortion exclusively occurred in the matrix, while distortion in the particle is rather small or even ignorable. This occurs due to the fact that Young's modulus of Y2Ti2O7 is much larger than the Fe base matrix.51
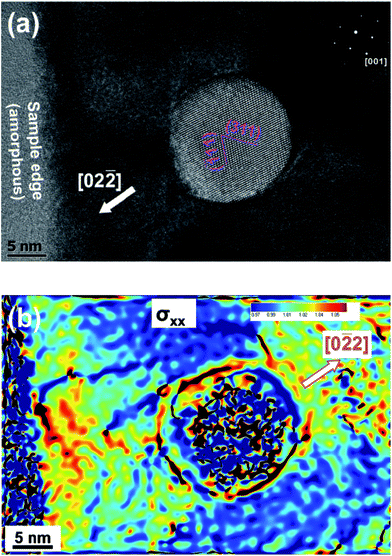 | ||
| Fig. 5 (a) A HRTEM image of a semi-coherent Y2Ti2O7 particle, (b) strain map generated by the GPA method from (a). | ||
Compared to the measurement of interfacial misfit strain by HRTEM, the diffraction contrast method in this work has the advantage of fast statistical measurement on a large number of particles by a single TEM image, as illustrated in Fig. 6. Interfacial misfit strain of most particles in Fig. 6 can be readily obtained by measuring the inter-spacings between “no-contrast” lines, which can also distinguish the difference in interfacial strain among different particles. For instance, it could be seen from Fig. 6 that interfacial strain varies from 3.3% to 4.9% among particles, possibly due to the local microstructural features such as dislocations. Fine particles (<3 nm) that are marked by dashed circles exhibited single no-contrast lines, indicating that misfit dislocations were not formed due to the strain relaxation.
 | ||
Fig. 6 Measurement of interfacial misfit strain of a large number of semi-coherent particles by a single two-beam (g02![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) condition TEM image. ) condition TEM image. | ||
Previously the “no-contrast” lines have been illustrated as moiré fringes, which are formed when two sets of lattices are overlapped. However, moiré fringes may not apply to semi-coherent particles that are smaller than 10 nm, as the interfacial misfit strain is dominating the two-beam contrast TEM images. For example, by overlapping (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1
1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )Matrix and (
)Matrix and (![[5 with combining macron]](https://www.rsc.org/images/entities/char_0035_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)Y2Ti2O7 planes and rotating around [011]Matrix by 2.5°, moiré fringes should be observable on particles with sizes of around 5 nm without interface lattice distortion (Fig. 7a). The moiré fringe spacing is about 2.5 nm and the angle between the moiré fringes and (
1)Y2Ti2O7 planes and rotating around [011]Matrix by 2.5°, moiré fringes should be observable on particles with sizes of around 5 nm without interface lattice distortion (Fig. 7a). The moiré fringe spacing is about 2.5 nm and the angle between the moiré fringes and (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1
1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )Matrix planes is about 30.2° according to eqn (2) and (3).52 The theoretical moiré fringes according to the OR between the Y2Ti2O7 lattice and matrix without distortion are illustrated in Fig. 7a. The sample was then tilted to be under g
)Matrix planes is about 30.2° according to eqn (2) and (3).52 The theoretical moiré fringes according to the OR between the Y2Ti2O7 lattice and matrix without distortion are illustrated in Fig. 7a. The sample was then tilted to be under g![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1, where interference lattice planes of (
1, where interference lattice planes of (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1
1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )Matrix and (
)Matrix and (![[5 with combining macron]](https://www.rsc.org/images/entities/char_0035_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)Y2Ti2O7 are edge on. In this study, no such fringes on fine particles were observed under g
1)Y2Ti2O7 are edge on. In this study, no such fringes on fine particles were observed under g![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1 (Fig. 7b). Several other two-beam conditions such as g112, g(13
1 (Fig. 7b). Several other two-beam conditions such as g112, g(13![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )were investigated, and no fringes were observed. It shows that a moiré fringe explanation does not apply here. Moiré fringes were not formed under these conditions due to the fact that the image contrast is dominated by the distorted interface instead of perfect crystals of Y2Ti2O7 and the austenite matrix. Tilting by 2.5° between (
)were investigated, and no fringes were observed. It shows that a moiré fringe explanation does not apply here. Moiré fringes were not formed under these conditions due to the fact that the image contrast is dominated by the distorted interface instead of perfect crystals of Y2Ti2O7 and the austenite matrix. Tilting by 2.5° between (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1
1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )Matrix and (
)Matrix and (![[5 with combining macron]](https://www.rsc.org/images/entities/char_0035_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)Y2Ti2O7 planes indicates that the strain field is asymmetrical under g
1)Y2Ti2O7 planes indicates that the strain field is asymmetrical under g![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1. The combined lattice displacement parallel to g
1. The combined lattice displacement parallel to g![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif)
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1 is never (x ≠ 0), and g·R ≠ 0 according to eqn (1).
1 is never (x ≠ 0), and g·R ≠ 0 according to eqn (1).
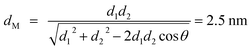 | (2) |
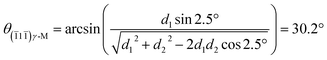 | (3) |
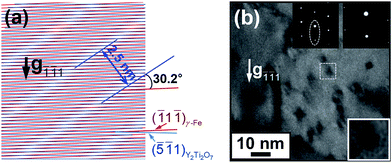 | ||
Fig. 7 (a) Moiré fringes formed by overlapping undistorted (![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1 1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) )Matrix and ( )Matrix and (![[5 with combining macron]](https://www.rsc.org/images/entities/char_0035_0304.gif) ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1)Y2Ti2O7 planes and rotating by 2.5°; (b) no such moiré fringes were observed on the TEM images taken under the condition. 1)Y2Ti2O7 planes and rotating by 2.5°; (b) no such moiré fringes were observed on the TEM images taken under the condition. | ||
4. Conclusion
This study gives a fast quantitative method for measurement of the interfacial strain around semi-coherent particles that are smaller than 10 nm. The underlying mechanism lies on the formation of “no-contrast” lines due to the symmetry of the interfacial strain field around semi-coherent particles under proper two-beam conditions. Application of this method on semi-coherent Y2Ti2O7 particles in austenitic ODS steel revealed an substantial decrease of the misfit strain by 51.9% compared to that estimated from undistorted lattices. This method is expected to contribute to the correlation between microstructure and mechanical strength of alloys that are strengthened by semi-coherent particles.Acknowledgements
The authors would like to thank the great help from the other members of FDS team. This work was supported by the One Hundred Talents Program of Chinese Academy of Sciences and the National Magnetic Confinement Fusion Science Program of China with Grant No. 2013GB108005.References
- S. B. Sinnotta and E. C. Dickey, Mater. Sci. Eng., R, 2003, 43, 1–59 CrossRef
.
- J. Chakhalian, J. W. Freeland, H.-U. Habermeier, G. Cristiani, G. Khaliullin, M. van Veenendaal and B. Keimer, Science, 2007, 318, 1114–1117 CrossRef CAS PubMed
.
- J. Mannhart and D. G. Schlom, Science, 2010, 327, 1607–1611 CrossRef CAS PubMed
.
- H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa and Y. Tokura, Nat. Mater., 2012, 11, 103–113 CrossRef CAS PubMed
.
- F. Huang, B. Cho, H.-S. Chung, S. B. Son, J. H. Kim, T.-S. Bae, H. J. Yun, J. I. Sohn, K. H. Oh, M. G. Hahm, J. H. Park and W.-K. Hong, Nanoscale, 2016, 8, 17598–17607 RSC
.
- C. Capdevila, M. M. Aranda, R. Rementeria, J. Chao, E. Urones-Garrote, J. Aldazabal and M. K. Miller, Acta Mater., 2016, 107, 27–37 CrossRef CAS
.
- A. Hirata, T. Fujita, Y. R. Wen, J. H. Schneibel, C. T. Liu and M. W. Chen, Nat. Mater., 2011, 10, 922–926 CrossRef CAS PubMed
.
- P. Luches, V. Bellini, S. Colonna, L. Di Giustino, F. Manghi, S. Valeri and F. Boscherini, Phys. Rev. Lett., 2006, 96, 106106 CrossRef CAS PubMed
.
- F. Ernst, Mater. Sci. Eng., R, 1995, 14, 97–156 CrossRef
.
- D. A. Shashkov, M. F. Chisholm and D. N. Seidman, Acta Mater., 1999, 47, 3939–3951 CrossRef CAS
.
- P. L. Galindo, S. Kret, A. M. Sanchez, J.-Y. Laval, A. Yáñez, J. Pizarro, E. Guerrero, T. Ben and S. I. Molina, Ultramicroscopy, 2007, 107, 1186–1193 CrossRef CAS PubMed
.
- S.-C. Wang, M.-Y. Lu, A. Manekkathodi, P.-H. Liu, H.-C. Lin, W.-S. Li, T.-C. Hou, S. Gwo and L.-J. Chen, Nano Lett., 2014, 14, 3241–3246 CrossRef CAS PubMed
.
- N. Homonnay, K. J. ÓShea, C. Eisenschmidt, M. Wahler, D. A. MacLaren and G. Schmidt, ACS Appl. Mater. Interfaces, 2015, 7, 22196–22202 CAS
.
- N. Li, S. K. Yadav, Y. Xu, J. A. Aguiar, J. K. Baldwin, Y. Q. Wang, H. M. Luo, A. Misra and B. P. Uberuaga, Sci. Rep., 2017, 7, 40148 CrossRef CAS PubMed
.
- J. L. Du, L. Y. Zhang, E. G. Fu, X. Ding, K. Y. Yu, Y. G. Wang, Y. Q. Wang, J. K. Baldwin, X. J. Wang and P. Xu, Appl. Surf. Sci., 2017, 410, 585–592 CrossRef CAS
.
- M. F. Ashby and L. M. Brown, Philos. Mag., 1963, 8, 1083–1103 CrossRef
.
- V. A. Philips, Acta Metall., 1966, 14, 1533–1547 CrossRef
.
- P. H. Pumphery and J. W. Edington, Acta Metall., 1974, 22, 89–94 CrossRef
.
- I. Ishida and M. Kiritani, Acta Metall., 1988, 36, 2129–2139 CrossRef CAS
.
- P. Dou, A. Kimura, T. Okuda, M. Inoue, S. Ukai, S. Ohnuki, T. Fujisawa and F. Abe, Acta Mater., 2011, 59, 992–1002 CrossRef CAS
.
- J. Ribis and Y. de Carlan, Acta Mater., 2012, 60, 238–252 CrossRef CAS
.
- T. Hu, J. H. Chen, J. Z. Liu, Z. R. Liu and C. L. Wu, Acta Mater., 2013, 61, 1210–1219 CrossRef CAS
.
- E. B. Watkins, A. Kashinath, P. Wang, J. K. Baldwin, J. Majewski and M. J. Demkowicz, Appl. Phys. Lett., 2014, 105, 041601 CrossRef
.
- X. Fan, D. Jiang, Q. Meng, Z. Lai and X. Zhang, Mater. Sci. Eng., A, 2006, 427, 130–135 CrossRef
.
- Y. Yamamoto, M. P. Brady, Z. P. Lu, P. J. Maziasz, C. T. Liu, B. A. Pint, K. L. More, H. M. Meyer and E. A. Payzant, Science, 2007, 20, 433–436 CrossRef PubMed
.
- G. R. Odette, M. J. Alinger and B. D. Wirth, Annu. Rev. Mater. Res., 2008, 38, 471–503 CrossRef CAS
.
- A. Kimura, R. Kasada, A. Kohyama, H. Tanigawa, T. Hirose, K. Shiba and R. L. Klueh, J. Nucl. Mater., 2007, 367, 60–67 CrossRef
.
- M. J. Alinger, G. R. Odette and D. T. Hoelzer, Acta Mater., 2009, 57, 392–406 CrossRef CAS
.
- Y. de Carlan, J. L. Bechade, P. Dubuisson, J. L. Seran, P. Billot, A. Bougault, T. Cozzika, S. Doriot, D. Hamon, J. Henry, M. Ratti, N. Lochet, D. Nunes, P. Olier, T. Leblond and M. H. Mathon, J. Nucl. Mater., 2009, 386, 430–432 CrossRef
.
- J. H. Schneibel, C. T. Liu, M. K. Miller, M. J. Mills, P. Sarosi, M. Heilmaierc and D. Sturm, Scr. Mater., 2009, 61, 793–796 CrossRef CAS
.
- P. Dou, A. Kimura, R. Kasada, T. Okuda, M. Inoue, S. Ukai, S. Ohnuki, T. Fujisawa and F. Abe, J. Nucl. Mater., 2013, 442, S95–S100 CrossRef CAS
.
- A. Kashinath, A. Misra and M. J. Demkowicz, Phys. Rev. Lett., 2013, 110, 086101 CrossRef CAS PubMed
.
- A. Ramar, N. Baluc and R. Schäublin, J. Nucl. Mater., 2009, 386, 515–519 CrossRef
.
- L. Hsiung, M. Fluss, S. Tumey, J. Kuntz, B. El-Dasher, M. Wall, B. Choi, A. Kimura, F. Willaime and Y. Serruys, J. Nucl. Mater., 2011, 409, 72–79 CrossRef CAS
.
- Y. Miao, K. Mo, B. Cui, W.-Y. Chen, M. K. Miller, K. A. Powers, V. McCreary, D. Gross, J. Almer, I. M. Robertson and J. F. Stubbins, Mater. Charact., 2015, 101, 136–143 CrossRef CAS
.
- S. Y. Zhong, J. Ribis, T. Baudin, N. Lochet, Y. de Carlan, V. Klosek and M. H. Mathon, J. Nucl. Mater., 2014, 452, 359–363 CrossRef CAS
.
- H. Oka, M. Watanabe, N. Hashimoto, S. Ohnuki, S. Yamashita and S. Ohtsuka, J. Nucl. Mater., 2013, 442, 164–168 CrossRef
.
- X. Mao, T. K. Kim, S. S. Kim, Y. S. Han and J. Jang, J. Nucl. Mater., 2015, 461, 329–335 CrossRef CAS
.
- D. Mukherji, R. Gilles, B. Barbier, D. Del Genovese, B. Hasse, P. Strunz, T. Wroblewski, H. Fuess and J. Rösler, Scr. Mater., 2003, 48, 333–339 CrossRef CAS
.
- A. G. Khachaturyan, S. Semenovskaya and T. Tsakalakos, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15909 CrossRef CAS
.
- S. Onaka, T. Fujii and M. Kato, Mech. Mater., 1995, 20, 329–336 CrossRef
.
- A. Kiris and E. Inan, Int. J. Solids Struct., 2006, 43, 4720–4738 CrossRef
.
- C. Shen, J. P. Simmons and Y. Wang, Acta Mater., 2006, 54, 5617–5630 CrossRef CAS
.
- Y. Gao, H. Liu, R. Shi, N. Zhou, Z. Xu, Y. M. Zhu, J. F. Nie and Y. Wang, Acta Mater., 2012, 60, 4819–4832 CrossRef CAS
.
- A. J. Vattré and M. J. Demkowicz, Acta Mater., 2015, 82, 234–243 CrossRef
.
- Y. Q. Sun, X. M. Gu and P. M. Hazzledine, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 220103 CrossRef
.
- Q. Huang, N. Baluc and Y. Dai, et al., J. Nucl. Mater., 2013, 442, S2–S8 CrossRef CAS
.
- Y. Wu, Z. Chen and L. Hu, et al., Nat. Energy, 2016, 1, 16154 CrossRef CAS
.
- X. Mao, K. H. Oh, S. H. Kang, T. K. Kim and J. Jang, Acta Mater., 2015, 89, 141–152 CrossRef CAS
.
- M. J. Hÿtch, E. Snoeck and R. Kilaas, Ultramicroscopy, 1998, 74, 131–146 CrossRef
.
- L. F. He, J. Shirahata, T. Nakayama, T. Suzuki, H. Suematsu, I. Ihara, Y. W. Bao, T. Komatsu and K. Niihara, Scr. Mater., 2011, 64, 548–551 CrossRef CAS
.
- M. Abolhassani and M. Mirzaei, Appl. Opt., 2007, 46, 7924–7926 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2017 |