Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The mechanical and thermodynamic properties of β-Si1−xC
Qiang Zhao *a,
Zheng Zhanga,
Yang Lia and
Xiaoping Ouyangabc
*a,
Zheng Zhanga,
Yang Lia and
Xiaoping Ouyangabc
aBeijing Key Laboratory of Passive Safety Technology for Nuclear Energy, North China Electric Power University, Beijing 102206, P. R. China. E-mail: qzhao@ncepu.edu.cn; Fax: +86 10 61773156; Tel: +86 10 61773165
bNorthwest Institute of Nuclear Technology, Xi’an 710024, P. R. China
cSchool of Materials Science and Engineering, Xiangtan University, Xiangtan 411105, P. R. China
First published on 31st May 2017
Abstract
By using the first-principles calculation method based on density functional theory (DFT), we investigated the stability, mechanical properties and thermodynamic performance of the carbon-rich β-Si1−xC. Our results show that the volume of the β-Si1−xC crystal decreases when the x value increases, while the density of β-Si1−xC increases when the x value increases. When the x value is smaller than 0.8148, the formation energy of β-Si1−xC increases when the x value increases, whereas when the x value is larger than 0.8148, the formation energy decreases when the x value increases.The binding energy value of β-Si1−xC declines with the increase of x value, which indicates that the stability of β-Si1−xC decreased as the x value increases. The bulk modulus, shear modulus and Young modulus increase upon increasing the x value, but the Poisson’s ratio of β-Si1−xC decreases when the x value increases. There is a nearly linear relationship between the thermodynamic properties of β-Si1−xC and the x value, and the change in the thermodynamic properties is mainly due to the change in the lattice vibration. Our results provide theoretical support for the development of β-SiC.
1 Introduction
Silicon carbide (SiC) has received more and more attention since the 1890s when it was discovered. SiC is a promising material that is used in the nuclear industry due to its excellent properties such as high corrosion resistance, good thermal conductivity, low neutron absorption cross section and retention rate of the fission gas. SiC is not only a cladding material1–5 that is used in light water reactors or a nuclear fuel coating material6–14 that is used in high temperature gas cooled reactors, but is also used in the structure of first wall materials15–21 that are used in fusion devices. SiC has many polytypes depending on the different stacking of the Si–C close-packed atomic plane.22–24 More than 200 polytypes have currently been reported from the wide variety of preferred stacking sequences.25 The most common polytypes are 3C, 4H, 6H and 15R, where the leading number shows the repetition of the Si–C pair and where C, H and R represent cubic, hexagonal and rhombohedral crystals, respectively. The 3C–SiC crystal is known as β-SiC, and our research in this paper is based on the 3C polytype matrix.With the development of the nuclear industry, research into SiC has never stopped. Y. Katoh,17 R. H. Jones26 and A. Hasegawa27 studied the application of SiC ceramic materials in the fusion field, and they found the critical issue of the application of SiC in the fusion field. L. L. Snead,28 G. Newsome29 and Y. Katoh30 studied the influence of neutron irradiation on SiC; their results showed that the swelling of SiC is associated with the dose of neutrons and the experimental temperature, and that the strength of SiC decreases after neutron irradiation. K. A. Terrani31 and J. G. Stone3 studied SiC that was used as fuel cladding. Their results indicated that the dissolved oxygen activity in water can greatly accelerate the performance degradation of SiC since it has a large reaction rate constant. Although irradiation of the particles led to swelling of the SiC, SiC provides a reliable, impermeable barrier to the release of fission products. All of the research works demonstrate that the application of silicon carbide in the nuclear industry is reasonable. There are a lot research works focusing on SiC that use the molecular dynamics method.32–35 However, a first-principles study on SiC requires more effort. Recent studies have shown that carbon fiber can reinforce SiC and improve its performance, and some scientists have studied SiC with different Si/C ratios using the molecular dynamics method.36,37 In this paper, we investigate the stability, mechanical and thermodynamic properties of β-Si1−xC by using the first-principles calculation method.
2 Computational details
Using the first-principles calculation method based on density functional theory (DFT),38,39 as implemented in the Cambridge serial total energy package (CASTEP),40 we investigated the stability, mechanical and thermodynamic properties of β-Si1−xC. CASTEP is an ab initio quantum mechanics theory software package based on DFT. The interaction between ions and electrons is described by the plane augmented wave (PAW) pseudopotential method, and the electron wave function is spread by plane wave basis sets. The exchange and correlation functions among the electrons are described by either a local density approximation (LDA) or a generalized gradient approximation (GGA). In this paper we used the GGA41–44 with a Perdew–Burke–Ernzerhol (PBE)45 form to describe the exchange and correlation functions among the electrons. After convergence tests, the parameters of our calculations were chosen as follows: the plane wave cutoff equals 500 eV, the space representation is reciprocal, the SCF tolerance equals 1.0 × 10−6 eV per atom, and k sampling with a 3 × 3 × 3 k-point mesh in the Brillouin zone was used. The optimal atomic positions were determined by satisfying the following conditions: (1) the maximum force on the atoms was smaller than 0.05 eV nm−1, (2) the maximum change of the energy per atom was smaller than 1.0 × 10−5 eV, (3) the maximum displacement was smaller than 0.001 Å and (4) the maximum stress of the crystal was smaller than 0.02 GPa. All of the properties of β-SiC that we calculated in this paper are based on the optimized crystal structure.Phonon calculations were carried out using the linear response method (density functional perturbation theory) applied with a norm-conserving pseudo-potential. A q-point grid of 10 × 10 × 10 was applied along with a cutoff energy of 500 eV for β-Si1−xC. The thermodynamic properties of β-Si1−xC were obtained via the resultant phonon dispersion curve. Based on the phonon calculations, the enthalpy (H), free energy (F), entropy (S) and heat capacity (CV) as functions of temperature at a finite temperature could be computed. The vibrational contributions to the thermodynamic parameters were evaluated using Debye’s quasi-harmonic approximation:
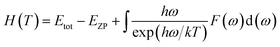 | (1) |
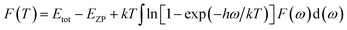 | (2) |
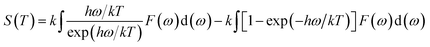 | (3) |
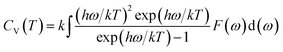 | (4) |
The Debye temperature, ΘD, can be estimated from analysis of the heat capacity using the following equations:
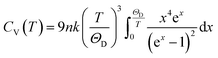 | (5) |
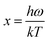 | (6) |
β-SiC is usually known as 3C–SiC and it possesses a cubic phase zinc blende structure. Every atom in SiC is surrounded by four heterogeneous atoms and they combine together through the directional strong tetrahedral sp3 bonds. The space group of β-SiC is F43m (196) and its crystal structure is shown in Fig. 1. In the cell, silicon atoms are located in the cubic vertex angles and the face centres and carbon atoms are located in the sites that are a quarter of the diagonal. In order to study the stability, mechanical and thermodynamic properties of β-Si1−xC, we choose a 2a0 × 2a0 × 2a0 supercell, where a0 is the lattice constant of a perfect β-SiC cell. To study the stability, mechanical and thermodynamics properties of β-Si1−xC with a series of different x values, we randomly replaced two silicon atoms with carbon atoms at every step, and we made sure to do this in a symmetrical manner as much as possible, e.g., the first silicon atom that will be replaced by a carbon atom is in the upper left corner of the supercell, the next silicon atom is in the lower right corner. Our calculations showed that the substituted carbon atoms preferred to be far away from each other in the supercell because the total energy of the supercell (when the substituted carbon atoms are far away from each other) was lower than that of the supercell with the substituted carbon atoms clustered together. When all of the silicon atoms in β-SiC were replaced by carbon atoms, we referred to it as diamond-C.
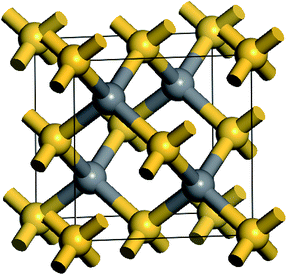 | ||
| Fig. 1 Schematic diagram of the β-SiC cell structure; the golden and gray balls correspond to silicon and carbon atoms, respectively. | ||
3 Results and discussion
3.1 Geometry optimization results
By optimizing the supercell, we can determine the stable structure of β-Si1−xC. The lattice constants and the densities of β-Si1−xC are shown in Fig. 2 and Table 1. Table 1 shows that our calculated lattice constants are in good agreement with the results of other researchers. Fig. 2(a) shows that the lattice constants decrease when the x value increases; this result is caused by the difference in the size of the carbon atoms and silicon atoms. We can describe the relationship between the lattice constants of β-Si1−xC and the x value using the equation a = 0.87381 − 0.09547x + 0.04033x2 − 0.10334x3. Fig. 2(b) shows that the density of β-Si1−xC increases when the x value increases; this is because the decline rate of the mass of the β-Si1−xC supercell is less than that of the volume.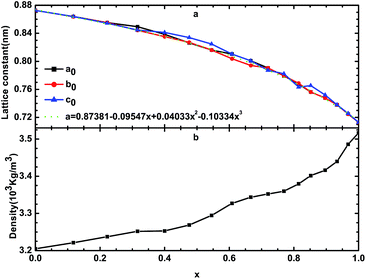 | ||
| Fig. 2 Lattice constants (a) and densities (b) of β-Si1−xC; a0, b0 and c0 are the lattice constants of β-Si1−xC; the dotted line is the line of best fit. | ||
| Symbol | a0/nm | B/GPa | G/GPa | E/GPa | ν |
|---|---|---|---|---|---|
| β-SiC | 0.436 | 212.519 | 189.643 | 324.026 | 0.246 |
| Cal.46 | 0.433 | 215 | 181.8 | 425.3 | 0.17 |
| Cal.47 | 0.438 | 207.026 | 142.374 | 347.469 | 0.22 |
| Exp. | 0.436 (ref. 48) | 225 (ref. 49) | 192 (ref. 50) | 314.2 (ref. 51) | 0.267 (ref. 49) |
| Diamond-C | 0.357 | 431.206 | 523.598 | 1029.379 | 0.102 |
| Cal.52 | 0.358 | 406.776 | 542.571 | 1046.993 | 0.071 |
| Cal.53 | 0.356 | 431.9 | 520.3 | 1113.7 | 0.077 |
| Exp. | 0.357 (ref. 54) | 443 (ref. 54) | 535 (ref. 54) | 1050 (ref. 48) | 0.1 (ref. 48) |
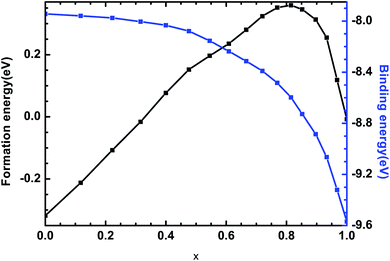
3.2 Formation energy and binding energy
The formation energy and binding energy are two important parameters that reflect the stability of the β-Si1−xC crystal structure. The computational formulae for calculating the crystal formation energy and binding energy are as follows:
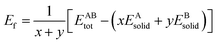 | (7) |
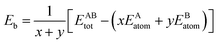 | (8) |
3.3 Mechanical properties
As an important structural material that is used in the nuclear industry, the mechanical properties of β-SiC are very important. We calculated the mechanical properties of β-Si1−xC with a series of different x values. Table 1 shows the mechanical properties of β-SiC and diamond-C; the results of our calculations are in good agreement with the results from other theoretical calculations and experimental data. Fig. 4 shows the mechanical properties of β-Si1−xC with different x values. On the whole, the values of the bulk modulus, shear modulus and Young’s modulus of β-Si1−xC increase when the x value is increased, and the Poisson’s ratio of β-Si1−xC decreases when the x value is increased. To our knowledge, the material is ductile if the value of G/B is smaller than 0.57, and the ductility of a material increases when the value of G/B decreases. The material is brittle if the value of G/B is larger than 0.57; the larger the value, the greater the brittleness of the material. The results of our calculations show that the value of G/B changes from 0.885 to 1.204 upon increasing the x value. No matter how large the value of x is, the β-Si1−xC crystal is a brittle material. β-Si1−xC becomes more and more brittle when the x value is increased, and we come to the same conclusion from the change in the Poisson’s ratio. In Fig. 4(c), there are some values of the Young’s modulus and the Poisson’s ratio that are different from the general trends. The reason for this phenomenon is the asymmetry of the silicon atoms’ positions as the silicon atoms are replaced by carbon atoms. In order to discuss the effects of supercell size on the results, we used 1a × 1a × 1a (8-atoms), 2a × 2a × 2a (64-atoms) and 3a × 3a × 3a (216-atoms) supercell models to check our conclusions in this paper. Fig. 5 shows the mechanical properties of β-Si1−xC based on a series of different supercell sizes, and the results show that the supercell size does not affect the conclusions about the mechanical properties of β-Si1−xC. The general trends shown in Fig. 4 and 5, of the elastic modulus values upon increasing the x value, can be explained by the differences in the bond strengths. The strengths of the bonds between carbon atoms and silicon atoms follow this rule: C–C > C–Si > Si–Si. The higher the number of silicon atoms that are replaced by carbon atoms, the more C–C bonds there are in the β-Si1−xC crystal. Therefore, the β-Si1−xC crystal becomes more difficult to destroy when the x value increases, and the hardness of β-Si1−xC increases when the x value increases.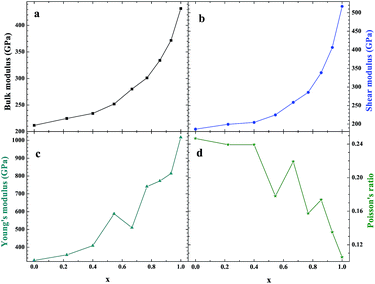 | ||
| Fig. 4 Mechanical properties of β-Si1−xC; bulk modulus (a), shear modulus (b), Young’s modulus (c) and Poisson’s ratio (d). | ||
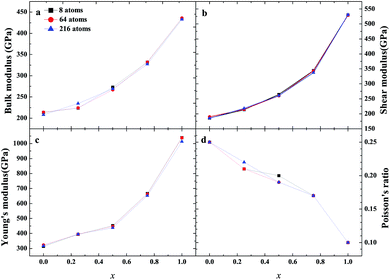 | ||
| Fig. 5 Mechanical properties of β-Si1−xC based on different supercell sizes; bulk modulus (a), shear modulus (b), Young’s modulus (c) and Poisson’s ratio (d). | ||
3.4 Thermodynamic properties
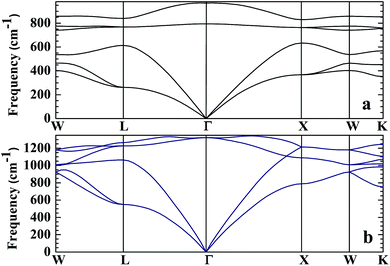
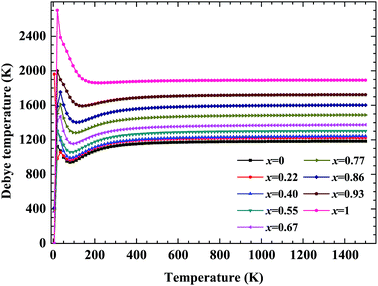
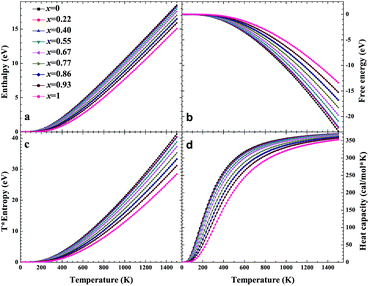
No matter where β-SiC as a structural material is used, whether in a fission reactor or in a fusion device, the thermodynamic properties of β-SiC are very important for its applications. We calculated the thermodynamic properties of β-Si1−xC in order to investigate the effects of carbon content on the thermodynamic properties of β-SiC. Fig. 6(a) and (b) show the phonon dispersion curves of β-SiC and diamond-C, respectively. The results of the phonon dispersion curve of β-SiC are in good agreement with Karch’s computational results.55–58 The difference between the phonon dispersion curves of β-SiC and diamond-C is not obvious, however the frequency of diamond-C is broader when compared with that of β-SiC. The phonon dispersion curves of all of the β-Si1−xC examples were calculated, however we only show the phonon dispersion curves of β-SiC and diamond-C in Fig. 6. Our results show that there is no imaginary frequency, which indicates that the structures of all of the β-Si1−xC examples are stable. The Debye temperature is an important physical property for materials, as it not only represents the interactions of atoms in materials, but is also closely related to the Young’s modulus, dilatation coefficients, specific heat and thermal conductivity. Fig. 7 shows the Debye temperatures of β-Si1−xC, and the results show that the Debye temperature of β-Si1−xC increases when the x value increases, which is in good agreement with the change in the Young’s modulus, which also increases when the x value increases. The Debye temperature of β-SiC determined from our calculations is in good agreement with the reported value in ref. 59.Based on phonon calculations and the Debye quasi-harmonic approximation, we calculated the enthalpy, free energy, entropy and heat capacity of β-Si1−xC. Fig. 8 shows the enthalpy, free energy, entropy and heat capacity of β-Si1−xC, respectively. At the same temperature the value of the free energy increases when the x value increases, and the enthalpy increases almost linearly with temperature and tends to display KbT behavior. The entropy increases slowly with increasing temperature when the temperature is below 300 K, and it increases rapidly when the temperature is above 300 K. As a whole, the enthalpy, entropy and heat capacity of β-Si1−xC decreases when the x value increases. The enthalpy of β-Si1−xC decreases when the x value increases, which suggests that the total energy of β-Si1−xC decreases when the x value increases. The free energy corresponds to the work outside that is converted from the system internal energy in the thermodynamics process. The value of the free energy of β-Si1−xC increases when the x value increases, which means that reducing the internal energy converts less work outside when the x value increases. The change of the free energy also demonstrates that the stability of β-Si1−xC becomes poorer and poorer, especially in high temperature region. The entropy represents the system energy that is not available. Fig. 8(c) shows that the entropy decreases when the x value increases, which demonstrates that less energy is not available when x increases. The heat capacity is the absorption energy when the system rises by one degree centigrade. The heat capacity of β-Si1−xC decreases when x increases; this result means that it becomes easier to heat β-Si1−xC when the x value increases. The thermal conductivity of SiC arises mainly through lattice vibration, and we can deduce the heat conductivity of β-SiC according to the phonon heat capacity. The reasons for the change in the thermodynamic properties are that the number of silicon atoms and carbon atoms changes when x increases, and the difference in atoms leads to the diversity of phonon frequency in the Brillouin zone for the β-Si1−xC structure.
4 Conclusion
In this paper we studied the stability, mechanical and thermodynamic properties of β-Si1−xC via the first-principles calculation method, and the results were as follows:(1) The supercell volume of β-Si1−xC decreases when the x value increases, but the density of β-Si1−xC increases when the x value increases.
(2) The stability of β-Si1−xC becomes poorer and poorer when the x value increases.
(3) The bulk modulus, shear modulus and Young’s modulus of β-Si1−xC increases when the x value increases, and the Poisson’s ratio decreases when x increases. β-Si1−xC becomes more brittle when the x value increases.
(4) The Debye temperature and free energy of β-Si1−xC increases when the x value increases, and the enthalpy, entropy and heat capacity of β-Si1−xC decreases as the x value increases.
All of our results are in good agreement with the existing theoretical and experimental works. The change in the volume and density of β-Si1−xC is associated with the difference of the atomic size. All of the β-Si1−xC examples are stable from the point view of the binding energy. The change in the mechanical properties of β-Si1−xC are mainly due to the changing internal bonds in the supercell. The change in the thermodynamic properties is associated with the difference in the lattice vibration, and the difference arises from the different number of silicon and carbon atoms. Our results suggest that there is a linear relationship between the mechanical properties and the carbon content, and the thermodynamic properties and the carbon content also demonstrate a linear relationship. Our works might provide a theoretical support for the development of carbon fiber reinforced β-SiC.
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 11275071 and 11305061, and the Fundamental Research Funds for the Central Universities under Grant No. 2017MS079.References
- H. Feinroth, A Multi-Layered Ceramic Composite for Impermeable Fuel Cladding for Commercial Water Reactors, Gamma engineering corporation technical report, 2008 Search PubMed.
- K. Yueh, D. Carpenter and H. Feinroth, Nucl. Eng. Int., 2010, 55, 14–16 CAS.
- J. G. Stone, R. Schleicher, C. P. Deck, G. M. Jacobsen, H. E. Khalifa and C. A. Back, J. Nucl. Mater., 2015, 466, 682–697 CrossRef CAS.
- D. M. Carpenter, Ph.D thesis, Massachusetts Institute of Technology, 2010.
- Y. Katoh, L. L. Snead, C. H. Henager, T. Nozawa, T. Hinoki, A. Iveković, S. Novak and S. G. de Vicente, J. Nucl. Mater., 2014, 455, 387–397 CrossRef CAS.
- R. Blackstone and E. H. Voice, J. Nucl. Mater., 1971, 39, 319–322 CrossRef CAS.
- R. J. Price, J. Nucl. Mater., 1969, 33, 17–22 CrossRef CAS.
- R. J. Price, Nucl. Technol., 1977, 35, 320–336 CAS.
- R. J. Price, J. Nucl. Mater., 1973, 48, 47–57 CrossRef CAS.
- W. Primak, L. H. Fuchs and P. P. Day, Phys. Rev., 1956, 103, 1184 CrossRef CAS.
- M. Balarin, Phys. Status Solidi B, 1965, 11, K67–K71 CrossRef CAS.
- D. Littler, Properties of reactor materials and the effects of radiation damage, Butterworths, 1962 Search PubMed.
- R. Stevens, Philos. Mag., 1972, 25, 523–528 CrossRef CAS.
- R. P. Thorne and V. C. Howard, Radiation-induced changes in porous cubic silicon carbide, Eng. Technical Report, United kingdom atomic energy authority, Culcheth, 1967 Search PubMed.
- C. H. Henager, B. N. Nguyen, R. J. Kurtz, T. J. Roosendaal, B. A. Borlaug, M. Ferraris, A. Ventrella and Y. Katoh, J. Nucl. Mater., 2015, 466, 253–268 CrossRef CAS.
- C. H. Henager and R. J. Kurtz, J. Nucl. Mater., 2011, 417, 375–378 CrossRef CAS.
- Y. Katoh, L. L. Snead, C. H. Henager, A. Hasegawa, A. Kohyama, B. Riccardi and H. Hegeman, J. Nucl. Mater., 2007, 367, 659–671 CrossRef.
- P. Colombo, B. Riccardi, A. Donato and G. Scarinci, J. Nucl. Mater., 2000, 278, 127–135 CrossRef CAS.
- S. Sharafat, R. H. Jones, A. Kohyama and P. Fenici, Fusion Eng. Des., 1995, 29, 411–420 CrossRef CAS.
- R. H. Jones and C. H. Henager, J. Nucl. Mater., 1995, 219, 55–62 CrossRef CAS.
- M. Ferraris, M. Salvo, C. Isola, M. A. Montorsi and A. Kohyama, J. Nucl. Mater., 1998, 258, 1546–1550 CrossRef.
- N. W. Jepps and T. F. Page, Prog. Cryst. Growth Charact., 1983, 7, 259–307 CrossRef CAS.
- P. Pirouz and J. W. Yang, Ultramicroscopy, 1993, 51, 189–214 CrossRef CAS.
- P. Shaffer, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 477–488 CrossRef CAS.
- G. R. Fisher and P. Barnes, Philos. Mag., 1990, 61, 217–236 CrossRef CAS.
- R. H. Jones, L. Giancarli, A. Hasegawa, Y. Katoh, A. Kohyama, B. Riccardi, L. L. Snead and W. J. Weber, J. Nucl. Mater., 2002, 307, 1057–1072 CrossRef.
- A. Hasegawa, A. Kohyama, R. Jones, L. Snead, B. Riccardi and P. Fenici, J. Nucl. Mater., 2000, 283, 128–137 CrossRef.
- L. L. Snead, Y. Katoh and S. Connery, J. Nucl. Mater., 2007, 367, 677–684 CrossRef.
- G. Newsome, L. L. Snead, T. Hinoki, Y. Katoh and D. Peters, J. Nucl. Mater., 2007, 371, 76–89 CrossRef CAS.
- Y. Katoh, T. Nozawa, L. L. Snead, K. Ozawa and H. Tanigawa, J. Nucl. Mater., 2011, 417, 400–405 CrossRef CAS.
- K. A. Terrani, Y. Yang, Y.-J. Kim, R. Rebak, H. Meyer and T. J. Gerczak, J. Nucl. Mater., 2015, 465, 488–498 CrossRef CAS.
- H. Kikuchi, R. K. Kalia, A. Nakano, P. Vashishta, P. S. Branicio and F. Shimojo, J. Appl. Phys., 2005, 98, 103524 CrossRef.
- F. Shimojo, I. Ebbsjö, R. K. Kalia, A. Nakano, J. P. Rino and P. Vashishta, Phys. Rev. Lett., 2000, 84, 3338 CrossRef CAS PubMed.
- F. Gao, H. Y. Xiao, X. T. Zu, M. Posselt and W. J. Weber, Phys. Rev. Lett., 2009, 103, 027405 CrossRef PubMed.
- W. H. Lee, X. H. Yao, W. R. Jian and Q. Han, Comput. Mater. Sci., 2015, 98, 297–303 CrossRef CAS.
- A. Adnan and S. F. Ferdous, Comput. Mater. Sci., 2015, 110, 331–339 CrossRef CAS.
- A. Adnan and S. F. Ferdous, Comput. Mater. Sci., 2015, 96, 354–359 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew and W. Yue, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8800 CrossRef.
- J. P. Perdew, J. Chevary, S. Vosko, K. A. Jackson, M. R. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- E. Konstantinova, M. J. V. Bell and V. Anjos, Intermetallics, 2008, 16, 1040–1042 CrossRef CAS.
- X. J. Liu, L. F. Li and F. Lu, Physics, 2013, 1745, 1301–1313 Search PubMed.
- http://www.ioffe.ru/SVA/NSM/Semicond/.
- D. W. Feldman, J. H. Parker Jr, W. J. Choyke and L. Patrick, Phys. Rev., 1968, 173, 787 CrossRef CAS.
- R. D. Carnahan, J. Am. Ceram. Soc., 1968, 51, 223–224 CrossRef CAS.
- P. Vashishta, R. K. Kalia, A. Nakano and J. P. Rino, J. Appl. Phys., 2007, 101, 103515 CrossRef.
- X. J. Liu, L. F. Li, Q. Q. Li, Y. Li and F. Lu, Mater. Sci. Semicond. Process., 2013, 16, 1369–1376 CrossRef CAS.
- H. Yao, L. Ouyang and W.-Y. Ching, J. Am. Ceram. Soc., 2007, 90, 3194–3204 CrossRef CAS.
- H. J. McSkimin and P. Andreatch Jr, J. Appl. Phys., 1972, 43, 2944–2948 CrossRef CAS.
- K. Karch, P. Pavone, W. Windl, D. Strauch and F. Bechstedt, Int. J. Quantum Chem., 1995, 56, 801–817 CrossRef CAS.
- K. Karch, P. Pavone, W. Windl, O. Schütt and D. Strauch, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17054 CrossRef CAS.
- O. Madelung, U. RÃűssler and M. Schulz, Diamond (C) phonon dispersion relations, phonon density of states, Springer, Berlin Heidelberg, 2001, pp. 1–11 Search PubMed.
- B. Monserrat and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 214304 CrossRef.
- A. Zywietz, K. Karch and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1791 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |