Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Investigation of the hole transport characterization and mechanisms in co-evaporated organic semiconductor mixtures
Yanping Wang *a,
Qingcheng Lianga,
Jinying Huangb,
Dongge Ma
*a,
Qingcheng Lianga,
Jinying Huangb,
Dongge Ma bc and
Yurong Jiaod
bc and
Yurong Jiaod
aSchool of Materials Science and Engineering, Changchun University of Science and Technology, Changchun 130022, People's Republic of China. E-mail: ypwang2015@163.com
bState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, People's Republic of China
cInstitute of Polymer Optoelectronic Materials and Devices, State Key Laboratory of Luminescent Materials and Devices, South China University of Technology, Guangzhou 510640, People's Republic of China
dDepartment of Chemistry and Chemical Engineering, Yulin University, Yulin, Shaanxi 719000, People's Republic of China
First published on 30th May 2017
Abstract
The hole transport characteristics in small molecule semiconductor mixtures of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN
NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN
TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP in the ratio of 2
CBP in the ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 have been investigated by admittance spectroscopy measurements. It is found that the hole mobility (10−5–10−4 cm2 V−1 s−1) variation with electric field in HAT-CN
1 have been investigated by admittance spectroscopy measurements. It is found that the hole mobility (10−5–10−4 cm2 V−1 s−1) variation with electric field in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB is the same as that in HAT-CN
NPB is the same as that in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC. The hole transport in HAT-CN
TAPC. The hole transport in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP is space-charge-limited current (SCLC) with exponential distribution traps, different from SCLC with free trap distributions of HAT-CN
CBP is space-charge-limited current (SCLC) with exponential distribution traps, different from SCLC with free trap distributions of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures. The hole mobility in the HAT-CN
TAPC mixtures. The hole mobility in the HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixture is obtained as 10−7–10−5 cm2 V−1 s−1, which is one or two orders of magnitude lower than those of the other two mixtures. It can be seen that the mobility exhibits strong field-dependence in low electric field region. The mobility slightly increases as the electric field increases and almost saturates in high electric field region. It is shown that the trapping effect leads to the much lower hole mobility. The hole transport mechanisms in the three mixtures have been further studied through energy level analysis and atomic force microscopy.
CBP mixture is obtained as 10−7–10−5 cm2 V−1 s−1, which is one or two orders of magnitude lower than those of the other two mixtures. It can be seen that the mobility exhibits strong field-dependence in low electric field region. The mobility slightly increases as the electric field increases and almost saturates in high electric field region. It is shown that the trapping effect leads to the much lower hole mobility. The hole transport mechanisms in the three mixtures have been further studied through energy level analysis and atomic force microscopy.
1 Introduction
In recent times, highly efficient organic optoelectronic devices1–8 have been obtained by using an organic heterojunction structure, including organic light emitting diodes (OLEDs) and organic solar cell (OSCs). As is well known, charge carrier transport is a crucial parameter affecting the performance of these devices. Furthermore, the systematic investigation of the charge transport characteristics in organic semiconductors is very important for establishing the relationship between the transport characteristics and device performance, and improving the performance of the devices. Therefore, it is necessary and desirable to study the transport characteristics in organic semiconductors. In contrast to the rapid progress made in the device performance, the understanding of the charge transport characteristics of the organic heterojunctions is still not clarified.So far the charge carrier transport characteristics in organic semiconductors have been usually analyzed by several techniques, such as time of flight (TOF),9,10 transient electroluminescence (TEL),11,12 space charge limited current (SCLC)13–15 and admittance spectroscopy (AS).16–21 In these techniques, notably, AS has been shown to be a feasible and powerful tool to explore the charge carrier transport kinetics and relaxation processes and involved in optoelectronic devices. In addition, it is applicable to charge carrier transport characteristics of organic semiconductor film whose thickness is approximately comparable to that of practical devices. It can also be applied without the need for a complex experimental setup.
The 1,4,5,8,9 and 11-hexaazatriphenylene-hexacarbonitrile (HAT-CN) material has been drawing a great deal of attention because it has a lot of interesting characteristics.22–28 It has been adapted as the charge generation layer in some tandem OLEDs for higher power efficiency due to its very good electron affinity. It has also been used to modify metal surface electronic properties due to its unoccupied molecular orbital (LUMO) almost close to the Fermi level. However, there are rare reports about the study on HAT-CN organic mixtures by AS measurements. In this work, we systematically investigated the hole transport characteristics and mechanisms in the mixtures of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN
NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN
TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP by current density–voltage characteristics, AS technique, energy level analysis and atomic force microscopy.
CBP by current density–voltage characteristics, AS technique, energy level analysis and atomic force microscopy.
2 Experimental
The hole-only devices were fabricated on glass substrates pre-coated with a 180 nm-thick indium tin oxide (ITO) film with a sheet resistance of ∼10 Ω per square. Before the fabrication process, the ITO surface was thoroughly cleaned in an ultrasonic bath using subsequently detergents and deionized water, dried at 120 °C. The device structure was ITO/HAT-CN (10 nm)/HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X (2
X (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 180 nm)/HAT-CN (10 nm)/Al. Here, X was N,N′-di(naphthalene-1-yl)-N,N′-diphenyl-benzidine (NPB), 4,4′-cyclohexylidenebis[N,N-bis(4-methylphenyl)benze namine] (TAPC) and 4,4′-bis(carbazol-9-yl)-biphenyl (CBP), respectively. Structures of organic molecules are depicted in Fig. 1. All organic materials were grown in succession by thermal evaporation in a high-vacuum (∼4 × 10−4 Pa) without breaking vacuum. The Al electrodes were deposited on the substrates through shadow masks. The active area of device is 4 × 4 mm2. During the deposition process, the rate was controlled with quartz crystal oscillators and monitored by a frequency counter and calibrated by a Dektak 6 M profiler (Veeco).
1, 180 nm)/HAT-CN (10 nm)/Al. Here, X was N,N′-di(naphthalene-1-yl)-N,N′-diphenyl-benzidine (NPB), 4,4′-cyclohexylidenebis[N,N-bis(4-methylphenyl)benze namine] (TAPC) and 4,4′-bis(carbazol-9-yl)-biphenyl (CBP), respectively. Structures of organic molecules are depicted in Fig. 1. All organic materials were grown in succession by thermal evaporation in a high-vacuum (∼4 × 10−4 Pa) without breaking vacuum. The Al electrodes were deposited on the substrates through shadow masks. The active area of device is 4 × 4 mm2. During the deposition process, the rate was controlled with quartz crystal oscillators and monitored by a frequency counter and calibrated by a Dektak 6 M profiler (Veeco).
The current density–voltage (J–V) characteristics were carried out using a Keithley 2400 sourcemeter integrated with a vacuum cryostat (Optistat DN-V, Oxford Instruments). The admittance was measured at room temperature by an Agilent E4980A precision LCR meter in the frequency range of 20 Hz–13 MHz with the oscillation amplitude of the ac voltage kept at 100 mV. The morphologies of the thin films on ITO substrates were tested by atomic force microscopy (AFM) (SPA 400, Seiko Instruments Inc.).
3 Results and discussion
3.1 Current density–voltage characteristics
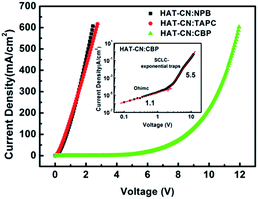
The J–V characteristics of the hole-only devices based on HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN
NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN
TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixtures are shown in Fig. 2. At a constant current density, the driving voltages of HAT-CN
CBP mixtures are shown in Fig. 2. At a constant current density, the driving voltages of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures are close and lower, demonstrating the similar hole transport ability. In our previous work,29 the J–V characteristics of the two devices with different mixing concentration (y) have been discussed in detail. The results showed that their hole conductions (y < 90%) exhibit space-charge-limited current (SCLC) with free trap distributions. Conversely, it is shown a higher voltage for HAT-CN
TAPC mixtures are close and lower, demonstrating the similar hole transport ability. In our previous work,29 the J–V characteristics of the two devices with different mixing concentration (y) have been discussed in detail. The results showed that their hole conductions (y < 90%) exhibit space-charge-limited current (SCLC) with free trap distributions. Conversely, it is shown a higher voltage for HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixture. As shown in the inset, it clearly show two distinct regions: (1) ohmic region, the slope of log
CBP mixture. As shown in the inset, it clearly show two distinct regions: (1) ohmic region, the slope of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J–log
J–log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V curve is about 1.1 at the lower voltage region. (2) SCLC with exponential trap distribution region, the slope of J–V curve in double logarithmic is about 5.5 at higher voltages. For organic semiconductor devices, the charge carrier mobility plays a crucial role in determining the J–V characteristics.
V curve is about 1.1 at the lower voltage region. (2) SCLC with exponential trap distribution region, the slope of J–V curve in double logarithmic is about 5.5 at higher voltages. For organic semiconductor devices, the charge carrier mobility plays a crucial role in determining the J–V characteristics.
In order to clearly demonstrate the similarities and differences in the three hole-only devices, the hole mobilities have been determined by using frequency-dependent AS.
3.2 Mobility characteristics
AS is technique based on the measurement of the frequency-dependent capacitance of an organic thin film. For a two-terminal device consisting of an organic semiconductor with a dielectric constant ε and a thickness d, holes are injected from the anode when it is applied a forward dc bias voltage (Vdc). In the case of application of a small ac signal (modulation), with an angular frequency ω = 2πf, the time-dependent injected charge current density j(t) can be given by:30
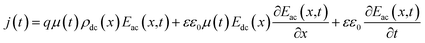 | (1) |
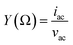 , where G, C and i are the conductance, capacitance and imaginary unit, respectively. It is shown that Y (Ω) can be obtained by applying a Fourier transform to eqn (1):
, where G, C and i are the conductance, capacitance and imaginary unit, respectively. It is shown that Y (Ω) can be obtained by applying a Fourier transform to eqn (1):
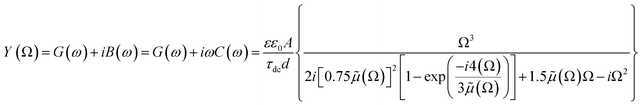 | (2) |
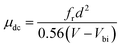 | (3) |
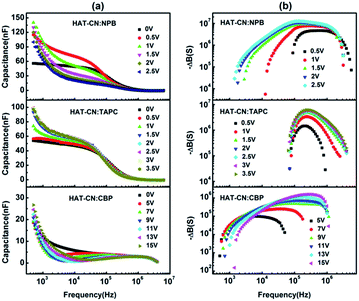
Fig. 3(a) shows C–f curves for the hole-only devices base on HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN
NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN
TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixtures at different applied bias voltages. In the low or intermediate frequency regions, clearly, the capacitances of the three devices decreased with frequency increasing. The reasons are as follows. When the ac-modulation is lower than the characteristic trapping–detrapping time constant, the trap states begin to respond and induce additional capacitive contribution. At further higher frequency, conversely, the trap states cannot follow the ac modulation, the capacitance drops to a plateau, leaving the geometrical capacitance (Cgeo). Toward high frequency, the capacitance becomes little lower than the Cgeo, which is determined by the transit time.31 In the frequency range higher than the fr, the capacitance comes close to the Cgeo because the period of the ac electric field is too short to redistribute the space charges in the mixture devices. As shown in Fig. 3(b), a clear maximum in −ΔB − f occurs at a well defined frequency fr for each device. On the base of eqn (3), the hole mobilities can be calculated, which are summarized in Fig. 4.
CBP mixtures at different applied bias voltages. In the low or intermediate frequency regions, clearly, the capacitances of the three devices decreased with frequency increasing. The reasons are as follows. When the ac-modulation is lower than the characteristic trapping–detrapping time constant, the trap states begin to respond and induce additional capacitive contribution. At further higher frequency, conversely, the trap states cannot follow the ac modulation, the capacitance drops to a plateau, leaving the geometrical capacitance (Cgeo). Toward high frequency, the capacitance becomes little lower than the Cgeo, which is determined by the transit time.31 In the frequency range higher than the fr, the capacitance comes close to the Cgeo because the period of the ac electric field is too short to redistribute the space charges in the mixture devices. As shown in Fig. 3(b), a clear maximum in −ΔB − f occurs at a well defined frequency fr for each device. On the base of eqn (3), the hole mobilities can be calculated, which are summarized in Fig. 4.
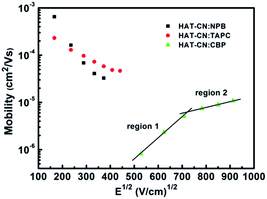 | ||
Fig. 4 Hole mobilities of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixtures against the square root of the electric-field strength. CBP mixtures against the square root of the electric-field strength. | ||
For HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures, the mobilities are in the range of 4.1 × 10−5–6.5 × 10−4 cm2 V−1 s−1 and 5.8 × 10−5–2.3 × 10−4 cm2 V−1 s−1, respectively. As expected from the J–V characteristics of the hole-only devices, HAT-CN
TAPC mixtures, the mobilities are in the range of 4.1 × 10−5–6.5 × 10−4 cm2 V−1 s−1 and 5.8 × 10−5–2.3 × 10−4 cm2 V−1 s−1, respectively. As expected from the J–V characteristics of the hole-only devices, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC have similar and higher hole mobilities. At the same electric field, the mobility (∼10−4 cm2 V−1 s−1) of the two mixtures calculated by AS measurements is one order of magnitude smaller than our previous result (∼10−3 cm2 V−1 s−1)29 obtained by SCLC technique, as shown in Fig. 5. It may be because the effect of the trap was not considered before. In fact, there exhibits the discrete or shallow trap states in HAT-CN
TAPC have similar and higher hole mobilities. At the same electric field, the mobility (∼10−4 cm2 V−1 s−1) of the two mixtures calculated by AS measurements is one order of magnitude smaller than our previous result (∼10−3 cm2 V−1 s−1)29 obtained by SCLC technique, as shown in Fig. 5. It may be because the effect of the trap was not considered before. In fact, there exhibits the discrete or shallow trap states in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures according to their C–f characteristics. As we know, the trap states can greatly influence the charge carrier mobility and even the device performance. In addition, the hole mobilities slightly decrease with the electric field increasing, which is in agreement to our previous result.29 The phenomenon of the slightly decreased mobility is considered as to be originated from the presence of certain energetic disorder.32,33 When the descent of the electrostatic potential is comparable and even transcends the energy barrier, for an along-field jump, the dwell time of a carrier on a site approaches the reciprocal rate for that jump because the jump reverse the electric field direction are gradually eliminated. As a result, the transport velocity will saturate with the electric field. Correspondingly, the carrier τdc does not change with the increment of applied voltage. This implies a linear decrease of the carrier mobility because it is controlled by energetically downward jump only that is not accelerated. For HAT-CN
TAPC mixtures according to their C–f characteristics. As we know, the trap states can greatly influence the charge carrier mobility and even the device performance. In addition, the hole mobilities slightly decrease with the electric field increasing, which is in agreement to our previous result.29 The phenomenon of the slightly decreased mobility is considered as to be originated from the presence of certain energetic disorder.32,33 When the descent of the electrostatic potential is comparable and even transcends the energy barrier, for an along-field jump, the dwell time of a carrier on a site approaches the reciprocal rate for that jump because the jump reverse the electric field direction are gradually eliminated. As a result, the transport velocity will saturate with the electric field. Correspondingly, the carrier τdc does not change with the increment of applied voltage. This implies a linear decrease of the carrier mobility because it is controlled by energetically downward jump only that is not accelerated. For HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP device, however, the hole mobility is in the range of 10−7–10−5 cm2 V−1 s−1. The mobility curve demonstrates two linear parts. (1) In low electric field region, it can be seen that the mobility (8.2 × 10−7–5.1 × 10−6 cm2 V−1 s−1) exhibits strong field-dependence and sharply increases as the applied electric field increases. (2) In high electric field region, the mobility (7.4 × 10−6–1.1 × 10−5 cm2 V−1 s−1) slightly increases as the electric field increases and almost saturates. This increase should be the trapping effect of trap states. When the electric field increased, the trap depth can be decreased by Poole–Frenkel effect, leading to the increasing mobility. As shown in the inset in Fig. 1, at high applied bias voltage, the J–V curve shows the conductance property of SCLC with exponential traps. This suggests that the hole transport in HAT-CN
CBP device, however, the hole mobility is in the range of 10−7–10−5 cm2 V−1 s−1. The mobility curve demonstrates two linear parts. (1) In low electric field region, it can be seen that the mobility (8.2 × 10−7–5.1 × 10−6 cm2 V−1 s−1) exhibits strong field-dependence and sharply increases as the applied electric field increases. (2) In high electric field region, the mobility (7.4 × 10−6–1.1 × 10−5 cm2 V−1 s−1) slightly increases as the electric field increases and almost saturates. This increase should be the trapping effect of trap states. When the electric field increased, the trap depth can be decreased by Poole–Frenkel effect, leading to the increasing mobility. As shown in the inset in Fig. 1, at high applied bias voltage, the J–V curve shows the conductance property of SCLC with exponential traps. This suggests that the hole transport in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP mixture is trap-controlled. It is clearly evident that the trapping effect leads to the much lower hole mobility.
CBP mixture is trap-controlled. It is clearly evident that the trapping effect leads to the much lower hole mobility.
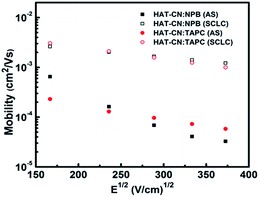 | ||
Fig. 5 Hole mobilities of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures against the square root of the electric-field strength obtained by AS and SCLC techniques, respectively. TAPC mixtures against the square root of the electric-field strength obtained by AS and SCLC techniques, respectively. | ||
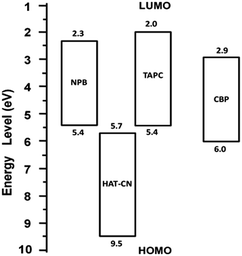
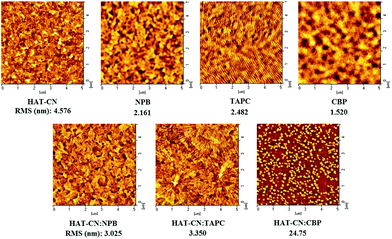
3.3 Holes transport mechanisms of mixtures
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP device. The hole mobility of the device is very low due to the influence of traps.
CBP device. The hole mobility of the device is very low due to the influence of traps.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP is as high as 24.75 nm, which is unfavorable for the hole transport. It is further explained the reason of the lowest holes mobility in HAT-CN
CBP is as high as 24.75 nm, which is unfavorable for the hole transport. It is further explained the reason of the lowest holes mobility in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP device. On the contrary, the RMS of HAT-CN
CBP device. On the contrary, the RMS of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC is 3.025 nm and 3.350 nm, respectively, which is relatively small and close. It is suggested that they have high and similar hole mobilities.
TAPC is 3.025 nm and 3.350 nm, respectively, which is relatively small and close. It is suggested that they have high and similar hole mobilities.
4 Conclusions
In summary, we have studied the hole transport characteristics and mechanisms of the three small molecule mixtures of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB, HAT-CN
NPB, HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC and HAT-CN
TAPC and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP. The current–voltage characteristics show that the holes conductions are both SCLC. The hole mobilites of HAT-CN
CBP. The current–voltage characteristics show that the holes conductions are both SCLC. The hole mobilites of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC are determined to be orders of ∼10−4 cm2 V−1 s−1 by AS measurements, which slightly decrease as the electric field increases. Nevertheless, the hole transport in HAT-CN
TAPC are determined to be orders of ∼10−4 cm2 V−1 s−1 by AS measurements, which slightly decrease as the electric field increases. Nevertheless, the hole transport in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP is SCLC with exponential distribution traps. The hole mobility of HAT-CN
CBP is SCLC with exponential distribution traps. The hole mobility of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP is obtained from 8.2 × 10−7 to 1.1 × 10−5 cm2 V−1 s−1, which shows two regions. At low electric field region, the hole mobility (8.2 × 10−7–5.1 × 10−6 cm2 V−1 s−1) sharply increases with increasing the electric field. Whereas at high electric field region, the mobility (7.4 × 10−6–1.1 × 10−5 cm2 V−1 s−1) slightly increases with increasing the electric field, and almost reaches saturate with the electric field, which should result from the trapping of trap states. Furthermore, the energy level analysis suggests that there are charge carrier generation in HAT-CN
CBP is obtained from 8.2 × 10−7 to 1.1 × 10−5 cm2 V−1 s−1, which shows two regions. At low electric field region, the hole mobility (8.2 × 10−7–5.1 × 10−6 cm2 V−1 s−1) sharply increases with increasing the electric field. Whereas at high electric field region, the mobility (7.4 × 10−6–1.1 × 10−5 cm2 V−1 s−1) slightly increases with increasing the electric field, and almost reaches saturate with the electric field, which should result from the trapping of trap states. Furthermore, the energy level analysis suggests that there are charge carrier generation in HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC. The CBP molecule acts as a trap during the hole transport process. AFM images clearly show the film surfaces of HAT-CN
TAPC. The CBP molecule acts as a trap during the hole transport process. AFM images clearly show the film surfaces of HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NPB and HAT-CN
NPB and HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TAPC mixtures are relatively smooth, which is beneficial to the hole transport. The HAT-CN
TAPC mixtures are relatively smooth, which is beneficial to the hole transport. The HAT-CN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CBP film exhibits much rough, indicating the poor hole transport ability. Our results further demonstrate that AS is a simple and powerful tool for the characterization of charge carrier transport properties in organic semiconductor mixtures. We believe that our results will provide critical theoretical information for material selection, device structure design and performance analysis.
CBP film exhibits much rough, indicating the poor hole transport ability. Our results further demonstrate that AS is a simple and powerful tool for the characterization of charge carrier transport properties in organic semiconductor mixtures. We believe that our results will provide critical theoretical information for material selection, device structure design and performance analysis.
Acknowledgements
The authors gratefully acknowledge the National Natural Science Foundation of China (51333007, 91433201, 61204059), Ministry of Science and Technology of China (973 program No. 2013CB834805), the Foundation of Jilin Research Council (2012ZDGG001, 20130206003GX), Chinese Academy of Sciences (KGZD-EW-303-3), Scientific Research Foundation of the Education Department of Shaanxi Province, China (15JK1849) for the support of this research.References
- G. Yu, J. Gao, J. C. Hummelen and A. J. Heeger, Science, 1995, 270, 1789–1791 CAS.
- L. S. Liao and K. P. Klubek, Appl. Phys. Lett., 2008, 92, 223311 CrossRef.
- W. S. Jeon, J. S. Park, L. Li, D. C. Lim, Y. H. Son, M. C. Suh and J. H. Kwon, Org. Electron., 2012, 13, 939–944 CrossRef CAS.
- Q. X. Guo, H. D. Sun, J. X. Wang, D. Z. Yang, J. S. Chen and D. G. Ma, J. Mater. Chem. C, 2016, 4, 376–382 RSC.
- H. D. Sun, Q. X. Guo, D. Z. Yang, Y. H. Chen, J. S. Chen and D. G. Ma, ACS Photonics, 2015, 2, 271–279 CrossRef CAS.
- L. Burtone, D. Ray, K. Leo and M. Riede, J. Appl. Phys., 2012, 111, 064503 CrossRef.
- N. Gasparini, S. Righi, F. Tinti, A. Savoini, A. Cominetti, R. Po and N. Camaioni, ACS Appl. Mater. Interfaces, 2014, 6, 21416–21425 CAS.
- W. L. Ma, C. Y. Yang, X. Gong, K. Lee and A. J. Heeger, Adv. Funct. Mater., 2005, 15, 1617–1622 CrossRef CAS.
- M. Redecker, D. D. C. Bradley, M. Inbasekaran and E. P. Woo, Appl. Phys. Lett., 1998, 73, 1565 CrossRef CAS.
- A. J. Campbell, D. D. C. Bradley and H. Antoniadis, J. Appl. Phys., 2001, 89, 3343 CrossRef CAS.
- P. W. M. Blom and M. C. J. M. Vissenberg, Phys. Rev. Lett., 1998, 80, 3819 CrossRef CAS.
- S. C. Tse, H. H. Fong and S. K. So, J. Appl. Phys., 2003, 94, 2033 CrossRef CAS.
- D. Poplavskyy, J. Nelson and D. D. C. Bradley, Appl. Phys. Lett., 2003, 83, 707 CrossRef CAS.
- N. L. Hong, X. Q. Qiu, W. Y. Deng, Z. C. He and Y. Li, RSC Adv., 2015, 5, 90913–90921 RSC.
- P. Anjaneyulu, C. S. Suchand Sangeeth and R. Menon, J. Appl. Phys., 2010, 107, 093716 CrossRef.
- M. Hoping, C. Schildknecht, H. Gargouri, T. Riedl, M. Tilgner, H. H. Johannes and W. Kowalsky, Appl. Phys. Lett., 2008, 92, 213306 CrossRef.
- S. Bellani, A. Iacchetti, M. Porro, L. Beverina, M. R. Antognazza and D. Natali, Org. Electron., 2015, 22, 56–61 CrossRef CAS.
- S. Ishihara, H. Hase, T. Okachi and H. Naito, Org. Electron., 2011, 12, 1364–1369 CrossRef CAS.
- S. W. Tsang, S. C. Tse, K. L. Tong and S. K. So, Org. Electron., 2006, 7, 474–479 CrossRef CAS.
- E. Ehrenfreund, C. Lungenschmied, G. Dennler, H. Neugebauer and N. S. Sariciftci, Appl. Phys. Lett., 2007, 91, 012112 CrossRef.
- K. H. Chan and S. K. So, J. Photonics Energy, 2011, 1, 011011 CrossRef.
- J. You, L. Dou, K. Yoshimura, T. Kato, K. Ohya, T. Moriarty, K. Emery, C. C. Chen, J. Gao, G. Li and Y. Yang, Nat. Commun., 2013, 4, 1446 CrossRef PubMed.
- Y.-K. Kim, K. J. Won and Y. Park, Appl. Phys. Lett., 2009, 94, 063305 CrossRef.
- P. S. Szalay, J. R. Galan-Mascaros, B. L. Schottel, J. Bacsa, L. M. Perez, A. S. Ichimura, A. Chouai and K. R. Dunbar, J. Cluster Sci., 2004, 15, 503–530 CrossRef CAS.
- P. Frank, N. Koch, M. Koini, R. Rieger, K. Müllen, R. Resel and A. Winkler, Chem. Phys. Lett., 2009, 473, 321 CrossRef CAS.
- H. Glowatzki, B. Broker, R. P. Blum, O. T. Hofmann, A. Vollmer, R. Rieger, K. Mullen, E. Zojer, J. P. Rabe and N. Koch, Nano Lett., 2008, 8, 3825–3829 CrossRef CAS PubMed.
- L. S. Liao and K. P. Klubek, Appl. Phys. Lett., 2008, 92, 223311 CrossRef.
- D. H. Kim and T. W. Kim, Org. Electron., 2014, 15, 3452–3457 CrossRef CAS.
- Y. P. Wang, J. Y. Huang, J. S. Chen, X. F. Qiao, D. Z. Yang, D. G. Ma and L. S. Dong, Chin. Phys. Lett., 2016, 33, 027302 CrossRef.
- S. W. Tsang, S. K. So and J. B. Xu, J. Appl. Phys., 2006, 99, 013706 CrossRef.
- J. Shao and G. T. Wright, Solid-State Electron., 1961, 3, 291–303 CrossRef.
- A. J. Mozer, N. S. Sariciftci, A. Pivrikas, R. Österbacka, G. Juška, L. Brassat and H. Bässler, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035214 CrossRef.
- K. Seki and M. Tachiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 014305 CrossRef.
- K. S. Yook, S. O. Jeon and J. Y. Lee, Thin Solid Films, 2009, 517, 6109–6111 CrossRef CAS.
- K. Goushi, R. Kwong, J. J. Brown, H. Sasabe and C. Adachi, J. Appl. Phys., 2004, 95, 7798 CrossRef CAS.
- J. Wünsche, S. Reineke, B. Lüssem and K. Leo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245201 CrossRef.
- M. E. Kondakova, T. D. Pawlik, R. H. Young, D. J. Giesen, D. Y. Kondakov, C. T. Brown, J. C. Deaton, J. R. Lenhard and K. P. Klubek, J. Appl. Phys., 2008, 104, 094501 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |