 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On AunAt clusters as potential astatine carriers†
Sławomir Ostrowski,
Agnieszka Majkowska-Pilip,
Aleksander Bilewicz* and
Jan Cz. Dobrowolski *
*
Institute of Chemistry and Nuclear Technology, 16 Dorodna Street, 03-195 Warsaw, Poland. E-mail: a.bilewicz@ichtj.waw.pl; j.dobrowolski@nil.gov.pl; Fax: +48 22 811 1532; Fax: +48 22 811 1917; Tel: +48 22 504 1357 Tel: +48 22 504 1086
First published on 20th July 2017
Abstract
To understand interactions between astatine atoms with gold clusters the AunAt and AunX clusters, n = 12 or 13, X = F, Cl, Br, and I, were calculated at the DFT level using basis sets with a quasi-relativistic pseudopotential and the D3 Grimme correction for the dispersion interactions. Among the studied clusters of various geometries, the interaction energy of At to the clusters is the smallest. Yet, consideration of the electron detachment from the X− anion and generation of a H2 molecule and OH− anion from water shows that the formation of the astatine gold clusters is favored.
Alpha particle emitting isotopes are of considerable interest for radionuclide therapy because of their high cytotoxicity and short path length. Due to the relatively high availability, 211At is actually the most promising α emitter for targeted radiotherapy. Attaching 211At to biomolecules targeting cancer cells is crucial for its application in the radionuclide therapy. Although astatine is generally treated as a halogen (X), it also shows a significant metallic character in certain conditions.1 The strength of aryl carbon–halogen bond for astatine is significantly lower than that for iodine which precludes the use of standard direct radio-iodination methods for labelling monoclonal antibodies (mAbs) with 211At.2 Such methods lead to unstable products resulting in rapid in vivo loss of 211At. It is well known that iodine has a high affinity for the noble metal surface and the degree of specific adsorption of halides on the gold surface increases in the order F− < Cl− < Br− < I−. In particular, the F− ion has the lowest affinity and, specifically, adsorbs on the metal surface weakly. The Cl−, Br−, and I− ions are able to chemisorb on the gold surface forming an Au–X bond.3 This phenomenon was applied to elaboration of a new method for iodination of biomolecules using the gold nanoparticle as a metal bridge between 125I and a biomolecule.4 Taking into account the increasing bond strength between Au surface and the halogen atom in order F− < Cl− < Br− < I−, we can assume that astatide, the heaviest halogen anion, will bind to the Au surface even stronger than iodide. Our recent experimental studies have shown that astatine is indeed very strongly adsorbed on the gold surface and allows to use gold nanoparticles as a bridge between 211At and a biomolecule.5 Moreover, the 211At bioconjugates were very stable in human blood serum and cerebrospinal fluid.5
The aim of this study was to understand interactions between At and gold clusters using computational methods. To ensure a compromise between computational costs and stay close to reality we decided to model At interactions with Au13 clusters. The Au13 cluster with the central atom surrounded by a single shell of 12 atoms is the first from the class of full-shell clusters.6 It is known experimentally. Indeed, the crystal structures of [Au13(PMe2Ph)10Cl2](PF6)3 and [Au13(dppmH)6](NO3)n, already solved in 1981, contain the centred icosahedral Au cluster.7,8 Nowadays synthesis of compounds containing Au13 cluster is well established.9
So indeed, the Au13 clusters taken into account here, exist in real world, capture essential chemistry and physics and are more convenient for calculations than Au clusters of a larger size. However, the Au clusters applied in our experimental study on a carrier of the At atoms5 were synthesized by Turkevich and Brust–Schiffrin method yielding nanoparticle diameters from 20 to 200 Å. Thus, they displayed diameters at least three- to five-fold greater than the clusters considered in this study. Since volume scales as the cube of the radius, the number of the Au atoms in our experimental clusters was at least 350 rather than 13. On the other hand, the aim of this study was to find a rationale for using gold clusters as At carriers not to reproduce an exact cluster parameters. Therefore, the size of the studied clusters is a compromise allowing us estimation of the At interaction (binding) energy to the cluster at the level of theory providing a fairly acceptable accuracy.
The initial icosahedral Au13 structure was taken from references6–9 and optimized at the selected theory level‡ appeared to be slightly distorted (Fig. 1), while if constrained to conserve the Ih symmetry, it exhibited imaginary frequencies. Therefore, except the slightly distorted icosahedron (Au13-3, Fig. 1), we took several other high-symmetry geometries considered before for both Au12 and Au13 clusters (Fig. 1).17–21
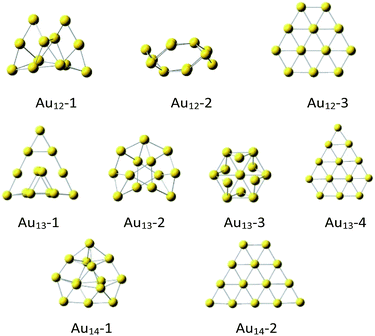 | ||
| Fig. 1 The DFT optimized‡ Au12, A13 and Au14 structures. | ||
Notice, that the non-planar Au12-1, Au13-1 and Au13-2, and Au14-1 are the most stable in the cluster of the same size (Table 1). It may seem surprising that the slightly distorted icosahedral Au13-3 structure is less stable than the most stable Au13 clusters by 17.5 kcal mol−1. However, in general, the high-symmetry (Ih, Oh, D3h, D5h) Au13 clusters tend to be less stable than those of lower symmetry.17 It is possible that this is a result of lack of external stabilisation forces in vacuum, while in crystals the most packed form of cluster is favorized.7,13,19 As expected,18 the planar Au12-3, Au13-4 and Au14-2 clusters are definitely the least stable (Table 1). Energetics of the quartet spin state considered for the Au13 systems indicated doublets to be always significantly more stable than quartets (see ESI†).
| Cluster | E | ΔE | G298 | ΔG298 kcal mol−1 |
|---|---|---|---|---|
| Au12-1 | −1629.405910 | 0.0 | −1629.474373 | 0.0 |
| Au12-2 | −1629.393431 | 7.8 | −1629.462010 | 7.8 |
| Au12-3 | −1629.357086 | 30.7 | −1629.429677 | 28.1 |
| Au13-1 | −1765.181138 | 0.0 | −1765.254652 | 0.3 |
| Au13-2 | −1765.181041 | 0.1 | −1765.255102 | 0.0 |
| Au13-3 | −1765.153717 | 17.2 | −1765.227080 | 17.6 |
| Au13-4 | −1765.129280 | 32.6 | −1765.206241 | 30.7 |
| Au14-1 | −1901.021432 | 0.0 | −1901.094858 | 0.0 |
| Au14-2 | −1900.902310 | 74.8 | −1900.980926 | 71.5 |
To model halogen–Au cluster interaction, first, we assumed that the halogen atom interacts with the cluster surface rather than is placed as one of the inner cluster atoms. In the case of planar clusters, introductory calculations indicated that the position in plane is more stable that any of the out of plane ones. Only a few, out of a multitude combinatorially possible, positions of the halogen atom on each Au cluster could be taken into account. For each halogen, the structures of those few positions were optimized. The structures fall into a few types, which however, locally are quite different. This is because in series of halogens, their electronegativities, volumes, ionization potentials, electron affinities, etc. differ a lot. The finding for all halogens were generalized, remembering that the objective of this study was to find a tendency for all halogens rather than a strict rule for a given type of cluster.
For all Aun clusters, series of similar neutral AunX structures were optimized (Fig. 2). It appeared that the heavier the halogen the less stable the cluster (Table 2). This is not unexpected because the halogen electronegativity decreases with its mass from 3.98 for fluorine to ca. 2.2 for astatine.22 Indeed, already for the AuX molecules the interaction energies decrease monotonically from ca. −110 kcal mol−1 for fluorine to −90 kcal mol−1 for astatine. For most of the Au12X and Au13X clusters such a trend is preserved, although it is not always monotonic.
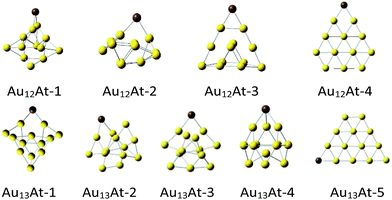 | ||
| Fig. 2 The DFT optimized‡ Au12At and Au13At structures. | ||
| ΔE | F | Cl | Br | I | At |
|---|---|---|---|---|---|
| AuX | −108.77 | −101.57 | −98.53 | −96.23 | −92.74 |
| Au12X-1 | −56.1 | −49.4 | −45.2 | −46.0 | −39.0 |
| Au12X-2 | −57.7 | −52.2 | −49.8 | −52.2 | −45.7 |
| Au12X-3 | −83.8 | −75.9 | −77.1 | −76.3 | −68.0 |
| Au12X-4 | −55.8 | −47.7 | −43.1 | −42.7 | −34.8 |
| Au13X-1 | −96.8 | −88.0 | −83.8 | −83.3 | −80.1 |
| Au13X-2 | −93.7 | −86.7 | −82.4 | −82.3 | −79.6 |
| Au13X-3 | −111.6 | −104.6 | −100.2 | −100.1 | −96.1 |
| Au13X-4 | −86.8 | −80.1 | −75.7 | −75.8 | −73.1 |
| Au13X-5 | −40.4 | −31.4 | −25.2 | −23.0 | −19.0 |
Remark, that the Au12X-3 structure is the most whereas the Au12X-4 one is the least stable. They are derived from the Au12-1 and Au12-3 clusters, respectively, which are the most and the least stable as well. However, the Au12X-1 structures are obtained from the most stable Au12-1 cluster, yet, the halogen stabilization energies in this very cluster are similar to the weakest Au12X-4 ones.
On the other hand, the most stable Au13X-3 structures are obtained from the Au13-2 clusters which are (one of two) the most stable and the least stable Au13X-5 structures are obtained from the least stable planar Au13-4 clusters. Notice however, that the Au13X-1 and Au13X-2 systems were also obtained from the most stable the Au13-1 and Au13-2 clusters but yield Au13X systems which are ca. 15 kcal mol−1 less stable than Au13X-3 ones. Comparison of the geometries of the clusters shows that within the given type of the AunX clusters its structure does not vary much with the halogen. In contrast, the site the halogen is attached to the Aun cluster significantly changes the interaction energy whether the parent gold cluster was very stable or not. Nevertheless, regardless the given AunX cluster type the halogen–gold cluster interaction energy decreases from F to At atom. Finally notice, that as for the Au13 clusters, the Au12X ones in the quartet spin state are always significantly less stable than doublets (see ESI†).
The decreasing interaction energy between halogen and gold cluster in AunX systems as the atomic number of halogen is increased would suggest that the same tendency could obey the gold clusters as a halogen carriers in water environment. In fact, in most cases the opposite is true. For example, in aqueous solutions the degree of specific adsorption on a gold surface increases in the order F− < Cl− < Br− < I−. Especially, F− has the lowest affinity and only nonspecifically or weakly specifically adsorbs on gold surface. Such an effect was observed in the case of adsorption of halides on gold electrode surfaces22 and aggregation of gold nanoparticles induced by halides adsorption.23 Indeed, to form an AunX cluster, the X− halide anion must be oxidized to the X0 free halogen form. As a result, the released electron is attached to water molecule and the H2 molecule and OH− anion are formed:
| X− + Aun + H2O → AunX + ½H2 + OH− | (1) |
The energy balance of the above reaction demonstrates that the stabilization energy of the halogen atom at the Au12 and Au13 clusters in water environment tend to increase from F to At (Table 3).
| System | X | ||||
|---|---|---|---|---|---|
| F | Cl | Br | I | At | |
| X2 + 2e → 2X− | −66.09 | −33.90 | −26.75 | −16.60 | −6.00 |
| AuX | −66.18 | −75.08 | −75.61 | −78.38 | −80.20 |
| Au12X-1 | −13.51 | −22.91 | −22.28 | −28.15 | −26.46 |
| Au12X-2 | −15.11 | −25.71 | −26.88 | −34.35 | −33.16 |
| Au12X-3 | −41.21 | −49.41 | −54.18 | −58.45 | −55.46 |
| Au12X-4 | −13.21 | −21.21 | −20.18 | −24.85 | −22.26 |
| Au13X-1 | −54.21 | −61.51 | −60.88 | −65.45 | −67.56 |
| Au13X-2 | −51.11 | −60.21 | −59.48 | −64.45 | −67.06 |
| Au13X-3 | −69.01 | −78.11 | −77.28 | −82.25 | −83.56 |
| Au13X-4 | −44.21 | −53.61 | −52.78 | −57.95 | −60.56 |
| Au13X-5 | 2.19 | −4.91 | −2.28 | −5.15 | −6.46 |
In conclusion, we have computationally confirmed the higher stability of the Au12At and Au13At clusters in water environment than stability of the analogous clusters with lighter halogens. Our experimental studies already signalized a high therapeutic potential of 211At labelled gold nanoparticles functionalized with substance P and trastuzumab towards glioma cells and HER2 positive breast and ovarian cancers. These two findings open new perspectives for optimization novel 211At labelled gold nanoparticles functionalized with different biomolecules for cancer targeting therapy.
Acknowledgements
This work was supported by Grant 2013/11/B/ST4/00516 from the National Science Center in Poland. The computational Grant from the Świerk Computing Centre (CIŚ) is gratefully acknowledged. Critical comments of anonymous referees to this paper are gratefully acknowledged.Notes and references
- J. Champion, M. Seydou, A. Sabatie-Gogova, E. Renault, G. Montavon and N. Galland, Phys. Chem. Chem. Phys., 2011, 13, 14984–14992 RSC.
- K. Berei and L. Vasaros, “Organic Chemistry of Astatine”, Hungarian Academy of Sciences, Central Research Institute for Nuclear Physics, Budapest, 114, Hungary, 1981 Search PubMed.
- Z. Zhang, H. Li, F. Zhang, Y. Wu, Z. Guo, L. Zhou and J. Li, Langmuir, 2014, 30, 2648–2659 CrossRef CAS PubMed.
- Y.-H. Kim, J. Jeon, S. H. Hong, W.-K. Rhim, Y.-S. Lee, H. Youn, J.-K. Chung, M. C. Lee, D. S. Lee, K. W. Kang and J.-M. Nam, Small, 2011, 7, 2052–2060 CrossRef CAS PubMed.
- A. Bilewicz, Ł. Janiszewska, P. Kozmiński, M. Łyczko, M. Pruszyński, J. Jastrzębski, J. Choiński, A. Stolarz, A. Trzcińska, K. Szkliniarz and W. Zipper, Eur. J. Nucl. Med. Mol. Imaging, 2015, 42, S245 Search PubMed.
- G. Schmid, Metal Nanoparticles: Electronic Properties, Bioresponse, and Synthesis, Encyclopedia of Inorganic and Bioinorganic Chemistry, Wiley, 2011–2012 Search PubMed.
- C. E. Briant, B. R. C. Theobald, J. W. White, L. K. Bell, D. M. P. Mingos and A. J. Welch, J. Chem. Soc., Chem. Commun., 1981, 201–202 RSC.
- J. W. A. van der Velden, F. A. Vollenbroek, J. J. Bour, P. T. Beurskens, J. M. M. Smits and W. P. Bosnian, Recl. Trav. Chim. Pays-Bas, 1981, 100, 148–152 CrossRef CAS.
- Y. Shichibu, K. Suzuki and K. Konishi, Nanoscale, 2012, 4, 4125–4129 RSC.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- E. Weintraub, T. M. Henderson and G. E. Scuseria, J. Chem. Theory Comput., 2009, 5, 754–762 CrossRef CAS PubMed.
- B. Civalleri, D. Presti, R. Dovesia and A. Savin, Chem. Modell., 2012, 9, 168–185 CAS.
- http://www.tc.uni-koeln.de/PP/clickpse.en.html.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- A. S. Menon and L. Radom, J. Phys. Chem. A, 2008, 112, 13225–13230 CrossRef CAS PubMed.
- J. Sun, X. Xie, B. Cao and H. Duan, Comput. Theor. Chem., 2017, 1107, 127–135 CrossRef CAS.
- D. A. Götz, R. Schäfer and P. Schwerdtfeger, J. Comput. Chem., 2013, 34, 1975–1981 CrossRef PubMed.
- S. Takano, S. Yamazoe and T. Tsukuda, APL Mater., 2017, 5, 053402 CrossRef.
- H. M. Lee, M. Ge, B. R. Sahu, P. Tarakeshwar and K. S. Kim, J. Phys. Chem. B, 2003, 107, 9994–10005 CrossRef CAS.
- H. Häkkinen, B. Yoon, U. Landman, X. Li, H.-J. Zhai and L.-S. Wang, J. Phys. Chem. A, 2003, 107, 6168–6175 CrossRef.
- O. M. Magnussen, Chem. Rev., 2002, 102, 679–726 CrossRef CAS PubMed.
- Z. Zhang, H. Li, F. Zhang, Y. Wu, Z. Guo, L. Zhou and J. Li, Langmuir, 2014, 30, 2648–2659 CrossRef CAS PubMed.
- CRC Handbook of Chemistry and Physics, ed. D. R. Lide, Internet Version 2005, http://www.hbcpnetbase.com, CRC Press, Boca Raton, FL, 2005 Search PubMed.
- J. Champion, C. Alliot, E. Renault, B. M. Mokili, M. Chérel, N. Galland and G. Montavon, J. Phys. Chem. A, 2010, 114, 576–582 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of all studied systems and energetics of the selected systems are available. See DOI: 10.1039/c7ra05224c |
| ‡ The computations were performed using the LC-ωPBE functional10–12 combined with the Stuttgart/Cologne Group (SDD) basis sets with quasi-relativistic pseudopotential13 and the D3 Grimme correction14 for the dispersion interactions as implemented in Gaussian 09 suite of programs.15 For open-shell systems the spin contamination was checked to be small.16 For more details see ESI.† |
| This journal is © The Royal Society of Chemistry 2017 |
