Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational design of polymers: poly(ester amide) and polyurethane†
Yuichiro Fukuda ,
Kohei Miyamae
,
Kohei Miyamae and
Yuji Sasanuma
and
Yuji Sasanuma *
*
Department of Applied Chemistry and Biotechnology, Graduate School and Faculty of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan. E-mail: sasanuma@faculty.chiba-u.jp; Fax: +81 43 290 3394; Tel: +81 43 290 3394
First published on 4th August 2017
Abstract
A methodology for conformational analysis of polymers including both ester and amide groups in the repeating unit has been developed by exemplifying a poly(ester amide), poly(oxyethylene-iminosuccinyl) (abbreviated herein as PEA), and a polyurethane, poly(oxy-1,2-ethanediyloxycarbonylimino-1,2-ethanediyliminocarbonyl) (PU). The repeating units have been divided into two parts, each of which has been represented by a small model compound with the same bond sequence that the polymer includes. To determine which molecular orbital (MO) theory is appropriate for the models, B3LYP, M06-2X, and MP2 calculations were compared with NMR observations. Consequently, the M06-2X or MP2 electronic energy with the B3LYP geometry was shown to yield reliable conformer free energies. Both PEA and PU were found to prefer bent conformations with a number of gauche states owing to intramolecular N–H⋯O and C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attractions. The characteristic ratio and configurational entropy, calculated by the refined rotational isomeric state scheme with the MO energies, were, respectively, obtained as follows: 5.39 and 5.8 × 10−2 cal K−1 g−1 (PEA); and 5.40 and 5.6 × 10−2 cal K−1 g−1 (PU). Both polymers show equivalent characteristics, however, the ratios (fU/f) of the internal energy contribution (fU) to the total restoring force (f) in chain elasticity, evaluated from the temperature coefficient of the characteristic ratio, are greatly different: −0.13 (PEA); and 0.21 (PU). This means that the urethane chain is more likely to behave as an elastomer than the ester amide chain. The possibility that poly(ester amide)s and polyurethanes will become biodegradable is also discussed in terms of the primary structures.
C attractions. The characteristic ratio and configurational entropy, calculated by the refined rotational isomeric state scheme with the MO energies, were, respectively, obtained as follows: 5.39 and 5.8 × 10−2 cal K−1 g−1 (PEA); and 5.40 and 5.6 × 10−2 cal K−1 g−1 (PU). Both polymers show equivalent characteristics, however, the ratios (fU/f) of the internal energy contribution (fU) to the total restoring force (f) in chain elasticity, evaluated from the temperature coefficient of the characteristic ratio, are greatly different: −0.13 (PEA); and 0.21 (PU). This means that the urethane chain is more likely to behave as an elastomer than the ester amide chain. The possibility that poly(ester amide)s and polyurethanes will become biodegradable is also discussed in terms of the primary structures.
Introduction
In state-of-the-art polymer science and engineering, polymeric materials are often required to exhibit different physical properties and functions appropriate for specific applications. For instance, a gene delivery polymer is expected to be highly efficient at transfection, and posses proper hydrophilicity and weak cytotoxicity.1 However, it is very difficult or essentially impossible to find a synthetic homopolymer that satisfies all the above requirements. As an alternative, one can choose a linear mosaic of different structural units, each of which shows a particular function. In the case of a gene delivery polymer, one may adopt poly(ethylene imine) for transfection, poly(ethylene oxide) for hydrophilicity, and a biodegradable polymer such as poly(L-lactide) or poly(ε-caprolactone) for non-cytotoxicity.1,2 Herein, such a structural unit is designated as a functional unit (FU) regardless of whether it is a polymer, an oligomer, or a monomer. In expectation that all the desired functions would be realized, one often synthesizes block copolymers composed of different FUs. If the individual monomeric units keep their inherent characteristics, their random copolymers must also be worth synthesizing and utilizing. Table S1 (ESI†) is a list of various FUs that we have so far characterized in detail. Each FU exhibits distinctive attractive and repulsive interactions due to the electronic structure of the included heteroatom(s), and the interactions result in conformational characteristics of the polymer.The interaction energies of a given FU can be derived from high-accuracy molecular orbital (MO) calculations on small model compounds that have the same bond sequence that the FU includes. Table S1 (ESI†) also shows types of interaction, values of characteristic ratios (〈r2〉0/nl2) calculated from the rotational isomeric state (RIS) scheme for the polymeric FUs in the Θ state,3,4 and the MO theories, which provide reliable conformational energies. Here, r is the end-to-end distance of the polymer, n is the number of skeletal bonds, and l is the bond length. The 〈r2〉0/nl2 value is a criterion for the flexibility/rigidity of the FU.
In polymers, the FUs are connected to each other by covalent bonds, whereas supramolecules are assembled with the aid of non-covalent linkages such as hydrogen bonds and weak attractive interactions that are reconfigurable and reconnectable.5,6 Therefore, to fabricate supramolecules as desired, we must recognize the attraction and repulsion of the FUs in advance and design geometrical relations between the non-covalent connections. It is particularly important to design the molecular architecture from a stereochemical viewpoint because we are too accustomed to two-dimensional structural formulas such as those in Fig. 1, where two FUs, a poly(ester amide) and a polyurethane, are depicted in the all-trans conformation and the carbonyl groups stick out alternately in opposite directions. As will be shown later, however, the most stable conformations of the two FUs are largely bent; each FU is represented by two model compounds, whose most stable forms are shown in Fig. 2.
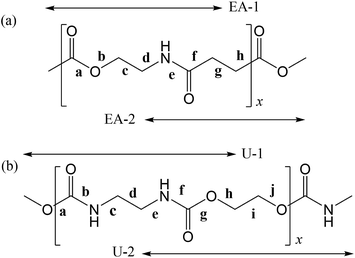 | ||
| Fig. 1 (a) Poly(oxyethylene-iminosuccinyl) (abbreviated as PEA) and (b) poly(oxy-1,2-ethanediyloxycarbonylimino-1,2-ethanediyliminocarbonyl) (PU). The repeating units are divided into two parts, which are represented by small model compounds: 2-acetamidoethyl acetate (designated herein as EA-1) and methyl 4-(methylamino)-4-oxobutanoate (EA-2) for PEA; and dimethyl ethane-1,2-diyldicarbamate (U-1) and ethane-1,2-diyl bis(methylcarbamate) (U-2) for PU. For the model compounds, see Fig. 2. | ||
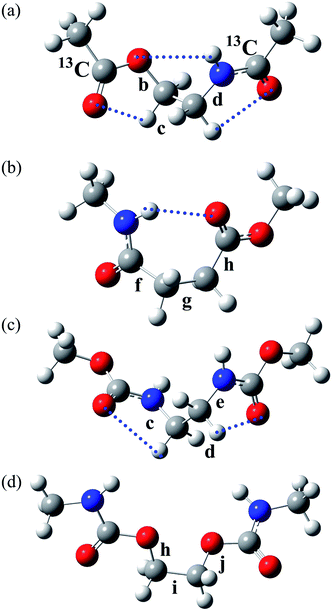 | ||
| Fig. 2 The most stable conformers (with the lowest ΔGk) of the model compounds: (a) EA-1, g+g+g+; (b) EA-2, g+g−t; (c) U-1, g+g+g+; and (d) U-2, tg+t. The rotatable bonds are designated as shown, and the symbols correspond to those shown in the polymers illustrated in Fig. 1. The EA-1 compound, whose carbonyl carbon atoms are labelled with 13C, was also prepared for NMR measurements and designated as EA-1-13C. The dotted lines represent weak attractive interactions predicted by MO calculations. | ||
The amide group (–NHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–) forms comparatively strong hydrogen bonds in natural and synthetic products: in α-helices and β-sheets in polypeptides; in adenine–thymine and guanine–cytosine pairs in DNA; and in parallel and anti-parallel pleated sheets of nylons. The amide group plays a major role in the formation of the higher-order structure and acts as a juncture in supramolecules.7 The NHC(
O)–) forms comparatively strong hydrogen bonds in natural and synthetic products: in α-helices and β-sheets in polypeptides; in adenine–thymine and guanine–cytosine pairs in DNA; and in parallel and anti-parallel pleated sheets of nylons. The amide group plays a major role in the formation of the higher-order structure and acts as a juncture in supramolecules.7 The NHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) atoms are located on a plane. However, if the carbonyl oxygen atoms of a planar aromatic amide –NHC(
O) atoms are located on a plane. However, if the carbonyl oxygen atoms of a planar aromatic amide –NHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C6H4–C(
O)–C6H4–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)NH– are replaced with sulfur, the resultant thioamide group, –NHC(
O)NH– are replaced with sulfur, the resultant thioamide group, –NHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)–C6H4–C(
S)–C6H4–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S)NH–, adopts six rotational isomeric states around the benzene ring.8 As the energy differences between the six rotamers are as small as ∼0.1 kcal mol−1, the thioamide group undergoes nearly free rotation. In addition, the N–H⋯S
S)NH–, adopts six rotational isomeric states around the benzene ring.8 As the energy differences between the six rotamers are as small as ∼0.1 kcal mol−1, the thioamide group undergoes nearly free rotation. In addition, the N–H⋯S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attraction is weaker than the N–H⋯O
C attraction is weaker than the N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attraction. Therefore, we must investigate rotational isomeric states and interactions of the amide group and its variants individually.
C attraction. Therefore, we must investigate rotational isomeric states and interactions of the amide group and its variants individually.
This study deals with a poly(ester amide), poly(oxyethylene-iminosuccinyl) (abbreviated as PEA and illustrated in Fig. 1a), and a polyurethane, poly(oxy-1,2-ethanediyloxycarbonylimino-1,2-ethanediyliminocarbonyl) (abbreviated as PU and illustrated in Fig. 1b). The monomeric unit of PEA consists of two ethylene groups, one amide group, and one ester group, and that of PU comprises two ethylene and two urethane groups. The urethane group corresponds to a combined form of an ester and an amide unit. Thus, PEA and PU are quite similar in terms of their primary structure. Both amide and urethane groups may form N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds, and the C
C hydrogen bonds, and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond of the ester group would also participate in hydrogen bonding. Therefore, these FUs are useful for us to understand the conformational characteristics and physical properties of both ester and amide groups in these compounds. In this study, we eventually investigated some rather complicated FUs via a number of FUs listed in Table S1 (ESI†) and attempted to establish a method for conformational analysis of poly(ester amide)s and polyurethanes.
O bond of the ester group would also participate in hydrogen bonding. Therefore, these FUs are useful for us to understand the conformational characteristics and physical properties of both ester and amide groups in these compounds. In this study, we eventually investigated some rather complicated FUs via a number of FUs listed in Table S1 (ESI†) and attempted to establish a method for conformational analysis of poly(ester amide)s and polyurethanes.
It is also of interest to us that poly(ester amide)s and polyurethanes have been used for practical materials and recently have become increasingly attractive, partly because some of them possess biodegradability.9,10 The PEA and PU polymers studied here were already synthesized but nevertheless have been hardly characterized: PEA was prepared from succinic anhydride and 2-amino-1-ethanol and was found to be semi-crystalline (weight-average molecular weight: 13.1 kDa and melting point (Tm): 190 °C).11 Semi-crystalline PU was prepared by interfacial polycondensation between ethylene diamine and ethylene bis(chloroformate), and its Tm was reported as 225 °C.12
At the beginning of this study, we attempted to establish a method for MO calculations appropriate for the aliphatic ester–amide and urethane FUs. Our studies have proven that geometrical optimization by the B3LYP density functional and electronic energy calculation by the MP2 theory with basis sets of medium sizes usually yield satisfactory results, as shown in Table S1 (ESI†). As far as aromatic polyesters and polyamides are concerned, however, the MP2//B3LYP combination fails to reproduce NMR observations.8,13,14 This is because the MP2 theory tends to overestimate π/π and C–H/π attractions of aromatic polyesters, and the self-consistent reaction field (SCRF) calculations can not satisfactorily reproduce the effects of irritant and polar solvents on hydrogen bonds of polyamides. Therefore, we have searched for a MO theory and solvation model suitable for PEA and PU through comparison with NMR experiments on the model compounds shown in Fig. 2. On the basis of the reliable MO calculations thus established, we have investigated the conformational characteristics and intramolecular interactions of the two FUs, and evaluated the configurational properties of the two polymers by the refined RIS scheme.15 This article reports the processes and results in detail and discusses the differences between PEA and PU, especially in terms of chain elasticity and biodegradability.
Methods
Synthesis of EA-1 and EA-1-13C
Acetyl chloride (0.91 mL, 13 mmol) was added dropwise with a syringe to 2-aminoethanol (0.31 mL, 5.1 mmol) and pyridine (4.1 mL, 51 mmol), and then the mixture was stirred under a nitrogen atmosphere at 40 °C for 27 h. After the solvent was removed on a rotary evaporator, diethyl ether was added to the residue to precipitate pyridinium chloride, which was removed by filtration. The filtrate was condensed, and the residue was dried in vacuo overnight to yield a yellowish viscous liquid, which was identified as EA-1 by 1H and 13C NMR spectroscopy. In preparation of EA-1-13C, acetyl chloride-13C was used instead of acetyl chloride.Synthesis of U-1
Ethylenediamine (1.2 mL, 18 mmol), dimethyl carbonate (3.0 mL, 36 mmol), sodium acetate (0.36 g, 4.4 mmol), and ethanol (9.0 mL) were mixed in a four-necked flask equipped with a reflux condenser connected to a drying tube of calcium chloride.16 The mixture was stirred under a nitrogen atmosphere at 75 °C for 15 h. After ethanol was removed on a rotary evaporator, the residue was dried under reduced pressure at 50 °C to yield a white solid. The crude product was dissolved in chloroform and filtrated to remove sodium acetate. The filtrate was condensed, dried in vacuo at 50 °C for 2 h, dissolved in toluene (50 mL) at 80 °C, and allowed to stand still to form white crystallites, which were collected and dried in vacuo at 50 °C for 2 h. The product was identified by 1H and 13C NMR spectroscopy as U-1.Synthesis of U-2
Ethylene carbonate (44 g, 0.5 mol) and methylamine aqueous solution (40%, 61.5 mL) were mixed in a four-necked flask equipped with a reflux condenser and a thermometer and stirred at 15–20 °C for 1 h.17 After water was removed on a rotary evaporator, the residue was distilled under reduced pressure to collect a fraction at ca. 170 °C and 7 mmHg. The product was 2-hydroxyethyl methylcarbamate.The prepared 2-hydroxyethyl methylcarbamate (3.8 g, 32 mmol) and dibutyltin dilaurate (0.40 g, 0.63 mmol) were stirred in an eggplant flask at 170 °C for 1 h and then distilled at 170 °C and 30 mmHg to remove a by-product, ethylene glycol. The residue underwent suction filtration to be separated into a white cake and a yellow filtrate. The former was dissolved in toluene (50 mL), heated to 80 °C, cooled to room temperature, and allowed to stand still to form white crystallites, which were collected by filtration and dried in vacuo at 30 °C for 2 h. The product was identified by 1H and 13C NMR spectroscopy as U-2.
NMR measurements
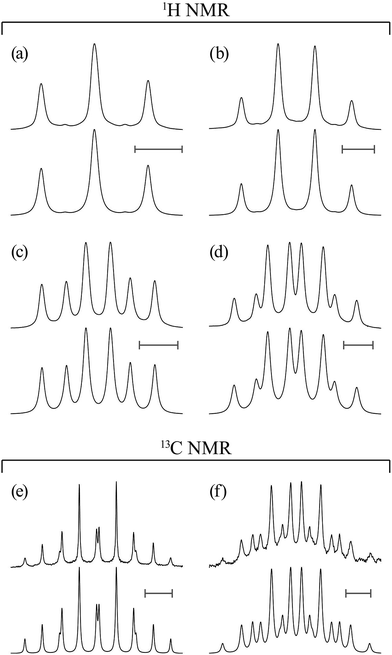
Proton (13C) NMR spectra were measured at 500 MHz (126 MHz) on a JEOL JNM-ECA500 spectrometer in the Center for Analytical Instrumentation of Chiba University. The sample temperature was changed step-wise from 15 or 25 to 55 °C at intervals of 10 °C and maintained there within ±0.1 °C. Free induction decays of 32k (64k) points were accumulated 32 (128) times, fully zero-filled, and underwent Fourier transform. The pulse width and recycle delay were 5.7 (3.27) μs and 3.0 (2.0) s, respectively. In the 13C NMR experiments, the gated decoupling technique was used under the conditions written in parentheses. The above numerical data are typical examples; the experimental conditions were adjusted to each sample. The NMR solvents were benzene-d6 (C6D6), chloroform-d (CDCl3), methanol-d4 (CD3OD), dimethyl-d6 sulfoxide (DMSO-d6, (CD3)2SO), and deuterium oxide (water-d2, D2O), and 5 mm NMR sample tubes were used. The 1H and 13C NMR spectra thus obtained were simulated with the gNMR program18 to yield chemical shifts and coupling constants.MO calculations on model compounds
Density functional theory and ab initio MO calculations were carried out with the Gaussian09 program19 installed on a Hitachi SR16000 server in the Institute of Management and Information Technologies of Chiba University. For each conformer of the model compounds, the geometrical parameters were fully optimized at the B3LYP/6-311+G(2d,p) level20 under tight convergence, and then the thermochemical energies at 25 °C and 1 atm were evaluated by the frequency computations at the same level. With the optimized geometry, the electronic energy was computed at the MP2/6-311+G(2d,p)21 and M06-2X/6-311+G(2d,p) levels.22 The Gibbs free energy was evaluated from the electronic and thermochemical energies, being expressed herein as the difference from that of a given conformer and represented as ΔGk (k: conformer). The solvent effect on the electronic energy was evaluated by the polarizable continuum model (PCM) using the integral equation formalism variant (IEFPCM)23 and the conductor-like PCM model (CPCM).24The geometrical parameters required for the refined RIS calculations on PEA and PU were chosen out of those optimized for the model compounds. Vicinal 1H–1H and 13C–1H coupling constants for the NMR analysis were calculated at the B3LYP/6-311++G(3df,3pd) level.25
Herein, the dihedral angle is defined according to the tradition in polymer science:3 trans (t) ∼ ±0° and gauche± (g±) ∼ ±120°. The dihedral angle here (ϕ) is related to that (Φ) recommended by IUPAC26 according to Φ = −sign(ϕ)(180 − |ϕ|), and vice versa ϕ = −sign(Φ)(180 − |Φ|), where the function, sign(ϕ), returns the sign (plus or minus) of ϕ.
Results and discussion
Conformational analysis of EA-1 and EA-2
| Solventb | Temp. (°C) | JOCH | JHH | J′HH | JNCH | JNHH |
|---|---|---|---|---|---|---|
| a In Hz. For more detailed data, see Table S2 (ESI†).b Symbols: C6D6, benzene-d6; CDCl3, chloroform-d; (CD3)2SO, dimethyl-d6 sulfoxide (abbreviated as DMSO-d6); D2O, deuterium oxide (water-d2).c Not available. | ||||||
| C6D6 | 15 | 3.33 | 6.66 | 4.72 | 3.50 | 5.85 |
| 25 | 3.33 | 6.66 | 4.72 | 3.50 | 5.85 | |
| 35 | 3.35 | 6.60 | 4.72 | 3.50 | 5.85 | |
| 45 | 3.36 | 6.60 | 4.78 | 3.50 | 5.85 | |
| 55 | 3.38 | 6.60 | 4.79 | 3.50 | 5.85 | |
| CDCl3 | 25 | 3.18 | 6.78 | 3.90 | 3.32 | 5.74 |
| (CD3)2SO | 25 | 3.19 | 6.52 | 4.96 | 3.76 | 5.70 |
| D2O | 25 | 3.13 | 6.76 | 3.80 | 3.80 | —c |
In Table 2, the vicinal coupling constants are expressed as a function of bond conformation, i.e. the trans (pt) and gauche (pg) fractions. The coefficients (JC, J′E, JG, and JT) of the equations, defined in Fig. 4, were chosen from the well-known Karplus equations, a cyclic compound with the same bond sequence that EA-1 has, and MO calculations on EA-1 itself. Their sources and numerical values are described in footnotes of Table 3. The trans fractions of the three bonds, O–C, C–C, and C–N, of EA-1, obtained from the equations in Table 2, are listed in Tables 3 and S3 (ESI†). The pt values seem to depend somewhat on the used coefficients but generally stay within narrow ranges. The trans fractions of the C–N bond were derived from JNCH and JNHH; however, the results do not agree well for the (CD3)2SO solution. This is partly because the NH proton undergoes strong solvent effects when EA-1 is dissolved in polar solvents. Actually, the JNHH value could not be obtained from the D2O solution. Nevertheless, we can clearly conclude that the O–C, C–C, and C–N bonds possess trans, gauche, and gauche preferences, respectively.
| Compound | Bonda | Coupled nuclei | Equationb | Table | Figure |
|---|---|---|---|---|---|
| a See Fig. 2.b By definition, pt + pg = 1. For the coefficients (JT, JG, JC, and J′E) of the equations, see the footnotes of Tables 3 and 7. | |||||
| EA-1 & EA-1-13C | b: O–C | 13C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O–CH2 O)O–CH2 |
JOCH = [(JG1 + JG2)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′T + J′G)/2] pt + [(J′T + J′G)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
1, S2 (ESI†) | 4 |
| c: C–C | CH2–CH2 | JHH = JG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′T + J′′G)/2] pt + [(J′T + J′′G)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
1, S2 (ESI†) | 4 | |
J′HH = JT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′G + J′′′G)/2] pt + [(J′G + J′′′G)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
1, S2 (ESI†) | ||||
| d: C–N | CH2–NH13C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
JNCH = [(JG1 + JG2)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′T + J′G)/2] pt + [(J′T + J′G)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
1, S2 (ESI†) | 4 | |
| CH2–NH | JNHH = [(JC1 + JC2)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′E + J′C)/2] pt + [(J′E + J′C)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
1, S2 (ESI†) | |||
| U-1 | c & e: N–C | NH–CH2 | JNHH = [(JC1 + JC2)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′E + J′C)/2] pt + [(J′E + J′C)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
S5 (ESI†) | 7 |
| U-1 & U-2 | d & i: C–C | CH2–CH2 | JHH = JG![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + [(J′T + J′′G)/2] pt + [(J′T + J′′G)/2]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
S5 (ESI†) | 7 |
J′HH = JT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pt + J′G pt + J′G![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pg pg |
S5 (ESI†) | ||||
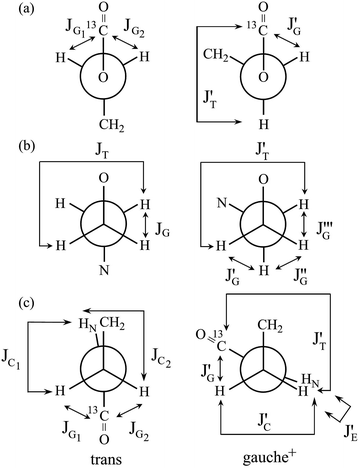 | ||
| Fig. 4 Newman projections for rotamers around the (a) b: O–C, (b) c: C–C, and (c) d: C–N bonds of EA-1, illustrating the coefficients (JC, J′E, JG, and JT) of the equations given in Table 2. For the bond symbols, see Fig. 2a. | ||
| Solvent | Temp. (°C) | Bondb | |||||||
|---|---|---|---|---|---|---|---|---|---|
| b: O–C | c: C–C | d: C–N | |||||||
| JOCH | JHH and J′HH | JNCH | JNHH | ||||||
| Set Ac | Set Bd | Set Ce | Set Df | Set Eg | Set Fh | Set Gi | Set Hj | ||
| a For more detailed data, see Table S3 (ESI†).b See Fig. 2a.c With the coupling constants calculated from a Karplus equation proposed by Tvaroška and Gajdoš:27 JG1 + JG2 = 2.42 Hz and J′T + J′G = 9.53 Hz.d With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JG1 + JG2 = 2.26 Hz and J′T + J′G = 9.87 Hz.e With the coupling constants of 2-methylmorpholine: e.g. JT = 11.62, JG = 2.35, J′T = 11.62, J′G = 3.33, J′′G = 1.21, and J′′′G = 2.51 Hz for the chloroform solution. For details, see ref. 28.f With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JT = 11.12, JG = 4.82, J′T = 10.07, J′G = 2.25, J′′G = 1.96, and J′′′G = 1.82 Hz.g With the coupling constants calculated from a Karplus equation proposed by Kao and Barfield:29 JG1 + JG2 = 1.96 Hz and J′T + J′G = 7.56 Hz.h With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JG1 + JG2 = 1.57 Hz and J′T + J′G = 8.03 Hz.i With the coupling constants calculated from a Karplus equation proposed by Ludvigsen et al.:30 JC1 + JC2 = 8.13 Hz and J′E + J′C = 12.09 Hz.j With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JC1 + JC2 = 5.16 Hz and J′E + J′C = 12.48 Hz. | |||||||||
| C6D6 | 15 | 0.40 | 0.42 | 0.14 | 0.22 | 0.10 | 0.16 | 0.10 | 0.11 |
| 25 | 0.40 | 0.42 | 0.14 | 0.22 | 0.10 | 0.16 | 0.10 | 0.11 | |
| 35 | 0.40 | 0.42 | 0.14 | 0.23 | 0.10 | 0.16 | 0.10 | 0.11 | |
| 45 | 0.40 | 0.41 | 0.15 | 0.23 | 0.10 | 0.16 | 0.10 | 0.11 | |
| 55 | 0.39 | 0.41 | 0.15 | 0.23 | 0.10 | 0.16 | 0.10 | 0.11 | |
| CDCl3 | 25 | 0.45 | 0.46 | 0.07 | 0.15 | 0.16 | 0.22 | 0.15 | 0.14 |
| (CD3)2SO | 25 | 0.44 | 0.46 | 0.17 | 0.25 | 0.01 | 0.08 | 0.17 | 0.15 |
| D2O | 25 | 0.46 | 0.47 | 0.07 | 0.14 | 0.00 | 0.07 | — | — |
| MO theoryc | Solvent | Solvation | ΔGkb (kcal mol−1) | |||||
|---|---|---|---|---|---|---|---|---|
| Existing conformer (in bonds b–d)b | ||||||||
| ttg+ | tg+g+ | g+tg− | g+g+g+ | g+g+g− | g+g−t | |||
| a Relative to the free energy of the ttg+ conformer. Abbreviations: IEFPCM, the polarizable continuum model using the integral equation formalism variant; CPCM, the conductor-like polarizable continuum model; DMSO, dimethyl sulfoxide; B3LYP, Becke’s three parameter hybrid functionals with the correlation functional of Lee, Yang, and Parr;20 MP2, a Hartree–Fock calculation followed by the Moller–Plesset correlation energy correction truncated at the second-order;21 and M06-2X, the hybrid functional of Zhao and Truhlar.22b The geometrical optimization was carried out at the B3LYP/6-311+G(2d,p) level. Of 27 (=33) possible conformers, only 6 conformations remained. For the bond symbols, see Fig. 2a.c The basis set of 6-311+G(2d,p) was used for all the MO theories. | ||||||||
| M06-2X | Benzene | IEFPCM | 0.00 | −0.76 | 0.11 | −0.96 | 0.53 | −0.57 |
| MP2 | 0.00 | −0.92 | 0.14 | −1.04 | 0.30 | −0.59 | ||
| B3LYP | Chloroform | IEFPCM | 0.00 | −0.70 | 0.77 | −0.25 | 2.22 | 0.39 |
| CPCM | 0.00 | −0.65 | 0.85 | −0.22 | 2.19 | 0.56 | ||
| M06-2X | IEFPCM | 0.00 | −0.60 | 0.34 | −0.77 | 0.63 | −0.16 | |
| CPCM | 0.00 | −0.54 | 0.43 | −0.73 | 0.58 | 0.02 | ||
| MP2 | IEFPCM | 0.00 | −0.76 | 0.35 | −0.86 | 0.40 | −0.21 | |
| CPCM | 0.00 | −0.70 | 0.44 | −0.83 | 0.36 | −0.04 | ||
| B3LYP | DMSO | IEFPCM | 0.00 | −0.52 | 1.07 | −0.03 | 2.29 | 0.94 |
| CPCM | 0.00 | −0.51 | 1.09 | −0.02 | 2.29 | 0.96 | ||
| M06-2X | IEFPCM | 0.00 | −0.41 | 0.65 | −0.54 | 0.66 | 0.39 | |
| CPCM | 0.00 | −0.40 | 0.66 | −0.54 | 0.65 | 0.42 | ||
| MP2 | IEFPCM | 0.00 | −0.56 | 0.64 | −0.64 | 0.43 | 0.30 | |
| CPCM | 0.00 | −0.55 | 0.66 | −0.64 | 0.43 | 0.33 | ||
| M06-2X | Water | IEFPCM | 0.00 | −0.39 | 0.66 | −0.53 | 0.66 | 0.42 |
| MP2 | 0.00 | −0.55 | 0.66 | −0.63 | 0.43 | 0.33 | ||
From the free energies, the bond conformations were calculated as listed in Tables 5 and S4 (ESI†). The M06-2X and MP2 results agree well with the NMR data (Tables 3 and S3 (ESI†)), regardless of the solvation model used. Therefore, we have decided to adopt the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) combination and the IEFPCM model for all the model compounds of PEA and PU because this computation has yielded satisfactory results consistent with NMR experiments for most FUs that we have considered (Table S1 (ESI†)). The reliable MP2 calculations indicated that the first and second most stable conformers of EA-1 are g+g+g+ and tg+g+, respectively. As all the model compounds treated here are symmetrical, i.e. achiral, for example, g+g+g+ and its mirror image, g−g−g−, have the same free energy and hence exist at an identical probability. Therefore, the results and discussion herein are represented by either conformer.
| Solvent | Solvation model | Temp. (°C) | Bondb | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| b: O–C | c: C–C | d: C–N | |||||||||
| B3LYPc | M06-2Xd | MP2e | B3LYPc | M06-2Xd | MP2e | B3LYPc | M06-2Xd | MP2e | |||
| a For more detailed data, see Table S4 (ESI†).b See Fig. 2a.c At the B3LYP/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level.d At the M06-2X/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level.e At the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level. | |||||||||||
| Benzene | IEFPCM | 15 | 0.34 | 0.37 | 0.13 | 0.11 | 0.19 | 0.17 | |||
| 25 | 0.34 | 0.37 | 0.14 | 0.11 | 0.20 | 0.17 | |||||
| 35 | 0.34 | 0.37 | 0.14 | 0.12 | 0.20 | 0.17 | |||||
| 45 | 0.34 | 0.37 | 0.15 | 0.12 | 0.20 | 0.17 | |||||
| 55 | 0.34 | 0.37 | 0.15 | 0.13 | 0.20 | 0.18 | |||||
| Chloroform | IEFPCM | 25 | 0.65 | 0.39 | 0.41 | 0.19 | 0.16 | 0.14 | 0.08 | 0.14 | 0.12 |
| CPCM | 25 | 0.66 | 0.40 | 0.41 | 0.20 | 0.17 | 0.14 | 0.06 | 0.11 | 0.10 | |
| DMSO | IEFPCM | 25 | 0.70 | 0.45 | 0.45 | 0.24 | 0.20 | 0.17 | 0.04 | 0.08 | 0.08 |
| CPCM | 25 | 0.70 | 0.45 | 0.45 | 0.24 | 0.20 | 0.17 | 0.04 | 0.08 | 0.07 | |
| Water | IEFPCM | 25 | 0.45 | 0.45 | 0.20 | 0.17 | 0.08 | 0.07 | |||
In a previous study,28 we carried out conformational analysis of N-(2-methoxyethyl)methylamine (CH3OCH2CH2NHCH3). Its most stable conformer is the tgt form with an intramolecular N–H⋯O attraction. It seems that the g+g+g+ conformer of EA-1 has two C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attractions as well as an N–H⋯O one (Fig. 2a); the outer carbonyl groups influence the conformational preference of the inner portion of EA-1.
C attractions as well as an N–H⋯O one (Fig. 2a); the outer carbonyl groups influence the conformational preference of the inner portion of EA-1.
The model compound, EA-1, represents bonds a–e of PEA (Fig. 1a). As a model for bonds f–h of PEA, we have employed EA-2 (Fig. 2b). As a result of the geometrical optimization for all conceivable conformers of EA-2, only five conformations remained. Around bonds f and h, unusual eclipsed forms as well as the three staggered states (t, g+, and g−) were suggested to exist: cisN–C in bond f; and cisH–O and cisC–O in bond h (Fig. 5). The ΔGk values of the five conformers and the bond conformations of bonds f–h are given in the upper and lower parts of Table 6, respectively. In benzene and chloroform, the most stable conformer was indicated to be g+g−t, whereas in polar solvents such as DMSO and water, the ttt conformation would be more likely to exist. This probably depends on whether an intramolecular N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attraction is formed (in g+g−t, Fig. 2b) or not (in ttt). The polar solvents may disturb the intramolecular interaction.
C attraction is formed (in g+g−t, Fig. 2b) or not (in ttt). The polar solvents may disturb the intramolecular interaction.
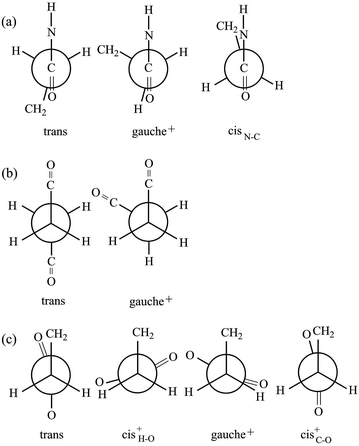 | ||
Fig. 5 Newman projections for rotamers around the (a) f: C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–C, (b) g: C–C, and (c) h: C–C( O)–C, (b) g: C–C, and (c) h: C–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) bonds of EA-2. For the bond symbols, see Fig. 2b. O) bonds of EA-2. For the bond symbols, see Fig. 2b. | ||
| Solvent | ΔGka (kcal mol−1) | ||||
|---|---|---|---|---|---|
| ttt | ttg+ | g+g−t | tg+(cisC–O) | (cisN–C)g+(cis+H–O) | |
| a At the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level with the IEFPCM solvation model. The five conformations were obtained from the geometrical optimization.b For the rotamers (ξ) of each bond, see Fig. 5.c See Fig. 2b. | |||||
| Benzene | 0.00 | 0.57 | −0.45 | 0.42 | 2.03 |
| Chloroform | 0.00 | 0.47 | −0.18 | 0.24 | 1.95 |
| DMSO | 0.00 | 0.37 | 0.08 | 0.04 | 1.85 |
| Water | 0.00 | 0.37 | 0.09 | 0.03 | 1.85 |
Conformational analysis of U-1 and U-2
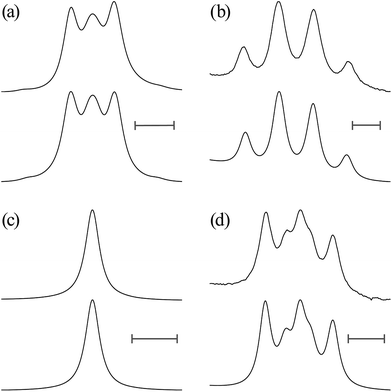
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)–NH group with the polar NMR solvents. For U-2, therefore, only the vicinal coupling constants at 15 and 25 °C are presented in Table S5 (ESI†). The equations for the analysis are given in Table 2, the coefficients (JC, JE, JG, and JT) are defined in Fig. 7, and their numerical values are written in the footnotes of Table 7. The trans fractions thus determined are listed in Tables 7 and S6 (ESI†). Despite the limited data, it is obviously indicated that the N–C and C–C bonds of U-1 and the C–C bond of U-2 prefer the gauche states.
O)–NH group with the polar NMR solvents. For U-2, therefore, only the vicinal coupling constants at 15 and 25 °C are presented in Table S5 (ESI†). The equations for the analysis are given in Table 2, the coefficients (JC, JE, JG, and JT) are defined in Fig. 7, and their numerical values are written in the footnotes of Table 7. The trans fractions thus determined are listed in Tables 7 and S6 (ESI†). Despite the limited data, it is obviously indicated that the N–C and C–C bonds of U-1 and the C–C bond of U-2 prefer the gauche states.
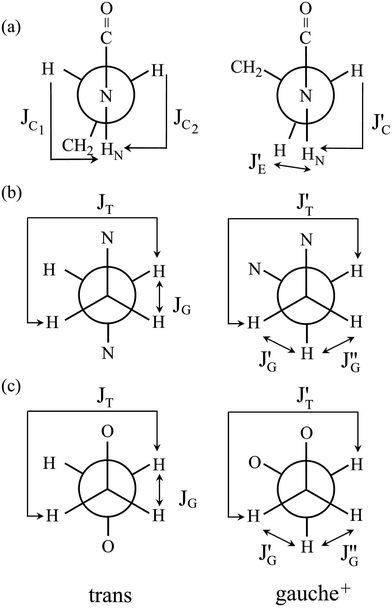 | ||
| Fig. 7 Newman projections for rotamers around the (a) c and e: N–C and (b) d: C–C bonds of U-1 and the (c) i: C–C bond of U-2, illustrating the coefficients (JC, J′E, JG, and JT) of the equations given in Table 2. For the bond symbols, see Fig. 2c and d. | ||
| Medium | Temp. (°C) | U-1b | U-2b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c & e: N–C | d: C–C | h & j: O–C | i: C–C | ||||||||
| NMR | MOc | NMR | MOc | MOc | NMR | MOc | |||||
| Set Ad | Set Be | Set Cf | Set Dg | Set Eh | Set Fi | ||||||
| a For more detailed data, see Table S6 (ESI†).b For the bond symbols, see Fig. 2c and d.c At the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level with the IEFPCM solvation model.d With the coupling constants calculated from a Karplus equation proposed by Ludvigsen et al.:30 JC1 + JC2 = 7.98 Hz and J′E + J′C = 12.44 Hz.e With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JC1 + JC2 = 4.77 Hz and J′E + J′C = 13.03 Hz.f With the coupling constants of 2-methylpiperazine:31 JT = 11.92, JG = 2.77, J′T = 11.92, J′G = 3.19, and J′′G = 1.92 Hz for the methanol solution; JT = 11.49, JG = 2.74, J′T = 11.49, J′G = 3.05, and J′′G = 2.14 Hz for the DMSO solution.g With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JT = 10.33, JG = 4.51, J′T = 10.38, J′G = 2.62, and J′′G = 1.65 Hz.h With the coupling constants optimized for ethylene oxides:32 JT = J′T = 11.4 Hz and JG = J′G = J′′G = 2.3 Hz.i With the coupling constants calculated from MO calculations at the B3LYP/6-311++G(3df,3pd) level: JT = 11.33, JG = 4.96, J′T = 10.73, J′G = 1.39, and J′′G = 2.49 Hz.j The satellite of U-2 was broadened at temperatures above 25 °C. | |||||||||||
| Gas | 25 | 0.16 | 0.14 | 0.46 | 0.24 | ||||||
| Methanol | 25 | 0.19 | 0.19 | 0.24 | 0.15 | 0.64 | 0.08 | 0.15 | 0.13 | ||
| DMSO | 25 | 0.18 | 0.17 | 0.19 | 0.18 | 0.21 | 0.15 | 0.64 | 0.04 | 0.11 | 0.13 |
| 35 | 0.21 | 0.18 | 0.19 | 0.18 | 0.22 | 0.15 | 0.63 | —j | —j | 0.13 | |
| 45 | 0.23 | 0.20 | 0.19 | 0.19 | 0.23 | 0.16 | 0.63 | — | — | 0.14 | |
| 55 | 0.23 | 0.20 | 0.19 | 0.20 | 0.24 | 0.16 | 0.62 | — | — | 0.14 | |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–C–H attraction; the outer ester groups appear to influence the inner NH–CH2–CH2–NH portion. On the other hand, the tg+t stabilization in the C(
O⋯H–C–H attraction; the outer ester groups appear to influence the inner NH–CH2–CH2–NH portion. On the other hand, the tg+t stabilization in the C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O–CH2–CH2–OC(
O)O–CH2–CH2–OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) bonds of U-2 has also been found for poly(ethylene terephthalate) (ΔGk = −1.2 kcal mol−1)33 and poly(ethylene succinate) (−1.3 kcal mol−1).34 The outer NH groups of U-2 seem not to disturb the tg+t preference inherent to the diester bond sequence.
O) bonds of U-2 has also been found for poly(ethylene terephthalate) (ΔGk = −1.2 kcal mol−1)33 and poly(ethylene succinate) (−1.3 kcal mol−1).34 The outer NH groups of U-2 seem not to disturb the tg+t preference inherent to the diester bond sequence.
| Conformerd | ΔGa (kcal mol−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| U-1b | U-2c | |||||||
| Gas | MeOH | DMSO | Gas | MeOH | DMSO | |||
| a At the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) level with the IEFPCM solvation model.b Relative to the g+g+g+ conformer.c Relative to the ttt conformer.d The blank represents that the potential minimum was not found by the geometrical optimization. | ||||||||
| t | t | t | 0.00 | 0.00 | 0.00 | |||
| t | t | g+ | −0.49 | −0.33 | −0.33 | |||
| t | g+ | t | −1.02 | −1.56 | −1.57 | |||
| t | g+ | g+ | −0.67 | −0.99 | −1.00 | |||
| t | g+ | g− | 0.64 | 0.37 | 0.37 | |||
| g+ | t | g+ | 2.78 | 1.24 | 1.20 | |||
| g+ | t | g− | 0.77 | 0.74 | 0.75 | 0.03 | 0.67 | 0.69 |
| g+ | g+ | g+ | 0.00 | 0.00 | 0.00 | −0.75 | −0.41 | −0.40 |
| g+ | g+ | g− | 2.05 | 1.27 | 1.26 | −0.32 | −0.16 | −0.16 |
| g+ | g− | g+ | 1.64 | 1.56 | 1.56 | |||
The trans fractions of U-1 and U-2, calculated from the ΔGk values, are compared in Tables 7 and S6 (ESI†) with the NMR data. The agreement between theory and experiment is good enough for us to conclude that the MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) calculation with the IEFPCM model should also be applicable to the urethane models.
Configurational properties of PEA and PU
As shown above, the MO calculations at the MP2//B3LYP level are suitable for the ester–amide and urethane models. Therefore, the configurational properties of PEA and PU were calculated with the MO energies and geometrical parameters. What we call the refined RIS method15 has advantages compared with the conventional RIS scheme:3,4 all geometrical parameters are dependent on (variable with) conformations of the current and neighboring bonds. The ΔGk energies of the model compounds, not being separated into first-, second-, and higher-order interaction energies, were directly introduced into the refined RIS computations.35 The conformational energies over bonds a–e and f–h of PEA were taken from the ΔGk values of EA-1 and EA-2 in DMSO, respectively (Fig. 1). In a similar manner, the conformational energies of PU were determined from the ΔGk values of U-1 and U-2 in DMSO.The results of the refined RIS calculations are summarized in Table 9. The characteristic ratio (〈r2〉0/nl2) of PEA is 5.39, almost the same as that (5.40) of PU. However, the temperature coefficient (dln〈r2〉0/dT × 103) of PEA is negative (−0.45), whereas that of PU is positive (0.69). The temperature coefficient at T0 was calculated using the finite-difference method:
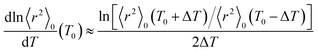 | (1) |
| PEA | PU | |
|---|---|---|
a Calculated from the MO energies including the solvent effect of DMSO.b Sconf = (R/x)[ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z + T(d(ln Z + T(d(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z))/(dT)] where R is the gas constant, x is the degree of polymerization, T is the absolute temperature, and Z is the partition function of the whole chain.c Symbols: Z))/(dT)] where R is the gas constant, x is the degree of polymerization, T is the absolute temperature, and Z is the partition function of the whole chain.c Symbols: ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) , averaged bond length (in Å); , averaged bond length (in Å); ![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) , averaged bond angle (in deg.); and , averaged bond angle (in deg.); and 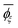 , average dihedral angle (in deg.) of the ξ conformation. , average dihedral angle (in deg.) of the ξ conformation. |
||
| 〈r2〉0/nl2 (x → ∞) | 5.39 | 5.40 |
| dln〈r2〉0/dT × 103 (K−1) | −0.45 | 0.69 |
| Sconfb (cal K−1 mol−1) | 8.28 | 9.73 |
| fU/f | −0.13 | 0.21 |
| Geometryc | Bond | ![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) |
![[l with combining macron]](https://www.rsc.org/images/entities/i_char_006c_0304.gif) |
![[small theta, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c9.gif) |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | 1.353 | 116.4 | 1.365 | 110.4 | ||||||
| b | 1.447 | 109.8 | ±93.0 | 1.355 | 122.1 | |||||
| c | 1.520 | 113.0 | ±116.3 | 1.454 | 113.3 | ±93.7 | ||||
| d | 1.452 | 122.6 | ±72.7 | 1.530 | 113.3 | ±115.8 | ||||
| e | 1.366 | 116.2 | 1.454 | 122.1 | ±93.7 | |||||
| f | 1.526 | 112.5 | ±90.3 | ±174.1 | 1.355 | 110.4 | ||||
| g | 1.529 | 114.3 | ±106.4 | 1.365 | 115.6 | |||||
| h | 1.512 | 111.8 | ± 13.2 | ±66.9 | ±172.4 | 1.437 | 109.6 | ±90.0 | ||
| i | 1.509 | 109.6 | ±111.7 | |||||||
| j | 1.437 | 115.6 | ±90.0 |
The Sconf value (in units of calories per Kelvin per mole) represents the conformational freedom of the unperturbed polymeric chain (e.g. in the melt and the amorphous state). Because PEA and PU have different monomer sizes, it is preferable that the unit should be changed to cal K−1 g−1. Then, PEA and PU are suggested to have close Sconf values of 5.8 × 10−2 and 5.6 × 10−2 cal K−1 g−1, respectively. The geometrical parameters averaged over all the possible conformations at 25 °C are also listed in Table 9.
Chain elasticity
If the ester amide or urethane unit is introduced into a polymeric network as a functional unit, it may show an elastic behavior. We can discuss the potentiality on the basis of the pioneering work of Flory et al.36–40The tension (f) of an elastomer is known to be expressed as:41
| f = fU + fS | (2) |
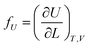 | (3) |
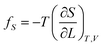 | (4) |
The ratio fU/f can be related to the temperature coefficient of the unperturbed chain dimension by:36–40
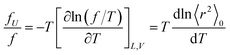 | (5) |
Polyethylene is known to exhibit negative fU/f values of ca. −0.4.36,38,42 As the temperature increases (ΔT > 0, where Δ means the change), the trans conformations partly change to more distorted gauche states of higher energy (Δ〈r2〉0 < 0), therefore dln〈r2〉0/dT < 0. When the polyethylene chain shrinks (ΔL < 0), the internal energy increases (ΔU > 0) owing to the trans-to-gauche conversion: (ΔU/ΔL ≈ (∂U/∂L) < 0). The negative fU/f vitiates the entropic elasticity, because fS must always be positive.
Positive fU/f values have often been found for elastomers, for example, natural rubber (0.12–0.18), polydimethylsiloxane (0.13–0.30), and cis-1,4-polybutadiene (0.10–0.17).42 The PU chain here also shows a positive value of 0.21. This is because PU strongly prefers distorted conformations: in bonds c–e, g+g+g+; and in bonds h–j, tg+t, tg+g+, and g+g+g+. As temperature increases, the distortion relaxes and the chain dimension increases: dln〈r2〉0/dT > 0. The stretching (contraction) of the PU chain increases (decreases) the internal energy: (∂U/∂L) > 0. This nature of PU supports the entropic elasticity. On the other hand, PEA will behave like polyethylene because of the negative fU/f. Therefore, the urethane unit is more likely to behave as an elastomer than the ester amide unit.
Although it is well established that rubber-like elasticity is entirely of intramolecular origin,43 the as-synthesized PU may not necessarily act as an elastomer. This is because the chain must also satisfy the following requirements to exhibit rubber-like elasticity: the chain must have a high degree of flexibility and mobility and, in addition, join a network structure.43 Probably, as needed, the polymer must become amorphous (by e.g. quenching), cross-linked, diluted with a plasticizer to lower the glass transition temperature, and/or foamed. Or, as mentioned in the Introduction, if the oligo-urethane is incorporated into a polymeric mosaic, it may behave as an elastomeric functional unit. The repeating units of PEA and PU include the same atomic groups, two ethylene, ester, and amide groups, but their arrangements in the backbone are different. The cardinal principle of polymer science and molecular biology, “higher-order structures, physical properties, and functions of a polymer originate from its primary structure”, should be emphasized. The difference between PEA and PU in atomic arrangement generates the differences in physical properties.
Biodegradability
Poly(ester amide)s have often been rendered biodegradable by introducing degradable components such as lactic acid, glycolic acid, and ε-caprolactone units into the ester part of the main chain.9,44–47 Then, the ester and amide moieties of poly(ester amide)s are considered to be different FUs. If the former and latter units are, respectively, a biodegradable ester and an α-amino acid, the decomposed products would be non-toxic to humans. Therefore, such poly(ester amide)s may be used for biomedical materials.The biodegradability of polyurethanes has been investigated from a microbiological viewpoint.10,48,49 The findings may be summarized as follows: (1) polyester-type polyurethanes are more susceptible to microbial attack than polyether-type ones; (2) polyurethanes with long repeating units are more readily degradable than those with short monomers; (3) the amorphous regions are degraded prior to the crystallites; and (4) the biodegradation of polyester-type polyurethanes is mainly due to the hydrolysis of the ester bonds by lipases and their homologs. In addition, aliphatic polyurethanes with different numbers of carbon atoms in the backbone, being close to the PU considered here in terms of the primary structure, have been reported to be biodegradable.10,48,49
Previous studies on biodegradable polymers48,50–52 have indicated that lipases are apt to degrade aliphatic polyesters with comparatively many methylene groups. Our conformational analysis of poly(ethylene succinate) and poly(butylene succinate)34 has indicated that such polyesters will selectively adopt extended and planar structures and can enter narrow crevices of lipases. The active site for hydrolyzing the ester bond is located inside the crevice. Therefore, the lipases may hardly degrade the PEA and PU chain because they strongly prefer the distorted conformations. It is well-known that the CH2–CH2 bond adjacent to the O–C bond in O–(CH2)z–O sequences of esters and ethers prefers the gauche form,53 and that the gauche stability of the bond generally decreases with increasing number of methylene units between the two oxygen atoms.13,14,33,34,54–56 If the ester and amide groups of the poly(ester amide)s ([–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O(CH2)yNHC(
O)O(CH2)yNHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)(CH2)z–]x) or urethane groups of the polyurethanes ([–C(
O)(CH2)z–]x) or urethane groups of the polyurethanes ([–C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)NH(CH2)yNHC(
O)NH(CH2)yNHC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O(CH2)zO–]x) are separated by at least four methylene units (z ≥ 4), these FUs would more readily form planar structures and possibly approach the active sites of lipases. Such poly(ester amide)s and polyurethanes are expected to exhibit some level of biodegradability. This prediction is consistent with the above-mentioned microbiological findings.
O)O(CH2)zO–]x) are separated by at least four methylene units (z ≥ 4), these FUs would more readily form planar structures and possibly approach the active sites of lipases. Such poly(ester amide)s and polyurethanes are expected to exhibit some level of biodegradability. This prediction is consistent with the above-mentioned microbiological findings.
Summary
To elucidate the effects of ester and amide groups on the conformational characteristics and physical properties of polymers, this study has dealt with a simple poly(ester amide) and polyurethane, PEA and PU. Each repeating unit was divided into two moieties, which have been represented by model compounds: EA-1 and EA-2 for PEA; and U-1 and U-2 for PU. These compounds were prepared and subjected to NMR measurements to determine the bond conformations. To examine the applicability of MO theories to the models, B3LYP, M06-2X, and MP2 calculations with the IEFPCM and CPCM solvation models were applied to EA-1 and compared with the NMR experiments. The M06-2X and MP2 energies with the B3LYP geometry satisfactorily reproduced the NMR data, and the IEFPCM and CPCM models made no essential differences. Therefore, MP2/6-311+G(2d,p)//B3LYP/6-311+G(2d,p) calculations with the IEFPCM model were employed to calculate the conformer free energies of all the four model compounds and suggested that the models form intramolecular N–H⋯O and C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C attractions and strongly prefer distorted structures including gauche bonds.
C attractions and strongly prefer distorted structures including gauche bonds.
The refined RIS calculations for the PEA and PU chains at 25 °C yield essentially the same characteristic ratios of ca. 5.4, whereas the temperature coefficients (dln〈r2〉0/dT × 103) of PEA and PU were negative (−0.45) and positive (0.69), respectively. Therefore, in PEA, the energy elasticity works against the entropic elasticity, whereas in PU, the former works with the latter. The results suggest the possibility that the PU chain would act as an elastomer under suitable conditions. In addition, the biodegradability of poly(ester amide)s and polyurethanes has been discussed in terms of their primary structures, and chemical modifications to render these polymers biodegradable have also been proposed.
In conclusion, PEA and PU, if chemically modified as needed, are expected not only to play the role of junctures of polymer networks and architectures but also to become more functional. Computational science will be increasingly helpful for molecular and materials design.57–59
Acknowledgements
This study was partially supported by the Grants-in-Aid for Scientific Research (C) (22550190 and 16K05906) from the Japan Society for the Promotion of Science.References
- E. Wagner and J. Kloeckner, Adv. Polym. Sci., 2006, 192, 135–173 CrossRef CAS
.
- Y. Yuan, C.-J. Zhang and B. Liu, Angew. Chem., Int. Ed., 2015, 54, 11419–11423 CrossRef CAS PubMed
.
- P. J. Flory, Statistical Mechanics of Chain Molecules, Wiley & Sons, New York, USA, 1969 Search PubMed
.
- W. L. Mattice and U. W. Suter, Conformational Theory of Large Molecules: The Rotational Isomeric State Model in Macromolecular Systems, Wiley-Interscience, New York, USA, 1994 Search PubMed
.
- J.-M. Lehn, Supramolecular Chemistry: Concepts and Perspectives, VCH, Weinheim, Germany, 1995 Search PubMed
.
- I. M. Atkinson and L. F. Lindoy, Self Assembly in Supramolecular Systems, Royal Society of Chemistry, London, UK, 2000 Search PubMed
.
- A. Greenberg, C. M. Breneman and J. F. Liebman, The Amide Linkage: Selected Structural Aspects in Chemistry, Biochemistry, and Materials Science, Wiley-Interscience, New York, USA, 2000 Search PubMed
.
- M. Nagasawa, T. Ishii, D. Abe and Y. Sasanuma, RSC Adv., 2015, 5, 96611–96622 RSC
.
- A. C. Fonseca, M. H. Gil and P. N. Simões, Prog. Polym. Sci., 2014, 39, 1291–1311 CrossRef CAS
.
- G. T. Howard, in Microbial Degradation of Xenobiotics, Environmental Science and Engineering, ed. S. N. Singh, Springer, Berlin, Germany, 2012, ch. 14 Search PubMed
.
- T. Fey, M. Hölscher, H. Keul and H. Höcker, Polym. Int., 2003, 52, 1625–1632 CrossRef CAS
.
- E. L. Wittbecker and M. Katz, J. Polym. Sci., Part A: Polym. Chem., 1959, 40, 367–375 CAS
.
- Y. Sasanuma and N. Suzuki, Macromolecules, 2009, 42, 7203–7212 CrossRef CAS
.
- Y. Sasanuma, Y. Wagai, N. Suzuki and D. Abe, Polymer, 2013, 54, 3904–3913 CrossRef CAS
.
- Y. Sasanuma, S. Asai and R. Kumagai, Macromolecules, 2007, 40, 3488–3497 CrossRef CAS
.
- D.-L. Sun, S.-J. Xie, J.-R. Deng, C.-J. Huang, E. Ruckenstein and Z.-S. Chao, Green Chem., 2010, 12, 483–490 RSC
.
- V. V. Mikheev, Russ. J. Org. Chem., 1989, 25, 2028–2029 Search PubMed
.
- P. H. Budzelaar, gNMR, version 5.0, IvorySoft & Adept Scientific plc, Letchworth, U.K., 2004 Search PubMed
.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision B01, Gaussian Inc., Wallingford CT, USA, 2009 Search PubMed
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- C. Moller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef CAS
.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed
.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef
.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed
.
- T. Helgaker, M. Watson and N. C. Handy, J. Chem. Phys., 2000, 113, 9402–9409 CrossRef CAS
.
- IUPAC, Compendium of Chemical Terminology, ed. A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, UK, 2nd edn (the “Gold Book”), 1997 Search PubMed
.
- I. Tvaroška and J. Gajdoš, Carbohydr. Res., 1995, 271, 151–162 CrossRef
.
- Y. Sasanuma, R. Kumagai and K. Nakata, Macromolecules, 2006, 39, 6752–6764 CrossRef CAS
.
- L.-F. Kao and M. Barfield, J. Am. Chem. Soc., 1985, 107, 2323–2330 CrossRef CAS
.
- S. Ludvigsen, K. V. Andersen and F. M. Poulsen, J. Mol. Biol., 1991, 217, 731–736 CrossRef PubMed
.
- Y. Sasanuma, S. Hattori, S. Imazu, S. Ikeda, T. Kaizuka, T. Iijima, M. Sawanobori, M. A. Azam, R. V. Law and J. H. G. Steinke, Macromolecules, 2004, 37, 9169–9183 CrossRef CAS
.
- K. Tasaki and A. Abe, Polymer J., 1985, 17, 641–655 CrossRef CAS
.
- Y. Sasanuma, Macromolecules, 2009, 42, 2854–2862 CrossRef CAS
.
- Y. Sasanuma, Y. Nonaka and Y. Yamaguchi, Polymer, 2015, 56, 327–339 CrossRef CAS
.
- Y. Sasanuma, Y. Ogawa and M. Matsumoto, Phys. Chem. Chem. Phys., 2010, 12, 14619–14628 RSC
.
- P. J. Flory, C. A. J. Hoeve and A. Ciferri, J. Polym. Sci., 1959, 34, 337–347 CrossRef CAS
.
- P. J. Flory, A. Ciferri and C. A. J. Hoeve, J. Polymer Sci., 1960, 45, 235–236 CrossRef CAS
.
- A. Ciferri, C. A. J. Hoeve and P. J. Flory, J. Am. Chem. Soc., 1961, 83, 1015–1022 CrossRef CAS
.
- J. E. Mark, J. Chem. Educ., 1981, 58, 898–903 CrossRef CAS
.
- J. E. Mark, J. Chem. Educ., 2002, 79, 1437–1443 CrossRef CAS
.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, USA, 1953 Search PubMed
.
- J. E. Mark, Macromol. Rev., 1976, 11, 135–159 CrossRef CAS
.
- J. E. Mark, in Physical Properties of Polymers, Cambridge University Press, Cambridge, UK, 2003, pp. 3–71 Search PubMed
.
- J. Tuominen and J. V. Seppälä, Macromolecules, 2000, 33, 3530–3535 CrossRef CAS
.
- M. Vera, M. Admetlla, A. Rodríguez-Galán and J. Puiggalí, Polym. Degrad. Stab., 2005, 89, 21–32 CrossRef CAS
.
- E. Botines, M. T. Casas and J. Puiggalí, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 815–825 CrossRef CAS
.
- J. E. Báez, D. Ramírez, J. L. Valentín and Á. Marcos-Fernández, Macromolecules, 2012, 45, 6966–6980 CrossRef
.
- Y. Tokiwa, B. P. Calabia, C. U. Ugwu and S. Aiba, Int. J. Mol. Sci., 2009, 10, 3722–3742 CrossRef CAS PubMed
.
- G. T. Howard, Int. Biodeterior. Biodegrad., 2002, 49, 245–252 CrossRef CAS
.
- H. Pranamuda, A. Tsuchii and Y. Tokiwa, Macromol. Biosci., 2001, 1, 25–29 CrossRef CAS
.
- Y. Tokiwa and A. Jarerat, Macromol. Symp., 2003, 201, 283–290 CrossRef CAS
.
- Y. Tokiwa and B. P. Calabia, Biotechnol. Lett., 2004, 26, 1181–1189 CrossRef CAS PubMed
.
- Y. Sasanuma, in Annual Reports on NMR Spectroscopy, ed. G. A. Webb, Academic Press, Elsevier Science, Oxford, UK, 2003, vol. 49, ch. 5, pp. 213–280 Search PubMed
.
- Y. Sasanuma, H. Ohta, I. Touma, H. Matoba, Y. Hayashi and A. Kaito, Macromolecules, 2002, 35, 3748–3761 CrossRef CAS
.
- Y. Sasanuma and A. Watanabe, Macromolecules, 2006, 39, 1646–1656 CrossRef CAS
.
- R. V. Law and Y. Sasanuma, Macromolecules, 1998, 31, 2335–2342 CrossRef CAS
.
- Computer Simulation of Polymers, ed. R. J. Roe, Prentice Hall, Upper Saddle River, New Jersey, USA, 1991 Search PubMed
.
- Computer Simulation of Polymeric Materials: Application of the OCTA System, ed. Japan Association for Chemical Innovation, Springer, Singapore, 2016 Search PubMed
.
- T. K. Mukhopadhyay and A. Datta, J. Phys. Chem. C, 2017, 121, 10210–10223 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Characteristics of various functional units (Table S1); observed vicinal coupling constants of EA-1 and EA-1-13C (Table S2); trans fractions of EA-1 determined from NMR experiments (Table S3); trans fractions of EA-1 evaluated from MO calculations (Table S4); observed vicinal coupling constants of U-1 and U-2 (Table S5); and trans fractions of U-1 and U-2 (Table S6). See DOI: 10.1039/c7ra05395a |
| This journal is © The Royal Society of Chemistry 2017 |