Open Access Article
Open Access ArticleBand structure engineering of borophane by first principles calculations
Zhi-Qiang Wang a,
Tie-Yu Lüa,
Hui-Qiong Wangab,
Yuan Ping Fengc and
Jin-Cheng Zheng
a,
Tie-Yu Lüa,
Hui-Qiong Wangab,
Yuan Ping Fengc and
Jin-Cheng Zheng *abd
*abd
aDepartment of Physics, Collaborative Innovation Center for Optoelectronic Semiconductors and Efficient Devices, Xiamen University, Xiamen 361005, China. E-mail: jczheng@xmu.edu.cn
bXiamen University Malaysia, 439000 Sepang, Selangor, Malaysia
cDepartment of Physics, National University of Singapore, Singapore 117542, Singapore
dFujian Provincial Key Laboratory of Theoretical and Computational Chemistry, Xiamen University, Xiamen 361005, China
First published on 11th October 2017
Abstract
We exploited the band structure engineering in W-borophane, the most stable conformer of the fully hydrogenated borophene in the literature, by first principles calculations. Uniaxial strains along the a and b direction, biaxial strains, shear strains, H vacancy and B–H dimer vacancy defects have been considered. Our results show that uniaxial strains along the a, b directions and biaxial strain can not open the band gap for W-borophane. However, band gap opening can be achieved by applying shear strain. The shear strain induced band gap is 53 meV when the applied shear strain is only 0.01. The band gap increases with the increasing shear strain. When the shear strain reaches 0.12, the band gap can reach up to 538 meV. Two different exchange–correlation potentials have been used to confirm the band gap opening. The excellent dynamical stability of W-borophane under shear strain has been proved by the phonon dispersion, indicating that applying shear strain is an effective and feasible approach to open the band gap for W-borophane. In addition, the Dirac cone of W-borophane is maintained well under the uniaxial and biaxial strains. In free-state, the Dirac fermions of W-borophane possess an ultrahigh Fermi velocity (2.13 × 106 m s−1) which is higher than that of graphene. It is very interesting that the Fermi velocities of W-borophane can be tuned in a wide range of values by applying uniaxial and biaxial strain.
Introduction
Recently, a two-dimensional (2D) boron sheet (borophene) was synthesized on a silver substrate under ultrahigh-vacuum1,2 and has attracted much attention.3–10 Borophene possesses high anisotropy in its mechanical properties, electrical conductivity, lattice thermal conductivity, surface ion transport and optical properties.11–15 High intrinsic catalytic activity of borophene for the hydrogen evolution reaction also has been reported.16 It has been proposed that borophene is the lightest catalyst for the hydrogen and oxygen evolution reaction.17 Furthermore, the catalytic performance can be improved by carbon dopants.17 Due to the high theoretical specific capacity and ultrafast ion transport property, which is strongly associated with the rate performance,18,19 borophene is a promising anode material for Li, Na, K, Mg and Al ion batteries.9,20–23 However, borophene is unstable against long-wavelength transversal waves, owing to the small imaginary frequency along the Γ–X direction in the phonon dispersion.24 It has been proposed that borophene can be stabilized by hydrogenation.24,25 The fully hydrogenated borophene (borophane) has a direction-dependent Dirac cone, and the Dirac fermions possess an ultrahigh Fermi velocity.24 Due to the ultrahigh Fermi velocity and excellent mechanical performance, borophane has a vast prospect of application in nanoelectronics devices. For example, theoretical calculations indicated that borophane can be used for the detection for volatile alcohol vapors.26 It is imperative to open the band gap of borophane for a broader application. Strain engineering is a common and effective approach to tune the physical and chemical properties of materials.27–34 It is reported that the band gap of graphene can be opened by applying a sine-like inhomogeneous deformation along any direction but the armchair one.35 Furthermore, it has been proposed that opening gap of graphene could be achieved by shear strains. The strain induced band gap can reach up to 0.9 eV.36 Gap opening of graphene can also be achieved by designing topological-defect lattices.37 In addition, hydrogenation and fluorination are both effective approaches to open the band gap for graphene.38,39 More specifically, the energy gaps of fully hydrogenated and fluorinated graphene are 4.62 and 3.45 eV, respectively.39 To date, the band structure engineering of borophane has not been reported, and would be the focus of the present study.In this work, the band structures of W-borophane under uniaxial strains along the a and b directions, biaxial strains, and shear strains have been studied by first principles calculations. Our results show that uniaxial strains along the a, b directions and biaxial strains are unable to open the band gap of W-borophane. However, the band gap opening can be achieved by shear strains. Moreover, we examined the dynamical stability of W-borophane under shear strains by the phonon dispersion. In addition, our results show that the Fermi velocities of the Dirac fermions in W-borophane can be tuned in a wide range of values by applying the uniaxial and biaxial strains. Finally, the spin-polarized band structure and charge density distribution of W-borophane with the H and B–H dimer vacancy defect have been studied, respectively.
Computational details
All calculations are carried out in the Quantum-Espresso package.40 Ultrasoft pseudopotentials41 are utilized for all atoms and the exchange–correlation approximation is evaluated through the Perdew–Burke–Ernzerhof (PBE)42 functional. The kinetic-energy cutoff of plane-waves is set to be 50 Ry. The atomic positions are fully relaxed, until the forces on all atoms are less than 0.01 eV Å−1. A large vacuum region (20 Å) is included along the z direction to eliminate the interlayer interactions. Linear response theory has been utilized to calculate the phonon dispersion. During the calculation of the dynamic matrix element, the threshold for self-consistency is 1.0 × 10−12. In order to further affirm the band gap opening, Becke–Lee–Yang–Parr (BLYP) exchange–correlation functional has been used to calculate the band structure of W-borophane and chair-like (C-borophane) under shear strains. In addition, the spin-polarized calculations are performed to obtain the spin-polarized band structure and charge density distribution of W-borophane with the H vacancy and B–H dimer vacancy defects, respectively.Results and discussion
Uniaxial and biaxial strains
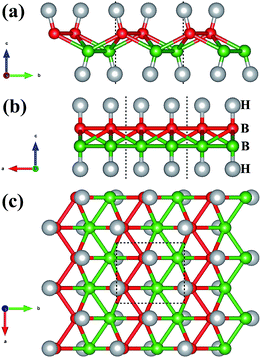
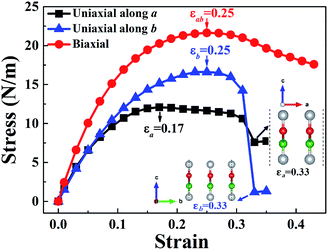
The crystal structure of W-borophane is displayed in Fig. 1. The unit cell is marked by the black dashed rectangle which contains four B and four H atoms. B and H atoms are staggered along both the a and b directions. W-borophane has a buckled configuration and the buckling height is 0.89 Å under free-state, which is slightly smaller than that of borophene (0.91 Å),11 but larger than that of C-borophane (0.81 Å).43 For W-borophane, the optimized lattice constants are 3.039 and 3.379 Å along the a and b directions, respectively, which are in good agreement with previous theoretical results.44The stress–strain curves of W-borophane under uniaxial strain along the a and b directions, and biaxial strains are displayed in Fig. 2. For applying the biaxial tensile strains, we change the lattice constants a and b with the equal proportion. The corresponding stress under the biaxial tensile strains is the vectorial resultant of the a and b direction component stresses. From the stress–strain curves, we can find that the ultimate tensile strains are 0.17, 0.25 and 0.25 for uniaxial strains along the a, b directions and biaxial direction, respectively. The corresponding ideal strengths are 12.08, 16.60 and 21.63 N m−1, respectively. Under small uniaxial and biaxial strains, the stresses increase with the increasing strains. There exists a sharp decrease when the uniaxial strains reach 0.33 along the a and b directions. From the two illustrations in Fig. 2 we can find that the crystal structure of W-borophane has been destroyed when the uniaxial strains reach 0.33 along the a and b directions. The ultimate tensile strains of W-borophane (0.17) is larger than that of C-borophane (0.12)43 along the a direction. In order to understand the different mechanical stabilities of C- and W-borophane along the a direction, the crystal structure of C-borophane has been compared with that of W-borophane. For C-borophane, B atoms are aligned along the a direction. However, for W-borophane, B atoms are staggered by a zigzag mode along the a direction which is very important to release the a direction uniaxial strain.43 Hence, W-borophane shows more superior mechanical properties along the a direction than C-borophane.
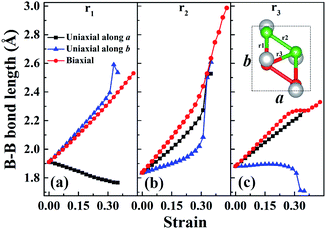
In order to understand the anisotropic mechanical property of W-borophane, we calculated the buckling heights of W-borophane under the uniaxial along the a, b directions and biaxial tensile strains. The buckling height is an important parameter for buckled 2D materials. The buckling height of W-borophane decreases under the a, b direction uniaxial and biaxial tensile strains, as shown in Fig. 3. It is easy to understand that tensile strains can stretch the pucker of W-borophane, leading to the decrease of the buckling height. However, under the a and b direction uniaxial strains, there exists a sudden jump when the tensile strains reach 0.33 that is corresponding to the rupture. Furthermore, the B–B bond lengths under the uniaxial along a, b directions and biaxial tensile strains have been calculated. For the convenience of description, we labelled the three inequitable B–B bonds in the unit cell as r1, r2 and r3, respectively, as shown in the inserted picture of Fig. 4c. Under the a direction uniaxial tensile strains, the bond lengths of r2 and r3 increase with the increasing strains, but the bond length of B–B bond r1 decreases with the increasing strains. Under the b direction uniaxial tensile strains, the bond lengths of r1 and r2 increase with the increasing strains. The bond length of r3 keeps almost unchanged, however, there is a sharp decrease when the b direction uniaxial strain reaches 0.33. Under the biaxial tensile strains, the bond lengths of r1, r2 and r3 all increase with the increasing strains. In order to understand the contraction of B–B bond r1 under a direction tensile strains, the Poisson's ratio of W-borophane has been taken into consideration. It is reported that the Poisson's ratios of W-borophane are 0.132 and 0.117 along the a and b direction,23 respectively. The positive Poisson's ratio indicates that W-borophane tends to contract in the directions transverse to the direction of stretching. More specifically, under the a direction tensile strains, the lattice constant along the b direction will decrease, leading to the contraction of r1 which is parallel to the b direction from the top view.
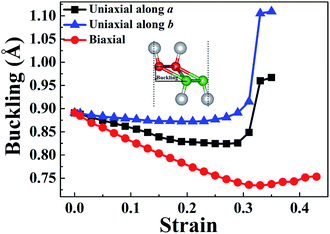 | ||
| Fig. 3 The strain-dependent buckling height of W-borophane under uniaxial strains along the a and b directions, respectively, and biaxial strains. | ||
The band structure of W-borophane under uniaxial strain along the a and b directions, biaxial strains has been calculated, as shown in Fig. 5. W-borophane possesses a Dirac cone along the Γ–Y direction. We found that the Dirac cone maintains well under the uniaxial and biaxial strains. More specifically, when the a direction uniaxial strain is between −0.17 and 0.05, the b direction uniaxial strain is between −0.05 and 0.23, and the biaxial strain is between −0.13 and 0.29, the Dirac cone maintains well and the Dirac point locates at the Fermi level perfectly. It is reported that the Dirac cone of W-borophane is mainly contributed by the px and py orbitals of B atoms.24 The Fermi velocities of the Dirac fermions can be obtained by the expression ν = E(k)/(ħk). As shown in the illustration of Fig. 6b, we define the E(k)/(ħk) value of the band (black curve) corresponding to the px orbital as νpx. Similarly, we define the E(k)/(ħk) value of the band (red curve) corresponding to the py orbital as νpy. Under the free-state, the Fermi velocities νpx and νpy of W-borophane are 1.15 × 106 and 2.13 × 106 m s−1, respectively. The Fermi velocities νpx and νpy of W-borophane under the a, b direction uniaxial and biaxial strains are shown in Fig. 6. First of all, the Fermi velocities of W-borophane can been tuned in a wide range of values by controlling the applied strains. The compression of the lattice constant along a direction and stretching of the lattice constant along b direction can enlarge the Fermi velocity νpx. On the contrary, the compression of the lattice constant along b direction and stretching of the lattice constant along a direction can enlarge the Fermi velocity νpy. The biaxial strains impose slight effect on Fermi velocity νpx, the Fermi velocity νpy decreases with the increasing biaxial tensile strains.
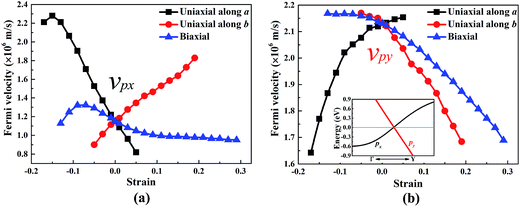 | ||
| Fig. 6 The Fermi velocity νpx and νpy of W-borophane under the uniaxial strains along the a and b directions, respectively, and biaxial strain. | ||
Shear strains
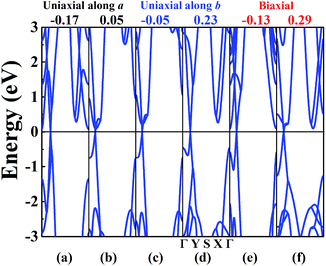
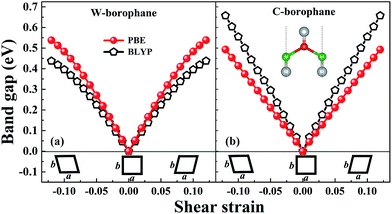
In order to achieve the band gap opening, shear strain has also been taken into consideration because shear strain is a common and effective approach to open the energy band gap of 2D Dirac materials. Therefore, we calculated the band structure of W-borophane under shear strains, as shown in Fig. 7. Positive and negative shear strains have been taken into consideration. Under free-state, the angle γ between lattice vectors along the a and b direction is 90°. Under the positive (negative) shear strains, the angle γ becomes smaller (larger) than 90°. The corresponding schematics have been shown in the Fig. 8 as small illustrations. Under 0.01 and 0.04 shear strain, the opening band gaps are 53 and 220 meV, respectively. Furthermore, the band gap become 538 meV when the shear strain reaches 0.12, indicating that shear strain is an effective approach to open the band gap of W-borophane. The band gap of C- and W-borophane under different shear strains are shown in Fig. 8. In order to further affirm the band gap opening, Becke–Lee–Yang–Parr exchange–correlation functional has been used. The shear strain induced band gap under PBE and BLYP level are consistent. The band gap enlarges with the increasing shear strains with different rates for PBE and BLYP. In order to present the relationship between the strain induced energy gap Eg and shear strain εshear more clearly, the corresponding function formula has been fitted under small shear strains. Under small shear strains, the linear relationship between Eg and εshear can be observed. More specifically, under the PBE level, for C-borophane, the formula is Eg = 4.1 × εshear; however, for W-borophane, the formula is Eg = 5.4 × εshear under small shear strains. Similarly, the band gap opening of 8-Pmmn borophene which is a 2D Dirac material by shear strains has been reported in literature.3 For 8-Pmmn borophene, the formula is Eg = 2.4 × εshear under small shear strains. The coefficient of W-borophane is larger than that of C-borophane and 8-Pmmn borophene, indicating that the shear strain is a more effective way to tune the band gap of W-borophane. For W-borophane, the non-linear relationship can be observed when the shear strain is larger than 0.05. Uniaxial along the a, b direction and biaxial strains cannot change the symmetry of borophane. But shear strain can effectively break the symmetry, leading to the strain induced band gap opening. For example, under free-state, the angle γ between the lattice vectors along the a and b direction is 90°. However, under 0.04 (−0.04) shear strain, the angle γ of W-borophane changes to 87.71° (92.29°), corresponding to the change of symmetry. Similar phenomenon has been observed in graphene.35,36,45 In order to estimate the dynamical stability of W-borophane under shear strains, we calculated the phonon dispersion. The phonon dispersions of W-borophane under shear strains are shown in Fig. 9. No imaginary frequencies were found along the high-symmetry directions of W-borophane under shear strains, indicating that W-borophane possesses excellent dynamical stability under shear strains. Due to the impressive strain induced band gap and the excellent dynamical stability, shear strains is an effective and feasible approach to open the band gap for W-borophane.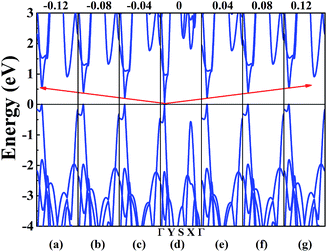 | ||
| Fig. 7 The band structure of W-borophane under shear strains of (a) −0.12, (b) −0.08, (c) −0.04, (d) 0, (e) 0.04 (f) 0.08 and (g) 0.12. | ||
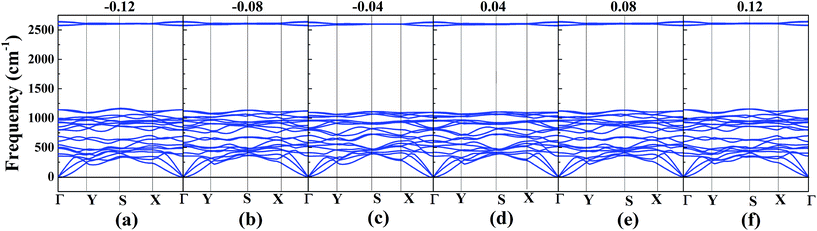 | ||
| Fig. 9 The phonon dispersion of W-borophane under shear strains of (a) −0.12, (b) −0.08, (c) −0.04, (d) 0.04, (e) 0.08 and (f) 0.12. | ||
H and B–H dimer vacancy defect
Vacancy defects are usually inevitable in the experimental process. Furthermore, the electronic structures of 2D materials are strongly influenced by vacancy defects.46–49 For example, the defect-induced magnetism has been observed in graphene. For borophane, low B–H dimer vacancy formation energy has been reported in our previous work,25 indicating that B–H dimer vacancy defect is feasible, experimentally. In addition, we have calculated the band structure of W-borophane with one H and B–H dimer vacancy defect in a 2 × 3 × 1 supercell which contains 48 atoms, respectively. Spin polarization has been taken into consideration. The spin-polarized band structures have been shown in Fig. 10. From the spin-polarized band structures, we can find that both H and B–H dimer vacancy defect cannot open the band gap for W-borophane. The two band structures both show metallic characteristics. It is interesting that the spin-up band structure curve of W-borophane with B–H dimer vacancy defect is completely overlapping with the spin-down band structure, indicating that B–H vacancy defect cannot lead to the appearance of magnetism. However, H vacancy defect can result in the rise of magnetism. More specifically, the H vacancy defect induced magnetic moment is as high as 0.53 μB. The spin-polarized state is more stable than the non-spin-polarized state, but the energy difference is only 6.51 meV. In order to show the vacancy induced magnetism phenomenon more clearly, we calculated the difference in spin charge density between the spin-up and spin-down states of W-borophane with the H vacancy defect, as shown in Fig. 11. The H atom vacancy induced magnetism phenomenon is obvious.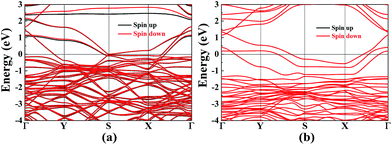 | ||
| Fig. 10 The band structures of W-borophane with the (a) H vacancy and (b) B–H dimer vacancy defect, respectively. | ||
Conclusions
We have studied the band structure engineering of borophane by first principles calculations. Uniaxial strains along the a and b directions, biaxial strains, shear strains, H vacancy and B–H dimer vacancy defects have been considered. Our results show that the mechanical properties of W-borophane is highly anisotropic. The ultimate tensile strains are 0.17, 0.25 and 0.25 for uniaxial strains along the a, b directions and biaxial strain, respectively. The corresponding ideal strengths are 12.08, 16.60 and 21.63 N m−1, respectively. Uniaxial strains along the a, b directions and the biaxial strain all cannot open the band gap for W-borophane. However, band gap opening can be achieved by applying shear strains. Under 0.01 and 0.04 shear strain, the opening band gaps are 53 and 220 meV, respectively. The shear strain induced band gap increases with the increasing shear strains. The band gap can reach up to 538 meV when the shear strain reaches 0.12. The shear strain induced band gap opening has been confirmed by two different exchange–correlation functionals. The excellent dynamical stability of W-borophane under shear strains has also been proved by the phonon dispersion, indicating that applying shear strains is an effective and feasible approach to open the band gap for W-borophane. It is very interesting that the Fermi velocities of the Dirac fermions in W-borophane can be tuned in a wide range of values by uniaxial and biaxial strains. Furthermore, H vacancy and B–H dimer vacancy defects cannot open the band gap for W-borophane. Finally, magnetism phenomenon has been observed for W-borophane with H vacancy defect.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Fundamental Research Funds for Central Universities (Grant No. 20720160020, 2013121010), the Natural Science Foundation of Fujian Province, China (Grant No. 2015J01029), Special Program for Applied Research on Super Computation of the NSFC-Guangdong Joint Fund (the second phase), the National Natural Science Foundation of China (No. 11335006, 51661135011). TYL acknowledges the National University of Singapore for hosting his visit during which part of the work reported here was carried out.Notes and references
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- B. J. Feng, J. Zhang, Q. Zhong, W. B. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. H. Wu, Nat. Chem., 2016, 8, 563–568 CrossRef CAS PubMed.
- A. Lopez-Bezanilla and P. B. Littlewood, Phys. Rev. B, 2016, 93, 241405(R) CrossRef.
- B. Peng, H. Zhang, H. Z. Shao, Y. F. Xu, R. J. Zhang and H. Y. Zhu, J. Mater. Chem. C, 2016, 4, 3592–3598 RSC.
- J. Carrete, W. Li, L. Lindsay, D. A. Broido, L. J. Gallego and N. Mingo, Mater. Res. Lett., 2016, 4, 204–211 CrossRef CAS.
- R. C. Xiao, D. F. Shao, W. J. Lu, H. Y. Lv, J. Y. Li and Y. P. Sun, Appl. Phys. Lett., 2016, 109, 122604 CrossRef.
- J. H. Yuan, L. W. Zhang and K. M. Liew, RSC Adv., 2015, 5, 74399–74407 RSC.
- H. S. Liu, J. F. Gao and J. J. Zhao, Sci. Rep., 2013, 3, 3238 CrossRef PubMed.
- X. M. Zhang, J. P. Hu, Y. C. Cheng, H. Y. Yang, Y. G. Yao and S. Y. Yang, Nanoscale, 2016, 8, 15340–15347 RSC.
- H. B. Shu, F. Li, P. Liang and X. S. Chen, Nanoscale, 2016, 8, 16284–16291 RSC.
- H. F. Wang, Q. F. Li, Y. Gao, F. Miao, X. F. Zhou and X. G. Wan, New J. Phys., 2016, 18, 073016 CrossRef.
- J. E. Padilha, R. H. Miwa and A. Fazzio, Phys. Chem. Chem. Phys., 2016, 18, 25491–25496 RSC.
- H. Y. Sun, Q. F. Li and X. G. Wan, Phys. Chem. Chem. Phys., 2016, 18, 14927–14932 RSC.
- Z. H. Cui, E. Jimenez-Izal and A. N. Alexandrova, J. Phys. Chem. Lett., 2017, 8, 1224–1228 CrossRef CAS PubMed.
- A. Lherbier, A. R. Botello-Méndez and J.-C. Charlier, 2D Materials, 2016, 3, 045006 CrossRef.
- L. Shi, C. Y. Ling, Y. X. Ouyang and J. L. Wang, Nanoscale, 2016, 9, 533–537 RSC.
- S. H. Mir, S. Chakraborty, P. C. Jha, J. Wärnå, H. Soni, P. K. Jha and R. Ahuja, Appl. Phys. Lett., 2016, 109, 053903 CrossRef.
- Z. Q. Wang, M. S. Wu, B. Xu and C. Y. Ouyang, J. Alloys Compd., 2016, 658, 818–823 CrossRef CAS.
- Z. Q. Wang, Y. C. Chen and C. Y. Ouyang, Phys. Lett. A, 2014, 378, 2449–2452 CrossRef CAS.
- H. R. Jiang, Z. H. Lu, M. C. Wu, F. Ciucci and T. S. Zhao, Nano Energy, 2016, 23, 97–104 CrossRef CAS.
- L. Shi, T. S. Zhao, A. Xu and J. B. Xu, Sci. Bull., 2016, 61, 1138–1144 CrossRef CAS.
- B. Mortazavi, A. Dianat, O. Rahaman, G. Cuniberti and T. Rabczuk, J. Power Sources, 2016, 329, 456–461 CrossRef CAS.
- Y. Zhang, Z. F. Wu, P. F. Gao, S. L. Zhang and Y. H. Wen, ACS Appl. Mater. Interfaces, 2016, 8, 22175–22181 CAS.
- L. C. Xu, A. J. Du and L. Z. Kou, Phys. Chem. Chem. Phys., 2016, 18, 27284–27289 RSC.
- Z. Q. Wang, T. Y. Lü, H. Q. Wang, Y. P. Feng and J. C. Zheng, Sci. Rep., 2017, 7, 609 CrossRef PubMed.
- V. Nagarajan and R. Chandiramouli, J. Mol. Graphics Modell., 2017, 73, 208–216 CrossRef CAS PubMed.
- T. Y. Lü, J. C. Zheng and Y. F. Zhang, ChemPhysChem, 2015, 16, 3015–3020 CrossRef PubMed.
- T. Y. Lü, X. X. Liao, H. Q. Wang and J. C. Zheng, J. Mater. Chem., 2012, 22, 10062–10068 RSC.
- N. Wei, Y. Chen, K. Cai, J. H. Zhao, H. Q. Wang and J. C. Zheng, Carbon, 2016, 104, 203–213 CrossRef CAS.
- N. Wei, L. Q. Xu, H. Q. Wang and J. C. Zheng, Nanotechnology, 2011, 22, 105705 CrossRef PubMed.
- J. C. Zheng and Y. M. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 024509 CrossRef.
- M. S. Wu, B. Xu and C. Y. Ouyang, J. Mater. Sci., 2016, 51, 4691–4696 CrossRef CAS.
- H. J. Yan, Z. Q. Wang, B. Xu and C. Y. Ouyang, Funct. Mater. Lett., 2012, 05, 1250037 CrossRef.
- F. H. Ning, S. Li, B. Xu and C. Y. Ouyang, Solid State Ionics, 2014, 263, 46–48 CrossRef CAS.
- I. I. Naumov and A. M. Bratkovsky, Phys. Rev. B, 2011, 84, 245444 CrossRef.
- G. Cocco, E. Cadelano and L. Colombo, Phys. Rev. B, 2010, 81, 241412 CrossRef.
- J. D. Silva-Araújo, H. Chacham and R. W. Nunes, Phys. Rev. B, 2010, 81, 193405 CrossRef.
- R. Balog, B. Jorgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Laegsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekaer, Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- A. Bhattacharya, S. Bhattacharya and G. P. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075454 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- Z. Q. Wang, T. Y. Lü, H. Q. Wang, Y. P. Feng and J. C. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 31424–31430 RSC.
- Y. L. Jiao, F. X. Ma, J. Bell, A. Bilic and A. J. Du, Angew. Chem., Int. Ed., 2016, 55, 10448–10451 CrossRef.
- M. Farjam and H. Rafii-Tabar, Phys. Rev. B, 2009, 80, 167401 CrossRef.
- R. Li, Z. L. Liu, W. Q. Ma and Y. G. Tan, AIP Adv., 2016, 6, 055204 CrossRef.
- F. Hao and X. Chen, J. Appl. Phys., 2016, 120, 165104 CrossRef.
- W. Hu and J. L. Yang, J. Phys. Chem. C, 2015, 119, 20474–20480 CAS.
- O. V. Yazyev and L. Helm, Phys. Rev. B, 2007, 75, 125408 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |