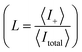Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
1/f pink chaos in nanopores
Vishal V. R. Nandigana *a and
N. R. Alurub
*a and
N. R. Alurub
aDepartment of Mechanical Engineering, Indian Institute of Technology, Madras, Chennai 600036, India. E-mail: nandiga@iitm.ac.in; Web: https://mech.iitm.ac.in/meiitm/personnal/dr-vishal-v-r-nandigana/ Tel: +91-44-2257-4668
bDepartment of Mechanical Science and Engineering, Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana – Champaign, Urbana, Illinois 61801, USA
First published on 28th September 2017
Abstract
Nanopores have been used for myriad applications ranging from water desalination, gas separation, fluidic circuits, DNA sequencing, and preconcentration of ions. In all of these applications noise is an important factor during signal measurement. Noisy signals disrupt the exact measuring signal in almost all of these applications. In this paper, we rationalize whether current oscillations should be classified only as noise or the physical disturbance in ionic charges has some other meaning. We infer that the physical disturbance in ionic charges and the current oscillations are not noise but can be chaos. Chaos is present in the system due to depletion of the ions, created by nonequilibrium anharmonic distribution in the electrostatic potential. In other words, multiple electric potential wells are observed in the nanoporous system. The multiple electric potential wells leads to bi-directional hopping of ions as the ions transport through the pore. The bi-directional hopping results in current oscillations. This paper suggests that chaos exists from a deterministic perspective and that there is no stochastic element leading to current oscillations. We prove this case by considering a simple oscillator model involving the electrostatic and dissipative forces in order to model ionic current. We observed current oscillations even in the absence of a stochastic noise force. Hence, we state that current oscillations in nanopores can be due to chaos as well and not necessarily due to noise. Furthermore, the color associated with the chaotic spectrum is not brown but pink, with 1/f type dynamics similar to the 1/f type pink noise presented by theorists and experimentalists. However, the 1/f type pink chaos exists due to deterministic current oscillations and not due to a stochastic fluctuating noise force.
I. Introduction
Ionic logic-based circuits have witnessed a tremendous surge in recent years, ranging from single molecule sensing,2,3 DNA sequencing,1,4–6 nanopower generators7 and electrolyte cells.8 The unsupported electrolyte is actively impelled across the ion membrane under an electric potential. One of the measuring signals is the current as ions are transported through the pore. Recently, it was found that the current signal has built-in oscillations as the ions traverse through the pore. These oscillations have been confirmed as noise by earlier theorists.9–13 The noise is perceived as random statistical fluctuation in the electrical current signal. Variations in noise were explained earlier by the mechanistic motion of the charges due to surface defects, or else they were perceived as thermal fluctuations within the purview of the classical fluctuation–dissipation theorem.14 Several instances of noise in membrane phenomenology occur due to the cooperative motion of ions due to random memory force. In other words, a noise force is used to model the mobility of the ions. Not only were the current oscillations perceived as noise but the resulting current spectra had a 1/f type pink noise in the low frequency regime. What causes the ionic membranes in electrolyte cells to exhibit pink noise is a subject for inspection. Several of these notions employ fluctuations in the inherent ionic mobility of the electrolyte.9 Another reason pertains to the stochastic variation in the protonation and deprotonation reactions near the charge site of the membrane surface. Finally, experimentalists have also argued that the membrane structural constituents also prompt the low frequency pink noise.10,12 Now, to what extent colored pink noise is the true state representation of the current dynamics under a dynamical driving/dissipative potential is a challenging question. Is it possible that physical disturbance in the ionic charges and current oscillations in the ion-selective membranes can be triggered by some phenomenon other than statistical fluctuation, namely noise? In this paper, we state that the physical disturbance in ionic charges is due to chaos, and current oscillations can be perceived as chaos as well and we need not restrict ourselves in claiming current oscillations as noise. We note that chaos occurs when the potential of mean force on a charged ion is anharmonic in the nonequilibrium state space. In other words, a multi-well potential acts on the charged ion when the ion is driven under an electric field. The anharmonic or multi-well potentials arise due to the depletion of ions owing to the charge conservation. The depleted ions create an electric field barrier that prevents other ions from entering into the nanopore. This causes the ions to hop in a bi-directional manner before the ions enter into the nanopore. The bi-directional hopping of ions results in current oscillations leading to chaos. We argue that the oscillations observed in the current signal have a deterministic origin and do not arise due to stochastic fluctuations postulated by earlier theorists. In this study we also observe that the spectrum of the current oscillations is pink in color as it exhibits “1/f” type dynamics similar to pink noise.In this work, we understand that the origin of chaos occurs when the nanomembrane is selective to ions. More precisely, the membrane is ideally selective to one particular type of ion which is opposite to the membrane charge. The disproportionate opposing charge has the space to confine a linear and anharmonic potential under an external electric field given by the mean field approximation. That means a multi-well potential exists in an ideal ion-selective nanoporous membrane when an electric field is applied on the ion. In the case of a non-ideal membrane, we cease to observe chaos. Now, the transport of charge over an electrostatic force in an ideal-membrane results in electrostatic potential instability due to the existence of multiple potential wells. We propose this mechanism as the ‘Potential-charge momentum theorem’. We further demonstrate a simple anharmonic oscillator model, calling it the ‘VN Oscillator model’ which stands for Variational Non-equilibrium potential oscillator, to explain the chaos mechanism. The current oscillations in the ideally selective nanoporous membrane can be applied in the field of nanopore sensing for DNA sequencing and chemical reactions. Furthermore, the current oscillations can be understood to manipulate fluid flow in fluidic logic circuits in areas of combinatorial chemistry, biology and electronic applications.
II. Theory
A. Charge oscillator model
Before looking at the VN oscillator model, we first disclose a unique charge-transfer and potential-dissipation model to uncover the notion of chaos that is exhibited by ion-selective nanogating channels. To demonstrate this phenomenon, we discerned the idea of the Maxwell model, ∇·![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) = δρf, where
= δρf, where ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) is the electric displacement vector field accounting for the effects of free and bound charge within the open-ended state space and δρf is the free charge in space (ionic charge) confined within a given volume. The free charge is a derivative of the total charge, δρ, which is the sum total of the free and bounded charges (δρb); δρ = δρb + δρf. The electric displacement field was demarcated using the constitutive relationship
is the electric displacement vector field accounting for the effects of free and bound charge within the open-ended state space and δρf is the free charge in space (ionic charge) confined within a given volume. The free charge is a derivative of the total charge, δρ, which is the sum total of the free and bounded charges (δρb); δρ = δρb + δρf. The electric displacement field was demarcated using the constitutive relationship 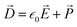 , where P is the polarization density whose divergence envisions the density of bound charges, ∇·
, where P is the polarization density whose divergence envisions the density of bound charges, ∇·![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) = δρb, and
= δρb, and 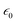 is the dielectric permittivity of free space. The stretching and compressive nature of the electric field (
is the dielectric permittivity of free space. The stretching and compressive nature of the electric field (![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ) triggered the total charge in the confined ion gating regime,
) triggered the total charge in the confined ion gating regime, 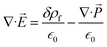 . The negative divergence in polarization density implied that the charge transfer of the bound charge was directionally dissimilar to the free charge because of the dielectric polarization. In a linear, homogeneous and isotropic dielectric with the electric field instantaneously varying with time, the polarization density is constituted by
. The negative divergence in polarization density implied that the charge transfer of the bound charge was directionally dissimilar to the free charge because of the dielectric polarization. In a linear, homogeneous and isotropic dielectric with the electric field instantaneously varying with time, the polarization density is constituted by 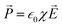 , where χ is the degree of polarization in conjunction with the electric field. The electric field caused the bound and free charges to polarize in space constituting Gauss’s theorem,
, where χ is the degree of polarization in conjunction with the electric field. The electric field caused the bound and free charges to polarize in space constituting Gauss’s theorem, 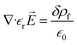 . The equation was arrived at by substituting the polarization density
. The equation was arrived at by substituting the polarization density ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) in the previous ∇·
in the previous ∇·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) equation.
equation. 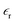 is the dielectric permittivity of the medium (water) and correlated with the degree of polarization, χ, by
is the dielectric permittivity of the medium (water) and correlated with the degree of polarization, χ, by 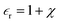 . The notion of Maxwell’s electric displacement field and electric flux conservation was conferred upon the ion gating membrane resulting in the governing equation
. The notion of Maxwell’s electric displacement field and electric flux conservation was conferred upon the ion gating membrane resulting in the governing equation 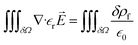 , where the electric field is related to the Coulomb potential (ϕ),
, where the electric field is related to the Coulomb potential (ϕ), ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) = −∇ϕ, and δΩ is the gating membrane. We radially averaged the governing equation to give
= −∇ϕ, and δΩ is the gating membrane. We radially averaged the governing equation to give 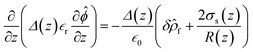 after invoking Gauss’s law,
after invoking Gauss’s law, 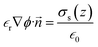 , where
, where ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) is the unit normal to the surface and z is the axial direction of the membrane system. The above area-averaged model was configured across the inhomogeneous system, namely along the nanopores and micropores. Δ(z) is the cross-sectional area, accounting for the micro and nanogating membrane radius given by R(z), and σs(z) is the variational surface charge density of the nanogating membrane along with the microporous membrane. Now, we can inspect the transfer of charges with the mass transfer of ions. The dynamic mass transfer of ions is correlated by the diffusive ionic gradients along with the electric mobility polarization density formulated by cΩ
is the unit normal to the surface and z is the axial direction of the membrane system. The above area-averaged model was configured across the inhomogeneous system, namely along the nanopores and micropores. Δ(z) is the cross-sectional area, accounting for the micro and nanogating membrane radius given by R(z), and σs(z) is the variational surface charge density of the nanogating membrane along with the microporous membrane. Now, we can inspect the transfer of charges with the mass transfer of ions. The dynamic mass transfer of ions is correlated by the diffusive ionic gradients along with the electric mobility polarization density formulated by cΩ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) , where cΩ is the degree of polarization of the ion required to translocate the ion in the presence of an electric field. We call this model the ‘charge oscillator model’. The rate of change of the ionic charge that was radially averaged was given as
, where cΩ is the degree of polarization of the ion required to translocate the ion in the presence of an electric field. We call this model the ‘charge oscillator model’. The rate of change of the ionic charge that was radially averaged was given as 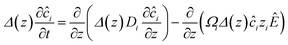 , where Ωi is the mobility of the individual ions which is related to the diffusion coefficient of each ion (Di) given by Einstein’s relation,
, where Ωi is the mobility of the individual ions which is related to the diffusion coefficient of each ion (Di) given by Einstein’s relation, 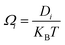 . KBT is the thermal energy with KB being the Boltzmann constant and T being the absolute thermodynamic temperature. The concentration of ions within the control volume was radially averaged and defined as ĉi. zi is the valence of each ion and
. KBT is the thermal energy with KB being the Boltzmann constant and T being the absolute thermodynamic temperature. The concentration of ions within the control volume was radially averaged and defined as ĉi. zi is the valence of each ion and 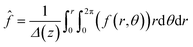 denotes the area-averaged mapping function. The current density in the system was given as
denotes the area-averaged mapping function. The current density in the system was given as 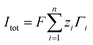 , where
, where 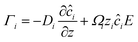 is the total area-averaged flux of each ion. The total current across the nanogating membrane was manifested from the current density by multiplication with the membrane cross-sectional area.
is the total area-averaged flux of each ion. The total current across the nanogating membrane was manifested from the current density by multiplication with the membrane cross-sectional area.
The coupled electric displacement field and charge transfer governing equations were numerically solved using the finite volume method in OpenFOAM15 (Open Field Operation and Manipulation). The details regarding the solver implementation are discussed elsewhere.16–19
B. VN oscillator model
We now discuss another simple oscillator model proposed by us to understand the notion of chaos. We call this oscillator model the ‘variational non-equilibrium potential oscillator’ or VN oscillator. In this model, we assumed that the nanogating membrane was ideally selective to one type of ion, i.e., the membrane allowed only ions of opposite polarity to that of the membrane charge. The model states that the mass transfer of each dissimilar ion with respect to the charge of the ion (qi) constituted the equation of motion of the charged particle, manifesting current:
with respect to the charge of the ion (qi) constituted the equation of motion of the charged particle, manifesting current:  . The mass transfer rate was mapped to the charge transfer rate
. The mass transfer rate was mapped to the charge transfer rate 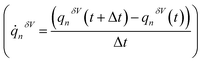 which was again mapped to the Eulerian space inferred in the net ion motion
which was again mapped to the Eulerian space inferred in the net ion motion 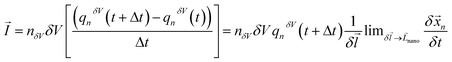 , where nδV is the number of ionic charges in the control volume δV, varying across the nanopore and micropore. qnδV is the charge of the ionic particle, Δt is the time step and δl is the length of the gating membrane accounting for either the micro or nanomembrane. We propose a theorem called the ‘potential charge-momentum theorem (PCM)’ to rationalize the displacement of a charged particle,
, where nδV is the number of ionic charges in the control volume δV, varying across the nanopore and micropore. qnδV is the charge of the ionic particle, Δt is the time step and δl is the length of the gating membrane accounting for either the micro or nanomembrane. We propose a theorem called the ‘potential charge-momentum theorem (PCM)’ to rationalize the displacement of a charged particle, ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) n. The theorem solves Newton’s law of motion for a coarse grained charged particle given by
n. The theorem solves Newton’s law of motion for a coarse grained charged particle given by 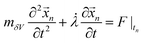 , where mδV is the mass of the ionic particle,
, where mδV is the mass of the ionic particle, ![[small lambda, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e152.gif) = 1/Ω is the mass transfer rate of the confined momentized particle given as
= 1/Ω is the mass transfer rate of the confined momentized particle given as 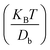 , Db is the bulk diffusion coefficient of the ionic particle, (KBT) is the thermal energy of the ionic particle, and F|tn is the mean force harnessed at time tn by the ionic particle. The mean interaction potential force produced by electrostatic interaction is
, Db is the bulk diffusion coefficient of the ionic particle, (KBT) is the thermal energy of the ionic particle, and F|tn is the mean force harnessed at time tn by the ionic particle. The mean interaction potential force produced by electrostatic interaction is 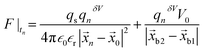 , where qs = σsδS is the charge constituted by the surface of the nano and micro membrane and δS is the surface area of the membrane. σs is the surface charge density of the micro or nanogating membrane. An electrostatic potential, V0, was applied across the micro-nanoporous architecture within a distance of |
, where qs = σsδS is the charge constituted by the surface of the nano and micro membrane and δS is the surface area of the membrane. σs is the surface charge density of the micro or nanogating membrane. An electrostatic potential, V0, was applied across the micro-nanoporous architecture within a distance of |![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) b2 −
b2 − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) b1|.
b1|. ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) 0 is the position of the charged nano-membrane. The PCM model was marched in time for Δt using a well known velocity-verlet algorithm:
0 is the position of the charged nano-membrane. The PCM model was marched in time for Δt using a well known velocity-verlet algorithm: 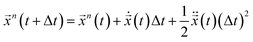 .20 The ionic particle acceleration at (t + Δt) was configured using the interaction potential force at
.20 The ionic particle acceleration at (t + Δt) was configured using the interaction potential force at ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) n(t + Δt). Finally, the velocity is
n(t + Δt). Finally, the velocity is 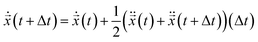 . Note, while calculating the velocity
. Note, while calculating the velocity 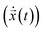 and acceleration
and acceleration 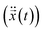 we had to substitute the right length δl and surface charge σs to account for the micro and nanopore membranes.
we had to substitute the right length δl and surface charge σs to account for the micro and nanopore membranes.
III. Simulation details
The simulated domain consisted of a nanopore of length Ln = 0.5 μm and diameter dn = 10 nm. The diameter of the micropore was dmicro = 500 nm, while the length of the micropore was Lmicro = 4 μm. Phosphate buffer of a constant concentration (0.39 mM NaH2PO4 and 0.61 mM Na2HPO4) was used in all of the simulations. The temperature was T = 300 K. The diffusivities of Na+, H2PO4− and HPO42− are 1.33 × 10−9 m2 s−1, 0.879 × 10−9 m2 s−1, and 0.439 × 10−9 m2 s−1, respectively. We assumed the dielectric constant of the aqueous solution to be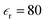 .21 We also assumed zero surface charge density on the walls of the micropore, σm = 0, as they were away from the nanopore membrane and could not have an influence on the transport. The charge on the walls of the nanopore was assumed to vary from σn = 0 mC m−2 to σn = −30 mC m−2. The voltage V0 was varied from V = 0 V to V = 100 V.
.21 We also assumed zero surface charge density on the walls of the micropore, σm = 0, as they were away from the nanopore membrane and could not have an influence on the transport. The charge on the walls of the nanopore was assumed to vary from σn = 0 mC m−2 to σn = −30 mC m−2. The voltage V0 was varied from V = 0 V to V = 100 V.
In the VN oscillator model, the mass mδV = 7 × 10−12 kg to match the charge oscillator model and the distance x0 = Lmicro,|![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) b2 −
b2 − ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) b1| = Ln + 2Lmicro. At time t = 0, the initial charge was assumed to be equal to the surface charge, qnδV|t=0 = σnδS, with δS = πdnLn. The time step used in the simulation was 1 ns. The total time of the simulation was 3 ms.
b1| = Ln + 2Lmicro. At time t = 0, the initial charge was assumed to be equal to the surface charge, qnδV|t=0 = σnδS, with δS = πdnLn. The time step used in the simulation was 1 ns. The total time of the simulation was 3 ms.
IV. Results
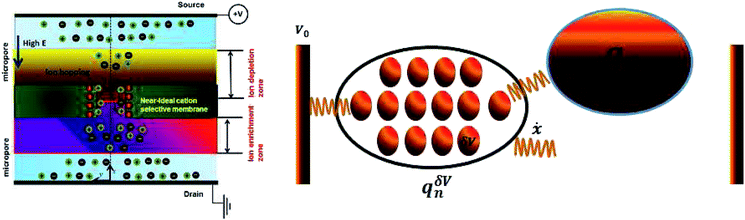
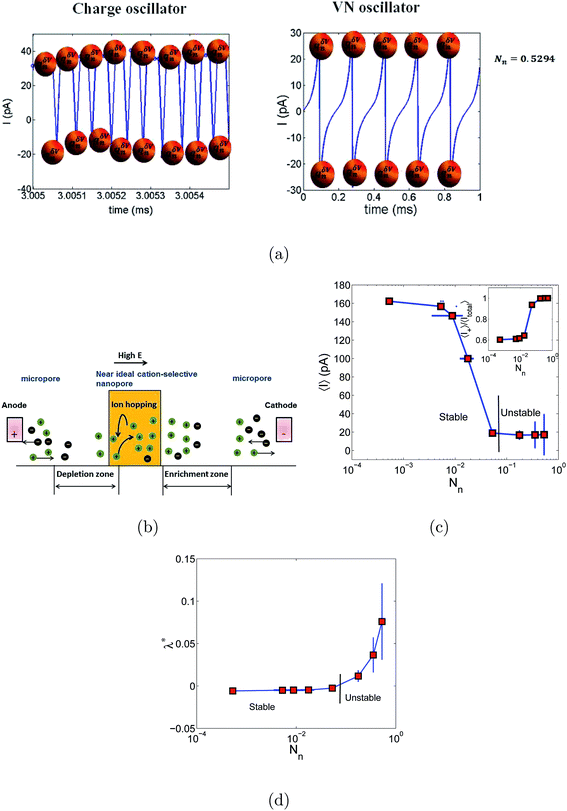
Schematics of the dynamic charge oscillator model and VN oscillator model are shown in Fig. 1. On solving the charge oscillator model, we observed that the current oscillated with time. The oscillations were bi-directional, indicating that the ions hop back and forth as they enter into the nanopore. The results are shown in Fig. 2(a). Interestingly, the VN oscillator model also showed similar current oscillations where the ion hops bidirectionally similar to the charge oscillator model (see Fig. 2(a)). The magnitude of the oscillations was similar to that of the charge oscillator model, thus indicating that our notion of representing the charge dynamics as a simple potential-dissipative oscillator model is sufficient to capture the physics.A. Origin of chaos
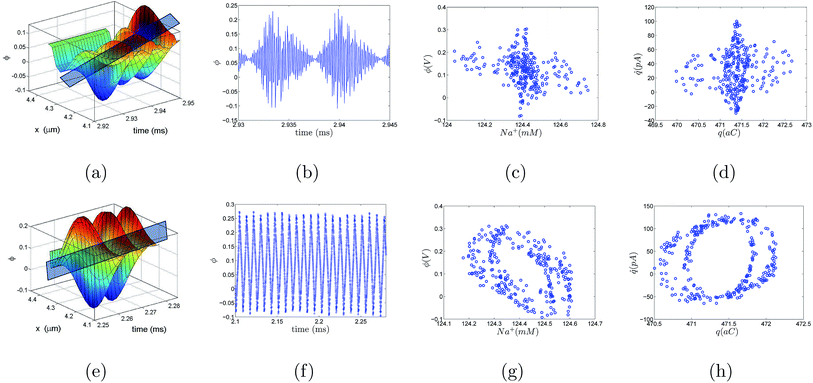
We are now interested in answering the question ‘why do these oscillations arise’? The oscillations are due to the depletion of ions near the micro-nano interface region, owing to the charge conservation. To elaborate, let us consider an ideal cation selective nanogating membrane as considered in this study. In an ideal cation selective nanopore, only cations are allowed to enter into the nanopore. When an electric field was applied from an anode to cathode, the anions were repelled from the cathode and from the cation-selective membrane (since the membrane allows only cations). Thus, the anions were accumulated or enriched near the cathode-nanogating membrane interface. To maintain neutrality, the cations were also enriched at this interface. At the anode-membrane interface the anions were repelled from the cation selective membrane due to electrostatic repulsion and attracted towards the anode due to electrostatic attraction, thus the anions were depleted at the anode-nanogating membrane interface. To maintain neutrality, the cations were also depleted at this interface. We observed that this depletion region was very strong for ideal ion-selective nanopores, resulting in non-equilibrium anharmonic potential and an electric barrier. The potential and the electric barrier creates an instability in the ionic charges near the interface. This instability results in bi-directional hopping of ions leading to chaos. From our understanding, this observation of bi-directional hopping of ions is made for the first time in the literature. A schematic of ion enrichment and ion depletion is shown in Fig. 2(b). We note that such oscillations were observed when the nanopore was ideally ion selective to one particular type of ion. Furthermore, we observed a stable current when the membrane was non-ideal, i.e., when the membrane allowed both cations and anions. We played with the ideality of the nanopore using the surface charge density. For nanoporous surface charge densities between σn = 0 mC m−2 and σn = –3 mC m−2, we did not observe current oscillations nor bi-directional hopping of the ions. Only for the nanoporous surface charge density of σn ≥ −10 mC m−2 did we observe an ideal ion-selective nature of the nanopore and current oscillations and chaos. Such large surface charge density nanopores can be assumed to be present for aluminum oxide nanopores.22 We would like to stress the fact that neither the charge oscillator model nor the simple VN oscillator model takes into account any statistical fluctuating force to observe these oscillations. Even the earlier theorists’ confirmation of necessitating the fluctuating ionic mobility or nano membrane surface charge fluctuating force to observe current oscillations is not considered in either of these models. The oscillator models manifest current oscillations and chaos in view of dynamic potential instability. Thus, in our study, we state that current oscillations can also be viewed from a chaos perspective and we need not limit ourselves to analyzing current oscillations from a noise perspective.When the physics of chaos occurs in nanogating membranes is the next interesting question one has to argue. The key to this lies in our proposed non-dimensional Nandigana number, 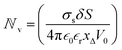 . The Nandigana number is arrived at by non-dimensionalizing the VN oscillator model. We considered the following terms to non-dimensionalize the VN oscillator model: distance x is normalized by xΔ = 1 nm; time t by tΔ = 1 ns; diffusion coefficient D by DΔ = 1 nm2 ns−1; charge q by qΔ = σsdS; and potential V by V0. The derived Nandigana number correlates the influence of the surface charge density of the membrane with the applied electric potential. The scale of the Nandigana number should be of the order of 0.17 to visualize potential instability instigating chaos. At this Nandigana number, the surface charge density of the nanopore was −10 mC m−2, when the nanopore was ideally ion-selective. The relationship of the current with the Nandigana number is shown in Fig. 2(c) using the charge oscillator model. The figure shows that the ion dynamics were stable until a Nandigana number of 0.05294 and we see unstable ion dynamics for Nv > 0.05294. Under such a Nandigana number, the nanoporous surface charge density was greater than ¬3 mC m−2. To truly note that the current oscillations were indeed chaotic in nature, we calculated the positive Lyapunov exponent using the current oscillations. The notion of determining the Lyapunov exponent infers upon the dimensionality of the system. In this study, we focused our attention towards the calculation of the maximum Lyapunov exponent, λ*, from the current–time map. We formed two state vectors,
. The Nandigana number is arrived at by non-dimensionalizing the VN oscillator model. We considered the following terms to non-dimensionalize the VN oscillator model: distance x is normalized by xΔ = 1 nm; time t by tΔ = 1 ns; diffusion coefficient D by DΔ = 1 nm2 ns−1; charge q by qΔ = σsdS; and potential V by V0. The derived Nandigana number correlates the influence of the surface charge density of the membrane with the applied electric potential. The scale of the Nandigana number should be of the order of 0.17 to visualize potential instability instigating chaos. At this Nandigana number, the surface charge density of the nanopore was −10 mC m−2, when the nanopore was ideally ion-selective. The relationship of the current with the Nandigana number is shown in Fig. 2(c) using the charge oscillator model. The figure shows that the ion dynamics were stable until a Nandigana number of 0.05294 and we see unstable ion dynamics for Nv > 0.05294. Under such a Nandigana number, the nanoporous surface charge density was greater than ¬3 mC m−2. To truly note that the current oscillations were indeed chaotic in nature, we calculated the positive Lyapunov exponent using the current oscillations. The notion of determining the Lyapunov exponent infers upon the dimensionality of the system. In this study, we focused our attention towards the calculation of the maximum Lyapunov exponent, λ*, from the current–time map. We formed two state vectors, ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n1 and
n1 and ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n2, from the current signal at an initial time with a distance of ||
n2, from the current signal at an initial time with a distance of ||![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n1 −
n1 − ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n2|| = δ0 ≪ 1. The ion trajectories from the initial distance travelled in time Δt were used to map the new state vector distance, δΔt = ||
n2|| = δ0 ≪ 1. The ion trajectories from the initial distance travelled in time Δt were used to map the new state vector distance, δΔt = ||![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n1+Δt −
n1+Δt − ![[I with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0049_20d1.gif) n2+Δt||. The maximum Lyapunov exponent (λ*) in this vector space was formed as
n2+Δt||. The maximum Lyapunov exponent (λ*) in this vector space was formed as 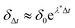 ; δΔt ≪ 1 and Δt ≫ 1. When λ* was positive, we observed an exponential divergence of the current time series data, resulting in dynamic instability or chaos. The maximum Lyapunov exponent was calculated from the current dynamics using TISEAN software.23 The transition from a stable current signal to a chaotic current signal in terms of the maximum Lyapunov exponent is shown in Fig. 2(d). We observed chaos when the pore was ion selective. The transference number is defined as the current due to positive ions compared to the total current. We considered the positive ions since the pore was cation selective. We observed that when Nv > 0.05294, the majority of the current was contributed by the cation, as the transference number was almost equal to 1 (see Fig. 2(c)), thus indicating that the pore was ideally selective to one type of ion. At this transference number and Nandigana number, we observed the transition from stable current dynamics to unstable or chaotic current dynamics (see Fig. 2(c)).
; δΔt ≪ 1 and Δt ≫ 1. When λ* was positive, we observed an exponential divergence of the current time series data, resulting in dynamic instability or chaos. The maximum Lyapunov exponent was calculated from the current dynamics using TISEAN software.23 The transition from a stable current signal to a chaotic current signal in terms of the maximum Lyapunov exponent is shown in Fig. 2(d). We observed chaos when the pore was ion selective. The transference number is defined as the current due to positive ions compared to the total current. We considered the positive ions since the pore was cation selective. We observed that when Nv > 0.05294, the majority of the current was contributed by the cation, as the transference number was almost equal to 1 (see Fig. 2(c)), thus indicating that the pore was ideally selective to one type of ion. At this transference number and Nandigana number, we observed the transition from stable current dynamics to unstable or chaotic current dynamics (see Fig. 2(c)).
Using the VN oscillator model, we could track the position of the charged ionic particle. Fig. 3(a) shows the ionic particle near the entrance of the micro-nanopore, i.e., when the particle reached x = 4 μm, the particle was repelled from the cation selective nanopores due to electrostatic interaction of the particle with the charged membrane and applied electric potential. There is electrostatic repulsion resulting in the ionic particle tracing back to its initial position, i.e., the particle moved back to x = 0. The charged particle tracing back to its initial position led to depletion of the ions near the micro-nanogating membrane junction, i.e., at x = 4 μm as shown in Fig. 3(a). This physics was observed when the Nandigana number = 0.5294. The action was repeated every time the charged particle moved near to the micro-nanogating membrane junction. Hence, the particle oscillated with time giving rise to instability and chaos. To get a better idea of the physics, we looked at the dynamics at a low Nandigana number = 0. At this Nandigana number, the charged particle did not interact with the membrane surface, since at this number the surface charge density of the nanomembrane was zero, allowing both cations and anions to enter into the pore. Thus, the electrostatic repulsion was absent at this Nandigana number, resulting in transport of the charged particle through the pore. We see a linear transport of the charged particle with time revealing that the particle was transported through the micropore to the nanopore and to the other end of the reservoir. The dynamics are shown in Fig. 3(a). Hence, we could control the stability of the particle motion using our VN oscillator model. Using our VN oscillator model we also showed how the charge acted on the particle. Fig. 3(b) shows that as the particle neared the nanogating membrane, i.e. at x = 4 μm, the particle was repelled from the nanomembrane. Furthermore, the charge of the particle decreased due to electrostatic repulsion. Thus we see a decrease of the charge at x = 4 μm (see Fig. 3(a) and (b) together). When the particle reached the entrance, i.e., at x = 0, the charge increased on the particle due to electrostatic interaction of the particle with the voltage, V0. Hence, as the particle oscillated between x = 4 μm and x = 0, the charge decreased and then increased periodically. The results are shown in Fig. 3(b). The charge oscillations resulted in current oscillations, leading to instability and chaos. The dynamics shown in Fig. 3(b) were at Nv = 0.5294. Thus, these two figures illustrate the depletion of ions and electrostatic repulsion experienced by the charged particle near the nano membrane.
B. Power spectral density
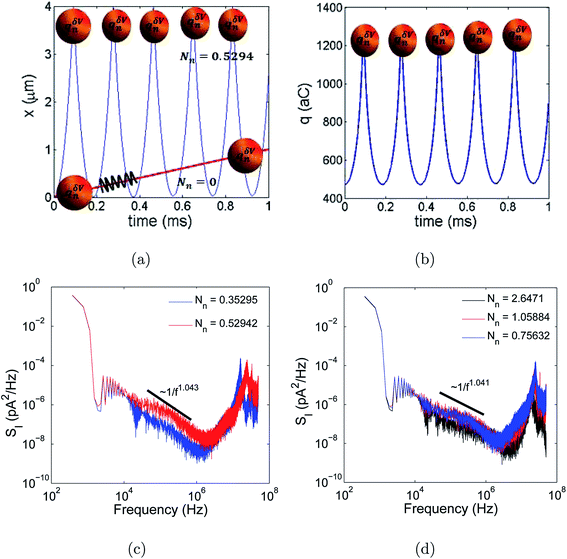
Finally, we need to resolve the conundrum of whether chaos has color. To answer this query, we probed the current dynamics by reviewing the power spectra of the current dynamics. The temporal power spectral density (SI) was analyzed in a frequency range of 0 to fs = 1/Δt and was obtained using the Welch method.24 The current signal was divided into the longest sections to obtain close to, but not exceeding, 8 segments with 50% overlap. Each section was windowed with a Hamming window. The spectral estimate was evaluated by averaging the modified periodograms for a frequency range [0–fs/2]. The power spectral density in Fig. 3(c) and (d) shows a power-law dependence (1/fα) with the frequency. The exponent α was close to 1 in this frequency range, similar to that of the pink noise phenomenon. However, we rationalized that the dynamics are pink chaos and not pink noise. This is because the pink chaos originates due to instability in the electrostatic potential which is a deterministic phenomenon in contradiction to needing a random memory force which was postulated by earlier theorists and experimentalists9–12 when observing pink noise. Thus, the dynamics of the current are pink chaos according to our understanding.C. Current-charge phase maps
Similar to the VN oscillator model, the charge oscillator model also depicted interesting physics. The anharmonic distribution in the electrostatic potential leading to multiple potential wells is shown in Fig. 4(a). A section of the potential was sliced along the time plane, and we see the potential-time dynamics in Fig. 4(b). We observed oscillating potential dynamics due to depletion of ions near the micro-nanogating junction. The oscillations changed their sign, indicating that the particle changed its direction as it oscillated in the pore. At Nv = 0.52942, the oscillations were not exactly bi-directional at every time interval, i.e., the oscillations were not periodical but still we observed the particle change its direction, revealing the bi-directional hopping nature of the ionic particle. The phase map between the charged ionic particle and the potential (see Fig. 4(c)) shows a chaotic distribution of ions in space at a high Nv. The current-charge phase map in Fig. 4(d) shows that the current oscillated between −20 pA to 100 pA when the charge was between 471.5 aC and 472 aC. The oscillations were chaotic and bi-directional due to the depletion of ions near the micro-nanogating membrane junction. The periodical bi-directional hopping of ions and the electric potential are shown in Fig. 4(e) and (f), respectively. These oscillations were observed at a relatively higher value of Nv = 1.058. The charge-potential phase map in Fig. 4(g) and the current-charge phase map in Fig. 4(h) show two circles indicating that the potential and current in these phase maps change their signs periodically resulting in bi-directional hopping of ions leading to instability and chaos.We now think back to the VN oscillator model to derive analytical expressions for the charge transfer. We considered the VN oscillator model without taking into account the ion acceleration. The model reduced down to 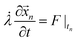 . Solving this equation analytically and substituting the velocity,
. Solving this equation analytically and substituting the velocity, 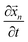 , in the ionic current expression, we obtained the charge on the ionic particle using
, in the ionic current expression, we obtained the charge on the ionic particle using 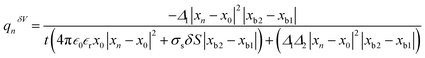 , where
, where 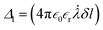 , δl varied along the ion particle displacement motion accounting for micropores and nanopores and Δ2 was obtained by invoking the initial particle charge condition, qnδV = −ZσnδS at time t = 0 and the position of the charged particle at the origin, xn = 0 in the above analytical equation. Z was the valence of the ion transporting through the pore. Note, if the pore is selective for monovalent ions, Z is 1, and similarly for divalent ions, Z = 2. This results in
, δl varied along the ion particle displacement motion accounting for micropores and nanopores and Δ2 was obtained by invoking the initial particle charge condition, qnδV = −ZσnδS at time t = 0 and the position of the charged particle at the origin, xn = 0 in the above analytical equation. Z was the valence of the ion transporting through the pore. Note, if the pore is selective for monovalent ions, Z is 1, and similarly for divalent ions, Z = 2. This results in 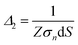 . This model also resulted in the bi-directional hopping of charge and current when we assume the ions are displaced in a bi-directional manner. This illustrated that the acceleration of the ionic particle was not necessary to observe current oscillations and chaos. Only the electrostatic interaction of the ions with the membrane surface and the dissipative ionic particle force were necessary to observe the current oscillations.
. This model also resulted in the bi-directional hopping of charge and current when we assume the ions are displaced in a bi-directional manner. This illustrated that the acceleration of the ionic particle was not necessary to observe current oscillations and chaos. Only the electrostatic interaction of the ions with the membrane surface and the dissipative ionic particle force were necessary to observe the current oscillations.
V. Conclusion
In conclusion, we show that for an ideally ion-selective nanopore, current oscillations can also exist due to chaos rather than noise. We observed chaos along with bi-directional hopping of ions due to depletion of ions at the micro-nanopore junction. The depletion of ions resulted in non-equilibrium instability in the electrostatic potential. Furthermore, the temporal power spectra map of the charged ion particle shows that the color of chaos is pink, with 1/f type dynamics similar to the 1/f type pink noise observed by fellow experimentalists. However, we note that pink chaos exists in nanopores and not pink noise as the oscillations observed are deterministic in nature. Thus, we think that, one can not argue that the current oscillations observed in experiments as mere noise, chaos can also be a new way of comprehending the current signals observed in experiments and other numerical simulations. We believe that the observation of bi-directional current hopping and current oscillations can lay pathways for nanopore sensing in areas of DNA sequencing and chemical reaction units along with paving new avenues to use current oscillations for fluidic logic circuits for flow manipulation in biology, combinatorial chemistry and electronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation (NSF) under grants 1264282, 1420882 and 1506619 and the AFOSR under grant FA9550-12-1-0464. The authors gratefully acknowledge the use of the parallel computing resource provided by the University of Illinois. This work was done when V. N. was at the University of Illinois.References
- Z. Chen, Y. Jiang, D. R. Dunphy, D. P. Adams, C. H. N. Liu, N. Zhang, G. Xomeritakis, X. Jin, N. R. Aluru, S. J. Gaik, H. W. Hillhouse and C. J. Brinker, DNA translocation through an array of kinked nanopores, Nat. Mater., 2010, 9, 667 CrossRef CAS PubMed.
- S. Howorka and Z. Siwy, Nanopore analytics: sensing of single molecules, Chem. Soc. Rev., 2009, 38, 2360 RSC.
- O. A. Saleh and L. L. Sohn, An artificial nanopore for molecular sensing, Nano Lett., 2003, 3, 37 CrossRef CAS.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Characterization of individual polynucleotide molecules using a membrane channel, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770 CrossRef CAS.
- H. Chang, F. Kosari, G. Andreadakis, M. A. Alam, G. Vasmatzis and R. Bashir, DNA-mediated fluctuations in ionic current through silicon oxide nanopore channels, Nano Lett., 2004, 4, 1551 CrossRef CAS.
- J. B. Heng, C. Ho, T. Kim, R. Timp, A. Aksimentiev, Y. V. Grinkova, S. Sligar, K. Schulten and G. Timp, Sizing DNA using a nanometer-diameter pore, Biophys. J., 2004, 87, 2905 CrossRef CAS PubMed.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. V. R. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Single-layer MoS2 nanopores as nanopower generators, Nature, 2016, 536, 197–200 CrossRef CAS PubMed.
- E. V. Dydek, B. Zaltzman, I. Rubinstein, D. S. Deng, A. Mani and M. Z. Bazant, Overlimiting current in a microchannel, Phys. Rev. Lett., 2011, 107, 118301 CrossRef PubMed.
- M. R. Powell, I. Vlassiouk, C. Martens and Z. S. Siwy, Nonequilibrium 1/f noise in rectifying nanopores, Phys. Rev. Lett., 2009, 103, 248104 CrossRef PubMed.
- Z. Siwy and A. Fulinski, Origin of 1/fα noise in membrane channel currents, Phys. Rev. Lett., 2002, 89, 158101 CrossRef CAS PubMed.
- R. M. M. Smeets, U. F. Keyser, M. Wu, N. H. Dekker and C. Dekker, Nanobubbles in solid-state nanopores, Phys. Rev. Lett., 2006, 97, 088101 CrossRef CAS PubMed.
- R. M. M. Smeets, N. H. Dekker and C. Dekker, Low-frequency noise in solid-state nanopores, Nanotechnology, 2009, 20, 095501 CrossRef CAS PubMed.
- R. M. M. Smeets, U. F. Keyser, N. H. Dekker and C. Dekker, Noise in solid-state nanopores, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 417 CrossRef CAS PubMed.
- H. Nyquist, Thermal agitation of electric charge in conductors, Phys. Rev., 1928, 32, 110–113 CrossRef CAS.
- http://www.openfoam.com/, 2011.
- V. V. R. Nandigana and N. R. Aluru, Understanding anomalous current–voltage characteristics in microchannel–nanochannel interconnect devices, J. Colloid Interface Sci., 2012, 384, 162 CrossRef CAS PubMed.
- V. V. R. Nandigana and N. R. Aluru, Nonlinear electrokinetic transport under combined ac and dc fields in micro/nanofluidic interface devices, J. Fluids Eng., 2013, 135, 021201 CrossRef.
- V. V. R. Nandigana and N. R. Aluru, Characterization of electrochemicalproperties of a micro-nanochannel integrated system using computational impedance spectroscopy (cis), Electrochim. Acta, 2013b, 105, 514–523 Search PubMed.
- V. V. R. Nandigana and N. R. Aluru, Avalanche effects near nano-junctions, Phys. Rev. E, 2016, 94, 012402 CrossRef PubMed.
- L. Verlet, Computer experiments on classical fluids. i. thermodynamical properties of Lennard-Jones molecules, Phys. Rev., 1967, 159, 98–103 CrossRef CAS.
- B. Hille, Ion Channels of Excitable Membranes, Sinauer Associates Inc., Sunderland, MA, 3rd edn, 2001 Search PubMed.
- B. M. Venkatesan, D. Estrada, S. Banerjee, X. Jin, V. E. Dorgan, M. Bae, N. R. Aluru, E. Pop and R. Bashir, Stacked graphene-Al2O3 nanopore sensors for sensitive detection of DNA and DNA-protein complexes, ACS Nano, 2012, 6, 441–450 CrossRef CAS PubMed.
- R. Hegger, H. Kantz and T. Schreiber, Practical implementation of nonlinear time series methods: the TISEAN package, Chaos, 1999, 9, 413 CrossRef PubMed.
- P. D. Welch, The use of fast Fourier transform for the estimation of power spectra: a method based on time-averaging over short, modified periodograms, IEEE Trans. Audio Electroacoust., 1967, 15, 70–73 CrossRef.
| This journal is © The Royal Society of Chemistry 2017 |

![[Doublestruck N]](https://www.rsc.org/images/entities/i_char_e171.gif)