Open Access Article
Open Access ArticleStructural, magnetic and electrical properties in Al-substitued NiZnCo ferrite prepared via the sol–gel auto-combustion method for LTCC technology
Le-Zhong Li *a,
Xiao-Xi Zhonga,
Rui Wanga,
Xiao-Qiang Tua,
Lei Hea,
Rong-Di Guob and
Zhi-Yong Xuc
*a,
Xiao-Xi Zhonga,
Rui Wanga,
Xiao-Qiang Tua,
Lei Hea,
Rong-Di Guob and
Zhi-Yong Xuc
aSichuan Province Key Laboratory of Information Materials and Devices Application, College of Optoelectronic Technology, Chengdu University of Information Technology, Chengdu 610225, People's Republic of China. E-mail: lezhong_li@163.com
bState Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu 610054, China
cSchool of Electronic Information & Mechanical Electrical Engineering, Zhaoqing University, Zhaoqing, 526061, China
First published on 10th August 2017
Abstract
Al-substituted NiZnCo ferrite, Ni0.4Zn0.5Co0.1AlxFe2−xO4 (0 ≤ x ≤ 0.20), were synthesized by the sol–gel auto-combustion method. The effects of Al substitution on the structural, magnetic and electrical properties have been investigated. The X-ray diffraction patterns show that the lattice parameter decreases with the increase of Al substitution. The SEM images show that the grain size decreases with the increase of Al substitution. The initial magnetic permeability reaches the maximum value when Al substitution is 0.05. The resonance frequency is inversely proportional to initial magnetic permeability which obeys Snoek's law. The temperature coefficient reaches the maximum value when Al substitution is 0.05, and it has the minimum value when Al substitution is 0.20. The Curie temperature decreases with the increase of Al temperature due to the number of nonmagnetic Al3+ ions increase results in the decrease of superexchange interaction. The saturation magnetization and coercivity of the ferrite decrease linearly with the increase of Al substitution. The real dielectric constant of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite decreases exponentially as frequency increases, and the dielectric constants decrease with the increase of Al substitution. The direct-current resistivity decreases and follows an exponential decay with the increase of temperature, and it increases with Al substitution.
1. Introduction
Low-temperature co-fired ceramic (LTCC) is one of the key technologies for manufacturing multilayered ceramic structures, which has comprehensively been used in the integration of passive components into monolithic devices. There are several layers of substrate material in which are buried capacitor, inductor, resistor, resonator, and filter components in the module.As a kind of soft magnetic ferrite, the polycrystalline NiCuZn ferrites extensively used in multilayer chip inductors (MLCI) because they exhibit excellent magnetic properties, high electrical resistivity, and good chemical stability.1–5
To integrate ferrite materials in LTCC technology, their sintering temperatures have to be reduced to less than 950 °C to avoid Ag diffusion and shrinkage since the melting temperature of silver metallization is 962 °C. However, sintering temperatures of typical ferrite materials are much higher than 950 °C. Under this condition, there are main two approaches to obtain dense samples with optimized microstructures after firing below 950 °C. One approach is to introduce single or multiple effective sintering additives to NiCuZn ferrite to form liquid phases in grain boundaries for promoting the densification and reducing the sintering temperature.5–10 Another approach to obtain dense ferrite materials after firing below 950 °C is by using high sinter-active ferrite powders prepared by alternative synthesis routes.11–14
In present work, NiZnCo ferrite nanopowders were prepared by the sol–gel auto-combustion method due to it has advantages of being able to use inexpensive precursors and a simple preparation process. Especially, the well dispersed homogenous, nano-sized and high sinter-active ferrite powder can be obtained at low sintering temperature.13 Accordingly, the effects of Al substitution on the structural, magnetic and electrical properties of NiZnCo ferrite after firing at 950 °C are investigated.
2. Experimental procedures
2.1. Preparation of Al-substituted NiZnCo ferrite
The samples of Ni0.4Zn0.5Co0.1AlxFe2−xO4 (x = 0, 0.05, 0.10, 0.15, 0.20) ferrite nanopowders were synthesized by the sol–gel auto-combustion method. The preparation process of nanopowders had been reported in our previous work.15 And then, the dried nanopowders were granulated with 10% poly-vinyl alcohol (PVA). The powder was pressed into samples with toroidal (Φ12 mm × Φ8 mm × h5 mm) and disc shape (Φ10 mm × h5 mm), which were sintered at 950 °C for 4 h in air to yield the final samples.2.2. Characterization and property measurements
The phase identification of the prepared ferrite samples was performed by DX 2700 X-ray diffractometer (XRD) (Cu target, Kα radiation, λ = 1.5406 Å) at room temperature. The microstructures were observed by the JEOL JSM-6490L scanning electron microscope (SEM). The frequency dependence of initial permeability of the prepared ferrite samples were measured by HP4291B impedance analyzer from 1 MHz to 1.8 GHz. The temperature dependence of initial permeability of the prepared ferrite samples were measured by WK 6500P LCR meter bridge from room temperature to 300 °C. The hysteresis loops of samples were measured at room temperature by using a TOEI VSM-5S-15 vibrating sample magnetometer (VSM). The dielectric constant (ε′) measurement were carried out using WK 6500P LCR meter bridge in the frequency range from 100 Hz to 10 MHz at room temperature. The dc resistivity was measured with Keithley 6517B high resistance meter at the temperature ranging from room temperature to 230 °C using silver-paste contacts on both sides of disc samples.3. Results and discussion
3.1. Structural properties
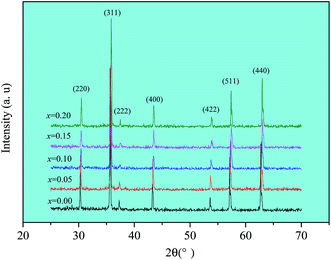
X-ray diffraction patterns of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrites are shown in Fig. 1. The patterns match well with the characteristic reflections of cubic spinel structure and without unidentified extra peaks within the experimental error and measurement precision. The lattice parameter (a) and X-ray density (dx) of all samples are calculated according to XRD data and the results are shown in Table 1. The lattice parameter and X-ray density decrease from 0.8355 nm to 0.8310 nm and 5.42 g cm−3 to 5.37 g cm−3, respectively. The lattice parameter decrease with increasing Al substitution can be attributed to the smaller ionic radius of Al3+ (0.051 nm) compared to Fe3+ ions (0.067 nm). As the smaller ionic radius Al3+ ions replace larger ionic radius Fe3+ ions in lattice sites, which can result in the shrinkage in the unit cell dimensions. The substitution of Fe3+ ions of higher atomic weight (55.845) with lower atomic weight Al3+ ions (26.982) results in the decrease of molecular weight from 237.8 to 232.0. Consequently, it leads to the X-ray density decrease.| x | 0.00 | 0.05 | 0.10 | 0.15 | 0.20 |
|---|---|---|---|---|---|
| a (nm) | 0.8355 | 0.8342 | 0.8325 | 0.8316 | 0.8310 |
| d (g cm−3) | 4.32 | 4.63 | 4.61 | 4.53 | 4.45 |
| dx (g cm−3) | 5.42 | 5.41 | 5.40 | 5.39 | 5.37 |
| P (%) | 20.25 | 14.42 | 14.64 | 15.92 | 17.15 |
Fig. 2 shows the cross section morphologies of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite. It demonstrates that the grain size decreases with the increase of Al substitution, which indicates that Al substitution inhibits the crystal growth. Similar variation in grain size with the increase of Al sustitution is also obtained in MnZn, Co, Ni, and NiZn ferrite system.16–20 It is due to small amount of aluminum oxide can be segregated at grain boundaries which inhibits the boundary movement as the second phase particle in the final sintering stage20 which can be confirmed by the EDS analysis in the grain interior and grain boundary (Fig. 3). Eventually, the grain size decreases with Al substitution increasing.
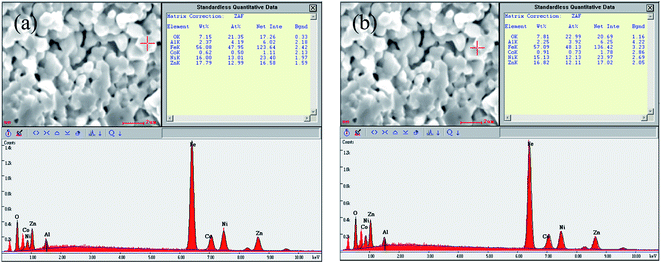 | ||
| Fig. 3 EDS analysis (a) in the grain interior and (b) grain boundary of Ni0.4Zn0.5Co0.1Al0.1Fe1.9O4 ferrite. | ||
3.2. Magnetic properties
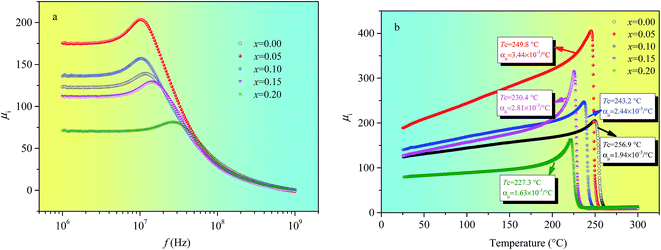
Fig. 4 illustrates the frequency and temperature dependence of the initial magnetic permeability of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite. Fig. 4(a) indicates that the initial magnetic permeability reaches the maximum value when Al substitution (x) is 0.05. As shown in Table 1, the density (d) have the maximum value and the porosity is the lowest when x = 0.05 indicates that proper Al substitution can increase the density of NiZnCo ferrite, which leads to the domain wall movement and domain rotation become easier. And then, the initial magnetic permeability increases with Al substitution. Moreover, the magnetocrystalline anisotropy constant (K1) of magnetic ions is a constant except zero and the value of K1 for nonmagnetic ions is zero, so the nonmagnetic Al3+ ions substitution can result in the decrease of K1. And the initial permeability is inversely proportional to K1, hence the decrease of K1 is another reason to make the initial magnetic permeability increase. However, the decrease of initial magnetic permeability when Al substitution excess 0.05 may be due to the inhomogeneous distribution of Al3+ ions and lattice deformation with excessive Al substitution which can result in the increase of inner stress. In addition, Fig. 4(a) also indicates that the resonance frequency initially decreases and then increases with increasing Al substitution. In other words, the resonance frequency is inversely proportional to initial magnetic permeability which obeys the Snoek's law.21The temperature coefficient of μi (αμ) among the temperature range T1 and T2 can be defined as αμ = (μ2 − μ1)/(T2 − T1)μ1. Fig. 4(b) indicates that Al substitution has an effect on the temperature coefficients of NiZnCo ferrite. The temperature coefficient of μi is obtained within the temperature range from 50 °C to 150 °C because the variation of μi with temperature is linear. αμ reaches the maximum value (3.44 × 10−3 °C−1) with Al substitution is 0.05, which mainly due to the decrease of magnetocrystalline anisotropy energy with proper Al substitution. And αμ has the minimum value (1.63 × 10−3 °C−1) when Al substitution is 0.20, which properly due to the increase of inner stress because the inhomogeneous distribution of Al3+ ions and lattice deformation with excessive Al substitution. Fig. 4(b) also shows that the Curie temperature (Tc) decreases with the increase of Al temperature which mainly due to the number of magnetic ions present in the two sublattices and their superexchange interactions. The strength of the superexchange interactions depends on the angle and distance between the two metal cations. And among them AB interaction is the strongest one and AA interaction is the weakest one.22 Therefore, AB superexchange interaction becomes weaker because the magnetic Fe3+ ions are being replaced by the nonmagnetic Al3+ ions at B site. So, Tc decreases with the increase of Al substitution since it is determined by an overall strength of the A–B superexchange interaction.
Fig. 5(a) shows the hysteresis loops of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite. The saturation magnetization (Ms) and coercivity (Hc) of ferrite as a function of Al substitution (x) are shown in Fig. 5(b). Ms and Hc decrease linearly with the increase of Al substitution.
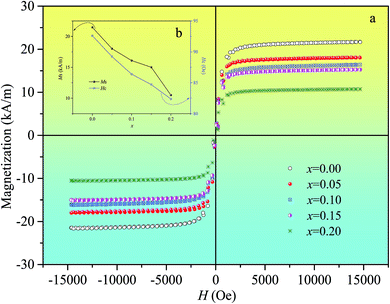 | ||
| Fig. 5 Hysteresis loops (a), and variation of Ms and Hc with different substitution (b) of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite. | ||
Magnetic properties of ferrites are influenced by many factors, such as structure, composition, defects, crystallite size, internal strain and cation distribution. According to Néel's two sublattice model of ferrimagnetisms,22 the magnetic moment of cubic spinel ferrite can be calculated by M = |MB − MA|, where MA and MB are the magnetizations of A and B-sites respectively. Since the magnetic Fe3+ ions (5 μB) are replaced by non-magnetic Al3+ ions (0 μB) at B-sites leads to a reduction of the magnetic ions density, which results in the decrease of the net magnetic moment at the B-sublattice (MB) and hence the net overall magnetic moment decrease. Furthermore, the decrease of grain size and increase of internal stress due to the formation of lattice dislocation and the increase of porosity with excessive Al substitution also can make Ms decrease. Eventually, Ms decreases with the increase of Al substitution.
Hc as a function of Al substitution (x) is shown in Fig. 5(b). It is observed that Hc monotonously decreases with the increase of Al substitution. On the one hand, the decrease in Hc value due to the nonmagnetic ions enter the lattices can result in the decrease of magnetocrystalline anisotropy energy. On the other hand, according to the Stoner–Wohlfarth mono-domain theory,23 Hc increases with the increase of crystallite size when the crystallite is mono-domain structure. And the transition from mono-domain to multi-domains is supposed to occur when the grain size is around 2.9 μm.24 So, from Fig. 2, the crystallite with mono-domain structure is another possible reason for the decrease of Hc with Al substitution.
3.3. Electrical properties
The frequency dependence of the real dielectric constant (ε′) of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite in a frequency range from 100 Hz to 10 MHz at room temperature is shown in Fig. 6. The dielectric constant is calculated using the following equation:
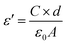 | (1) |
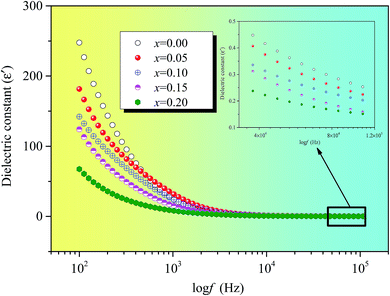
Fig. 6 indicates that the real dielectric constant of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite decreases exponentially as frequency increases. The real dielectric constant decreases rapidly in low frequency region while it approaches almost frequency independent in high frequency region for all the compositions under investigation.
The dielectric polarization in ferrites is similar with the conduction hopping mechanism. Hopping between Fe2+ and Fe3+ the local displacement of electrons in the direction of the applied field occurs and these electrons determine the polarization.25 The alternating electric field causes the localized charges accumulation at grain boundaries and results in interfacial polarization. At lower frequencies, the real dielectric constant decreases rapidly due to the space charges are able to follow the frequency of the alternating field. The polarization decreases with increasing frequency and then reaches a constant value due to the fact that beyond a certain external field frequency, as a result electron exchange between Fe2+ and Fe3+ ions don't obey the variant in an alternating field. The large value of dielectric constant at lower frequency is due to the predominance of species like Fe2+ ions, interfacial dislocation piles up, oxygen vacancies, grain boundary defects, and so on.25 At the same time, the decrease in the real dielectric constant with frequency because any species contributing to polarizability is found to show lagging behind the applied field at a certain higher frequencies.
Polarisation in ferrites mainly attributed to the Fe2+ ions existence because hopping between Fe2+ and Fe3+ the local displacement of electrons determine the polarization. The more Fe2+ ions, the higher dielectric constant because Fe2+ ions are easily polarizable. The insert figure of Fig. 6 clearly demonstrates that the dielectric constants decrease with the increase of Al substitution at 100 kHz. The decrease of dielectric constant can be explained on the basis of the number of available Fe2+ ions on B sites. And the n-type charge transfer in ferrites is due to the hopping of electrons from Fe2+ to Fe3+ ions according to Fe2+ ↔ Fe3+ + e−. With the increase of Al substitution, Fe2+ ions must be decreasing.26 Therefore, the polarization is weakened which results in the dielectric constant decrease with the increase of Al substitution.
Fig. 7(a) shows the temperature dependence of direct-current resistivity (ρd) for Ni0.4Zn0.5Co0.1AlxFe2−xO4 (x = 0–0.20) ferrite. It is clear that the investigated samples have semi-conducting behavior, in which ρd decreases and follows an exponential decay with the increase of temperature. At the same time, ρd increases with Al substitution. It is well known that the conduction mechanism for ferrites is predominantly due to hopping of electrons between Fe2+ and Fe3+ ions (Fe2+ ↔ Fe3+ + e−).27 As discussed previously, Fe2+ ions must be decreasing with the increase of Al substitution, which hinders the electron hopping between Fe3+ and Fe2+ ions and then it results in the increase of ρd.
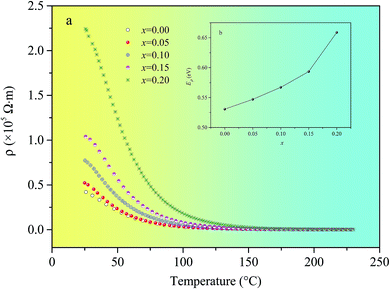 | ||
| Fig. 7 Temperature dependence of ρd (a) and variation of Eρ with x (b) for Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite. | ||
The hopping probability not only depends upon the separation between the ions involved but the activation energy.28 The relationship between direct-current resistivity and temperature obeys the well-known Arrhenius equation as29
ρd = ρ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Eρ/kT) exp(Eρ/kT)
| (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ against l/T, the activation energies Eρ can calculated from eqn (2).30 It is noticed that the values of activation energies increased from 0.531 eV (x = 0) to 0.659 eV (x = 0.20) (Fig. 7(b)). The result indicates that the activation energy is influenced by Al substitution. The hopping depends upon the activation energy, which is associated with the electrical energy barrier experienced by the electrons during hopping. And the electronic conduction in ferrites is formed by hopping of electrons between ions of the same element present in more than one valance state, distributed randomly over crystallographically equivalent lattice sites. In other word, the electrical energy barrier becomes much higher when the Fe3+ ions are being replaced by the different element ions at the same lattice sites. So, the activation energy Eρ increases with increasing Al substitution.
ρ against l/T, the activation energies Eρ can calculated from eqn (2).30 It is noticed that the values of activation energies increased from 0.531 eV (x = 0) to 0.659 eV (x = 0.20) (Fig. 7(b)). The result indicates that the activation energy is influenced by Al substitution. The hopping depends upon the activation energy, which is associated with the electrical energy barrier experienced by the electrons during hopping. And the electronic conduction in ferrites is formed by hopping of electrons between ions of the same element present in more than one valance state, distributed randomly over crystallographically equivalent lattice sites. In other word, the electrical energy barrier becomes much higher when the Fe3+ ions are being replaced by the different element ions at the same lattice sites. So, the activation energy Eρ increases with increasing Al substitution.
4. Conclusions
Al-substituted NiZnCo ferrite, Ni0.4Zn0.5Co0.1AlxFe2−xO4 (0 ≤ x ≤ 0.20), were synthesized by the sol–gel auto-combustion method. The influences of Al substitution on the structural, magnetic and electrical properties have been investigated. The lattice parameter and grain size decrease with the increase of Al substitution. The initial magnetic permeability reaches the maximum value when Al substitution is 0.05. The resonance frequency is inversely proportional to initial magnetic permeability which obeys the Snoek's law. The temperature coefficient reaches the maximum value (3.44 × 10−3 °C−1) with Al substitution is 0.05 due to the decrease of magnetocrystalline anisotropy energy with proper Al substitution, and it has the minimum value (1.63 × 10−3 °C−1) when Al substitution is 0.20 because the inhomogeneous distribution of Al3+ ions and lattice deformation with excessive Al substitution. The Curie temperature decreases with the increase of Al temperature due to the number of nonmagnetic Al3+ ions increase results in the decrease of superexchange interaction. The saturation magnetization and coercivity of the ferrite decrease linearly with the increase of Al substitution. The real dielectric constant of Ni0.4Zn0.5Co0.1AlxFe2−xO4 ferrite decreases exponentially as frequency increase, and the dielectric constants decrease with the increase of Al substitution. The direct-current resistivity decreases and follows an exponential decay with the increase of temperature which indicate that the investigated samples have semi-conducting behavior, and it increases with Al substitution.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant no. 51502025.References
- D. Stoppels, J. Magn. Magn. Mater., 1996, 160, 323–328 CrossRef CAS.
- H. I. Hsiang, W. C. Liao, Y. J. Wang and Y. F. Cheng, J. Eur. Ceram. Soc., 2004, 24, 2015–2021 CrossRef CAS.
- T. Krishnaveni, B. R. Kanth, V. S. R. Raju and S. R. Murthy, J. Alloys Compd., 2006, 414, 282–286 CrossRef CAS.
- P. Guzdek, J. Kulawik, K. Zaraska and A. Bieńkowski, J. Magn. Magn. Mater., 2010, 322, 2897–2901 CrossRef CAS.
- S. Zhang, L. Jia, H. Zhang, J. Li, T. Zhou and B. Liu, J. Appl. Phys., 2014, 115, 17A524 CrossRef.
- X. Wang, Y. Li, J. Li, G. Yu, L. Zuo and H. Zhang, J. Mater. Sci.: Mater. Electron., 2014, 25, 4230–4234 CrossRef CAS.
- W. Ling, IEEE Trans. Magn., 2014, 50, 1–4 Search PubMed.
- J. C. Jao, P. Li and S. F. Wang, Jpn. J. Appl. Phys., Part 1, 2007, 46, 5792–5796 CrossRef CAS.
- X. M. Cui, J. Zhou, B. Li and Z. F. Tong, Mater. Manuf. Processes, 2007, 22, 251–255 CrossRef CAS.
- W. Ling, H. Zhang, Y. Li, D. Chen, Q. Wen and J. Shen, J. Appl. Phys., 2010, 107, 09D911 CrossRef.
- Q. Yang, H. Zhang, Y. Liu, Q. Wen and L. Jia, Mater. Lett., 2012, 79, 103–105 CrossRef CAS.
- K. O. Low and F. R. Sale, J. Magn. Magn. Mater., 2003, 256, 221–226 CrossRef CAS.
- T. T. Ahmed, I. Z. Rahman and M. A. Rahman, J. Mater. Process. Technol., 2004, 153, 797–803 CrossRef.
- J. Mürbe and J. Töpfer, J. Eur. Ceram. Soc., 2012, 32, 1091–1098 CrossRef.
- L. Z. Li, Z. Yu, Z. W. Lan, K. Sun and C. J. Wu, Ceram. Int., 2014, 40, 13917–13921 CrossRef CAS.
- M. A. Gabal, A. M. Abdel-Daiem, Y. M. Angari and I. M. Ismail, Polyhedron, 2013, 57, 105–111 CrossRef CAS.
- L. Kumar and M. Kar, J. Magn. Magn. Mater., 2011, 323, 2042–2048 CrossRef CAS.
- B. K. Kuanr, S. R. Mishra, L. Wang, D. Conte, D. Neupane, V. Veerakumar and Z. Celinski, Mater. Res. Bull., 2016, 76, 22–27 CrossRef CAS.
- R. S. Biasi and H. F. Santos, Ceram. Int., 2017, 43, 4557–4561 CrossRef.
- A. A. Birajdar, S. E. Shirsath, R. H. Kadam, M. L. Mane, D. R. Mane and A. R. Shitre, J. Appl. Phys., 2012, 112, 053908 CrossRef.
- J. L. Snoek, Physica, 1948, 14, 207–217 CrossRef CAS.
- D. F. Wan and X. L. Ma, The Physics of Magnetism, UESTC Press, Chengdu, 1994 Search PubMed.
- E. C. Stoner and E. P. Wohlfarth, IEEE Trans. Magn., 1991, 27, 3475–3518 CrossRef CAS.
- P. J. Zagg, P. J. Valk and M. T. Rekveldt, Appl. Phys. Lett., 1996, 69, 2927–2929 CrossRef.
- M. Naeem, N. A. Shah, I. H. Gul and A. Maqsood, J. Alloys Compd., 2009, 487, 739–743 CrossRef CAS.
- A. A. Sattar, H. M. El-Sayed, K. M. El-Shokrofy and M. M. El-Tabey, J. Appl. Sci., 2005, 3, 162–168 Search PubMed.
- E. J. W. Verwey and J. H. De Boer, Recl. Trav. Chim. Pays-Bas, 1936, 55, 531–540 CrossRef CAS.
- A. Lakshman, P. S. V. S. Rao, B. P. Rao and K. H. Rao, J. Phys. D: Appl. Phys., 2005, 38, 673–678 CrossRef CAS.
- U. V. Chhaya and R. G. Kulkarni, Mater. Lett., 1999, 39, 91–96 CrossRef CAS.
- A. Thakur, P. Mathur and M. Singh, J. Phys. Chem. Solids, 2007, 68, 378–381 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |