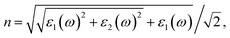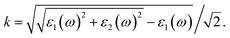Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
First-principles study on the electronic, optical and thermodynamic properties of ABO3 (A = La,Sr, B = Fe,Co) perovskites
Ting Jia a,
Zhi Zeng*abc,
H. Q. Linc,
Yuhua Duan
a,
Zhi Zeng*abc,
H. Q. Linc,
Yuhua Duan d and
Paul Ohodnickid
d and
Paul Ohodnickid
aKey Laboratory of Materials Physics, Institute of Solid State Physics, Chinese Academy of Sciences, Hefei 230031, P. R. China. E-mail: zzeng@theory.issp.ac.cn
bDepartment of Physics, University of Science and Technology of China, Hefei, 230026, P. R. China
cBeijing Computational Science Research Center, Beijing 100084, P. R. China
dNational Energy Technology Laboratory, United States Department of Energy, Pittsburgh, Pennsylvania 15236, USA
First published on 8th August 2017
Abstract
The electronic, optical and thermodynamic properties of ABO3 (A = La,Sr, B = Fe,Co) perovskites are investigated using first-principles calculations. The obtained results indicate that SrCoO3 and SrFeO3 are metals, while LaCoO3 and LaFeO3 are insulators and all of them exhibit strong hybridization of the Fe/Co-3d and O-2p orbitals. By correlating the energy band structures with the peaks of the imaginary part of the dielectric function, we obtained the origin of each electron excitation to provide information about the active bands for the corresponding optical transitions observed in the experiment. Moreover, the Debye temperatures θD obtained from the phonon frequencies are comparable to the available data. Finally, the thermodynamic properties of the Helmholtz free energy F, entropy S, and constant-volume heat capacity Cv are investigated based on the phonon spectra.
1 Introduction
Perovskites in the form of ABO3 (A = alkaline-earth metal or La, B = 3d transition metal) are a plentiful family of compounds, which exhibit novel properties, such as colossal magnetoresistance, ferroelectricity and superconductivity, which make them attractive in technological applications such as in catalysis, sensor devices, magnetoresistance devices and spintronics.1–6 The extensive investigations into ABO3 not only have technical importance, but also originate from the fundamental interest in the physics of their multiple phases. In the ABO3 system, the A sites are divalent or trivalent metals, occupied for example by Sr or La atoms. Correspondingly the B sites are tetravalent or trivalent atoms, occupied for example by Co or Fe atoms, resulting in perovskites with desired properties and performances. Usually, the B cations generally determine the physical properties by either the localized or collective behavior of the d electrons. Of course, the valency of the B sites depends on the valency of the A cations, by which the valency of the B transition metal ions change and thus lead to unusual electronic and magnetic properties.Therefore, the variety of A and B atoms can tailor the structural, electronic, magnetic and other related properties of the perovskites, depending on the size and valence electrons of the A and B atoms. Here, we choose the system of Sr2+ and La3+ for the A sites, corresponding to Fe/Co4+ and Fe/Co3+ for the B sites. Both experimental and theoretical studies have been widely carried out on these traditional materials. SrCoO3 has been clarified to be a ferromagnetic metal (TC = 280 K) with an intermediate-spin d5 state7–10 or a high-spin d6L (where L denotes a ligand hole) state of Co4+.11 SrFeO3 is a helical-type antiferromagnet (TN = 130 K) with a high-spin Fe4+ ion.12,13 Comparatively, there are many more phase transitions in LaCoO3 and LaFeO3. LaCoO3 is a nonmagnetic insulator with low-spin Co3+ at low temperatures, but undergoes a transition to a paramagnetic insulator above 90 K and to a paramagnetic metal with high-spin above 500 K.14–20 The presence of an IS state at 90–500 K (ref. 21) and the structural transition from R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c to R
c to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) at 648 K (ref. 22–24) are controversial. For LaFeO3, a structural transition from Pbnm to R3c has been observed at 1228 K as well as a subsequent transition to Pm3m at 2140 K.25 LaFeO3 is a G-type antiferromagnet above TN = 735 K.26–28 However, there is little research on the optical and thermodynamic properties.29–31 Moreover, these data are important both in providing a reference for future research and in improving the range of practical applications. Therefore, in this work, we focus on the ground state at low temperatures to systematically investigate the electronic, optical and thermodynamic properties using first-principles calculations. Our results show that the divalent A sites of SrCoO3 and SrFeO3 are metals, while the trivalent A sites of LaCoO3 and LaFeO3 are insulators, all of which are consistent with experimental results.8,9,32,33 Based on the electronic structures, their optical and thermodynamic properties are further investigated and summarized to provide a comparison for the experiments.
at 648 K (ref. 22–24) are controversial. For LaFeO3, a structural transition from Pbnm to R3c has been observed at 1228 K as well as a subsequent transition to Pm3m at 2140 K.25 LaFeO3 is a G-type antiferromagnet above TN = 735 K.26–28 However, there is little research on the optical and thermodynamic properties.29–31 Moreover, these data are important both in providing a reference for future research and in improving the range of practical applications. Therefore, in this work, we focus on the ground state at low temperatures to systematically investigate the electronic, optical and thermodynamic properties using first-principles calculations. Our results show that the divalent A sites of SrCoO3 and SrFeO3 are metals, while the trivalent A sites of LaCoO3 and LaFeO3 are insulators, all of which are consistent with experimental results.8,9,32,33 Based on the electronic structures, their optical and thermodynamic properties are further investigated and summarized to provide a comparison for the experiments.
2 Computational details
Density functional theory (DFT) calculations were performed using the projector-augmented wave (PAW) method34 implemented in the Vienna ab initio simulation package (VASP).35 The exchange–correlation energy is described by the local spin density approximation (LSDA), or generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional.36 To account for the strong electron correlation of the Fe and Co ions, all calculations were performed using the Dudarev formalism37 of the plus Hubbard U correction with U = 4 eV, which performs better in describing structures and band gaps with our choice of U values (U = 4 and 5 eV). The cutoff energy for the plane-wave basis set is 400 eV, and an 11 × 11 × 11 Monkhorst–Pack k-point mesh38 for SrCoO3 and SrFeO3, a 5 × 5 × 3 mesh for LaCoO3 and a 6 × 4 × 6 mesh for LaFeO3 were used. All of the shape, volume and ionic coordinates were fully relaxed until the total energy was changed within 10−8 eV per atom and the Hellmann–Feynman force on each atomic site is less than 0.0001 eV Å−1 for the following phonon calculations.It is known that all of the optical constants, such as the refractive index n and the extinction coefficient k, can be derived from the dielectric function ε = ε1(ω) + iε2(ω). The imaginary part ε2(ω) of the dielectric function is calculated from the momentum matrix elements between the occupied and unoccupied wave functions. The real part ε1(ω) of the dielectric function is evaluated from the imaginary part ε2(ω) by the Kramers–Kronig relationship.39
The phonon dispersion and thermodynamic properties were calculated from the harmonic interatomic force constants using the finite displacement method via the PHONONPY package.40 The 2 × 2 × 2 supercell and 5 × 5 × 5 k mesh for SrCoO3 and SrFeO3, the 2 × 2 × 1 supercell and 3 × 3 × 3 k mesh for LaCoO3 and the 2 × 1 × 2 supercell and 3 × 5 × 3 k mesh for LaFeO3 were applied to calculate the force constants.
3 Results and discussion
3.1 Structures
ABO3 compounds contain a rich family of crystal structures, such as simple cubic, tetragonal, orthorhombic, rhombohedral etc. Moreover, the structure of one given ABO3 compound is complicated due to phase transitions at different temperatures. For example, the structure of LaFeO3 changes from an orthorhombic Pbnm phase to rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c at 1228 K and subsequently to cubic Pm
c at 1228 K and subsequently to cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 2140 K.25 Considering that the properties of the ground state at 0 K are investigated by DFT, we used the crystal structures reported from experiments at low temperatures. SrCoO3 has a perfect perovskite cubic structure with the space group Pm3m
m at 2140 K.25 Considering that the properties of the ground state at 0 K are investigated by DFT, we used the crystal structures reported from experiments at low temperatures. SrCoO3 has a perfect perovskite cubic structure with the space group Pm3m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 (Fig. 1(a)). SrFeO3 has a little distortion to a tetragonal structure with space group P4/mmm
7 (Fig. 1(a)). SrFeO3 has a little distortion to a tetragonal structure with space group P4/mmm![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 12 (Fig. 1(b)). For compounds with smaller A site ionic radii, the crystal structures of LaCoO3 and LaFeO3 are more distorted to a rhombohedral R
12 (Fig. 1(b)). For compounds with smaller A site ionic radii, the crystal structures of LaCoO3 and LaFeO3 are more distorted to a rhombohedral R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure14 (Fig. 1(c)) and an orthorhombic Pbnm structure25 (Fig. 1(d)), respectively. Similarly, the magnetic structures used here are the ground states at low temperatures both from experiment and theory, that are the ferromagnetic structure for SrCoO3,8–11 the nonmagnetic structure for LaCoO3 (ref. 15, 20 and 29) and the G-type antiferromagnetic structure for LaFeO3.26–28 For SrFeO3, the ground magnetic state is a non-collinear antiferromagnet with a spiral structure, as shown by experiment.13 Since the non-collinear magnetic ordering has little influence on the optical and thermodynamic properties, and ferromagnetism has been clarified to be the most stable state among all collinear magnetic phases,9,41 we selected ferromagnetism as the magnetic structure of SrFeO3 in the following calculations.
c structure14 (Fig. 1(c)) and an orthorhombic Pbnm structure25 (Fig. 1(d)), respectively. Similarly, the magnetic structures used here are the ground states at low temperatures both from experiment and theory, that are the ferromagnetic structure for SrCoO3,8–11 the nonmagnetic structure for LaCoO3 (ref. 15, 20 and 29) and the G-type antiferromagnetic structure for LaFeO3.26–28 For SrFeO3, the ground magnetic state is a non-collinear antiferromagnet with a spiral structure, as shown by experiment.13 Since the non-collinear magnetic ordering has little influence on the optical and thermodynamic properties, and ferromagnetism has been clarified to be the most stable state among all collinear magnetic phases,9,41 we selected ferromagnetism as the magnetic structure of SrFeO3 in the following calculations.
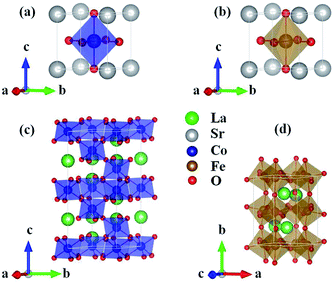 | ||
| Fig. 1 Crystal structures of the unit cells for (a) SrCoO3, (b) SrFeO3, (c) LaCoO3 and (d) LaFeO3 used in our calculations. | ||
Based on the lattice parameters from the experiment, a full structural optimization was performed using GGA, GGA+U and LSDA+U methods. As shown in Table 1, the lattice constants obtained by GGA+U are much closer to the experimental values than for those obtained by GGA, even for SrCoO3 and SrFeO3 with metal characteristics. Therefore, the correlation U is necessary for the correct prediction of structural information and the following properties which are sensitive to the fine structure. In addition, within the LSDA+U method, lattice constants are significantly underestimated compared to those obtained by the GGA+U method and experimentally. Therefore, we selected the most suitable method, GGA+U, for further calculations.
| Compounds | Methods | a | b | c |
|---|---|---|---|---|
| SrCoO3 | GGA | 3.8038 | 3.8038 | 3.8038 |
| GGA+U | 3.8174 | 3.8174 | 3.8174 | |
| LSDA+U | 3.7274 | 3.7274 | 3.7274 | |
| Experiment7 | 3.8550 | 3.8550 | 3.8550 | |
| GGA | 3.8156 | 3.8156 | 3.8179 | |
| SrFeO3 | GGA+U | 3.8489 | 3.8489 | 3.8513 |
| LSDA+U | 3.7471 | 3.7471 | 3.7487 | |
| Experiment12 | 3.8570 | 3.8570 | 3.8690 | |
| GGA | 5.4440 | 5.4440 | 12.8942 | |
| LaCoO3 | GGA+U | 5.4272 | 5.4272 | 12.9116 |
| LSDA+U | 5.3119 | 5.3119 | 12.6911 | |
| Experiment14 | 5.4427 | 5.4427 | 13.0899 | |
| GGA | 5.4438 | 7.6903 | 5.4758 | |
| LaFeO3 | GGA+U | 5.5607 | 7.8267 | 5.5311 |
| LSDA+U | 5.2145 | 7.5080 | 5.3292 | |
| Experiment25 | 5.5659 | 7.8534 | 5.5544 |
3.2 Electronic properties
The band structures and partial density of states (PDOS) are shown in Fig. 2. The compounds with lower valence A sites, SrCoO3 and SrFeO3, are both metals, which is consistent with experiments and previous calculation results.8–11,41 The orbitals at the Fermi energy are mainly contributed to by the Fe/Co and O ions. The occupied configurations of d6L for Co4+ and d5L for Fe4+ reflect the strong hybridization of the Fe/Co-3d and O-2p orbitals and are consistent with the negative charge transfer regime of SrCoO3 and SrFeO3 reported before.8,9,11 These hybridized orbitals give rise to the conduction bands (CBs) and dominate the properties of these oxides, as expected in the case of perovskite oxides. The CBs in the range of 7 to 11 eV are mainly occupied by Sr-4d orbitals. Since Fe4+ has one electron less than Co4+, there is little difference at the Fermi level. The minority spin Co-3d states of SrCoO3 are partially occupied and thus cross the Fermi level, reflecting an intermediate-spin state and the metal characteristics of both majority and minority spin. This metal behavior is different from the result of the half metal by the unrestricted Hartree–Fock method,10 but is similar to the result given by the LSDA+DMFT method.11 Furthermore, such an intermediate-spin ground state of SrCoO3 has been confirmed by the experimental Co-2p X-ray absorption spectroscopy spectrum, and also the strong hybridization of the d6L state is key to explain the experimental spectrum.8,9 Unlike SrCoO3, the minority spin Fe-3d states of SrFeO3 are fully unoccupied, corresponding to the insulating behavior of minority spin and thus the half-metallic property of SrFeO3. Our result of a half-metallic characteristic of ferromagnetic SrFeO3 is slightly different from the metal results from the paramagnetic and antiferromagnetic calculations.42 In addition, Fe4+ is a high-spin state with fully occupied up-spin and unoccupied down-spin Fe-3d orbitals. Considering the charge from the O-2p orbitals, the ground state of Fe4+ is a high-spin d5L configuration, which agrees with the electronic structure of SrFeO3 obtained by X-ray photoemission and ultraviolet photoemission spectroscopy investigations.43 This negative charge transfer regime is characteristic of compounds with transition metal ions in relatively high oxidation states. The high-valence states of Co4+ and Fe4+ in SrCoO3 and SrFeO3 correspond to reduced potential energy, which is comparable with or even lower than that of O-2p. As a result, there are charge transfers from O-2p to Fe/Co-3d and thus covalent contributions to the bonding in SrCoO3 and SrFeO3.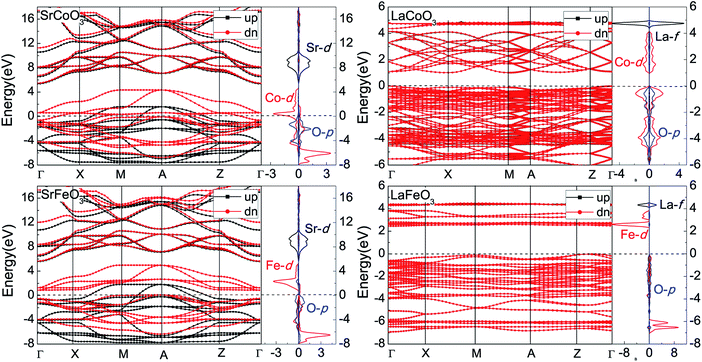 | ||
| Fig. 2 The band structures and partial density of states for SrCoO3, SrFeO3, LaCoO3 and LaFeO3. The zero of the energy scale is the position of the Fermi level. | ||
While for the compounds with higher valence A sites, LaCoO3 and LaFeO3 with relatively low-valence Co3+ and Fe3+ cations are more ionic than SrCoO3 and SrFeO3. As shown in Fig. 2, LaCoO3 and LaFeO3 are both insulators, with band gaps of 0.8 and 2.2 eV, which are similar to the experimental results of 0.6 (ref. 32) and 2.1 eV.33 For LaCoO3, the occupation numbers of the up and down spin states are nearly the same, so the Co3+ is the low-spin state and the system is a nonmagnet. The valence bands (VBs) are dominated by the hybridization bands of Co-t2g and O-2p; the lowest CBs are Co-eg, and the highest CBs are La-4f. The shape and peak locations are similar to existing results.29 Although the spin-state transition of LaCoO3 at high temperature is controversial, the low-spin ground state at low temperature has reached an agreement by comparing it with the photoemission spectrum.44 For LaFeO3, since the ground state that we calculated is antiferromagnetic, both the up-spin and down-spin states are equal, showing a spin degenerate band structure. However, the PDOS of the up-spin states exhibit spin polarization, especially the Fe-3d orbitals. The up-spin states of the Fe-3d orbitals are fully occupied and down-spin ones are nearly unoccupied, which shows high-spin Fe3+ in LaFeO3. There are also hybridization bands of Fe-3d and O-2p near the Fermi level, and the relatively deeper VBs are the fully occupied Fe-3d orbitals. The lowest CBs are the empty Fe-t2g orbitals, which have smaller bandwidths and dispersion than the nearest VBs of Fe-eg, due to the direct overlap of eg with O-2p, which is consistent with previous calculation results.31 The upper narrow and flat CBs in the range of 4.5 to 5 eV are also localized La-4f. Our results are in good agreement with experimental data of the X-ray absorption spectra.45
3.3 Optical properties
The optical constants of the dielectric function are shown in Fig. 3. The peaks of the imaginary part of the dielectric function ε2(ω) are related to electron excitation and thus directly connected to the energy band structure. The first peaks of SrCoO3 and SrFeO3 at about 1–2 eV are ascribed to the transitions from the occupied O-2p to the unoccupied Co/Fe-3d or the d–d transition of the Co/Fe-3d states. This peak is very pronounced and higher than the other peaks, which demonstrates that a large number of interband transitions occur at this same energy, corresponding to the concentration of energy bands near the Fermi level. The second peak at about 9 eV is mainly due to the transition from occupied O-2p orbitals to empty Sr-4d orbitals. However, as far as we know no experimental measurements exist for comparison with our theoretical predictions. For LaCoO3 and LaFeO3, the absorptive edges of imaginary part ε2(ω) start at about 0.5 eV and 2.0 eV respectively, relating to the band gaps. In addition, there are relatively more peaks for LaCoO3 and LaFeO3. For LaCoO3, the first two peaks at around 2 eV and 5 eV are attributed to the transitions from the occupied O-2p centered around −0.5 eV and −4 eV below the Fermi level to the empty Co-3d, respectively. These two peaks in the experiment merge to a strong absorption region in the energy region of 1–5 eV.30 However, the optical properties from the experiment were measured at room temperature so that other spin-states may be mixed, while our calculation results are based on totally low-spin ground states. Therefore, there are some discrepancies. The other peak near 9 eV is contributed to by the transition from the occupied O-2p and Co-3d centered around −4 eV to the empty La-4f near 5 eV. While for LaFeO3, there are only two main peaks below 10 eV. The first one below 5 eV comes from the transition between the occupied O-2p centered around −2 eV and the empty Fe-3d just above 2 eV. The second one between 6 and 10 eV is from multiple transitions: the transition from the occupied O-2p to the empty Fe-3d, the intersite d–d transition between the VB and CB of the Fe-3d centered around −6 and 3 eV, or the transition from the occupied Fe-3d to the CB of La-4f at −4 eV. These two peaks agree well with the experimental results.31 All of the peaks above 20 eV for LaCoO3 and LaFeO3 correspond to the excitation of the inner electrons to the CB (not shown in the band structures).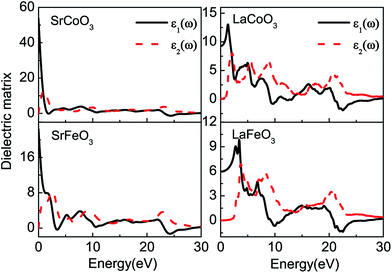 | ||
| Fig. 3 The real parts ε1(ω) and imaginary parts ε2(ω) of the complex dielectric function for SrCoO3, SrFeO3, LaCoO3 and LaFeO3. | ||
Based on the dielectric function, the optical properties, such as the refractive index n and the extinction coefficient k, could be obtained by the equations
Our results of n and k as a function of photon wavelength λ are displayed in Fig. 4, both of which oscillate in the short wavelength range. The refractive indices n of LaCoO3 and LaFeO3 increase to a maximum and decay to a static value (ω = 0 or λ → ∞) of 3.04 and 2.44, while those of SrCoO3 and SrFeO3 should further increase with increasing λ and finally decay to static values of 7.08 and 4.67 (not shown here). Generally, the static refractive indices of the SrCoO3 and SrFeO3 metals are relatively larger than those of the LaCoO3 and LaFeO3 insulators. Since the refractive index n and extinction coefficient k are directly proportional to real part ε1(ω) and the imaginary ε2(ω) of the dielectric function, both of them are directly connected to the energy band structure and they are equivalent in describing the optical properties. The extinction coefficient k is similar to the imaginary part of the dielectric function ε2(ω), which is directly related to electron excitation. The peaks of k directly correspond to those of ε2(ω) we analyzed above, but the wavelength dependence of the extinction coefficient k is shown here. The values of k go down to 0 at about 1000 nm and 500 nm for LaCoO3 and LaFeO3, respectively. These optical gaps are due to their insulating behavior, which is absent for SrCoO3 and SrFeO3. The refractive index n and extinction coefficient k provided here are used for experimental comparison.
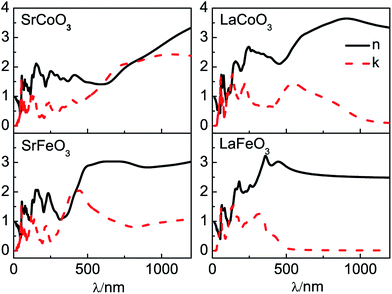 | ||
| Fig. 4 The optical parameters of the refractive index n and extinction coefficient k for SrCoO3, SrFeO3, LaCoO3 and LaFeO3. | ||
3.4 Thermodynamic properties
To obtain the temperature dependence of the thermodynamic parameters, the phonon spectrum was firstly calculated using a finite displacement method. As shown in Fig. 5, there are no imaginary phonon modes for all of these compounds, indicating their dynamical stability. Since the wave number is proportional to the number of atoms, there are 15, 90 and 60 phonon bands for SrCoO3(SrFeO3), LaCoO3 and LaFeO3 with 5, 30 and 20 atoms per unit cell, respectively. Besides, the phonon PDOS that are presented in Fig. 5 match the phonon dispersion. The flat regions of the phonon-dispersion curves, which correspond to the peaks in the phonon PDOS, indicate the localization of the states. These phonon spectra can be divided into three parts: (1) the low frequency modes of the acoustic phonon branches below about 4 THz are mainly contributed to by La/Sr atoms together with slight contributions from other atoms. (2) The middle frequency range of the optical branches are mixed Fe/Co–O modes (4–12 THz for SrCoO3 and SrFeO3, and 4–16 THz for LaCoO3 and LaFeO3). (3) The high frequency mode optical branches are nearly always contributed by O atoms. This is consistent with the fact that other atoms are much heavier than O atoms, as frequency is inversely proportional to atomic mass. In addition, the maximum values of the vibrational frequency for LaCoO3 and LaFeO3 are larger than those for SrCoO3 and SrFeO3. This suggests a stronger bonding in LaCoO3 and LaFeO3.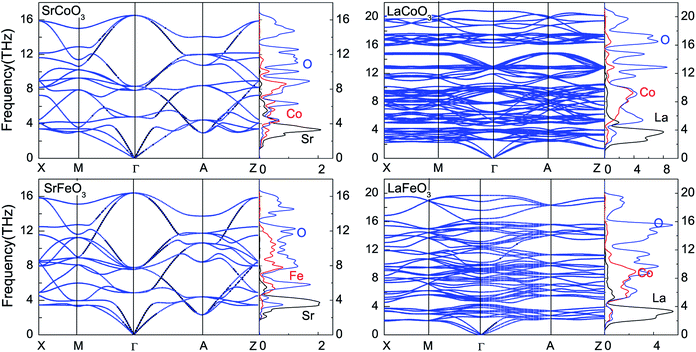 | ||
| Fig. 5 Phonon dispersion curves and partial density of states for SrCoO3, SrFeO3, LaCoO3 and LaFeO3. | ||
The Debye temperature θD is an important parameter for the thermophysical properties of materials. This fundamental parameter is useful for the analysis of the specific heat, thermal conductivity and melting temperature. The Debye temperature is not a strictly determined parameter, but is obtained through well established empirical or semiempirical formulae. Here, we calculated it from the highest frequency of the normal mode vibration (Debye frequency) ωm,
| θD = ħωmn1/3/kB, |
Furthermore, the thermodynamic functions can be obtained by the phonon spectrum, assuming that the lattice vibrational degrees of freedom play a more noticeable role than the electronic degrees of freedom. As shown in Fig. 6, the temperature dependence of the Helmholtz free energy F, entropy S, and constant-volume heat capacity Cv are calculated within the harmonic approximation. With an increase in temperature, the free energy decreases, while both the entropy and heat capacity increase from zero at 0 K, all of which conform to the third law of thermodynamics. Moreover, at low temperatures that are much lower than the Debye temperatures, the constant-volume heat capacity Cv is proportional to temperature T3. The contribution of the lattice heat capacity at low temperatures is mainly from the long wavelength vibration modes of the lattice, which could be approximated by treating the lattice as a continuum. However, at high temperatures, Cv tends to the Dulong–Petit classical limit which is proportional to the number of atoms per unit cell.
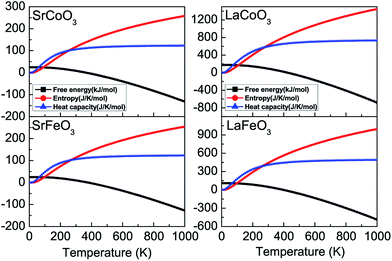 | ||
| Fig. 6 The thermodynamic parameters of free energy, entropy, and constant volume heat capacity for SrCoO3, SrFeO3, LaCoO3 and LaFeO3. | ||
4 Conclusions
In summary, the electronic, optical and thermodynamic properties of ABO3 (A = La,Sr and B = Fe,Co) perovskites are investigated using first-principles calculations. The structural parameters we optimized and the energy gaps we obtained by the GGA+U method are in good agreement with the experimental data. The strong hybridization of the Fe/Co-3d and O-2p orbitals dominates the properties of these oxides, which is a common characteristic for perovskite oxides. Based on the electronic structure, the dielectric function, refractive index and extinction coefficient are obtained and discussed. The static refractive indices of SrCoO3 and SrFeO3 are relatively larger than those of LaCoO3 and LaFeO3. Furthermore, based on the phonon frequencies, we obtained Debye temperatures θD that are comparable to the available data. Finally, by using the calculated phonon dispersion, the thermodynamic properties of the Helmholtz free energy, entropy, and constant-volume heat capacity are obtained within the harmonic approximation, all of which conform to the third law of thermodynamics. Finally, ABO3 perovskites are flexible systems as their properties can be adjusted or enhanced for specific applications by chemical doping at the A or B cation sites. Therefore, the doped (La,Sr)(Fe,Co)O3 compounds will be investigated to improve the performance of the pure parent materials in our further work.Acknowledgements
This work was supported by the National Science Foundation of China under Grant No. 11534012, and U1230202 (NSAF), the special Funds for Major State Basic Research Project of China (973) under Grant No. 2012CB933702 and the Director Grants of CASHIPS. The calculations were partly performed in the Center for Computational Science of CASHIPS, the ScGrid of the Supercomputing Center and the Computer Network Information Center of the Chinese Academy of Sciences, and partly using the Tianhe-2JK computing time award at the Beijing Computational Science Research Center (CSRC).References
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed
.
- A. J. Millis, Nature, 1998, 392, 147–150 CrossRef CAS
.
- T. Arakawa, H. Kurachi and J. Shiokawa, J. Mater. Sci., 1985, 20, 1207–1210 CrossRef CAS
.
- A. A. Bokov and Z.-G. Ye, J. Mater. Sci., 2006, 41, 31–52 CrossRef CAS
.
- A. M. Schultz, T. D. Brown, M. P. Buric, S. Lee, K. Gerdes and P. R. Ohodnicki, Sens. Actuators, B, 2015, 221, 1307–1313 CrossRef CAS
.
- A. M. Schultz, T. D. Brown and P. R. Ohodnicki, J. Phys. Chem. C, 2015, 119, 6211–6220 CAS
.
- Y. Wang, L. Yu, J. Wang, L. Chen, W. Gao, X. Du and L. Biao, Mater. Lett., 2012, 75, 39–41 CrossRef CAS
.
- R. H. Potze, G. A. Sawatzky and M. Abbate, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 11501–11506 CrossRef CAS
.
- M. Abbate, G. Zampieri, J. Okamoto, A. Fujimori, S. Kawasaki and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165120 CrossRef
.
- M. Zhuang, W. Zhang, A. Hu and N. Ming, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 13655–13659 CrossRef CAS
.
- J. Kuneš, V. Křápek, N. Parragh, G. Sangiovanni, A. Toschi and A. V. Kozhevnikov, Phys. Rev. Lett., 2012, 109, 117206 CrossRef PubMed
.
- S. Diodati, L. Nodari, M. M. Natile, U. Russo, E. Tondello, L. Lutterotti and S. Gross, Dalton Trans., 2012, 41, 5517 RSC
.
- T. Takeda, Y. Yamaguchi and H. Watanabe, J. Phys. Soc. Jpn., 1972, 33, 967–969 CrossRef CAS
.
- C. Autret, J. Hejtmánek, K. Knížek, M. Maryško, Z. Jirák, M. Dlouhá and S. Vratislav, J. Phys.: Condens. Matter, 2005, 17, 1601–1616 CrossRef CAS
.
- M. Señarís-Rodríguez and J. Goodenough, J. Solid State Chem., 1995, 116, 224–231 CrossRef
.
- P. G. Radaelli and S.-W. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 094408 CrossRef
.
- K. Asai, A. Yoneda, O. Yokokura, J. M. Tranquada, G. Shirane and K. Kohn, J. Phys. Soc. Jpn., 1998, 67, 290–296 CrossRef CAS
.
- M. W. Haverkort, Z. Hu, J. C. Cezar, T. Burnus, H. Hartmann, M. Reuther, C. Zobel, T. Lorenz, A. Tanaka, N. B. Brookes, H. H. Hsieh, H.-J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2006, 97, 176405 CrossRef CAS PubMed
.
- A. Podlesnyak, S. Streule, J. Mesot, M. Medarde, E. Pomjakushina, K. Conder, A. Tanaka, M. W. Haverkort and D. I. Khomskii, Phys. Rev. Lett., 2006, 97, 247208 CrossRef CAS PubMed
.
- T. Saitoh, T. Mizokawa, A. Fujimori, M. Abbate, Y. Takeda and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 4257–4266 CrossRef CAS
.
- M. A. Korotin, S. Y. Ezhov, I. V. Solovyev, V. I. Anisimov, D. I. Khomskii and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 5309–5316 CrossRef CAS
.
- J. B. Goodenough and P. M. Raccah, J. Appl. Phys., 1965, 36, 1031–1032 CrossRef CAS
.
- P. M. Raccah and J. B. Goodenough, Phys. Rev., 1967, 155, 932–943 CrossRef CAS
.
- G. Thornton, B. Tofield and A. Hewat, J. Solid State Chem., 1986, 61, 301–307 CrossRef CAS
.
- S. M. Selbach, J. R. Tolchard, A. Fossdal and T. Grande, J. Solid State Chem., 2012, 196, 249–254 CrossRef CAS
.
- S. Stølen, F. Grønvold, H. Brinks, T. Atake and H. Mori, J. Chem. Thermodyn., 1998, 30, 365–377 CrossRef
.
- S. Parida, S. Rakshit and Z. Singh, J. Solid State Chem., 2008, 181, 101–121 CrossRef CAS
.
- D. D. Sarma, N. Shanthi, S. R. Barman, N. Hamada, H. Sawada and K. Terakura, Phys. Rev. Lett., 1995, 75, 1126–1129 CrossRef CAS PubMed
.
- A. Laref and S. Jun Luo, J. Phys. Soc. Jpn., 2010, 79, 064702 CrossRef
.
- L. V. Nomerovannaya, A. A. Makhnev, S. V. Streltsov, I. A. Nekrasov, M. A. Korotin, S. V. Shiryaev, G. L. Bychkov, S. N. Barilo and V. I. Anisimov, J. Phys.: Condens. Matter, 2004, 16, 5129–5136 CrossRef CAS
.
- M. D. Scafetta, A. M. Cordi, J. M. Rondinelli and S. J. May, J. Phys.: Condens. Matter, 2014, 26, 505502 CrossRef PubMed
.
- A. Chainani, M. Mathew and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 9976–9983 CrossRef CAS
.
- T. Arima, Y. Tokura and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17006–17009 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef
.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef
.
- I. R. Shein, Phys. Solid State, 2005, 47, 2082 CrossRef CAS
.
- S. Mathi Jaya, R. Jagadish, R. S. Rao and R. Asokamani, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 13274–13279 CrossRef CAS
.
- A. E. Bocquet, A. Fujimori, T. Mizokawa, T. Saitoh, H. Namatame, S. Suga, N. Kimizuka, Y. Takeda and M. Takano, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 1561–1570 CrossRef CAS
.
- M. Abbate, R. Potze, G. A. Sawatzky and A. Fujimori, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7210–7218 CrossRef CAS
.
- Z. Y. Wu, M. Benfatto, M. Pedio, R. Cimino, S. Mobilio, S. R. Barman, K. Maiti and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 2228–2233 CrossRef CAS
.
- D. T. Morelli and G. A. Slack, in High Thermal Conductivity Materials, Springer-Verlag, New York, 2006, pp. 37–68 Search PubMed.
- S. Balamurugan, K. Yamaura, A. B. Karki, D. P. Young, M. Arai and E. Takayama-Muromachi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 172406 CrossRef
.
- H. Rached, D. Rached, M. Rabah, R. Khenata and A. H. Reshak, Phys. B, 2010, 405, 3515–3519 CrossRef CAS
.
- C. He, H. Zheng, J. F. Mitchell, M. L. Foo, R. J. Cava and C. Leighton, Appl. Phys. Lett., 2009, 94, 102514 CrossRef
.
| This journal is © The Royal Society of Chemistry 2017 |