Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Field-driven pattern formation in nematic liquid crystals: mesoscopic simulations of electroconvection
Kuang-Wu Lee * and
Thorsten Pöschel
* and
Thorsten Pöschel
Institute for Multiscale Simulation, Erlangen-Nuremburg University, Erlangen, Germany. E-mail: jeff.lee@fau.de
First published on 31st August 2017
Abstract
As an environment for rich pattern formation, the electroconvection (EC) of nematic liquid crystals (LCs) is studied via fully nonlinear simulations for the first time. Previously, EC was mostly studied by experiments or by linear/weakly nonlinear hydrodynamic theory for its instability criteria. While the negative dielectric LCs are used in most EC analytical and experimental investigations, EC with positive dielectric LCs is limited to experiments only, due to their more complex nonlinear behavior. In this work we take a step beyond the existing weakly nonlinear EC research by using a fully nonlinear particle-based simulation. To investigate the distinct dynamics of positive and negative dielectric LCs, we modified the molecular potential in the LC stochastic rotational model (LC SRD) [Lee et al., J. Chem. Phys., 2015, 142, 164110] to incorporate the dielectric characteristics and the field-particle interaction. As a result, different convection patterns known in the EC experiments were observed in our simulations, for which those patterns appeared orderly, as a function of external field strength. The simulated director and flow fields correspond to each other well, as found in our experiments. For the positive dielectric LC, we discovered a net directional flow accompanying the travelling EC rolls. This numerical model and its hydrodynamic analysis could be used for precise flow control at the micro-scale, such as nematic colloidal transportation in microfluidics.
1 Introduction
Electroconvection1 in nematic liquid crystals has been an interesting topic since its discovery in 1963 by Williams.2 It has attracted a great amount of attention due to its rich pattern formation phenomena and profound potentials in industrial applications. Similar to Rayleigh-Bénard convection (RBC) in simple fluids, EC is a demonstration of hydrodynamic instability resulting from the competition between an external driving force and the internal dissipation force. The scientific interests on EC and RBC are mainly focused on the phase transitions from the homogeneous state to regular and turbulent patterns.From an industrial point of view, EC related instabilities are of fundamental importance because most of the liquid crystal displays (LCDs) are driven by an external electric field. Because the DC electric field degrades the LC molecular structure over time, an AC electric field, ranging from 60–600 Hz, is mostly used for display usage. Over this frequency range, a low driving electric field is enough for EC instability, which is usually accompanied with topological defects that destroy the optical properties of LCDs. On the other hand, a low driving electric field is desirable for low consumption, therefore the search for a stable operational frequency range without a turbulent EC pattern is one of the important topics within the LCD industry.
To improve the energy efficiency in LCD operations further, tunable cholesteric liquid crystals (CLCs) are now within the scope of the next generation of advanced photonic devices.3 One of the questions to answer, in the area of EC patterns in external fields, is the relationship between generated complex defects and helical superstructures. Very recently, promising experimental results have shown that the zigzag defect pattern in CLCs can be controlled by manipulating UV/visible light under certain electric field conditions.4 To fully understand the connection between the applied field and the nonlinear helical superstructures, nonlinear numerical simulation is desired.
Another potential application of EC lies in the guided colloidal transport in LC microfluidics. Sasaki et al.5 created a caterpillar type nematic colloidal chain which could be transported by the EC in the microfluidic channel. This guided colloidal chain was also shown to carry a silicone oil droplet and a glass rod as loaded micro-cargos in the channel. The controlled transport processes are important for drug delivery, lab-on-a-chip applications, and guided self-assembly.
To understand the generation of EC in liquid crystals, a free-charge in field model was proposed as the driving mechanism by Carr and Helfrich.6 Linear perturbation theory was subsequently applied to the EC system to study the onset of the instabilities.7 Beyond the linearly studied EC onset, weakly nonlinear theory considering mean flow effects8 was used to study the evolution from ordered periodic to weakly turbulent patterns. As in many systems that undergo phase transition, it is observed that the generation of EC rolls is closely related to the thermal noise level of the system.9 In their work the system’s intrinsic thermal noise corresponds to the director fluctuation at the EC onsets, indicating that the external electric field feeds energy to the most unstable eigenmode, hence causing the instability growth.
Despite the abundant exciting experimental works and the weakly nonlinear theory for instability analysis, numerical investigations for the full EC development still fall behind. EC is essentially a highly nonlinear phenomenon, therefore a numerical investigation is necessary for an EC evolution study. To analyze this complex reaction-diffusion process, the weakly nonlinear simulations10 were performed by neglecting the higher order perturbation terms in the hydrodynamic equations. This approach was used to study the transition from normal to oblique EC rolls. In addition, the optical properties of the EC patterns in thin cells were studied using the finite-difference-time-domain (FDTD) method,11 for which the reflective and transmitted lights of normal EC rolls are derived from the presumed background director and flow fields.
One of the important topics in EC evolution is the dynamics of topological defects generated by positive and negative types of LC. By simulating the LC rotation on lattices using the Lebwohl–Lasher potential,12 it was found that the applied external electric field can remove certain types of defect charge. Nevertheless, the coupling of the director and flow fields is still neglected in their 2D model, and fully coupled dynamics should be restored to describe the flow dynamics precisely. In conclusion, a fully nonlinear simulation of a self-consistent EC evolution is still needed.
In this work we introduce the particle-based stochastic rotation dynamics (SRD) model to study the nonlinear evolution of EC. Our numerical approach is based on the recently developed LC SRD model by Lee et al.,13 in which they studied the rheology of a nematic LC in Couette flow, and the dynamics of its topological defects. In their work the thermal fluctuation determines the nematic-isotropic phase transition in the NLC, and, similarly, the EC generation discussed here is also a phase transition that is controlled by the thermal fluctuation.9
We modify the molecular potential to couple the LC rotation and the external electric field. Positive and negative types of liquid crystal, such as 5CB and MBBA, are modeled by tuning the dielectric tensor, εa = ε∥ − ε⊥. The EC director-flow patterns are revealed and the polarized reflections are compared accordingly. We address the similarities and differences between the generated patterns when different types of liquid crystal are used.
Although not addressed in the current work, our numerical model can be easily modified to study the recently discovered dual-frequency NLC, which is a mixture of positive and negative dielectric NLCs, and has the industrially desired ability to quickly switch between planar/homeotropic orientations.14 This reported model can be viewed as a proof of concept for the numerical study of the highly nonlinear field-flow coupling dynamics in dual-frequency NLCs.
2 Numerical model
Stochastic rotation dynamics15 (SRD) was used as a basis to construct our numerical model. Standard SRD is a particle-based algorithm that consists of two steps, i.e. the free streaming step for updating the particle positions, and the rotational step to change the particle velocity during particle collisions. For anisotropic fluids such as liquid crystals, one extra degree of freedom is added to the particle orientation, i.e. the particle director,![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i. One must notice that the rotation of particle translation velocity,
i. One must notice that the rotation of particle translation velocity, ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i, is different from the rotation of the particle director,
i, is different from the rotation of the particle director, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i, and their dynamics are controlled by different equations of motion.
i, and their dynamics are controlled by different equations of motion.
On the other hand, a liquid crystal is a material which has strong coupling between the fluid velocity ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) i and the director field
i and the director field ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i, hence a complete LC model should have feedback from each. The validation of a liquid crystal model using SRD was proposed by Lee et al.,13 and, almost simultaneously, an independently developed model was also proposed by Shendruk and Yeomans.16 Several important LC phenomena are successfully observed in their particle-based mesoscopic models, e.g. the first-order nematic-isotropic phase transition, the dynamics of topological defects, and the non-Newtonian shear-banding effect.
i, hence a complete LC model should have feedback from each. The validation of a liquid crystal model using SRD was proposed by Lee et al.,13 and, almost simultaneously, an independently developed model was also proposed by Shendruk and Yeomans.16 Several important LC phenomena are successfully observed in their particle-based mesoscopic models, e.g. the first-order nematic-isotropic phase transition, the dynamics of topological defects, and the non-Newtonian shear-banding effect.
The advantages of a particle-based algorithm over a nematohydrodynamic approach are that the particle model avoids phase-space scanning to find out the initial unstable wave modes, and there is no need to presume non-zero amplitudes for the unstable eigenmodes.
The nematohydrodynamic system we aim to simulate can be described by the simplified Ericksen–Leslie model.17 The governing equations for the cell-wise bulk flow ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) and director
and director ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) are as follows:13,18
are as follows:13,18
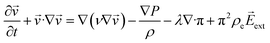 | (1) |
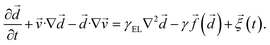 | (2) |
In eqn (1), π = ∇![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) T·∇
T·∇![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) , which is the Ericksen–Leslie stress tensor. The charge density, ρe = ∇(ε
, which is the Ericksen–Leslie stress tensor. The charge density, ρe = ∇(ε![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ), is obtained from Poisson’s equation, where the dielectric tensor is εi,j = ε⊥δi,j + εadidj. In eqn (2), the molecular field f(d→i) = ∂Ui/∂d→i is the vector derivative of the molecular potential. The molecular potential in the presence of the external electric field
), is obtained from Poisson’s equation, where the dielectric tensor is εi,j = ε⊥δi,j + εadidj. In eqn (2), the molecular field f(d→i) = ∂Ui/∂d→i is the vector derivative of the molecular potential. The molecular potential in the presence of the external electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) is a modified Lebwohl–Lasher type,19
is a modified Lebwohl–Lasher type,19
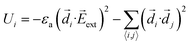 | (3) |
The numerical procedures, similar to those used by Lee et al.,13 are to use particle-based SRD to replace most parts of the Navier–Stokes equation. The linear momentum is further corrected by the angular momentum from the LC rotations, due to particle alignment and the external electric field, which are the last two terms in eqn (1). It is seen in eqn (2) that the modification of the particle directors ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i is based on the molecular field, shown in eqn (3), and the shear-flow felt by the particle. Also, because the mesoscopic timescale is longer than the microscopic molecular equi-partition timescale, thermal noise
i is based on the molecular field, shown in eqn (3), and the shear-flow felt by the particle. Also, because the mesoscopic timescale is longer than the microscopic molecular equi-partition timescale, thermal noise ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) (t) controls the rotational velocity distribution of the particles as well. Therefore the particle-based director rotational rule for SRD particles is:
(t) controls the rotational velocity distribution of the particles as well. Therefore the particle-based director rotational rule for SRD particles is:
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (n + 1) = (n + 1) = ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (n) + [ (n) + [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) (n)·∇ (n)·∇![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) − γf( − γf(![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) )]dt + )]dt + ![[small xi, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1cd.gif) (t)dt. (t)dt.
| (4) |
This is an over-damped Langevin equation in discrete form, for which the equivalent potential is a complicated combination of the molecular field, external electric field and flow gradient field. This director update rule is similar to the direct angular momentum balance used by Shendruk and Yeomans,16 and the angular momentum gain of LC particles is balanced in the Navier–Stokes equation as the last term in eqn (1). The detailed numerical implementation of the model used here can be found in the report by Lee et al.,13 and the improvements considered in this study are the new molecular potential and its resulting momentum balance term in bulk velocity.
Different nematic liquid crystals exhibit different dielectric properties when they are subjected to an external electric field. Positive LCs (ε∥ > ε⊥) are polarized along the long-axis of the molecules, therefore they align parallel to the electric field. On the other hand, negative LCs (ε∥ < ε⊥) are polarized along the short-axis, leading to perpendicular alignment. This effect is clearly seen in the molecular potential Ui. When a positive LC is considered (εa = ε∥ − ε⊥ > 0), the minimum values of potential Ui appear when ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i∥
i∥![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) , and when a negative LC is considered, the minimum values appear when
, and when a negative LC is considered, the minimum values appear when ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i⊥
i⊥![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) .
.
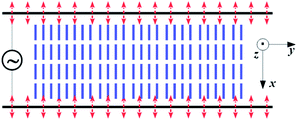
The commonly considered EC environment has two parallel planar anchoring plates that embrace nematic LCs with a small separation, typically of the order of ∼100 μm. An AC electric field is applied between these two plates.
The simulations in this study are prepared with the following parameters: the SRD rotation angle for particle velocity, αSRD, is 120°, and the mass and moment of inertia for SRD particles are mi = 1 and Ii = 27. This mass-inertia ratio represents an elongated molecular shape for nematic liquid crystals. The average number of SRD particles per cell 〈NCi〉 = 70, which avoids an unrealistic high thermal noise. The normalized grid size of ds = 1 and time step of dt = 1 are used, while a 3D simulation domain, (x,y,z) = ([1 8],[1 45],[1 45]), represents a thin slab geometry.
To guarantee a liquid behavior in this particle-based algorithm, SRD super-cell collision20 is used to keep the finite compressibility small. A spatially uniform AC electric field is applied in the cross-plate direction, ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) x(t) = Ex0
x(t) = Ex0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt). The amplitude Ex0 and modulating frequency ω are the primary free parameters for the EC pattern generation. Other LC material parameters are the relaxation constant, γ = 0.04, and the average thermal velocity in each degree of freedom, vth,s = 0.3 ds/dt, where s ∈ (x,y,z, θ) refers to the dimensions.
cos(ωt). The amplitude Ex0 and modulating frequency ω are the primary free parameters for the EC pattern generation. Other LC material parameters are the relaxation constant, γ = 0.04, and the average thermal velocity in each degree of freedom, vth,s = 0.3 ds/dt, where s ∈ (x,y,z, θ) refers to the dimensions.
Surface anchoring, which provides the orientation tendency for LC molecules near the walls, is implemented by assuming stationary ghost LC particles in the walls. The near-wall alignment for LC fluid particles is established via the molecular potential contributed from these wall ghost particles. Two types of anchoring condition are used in this study, i.e. the homeotropic anchoring for positive dielectric LCs and planar anchoring for negative dielectric LCs.
3 Simulation results and discussion
The EC patterns have been mostly studied using a negative type LC such as MBBA. This is due to that fact that the weakly nonlinear theory predicts a positive type LC, such as 5CB, would exhibit more complex nonlinear behavior.21 Positive dielectric LCs have not been extensively studied either analytically or numerically, although they are widely used in the LCD industry.By creating positive and negative types of LC in simulation, we specified the different parallel and perpendicular dielectric constants to generate different orientation tendencies under an electric field. For the positive LC the parallel and perpendicular dielectric constants ε∥ = 9 and ε⊥ = 1 are used such that εa = 9. For the negative LC we used ε∥ = 1 and ε⊥ = 9, and the corresponding dielectric anisotropy εa = 1/9.
The simulation results of these LCs are discussed separately in the following sections.
3.1 Negative LC
Different from the Fréedericksz transition, where the external force drives the LC system away from its equilibrium configuration, EC is generated by an external electric field that tends to maintain the original equilibrium.A typical configuration of EC with a negative dielectric LC is shown in Fig. 1. Because the perpendicular dielectric constant is greater than the parallel one, negative LCs tend to be polarized in the molecular short axis when an external electric field is applied. This implies that the negative LCs tend to align perpendicularly to the applied electric field. This orientation tendency in the electric field is actually along the original equilibrium direction, therefore, intuitively, one would assume the external field has no destabilizing effect on negative dielectric LCs.
However it has been long known that this external field indeed destabilizes the system, and introduces free energy to drive the system away from equilibrium. This contradiction of the stabilization of the system under an electric field can actually be understood by examining the last term in eqn (1), which has a non-zero value if the charge density ρe appears.
This term works as a source term in the Navier–Stokes equation, for which it now becomes a reaction-diffusion type equation. A system with the source term has chaotic behavior when the driving source term surpasses diffusion. In an environment without free charges, such as in pure nematic LCs, the instantaneous charge density is only induced by the thermal distribution of LC directors. These bound charges can also move under the external electric field as free charges.
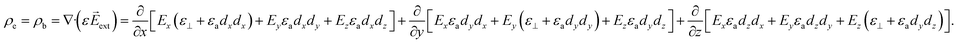 | (5) |
This system of thermal fluctuation always exists in a non-zero temperature environment, hence the spatial derivatives in eqn (5) always have finite values. This effect is preserved naturally in a particle-based approach, due to the coarse graining of particle motions.
Fig. 2 shows the typical EC convection with the negative LC under a DC electric field. Panels a, b and c are the xy projections of the directors, bound charge and flows. It can be seen that the original y-parallel directors are bent, along with the convection flow patterns. The cross-plate DC electric field is along the positive x direction, ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) x, in this simulation. Charge density is plotted in panel b, and it shows perfectly that the positive charge areas (yellow) have upward flow while the negative charge areas (blue) have downward flow. Our simulated flow and director fields are without free charges, and they are characteristically identical to the EC experiments which have always assumed free-charges to be primary drivers in EC (e.g. in the EC for nematic colloid transportation5).
x, in this simulation. Charge density is plotted in panel b, and it shows perfectly that the positive charge areas (yellow) have upward flow while the negative charge areas (blue) have downward flow. Our simulated flow and director fields are without free charges, and they are characteristically identical to the EC experiments which have always assumed free-charges to be primary drivers in EC (e.g. in the EC for nematic colloid transportation5).
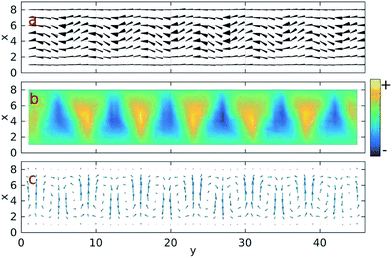 | ||
| Fig. 2 The typical EC with negative dielectric LCs is shown here. Panel a is the x–y projection of the directors, while panel c is the x–y projection of the flows. The middle panel b shows the bound charges seen in the x–y plane, for which they are calculated according to eqn (5). | ||
The EC pattern formation is usually studied in the voltage-frequency phase-space. In experiments it is discovered that, for a fixed AC frequency and increasing electric field, phase transitions can be seen from the transforming polarized reflection, from planar reflection to strip and connected lines.2,22 To see if this tendency exists in our model we used the same system setups and increased the driving electric field.
The EC patterns are seen from the reflection of incident y-polarized light, and the luminosity is calculated by:
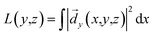 | (6) |
The originally unperturbed LC directors would start to develop regular EC patterns when the driving electric field increases. As the electric field increased further, the regular EC patterns evolved into oblique/connected convection rolls, and this is called a turbulent state.
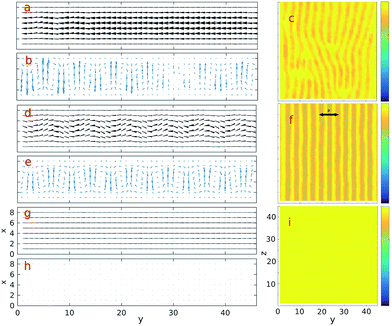
It can be seen in Fig. 3 that the simulated tendency corresponds well with the theoretical prediction.21 The EC simulation results with the negative LC show, in order, the turbulent Williams, stationary Williams and planar phases (from top to bottom) when the field strength increases. The simulation frequency is normalized to the time-step (1/dt), and for the cases shown in Fig. 3, the field frequency is f = 5 × 10−7. The electric fields corresponding to these three regimes are Ex = 150 (turbulent Williams), Ex = 75 (stationary Williams) and Ex = 25 (planar).
In the lower panels (g–i), the system is still in the planar regime with Ex = 25, i.e. the reflection of incident polarized light (panel i) is strong. The LC directors are not bent from equilibrium positions at all, and the flow velocity is only about the same as the thermal fluctuation level, as seen in panel h of Fig. 3. In the planar regime, the flow caused by the external field is small and quickly dissipated by the fluid viscosity.
When the applied electric field reaches the transition value, the collective flows are suddenly generated and they are self-organized into convection roll patterns (as seen in panels d–f of Fig. 3). The LC directors exhibit corresponding bending at the flow driving zones, i.e. the upward bending corresponds to downward driving and vice versa. The patterns of reflected light are periodically in bright–dark stripes (panel f), and the separation of bright–bright stripes (Sbb,– ≃ 3.6 ds) is about half of the channel height, Lx = 7 ds. This result agrees well with previous experiments.5
If the driving electric field goes higher, the fluid viscosity can no longer dissipate the exceeding energy from the driven flows, hence the system evolves from a stationary Williams into a turbulent Williams regime. Localized reflection structures appear dynamically, i.e. the dislocation of striped EC rolls evolves in time. This is seen in panel c of Fig. 3 as a simulation snapshot, and its corresponding LC director (panel a) and flow convection (panel b) are less-organized structures.
To study the full evolution in EC phenomena one should, in principle, take a fully nonlinear approach because the linear/weakly nonlinear assumption, i.e. E = E0 + E′ and E′ ≪ E0, is no longer valid. The most significant signature of the turbulent regime is the non-steady oblique/connected EC rolls.8 The dynamics of those localized structures can only be studied either experimentally or via nonlinear simulations.
It is noted here that, although not shown here, in a much larger electric field, the reflection patterns become patch-like and the flow field is completely randomized.
3.2 Positive LC
In this section the more complicated EC behaviors of a positive LC are investigated by assuming positive dielectric anisotropy. Most of the particle parameters are kept the same as those used for the negative LC, except the dielectric constants for the positive LC are now ε∥ = 9 and ε⊥ = 1, such that εa = 9. Stationary ghost LC particles, orientating perpendicularly to the surface, are assumed in the walls. These ghost particles provide a homeotropic anchoring effect for LC fluid molecules.The EC configuration of the positive dielectric LC is shown in Fig. 4, for which the applied electric field is still along the x direction, which is the same as for the negative dielectric LC, but the boundary anchoring is now homeotropic to the channel surfaces. This initial configuration allows the positive dielectric LCs to orientate perpendicular to the surfaces, i.e. ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) initial∥
initial∥![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) . The external electric field causes charge separation along the long axis of the LC molecules, indicating that the LCs have the tendency to be aligned with the field. This external field seemingly provides a stabilized force for the LC orientations, and the initial configuration is in a stable state at first glance.
. The external electric field causes charge separation along the long axis of the LC molecules, indicating that the LCs have the tendency to be aligned with the field. This external field seemingly provides a stabilized force for the LC orientations, and the initial configuration is in a stable state at first glance.
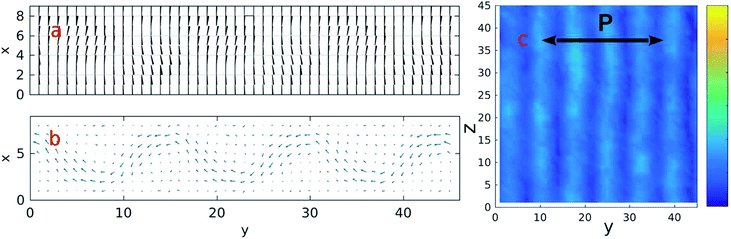
The simulation result is shown in Fig. 5, for which some simulation parameters are used, including the AC field frequency f = 5 × 10−7 and the electric field Ex = 25. The x–y projections of the LC director and the flow fields are shown in panels a and b, and the reflection of the incident polarized light is plotted in the panel c. It is seen in panel a that the simulated LC directors are not exactly the same as those inferred from previous literature (e.g. Fig. 2 in Buka et al.23), i.e. the bending of directors is not symmetric and circular convection cells do not exist.
Surprisingly, our simulation results exhibit a net directional flow, either to the right or to the left of the channel. Not only the net directional flow but also the polarized reflection show a propagating behavior, i.e. the reflection stripes (shown in panel c) move to the right with time when the net flow goes left, and vice versa. This simulation result corresponds to the propagating reflection structures discovered in previous EC experiments.24 In previous work the propagating reflection (which is called a travelling wave, TW) is discussed under different driving electric fields, but the unique directional flow was not discovered or discussed. In our simulation we found that the propagating reflection and the directional flow are counterparts to each other, and they always appear together.
4 Conclusions
The electroconvection is studied via full nonlinear simulations for the first time. We proposed a new particle-based numerical algorithm to study the dynamics of nematic liquid crystals under the external electric field. Nematic liquid crystals with positive and negative dielectric properties are both considered in this model. This particle-based model clearly shows the dependence of energy input and the system response to a pattern formation. Furthermore, those details that are difficult to measure, such as the zonal flows in the convection cells, can also be easily obtained in simulations. We think that this can benefit the experimental setups when the system becomes more complicated, such as adding a colloid suspension in the convection channel.5It is also noted that the EC simulations presented here are without free-charges, i.e. the bound charges due to the flexoelectric effect are the main causes of EC in pure nematic LCs. The bound charges are due to the non-vanishing spatial derivatives of directors, as seen in the charge calculation, and this effect is intrinsic to the particle-based methods that possess thermal fluctuations.
For the commonly used negative dielectric LC, the known planar, stationary and turbulent Williams patterns are observed in order by increasing the driving electric field. They are clearly seen in the reconstructed reflection patterns.
One of the interesting findings in our simulations is, although they look similar at first glance, the EC of positive and negative LCs is actually very different in their dynamics. As demonstrated in the experiments, the EC patterns with a positive LC can be a propagating phenomenon, however our simulation reveals that the corresponding flow field is actually directional.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the helpful discussions with Christian Bahr and Marco Mazza from MPIDS Göttingen, and Takeaki Araki from Kyoto University. We acknowledge funding by Deutsche Forschungsgemeinschaft through the Cluster of Excellence “Engineering of Advanced Materials”, ZISC, FPS and grant PO472-22/1.References
- P. H. Roberts, Q. J. Mech. Appl. Math., 1969, 22, 211–220 CrossRef.
- R. Williams, J. Chem. Phys., 1963, 39, 384–388 CrossRef CAS.
- H. Xie, L. Wang, H.-H. Wang, C. Zou, M. Wang, B.-Y. Wang, Z. Chen, L.-Y. Zhang, X.-G. Zhang, Z. Yang and H. Yang, Liq. Cryst., 2015, 42, 1698 CrossRef CAS.
- Z.-G. Zheng, R. S. Zola, H. K. Bisoyi, L. Wang, Y.-N. Li, T. J. Bunning and Q. Li, Adv. Mater., 2017, 29, 1701903 CrossRef PubMed.
- Y. Sasaki, Y. Takikawa, V. S. R. Jampani, H. Hoshikawa, T. Seto, C. Bahr, S. Herminghaus, Y. Hidaka and H. Orihara, Soft Matter, 2014, 10, 88138820 RSC.
- E. F. Carr, Mol. Cryst. Liq. Cryst., 1969, 7, 253–269 CrossRef CAS; W. Helfrich, J. Chem. Phys., 1969, 51, 4092 CrossRef.
- L. C. G. Orsay, Phys. Rev. Lett., 1970, 25, 1642–1643 CrossRef.
- E. Bodenschatz, W. Zimmermann and L. Kramer, J. Phys., 1988, 49, 1875–1899 CAS.
- I. Rehberg, S. Rasenat, M. de la Torre Juarez, W. Schopf, F. Horner, G. Ahlers and H. R. Brand, Phys. Rev. Lett., 1991, 67, 596–599 CrossRef CAS PubMed.
- A. G. Rossberg, A. Hertrich, L. Kramer and W. Pesch, Phys. Rev. Lett., 1989, 76, 4729–4732 CrossRef PubMed.
- C. Bohley, J. Heuer and R. Stannarius, J. Opt. Soc. Am. A, 2005, 22, 2818–2826 CrossRef PubMed.
- B. F. de Oliveira, P. P. Avelino, F. Moraes and J. C. R. E. Oliveira, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 041707 CrossRef CAS PubMed.
- K.-W. Lee and M. G. Mazza, Soft Matter, 2015, 142, 164110 Search PubMed.
- M. Mrukiewicz, P. Perkowski, W. Piecek, R. Mazur, O. Chojnowska and K. Garbat, J. Appl. Phys., 2015, 118, 173104 CrossRef.
- A. Malevanets and R. Kapral, J. Chem. Phys., 1999, 110, 8605 CrossRef CAS.
- T. N. Shendruk and J. M. Yeomans, Soft Matter, 2015, 11, 5101 RSC.
- F.-H. Lin and C. Liu, Comm. Pure Appl. Math., 1995, 48, 501 CrossRef.
- N. Breindl, G. Schneider and H. Uecker, Proc. Equadiff-11, 2005, pp. 1–10 Search PubMed.
- F.-H. Lin and C. Liu, Phys. Rev. A, 1972, 6, 426 CrossRef.
- T. Ihle, E. Tuzel and D. M. Kroll, Europhys. Lett., 2006, 73, 664670 CrossRef.
- L. Kramer and W. Pesch, Annu. Rev. Fluid Mech., 1995, 27, 515–541 CrossRef.
- A. P. Kapustin and L. S. Larinova, Kristallografiya, 1964, 9, 297 CAS , in Russian.
- A. Buka, B. Dressel, W. Otowski, K. Camara, T. Toth-Katona, L. Kramer, J. Lindau, G. Pelzl and W. Pesch, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051713 CrossRef CAS PubMed.
- V. A. Raghunathan, P. R. Maheswara Murthy and N. V. Madhusudana, Curr. Sci., 1990, 59, 506–509 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |