Deciphering chemical bonding in B_nH_n²⁻ (n = 2–17): flexible multicenter bonding

Abstract

It is well known that closo-borane dianions B_nH_n²⁻ are stable aromatic cages and possess n + 1 valence electron pairs, in accordance with Wade's rules. However, the electronic structures of closo-B_nH_n²⁻ cannot be explained by a Lewis structure because of their electron-deficient character, while recent theoretical and experimental studies reveal that multicenter bonding is a key part in their electronic structures. In this work, flexible multicenter bonding of B_nH_n²⁻ (n = 2–17) is studied using the adaptive natural density partitioning (AdNDP) method in order to get insight into their stability and aromaticity. The large HOMO–LUMO gaps and negative NICS values indicate their close-shell electronic structure. Further chemical bonding analysis shows that all 2n + 2 delocalized valence electrons in closo-B_nH_n²⁻ are involved in various delocalized σ and π multicenter bonding systems on their cage surface, well matched with different symmetric configurations. There are five types of multicenter bonds, including an open 3c–2e BBB bond, closed 3c–2e BBB bond, 4c–2e bond, 8c–2e bond and a fully delocalized bond, which are delocalized on a B₃ broken-line, B₃ triangle, B₄ rhombus, B₈ double-ring and the whole surface of the boron cage, respectively. Our work reveals the flexibility of multicenter bonding in diversified closo-B_nH_n²⁻ clusters, giving new insights into the bonding nature of B_nH_n²⁻.

---

1. Introduction

The chemistry of boron is intriguing due to its electron-deficient character and delocalized bonding pattern. As a result, boron based clusters have rich forms of nanostructures, including quasi-planar, ring, two-dimensional sheet and cage.^1–22 Over the past decade, small boron clusters have been systematically characterized both experimentally and theoretically to exhibit planar or quasi-planar structures in their ground states except for B₁₄, but undergo the 2D-3D transition at B₂₀ for neutral, at B₂₇⁻ for anionic and at B₁₆⁺ for cationic clusters.^5,23–29 The double-ring tubular B₂₀ is confirmed to be stable and aromatic.^30–32 The B₄₀ cage is the first all-boron fullerene composed of hexagons and heptagons, according to the theoretical and experimental observation by photoelectron spectroscopy.³³ In addition, there are also many fascinating sandwich-type complexes, metalloborospherenes, metal-centered boron molecular wheels and drums by doping metallic elements in boron clusters.^25,34–49 Chemical bonding analyses reveal that there is numerous flexible multicenter bonding in the electronic structures of all these clusters.

The polyhedral closo-borane B_nH_n²⁻ clusters have attracted much interest from theoretical and experimental chemists since their synthesis in the early 20th century,^50–58 especially for their bonding patterns. Lipscomb pointed out that the 3c–2e hydrogen bridge bond is the key part in the electronic structure of borane clusters, which was proved by experimental study. In 1971, Wade's rules gave the insight into topologic structures of deltahedral B_nH_n²⁻ clusters. It revealed that there are (n + 1) electron pairs delocalized on their closo cage surface, where n is the number of vertexes.⁵⁹ Mingos extended this principle to electron rich clusters to become popularly known as the Wade–Mingos rules.^60,61 In 1977, King and co-workers investigated the three-dimensional aromaticity in B_nH_n²⁻ using algebraic graph-theoretical methods, providing the theoretical basis for the stability of these clusters.⁶² Whereafter, O'Neill and Wade tried to apply the Kekulé-type structures which using chemical bonding instead of the delocalized structures to closo-borane dianions for suggesting the existence of 3c–2e bonds.^63,64 In 2011, Lentz group obtained crystal structures of B₁₀H₁₀²⁻ and B₁₂H₁₂²⁻, and revealed that both of them have 3c–2e bonds by electron density and atoms-in-molecules (AIM) analysis.⁶⁵

Previous study reveals the structures and stability of closo-borane B_nH_n²⁻ from their topologic structures according to Wade's rules, rather than in the view of chemical bonding. However, the chemical bonding pattern in the series of closo-borane B_nH_n²⁻ has not been studied yet. As multicenter bonding is a popular language in the community of chemistry which is wildly used to interpret the electronic structure, stability and aromaticity of boron clusters, in this paper we try to reveal the nature of electronic structure in borane dianions B_nH_n²⁻ (n = 2–17) series from this way.

2. Computational methods

In this article, the geometrical structures of borane dianions B_nH_n²⁻ (n = 2–17) are optimized using TPSSh functional which has been proved to be reliable in the study of boron clusters.^66–70 The optimization and the calculations of the nucleus-independent chemical shifts (NICS)⁷¹ are performed at the TPSSh/6-311+G* level, the HOMO–LUMO gaps are estimated using time-dependent density-functional theory (TD-DFT) method. NICS value is a popular measurement for aromaticity, where negative value indicates aromaticity, and positive value implies antiaromaticity. The vibrational frequencies are also checked to confirm the stability of structures at the same level of theory. All the DFT calculations are carried out in GAUSSIAN 09 package.⁷² Chemical bonding analysis are performed using the adaptive natural density partitioning (AdNDP) method.⁷³ The AdNDP analysis is an effective tool developed by Boldyrev's group for deciphering the nature of the localized and delocalized bonds in boron clusters.^14,74–76 Since the size of basis sets does not affect much of the AdNDP calculations, the 3-21G basis set is employed. Noncovalent interaction (NCI)⁷⁷ are plotted using Multiwfn⁷⁸ and VMD packages.⁷⁹ The visualization of the AdNDP results are realized using the MOLEKEL 5.4.0.8 program.⁸⁰

3. Results and discussion

3.1 Geometries and stability

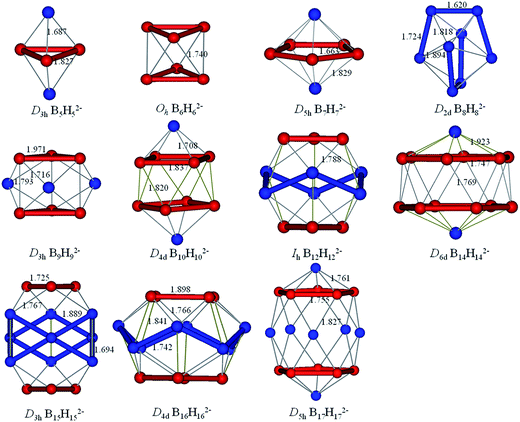
The borane dianions B_nH_n²⁻ (n = 2–17) series are optimized at TPSSh/6-311+G* level. The B_nH_n²⁻ (n = 6–12) and (n = 4, 5, 13–17) have been observed experimentally and investigated theoretically, respectively.^{51–55,81,82} In order to grasp the structural features and assure the integrity in this family, B_nH_n²⁻ with n = 2 and 3 are considered as well. The structures of borane dianions are taken from the previous studies of Lipscomb, Schleyer, Dreuw, and their co-workers.^50,81,82 Fig. 1 plots the geometric structures of B_nH_n²⁻ (n = 2–17). B₂H₂²⁻ and B₃H₃²⁻ are isovalent to C₂H₂ and C₃H₃⁺, as we expected, they possess alike linear and planar structures, respectively. B₄H₄²⁻ is neither planar nor tetrahedral, but somewhere in between, exhibiting a D_2d-symmetric geometry. Borane dianions B_nH_n²⁻ (n = 5–17) start to favor closo-structures with increasing cluster size, including n + 1 electron pairs, in accordance with Wade's rules. The smallest member of closo-borane family that has been synthesized is B₆H₆²⁻, of which calculated bond length is 1.740 Å close to the experimental value (1.700 Å).⁸³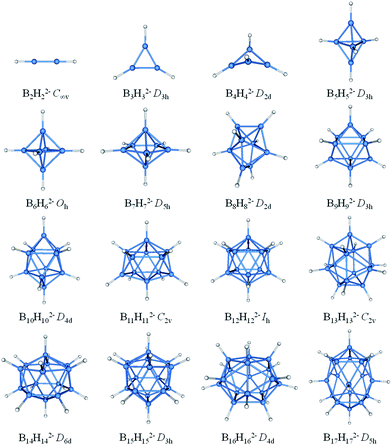

Fig. 1 Optimized geometries for borane dianions B_nH_n²⁻ (n = 2–17) at TPSSH/6-311+G* level of theory. B-blue; H-white.

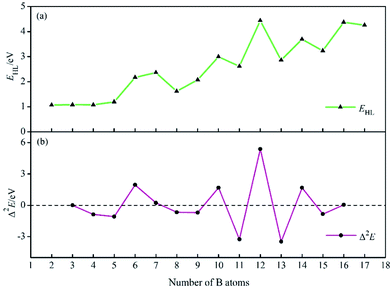
To investigate the stability of B_nH_n²⁻ series, the HOMO–LUMO energy gaps (E_HL) are computed using TPSSH/6-311+G* level. As shown in Fig. 2a, the HOMO–LUMO energy gaps at n ≤ 4 are lower than ones at n ≥ 5, the reason is supposed be that the structures are open-shaped at n ≤ 4, but getting closed at n ≥ 5. Moreover, for B_nH_n²⁻ (n ≥ 5), there are four valleys at n = 8, 11, 13, 15, probably due to the lower symmetry of clusters comparing with other borane dianions. The relative stability of the system is further evaluated with the second-order difference in the total energies (Δ²E), which can be defined as: Δ²E(B_nH_n²⁻) = E(B_n−1H_n−1²⁻) + E(B_n+1H_n+1²⁻) − 2E(B_nH_n²⁻), where E(B_n−1H_n−1²⁻), E(B_n+1H_n+1²⁻), E(B_nH_n²⁻) are total energies of the clusters B_n−1H_n−1², B_n+1H_n+1²⁻, B_nH_n²⁻. The second-order difference in energies is previously applied to study the relative stability of other boron clusters, and in its curves, positive peaks correspond to more relatively stable structures.^84,85 The Δ²E plot in Fig. 2b shows that, four peaks present at B₆H₆²⁻, B₁₀H₁₀²⁻, B₁₂H₁₂²⁻, B₁₄H₁₄²⁻, suggesting their higher relative stability than their neighbours. In addition, it can be found that, each positive Δ²E value in Fig. 2b can correspond to a peak in Fig. 2a, the highest Δ²E and E_HL value is found for B₁₂H₁₂²⁻, indicating the highest one in the series of dianions considered.

Fig. 2 HOMO–LUMO energy gaps E_HL (a) and the second-order differences in energy Δ²E (b) of B_nH_n²⁻ (n = 2–17).

3.2 Chemical bonding patterns

The theoretical study in 1963, Lipscomb's topological model involving styx numbers and rules inferred that closo-B_nH_n²⁻ had (n − 2) 3c–2e BBB bonds and three 2c–2e BB bonds, which was somewhat limited in applicability.^50,86 Until today, the bonding nature of closo-B_nH_n²⁻ is still one of the many intrigued mysteries in chemistry because of their complicated structure and electron deficiency. Apart from theoretical calculations of geometries, energies and aromaticity for closo-borane, no attempt to characterize chemical bonding in this family by means of AdNDP method has been carried out. Herein, chemical bonding analysis by AdNDP gives a more straightforward evidence for the multicenter bonding in B_nH_n²⁻ (n = 2–17). The AdNDP method is wildly applied for closed-shell species recovering both the classical Lewis bonding concepts (lone-pairs and 2c–2e bonds) and the delocalized nc–2e bonds.

As shown in Fig. 3, B–B bond lengths in B₂H₂²⁻ is 1.507 Å somewhat longer than a typical B≡B bond, while the B–B distance in B₃H₃²⁻ is 1.634 Å between single B–B and double B=B bonds. In contrast with the previously reported C₂H₂ and C₃H₃⁺ both geometries and bonds are similar for B₂H₂²⁻ and B₃H₃²⁻, respectively.⁸⁷ Then, we succeed in finding all expected multicenter bonds in these two clusters. For B₂H₂²⁻, there are two 2c–2e σ-BH bonds and three 2c–2e BB bonds (B≡B triple bonds, including one σ and two π bonds) with occupy number (ON) 1.99|e|, 2.00|e|, respectively. In B₃H₃²⁻, there are three 2c–2e σ-BH bonds, three 2c–2e σ-BB bonds and one delocalized 3c–2e π-BBB bond (ON = 2.00|e|, 1.95|e| and 2.00|e|, respectively). Similarly, B₄H₄²⁻ has 10 valence electrons, featuring four 2c–2e σ-BH bonds, four 2c–2e σ-BB bonds and one 4c–2e delocalized over four boron atoms π-bond. Thus, bonding systems in boron framework of B₃H₃²⁻ and B₄H₄²⁻ are π-aromatic (2 electrons on one delocalized π-bond). B₅H₅²⁻ is the least stable member in closo-B_nH_n²⁻ and has never been synthesized. It has a three-membered ring with two caps in D_3h symmetry, the equatorial bonds are 1.827 Å and the axial bonds are 1.687 Å. Besides five 2c–2e σ-BH bonds, AdNDP analysis gives two bonding patters of the remained electrons of B₅H₅²⁻. Pattern I includes three 3c–2e boron bridge σ bonds in the vertical direction and three delocalized 4c–2e σ bonds. Note that the open 3c–2e σ-BBB bond is formed by two apical B atoms and one of equatorial B atoms, while the apical B atom provides half of electron and the equatorial B atom provides one electron, respectively, such boron bridge bond was only observed previously in neutral borane (such as B₁₀H₁₄).⁵⁰ Pattern II includes six 3c–2e σ-BBB bonds on six triangles with ON = 1.90|e| which is smaller than the open one. Thus, we think pattern I is more reasonable.

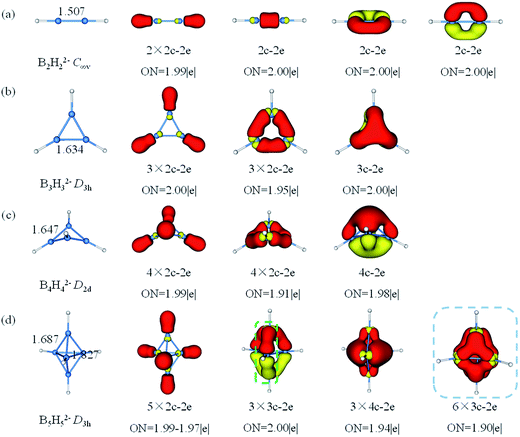Fig. 3 Structures and AdNDP localized natural bonding orbitals of borane dianions. (a) B₂H₂²⁻ (b) B₃H₃²⁻ (c) B₄H₄²⁻ (d) B₅H₅²⁻. B-blue; H-white.

The results of AdNDP analysis of B_nH_n²⁻ (n = 6–8) are plotted in Fig. 4. B₆H₆²⁻ is octahedral resonance structure, two bonding patterns are given in consideration of resonance effect. Pattern I includes six 2c–2e σ-BH bonds, six 3c–2e σ-BBB bonds and one delocalized 6c–2e σ bond, which is selected one of three-fold axis as main axis on account of the resonance effect. From pattern II, these 6c–2e orbitals can be clearly viewed as super S, P_x,y,z and D_xy,yz,xz orbitals. According to the spherical Jellium model,⁸⁸ 18-electron is the most stable magic number (S²P⁶D¹⁰). The five D orbitals split into two sets in the octahedral field, and energy level of the double-degenerate orbital (D_z² and D_x²−y²) increase due to the repulsion of BH bonds. Thus, 14-electron becomes stable magic number. For D_5h B₇H₇²⁻, the equatorial bonds are 1.663 Å indeed smaller than the axial bonds (1.829 Å), which is prone to form 4c–2e bond. The σ-bonding framework includes seven 2c–2e σ-BH bonds and five delocalized 4c–2e σ bonds, the π-bonding framework consists of three delocalized 7c–2e π bonds. This type of π-bonding framework of B₇H₇²⁻ is analogous to that of benzene. The bonding in B₈H₈²⁻ can be explained by the formation of eight 2c–2e σ-BH bonds, four 3c–2e σ bonds, four 4c–2e σ bonds and one delocalized 8c–2e π bonds.

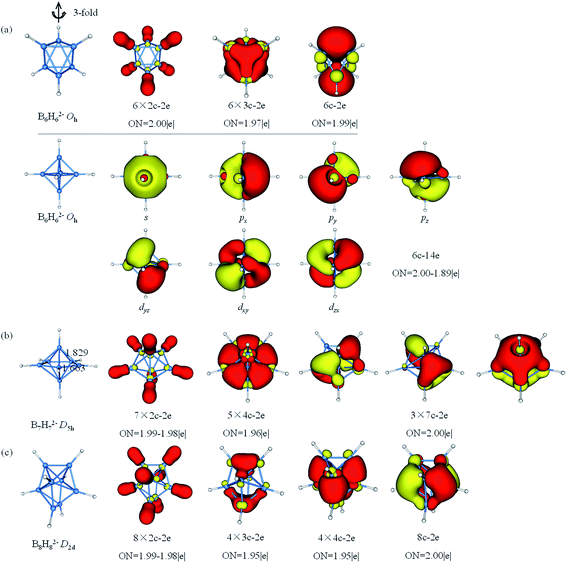Fig. 4 Structures and AdNDP localized natural bonding orbitals of borane dianions. (a) B₆H₆²⁻ (b) B₇H₇²⁻ (c) B₈H₈²⁻. B-blue; H-white.

The AdNDP analysis of B_nH_n²⁻ (n = 9–11) are shown in Fig. 5. The B₉H₉²⁻ has a D_3h symmetry which can be divided into three layers (each layer has three B atoms). The AdNDP results reveal that there are 2c–2e σ-BH bonds, six 3c–2e σ bonds and four delocalized 9c–2e bonds. The six 3c–2e σ-BBB bonds are formed by six triangular lattices of middle layer B atoms bonding with top and bottom B₃ triangles. The four 9c–2e delocalized bonds can be classified into two sets including three 9c–2e delocalized π bonds and one 9c–2e delocalized σ bond, giving rise to double aromaticity (the delocalized π-system has 6 electrons following the (4n + 2) rule for π-aromaticity and similarly for the delocalized σ-system). B₁₀H₁₀²⁻ is square anti-prism geometry with two caps in D_4d symmetry. Three different distances of two B atoms are given in Fig. 5b, the bond lengths of two equatorial B atoms in (1.837 Å) or between (1.820 Å) two four-membered rings are clearly longer than the B–B distance (1.708 Å) between apical and equatorial B atoms. Thus, we guess that there are multicenter bonds in B₈ “double-ring”. The AdNDP analysis reveals ten 2c–2e σ-BH bonds, eight 3c–2e σ-BBB bonds and three delocalized 8c–2e σ bonds, leading to σ-aromaticity. There are 46 valence electrons altogether in B₁₁H₁₁²⁻ with C_2v symmetry. The results of the AdNDP analysis include eleven 2c–2e σ-BH bonds and twelve 3c–2e σ-BBB bonds with occupation numbers ranging from 1.77–1.92|e|.

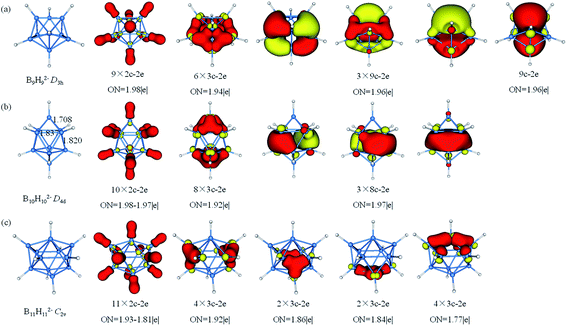Fig. 5 Structures and AdNDP localized natural bonding orbitals of borane dianions. (a) B₉H₉²⁻ (b) B₁₀H₁₀²⁻ (c) B₁₁H₁₁²⁻. B-blue; H-white.

The AdNDP analysis of B_nH_n²⁻ (n = 12–14) are displayed in Fig. 6. The icosahedral B₁₂H₁₂²⁻ cluster is the most stable molecule among polyhedral boranes observed experimentally up to now.^52,89,90 All of B atoms in I_h B₁₂H₁₂²⁻ are equivalent, therefore, it can be treated for AdNDP analysis in similar way as B₆H₆²⁻. Pattern I includes twelve 2c–2e σ-BH bonds, six 3c–2e σ-BBB bonds, six 4c–2e σ bonds and one delocalized 12c–2e bond. From pattern II, these orbitals are fulfilled with 26 valence electrons (S²P⁶D¹⁰F⁸), the B₁₂H₁₂²⁻ possesses thirteen 12c–2e bonds and forms the closed-shell spherical structure. Similarly, seven F orbitals split into two sets in an icosahedral field, and only the lower quadruple-degenerate orbitals are filled. Both B₁₃H₁₃²⁻ and B₁₁H₁₁²⁻ are in lowest symmetry and have a relatively simple bonding pattern in this family. The B₁₃H₁₃²⁻ dianion has 54 valence electrons that form thirteen 2c–2e σ-BH bonds and fourteen delocalized 3c–2e σ-BBB bonds distributing on the left and right, top and bottom, front and back, in an overall symmetry of C_2v. B₁₄H₁₄²⁻ is composed of two six-membered rings and two caps with D_6d symmetry. In contrast to the bond lengths in B₁₀H₁₀²⁻, B₁₄H₁₄²⁻ tends to bond between two six-membered rings. B₁₄H₁₄²⁻ possesses fourteen 2c–2e σ-BH bonds, twelve 3c–2e σ-BBB bonds on twelve B₃ triangles forming a “double-ring”, and three delocalized 14c–2e delocalized σ bonds, making the contribution to the σ-aromaticity of B₁₄H₁₄²⁻.

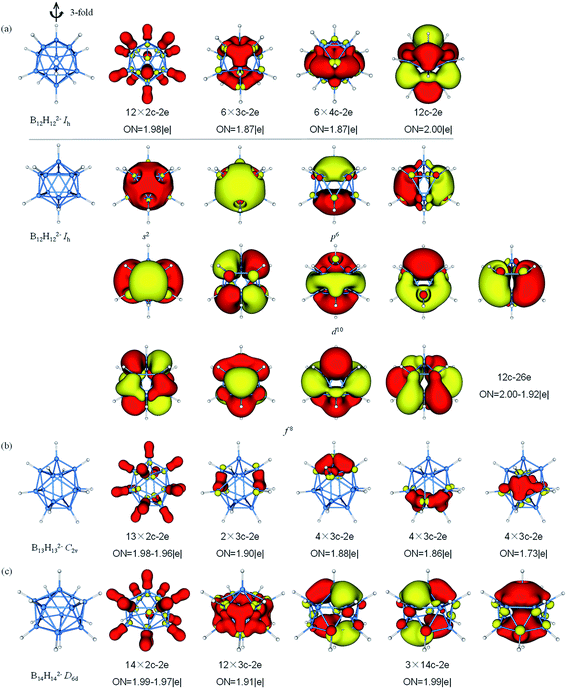Fig. 6 Structures and AdNDP localized natural bonding orbitals of borane dianions. (a) B₁₂H₁₂²⁻ (b) B₁₃H₁₃²⁻ (c) B₁₄H₁₄²⁻. B-blue; H-white.

The fifteen B atoms of D_5h B₁₅H₁₅²⁻ can be classified into five three-membered rings of which can be available for bonding. There are 62 valence electrons in B₁₅H₁₅²⁻, AdNDP analysis (Fig. 7) yields fifteen 2c–2e σ-BH bonds involving all atoms, six 3c–2e σ-BBB bonds which are shared by six B₃ triangles, three delocalized 4c–2e σ bonds around the middle of cage, six delocalized 4c–2e σ bonds covering on surface and one delocalized 15c–2e bond. The D_4d B₁₆H₁₆²⁻ features a similar bonding pattern of B₁₂H₁₂²⁻, with sixteen 2c–2e σ-BH bonds, eight 3c–2e σ-BBB bonds, eight delocalized 4c–2e σ bonds (are in a cycle just like a lantern) and one delocalized 16c–2e bond. B₁₇H₁₇²⁻ is regard as “a hot candidate” for synthesis due to its high stability, aromaticity and symmetry through the theoretical study.⁸¹ The 70 valence electrons in B₁₇H₁₇²⁻ can be divided into three sets. The first set consists of localized bonding elements, seventeen 2c–2e σ-BH bonds, while the other two sets are composed of delocalized bonding elements, fifteen 4c–2e σ bonds (on the top, around the waist and at the bottom) and three 17c–2e delocalized bonds. The delocalized bonding can be viewed as three concentric σ-systems and one π-system, satisfying the (4n + 2) rule for aromaticity, the similar delocalized bonding has been investigated in planar B₁₃⁺ which has two concentric σ-systems and one π-system.⁹¹

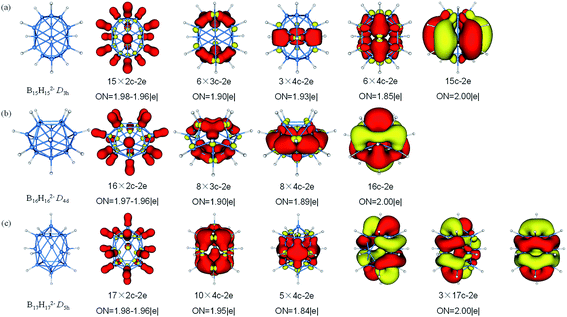Fig. 7 Structures and AdNDP localized natural bonding orbitals of borane dianions. (a) B₁₅H₁₅²⁻ (b) B₁₆H₁₆²⁻ (c) B₁₇H₁₇²⁻. B-blue; H-white.

3.3 Aromaticity

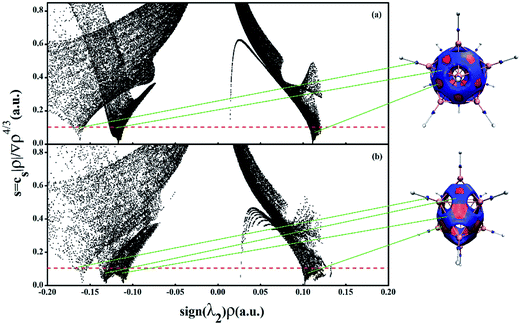
From all above, it is believed that borane dianions with cage structure are highly stable from their relative energies. The stability and aromaticity can also be analyzed with the aid of a noncovalent interaction (NCI) method. The NCI index is based on the electron density (ρ) and the reduced density gradient (RDG, s = 1/[2(3π²)^1/3]|∇ρ|/ρ^4/3), which can indicate the presence of noncovalent interactions with low-s low-ρ and covalent bonds with low-s high-ρ. The second ingredient of the NCI index adopts the second density Hessian eigenvalue (λ₂) to distinguish between bonding interactions (λ₂ < 0) and non-bonding interactions (λ₂ > 0). We believe that the NCI characteristic peak with disparate values of borane cage depends on their bonding patterns and all delocalized valence electrons distribute on the cage surface.

Fig. 8 plots the reduced density gradient (s) versus electron density (ρ) multiplied by the sign of λ₂ and the low-gradient (s = 0.10) NCI isosurfaces of the cage structure B₁₂H₁₂²⁻ and B₁₀H₁₀²⁻. As is illustrated in Fig. 8a, the high density, low-gradient spikes lie at about sign (λ₂) ρ = −0.160 and −0.126 a.u. for B₁₂H₁₂²⁻, which represent strong covalent attractions. The more negative spike is clearly associated to the B–H covalent bonds which can be seen from NCI isosurfaces in the right part of Fig. 8, whereas the other strong attractive spike is the strong covalent interaction between boron atoms, indicating high stability and σ delocalization of B₁₂H₁₂²⁻ cage. Similarly, there are one attractive spike (−0.160 a.u.) and the other two attractive spike (−0.136 and −0.108 a.u.) associated to the B–H covalent bonds and strong covalent interaction between boron atoms for B₁₀H₁₀²⁻, which correspond to the blue regions of isosurfaces at the top (or bottom) and in the middle, respectively. Moreover, for B₁₂H₁₂²⁻ and B₁₀H₁₀²⁻, there are positive spikes at sign (λ₂) ρ = 0.119 and 0.103 a.u., respectively, which represent steric interactions among the boron atoms with the red regions of the isosurfaces. The results in Fig. 8 reveal that the spikes of B–H covalent interactions lie at about sign (λ₂) ρ = −0.160, and the rest of negative spikes with more intensive dots are because all the skeletal bonding electrons (in Wade's rules) of B₁₀H₁₀²⁻ and B₁₂H₁₂²⁻ are delocalized on the cage surface causing high stability. In addition, the number of NCI characteristic peak with negative values of B₁₀H₁₀²⁻ is one more than that of B₁₂H₁₂²⁻, which is due to the two different kinds of boron atoms in the former one, whereas the boron atoms of B₁₂H₁₂²⁻ are equivalent.

Fig. 8 Plots of the reduced density gradient versus the electron density multiplied by the sign of the second Hessian eigenvalue sign (λ₂) (left) and NCI isosurfaces using a blue-green-red color scale at s = 0.10 for B₁₂H₁₂²⁻ (a) and B₁₀H₁₀²⁻ (b), respectively.

In 2016, Poater and coworkers applied Hückel (4n + 2) rule and Wade's rules in closo-B_nH_n²⁻ to establish a connection between three-dimensional aromatic closo boron hydride clusters and planar aromatic annulenes.⁹² Herein, NCI is a direct evidence to identify the aromaticity of clusters, and the aromatic characteristic of B_nH_n²⁻ can obtain from their NICS value and electronic structures. We calculate the NICS values of above dianions except B₂H₂²⁻ out of consideration for its line structure. As shown in Fig. 9, the negative NICS values suggest that all structures are aromatic. It should be noted that the tendency is accordant with E_HL gaps and NICS values (one wanes and the other one waxes), which indicates their close-shell electronic structures. For B₃H₃²⁻ and B₄H₄²⁻, both of them have two π electrons obeying (4n + 2) Hückel rule with π-aromaticity. B_nH_n²⁻ with n = 5–17 possess large negative NICS values from −17.91 to −29.13 ppm as a comparison with that of benzene of −11.92 ppm. B₅H₅²⁻ is a watershed of structure and property in this system, which includes two categories of six delocalized σ electrons causing double σ-aromaticity in vertical and vertical direction, respectively. The O_h B₆H₆²⁻ and I_h B₁₂H₁₂²⁻ have two delocalized σ electrons along their five and ten 3-fold axis of symmetry as a consequence of resonance, respectively, showing large negative NICS values and E_HL gaps, which display high stability and strong aromaticity. The D_5h B₇H₇²⁻ has ten σ and six π delocalized electrons leading to (σ + π) aromaticity. B₈H₈²⁻ is less stable with lower E_HL gap and smaller negative NICS value in the lower D_2d symmetry, the reason is probably that, there are two π and sixteen σ delocalized electrons, rendering π-aromaticity and σ-antiaromatic in B₈H₈²⁻, according to the (4n + 2) rule for aromaticity and 4n rule for antiaromaticity, respectively, but finally the former is dominated and counteract the latter. Likewise, B₉H₉²⁻ and B₁₀H₁₀²⁻ are (σ + π) aromaticity and σ-aromaticity with 6π_delo–2σ_delo (six π delocalized and two σ delocalized) and 2σ_delo electrons, respectively. Both B₁₁H₁₁²⁻ and B₁₃H₁₃²⁻ have lower E_HL gaps and smaller negative NICS values than their neighbors, which perhaps on account of their lower symmetry, but are aromatic with close-shell electronic structures. The aromaticity of B₁₄H₁₄²⁻ derives from its six delocalized σ electrons. The delocalized electrons of B₁₅H₁₅²⁻ can be segmented into six parts, which include 5 × 6σ_delo electrons from top to bottom and 2σ_delo electrons around whole structure, according to Hückel rule. The result of B₁₆H₁₆²⁻ is similar to that of B₈H₈²⁻, but allowing higher aromaticity with higher symmetry. B₁₇H₁₇²⁻ also has high σ-aromaticity with four types of delocalized electrons (3 × 10σ_delo and 6σ_delo).

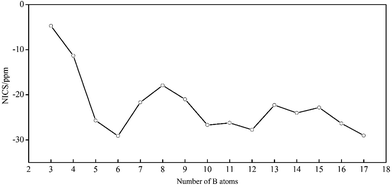Fig. 9 Plot of Nucleus-Independent Chemical Shifts (NICS) for borane dianions B_nH_n²⁻ (n = 3–17) (in ppm).

3.4 Flexibility of multicenter bonding

According to the bonding patterns of closo-B_nH_n²⁻, their available topologic structures are exhibited in different lines and colors. As depicted in Fig. 10, there are different types of delocalized multicenter bonds, including open 3c–2e bond, close 3c–2e bond, 4c–2e bond, 8c–2e bond and fully delocalized bond, which corresponds to B₃ broken-line, B₃ triangle, B₄ rhombus, B₈ double-ring and the whole surface of boron cage in closo-B_nH_n²⁻, respectively. The location of multicenter bond is related to the relative sizes of multi-membered rings and caps of clusters. In B₁₀H₁₀²⁻, the 3c–2e bonds distribute on B₃ triangles of two caps at the top and bottom but of two multi-membered rings for B₁₄H₁₄²⁻. Moreover, the bonding pattern of closo-B_nH_n²⁻ are diversified both with their symmetry and with different B–B bond lengths. In B₈H₈²⁻, B₁₂H₁₂²⁻ and B₁₆H₁₆²⁻, there are four, six and eight 3c–2e bonds on B₃ triangles, respectively, lying on the top and bottom, while the 4c–2e bonds distribute on B₄ rhombuses with longer B–B bond length. Thus, the flexibility of multicenter bonding can adapt well to all borane cages with different configurations. However, it is difficult to grasp clear generalizations of closo-borane clusters which is part of the attraction for study and distinct from carbon clusters.

Fig. 10 Topology structures for closo-borane dianions, B_nH_n²⁻ (n = 5–10, 12, 14–17).

4. Conclusion

The closo-borane dianion B_nH_n²⁻ (n = 6–12) are proven to be stable and aromatic through the joint experimental and theoretical study. However, the bonding nature of closo-B_nH_n²⁻ is still one of the mysteries in borane chemistry. In present work, we investigate the evolution rules of structures in B_nH_n²⁻ (n = 2–17) and decipher their stability and aromaticity in the view of chemical bonding. B_nH_n²⁻ with n = 2 and 3 are liner and planar structures, respectively, but undergo a transition between 2D and 3D structures at B₄H₄²⁻. B_nH_n²⁻ (n = 5–17) are inclined cage structures which have been explained by Wade's rules. There are (4n + 2) valence electrons in B_nH_n²⁻, the bonding in B₂H₂²⁻ and B₃H₃²⁻ are very similar to that in C₂H₂ and C₃H₃⁺, respectively. Moreover, in closo-B_nH_n²⁻, 2n valence electrons are involved in localized σ-BH bonds, the remaining (2n + 2) valence electrons are evenly delocalized in either multicenter σ/π bonds, forming an effective σ and π delocalized system causing high stability, and σ/π aromaticity. The bonding in B₅H₅²⁻ exits the 3c–2e open boron bridge bonds which was only observed in neutral borane preciously. For the high symmetry B₆H₆²⁻ and B₁₂H₁₂²⁻, one type of bonding patterns is given in a particular way in which any 3-fold axis has two delocalized valence electrons due to their resonance, while the other type of bonding patterns are listed in terms of superatom, both leading to high stability and aromaticity. In addition, we extend the concentric aromaticity of planar B₁₃⁺ to 3D B₁₅H₁₅²⁻ and B₁₇H₁₇²⁻ to explain their aromaticity. Moreover, it is found that the tendency of E_HL gaps in closo-B_nH_n²⁻ are in accordance with their NICS values which indicates their close-shell electronic structures. In short, the highlight of our work is deciphering chemical bonding in closo-B_nH_n²⁻, and the flexibility of multicenter bonding can adapt well to all borane cages with different configurations, making their stable and aromatic.

Acknowledgements

This work is financed by the National Natural Science Foundation of China (21573001), and by the Foundation of Distinguished Young Scientists of Anhui Province. The calculations were carried out at the High-Performance Computing Center of Anhui University.

References

1. R. Kawai and J. H. Weare, J. Chem. Phys., 1991, 95, 1151–1159.
2. I. Boustani, Chem. Phys. Lett., 1995, 240, 135–140.
3. A. Ricca and C. W. Bauschlicher Jr, Chem. Phys., 1996, 208, 233–242.
4. I. Boustani, Phys. Rev. B, 1997, 55, 426–438.
5. E. Oger, N. R. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
6. J. J. Zhao, L. Wang, F. Y. Li and Z. F. Chen, J. Phys. Chem. A, 2010, 114, 9969–9972.
7. R. X. He and X. C. Zeng, Chem. Commun., 2015, 51, 3185–3188.
8. T. B. Tai and M. T. Nguyen, Phys. Chem. Chem. Phys., 2015, 17, 13672–13679.
9. T. B. Tai, L. V. Duong, H. T. Pham, D. T. Mai and M. T. Nguyen, Chem. Commun., 2014, 50, 1558–1560.
10. C. B. Kah, M. Yu, P. Tandy, C. S. Jayanthi and S. Y. Wu, Nanotechnology, 2015, 26, 405701.
11. X. Y. Zhao, Q. Chen, H. R. Li, Y. W. Mu, H. G. Lu and S. D. Li, Phys. Chem. Chem. Phys., 2017, 19, 10998–11003.
12. Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754–760.
13. Q. Chen, S. Y. Zhang, H. Bai, W. J. Tian, T. Gao, H. R. Li, C. Q. Miao, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Angew. Chem., 2015, 127, 8278–8282.
14. Y. J. Wang, Y. F. Zhao, W. L. Li, T. Jian, Q. Chen, X. R. You, T. Ou, X. Y. Zhao, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 064307.
15. T. B. Tai and M. T. Nguyen, Nanoscale, 2015, 7, 3316–3317.
16. Z. A. Piazza, H. S. Hu, W. L. Li, Y. F. Zhao, J. Li and L. S. Wang, Nat. Commun., 2014, 5, 3113.
17. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563.
18. W. L. Li, Y. F. Zhao, H. S. Hu, J. Li and L. S. Wang, Angew. Chem., Int. Ed., 2014, 53, 5540–5545.
19. W. L. Li, Q. Chen, W. J. Tian, H. Bai, Y. F. Zhao, H. S. Hu, J. Li, H. J. Zhai, S. D. Li and L. S. Wang, J. Am. Chem. Soc., 2014, 136, 12257–12260.
20. A. P. Sergeeva, Z. A. Piazza, C. Romanescu, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 18065–18073.
21. A. P. Sergeeva, D. Y. Zubarev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2008, 130, 7244–7246.
22. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206.
23. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
24. L. J. Cheng, J. Chem. Phys., 2012, 136, 104301.
25. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
26. D. Z. Li, H. Bai, T. Ou, Q. Chen, H. J. Zhai and S. D. Li, J. Chem. Phys., 2015, 142, 014302.
27. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
28. B. Kiran, G. G. Kumar, M. T. Nguyen, A. K. Kandalam and P. Jena, Inorg. Chem., 2009, 48, 9965–9967.
29. T. B. Tai, D. J. Grant, M. T. Nguyen and D. A. Dixon, J. Phys. Chem. A, 2010, 114, 994–1007.
30. B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, PNAS, 2005, 102, 961–964.
31. T. B. Tai, A. Ceulemans and M. T. Nguyen, Chem.–Eur. J., 2012, 18, 4510–4512.
32. M. P. Johansson, J. Phys. Chem. C, 2009, 113, 524–530.
33. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
34. S. D. Li, J. C. Guo, C. Q. Miao and G. M. Ren, Angew. Chem., Int. Ed., 2005, 44, 2158–2161.
35. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2011, 50, 9334–9337.
36. B. P. Fokwa and M. Hermus, Angew. Chem., Int. Ed., 2012, 51, 1702–1705.
37. Y. Yuan and L. J. Cheng, J. Chem. Phys., 2013, 138, 024301.
38. L. F. Li, C. Xu, B. K. Jin and L. J. Cheng, Dalton Trans., 2014, 43, 11739–11744.
39. M. Mbarki, R. St Touzani and B. P. Fokwa, Angew. Chem., Int. Ed., 2014, 53, 13174–13177.
40. B. Mondal, B. Mondal, K. Pal, B. Varghese and S. Ghosh, Chem. Commun., 2015, 51, 3828–3831.
41. H. J. Zhai, A. N. Alexandrova, K. A. Birch, A. I. Boldyrev and L. S. Wang, Angew. Chem., Int. Ed., 2003, 42, 6004–6008.
42. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2013, 138, 134315.
43. S. Li, Z. Zhang, Z. Long and S. Qin, Sci. Rep., 2017, 7, 40081.
44. Q. Chen, H. R. Li, C. Q. Miao, Y. J. Wang, H. G. Lu, Y. W. Mu, G. M. Ren, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2016, 18, 11610–11615.
45. H. Bai, Q. Chen, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 941–945.
46. Q. Chen, T. Gao, W. J. Tian, H. Bai, S. Y. Zhang, H. R. Li, C. Q. Miao, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2015, 17, 19690–19694.
47. W. L. Li, T. Jian, X. Chen, H. R. Li, T. T. Chen, X. M. Luo, S. D. Li, J. Li and L. S. Wang, Chem. Commun., 2017, 53, 1587–1590.
48. W. L. Li, C. Romanescu, T. R. Galeev, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Am. Chem. Soc., 2012, 134, 165–168.
49. W. J. Tian, Q. Chen, X. X. Tian, Y. W. Mu, H. G. Lu and S. D. Li, Sci. Rep., 2016, 6, 8.
50. W. N. Lipscomb, Boron Hydrides, ed. W. A. Benjamin, New York, 1963.
51. M. F. Hawthorne and A. R. Pitochelli, J. Am. Chem. Soc., 1959, 81, 5519.
52. A. R. Pitochelli and F. M. Hawthorne, J. Am. Chem. Soc., 1960, 82, 3228–3229.
53. J. L. Boone, J. Am. Chem. Soc., 1964, 86, 5036.
54. F. Klanberg and E. Muetterties, Inorg. Chem., 1966, 5, 1955–1960.
55. F. Klanberg, D. R. Eaton, L. J. Guggenberger and E. L. Muetterties, Inorg. Chem., 1967, 6, 1271–1281.
56. F. Schluter and E. Bernhardt, Inorg. Chem., 2011, 50, 2580–2589.
57. N. Zint, A. Dreuw and L. S. Cederbaum, J. Am. Chem. Soc., 2002, 124, 4910–4917.
58. L. D. Brown and W. N. Lipscomb, Inorg. Chem., 1977, 16, 2989–2996.
59. K. Wade, J. Chem. Soc. D, 1971, 549, 792–793.
60. D. M. P. Mingos, Nature (London), Phys. Sci., 1972, 236, 99–102.
61. D. M. P. Mingos, Acc. Chem. Res., 1984, 17, 311–319.
62. R. B. King and D. H. Rouvray, J. Am. Chem. Soc., 1977, 9, 7834–7840.
63. M. E. O'Neill and K. Wade, THEOCHEM, 1983, 103, 259–268.
64. M. E. O'Neill and K. Wade, Polyhedron, 1984, 3, 199–212.
65. S. Mebs, R. Kalinowski, S. Grabowsky, D. Forster, R. Kickbusch, E. Justus, W. Morgenroth, C. Paulmann, P. Luger, D. Gabel and D. Lentz, Inorg. Chem., 2011, 50, 90–103.
66. Y. Yuan and L. J. Cheng, J. Chem. Phys., 2012, 137, 044308.
67. L. F. Li, C. Xu and L. J. Cheng, Comput. Theor. Chem., 2013, 1021, 144–148.
68. L. F. Li, C. Xu, B. K. Jin and L. J. Cheng, J. Chem. Phys., 2013, 139, 174310.
69. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
70. C. Xu, L. J. Cheng and J. L. Yang, J. Chem. Phys., 2014, 141, 124301.
71. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
72. M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision B. 01, Gaussian Inc., Wallingford, CT, 2010.
73. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
74. W. L. Li, T. Jian, X. Chen, T. T. Chen, G. V. Lopez, J. Li and L. S. Wang, Angew. Chem., 2016, 128, 7484–7489.
75. E. Osorio, J. K. Olson, W. Tiznado and A. I. Boldyrev, Chem.–Eur. J., 2012, 18, 9677–9681.
76. A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, J. Chem. Phys., 2011, 134, 224304.
77. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
78. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
79. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
80. U. Varetto, Molekel 5.4.0.8, Swiss National Supercomputing Centre, Manno, Switzerland.
81. P. v. R. Schleyer, K. Najafian and A. M. Mebel, Inorg. Chem., 1998, 37, 6765–6772.
82. A. Dreuw, N. Zint and L. S. Cederbaum, J. Am. Chem. Soc., 2002, 124, 10903–10910.
83. R. Schaeffer, Q. Johnson and G. S. Smith, Inorg. Chem., 1965, 4, 917–918.
84. J. F. Jia, L. J. Ma, J. F. Wang and H. S. Wu, J. Mol. Model., 2013, 19, 3255–3261.
85. D. T. Mai, L. V. Duong, T. B. Tai and M. T. Nguyen, J. Phys. Chem. A, 2016, 120, 3623–3633.
86. A. J. Welch, Chem. Commun., 2013, 49, 3615–3616.
87. D. Y. Zubarev and A. I. Boldyrev, J. Org. Chem., 2008, 73, 9251–9258.
88. B. K. Teo, J. Cluster Sci., 2014, 25, 883–891.
89. W. S. Hopkins, P. J. Carr, D. Huang, K. P. Bishop, M. Burt, T. B. McMahon, V. Steinmetz and E. Fillion, J. Phys. Chem. A, 2015, 119, 8469–8475.
90. G. S. Nevill and C. J. Tymczak, Nanoscale Res. Lett., 2012, 7, 236.
91. W. Huang, A. P. Sergeeva, H. J. Zhai, B. B. Averkiev, L. S. Wang and A. I. Boldyrev, Nat. Chem., 2010, 2, 202–206.
92. J. Poater, M. Sola, C. Vinas and F. Teixidor, Chem.–Eur. J., 2016, 22, 7437–7443.

---