Dimension-dependent band alignment and excitonic effects in graphitic carbon nitride: a many-body perturbation and time-dependent density functional theory study

Abstract

First-principles many-body theory and time-dependent density functional theory were used to study the dimension effects on the band alignment and optical properties of s-triazine and graphitic C₃N₄. The inclusion of quasiparticle corrections is very important to describe the quantum confinement and the enhancement of the electron–electron (e–e) interaction. The calculated quasiparticle gaps range from 4.0 eV (monolayer) to 3.21 eV (tetralayer). The position of the valence band maxima is found to be almost constant, whereas the conduction band minima show a strong quantum confinement effect with a variation of ∼0.7 eV respective to the bulk structure. The calculated frequency-dependent imaginary part of the dielectric function using the Bethe–Salpeter equation shows prominent excitonic effects, where there is a strong redistribution of the spectral weight to lower photon energies in the ultraviolet frequencies where the major part of the absorption occurs. On the other hand, a less intense excitonic absorption in the visible region is due to light polarization perpendicular to the surface plane. In contrast, time-dependent density functional theory also shows a redistribution of the spectral weight in the ultraviolet but it fails to describe the excitonic features in the visible region.

---

1 Introduction

The energy consumption projections¹ around the world have motivated, in the most recent decades, widespread research to find materials and technologies with capabilities to use solar energy as a principal source of power, in order to generate energy that is environmentally friendly and at the same time is produced at a low-cost. Since the pioneering work of Fujishima and Honda,² who demonstrated the capability of a TiO₂ anode and a Pt cathode under ultraviolet irradiation with an external bias to oxidize water, many interesting approaches have been studied to synthesize liquid fuels from carbon dioxide (CO₂). Nowadays some of those mechanisms have become promising alternatives to replace fossil fuels. In this context, many researchers around the world have devoted enormous efforts to find better candidates to be implemented as photocatalytic materials to reduce CO₂ to liquid fuels and, consequently, alleviate the global warming impact by generating clean energy. In spite of the huge efforts, a good candidate with the desirable properties: efficient absorption of visible light, high chemical stability under typical operating conditions, band edge positions that straddle the water or CO₂ redox potentials, and large hole diffusion length that is abundant in the earth’s crust^3,4 has not been found yet.

An active and stable photocatalyst is able to use light to drive reactions. The incoming photon energy can be used to stimulate certain desired reactions, otherwise, they are energetically unfavourable. Among the extensively studied photocatalytic materials, carbon nitrides (C₃N₄) have attracted attention due to their prominent properties such as high thermal stability, insolubility in most solvents, high surface area, easy processability, excellent stability, and low cost.^5–8 Additionally, C₃N₄ has been successfully implemented in hydrogen production,⁹ photocatalytic water splitting,¹⁰ and oxidation reactions,¹¹ among others. C₃N₄ possesses different allotropes,^12,13 the graphitic structures being the most stable under ambient conditions.^13,14 Among the graphitic structures, the 2D hexagonal pattern based structures (g-h-C₃N₄) are the most studied. G-h-triazine is made up from the polymerization and subsequent condensation of C₃H₃N₃ rings (triazine), into a graphitic solid that consists of C₃N₃ rings connected by a N bridge, and g-h-heptazine is built up from tri-s-triazine (C₆H₃N₆) ring units connected by planar amino groups. Different density functional theory studies have shown that the most stable coplanar structure at zero pressure is g-h-heptazine.^8,14,15 Experimentally many different techniques can be used to synthesize the graphitic carbon nitrides, and some investigations have found many physical and chemical factors that affect the performance of the photocatalytic activity in those graphitic compounds.^6,16–19 Up to today, a complete condensation of g-h-C₃N₄ with an ideal stoichiometric ratio of 0.75 has not been possible to obtain, and a small amount of hydrogen (≃2%) is always found.^5,20

In recent years, density functional theory calculations have been employed to study mainly the electronic and optical properties of the pristine g-h-C₃N₄, with different exchange–correlation functionals, and including or excluding van der Waals dispersive forces.^8,14,15,21 Theoretical studies have been focused on enhancing the electronic and photocatalytic properties of g-h-C₃N₄ by doping with different atoms.^22–25 However, recombination effects could be unfavourable for the photocatalytic performance in this material. Other interesting studies have incorporated quasiparticle corrections (G₀W₀) to accurately calculate the band gap,⁸ and others to solve the more computationally expensive Bethe–Salpeter equation for monolayer structures of g-h-triazine and g-h-heptazine.²⁶

A detailed knowledge of optical properties is always desirable to guide the photocatalytic applications. A comprehensive description of the optical properties is therefore of the utmost importance to clarify the role of the Coulomb interaction between electrons and holes, commonly called excitonic effects, which could modify the absorption properties. Additionally, the effect of quantum confinement on the optical properties of g-h-C₃N₄ is not totally understood, and it is well-known that the dimensionality strongly modifies the band alignment and the excitonic properties. In this paper, we applied state-of-the-art many-body Green’s function theory and Time-Dependent Density Functional Theory (TD-DFT) to investigate the quantum confinement and dimensionality effects on band gaps, band alignments and optical properties of g-h-triazine. We have chosen g-h-triazine due to its surface formation energy being higher in energy than that of g-h-heptazine, indicating that it would be easier to exfoliate g-h-heptazine than g-h-triazine. Additionally, its surfaces are almost coplanar making it easier to study the absorption process.¹⁵

2 Method of calculation

The slab models were constructed from the optimized bulk structure (for details see ref. 15) along the [001] crystallographic direction. We allowed all the ionic positions to relax without any symmetry restrictions to see any possible corrugation effects. The total energies, stress tensor and ionic forces were calculated via density functional theory using the projector augmented wave method,^27,28 as has been implemented in the VASP code.^28,29 The Román-Pérez and Soler³⁰ algorithm and the van der Waals density functional (vdW-DF) implementation by Klimeš et al.³¹ (OptB88) were used to take into account dispersive forces. Hard PAW potentials with the valence atomic configuration 2s²2p² for C and 2s²2p³ for N were used to relax the surfaces with a cut-off energy of 910 eV. All structural parameters, lattice constants, and atomic positions for each calculated system have been optimized by simultaneously minimizing all atomic forces and stress tensor components via the conjugate gradient method. Brillouin-zone integration was performed on a Monkhorst–Pack 6 × 6 × 1 k-mesh with a Gaussian broadening of 0.01 eV for full relaxation, and ionic forces were converged to 0.1 meV Å⁻¹ and the slab cohesive energy was converged to 5 meV with respect to the vacuum thickness of the periodically separated repeated slabs and the number of layers. For the calculation of the total energies a Γ-centred 6 × 6 × 1 k-mesh was used in conjunction with the tetrahedron method including Blöchl corrections.³²

The quasiparticle energies were calculated by a nonself-consistent GW approximation (G₀W₀),³³ where the Green function G₀ and the screened Coulomb W₀ are calculated using the OptB88 Kohn–Sham eigenvalues and eigenfunctions of the ground state structures. We kept the same input parameters as above, however, we used PAW potentials optimized specifically to yield accurate high-energy scattering properties up to 10 Ry above the vacuum level. This was achieved by placing one projector in the valence band and an additional projector typically 5–8 Ry above the vacuum level.

Then, we calculated the imaginary part of the dielectric function including local field effects by means of TDDFT with Bootstrap (BO) kernel³⁴ and the Bethe–Salpeter equation (BSE) beyond the Tamm–Dankoff approximation using the full-potential augmented-plane wave method with local orbitals.³⁵ The muffin-tin radii of C and N are set to R_MT = 1.225 a.u. The parameter R_MT|G + k|_max setting the number of plane waves was converged to 7. The irreducible wedge of the Brillouin zone was sampled with a uniformly spaced k-point grid of 12 × 12 × 9 and 6 × 6 × 4 for the RBO and BSE calculations, respectively. We used 128 empty bands for RBO, whereas the BSE Hamiltonian was set with 10 valence and 16 conduction states. Finally, the energy dispersion relations were adjusted by a scissor correction of the conduction bands to follow the QP energies. For consistency, the scissor corrections were done using the G₀W₀ band gap at the Γ-point.

3 Results and discussion

3.1 Electronic properties

In previous work in ref. 15, we calculated the band structure and band alignments incorporating quasiparticle corrections of bulk g-h-triazine and g-h-heptazine. In that work, we showed the vital importance of including van der Waals dispersive forces, in order to give an appropriate physical description of the surface properties of this two-dimensional material. From the structurally optimized parameters used in ref. 15, we have built different surfaces varying the number of layers. Fig. 1 shows the calculated band gaps as a function of the number of layers using standard density functional theory (OptB88) and quasiparticle (QP) corrections on top of the OptB88 exchange–correlation functional (OptB88+G₀W₀). The calculated quasiparticle OptB88+G₀W₀ (OptB88) gaps range from 4.0 (1.56) eV for the monolayer to 3.21 (1.47) eV for the tetralayer. The large QP corrections (from 2.44 eV for the monolayer to 1.74 eV for the tetralayer) can be explained by the role of quantum confinement. This quantum effect plays an important role in those low-dimensional systems, and additionally the enhancement of the e–e interaction due to the less effective screening increases the QP corrections as the number of layers decrease.³⁶ All the calculated band gaps decrease monotonically towards the expected bulk band gap, being almost linear in the case of OptB88. This behaviour in OptB88 indicates the poor physical contribution to the quantum and quasiparticle effects. The difference in band gaps for the monolayer and the bulk g-h-triazine with OptB88 is only 0.09 eV, indicating the importance of including the QP corrections to describe the quantum confinement and enhancement of the e–e interaction. The monolayer band gap agrees well with a previous result in ref. 26, where the used starting point for the G₀W₀ calculation was the LDA eigenvalues and eigenfunctions. Recently, it has become well-known that the starting point of G₀W₀ may affect the results,³⁷ and so we attribute the discrepancy in the monolayer band gap to the different starting points in the G₀W₀ calculation.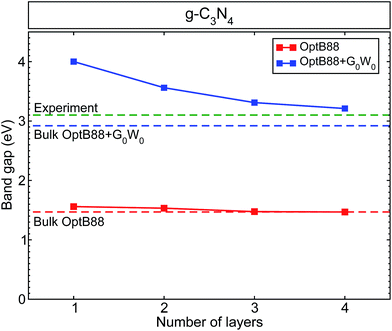

Fig. 1 The calculated band gap for graphitic-like C₃N₄ as a function of the number of layers. We have included as a reference the calculated band gap for bulk g-h-triazine with OptB88 (red dashed line), OptB88+G₀W₀ (blue dashed line), and the experimental value⁴⁰ (green dashed line).

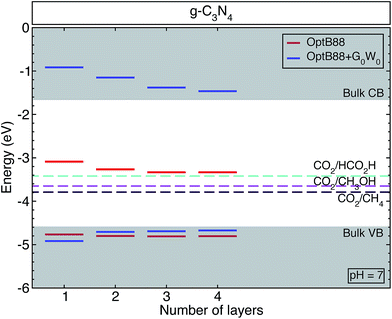
All the surfaces with both approximations (OptB88 and OptB88+G₀W₀) present a direct band gap at the Γ-point, where the top of the valence band and bottom of the conduction band are doubly degenerated. Similar to the bulk structure, the top of the valence band is mainly built up by N 3p_x,y-states with a small contribution from the C 2p_x,y-states and N 2s-states, whereas the bottom of the conduction band is built up by the hybridization of C 2p_z-states and N 3p_z-states (see Fig. S1, in the ESI†). An important factor in determining the photocatalytic activity of a material is the position of the band edges. To calculate accurately the band alignment in this system, we have used the slab model implemented in ref. 38. Thermodynamically, a redox reaction is favourable if the redox free energy lies within the band edges of the material. Fig. 2 shows the schematic representation of the calculated band edges as a function of the number of layers, with some selected important redox energies (at pH = 7) to produce fuels like methane, methanol, and formic acid using CO₂ as a reactant. The QP corrections with respect to OptB88 in the valence band maxima are rather small, whereas the important corrections in the positions of the conduction band minima show a strong enhancement of the e–e interaction. The variation of the QP values in those positions from the monolayer to the bulk is ∼0.7 eV. This enhancement of the e–e interaction is due principally to the fact that most of the conduction band minima are built from p_z orbitals, which extend into the vacuum region, and particularly in the monolayer the screening effects in those orbitals are rather small, indicating an intensification of the e–e interaction and causing the augmentation of the QP values. In contrast, in the in-plane bonds which are built mainly of p_x,y-states, the screening effects are determinant, and therefore the corrections in the QP values are small.

Fig. 2 The calculated band edges for graphitic-like C₃N₄ as a function of the number of layers. The gray shaded areas show the valence and conduction bands for bulk g-h-triazine calculated with OptB88+G₀W₀. We have also added, for comparison, the measured reduction reactions producing methane CH₄, methanol CH₃OH, and formic acid HCO₂H at pH = 7.

For a semiconductor to be implemented as a photocatalyst, the VBM (CBM) has to be more negative (positive) than the reduction (oxidation) potential. This requirement ensures that the reaction is favourable without a bias voltage. The free energies of some possible pathways to reduce CO₂ are located inside the band edges of the studied surfaces and bulk structure, indicating that g-h-triazine could be implemented as a photocatalytic material to reduce CO₂. However, the QP corrections move towards too high positive values for the CBM in those structures, thus for a better efficiency g-h-triazine must be functionalized to obtain a better performance of this material.

3.2 Optical properties

In Fig. 3, we present the average of the imaginary part of the dielectric function for the building block of g-h-triazine, commonly known as s-triazine (C₃H₃N₃) (left), and for the monolayer of g-h-triazine (right). The inclusion of the electron–hole (e–h) interaction generates important modifications in the dielectric function, where strongly bound exciton states appear below the onset of the IPA spectra. From the figure we can observe two contrasting effects, the influence of the quasiparticle corrections opening the band gap and the excitons causing a redshift in the absorption onset. In the left panel, the IPA onset starts around 6.6 eV with two other well-defined peaks around 8.8 eV and 9.4 eV. These main peaks describe the transition between the s-states to the p-states. The ALDA and BSE results are similar to the IPA, where the important differences are the spectral weight redistribution and the oscillator strength. The former has the same three peaks with a tiny redshift, with a considerable increment (decrease) in the first (other two) peak(s). In the latter the first (second) peak is moved towards higher (lower) energies (closer to the first), and the third peak presents a prominent shoulder around 8.2 eV. The right side of Fig. 3 shows the monolayer dielectric function of g-h-triazine. There is clear evidence of the fact that the e–h pair is poorly described by the ALDA kernel, which does not improve the results in the IPA. The main difference is in the spectral weight and in an energy enhancement with respect to the IPA peak.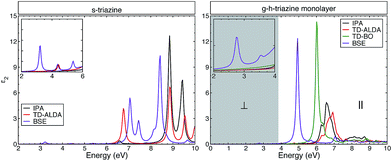

Fig. 3 The calculated average of the imaginary part of the dielectric function for s-triazine and a monolayer of g-h-triazine by independent particle approximation (IPA), TD-ALDA,⁴¹ TD-BO³⁴ and BSE. The grey shaded area highlights the energies where the monolayer shows a significant response to perpendicular light polarization and it does not present any response to parallel light polarization. A Lorentzian function with FWHM = 0.1 eV was used to broaden the calculated spectra.

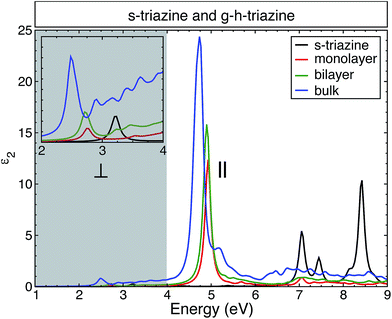
On the other hand, TD-BO and BSE present a strong exciton peak located in the ultraviolet region at 6.0 eV and 4.9 eV respectively. Both are redshifted with respect to the onset in the IPA (or ALDA) spectra, as one would expect. There are two other well-defined excitonic peaks located in the visible region at 2.75 eV and in the ultraviolet region at 3.6 eV. Those excitonic peaks are described only by the BSE and are absent from the TD-BO. The inset (see also the inset in the left panel) of this figure highlights the perpendicular light polarization of the monolayer, indicating a significant response to this polarization and that these peaks come from this component of the dielectric function. In this energy range, there is no response in the monolayer to the parallel light polarization. Those peaks are generated due to the strong excitonic effect and the less efficient screening (which commands the e–h interaction) in the monolayer of g-h-triazine. Additionally those peaks are not properly described by the other methods. Such excitonic peaks could make g-h-triazine surfaces exhibit some absorption of light in the visible region, and increase the photocatalytic activity of this material. Due to the failure of the TD-DFT exchange–correlation functionals used, we shall only use the BSE results for the remainder of the discussion.

A previous BSE study²⁶ was performed for the monolayer and bulk g-h-triazine. It was concluded that the monolayer surface does not respond for the light polarization perpendicular to the surface, in contradiction with the BSE results obtained here. As it was shown above, the optical response of s-triazine reveals an excitonic resonance in the near ultraviolet region (see Fig. 3), and because of the dimensionality changes of the system it becomes more prominent and situated in the visible region for the g-h-triazine monolayer. Finally, this feature is revealed by perpendicular light polarization on the monolayer. Additionally, the calculation for the bulk was done with too large an interlayer distance (4.05 Å), in comparison to the ideal value for these graphitic compounds (3.27 Å).^20,39 This huge interlayer distance modifies the electronic structure and, therefore, the optical properties of the bulk structure.

Fig. 4 shows the changes in the average of the imaginary part of the dielectric function for s-triazine and the g-h-triazine monolayer, bilayer, and bulk using BSE. In this figure, we can appreciate the changes in the excitonic peaks as we increase the dimensionality of the system. Increasing the number of layers generates a redshift in the excitonic peaks and an appreciable oscillator strength increment. The main absorption peaks in the middle of the ultraviolet region are located at 4.9 eV, 4.8 eV and 4.7 eV for the monolayer, bilayer and bulk, respectively. These peaks are generated by the response of the system to the parallel light polarization. In the inset, we observe an excitonic peak located at 3.2 eV in the near ultraviolet due to the s-triazine molecule. After increasing the dimensionality and dehydrogenating the surfaces, the excitonic peak is redshifted to the visible region relative to the s-triazine peak, and it is moved to 2.8 eV, 2.7 eV, and 2.5 eV for the monolayer, bilayer and bulk of g-h-triazine, respectively. These peaks are generated by the response of the surfaces to perpendicular light polarization. The role of the van der Waals interaction is apparent in this two-dimensional material, where this dispersive force does not generate an important screening effect, and then this weaker screening leads to an important excitonic effect in the bulk structure. The low dimensional structures are characterized by narrower peaks below the band gap, as in the bulk structure. The excitonic peaks in the visible spectrum are characterized by a small oscillator strength, and explain the poor absorption of g-h-C₃N₄ in the visible region. In order to quantify the absorption as the dimensionality changes in g-h-triazine, the average absorption coefficient for the monolayer, bilayer, and bulk is shown in Fig. 5 using BSE. It is noted that a redshift occurs in the absorption as the number of layers is increased. The excitonic absorption starts to be appreciable around 2.7 eV, 2.6 eV, and 2.2 eV for the monolayer, bilayer, and bulk g-h-triazine, respectively. Particularly in the case of the bulk structure, the absorption starts around 2.2 eV (α ∼ 0.8 × 10⁵), and then for energies around 2.8 eV it becomes almost constant (α ∼ 0.5 × 10⁵) until 4.5 eV, where it grows considerably to reach its maximum at 4.8 eV in the ultraviolet region. The quantum yield of g-h-C₃N₄ as a photocatalytic material in water splitting is reported to be around 0.1% at λ = 420–460 nm, even with the assistance of Pt,¹⁰ therefore those peaks located in the visible region are shown in Fig. 5 and their respective low absorption values explain the capability of g-h-C₃N₄, and particularly g-h-triazine, as a photocatalytic material to activate oxidative H₂O/O₂ and reductive H⁺/H₂ reactions for water splitting under visible irradiation, and also demonstrate its low efficiency.

Fig. 4 The calculated average of the imaginary part of the dielectric function for s-triazine and the g-h-triazine monolayer, bilayer and bulk using BSE. The grey shaded area highlights the energies where the extended structures show a significant response to perpendicular light polarization and they do not present any response to parallel light polarization. A Lorentzian function with FWHM = 0.1 eV was used to broaden the calculated spectra.

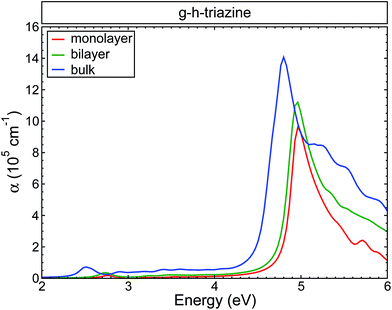Fig. 5 The calculated absorption coefficient for the g-h-triazine monolayer, bilayer and bulk using BSE. A Lorentzian function with FWHM = 0.1 eV was used to broaden the data.

4 Conclusions

In summary, we have studied the dimension effects on the band alignments and optical properties of s-triazine and graphitic C₃N₄ based on DFT, TD-DFT, the GW approximation, and the Bethe–Salpeter equation also taking into account van der Waals dispersive forces. In order to properly describe the quantum confinement and the enhancement of the electron–electron interaction, and consequently the less effective screening, quasiparticle corrections have to be included in all the calculations of g-h-C₃N₄. It is precisely the less effective screening that is responsible for the strong quantum confinement effect in the conduction band minima with a variation of ∼0.7 eV from the monolayer to the bulk structure, whereas the valence band maxima are found to be almost constant. The optical properties show a strong redistribution of the spectral weight to lower photon energies, the presence of excitonic peaks in the visible region is described only with the BSE equation, and is totally absent with TD-ALDA, TD-BO. The excitonic absorption in the visible region is due to light polarization perpendicular to the surface plane. Quantum confinement (dimensionality) effects are not the best route to improve the performance of g-h-C₃N₄ as a photocatalytic material in the visible region.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Universidad de San Buenaventura-Medellín (project code M4829) and by the Vatenskapsrådet (VR), Swedish Energy Agency, and STandUP for energy. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center at Linköping University and the Instituto Tecnológico Metropolitano ITM. J. M. O. G. would like to thank CODI – Vicerrectoría de Investigación – Universidad de Antioquia (Estrategia de Sostenibilidad 2016–2017).

References

1. N. S. Lewis and D. G. Nocera, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 15729–15735.
2. A. Fujishima and K. Honda, Nature, 1972, 238, 37–38.
3. C. Bohn, A. Agrawal, E. Walter, M. Vaudin, A. Herzing, P. Haney, A. Talin and V. Szalai, J. Phys. Chem. C, 2012, 116, 15290–15296.
4. Y. Ping, D. Rocca and G. Galli, Chem. Soc. Rev., 2013, 42, 2437.
5. X. Wang, S. Blechert and M. Antonietti, ACS Catal., 2012, 2, 1596–1606.
6. S. Cao, J. Low, J. Yu and M. Jaroniec, Adv. Mater., 2015, 27, 2150–2176.
7. T. Sano, S. Tsutsui, K. Koike, T. Hirakawa, Y. Teramoto, N. Negishi and K. Takeuchi, J. Mater. Chem. A, 2013, 1, 6489–6496.
8. Y. Xu and S.-P. Gao, Int. J. Hydrogen Energy, 2012, 37, 11072–11080.
9. Y. Wang, J. Yao, H. Li and D. Su, J. Am. Chem. Soc., 2011, 133, 2362–2365.
10. X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2008, 8, 76–80.
11. C. E. Chan Thaw, A. Villa, G. M. Veith, K. Kailasam, L. A. Adamczyk, R. R. Unocic, L. Prati and A. Thomas, Chem.–Asian J., 2012, 7, 387–393.
12. A. Y. Liu and M. L. Cohen, Science, 1989, 245, 841–842.
13. D. Teter and R. Hemley, Science, 1996, 271, 53–55.
14. J. Gracia and P. Kroll, J. Mater. Chem., 2009, 19, 3013–3019.
15. J. M. Osorio-Guillén, W. F. Espinosa-García and C. M. Araujo, J. Chem. Phys., 2015, 143, 094705.
16. I. Papailias, T. Giannakopoulou, N. Todorova, D. Demotikali, T. Vaimakis and C. Trapalis, Appl. Surf. Sci., 2015, 358, 278–286.
17. J. Lin, Z. Pan and X. Wang, ACS Sustainable Chem. Eng., 2014, 2, 353–358.
18. B. Lotsch and W. Schnick, Chem.–Eur. J., 2007, 13, 4956–4968.
19. S. Lyth, Y. Nabae, S. Moriya, S. Kuroki, M.-A. Kakimoto, J.-I. Ozaki and S. Miyata, J. Phys. Chem. C, 2009, 113, 20148–20151.
20. A. Thomas, A. Fischer, F. Goettmann, M. Antonietti, J.-O. Müller, R. Schlögl and J. M. Carlsson, J. Mater. Chem., 2008, 18, 4893–4908.
21. J. Cui, S. Liang, X. Wang and J.-M. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 23613–23618.
22. J. Liu, J. Alloys Compd., 2016, 672, 271–276.
23. Q. Guo, Y. Zhang, J. Qiu and G. Dong, J. Mater. Chem. C, 2016, 4, 6839–6847.
24. K. Ding, L. Wen, M. Huang, Y. Zhang, Y. Lu and Z. Chen, Phys. Chem. Chem. Phys., 2016, 18, 19217–19226.
25. X. Ma, Y. Lv, J. Xu, Y. Liu, R. Zhang and Y. Zhu, J. Phys. Chem. C, 2012, 116, 23485–23493.
26. W. Wei and T. Jacob, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085202.
27. P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
30. G. Román-Pérez and J. Soler, Phys. Rev. Lett., 2009, 103, 096102.
31. J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
32. P. Blöchl, O. Jepsen and O. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
33. M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 035101.
34. S. Sharma, J. K. Dewhurst, A. Sanna and E. Gross, Phys. Rev. Lett., 2011 DOI:10.1103/PhysRevLett.107.186401.
35. K. Dewhurst, S. Sharma, L. Nordström, F. Cricchio, F. Bultmark and H. Gross, http://elk.sourceforge.net.
36. L. Yang, M. L. Cohen and S. G. Louie, Nano Lett., 2007, 7, 3112–3115.
37. X. Leng, F. Jin, M. Wei and Y. Ma, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 532–550.
38. H. Jiang, J. Phys. Chem. C, 2012, 116, 7664–7671.
39. A. Schwarzer, T. Saplinova and E. Kroke, Coord. Chem. Rev., 2013, 257, 2032–2062.
40. V. Khabashesku, J. Zimmerman and J. Margrave, Chem. Mater., 2000, 12, 3264–3270.
41. Time-Dependent Density Functional Theory, ed. M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, vol. 706.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07134e

---