Open Access Article
Open Access ArticleFocused ultrasound actuation of shape memory polymers; acoustic-thermoelastic modeling and testing†
Aarushi Bhargavaa,
Kaiyuan Pengb,
Jerry Stiegb,
Reza Mirzaeifar *b and
Shima Shahaba
*b and
Shima Shahaba
aDepartment of Biomedical Engineering and Mechanics, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, USA
bDepartment of Mechanical Engineering, Virginia Polytechnic Institute and State University, Blacksburg, VA 24061, USA. E-mail: rmirzaei@vt.edu
First published on 25th September 2017
Abstract
Controlled drug delivery (CDD) technologies have received extensive attention recently. Despite recent efforts, drug releasing systems still face major challenges in practice, including low efficiency in releasing the pharmaceutical compounds at the targeted location with a controlled time rate. We present an experimentally-validated acoustic-thermoelastic mathematical framework for modeling the focused ultrasound (FU)-induced thermal actuation of shape memory polymers (SMPs). This paper also investigates the feasibility of using SMPs stimulated by FU for designing CDD systems. SMPs represent a new class of materials that have gained increased attention for designing biocompatible devices. These polymers have the ability of storing a temporary shape and returning to their permanent or original shape when subjected to external stimuli such as heat. In this work, FU is used as a trigger for noninvasively stimulating SMP-based systems. FU has a superior capability to localize the heating effect, thus initiating the shape recovery process only in selected parts of the polymer. The multiphysics model optimizes the design of a SMP-based CDD system through analysis of a filament as a constituting base-structure and quantifies its activation under FU. Experimental validations are performed using a SMP filament submerged in water coupled with the acoustic waves generated by a FU transducer. The modeling results are used to examine and optimize parameters such as medium properties, input power and frequency, location, geometry and chemical composition of the SMP to achieve favorable shape recovery of a potential drug delivery system.
I. Introduction
In the field of medicine, delivery of drugs in a controlled manner is being realized as a key factor for treating infections, cancer and many other diseases. Drug delivery refers to the methods for transporting a medication/drug compound into human body in a safe manner. Controlled drug delivery (CDD) technology has received extensive attention during the past three decades,1 mainly because of numerous advantages of this technology compared to the conventional methods.2 Despite significant recent achievements, controlled drug releasing systems still face major challenges in practice including chemical issues involved in synthesizing biocompatible drug containers, manipulating the releasing time of drugs in the body, delivering the drugs at a targeted location and utilizing a safe and noninvasive trigger to initiate drug release.3,4 In this research, we leverage the experimental, analytical and computational techniques to investigate the feasibility of using shape memory polymers (SMPs) and focused ultrasound (FU) for designing a CDD system. The design is used in a conceptual novel mechanism for simultaneously opening the drug container and pushing the particles out, which will significantly improve the rate of drug release at a targeted location.Smart materials are engineering materials that have one or more properties, which can be changed by external stimuli such as temperature, electric field, magnetic field or stress.5–8 SMPs are a relatively new class of smart materials that have the ability of storing a temporary shape and returning to their permanent or original shape9 when subjected to external stimuli such as heat, light or ultrasound.10–14 The shape memory responses to these stimuli fall broadly into three categories namely, chemo-responsive,15,16 thermo-responsive and photo-responsive. While thermo-responsive SMPs absorb heat to generate molecular motion and modify stiffness above a transition temperature for shape recovery, the shape memory effect in chemo-responsive SMPs is due to interaction with a solvent which alters/softens the transition component in the SMP. The plasticizing effect of the bound solvent molecules on the bonds of SMP molecules such as seen in the peak shift of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond in SMP in DMF solvent evidenced by Lu et al.,16 alters the transition temperature of chemo-responsive SMPs to initiate shape memory effect. Compared to other shape memory materials such as shape memory alloys17–19 and shape memory ceramics,20 SMPs are light weight, inexpensive, and can recover large deformations21–23 in a controlled manner. Development of SMP-based devices for medical applications such as stents for cardiovascular systems and self-tightening sutures has gained a lot of attention recently.3,9,24,25 Xue et al.26 developed self-expandable stents which exhibited ≈98% shape recovery at body temperature at a much faster rate compared to the best known self-expandable stents. Because of these advantages, during the past decade, SMPs have received increased interest in biomedical applications27 and advancing CDD systems.28 At present, the commercially available drug release devices still lack the capability of delivering drugs in a spatially and temporally controlled manner.29 The combination of SMPs and CDD leads us to a multidisciplinary research in order to reduce the drug side effects in patient body and frequency of taking drugs by patient, which means having more reliable and accurate treatment.
O bond in SMP in DMF solvent evidenced by Lu et al.,16 alters the transition temperature of chemo-responsive SMPs to initiate shape memory effect. Compared to other shape memory materials such as shape memory alloys17–19 and shape memory ceramics,20 SMPs are light weight, inexpensive, and can recover large deformations21–23 in a controlled manner. Development of SMP-based devices for medical applications such as stents for cardiovascular systems and self-tightening sutures has gained a lot of attention recently.3,9,24,25 Xue et al.26 developed self-expandable stents which exhibited ≈98% shape recovery at body temperature at a much faster rate compared to the best known self-expandable stents. Because of these advantages, during the past decade, SMPs have received increased interest in biomedical applications27 and advancing CDD systems.28 At present, the commercially available drug release devices still lack the capability of delivering drugs in a spatially and temporally controlled manner.29 The combination of SMPs and CDD leads us to a multidisciplinary research in order to reduce the drug side effects in patient body and frequency of taking drugs by patient, which means having more reliable and accurate treatment.
The shape memory effect of SMPs relies heavily on the external trigger provided. For use in in vivo applications, thermal activation through body heat has often been relied upon to trigger shape recovery.4 However, there is a need for more flexible stimuli as compared to fixed body heat temperature. Consequently, noninvasive triggers such as light,30–32 magnetic field,33,34 electrical field35,36 and radiofrequency wave34 have been employed. These triggers require special components such as magnetic or florescent particles to generate response, which can compromise the biodegradability and biocompatibility of SMPs. Thus, use of a safer and effective trigger is of utmost importance to achieve remotely controlled shape recovery. The use of FU an as external stimulus fulfils the above criteria. The underlying mechanism involves focusing ultrasound into a tight spot in domain area of millimeter scale, which causes selective and controlled heating of the medium at the spot. This localized heating also eliminates the need of incorporating special or responsive particles in the medium as shape deformation occurs due to heating caused by viscous shearing oscillation of molecules under ultrasound exposure.
Employing high-intensity FU has been researched for biomedical purposes for many years.37,38 The higher penetrating ability of acoustic waves as compared to light has been used for selective tissue necrosis in controlled volumes. Studies have been conducted reporting the use of ultrasound in acoustic energy transfer systems39–42 and for drug delivery43–45 especially from polyelectrolyte micro-containers,46 multilayered capsules44,47 and polymer micelles.48–51 In their study, Kost et al.43 irradiated ultrasound on a polymer matrix for releasing drugs entrapped in the matrix. Liu et al.52 and Han et al.53 conducted proof-of-concept experiments using FU to demonstrate shape recovery process of SMPs and obtain various intermediate shapes with the help of FU. The research done in recent years demonstrating the effect of FU on shape recovery behavior of polymers has been experimental in nature. The very limited literature lacks fully coupled modeling efforts to analytically solve the underlying problem and optimize a SMP-based CDD design.
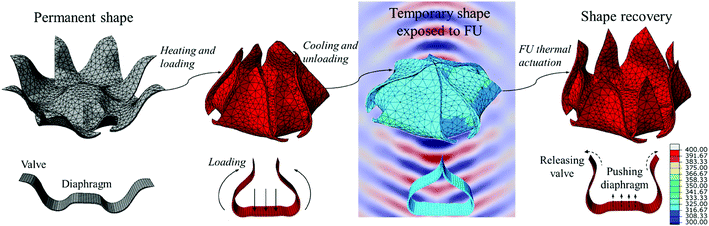
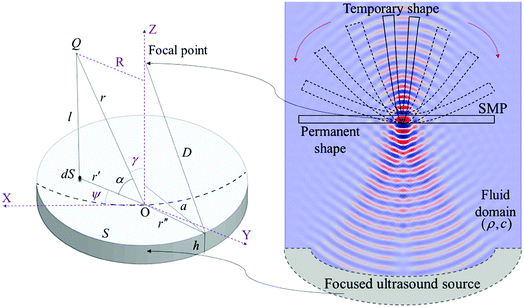
In this research, for the first time, we perform a multiphysics analytical and numerical modeling to optimize the design of a thermo-responsive SMP-based drug delivery system and quantify its activation under FU. This model provides the foundation for designing and testing SMP capsules, an example of which is schematically shown in Fig. 1 and further will be discussed in Section IV. The proposed design has the unique capabilities of (i) releasing the loaded drug at a controlled rate and (ii) releasing the drug accurately at targeted areas, thus, addressing the two major challenges of designing CDD systems. This design is based on the mechanism for simultaneously opening the drug container and pushing the particles out, which will significantly improve the drug release rate. The developed model in Fig. 1, uses FU as a trigger for stimulating the drug capsules in order to control the location of drug release. FU localizes the heating effect on a small area (about 1 mm2). This concentrated thermal field allows the activation of the shape recovery process only in a selected part of the polymer, even for the polymer immersed in water or living body.3,52,54,55 By turning off the ultrasound beam the shape recovery process can be paused at any time, which allows the polymer to have an intermediate but a stable shape.3,55 Therefore, by using FU we are able to release the loaded drug in a switchable manner.
In this paper, we implement a comprehensive set of analytical, numerical and experimental studies to design, analyze and test a coupled FU and SMP representative mechanism at a millimeter-scale framework. The model studies the acoustic-structure interaction of FU with SMP-based filaments to establish the relationship between input parameters (such as input power and frequency) with the acoustic, thermal and stress fields and shape recovery of SMPs. Medium properties such as absorption and nonlinearity, which significantly affect the pressure field of a propagative wave,56 are studied to analyze their influence on the shape memory behavior of polymer. The analytical-numerical model is validated through experiments using a high-intensity focused transducer in a water tank. Various concepts can be considered for the design of a SMP container subjected to FU, similar to the example shown in Fig. 1, however, the modeling effort is focused on the special case of a filament, as fundamental element of any container, stimulated by FU.
II. Theory
To design a SMP-based drug delivery system, development of a robust theoretical model which predicts the FU induced acoustic and thermal fields and subsequent mechanical behavior of SMP is essential. In this work, we present multiphysics acoustic-thermoelastic modeling for ultrasound actuation of SMP filaments. The analytical-numerical model is divided into three interconnected parts. The first part studies the focused acoustic pressure field in a multilayer domain which includes a SMP filament submerged in fluid, using Khokhlov–Zabolotskaya–Kuznetsov (KZK) equation.57,58 The equation is solved in a hybrid time–frequency domain using operator-splitting method and accounts for the effects of absorption, diffraction and nonlinear distortion in the medium. The second part provides a model based on Penne's bioheat equation59 to estimate the thermal field developed in SMPs as a result of FU. The temperature distribution of the polymer obtained from the second part is given to the third part which provides a framework to predict the mechanical stresses developed in SMPs and consequent shape recovery. A mechanical model is formulated by a compressible neo-Hookean constitutive equation, which assumes the SMPs behave as a thermoelastic material and predicts the thermally induced shape memory effect under FU. The constitutive model is numerically implemented in a user material subroutine (UMAT) in ABAQUS to model the deformation of the filament.The two common models used for simulating focused acoustic waves are KZK and Westervelt equations.57,58,60 In both models, the approach is based on the equations of continuum mechanics. However, existing analytical solutions fail to accurately incorporate the effects of nonlinearity, diffraction and absorption which strongly affect the acoustic wave propagation. Therefore numerical approaches have been adopted to obtain the solutions of focused hydroacoustic problems.61 The KZK equation is based on parabolic approximation and is applicable for quasi-planar waves of limited high frequencies.58 The equation holds good for directional sound beams and for focused transducers with small aperture angles (not more than 16°−18°).62,63 However, Soneson et al.64,65 have proved the applicability of KZK equation at higher aperture angles with good accuracy. The method assumes forward-wave propagation with nonlinear distortion in a direction normal to the propagation planes. On the other hand, Westervelt equation is a full-wave solution for wider aperture angles and highly focused beams. However, Westervelt equation requires fine discretization which makes it more time and memory inefficient. In this work, KZK equation is chosen to model the acoustic field of FU to reduce the computational cost.
Several theoretical models have been developed based on KZK equation, which adopt different numerical techniques to solve for the effects of absorption, diffraction and nonlinearity in the medium. However, the numerical algorithms become very time and memory consuming. Therefore, to reduce the computational burden, several approximations are made56,66,67 which include assuming one way (forward) wave propagation,68 solving governing equations in 2D when the system is axisymmetric,69 optimization of spatial grid70 and using a perfectly matching layer at the boundaries of computational grid domain to reduce spatial grid size and to avoid reflections from the edges of the grid.67 The most widely used numerical technique to solve KZK equation is a frequency-domain technique called the spectral method.71 The method substitutes a Fourier expansion of sound pressure in the KZK equation and then solves numerically. The method originally designed for monochromatic waves and tone bursts, was later modified to include the calculations for far field,72 focused beams56 and non-axisymmetric sources.73 In order to overcome the problem of high computational time required for solving nonlinearity term with spectral method, hybrid method was adopted by several researchers.74,75 The hybrid method based on KZK equation solves for the effects of absorption and diffraction in frequency domain and of nonlinearity in time domain. Pestorius and Blackstock76 validated the combined time and frequency-domain approaches through experiments to study the propagation of plane, finite-amplitude sound in the medium. Several others also adopted a pure time-domain algorithm to solve KZK equation for computational efficiency.70,77
The novel feature of the multiphysics model developed in this work is to use KZK equation with the hybrid method to study the behavior of SMPs in an acoustic field (where multiple domains are involved and medium nonlinearity is pronounced) and couple it with thermal and mechanical models to build a comprehensive framework for acoustic-thermal-structural study of SMPs. The theory is divided into three interconnected parts (A–C). Part A predicts the focused acoustic pressure field of SMPs immersed in water using nonlinear KZK equation which includes the effects of nonlinearity, absorption and diffraction (a linear analytical model for the pressure field due to focused transducers without including any nonlinear effects is given in ESI document†). We adopt the hybrid time-frequency approach using operator-splitting technique61 which accounts for these three effects separately at every integration step. Part B provides a model for calculating the thermal field developed in SMPs as a result of focused acoustic pressure. It uses the acoustic pressure field calculated in part A as an input to evaluate the heating response of the polymer. This FU induced thermal field triggers a mechanical response in the polymer and deforms the SMP. Part C provides a framework to estimate these mechanical stresses using the absorbed heat calculated in part B as an input to the framework and predicts the consequent shape recovery of the SMP.
For validation purposes, first we verify our coupled acoustic-thermoelastic theoretical model with simulations in COMSOL Multiphysics and experiments under linear conditions. Then, the developed coupled KZK-Penne's Bioheat theoretical model is employed to extract and optimize the acoustic and thermal fields under nonlinear effects, which cannot be easily simulated in a standard FEM environment. It is worth noting that although applying the nonlinear parameters in the COMSOL finite-element framework is practically difficult, it is still a valuable tool as it enables us to base the further analysis for optimizing the design of SMP-based drug delivery systems with complex geometrical 3D configurations. The simulation (ABAQUS) predicted deformation in SMP upon shape recovery process is compared with experiments as well.
A. Multiphysics modeling of acoustic-SMP interaction; nonlinear acoustic model
KZK equation is used to predict the nonlinear acoustic pressure field in fluid and SMP domains (shown in Fig. 2) using a numerical approach. This model incorporates absorption, diffraction and nonlinear effects of the medium in the wave equation. KZK equation is derived from mass and momentum conservation equations. In cylindrical form, it is given as57,58,60
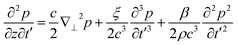 | (1) |
![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (R,t + R2/2cD)|z = 0,56,70 where
(R,t + R2/2cD)|z = 0,56,70 where ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (R,t + R2/2cD) shows the dependence of time on spatial dimension in source plane. A non-dimensional form of the KZK equation is
(R,t + R2/2cD) shows the dependence of time on spatial dimension in source plane. A non-dimensional form of the KZK equation is
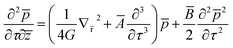 | (2) |
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) , is given as
, is given as ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) = p/p0.
= p/p0.
 | ||
| Fig. 2 Schematic representation (left) and finite-element simulation snapshot (right) of acoustic wave from a focused wave source to a shape memory polymer filament. | ||
Since the spherical spreading occurs from the focal point area, it becomes more convenient to normalize the z parameter to focal distance. The non-dimensional form of propagation distance, ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) in eqn (2) is
in eqn (2) is ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = z/D. The retarded time τ is normalized with angular source frequency ω0 and is given by τ = ω0(t − z/c). In eqn (2), the non-dimensional parameters G,
= z/D. The retarded time τ is normalized with angular source frequency ω0 and is given by τ = ω0(t − z/c). In eqn (2), the non-dimensional parameters G, ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) and Ā account for focusing gain, nonlinearity and attenuation effects in the medium, respectively. The focusing gain is given by G = zr/D, where zr is the Rayleigh distance of the unfocused source, given as zr = ω0a2/2c with a as the radius of the transducer. The nonlinearity term is
and Ā account for focusing gain, nonlinearity and attenuation effects in the medium, respectively. The focusing gain is given by G = zr/D, where zr is the Rayleigh distance of the unfocused source, given as zr = ω0a2/2c with a as the radius of the transducer. The nonlinearity term is ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = D/zs, where zs = ρc3/βp0ω0 is the plane wave shock formation distance. In addition, the parameter Ā is defined as Ā = āD, where ā = ξω2/2c3 is the attenuation coefficient at frequency ω. The non-dimensionalized form of Laplacian in eqn (2) is given by ∇
= D/zs, where zs = ρc3/βp0ω0 is the plane wave shock formation distance. In addition, the parameter Ā is defined as Ā = āD, where ā = ξω2/2c3 is the attenuation coefficient at frequency ω. The non-dimensionalized form of Laplacian in eqn (2) is given by ∇![[r with combining macron]](https://www.rsc.org/images/entities/char_0072_0304.gif) 2 = (∂2/∂
2 = (∂2/∂![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 2 + ∂/
2 + ∂/![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ∂
∂![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ), where
), where ![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = R/a. The source condition in non-dimensional form becomes
= R/a. The source condition in non-dimensional form becomes ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) =
= ![[f with combining circumflex]](https://www.rsc.org/images/entities/i_char_0066_0302.gif) (
(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,τ + G
,τ + G![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) 2)|
2)|![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = 0, which is valid for spherical transducers under the following three assumptions, given as sin2
= 0, which is valid for spherical transducers under the following three assumptions, given as sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ ≪ 2, G ≪ 8π/sin2
θ ≪ 2, G ≪ 8π/sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, and 1 ≪ ka ≪ 16π/sin3
θ, and 1 ≪ ka ≪ 16π/sin3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.56 Here θ is the half aperture angle, Fig. S1a,† and sin
θ.56 Here θ is the half aperture angle, Fig. S1a,† and sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = a/D. While the first assumption is a relatively weak restriction which requires the half aperture angle to be less than 25°, the other two are analogous and restrict the maximum focusing gain for a given aperture angle. Therefore, the given assumptions limit the domain of validity of KZK equation for a focused transducer. Since, the transducer geometry used for this research satisfies two of the necessary conditions, KZK equation is used to predict acoustic pressure field in SMP for time and memory efficiency.
θ = a/D. While the first assumption is a relatively weak restriction which requires the half aperture angle to be less than 25°, the other two are analogous and restrict the maximum focusing gain for a given aperture angle. Therefore, the given assumptions limit the domain of validity of KZK equation for a focused transducer. Since, the transducer geometry used for this research satisfies two of the necessary conditions, KZK equation is used to predict acoustic pressure field in SMP for time and memory efficiency.
Absorption refers to the thermal-viscous attenuation of the waves as they propagate through a medium leading to loss of energy of the wave. KZK equation includes the absorption effect in eqn (2) with the term
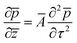 | (3) |
ā(f) = ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0fν 0fν
| (4) |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0 represents attenuation at source frequency ω0. Classical thermal-viscous attenuation uses a squared frequency dependency of the attenuation for fluids with ν = 2. However, for tissues, various experiments show that ν ranges from 0.60–2. A popular approach is to take ν = 1 for soft materials and polymers, but specific values of ν vary according to the type of material.79 It is assumed that attenuation in SMPs follow a similar frequency dependence law with ν = 1.
0 represents attenuation at source frequency ω0. Classical thermal-viscous attenuation uses a squared frequency dependency of the attenuation for fluids with ν = 2. However, for tissues, various experiments show that ν ranges from 0.60–2. A popular approach is to take ν = 1 for soft materials and polymers, but specific values of ν vary according to the type of material.79 It is assumed that attenuation in SMPs follow a similar frequency dependence law with ν = 1.
Nonlinearity arises due to variations of pressure with variation of density of the medium. It can also be expressed in terms of variations of sound velocity of a propagating wave in a medium. For example, as the wave propagates, the peaks of the wave may travel faster than the troughs thus distorting the structure of the wave. For a state p = p(ρ,s) where s is the specific entropy, Taylor series expansion expressing the variation of pressure p with density ρ under adiabatic conditions is given as p = {p0 + A[(ρ − ρ0)/ρ0] + B[(ρ − ρ0)/ρ0]2/2 +…}|s=s0,58,80 where p0 = p0(ρ0,s0). Here ρ0 and s0 represents the density and the specific entropy in the unperturbed state, respectively. The coefficients A and B represent the first and second order variation of pressure with density and are given as A = ρ0(∂p/∂ρ)|s=s0 and B = ρ02(∂2p/∂ρ2)|s=s0. The quantity B/A is known as the nonlinearity parameter and is expressed as
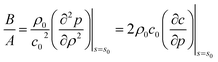 | (5) |
![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) integrates β into the KZK equation. Thus, the nonlinearity term in KZK equation, neglecting any diffraction and absorption effects, is expressed as
integrates β into the KZK equation. Thus, the nonlinearity term in KZK equation, neglecting any diffraction and absorption effects, is expressed as
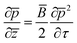 | (6) |
Eqn (6) has its origin in a simpler model known as Burger's equation.81 Burger's equation models quadratic nonlinearities and absorption effects in a propagating wave. It is a basic model to understand shock wave formation and propagation. The full non-dimensionalized form of Burger's equation is given by ∂![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) /∂
/∂![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = Ā∂2
= Ā∂2![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) /∂τ2 +
/∂τ2 + ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif)
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ∂
∂![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) /∂τ. Eqn (6) is the inviscid form of Burger's equation.
/∂τ. Eqn (6) is the inviscid form of Burger's equation.
The numerical approach to solve KZK equation was first introduced by Lee et al.70 The approach known as operator-splitting method involves solving for each of the three effects independently at each integration step and combining the effects before proceeding to the next step. Therefore, KZK equation, eqn (2), can be expressed in terms of independent terms as ∂![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) /∂
/∂![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) = oD(
= oD(![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ) + oA(
) + oA(![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ) + oN(
) + oN(![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) ), where first, second and third operators represent diffraction, absorption and nonlinear effects respectively. The current model uses operator splitting method to solve eqn (2) in a hybrid frequency–time domain approach82 for harmonic acoustic actuation of a submerged SMP filament. The pressure field is expressed in time domain as
), where first, second and third operators represent diffraction, absorption and nonlinear effects respectively. The current model uses operator splitting method to solve eqn (2) in a hybrid frequency–time domain approach82 for harmonic acoustic actuation of a submerged SMP filament. The pressure field is expressed in time domain as
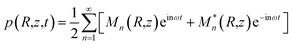 | (7) |
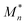 is the complex conjugate of pressure amplitude.83 Substituting eqn (7) in (2) and converting it into frequency domain, the non-dimensionalized KZK equation becomes
is the complex conjugate of pressure amplitude.83 Substituting eqn (7) in (2) and converting it into frequency domain, the non-dimensionalized KZK equation becomes
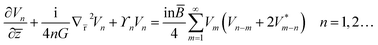 | (8) |
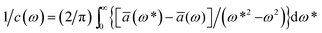 ,78 where ω* represents conjugate of the angular frequency and c(ω) is the phase velocity of the acoustic wave.
,78 where ω* represents conjugate of the angular frequency and c(ω) is the phase velocity of the acoustic wave.
At each integration step, the linear terms of eqn (8), given by,
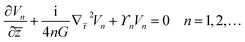 | (9) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≥ 0; 0 ≤
≥ 0; 0 ≤![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ≤ rmax, τmin ≤ τ ≤ τmax. The values of rmax, τmin and τmax are chosen such as to minimize numerical errors and depend on geometry of the transducer, absorption and nonlinearity parameters. Boundary conditions used for solving eqn (2) for a focused transducer are given as
≤ rmax, τmin ≤ τ ≤ τmax. The values of rmax, τmin and τmax are chosen such as to minimize numerical errors and depend on geometry of the transducer, absorption and nonlinearity parameters. Boundary conditions used for solving eqn (2) for a focused transducer are given as ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (
(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ,τmin) = 0,
,τmin) = 0, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (
(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) ,
,![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ,τmax) = 0,
,τmax) = 0, ![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) (
(![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) max,
max,![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ,τ) = 0, and ∂
,τ) = 0, and ∂![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) /∂
/∂![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) |
|![[r with combining macron]](https://www.rsc.org/images/entities/i_char_0072_0304.gif) = 0 = 0. The time window is chosen large enough to incorporate the effects of absorption, waveform steepening and any singularities.70 The lower and the upper limits of the time window are chosen as τmin = −(G + ω0T0 + 10π) and τmax = ω0T0 + 20π where T0 is the time duration of source wave.
= 0 = 0. The time window is chosen large enough to incorporate the effects of absorption, waveform steepening and any singularities.70 The lower and the upper limits of the time window are chosen as τmin = −(G + ω0T0 + 10π) and τmax = ω0T0 + 20π where T0 is the time duration of source wave.
At each integration step, the nonlinear terms in eqn (8) are converted into time domain using Inverse Fast Fourier Transform (IFFT) and solved for nonlinear pressure field using eqn (6). Soneson et al.83 proposed a criteria to determine the cases for which nonlinear effects can be neglected without significant errors, to improve computing efficiency in time domain. The criteria uses attenuation and nonlinearity parameters, ϒ and N respectively, to determine a cutoff value and decide if linear model is sufficient for the analysis. Thus, in this work, before the model computes for nonlinearity, a threshold cutoff amplitude is determined. If the pressure amplitude at each grid step is greater than the cutoff value, then the model accounts for nonlinearity and integrates eqn (6) using upwind method. The solution is then converted back to frequency domain and the numerical code marches to the next step. The term β = 4.50 in SMP and β = 3.50 in water58,84 incorporate the nonlinear effects in wave propagation. An input pressure at 6 W is used. The number of harmonics (n) included in the model are given by n = 2k, where k is an integer. To accurately model nonlinear effects, k ≥ 6 is used.
To solve for absorption and diffraction effects in frequency domain, Diagonally Implicit Runge–Kutta (DIRK) and Crank–Nicolson (CN) methods85,86 are used. The second order IRK method is used in the near field near boundaries to reduce oscillations while Crank–Nicolson is used in the far field region.82 The transition from DIRK to CN method is made at an axial grid length of ![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) ≈ 0.3. The methods use an axial step size of 0.06 mm with an axial grid length of up to 78 mm and radial step size of 0.12 mm with a radial grid length of up to 32 mm. A time step of 7.8 × 10−9 is applied for both methods. The axial grid step is taken smaller to account for nonlinearity and provides a stable and accurate solution. In SMP domain,
≈ 0.3. The methods use an axial step size of 0.06 mm with an axial grid length of up to 78 mm and radial step size of 0.12 mm with a radial grid length of up to 32 mm. A time step of 7.8 × 10−9 is applied for both methods. The axial grid step is taken smaller to account for nonlinearity and provides a stable and accurate solution. In SMP domain, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0 of 82.5 dB MHz−1 m−1 and in water, a value of 0.22 dB MHz−1 m−1 is used.84 The methods yield a tridiagonal finite-difference matrix which can be solved using Thomas algorithm.85
0 of 82.5 dB MHz−1 m−1 and in water, a value of 0.22 dB MHz−1 m−1 is used.84 The methods yield a tridiagonal finite-difference matrix which can be solved using Thomas algorithm.85
The results of the numerical code in MATLAB are further validated using COMSOL. A 2-D axisymmetric model is developed to solve for acoustic pressure in frequency domain and later for heat transfer in time domain. The input parameters of the transducer and the SMP properties (density, thermal conductivity and specific heat capacity) are obtained from experimental measurements.
B. Thermal modeling
The effects of focused ultrasound on soft tissues are well documented.87–89 A mathematical formulation to analyze the effects of ultrasound on tissues is given by Penne's bioheat equation which models the transfer of heat and generation of thermal field in the tissue domain. In this work, similar framework is used to evaluate the temperature T rise of the soft polymer as a result of FU heating. The modified Penne's Bioheat equation for SMP is given as59
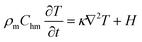 | (10) |
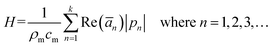 | (11) |
In eqn (10), ρm, Chm and κ denote the density, specific heat capacity and thermal conductivity of polymer. Parameter cm in eqn (11) denotes the sound speed in polymer and pn denotes the pressure field associated with each harmonic predicted by KZK equation in part A. The thermal equation is coupled with KZK equation through heating rate H. Heating rate takes into account the cumulative heating by all harmonics. The absorption ān in polymer associated with each harmonic n obeys the frequency dependent power law given by eqn (4) where ν = 1. The numerical algorithm in this paper solves eqn (10) using Crank–Nicolson operators for 40 s with a time step of 0.10 s. The radial and the axial step sizes are 0.24 mm and 0.25 mm, respectively.
C. Mechanical modeling of SMPs
Having obtained the temperature distribution from Section B, in this section, a SMP filament is modeled to predict the shape recovery process under focused ultrasound by applying the obtained thermal boundary conditions. SMPs are categorized as semi-crystalline shape memory polymers (CSMPs) and glassy shape memory polymers (GSMPs). GSMPs have both amorphous and glass regions, with Tg defined as the glass transition temperature above which the SMPs exist in amorphous form. In this study, the selected constitutive model takes into account the stress–strain response which depends on thermal expansion of polymers to predict the glass transition of GSMPs.90–92 The constitutive model involves four steps, the loading (amorphous phase), cooling (phase transition), unloading (glassy phase) and heating (phase transition) of the polymer filament. The constitutive model is numerically implemented in a user material subroutine (UMAT) in ABAQUS, a commercial finite-element software, to model the deformation and shape recovery of an L-shaped filament which is thermally activated by FU. The governing equations calculating the stresses during the whole cycle and the evolution rules for the glass volume fraction are given as following.90SMPs above the glass transition temperature show the characteristics of an elastomer. The stress 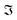 in the amorphous part of the SMPs is given as
in the amorphous part of the SMPs is given as
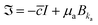 | (12) |
![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) is the Lagrange multiplier due to the constraints of incompressibility, I is an identity tensor, Bka is the left Cauchy stretch tensor and μa is the shear modulus of the amorphous phase. Here Bkais related to deformation gradient in amorphous phase,
is the Lagrange multiplier due to the constraints of incompressibility, I is an identity tensor, Bka is the left Cauchy stretch tensor and μa is the shear modulus of the amorphous phase. Here Bkais related to deformation gradient in amorphous phase, ![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) ka, as Bka =
ka, as Bka = ![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) ka
ka![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) kaT. The stored energy function for the amorphous phase, Ψa is given as
kaT. The stored energy function for the amorphous phase, Ψa is given as
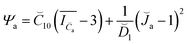 | (13) |
![[C with combining breve]](https://www.rsc.org/images/entities/i_char_0043_0306.gif) 10 = μa/2 and
10 = μa/2 and ![[D with combining breve]](https://www.rsc.org/images/entities/i_char_0044_0306.gif) 1 = 2/Ka are the coefficients related to shear modulus and bulk modulus, Ka, of the amorphous phase, respectively. Here ĪCa = tr(
1 = 2/Ka are the coefficients related to shear modulus and bulk modulus, Ka, of the amorphous phase, respectively. Here ĪCa = tr(![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) ka) and
ka) and ![[J with combining breve]](https://www.rsc.org/images/entities/i_char_004a_0306.gif) a is the volume ratio that can be determined by
a is the volume ratio that can be determined by ![[J with combining breve]](https://www.rsc.org/images/entities/i_char_004a_0306.gif) a = det(Bka)1/2.
a = det(Bka)1/2.
During cooling, as the temperature goes below the glass transition temperature, the glassy phase starts forming and both amorphous and glassy phase coexist at the same time. The stress for cooling phase of the cycle is given by
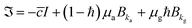 | (14) |
![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) kg, as Bkg =
kg, as Bkg = ![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) kg
kg![[F with combining breve]](https://www.rsc.org/images/entities/i_char_0046_0306.gif) kgT.
kgT.
After cooling stops and the polymer is below Tg, the formation of glassy phase stops. While the amorphous phase may not totally transit to glassy phase, the stress in the mixture is still given by eqn (14). The stored energy function for the glassy phase, Ψg is given as,
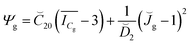 | (15) |
![[C with combining breve]](https://www.rsc.org/images/entities/i_char_0043_0306.gif) 20 = μg/2 and
20 = μg/2 and ![[D with combining breve]](https://www.rsc.org/images/entities/i_char_0044_0306.gif) 2 = 2/Kg are the coefficients related to shear modulus and bulk modulus, Kg, of the glassy phase respectively, and ĪCg = tr(
2 = 2/Kg are the coefficients related to shear modulus and bulk modulus, Kg, of the glassy phase respectively, and ĪCg = tr(![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) kg).
kg).
In the heating phase, SMPs return to the original shape as the temperature goes above Tg. Due to the melting of glassy phase, the final state of the material is stress free and is given by 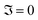 . The activation criterion for heating (starting of phase change) is governed by
. The activation criterion for heating (starting of phase change) is governed by
(1 − ħ)μaBka + μgħBkg = ![[c with combining macron]](https://www.rsc.org/images/entities/i_char_0063_0304.gif) I I
| (16) |
In a thermomechanical cycle, the change of glassy volume fraction controls the strain storage and release. Consistent with experimental results,92 this volume fraction is assumed to be a function of temperature T only. Based on this assumption, a phenomenological function is given by93
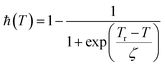 | (17) |
To implement the constitutive model in ABAQUS, UMAT provides the updated stress and the local tangent stiffness matrix, 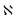 . Here
. Here 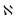 is a fourth-order tensor which is termed as the Jacobian matrix and provides the relationship for the stress and strain. The required Jacobian matrix format is given as
is a fourth-order tensor which is termed as the Jacobian matrix and provides the relationship for the stress and strain. The required Jacobian matrix format is given as
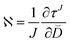 | (18) |
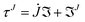 . Substituting τJ into eqn (18) gives
. Substituting τJ into eqn (18) gives 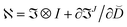 , where for a mixture of amorphous and glassy phases,
, where for a mixture of amorphous and glassy phases, 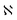 is given as
is given as
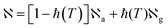 | (19) |
Solving eqn (18) and (19) delivers 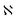 , which relates stresses to strains thus predicting shape recovery based on the detailed derivation given by Barot.95 In eqn (12–16), the shear modulus of the amorphous and glassy phases, μa and μg, are given as μa = Ea/2(1 + νa) and μg = Eg/2(1 + νg) where νa = 0.49 and νg = 0.40 are Poisson's ratios for the rubbery and glassy phases, respectively.27 The bulk modulus, Ka and Kg, in eqn (13) and (15) are given as Ka = Ea/3(1 − 2νa) and Kg = Eg/3(1 − 2νg).
, which relates stresses to strains thus predicting shape recovery based on the detailed derivation given by Barot.95 In eqn (12–16), the shear modulus of the amorphous and glassy phases, μa and μg, are given as μa = Ea/2(1 + νa) and μg = Eg/2(1 + νg) where νa = 0.49 and νg = 0.40 are Poisson's ratios for the rubbery and glassy phases, respectively.27 The bulk modulus, Ka and Kg, in eqn (13) and (15) are given as Ka = Ea/3(1 − 2νa) and Kg = Eg/3(1 − 2νg).
III. Experimental results and model validation
A. Experimental setup and SMP filament preparation
Experiments are conducted for a flat 25 mm long, 3 mm wide, 1.5 mm thick 95% TBA–5% DEGMA polymer filament. The H-104-4A SONIC Concepts FU transducer rests on the bottom of the tank (Fig. 3a and b). The tank of water is filled to a depth such that the focal point of the FU transducer is located at the surface of the water. Special care is taken to ensure the water doesn't spray when the transducer is activated, and that the exposure power is low enough to prevent sample degradation. In an attempt to prevent acoustic interference, a rigid sample holder is placed outside of the tank to suspend the SMP sample at the surface of the water. The sample is suspended in a way such that the lower surface is submersed in water, and the upper surface is exposed to air. The FLIR C2 thermal imaging camera is fixed so that the images are focused around the exposure area of the FU, as shown in Fig. 3. The camera has an imaging rate of once every four seconds. Duration of sinusoidal exposure is 20 continuous seconds, with most thermal measurements reaching 40 seconds to capture cool down. Data is processed with FLIR Tools software. Exposure power can be varied within the sample damage range. Fig. 3c shows shape recovery of a SMP filament exposed to FU.The monomer and the crosslinker that are utilized for fabrication of the SMP filament during the experiments are tert-butyl acrylate (TBA) and di(ethylene glycol)dimethacrylate (DEGMA) (molecular weight 550) respectively. The photo-initiator used for the UV curing process is 2,2-dimethoxy-2-phenyl-acetophenone. All chemicals are purchased from Sigma-Aldrich, and are not altered prior to use. Molds are created with dimensions of 150 mm × 100 mm from clear ultra-scratch resistant acrylic, and sealed with Loctite silicon sealant. Thickness of polymer filaments developed is varied as per the needs of the experiment, but is typically 1.5 mm. Curing is completed with a 100 W Blak-Ray B-100 AP High Intensity UV Lamp.
Depending on the desired composition, TBA is mixed with DEGMA in different volumetric ratios of 80–20; 90–10; 95–5; and 100–0, respectively. The crosslinker–monomer combination is mixed well for ten minutes with a stir plate after adding 1 wt% photo-initiator. The mixture is then transferred to the acrylic molds for curing. The UV light exposure lasts 20 minutes for each mold. The prepared SMP is then removed from the mold. All SMP samples have a permanent shape of a flat rectangle. The SMP film is cut to the desired geometry by either scoring the material or use of a rotary tool.
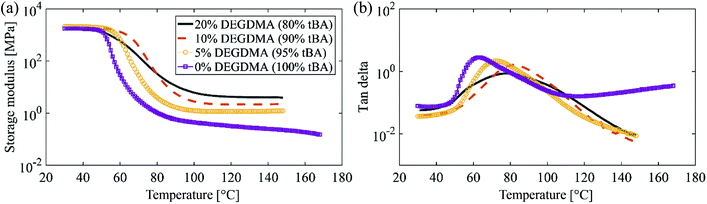
Dynamic mechanical analysis (DMA) is done for each of the aforementioned compositions. DMA measures storage modulus, Fig. 4a and tan delta, Fig. 4b (loss modulus and stiffness values are given in the ESI; Fig. S2a and S2b,† respectively). The ratio of the loss modulus to the storage modulus is the tan delta and is often called damping. It is a measure of the energy dissipation from a material. A TA Instuments-Q800 DMA is used with an oscillation rate of 1 Hz. The data is collected in 0.5 °C steps, and the temperature is ramped at a rate of 2 °C per minute. DMA analysis and the preliminary experiments for shape recovery behavior show that 95% TBA–5% DEGMA is the most suitable composition and is used for all further experiments and theoretical analysis in this paper. The preliminary tests show that the other compositions are either too brittle to be used practically or are easily damaged even at low input power to the transducer.
A hot disk thermal constants analyzer is utilized for evaluating thermal properties of the SMP filament. The hot disk hardware consists of a Keithley 2000 voltmeter, a Keithley 2400 sourcemeter, a Hot-disk bridge, and a computational device. After fabrication of SMP films, 14 disks of 15 mm diameter and 1 mm thickness are cut with a rotary tool. These sheets are clamped tightly in the sample holder for testing. The measurement method is verified with solid porcelain and sheets of PMMA with known thermal properties. The values of mechanical and thermal properties extracted from DMA analysis and hot disk experiment for 95% TBA–5% DEGMA are reported in Table 1. These values are later used in the entire research work for theoretical and experimental analysis of SMP filaments. The results obtained from DMA tests are also used to set the values of following parameters for the mechanical modeling in ABAQUS as ![[C with combining breve]](https://www.rsc.org/images/entities/i_char_0043_0306.gif) 10 = 0.28,
10 = 0.28, ![[C with combining breve]](https://www.rsc.org/images/entities/i_char_0043_0306.gif) 20 = 375,
20 = 375, ![[D with combining breve]](https://www.rsc.org/images/entities/i_char_0044_0306.gif) 1 = 0.072 and
1 = 0.072 and ![[D with combining breve]](https://www.rsc.org/images/entities/i_char_0044_0306.gif) 2 = 0.00054.
2 = 0.00054.
| Property | Value |
|---|---|
| Tg | 72 °C |
| Density, ρm | 1100 kg m−3 |
| Amorphous phase elastic modulus, Ea | 1.66 MPa |
| Glassy phase elastic modulus, Eg | 2100 MPa |
| Thermal conductivity, κ | 0.175 W m−1 K−1 |
| Specific heat capacity, Chm | 1050 J kg−1 K−1 |
B. Experimental results and acoustic-thermoelastic model validation
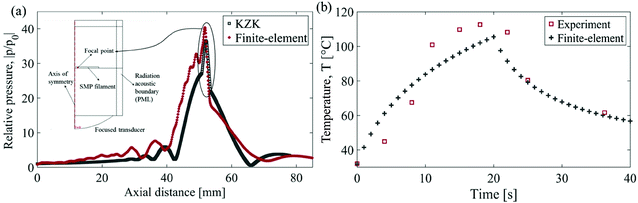
The acoustic-thermoelastic model in Section II is used to study the FU induced acoustic and thermal field as well as the shape memory behavior of the crossed-linked polymer. The theoretical acoustic pressure model is validated by finite-element simulation in COMSOL (Fig. 5a and b) and experiments. The SMP filament is exposed to focused acoustic waves in fluid domain (water), and boundaries of the fluid domain are defined to allow no reflection by employing perfectly matched layers in COMSOL. For harmonic actuation at the resonance frequency (0.5 MHz) of the FU transducer and 6 W input power, Fig. 5a shows the relative acoustic pressure field of the fundamental harmonic along axis of symmetry of the transducer, obtained from the KZK and finite-element models. The calculated acoustic pressure is normalized with respect to source pressure amplitude, p0. A good agreement is observed between the finite-element simulations and proposed analytical-numerical multiphysics model. The sudden jump observed in the pressure field at z ≅ 52 mm in Fig. 5a is due to the amplified effects of diffraction at the focal point and nonlinearity in the polymer. Fig. 5b experimentally validates the temperature of the thermal field developed at the focal point for a sonication period of 20 s with finite-element analysis. The overall agreement of temperature and pressure values between experiments, finite-element analysis and acoustic-thermoelastic model proves the robustness of the theoretical model developed in this work. The parameters used in the acoustic model, accounting for gain, attenuation and nonlinearity effects in water and polymer are listed in Table 2.| Parameter | Medium | |
|---|---|---|
| Water | SMP | |
![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0 (dB MHz−1 m−1) 0 (dB MHz−1 m−1) |
0.217 | 82.5 |
| β | 3.5 | 4.5 |
| G | 20.87 | 11.25 |
Fig. 6 shows the thermal images of the polymer to demonstrate the temperature rise with respect to time corresponding to Fig. 5b. The heating of polymer is due to absorption of acoustic energy as a result of viscous shearing exerted by ultrasound focused waves and subsequent release of energy in the form of heat.52 In the images, the highly concentrated spot in the center has the maximum temperature while the immediate surroundings outside of the focal spot has significantly lower temperatures. This shows a sharp temperature gradient from center to the edges of the polymer demonstrating the highly localized heating effect of focused ultrasound. As seen in the temperature curve in Fig. 5b, after 20 s, the ultrasound is switched off and the polymer immediately begins cooling down which is shown by the sharp temperature decay. This ability to change the temperature of the polymer in short range of time shows the capability of focused ultrasound to control the heating effect which is an important parameter to consider in designing of SMP-based CDD systems.
Having validated the acoustic-thermal model results and identified the mechanical and thermal parameters, a three dimensional filament is modeled to investigate the shape recovery of SMPs thermally induced by FU. The simulations of SMP's recovery process are performed by using a commercially available finite-element software package in ABAQUS (version 6.14, Dassault Systems Simulia Corp., Providence, RI, USA), with a user material subroutine (UMAT).
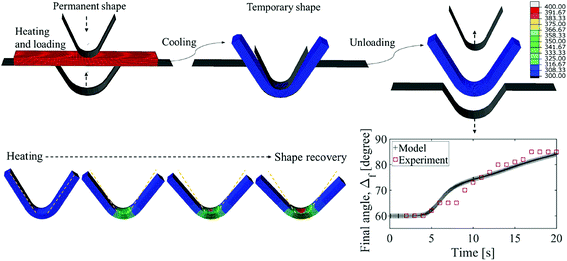
The SMP filament is modeled in ABAQUS using the properties given in Table 1. For the filament, the symmetry in x-direction and y-direction is applied to nodes that are on the central cross section and perpendicular to the x–y directions. Referring to Fig. 7, a punch and a die, defined as analytical rigid parts, are also introduced for modeling the loading process. The die is fixed and the punch is constrained in x and y directions, ux = 0 and uy = 0, while only z-direction movement is allowed. Contact between the punch/die parts and the filament is modeled as frictionless and we assume there is no thermal transfer between punch/die parts and the filament.
The initial temperature is set above the glass transition temperature and the filament is deformed at different angles ranging from 60° to 120°. After cooling and unloading, ultrasound thermal field data from acoustic-thermal model is imported and applied as a mapped temperature distribution field in the finite-element model, to simulate the heating stage of the mechanical model, at 6 W power of the transducer as shown in Fig. 7. The thermal field data obtained from Section B is exported from 0 to 20 s, divided into 4 sub steps (0–1, 1–5, 5–10, and 10–20 s) and applied as boundary conditions successively in the heating stage in the model. The inset in Fig. 7 compares the experimental and model predicted values of change in deformed angle against time for a filament with temporary initial angle of 60°. According to Fig. 7 and Table 3, the simulation results show a good agreement with experiments.
| Initial angle, Δi | Final angle, Δf | Angle change, Δ | ||
|---|---|---|---|---|
| Model | Experiment | Model | Experiment | |
| 60 | 84.06 | 85 | 24.19 | 25 |
| 90 | 110.14 | 110 | 20.23 | 21 |
| 120 | 135.38 | 135 | 15.52 | 15 |
C. Effects of various parameters
Experiments are conducted to estimate the threshold input acoustic power to the SMP filament beyond which the polymer gets damaged. Polymer filaments are exposed to input power ranging from 0–100 W. The filaments are then observed under OME-TOP metallurgical microscope PM-304I at a resolution of 100 μm. Experiments reveal that after a certain range of power, actuating polymers at higher powers result in surface scarring and cracking of the polymer filament as shown in Fig. 8. Besides visible changes, the polymer also undergoes structural changes such as temporary melting during ultrasound exposure which lead to unpredictable and non-repetitive rise in temperature of the polymer. The threshold power range is found to be within 6–10 W for the 1.5 mm thick filament above which the observed changes in temperature are non-uniform. | ||
| Fig. 8 Surface images of the polymer filament exposed to (a) no acoustic power, and (b1) 25 W (b2) 50 W (b3) 75 W (b4) 100 W. | ||
In the usage of FU technology combined with SMPs for designing an ultrasound responsive SMP-based CDD system, focused acoustic waves are strongly affected by the mutual influence of diffraction, absorption and nonlinearity of the medium. Therefore, investigating the influence of these effects in the focal area, on the FU induced heat generation in polymer and the resultant shape recovery are clearly of importance. In this section, various acoustic parameters are investigated in the polymer domain and the resulting acoustic and heating responses are explored in both the time and frequency domains. The nonlinear acoustic-thermal model is then coupled with the constitutive equations of SMPs to explore the dependence of shape recovery on the nonlinear parameters and compared with the results reported in the literature. Specifically, the input power and frequency-dependent nonlinear effects on shape recovery are studied.
Nonlinearity is a property which arises due to variation of speed of a propagating wave in a medium. Presence of higher harmonics due to transfer of energy from fundamental to higher harmonic components and distortion of waveform characterizes a nonlinear wave. The localization of the fundamental pressure field as well as the harmonics at the focal point is of utmost importance in evaluating the thermal effects of FU on SMP filament, because the amount of energy deposition is directly proportional to frequency-dependent absorption and on higher frequencies according to eqn (11). Thus, stronger nonlinear effects lead to stronger and higher number of harmonics creating enhanced localized energy deposition and therefore enhanced shape recovery of SMP.
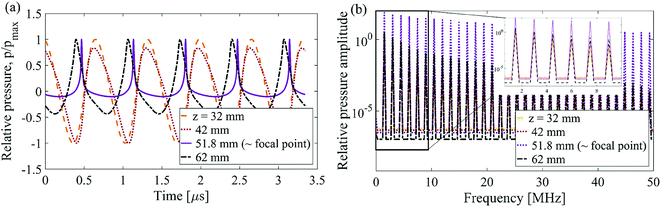
The relative pressure against axial distance from the transducer and the time histories of the relative acoustic pressure at the focal point, located in the polymer domain, are shown in Fig. 9, in response to harmonic excitation of the transducer at 6 W and 0.5 MHz. To study the nonlinearity effects and distortion of pressure waves in our experiments, a simulation using KZK equation is performed for the experimental case study in Section B with the parameters mentioned in Tables 1 and 2. Fig. 9a shows that the fundamental component has the highest pressure amplitude which indicates that most of the energy is concentrated in the fundamental component, with the second harmonic having only small amount of energy due to a low pressure amplitude. The remaining harmonics have negligible pressure amplitudes and therefore, negligible energy. The results in Fig. 9b show that the transducer settings assigned for the experimental case study to obtain the results in Fig. 5, result in a weak distortion of the waveform from the linear case, due to low value of nonlinear parameter, β, and energy contribution of only two harmonics (fundamental and second).
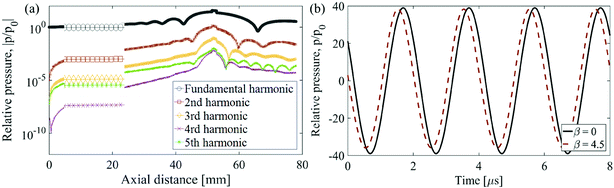 | ||
| Fig. 9 (a) Relative axial pressure magnitude and (b) linear and nonlinear relative pressure waveform at 6 W and 0.5 MHz. | ||
Having validated the analytical-numerical acoustic model in Fig. 5a against FEM simulations for the experimental case study with weak nonlinear effects, finite cases with strong nonlinearity are considered next (which cannot be efficiently simulated in a standard FEM environment). With increase in β alone for the polymer, the variation of speed with pressure in the polymer increases, which leads to stronger nonlinear effects with stronger harmonics and more distorted waveform as shown in Fig. 10. The waveforms are obtained at higher power and frequency (20 W and 1.5 MHz) to observe the nonlinear effects at a reasonable spatial scale and these values are different from input values used for experiments. With increase in β in Fig. 10a, the peak amplitude of the waveforms become narrower and increase drastically due to cumulative effect of stronger harmonics. This is further demonstrated in Fig. 10b where the increased transfer of energy from fundamental to other harmonic components with β leads to decrease in the relative pressure amplitude of the fundamental frequency and increased pressure amplitudes of higher harmonics.
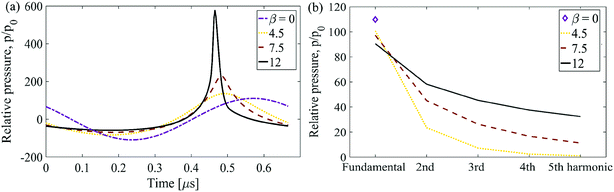 | ||
| Fig. 10 (a) Relative pressure waveforms and (b) amplitudes for first five harmonics at focal point for various nonlinearity parameter β. | ||
Nonlinear effects become more dominant with distance as well.58 The speed of a particle is different at various points in the waveform. Fig. 11 shows the distortion of the waveform at four different points along the propagation axis at 1.5 MHz and 20 W of power with β = 12 in water and β = 13 in polymer. The values of β are chosen to observe the nonlinear effects at a reasonable spatial scale. The increased distortion of the waves with distance is due to the increased strength of harmonics with wave propagation in the medium, Fig. 11b. In other words, nonlinear effects cumulate with distance. However, we observe that at the focal point where SMP filament is located, the narrowing of the waveform and the strength of the harmonics is the maximum. This is due to the presence of polymer at the focal point which has a higher β as compared to water and thus has increased nonlinear effect on the propagating acoustic waveform as compared to distance.
Absorption causes loss in the transmitted energy of the wave as it passes through a medium. The effect of absorption on wave attenuation is explained in Section II.A. The contribution of absorption to the pressure field is incorporated through the attenuation coefficient ā in the KZK model. To evaluate the influence of variation of attenuation coefficient of SMP at source frequency, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0, on the distortion of waveform and generation of harmonics, simulations are performed at 20 W and 1.5 MHz, keeping other properties of the polymer according to Table 1 and 2. Fig. 12 shows that with increase in attenuation coefficient of the polymer, the relative pressure amplitude and the number of harmonics do not increase or decrease. Attenuation counters the nearfield and nonlinearity effects. However, for focused sources56 the effect of absorption on the waveform is significantly less in the nearfield region due to dominant effects of nonlinearity. Similar observations by Hart et al.56 confirm the suppression of dissipation effects and their negligible influence on pressure field in the nearfield region.
0, on the distortion of waveform and generation of harmonics, simulations are performed at 20 W and 1.5 MHz, keeping other properties of the polymer according to Table 1 and 2. Fig. 12 shows that with increase in attenuation coefficient of the polymer, the relative pressure amplitude and the number of harmonics do not increase or decrease. Attenuation counters the nearfield and nonlinearity effects. However, for focused sources56 the effect of absorption on the waveform is significantly less in the nearfield region due to dominant effects of nonlinearity. Similar observations by Hart et al.56 confirm the suppression of dissipation effects and their negligible influence on pressure field in the nearfield region.
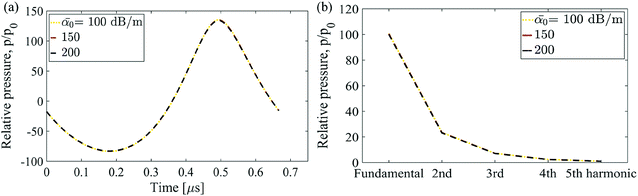 | ||
Fig. 12 (a) Relative pressure waveforms and (b) amplitudes for first five harmonics at focal point for various attenuation coefficient, ![[small alpha, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c2.gif) 0. 0. | ||
Most of the literature talks about nonlinearity effects on the pressure waveform due to distance. Very few studies examine the effect of other parameters on the distortion on the propagating sound wave in a medium. Fig. 13 and S3† show the relative pressure amplitudes at focal point in time and frequency domains for various excitation frequency and input power level, respectively. As input power is increased at a particular frequency, the amplitudes of all the harmonics increase, adding more energy available to each harmonic; however, there is no change in number of harmonics, Fig. S3b.† This results in low distortion of the waveform for increasing input power, Fig. 13b. On the other hand, increase in frequency at a fixed power level gives rise to more number of harmonics and significant distortion of waveform, Fig. 13a and S3a.† This occurs due to increased change of sound speed in the medium with increase in frequency. It is inferred that between the two transducer input parameters, frequency plays a more significant role, as compared to input power, in inducing nonlinearity in acoustic pressure field exposed to the SMP. The effects of acoustic nonlinearity on the induced thermal field in polymer is explained further in Fig. 14.
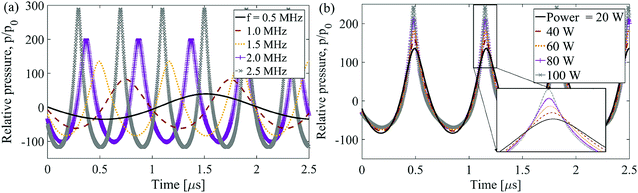 | ||
| Fig. 13 Relative pressure (with reference as source pressure, p0) at focal point in time domain for (a) various source frequency and 20 W input power; (b) various input power at 1.5 MHz. | ||
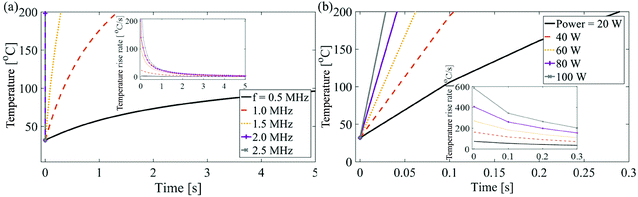
The concentration of the acoustic pressure fields of the higher harmonic components at the focal point leads to increased energy deposition because higher frequencies significantly influences the heating response of polymer, eqn (11). From Fig. S3a and b,† it is seen that at a particular acoustic pressure field in SMP domain, an increment in input power level causes more energy distribution from the fundamental to higher harmonics. Therefore, stronger high frequency components appear, as compared to applying an increment in the source frequency. Increase in power level enhances more localized energy deposition on the surface of SMP and therefore rapid increase of temperature. Fig. 14 shows that the temperature rise rate in SMP with power variations is significantly higher than the temperature rise rate due to increase in frequency. As a result, the rise in input power level onsets an earlier shape recovery and plays a more influential role in triggering heating effect in the polymer filament. However, increasing power should be done with care since the experiments in Fig. 8 show that actuating polymers at higher power levels result in surface damages. It is concluded that, the acoustic nonlinearity has a significant role in controlling the onset of shape recovery in ultrasound SMP-based systems; increment in excitation frequency results in smoother shape recovery whereas increase in power level makes a sudden shape recovery of the SMP.
Simulations are performed to explore the effects of polymer constitutive composition on the shape recovery behavior of SMP filament at a fixed ultrasound actuation power. Reference temperature, Tr in eqn (17), and the elastic modulus of amorphous phase, Ea, are the two parameters considered as variables in the simulations, while all other parameters are kept constant. Fig. 15a shows that the onset of shape recovery is delayed for the SMP with higher characteristic recovery temperature (Tr = 328 K), however the recovery ratios do not show a uniform trend. Fig. 15b shows that the SMP with higher elastic modulus in rubbery phase gives better shape recovery and therefore achieves larger change in initial angle. The reason is that the polymer with high elastic modulus (hard material) has a higher stored energy under the same deformation during loading stage as compared to a softer polymer with lower elastic modulus. Since for different compositions, the elastic moduli in glass phase are same, the polymer with larger stored energy has a better recovery ratio.
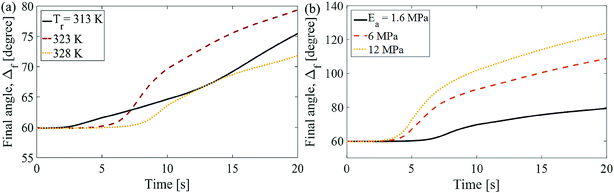 | ||
| Fig. 15 (a) Final angle vs. time for various (a) recovery temperature and (b) elastic moduli of amorphous phase. | ||
The effects of increasing the crosslinker content on material properties are shown in Fig. 4 and S2.† In Table 4, the results from simulation show that the sample with heavier crosslinking (with higher elastic modulus in amorphous phase) will have more shape recovery, which is consistent with Fig. 15b. It is worth emphasizing that in Fig. 15, the reference temperature and elastic modulus of amorphous phase are the only parameters which are varied in the simulations which is not the case in Table 4 (both reference temperature and elastic modulus are different for various compositions).
| Composition (%TBA–%DEGMA) | Tg [°C] | Final angle, Δf | Angle change, Δ |
|---|---|---|---|
| 70–30 | 106 | 105.20 | 45.20 |
| 80–20 | 78 | 87.87 | 27.87 |
| 90–10 | 82 | 79.36 | 19.36 |
To study the effect of geometric parameters and input power on the thermally induced shape recovery behavior of polymers, simulations are performed for varying thickness, width, initial angle of bending curvature of the filament and input power to the transducer. Fig. 16a shows the final angle (the angle of the deformed area after undergoing shape memory behavior) with time for a 3 mm wide filament with initial deformation of 60° at 6 W of input power for varying thickness. The change in final angle and therefore shape recovery is more in thicker filaments. The reason behind this trend is the increase in the available sample volume with increased thickness for absorbing heat, resulting in increased bulk temperature of the exposed sample and therefore more shape recovery.55 Thus, thickness plays an important role in determining shape memory behavior of a given filament.
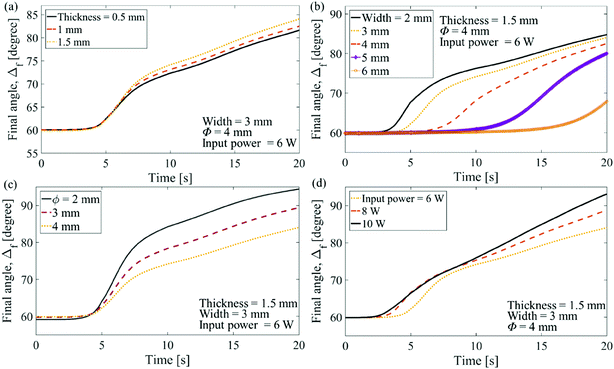 | ||
| Fig. 16 Final angle vs. time for various (a) thickness and (b) width of the SMP filament, (c) initial bending curvatures of the deformed area in mm, and (d) transducer input powers. | ||
Fig. 16b explores the effect of change in width of polymer filament on shape recovery behavior for a 1.5 mm thick filament with initial bending curvature of 60° at 6 W. The increase in width delays the onset of shape recovery and decreases the amount of shape recovery. It is observed that angle recovery onset time is related to the temperature at the edge nodes. Since the filaments have different width, the time taken by edge nodes of filaments with larger width to reach glass transition temperature is more. Thus, a larger width increases the zone of phase transformation and requires more time and energy to transform the overall exposed area and initiate the shape recovery, resulting in lesser change in initial angle.
The simulations of the filaments for various initial radii of curvature, Φ are conducted for a 3 mm wide and 1.5 mm thick filament heated at 6 W power of focused ultrasound. Fig. 16c shows that even though the filaments have almost same onset time, a sharper bending area leads to a larger deformation. Since the filaments have same width, the time for edge nodes on central cross section to reach the glass transition temperature is approximately the same. Hence, the filaments with different bending radius but same width have almost same recovery onset time. However, for a sharper bending area, the spreading phase transformation zone easily covers the whole bending area which results in a larger deformation for the sharper filament.
Fig. 16d shows the final angle with respect to time at various input powers. The thickness of the polymer filament is kept constant at 1.5 mm and initial angle of 60° is used for all powers. It is seen that higher input power results in higher shape recovery (more change in initial angle) of the polymer. This is expected as the increase in power will result in increase in absorption of energy, eqn (11), due to higher internal friction and therefore increase in energy subsequently released as heat.55 As power increases, the bulk temperature crosses Tg at an earlier time step thus initiating early shape recovery.
IV. SMP container design
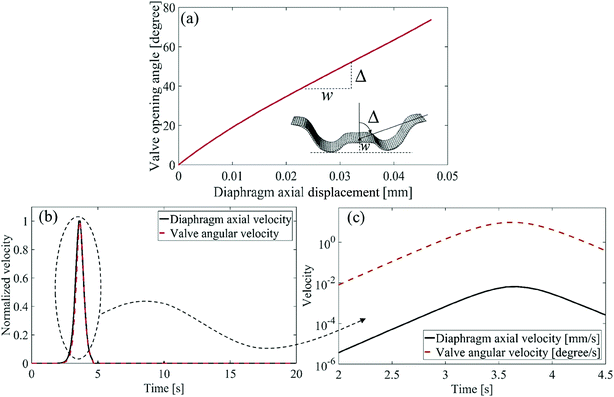
The theoretical model in this research aims to develop a mathematical framework for optimizing and evaluating the role of different input parameters, geometrical configuration, and medium properties on ultrasound actuated shape memory behavior of polymers through experimental validation. The efforts lead to propose a design for an ultrasound activated drug delivery container. A possible design for such a container is shown in Fig. 17. The 0.3 mm wide (diameter) container is a 2D representation of Fig. 1 and is composed of 0.01 mm thick layer of 95% TBA–5% DEGMA kept at the focal point of the ultrasound transducer. Fig. 17 shows the simultaneous displacement of the valve and diaphragm with time and the intermediary stages due to shape recovery under FU at 6 W. The color contour gives the temperature distribution inside the container.The design proposes a novel mechanism for simultaneously opening the drug container and pushing the particles out, which will significantly improve the rate of drug releasing. The movement of valve with respect to diaphragm is shown in Fig. 18a. Fig. 18b shows the normalized velocity (normalization is done with respect to the maximum velocity) of the diaphragm and valve is maximum within first five seconds suggesting the maximum release of drug particles occurs within first 5 seconds of ultrasound exposure. The time at which the normalized velocity attains maximum can be manipulated by varying the input power or geometric parameters of the container, thus controlling the drug release rate. Since the diaphragm velocity is lower than the valve velocity as shown in Fig. 18c, the drug release of particles is expected to be uniform, unhindered and regulated. It is worth noting here that we are only showing a proof of concept and the developed experimental-computational framework can be utilized for designing various ultrasound activated drug delivery containers, specifically tailored for different applications depending on the size of drug particles, target time for releasing the particles, and the size/shape of the container. This is the topic of a future communication by the authors.
V. Conclusions
This paper aims to present a combined acoustic-thermal-structural model to predict the shape recovery behavior of polymers under focused ultrasound. The numerical model provides the basis for designing spatially and temporally controlled drug delivery (CDD) systems. A theoretical framework is used to predict acoustic pressure field due to focused transducers, and the acoustic model is coupled with a thermal model to predict the developed temperature field due to focused ultrasound. The thermal field is then coupled to the mechanical model which solves for the stresses developed in the polymer and predicts the shape recovery of the system. Experiments are conducted to validate the numerical model. In addition to successful model validations against 3D finite-element simulations, a study on the effects of several system parameters is performed. The model is used to explore the effects of medium properties (nonlinearity and absorption), geometrical properties (thickness, width and initial deformation of the polymer filament) and input parameters (power and frequency) on shape recovery behavior of the polymer. The results show that while input source frequency has more influence on nonlinearity, input power plays a major role in achieving high temperature rise rates and thereby faster onset and increased shape recovery. Observations related to medium properties show that the coefficient of nonlinearity of the medium plays a significant role in distorting the waveform and generating more harmonics, thus increasing the energy deposition at the focal point and enhancing the shape recovery behavior. Our results will pave the way for designing more efficient drug delivery capsules at meso to nanoscale, and will shed light into the details of utilizing focused ultrasound for stimulating SMP-based mechanisms in drug delivery applications.Conflicts of interest
There are no conflicts to declare.References
- R. H. MuÈller, K. MaÈder and S. Gohla, Eur. J. Pharm. Biopharm., 2000, 50, 161–177 CrossRef.
- K. E. Uhrich, S. M. Cannizzaro, R. S. Langer and K. M. Shakesheff, Chem. Rev., 1999, 99, 3181–3198 CrossRef CAS PubMed.
- S. A. Martel-Estrada, I. Olivas-Armendáriz, C. A. Martínez-Pérez, T. Hernández, E. I. Acosta-Gómez, J. G. Chacón-Nava, F. Jiménez-Vega and P. E. García-Casillas, J. Mater. Sci.: Mater. Med., 2012, 23, 2893–2901 CrossRef CAS PubMed.
- T. Xie, Polymer, 2011, 52, 4985–5000 CrossRef CAS.
- R. Bogue, Assembly Automation, 2012, 32, pp. 3–7 Search PubMed.
- V. Giurgiutiu, J. Intell. Mater. Syst. Struct., 2000, 11, 525–544 CrossRef.
- I. Chopra, AIAA J., 2002, 40, 2145–2187 CrossRef CAS.
- M. V. Gandhi and B. S. Thompson, Smart materials and structures, Springer Science & Business Media, 1992 Search PubMed.
- A. Lendlein and S. Kelch, Angew. Chem., Int. Ed., 2002, 41, 2034–2057 CrossRef CAS.
- X. Chen, M. A. Dam, K. Ono, A. Mal, H. Shen, S. R. Nutt, K. Sheran and F. Wudl, Science, 2002, 295, 1698–1702 CrossRef CAS PubMed.
- X. Chen, F. Wudl, A. K. Mal, H. Shen and S. R. Nutt, Macromolecules, 2003, 36, 1802–1807 CrossRef CAS.
- C. e. Yuan, M. Z. Rong, M. Q. Zhang, Z. P. Zhang and Y. C. Yuan, Chem. Mater., 2011, 23, 5076–5081 CrossRef CAS.
- B. Ghosh and M. W. Urban, Science, 2009, 323, 1458–1460 CrossRef CAS PubMed.
- Y. Amamoto, H. Otsuka, A. Takahara and K. Matyjaszewski, Adv. Mater., 2012, 24, 3975–3980 CrossRef CAS PubMed.
- W. M. Huang, Y. Zhao, C. C. Wang, Z. Ding, H. Purnawali, C. Tang and J. L. Zhang, J. Polym. Res., 2012, 19, 9952 CrossRef.
- H. Lu, W. M. Huang, Y. Q. Fu and J. Leng, Smart Mater. Struct., 2014, 23, 125041 CrossRef.
- R. Mirzaeifar, PhD Thesis, Georgia Institute of Technology, 2013.
- R. Mirzaeifar, R. DesRoches, A. Yavari and K. Gall, Int. J. Solids Struct., 2013, 50, 1664–1680 CrossRef CAS.
- R. Mirzaeifar, R. DesRoches and A. Yavari, Continuum Mech. Thermodyn., 2011, 23, 363–385 CrossRef CAS.
- K. Uchino, Shape Memory Materials, 1998, pp. 184–202 Search PubMed.
- H. Meng and G. Li, Polymer, 2013, 54, 2199–2221 CrossRef CAS.
- C. Liu, H. Qin and P. T. Mather, J. Mater. Chem., 2007, 17, 1543–1558 RSC.
- D. Ratna and J. Karger-Kocsis, J. Mater. Sci., 2008, 43, 254–269 CrossRef CAS.
- S. S. Venkatraman, L. P. Tan, J. F. D. Joso, Y. C. F. Boey and X. Wang, Biomaterials, 2006, 27, 1573–1578 CrossRef CAS PubMed.
- C. M. Yakacki, R. Shandas, C. Lanning, B. Rech, A. Eckstein and K. Gall, Biomaterials, 2007, 28, 2255–2263 CrossRef CAS PubMed.
- L. Xue, S. Dai and Z. Li, Biomaterials, 2010, 31, 8132–8140 CrossRef CAS PubMed.
- B. L. Volk, PhD Thesis, Texas A&M University, 2012.
- C. Wischke and A. Lendlein, Pharm. Res., 2010, 27, 527–529 CrossRef CAS PubMed.
- J. Kost and R. Langer, Adv. Drug Delivery Rev., 2012, 64, 327–341 CrossRef.
- J. R. Kumpfer and S. J. Rowan, J. Am. Chem. Soc., 2011, 133, 12866–12874 CrossRef CAS PubMed.
- A. Lendlein, H. Jiang, O. Jünger and R. Langer, Nature, 2005, 434, 879–882 CrossRef CAS PubMed.
- K. C. Hribar, R. B. Metter, J. L. Ifkovits, T. Troxler and J. A. Burdick, Small, 2009, 5, 1830–1834 CrossRef CAS PubMed.
- U. N. Kumar, K. Kratz, W. Wagermaier, M. Behl and A. Lendlein, J. Mater. Chem., 2010, 20, 3404–3415 RSC.
- U. N. Kumar, K. Kratz, M. Heuchel, M. Behl and A. Lendlein, Adv. Mater., 2011, 23, 4157–4162 CrossRef CAS PubMed.
- K. Yu, Z. Zhang, Y. Liu and J. Leng, Appl. Phys. Lett., 2011, 98, 074102 CrossRef.
- Y. Liu, H. Lv, X. Lan, J. Leng and S. Du, Compos. Sci. Technol., 2009, 69, 2064–2068 CrossRef CAS.
- J. E. Kennedy, G. R. Ter Haar and D. Cranston, Br. J. Radiol., 2003, 76, 590–599 CrossRef CAS PubMed.
- G. ter Haar and C. Coussios, Int. J. Hyperthermia, 2007, 23, 89–104 CrossRef.
- S. Shahab and A. Erturk, Smart Mater. Struct., 2014, 23, 125032 CrossRef.
- S. Shahab, M. Gray and A. Erturk, J. Appl. Phys., 2015, 117, 104903 CrossRef.
- S. Shahab and A. Erturk, Contactless Ultrasonic Energy Transfer: Acoustic-Piezoelectric Structure Interaction Modeling and Performance Enhancement, American Society of Mechanical Engineers, 2014, p. V008T011A0955 Search PubMed.
- M. B. Nejad, A. Elnahhas, S. Jung and S. Shahab, Ultrasound acoustic energy for microbubble manipulation, International Society for Optics and Photonics, 2017, p. 101642H-101642H-101614 Search PubMed.
- J. Kost, K. Leong and R. Langer, Proc. Natl. Acad. Sci. U. S. A., 1989, 86, 7663–7666 CrossRef CAS.
- B. G. De Geest, A. G. Skirtach, A. A. Mamedov, A. A. Antipov, N. A. Kotov, S. C. De Smedt and G. B. Sukhorukov, Small, 2007, 3, 804–808 CrossRef CAS PubMed.
- H. Bruinewoud, PhD Thesis, Technical University Eindhoven, 2005.
- D. G. Shchukin, D. A. Gorin and H. Möhwald, Langmuir, 2006, 22, 7400–7404 CrossRef CAS PubMed.
- A. G. Skirtach, B. G. De Geest, A. Mamedov, A. A. Antipov, N. A. Kotov and G. B. Sukhorukov, J. Mater. Chem., 2007, 17, 1050–1054 RSC.
- G. A. Husseini, N. Y. Rapoport, D. A. Christensen, J. D. Pruitt and W. G. Pitt, Colloids Surf., B, 2002, 24, 253–264 CrossRef CAS.
- Y. Li, R. Tong, H. Xia, H. Zhang and J. Xuan, Chem. Commun., 2010, 46, 7739–7741 RSC.
- J. Wang, M. Pelletier, H. Zhang, H. Xia and Y. Zhao, Langmuir, 2009, 25, 13201–13205 CrossRef CAS PubMed.
- A. Marin, M. Muniruzzaman and N. Rapoport, J. Controlled Release, 2001, 75, 69–81 CrossRef CAS PubMed.
- B. Liu, H. Xia, G. Fei, G. Li and W. Fan, Macromol. Chem. Phys., 2013, 214, 2519–2527 CrossRef CAS.
- J. Han, G. Fei, G. Li and H. Xia, Macromol. Chem. Phys., 2013, 214, 1195–1203 CrossRef CAS.
- X. Lu, G. Fei, H. Xia and Y. Zhao, J. Mater. Chem. A, 2014, 2, 16051–16060 RSC.
- G. Li, G. Fei, B. Liu, H. Xia and Y. Zhao, RSC Adv., 2014, 4, 32701–32709 RSC.
- T. S. Hart and M. F. Hamilton, J. Acoust. Soc. Am., 1988, 84, 1488–1496 CrossRef.
- A. Rozanova-Pierrat, Mathematical analysis of Khokhlov-Zabolotskaya-Kuznetsov (KZK) equation, 2006 Search PubMed.
- M. F. Hamilton and D. T. Blackstock, Nonlinear acoustics, Academic press, San Diego, 1998 Search PubMed.
- F. P. Curra, P. D. Mourad, V. A. Khokhlova, R. O. Cleveland and L. A. Crum, IEEE Trans. Sonics Ultrason., 2000, 47, 1077–1089 CrossRef CAS PubMed.
- Y. Jing, D. Shen and G. T. Clement, IEEE Trans. Sonics Ultrason., 2011, 58(5), 1097–1101 CrossRef PubMed.
- J. Tavakkoli, D. Cathignol, R. Souchon and O. A. Sapozhnikov, J. Acoust. Soc. Am., 1998, 104, 2061–2072 CrossRef CAS PubMed.
- M. Solovchuk, T. W. H. Sheu and M. Thiriet, J. Acoust. Soc. Am., 2013, 134, 3931–3942 CrossRef PubMed.
- H. O'Neil, J. Acoust. Soc. Am., 1949, 21, 516–526 CrossRef.
- J. E. Soneson, J. Acoust. Soc. Am., 2012, 131, EL481–EL486 CrossRef PubMed.
- J. E. Soneson, R. Muratore and E. E. Konofagou, Practical limits of the parabolic approximation for focused ultrasound beams, AIP, 2012, pp. 357–361 Search PubMed.
- V. A. Khokhlova, S. S. Kashcheeva, M. A. Averkiou and L. A. Crum, Effect of selective absorption on nonlinear interactions in high intensity acoustic beams, AIP, 2000, pp. 151–154 Search PubMed.
- B. Ystad and J. Berntsen, Acust. Acta Acust., 1995, 3, 323–330 Search PubMed.
- J. Huijssen and M. D. Verweij, J. Acoust. Soc. Am., 2010, 127, 33–44 CrossRef CAS PubMed.
- V. W. Sparrow and R. Raspet, J. Acoust. Soc. Am., 1991, 90, 2683–2691 CrossRef.
- Y. S. Lee and M. F. Hamilton, J. Acoust. Soc. Am., 1995, 97, 906–917 CrossRef.
- S. I. Aanonsen, Numerical computation of the nearfield of a finite amplitude sound beam, University of Bergen, Department of Applied Mathematics, 1983 Search PubMed.
- M. F. Hamilton, J. N. Tjøtta and S. Tjøtta, J. Acoust. Soc. Am., 1985, 78, 202–216 CrossRef.
- T. Kamakura, M. Tani, Y. Kumamoto and K. Ueda, J. Acoust. Soc. Am., 1992, 91, 3144–3151 CrossRef.
- F. S. McKendree, A Numerical Solution of the Second-Order-Nonlinear Acoustic Wave Equation in One and in Three Dimensions, DTIC Document, 1981.
- K. Frøysa, J. N. Tjøtta and J. Berntsen, Advances in nonlinear acoustics, 1993, pp. 233–238 Search PubMed.
- F. Pestorius and D. Blackstock, Finite-Amplitude Wave Effects in Fluids, 1974, pp. 24–29 Search PubMed.
- R. O. Cleveland, M. F. Hamilton and D. T. Blackstock, J. Acoust. Soc. Am., 1996, 99, 3312–3318 CrossRef.
- K. R. Waters, M. S. Hughes, J. Mobley, G. H. Brandenburger and J. G. Miller, J. Acoust. Soc. Am., 2000, 108, 556–563 CrossRef PubMed.
- N. Jiménez, F. Camarena, J. Redondo, V. Sánchez-Morcillo, Y. Hou and E. E. Konofagou, Acta Acust. Acust., 2016, 102, 876–892 CrossRef.
- L. Bjørnø, Phys. Procedia, 2010, 3, 5–16 CrossRef.
- G. B. Whitham, Linear and nonlinear waves, John Wiley & Sons, 2011 Search PubMed.
- J. E. Soneson and E. S. Ebbini, A User-Friendly Software Package for HIFU Simulation, AIP, 2009, pp. 165–169 Search PubMed.
- J. E. Soneson and M. R. Myers, IEEE Trans. Sonics Ultrason., 2010, 57, 2450–2459 CrossRef PubMed.
- M. Wang and Y. Zhou, Int. J. Hyperthermia, 2016, 32, 569–582 CrossRef PubMed.
- W. F. Ames, Numerical methods for partial differential equations, Academic press, 2014 Search PubMed.
- A. Ostermann and M. Roche, Math. Comput., 1992, 59, 403–420 CrossRef.
- C. R. Hill, J. C. Bamber and G. Ter Haar, J. Acoust. Soc. Am., 2004, 116, 2707 CrossRef.
- G. Ter Haar, Prog. Biophys. Mol. Biol., 2007, 93, 111–129 CrossRef PubMed.
- W. Summer and M. K. Patrick, Ultrasonic therapy: A textbook for physiotherapists, Elsevier, 1964 Search PubMed.
- M. Khanolkar, J. Sodhi and I. J. Rao, 2010, DOI:10.1115/SMASIS2010-3694, 105–109.
- G. Barot, I. J. Rao and K. R. Rajagopal, IUST Int. J. Eng. Sci., 2008, 46, 325–351 CrossRef CAS.
- L. V. Brent, C. L. Dimitris and C. Yi-Chao, Smart Mater. Struct., 2010, 19, 075006 CrossRef.
- H. J. Qi, T. D. Nguyen, F. Castro, C. M. Yakacki and R. Shandas, J. Mech. Phys. Solids, 2008, 56, 1730–1751 CrossRef CAS.
- K. Yu and H. J. Qi, Soft Matter, 2014, 10, 9423–9432 RSC.
- G. Barot, Constitutive Modeling of the Thermo-mechanics Associated with Crystallizable Shape Memory Polymers, ProQuest, 2007 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07396h |
| This journal is © The Royal Society of Chemistry 2017 |