Open Access Article
Open Access ArticleRadiation enhanced uptake of Hg0(g) on iron (oxyhydr)oxide nanoparticles†
Uday Kurien a,
Zhenzhong Hub,
Heonho Leeb,
Ashu P. Dastoorc and
Parisa A. Ariya*ab
a,
Zhenzhong Hub,
Heonho Leeb,
Ashu P. Dastoorc and
Parisa A. Ariya*ab
aDepartment of Atmospheric and Oceanic Sciences, McGill University, 801 Sherbrooke West, Montreal, QC H3A 2K6, Canada. E-mail: parisa.ariya@mcgill.ca; Fax: +1-514-398-3797; Tel: +1-514-398-6931 Tel: +1-514-398-3615
bDepartment of Chemistry, McGill University, 801 Sherbrooke West, Montreal, QC H3A 2K6, Canada
cAir Quality Research Division, Environment and Climate Change Canada, 2121, Route Transcanadienne, Dorval, QC H9P 1J3, Canada
First published on 21st September 2017
Abstract
Despite the proposed importance of atmospheric mercury (Hg) cycling, little is known about its heterogeneous chemistry, specifically on ubiquitous dust particle surfaces in the environment. To address this gap in knowledge, we herein report the uptake coefficients for the uptake of Hg0(g) on iron (oxyhydr)oxides (γ-Fe2O3, α-FeOOH, α-Fe2O3 and Fe3O4) nanoparticles, employed as proxies for reactive components of mineral dust. Hg0(g)-particle interactions were studied in a batch set-up, at ambient pressure (760 ± 5 Torr) and temperatures (295 ± 2 K) with UV and visible irradiation (290 nm ≤ λ ≤ 700 nm). γ-Fe2O3, α-FeOOH and α-Fe2O3 demonstrated a ca. 40–900-fold increase in uptake kinetics upon irradiation, under our experimental conditions. In contrast, uptake kinetics on Fe3O4's surface displayed little dependence on irradiation. Relative humidity was shown to inhibit the effect of radiation on the uptake of Hg0(g) by α-Fe2O3. Size distributions, electronic properties, surface area and phase characterization of the iron(oxyhydr)oxide particles were studied to explain the uptake kinetics, and to provide insights into the mechanism of Hg0(g) loss. The adsorption capacity of Hg0(g) on α-Fe2O3 was determined from the adsorption isotherm fitted with Langmuir, Freundlich and Elovich adsorption models. The implications of the results to atmospheric chemical processes are herein discussed.
1. Introduction
Mercury (Hg) is a top priority contaminant of global interest. Gaseous elemental mercury (GEM, Hg0(g)), the predominant form of atmospheric Hg, has a lifetime of several months to years,1,2 and can have local, regional and global impacts. It is removed from the atmosphere via oxidation and deposition.3 Following deposition, Hg can be either re-emitted into the atmosphere, or methylated and subsequently bio-magnified, adversely impacting human health.4 As such, the international Minamata treaty was agreed upon by 128 countries to limit anthropogenic Hg emissions into the environment.5 The recent withdrawal of the US from the 2015 Paris Agreement, and the consequent reversal of its decision to reduce coal fired plants (the largest point source of anthropogenic Hg emissions) is expected to be potentially detrimental to global Hg mitigation efforts.Deposition of Hg can occur through wet and dry processes, such as the deposition of particulate bound mercury (PBM).6 Evidence from atmospheric and global modeling studies suggest that both dry and wet deposition pathways are important to the total deposition of Hg; however, owing to large uncertainties in dry deposition processes, estimates among models differ from each other by as much as a factor of 2 in North America and by an order of magnitude on the global scale.7 The inability to accurately quantify Hg dry deposition has, in part, been attributed to an incomplete understanding of the underlying physico-chemical processes driving Hg transformations.6
Of importance to these transformations, specifically the formation of PBM, are ubiquitous atmospheric aerosols. Despite substantial progress having been made in understanding atmospheric gas phase oxidation reactions of Hg0,8,9 and reduction reactions of Hg2+ on terrestrial surfaces,10 little is known about the impact of atmospheric aerosol surfaces on GEM. Published literature has speculated on the uptake of Hg0(g) by particulate matter in the atmosphere based on observations and theoretical analysis.11,12 However, to the best of our knowledge, experimental studies on the uptake of Hg0(g) with such surfaces are scarce.
Mineral dusts are common atmospheric aerosols, capable of acting as condensation nuclei influencing cloud formation, Earth's radiation budget and ultimately climate.13 Dust particles also provide surfaces for the reaction and uptake of trace atmospheric gases such as organic compounds.14 Metals and metal oxides are important reactive components of dust particles. Common metal oxides include those of iron and titanium such as Fe2O3, Fe3O4 (Fe2O3·FeO), FeOOH and TiO2.15 These oxides lend mineral dusts photo enhanced reactivity towards gases, such as the catalytic decomposition of O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and uptake and nucleation of SO2
16 and uptake and nucleation of SO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 and NO2.18 While the uptake of Hg0(g) on TiO2 is well documented19 a similar understanding of the photochemical aging processes on iron oxide surfaces is scarce.
17 and NO2.18 While the uptake of Hg0(g) on TiO2 is well documented19 a similar understanding of the photochemical aging processes on iron oxide surfaces is scarce.
It has been suggested that iron oxide fractions in fly-ash promote adsorption of Hg0(g) in simulated stack conditions.20 However, due to high temperatures and the complexity of the feed gas and particulate phase composition, little is known about the nature of Hg0(g)–iron oxide interactions at environmentally relevant conditions, after its emission. There are also recent theoretical investigations into mechanisms of Hg0–Fe2O3 interactions.21,22 These studies, however, do not address the impact of atmospheric relevant radiation on the reactions, particularly in the lower troposphere which is abundant in dust particles.
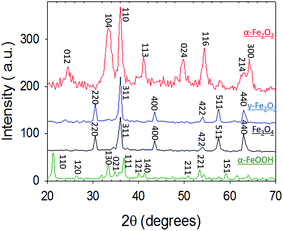
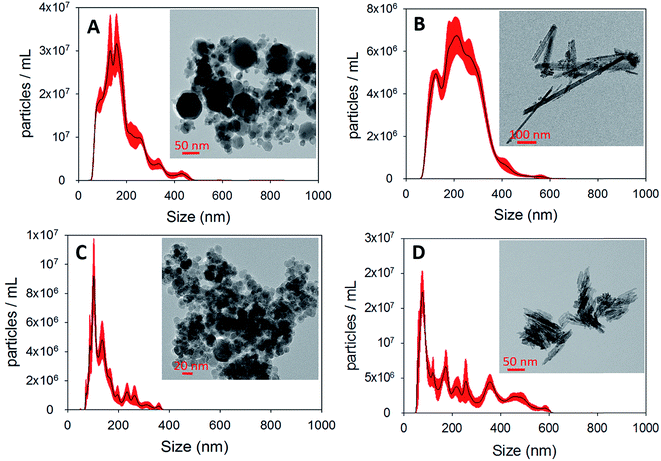
The objective of this work was, hence, to study the heterogeneous chemistry, influenced by photochemistry and humidity, of Hg0(g) on the reactive components of mineral dust and to provide insights on the photochemical aging processes in the troposphere. We performed uptake reactions of Hg0(g) on the surfaces of α-Fe2O3 (hematite), γ-Fe2O3 (maghemite), Fe3O4 (magnetite) and α-FeOOH (goethite) nanoparticles, used as proxies for the reactive components of mineral dust aerosols.23 The effects of common atmospheric parameters, such as irradiation and humidity, on the promotion or inhibition of these reactions were examined. Reaction kinetics were evaluated and reported as pseudo first order rate constants (k) and uptake coefficients (γ). We discuss our observations in relation to the particle properties obtained through multiple characterization techniques: Nanoparticle Tracking Analysis (NTA), Transmission Electron Microscopy (TEM), BET surface area, X-Ray Diffraction (XRD), X-ray Photoelectron Spectroscopy (XPS) and UV-Visible Diffuse Reflectance Spectroscopy (UV-Vis DRS). We also examine how our laboratory results may help improve global atmospheric Hg models.
2. Experimental section
The following sections detail the experimental procedures employed for the synthesis and characterization of the nanoparticles, the measurement of adsorption kinetics and adsorption isotherms. We provide detailed descriptions of the reaction chambers, Hg0(g) measurement techniques, methodology and kinetic models employed to evaluate the impact of radiation and relative humidity on the uptake reactions.2.1 Characterization of the iron (oxyhydr)oxide particles
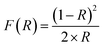 | (E1) |
2.2 Uptake and adsorption studies: impact of radiation and relative humidity
The uptake reactions were monitored by measuring the loss of Hg0(g) using Electron Ionization (EI) Mass Spectrometry (MS) performed with an Agilent G1540A Gas Chromatograph (GC) in tandem with a Hewlett Packard 5973 mass selective detector. Details of the method are presented in Section S1 of the ESI.† Prior to use, the particles were placed in the chamber and swirled to coat the inner walls of the chamber. The reaction chamber, containing the particles, was evacuated to ∼5 × 10−2 Torr, for 30 minutes, filled with extra dry air and then evacuated again. The process was repeated thrice, using a ChemGlass vacuum line fitted with an Edwards high vacuum pump and Edwards 2 stage pressure gauge, to maximize removal of surface adsorbed species prior to Hg0(g) uptake experiments.
Quantitative transfer of Hg0(g) into the reaction chamber was achieved by connecting stock flask (containing Hg0(l) in equilibrium with Hg0(g) in extra dry air) to the vacuum line and allowing Hg0(g) to diffuse to the evacuated reaction chamber. The amount of Hg0(g) transferred to the reaction chamber was controlled by tuning the pressure of the reaction chamber relative to that of the stock flask, maintained at ∼760 Torr. The final pressure of the reaction chamber was brought upto 760 ± 3 Torr with extra dry. The experiments were performed with an initial Hg0(g) concentration of 3 μg L−1 (±10%).
The order in which the reactants were introduced into the chamber was: (1) the particles, (2) water vapor, (3) Hg0(g) in air and finally (4) air as the make-up gas to raise the final pressure up to 760 Torr. The start time of the experiment (t = 0 minutes) is defined as the time when iron (oxyhydr)oxide particles, Hg0(g), water vapor and the make-up gas were present in the chamber at 760 Torr.
The reaction chamber was housed in an irradiation chamber equipped with appropriate broadband illumination sources for UV-A (315 ≤ λ ≤ 400 nm), UV-B (280 ≤ λ ≤ 315 nm) and visible (400 ≤ λ ≤ 700 nm) radiation. Details of the light sources and characterization of their radiation intensity and emission spectra are presented in Section S2 of the ESI.† The temperature of the irradiation chamber was monitored using a Fischer Scientific temperature probe.
| ln[Hg]t = k × t + ln[Hg]o | (E2) |
The pseudo first order rate constant (k) was expressed as the uptake coefficient (γ) defined as:30
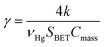 | (E3) |
Additionally, the statistical significance of the effect of radiation on Hg0(g) loss was calculated by comparing sample means of Hg0(g) concentrations post irradiation to Hg0(g) concentrations in control (dark) experiments using the 2 sample Student t-test with the Welch correction, to account for different sample sizes and variances. The t-tests were executed using the default algorithms in R programming language. A p value of less than 0.05 was used to identify statistically distinct samples in a 95% confidence interval.
2.3 Materials and supplies
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 solution of ferric chloride hexahydrate (FeCl3·6H2O) and ferrous chloride tetrahydrate (FeCl2·4H2O) in deoxygenated water maintained at 85 °C. The nanoparticles were recovered magnetically and rinsed thrice with warm deoxygenated water and allowed to dry in a vacuum oven maintained at 60 °C. The synthesized nanoparticles were stored in a vacuum desiccator for the duration of the experiments to minimize oxidation by atmospheric O2.
1 solution of ferric chloride hexahydrate (FeCl3·6H2O) and ferrous chloride tetrahydrate (FeCl2·4H2O) in deoxygenated water maintained at 85 °C. The nanoparticles were recovered magnetically and rinsed thrice with warm deoxygenated water and allowed to dry in a vacuum oven maintained at 60 °C. The synthesized nanoparticles were stored in a vacuum desiccator for the duration of the experiments to minimize oxidation by atmospheric O2.α-FeOOH nanoparticles were prepared by adding sodium hydroxide (NaOH) dropwise to an 85 °C deoxygenated solution of FeCl3·6H2O followed by addition of a trace amount of FeCl2·4H2O (nFe(II)/nFe(III) = 0.02). The solution was refluxed in air for 4 hours. The precipitate was washed 5 times with ultrapure water and dried in a vacuum oven at 50 °C.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4OH (28.0–30.0% NH3 weight basis, ACS reagent), NaOH (≥97.0%, ACS reagent), FeCl3·6H2O (≥97.0%, ACS reagent) and FeCl2·4H2O (≥98.0%), were purchased from Sigma-Aldrich and used without further purification.
NH4OH (28.0–30.0% NH3 weight basis, ACS reagent), NaOH (≥97.0%, ACS reagent), FeCl3·6H2O (≥97.0%, ACS reagent) and FeCl2·4H2O (≥98.0%), were purchased from Sigma-Aldrich and used without further purification.Extra dry air (19.5% ≤ O2 ≤ 23.5% and H2O < 10 ppm), from Praxair, was used as the diluent to prepare gas phase solutions of Hg0. 18.2 MΩ deionized water from a Milli-Q (Millipore) system was used to generate water vapor for experiments conducted with humidity.
3. Results and discussions
In this section, we report and discuss the physical and chemical characterization of the iron (oxyhydr)oxide particles, uptake coefficients, adsorption isotherms and the influence of humidity and irradiation on the uptake reactions. We subsequently integrate our observations to propose potential mechanisms for these reactions, and further conceptualize their implications for atmospheric Hg models.3.1 Characterization of iron (oxyhydr)oxides
3.2 Uptake of Hg0(g) on iron (oxyhydr)oxides
| k [min−1] | γ | γlight/γdark | ||
|---|---|---|---|---|
| Fe3O4 | Dark | (1.15 ± 0.17) × 10−2 | (1.09 ± 0.16) × 10−10 | 1.00 |
| Visible | (1.01 ± 0.10) × 10−2 | (9.66 ± 0.95) × 10−11 | 0.87 | |
| UV-A | (1.15 ± 0.21) × 10−2 | (1.09 ± 0.20) × 10−10 | 1.00 | |
| UV-B | (1.41 ± 0.19) × 10−2 | (1.35 ± 0.18) × 10−10 | 1.22 | |
| α-FeOOH | Dark | (1.71 ± 0.41) × 10−4 | (2.11 ± 0.51) × 10−12 | 1.00 |
| Visible | (1.87 ± 0.58) × 10−2 | (2.30 ± 0.71) × 10−10 | 109.35 | |
| UV-A | (1.62 ± 0.12) × 10−1 | (1.99 ± 0.14) × 10−9 | 947.36 | |
| UV-B | (9.67 ± 2.08) × 10−2 | (1.19 ± 0.25) × 10−9 | 565.49 | |
| γ-Fe2O3 | Dark | (9.50 ± 0.71) × 10−4 | (1.96 ± 0.14) × 10−11 | 1.00 |
| Visible | (4.64 ± 0.19) × 10−2 | (9.57 ± 0.39) × 10−10 | 48.84 | |
| UV-A | (7.95 ± 0.34) × 10−2 | (1.64 ± 0.70) × 10−9 | 83.68 | |
| UV-B | (4.19 ± 0.10) × 10−2 | (8.64 ± 0.21) × 10−10 | 44.10 | |
| α-Fe2O3 | Dark | (3.70 ± 2.12) × 10−4 | (2.81 ± 1.61) × 10−12 | 1.00 |
| Visible | (7.43 ± 1.07) × 10−2 | (5.64 ± 0.81) × 10−10 | 200.81 | |
| UV-A | (2.21 ± 0.22) × 10−1 | (1.59 ± 0.16) × 10−9 | 567.56 | |
| UV-B | (9.84 ± 1.35) × 10−2 | (7.47 ± 1.03) × 10−10 | 265.94 |
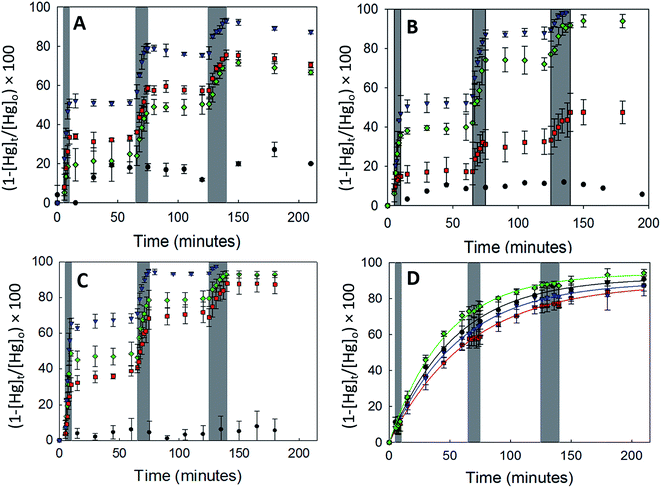
3.2.2.1 Uptake of Hg0(g) on γ-Fe2O3. Fig. 3A displays the loss of Hg0(g) on γ-Fe2O3 with the different types of irradiation. The x-axis and y-axis depict the percentage loss of Hg0(g) and time expressed in minutes, respectively. Grey bands represent periods of irradiation while the white spaces represent aging of the particles in the dark. It was observed that irradiation with visible, UV-A or UV-B radiation led to a rapid loss of Hg0(g). t-Tests confirmed that Hg0(g) concentrations after the irradiation pulses were statistically distinct from (a) Hg0(g) concentrations prior to the pulse and (b) control reactions done in dark conditions. Since significant Hg0(g) losses were not observed in (a) dark reactions with iron (oxyhydr)oxides and (b) irradiated controls without iron (oxyhydr)oxides, it was assumed that Hg0(g) losses were driven by the irradiated γ-Fe2O3 surfaces. The loss of Hg0(g) ceased with termination of each irradiation pulse, suggesting that aged γ-Fe2O3 surfaces were not involved in secondary reactions with Hg0(g) post radiation exposure.
Continuous curves for the radiation driven loss of Hg0(g) were obtained by splicing together changes in the concentration of Hg0(g) over the 3 irradiation pulses. The spliced curves are shown in ESI, Section S6.† Pseudo first order rate constants for the loss of Hg0(g) were obtained by fitting the data to the linearized form of the pseudo first order kinetic model. The model described the data well with R2 > 0.98 for irradiated experiments. Dark reactions, however, were found to have low coefficients of determination (R2 < 0.52) which were attributed to the changes in Hg0(g) concentrations being similar to the instrumental variability (±10%).
The rate coefficients were normalized by the mass loading and BET surface area of γ-Fe2O3 to yield the uptake coefficients. It should be noted that using BET surface area, instead of geometric surface area, underestimates the values of γ as all the surfaces may not participate in the uptake reaction.32 In real atmospheric and stack conditions iron (oxyhydr)oxides aerosols may be expected to be suspended in the air, increasing available surfaces for the uptake of Hg0(g). We therefore regard our reported values of γ to be the lower bound estimates of these reactions.
The values of k and γ are summarized in Table 1. Under similar initial reaction conditions of Hg0(g) and γ-Fe2O3 concentrations, temperature, humidity and reaction flask surface to volume ratio, γ values for irradiated experiments were ca. 40–80 times larger than dark reactions. The relative increase in γ was expressed as the ratio of the uptake coefficients on irradiation (γlight) to the uptake coefficients of dark reactions (γdark), and presented in the last column of Table 1. It was additionally found that γ varied with the wavelength bands of radiation used. γ for the loss of Hg0(g) was highest in UV-A > visible ≥ UV-B > dark. The dependence of γ on wavelength was suspected to be related to the optical properties of γ-Fe2O3, which were characterized with UV-Vis DRS.
Fig. 4 depicts a plot of the Kubelka–Munk function (top panel) and its first derivative (bottom panel) against wavelength (λ) of the iron (oxyhydr)oxides (the 250–800 nm spectra are present in ESI, Section S7†). The band gaps calculated in this study are in agreement with previously published values.33,34
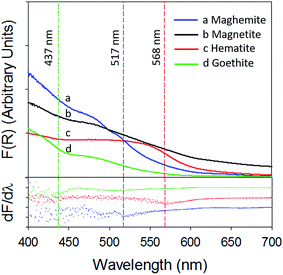 | ||
| Fig. 4 Kubelka–Munk function (top panel) and its first derivative (bottom panel) of (a) γ-Fe2O3 (blue) (b) Fe3O4 (black) (c) α-Fe2O3 (red) and (d) α-FeOOH (green). | ||
The band gap of γ-Fe2O3 was determined to be 2.39 eV (or 517 nm). Consequently, the entire UV-A band (315–400 nm), used in this study, was likely to have energies sufficient to promote electronic transitions in γ-Fe2O3. In contrast, electronic transitions due to visible radiation (400–700 nm) may have occurred only for λ < 517 nm. For λ > 517 nm, the incoming radiation was likely not energetically sufficient to promote transitions. As consequence of this only about 40–50% of the total impinged visible radiation may have excited electrons across the band gap, causing γ values to be lower with visible radiation than UV-A radiation. It is additionally possible that since electronic transitions in visible radiation arise from weaker indirect d–d transitions, compared to direct transitions in UV radiation,35,36 the associated reactions kinetics are lower than those for direct transitions.36
Following the previous discussion, it was expected that the entire UV-B band (280–315 nm) had sufficient energy to promote electronic transitions and therefore result in uptake coefficients similar to those obtained with UV-A radiation. γ values for UV-B radiation were, however, seen to be only about ∼50% of the γ values obtained with UV-A radiation. This apparent discrepancy was explained by the attenuation of UV-B radiation by the reaction chamber walls. The construction material of our reaction chambers – Pyrex (borosilicate glass)- is known to absorb UV-B radiation.37 The radiation transmitted through the reaction chamber walls, characterized with a PM100A power meter (Thor Labs), was attenuated by ∼53%, (characterization of radiation attenuation is presented in Section S2, Table S2 of the ESI†) thereby limiting its availability for the photolytic uptake of Hg0(g).
3.2.2.2 Uptake of Hg0(g) on α-Fe2O3 and α-FeOOH. To further explore the correlation between iron oxide band gaps and Hg0(g) loss kinetics, Hg0(g) uptake experiments, in dry air, were conducted with the additional iron oxides (α-Fe2O3, Fe3O4) and iron oxide-hydroxide (α-FeOOH).
α-Fe2O3 displayed similar adsorption characteristics as γ-Fe2O3, with enhanced Hg0(g) loss kinetics (Fig. 3C) upon irradiation, under our experimental conditions. The enhancement of uptake kinetics in visible light was lower than that of UV-A radiation (Table 1). This is in agreement with (a) the calculated band gap of 568 nm (Table 2) for α-Fe2O3, because of which half the visible band was expected to lack sufficient energy to promote transitions between the valence and conduction bands and (b) the promotion of weaker indirect d–d transitions with visible radiation compared to stronger direct transitions with UV radiation, as discussed before.36
| Iron oxide | Band gap (eV) | Specific surface area (m2 g−1) |
|---|---|---|
| Fe3O4 | — | 72.85 ± 0.63 |
| α-FeOOH | 2.83 | 56.51 ± 1.52 |
| γ-Fe2O3 | 2.39 | 33.78 ± 1.48 |
| α-Fe2O3 | 2.18 | 91.71 ± 0.35 |
Similar to our observations for γ-Fe2O3 and α-Fe2O3, we observed the loss of Hg0(g) on α-FeOOH when irradiated (Fig. 3B). However, in contrast to γ-Fe2O3 and α-Fe2O3, the activity in the visible region was only about 11.5% of that observed in UV-A irradiation experiments (Table 1). The calculated band gap for α-FeOOH was found to be 437 nm, which likely limited the spectrum of the visible region, capable of causing transitions, to 12% (400–437 nm) of the 400–700 nm visible band. It has been shown that for α-FeOOH the energies of direct band transitions decrease from 3.2 eV (λ = 387 nm) to a limiting value of 2.5 eV (λ = 495 nm), and energies of indirect transitions decrease from 2.1–1.6 eV (λ = 590–774 nm) with increasing particle size from 8 nm to 40 nm.38 Therefore it can be expected that size is a crucial factor in determining Hg0(g) loss on irradiated α-FeOOH.
It should be noted that the maximum uptake kinetics for Hg0(g) loss on α-Fe2O3 and α-FeOOH were observed with UV-A illumination. The increase in γ values were large; approximately 567 and 947-fold greater than dark reactions on the surfaces of α-Fe2O3 and α-FeOOH, respectively.
It was also observed that rate of loss of Hg0(g) on α-Fe2O3 and α-FeOOH in the presence of UV-B was, within limits of experimental uncertainty, half that of UV-A. This was attributed to the attenuation of UV-B radiation transmitted through the reaction chamber walls, as discussed before.
3.2.2.3 Uptake of Hg0(g) on Fe3O4. With Fe3O4, Hg0(g) losses were observed in the dark. Illumination with UV and visible radiation did not yield measurable changes in Hg0(g) loss kinetics relative to the dark reactions (Fig. 3D). Fe3O4 absorbed at all wavelengths examined in this study using UV-Vis DRS (ESI, Section S7†). No clear peaks were observed in the first derivative plot of Fe3O4 and it was therefore omitted from Fig. 4 to improve clarity. The mechanisms of the photolytic uptake of Hg0(g) on α-Fe2O3, α-FeOOH and γ-Fe2O3, and the reasons for the lack of photolytic activity on the surface of Fe3O4 are discussed in Section 3.6.
3.3 Effect of concentration on uptake kinetics and uptake coefficient
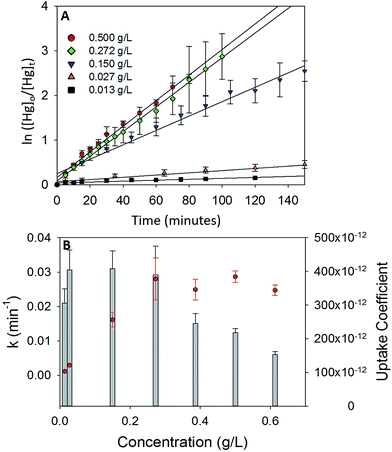
To study the dependence of γ on the mass loading of the iron oxides, adsorption experiments were done with varying concentrations of α-Fe2O3 (0.013 g L−1 to 0.613 g L−1) in visible light (Fig. 5A). On visual inspection, the coating was sparse for α-Fe2O3 concentration of 0.013 g L−1, yet increased steadily with increasing concentration up to 0.272 g L−1. At concentrations >0.272 g L−1 the coating appeared densest with excess α-Fe2O3 accumulating at the bottom of the reaction chamber.The calculated values of k and γ are shown in Fig. 5B. It was observed that k increased almost linearly with increasing concentrations of α-Fe2O3 from 0.013 g L−1 to 0.272 g L−1, however, a further increase in concentrations from 0.272 g L−1 to 0.613 g L−1 did not lead to a corresponding increase in k.
This stabilization of k was attributed to the non-participation of additional surfaces beyond a concentration of 0.272 g L−1. Since the adsorption process was photolytic, we expected only irradiated iron oxide surfaces to participate in the reaction. From reported penetration depths of radiation through α-Fe2O3 (118 nm at λ = 550 nm),39 light may be expected to travel only through a few monolayers of the α-Fe2O3 nanoparticle coating before being extinguished. Increases in mass loadings of α-Fe2O3, beyond 0.272 g L−1, presumably inhibited radiation from reaching α-Fe2O3 particles that were (a) further away from the illuminated surfaces and (b) accumulated at the bottom of the chamber. Since these additional surfaces were not irradiated, they were expected to not contribute to the photolytic uptake of Hg0(g) thereby limiting k values. Stabilization of k values was reflected in further underestimation of the uptake coefficients. While γ was similar for α-Fe2O3 loadings of 0.027–0.272 g L−1, it decreased on increasing α-Fe2O3 loading beyond 0.272 g L−1. This trend was explained via eqn (E3). Above concentrations of 0.272 g L−1, k values remained constant, while Cmass increased, leading to decreases in the calculated values of γ.
It was additionally observed that for the adsorption of Hg0(g) on α-Fe2O3 in visible light, γ values averaged over 3 trials were lower for experiments done in 5.5 L chambers (γ = (3.90 ± 0.59) × 10−10) than 2.0 L chambers (γ = (5.64 ± 0.81) × 10−10). The difference was proportional to the difference in the surface to volume (S/V) ratios of the reaction chambers ((S/V)5.5 L/(S/V)2.0 L = 0.717 and γ5.5 L/γ2.0 L = 0.709). The increase in uptake kinetics with S/V ratios of the reaction chambers was likely due to the larger abundance of iron oxide surfaces on the walls of the reaction chamber, relative to the bulk, that participated in the photolytic uptake of Hg0(g).
3.4 Effect of water vapor on uptake coefficient
The values of γ discussed so far have only dealt with the adsorption of Hg0(g) on the iron oxides in dry conditions. However, such conditions are unlikely in atmosphere due to the relative abundance of water vapor. To address the influence of water vapor, uptake reactions on α-Fe2O3 were performed at relative humidities of <1%, 33%, 66% and 95%, in the presence of visible and UV-A radiation. We opted to exclude supersaturation conditions to avoid secondary reactions (e.g., solid/aqueous condensed phase chemistry), which occurs close to or over saturation point.The reaction variables and uptake coefficients are summarized in Table 3. It was observed that γ decreased rapidly with increasing relative humidity. Even at the low relative humidity of 33%, γ decreased by 89% and 93% for visible radiation and UV-A radiation, respectively, relative to the dry reactions.
| Effect of humidity on the uptake coefficient | |||||||
|---|---|---|---|---|---|---|---|
| S. no. | Conc. (g L−1) | RH (%) | Radiation | k (min−1) | γ | γwet/γdry | γlight/γdark |
| 1 | 0.272 | 0 | Visible | (2.81 ± 0.61) × 10−2 | (3.90 ± 0.59) × 10−10 | 1.00 | 142.21 |
| 2 | 0.272 | 33 | Visible | (0.33 ± 0.03) × 10−2 | (0.46 ± 0.04) × 10−10 | 0.11 | 16.35 |
| 3 | 0.272 | 66 | Visible | (0.16 ± 0.01) × 10−2 | (0.22 ± 0.01) × 10−10 | 0.05 | 7.93 |
| 4 | 0.272 | 95 | Visible | (0.12 ± 0.03) × 10−2 | (0.17 ± 0.04) × 10−10 | 0.04 | 5.94 |
| 5 | 0.272 | 0 | UV-A | (3.20 ± 0.40) × 10−2 | (4.46 ± 0.41) × 10−10 | 1.00 | 158.56 |
| 6 | 0.272 | 33 | UV-A | (0.24 ± 0.02) × 10−2 | (0.33 ± 0.03) × 10−10 | 0.07 | 11.89 |
| 7 | 0.272 | 66 | UV-A | (0.16 ± 0.01) × 10−2 | (0.22 ± 0.01) × 10−10 | 0.05 | 7.92 |
| 8 | 0.272 | 95 | UV-A | (0.06 ± 0.01) × 10−2 | (0.08 ± 0.01) × 10−10 | 0.02 | 2.84 |
The decrease in the uptake kinetics was attributed to competitive adsorption between water molecules and Hg0(g) atoms for active sites on α-Fe2O3's surface. As shown in previous research, the introduction of water vapor at increasing relative humidity, results in further water uptake by hematite.16 Once adsorbed, water molecules may have inhibited contact between the surface sites and Hg0(g) atoms, thereby preventing its photolytic uptake. It should be noted that a previous study with a flow through system at elevated temperatures studied the effect of humidity, but not radiation, on Hg0(g) adsorption by α-Fe2O3. They reported that while water vapor concentrations of up to 2% promoted Hg0(g) uptake, concentrations above 2% inhibited Hg0(g) adsorption.40
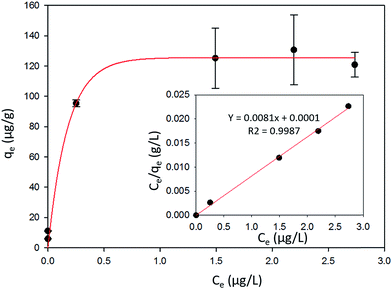
3.5 Adsorption isotherm
The Langmuir, Freundlich and Elovich models used in this study represent different physical basis for adsorption.
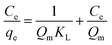 | (E4) |
The separation factor (RL) is defined as:
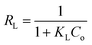 | (E5) |
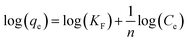 | (E6) |
A linear fit of log(qe) vs. log(Ce) yields the adsorption intensity (n) and the Freundlich adsorption isotherm constant (KF). The adsorption capacity (Qm) is obtained by replacing Ce by the initial Hg0(g) concentration (Co), in eqn (E6).41
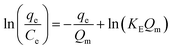 | (E7) |
The Elovich adsorption isotherm represents multilayer adsorption. The maximum adsorption capacity (Qm) and Elovich adsorption isotherm constant (KE) were obtained from the slope and intercept, respectively, of the linear fit of ln(qe/Ce) to qe.
| Model | Parameters | |||
|---|---|---|---|---|
| Langmuir | Qm (μg g−1) | KL (L μg−1) | RL | R2 |
| 125.00 | 20 | 0.02 | 0.99 | |
| Freundlich | Qm (μg g−1) | KF (μg g−1) (L g−1)n | n | R2 |
| 129.47 | 113.35 | 8.77 | 0.88 | |
| Elovich | Qm (μg g−1) | KE (L μg−1) | N.A. | R2 |
| 16.23 | 7730.32 | N.A. | 0.84 | |
The favorability of adsorption for the Langmuir and Freundlich adsorption isotherms are decided based on the separation factor (RL) and adsorption intensity (n) respectively. RL and n are characteristic of the adsorbent–adsorbate system. Adsorption is said to be favorable if 0 < RL < 1 and 1/n < 1 (or n > 1). The computed values of RL (0.02) and n (8.77) suggest that Hg0(g) adsorption onto α-Fe2O3 in the presence of visible light is highly favorable. The adsorption capacities of Hg on α-Fe2O3 were similar for the Langmuir and Freundlich models, yielding a maximum adsorption capacity of (127.23 ± 2.23) μg g−1.
3.6 Potential adsorption mechanism
Previous studies on the photolytic uptake of Hg0(g) by TiO2 have suggested electronic excitation from the Conductance Band (CB) to the Valence Band (VB) leads to superoxide and hydroxyl radical formation.42 The hydroxyl radicals have been proposed to react with Hg0 oxidizing it on the surface of TiO2. For γ-Fe2O3, α-Fe2O3 and α-FeOOH, the strong correlation of irradiation with Hg0(g) uptake considered in tandem with their band structure hints at similarities in the uptake mechanisms. Excitation to the CBs, from upper levels of the VBs are responsible for their respective optical absorption edges.43 The oxidation potential of the holes (h+) > +2.27 eV is sufficient to potentially generate hydroxyl radicals from surface water (Fig. 7A), which may then oxidize Hg0. Evidence for the formation of hydroxyl radicals on the surfaces of γ-Fe2O3, α-Fe2O3 and α-FeOOH surfaces have previously been reported.44–46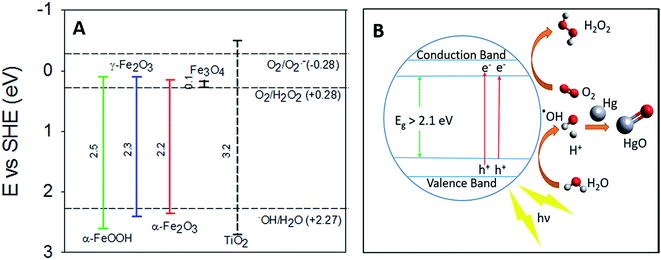 | ||
| Fig. 7 (A) Band gaps of TiO2, α-FeOOH, α-Fe2O3 and γ-Fe2O3 compared with redox potentials of hydroxyl, peroxide and superoxide radicals (the redox potentials described here are compiled from the work of Liu,33 Fujishima et al.,47 and Sherman34). (B) Graphical representation of proposed radiation enhanced Hg0(g) loss mechanism. | ||
The lack of radiation effects on uptake of Hg0 on magnetite surfaces maybe explained by Fe3O4's low band gap value (∼0.1 eV).33 Consequently, the oxidation potential of the holes (Fig. 7) generated is insufficient to produce the hydroxyl radicals required to oxidize Hg0.
Thermodynamic studies have suggested that direct HgO formation from the reaction of Hg0 and ˙OH is endothermic (ΔH = +90 kJ mol−1), while HgO formation in the pathway involving O2 is exothermic (ΔH = −118 kJ mol−1).48 We thus suspect that surface hydroxyls oxidized Hg0 to HgO via formation of an intermediate Hg–˙OH complex, which then reacted with molecular oxygen.
The reduction potential of γ-Fe2O3 CB electrons may favor the 2 e− reduction of oxygen to peroxides along with the formation of superoxides as reported for TiO2.42 The overall oxidation pathway, consistent with previously suggested mechanisms of iron oxide photo activity,49–51 may be represented by reactions R1–R6, yet due to the complexity of pathways for such reactions on iron (oxyhydr)oxide surfaces49,51–53 further experimental investigation on the precise mechanism is encouraged.
| Fe2O3 + hν → e− + h+ | (R1) |
| H2O + h+ → OH˙ + H+ | (R2) |
| O2 + 2e− + 2H+ → H2O2 | (R3) |
| H2O2 + e− → OH˙ + –OH | (R4) |
| Hg0 + OH˙ → ˙HgOH (+M) | (R5) |
| ˙HgOH + O2 → via intermdiates/surfaces → HgO(s) + HO2˙ | (R6) |
For convenience, the simplified reaction scheme is depicted in Fig. 7B.
Spent iron (oxyhydr)oxides were characterized with X-ray Photon Spectroscopy (XPS) and Energy Dispersive Analysis of X-ray (EDAX) to identify post reaction Hg speciation. We were unable to detect Hg because its surface concentrations (≈120 μg g−1) were lower than the working detection limit of the instruments (≈0.05% or 500 μg g−1).
Additionally, to check for the temperature dependent reversibility of Hg binding on α-Fe2O3, which could potentially affect the release of Hg in warmer climates, the reaction chamber, post reaction, was heated from 23 °C to 150 °C in an oil bath. Hg desorption was not detected up to 100 °C, however, at 110 °C Hg release back into the gas phase was observed. The maximum Hg0(g) released was ca. 10% of the initial concentration at 120 °C. Hg0(g) concentrations did not increase significantly on increasing the temperature to 150 °C or prolonged heating (65 minutes at 150 °C). Re-volatilization of those Hg0 atoms that were weakly adsorbed on the chamber walls (ca. 5%, as reported before) and α-Fe2O3 surfaces were likely responsible for the observed Hg signals. Since tropospheric temperatures are lower than the temperatures reported here, we expect that temperature alone will not affect the release of Hg bound to α-Fe2O3 particles in warmer climates. It is, however, possible that other atmospheric species such as water vapor and organic species such as BTEX in conjunction with temperature may affect α-Fe2O3 bound Hg differently. Such interactions are yet to be studied.
Although the focus of our studies was to understand the reactions of elemental mercury with ubiquitous dust particles and the effect of photochemical aging and the humidity on the particles, such nanoparticles can also be used for mercury remediation. There is already a wide range of promising natural42 and synthetic54,55 materials in literature and further investigation into exploiting the photoactivity of iron (oxyhydr)oxides for remediation processes is encouraged.
4. Conclusions and future work
In this study, we provided evidence for the uptake of Hg0(g) on the surfaces iron (oxyhydr)oxide particles. The uptake of Hg0(g) on α-FeOOH, γ-Fe2O3 and α-Fe2O3, was found to be significantly influenced by UV-visible radiation. In dark conditions, uptake of Hg0(g) on these iron oxides were comparable to wall losses, suggesting limited uptake of Hg0(g). Despite the inhibition of uptake reactions on α-Fe2O3 by humidity, γ values for these reactions (at RH ≤ 66%) were higher than γ values for Hg0(g) losses in dark. Additionally, while Hg0(g) uptake on the surfaces of α-FeOOH, γ-Fe2O3 and α-Fe2O3 were driven by UV-visible radiation, the uptake of Hg0(g) on Fe3O4 was not. The difference in uptake behavior of the iron (oxyhydr)oxides were attributed to their band gaps and consequently the redox potentials of the electron–hole pairs. It is important to note that while only 4 iron (oxyhydr)oxides were investigated in this study, we believe that other oxides and hydroxides of metals (such as manganese) with suitable band gaps may also be active in the photolytic capture of Hg0(g). This can potentially increase the number of chemical pathways available for the formation of PBM and deposition of Hg0(g), however, further studies are required to identify and characterize such reactions.Mercury models are used to assess the impact of changes in anthropogenic mercury emissions such as expected under the Minamata convention on mercury levels in environmental ecosystems; however, accurate representation of mercury chemistry in models remains a challenge. The long-range transport of mercury and its impact on global ecosystems are largely determined by the physicochemical processes involved in the removal of Hg0 from the atmosphere. Uptake of Hg0(g) on particulate matter in air and at terrestrial surfaces could explain a significant pathway for the deposition of Hg0. This study provides insights into the mechanism for gas-particle partitioning of Hg0 for selected ambient aerosol surfaces under various environmental conditions. Further studies are required to fully determine the mechanism involved in gas-particle interactions of Hg0 for different heterogeneous surfaces in the biosphere, and modeling studies are needed to investigate the impact of these processes on the lifetime of mercury in the atmosphere.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
| γ | Uptake coefficient |
| λ | Wavelength (nm) |
| νHg | Mean molecular velocity of Hg0(g) at 22.3 °C (m min−1) |
| Cmass | Mass loading of sorbent in reaction chamber (g m−3) |
| [C]e | Equilibrium concentration of Hg0(g) (μg L−1) |
| F(R) | Kubelka–Munk function |
| [Hg]o | Concentration of Hg0(g) at time t = 0 (μg L−1) |
| [Hg]t | Concentration of Hg0(g) at time t (μg L−1) |
| k | Pseudo-first order rate constant (min−1) |
| KE | Elovich isotherm constant (L μg−1) |
| KF | Freundlich isotherm constant (μg g−1) (L g−1)n |
| KL | Langmuir isotherm constant (L μg−1) |
| n | Adsorption intensity |
| qe | Equilibrium concentration of Hg0 on sorbent (μg g−1) |
| Qm | Maximum adsorption capacity of sorbent (μg g−1) |
| R2 | Coefficient of determination |
| R | Reflectance |
| RL | Separation factor |
| SBET | BET surface area of the sorbent (m2 g−1) |
| t | Time (minutes) |
| T | Temperature (°C) |
Acknowledgements
This study was supported by funding from Environment and Climate Change Canada. We are also grateful to NSERC and NSERC-CREATE Mines of Knowledge for partial financial support.References
- C. Seigneur, K. Vijayaraghavan, K. Lohman, P. Karamchandani and C. Scott, Environ. Sci. Technol., 2004, 38, 555–569 CrossRef CAS PubMed.
- C. T. Driscoll, R. P. Mason, H. M. Chan, D. J. Jacob and N. Pirrone, Environ. Sci. Technol., 2013, 47, 4967–4983 CrossRef CAS PubMed.
- F. M. M. Morel, A. M. L. Kraepiel and M. Amyot, Annu. Rev. Ecol. Syst., 1998, 29, 543–566 CrossRef.
- P. B. Tchounwou, W. K. Ayensu, N. Ninashvili and D. Sutton, Environ. Toxicol., 2003, 18, 149–175 CrossRef CAS PubMed.
- AMAP/UNEP, 2013. Technical Background Report for the Global Mercury Assessment 2013. Arctic Monitoring and Assessment Programme, Oslo, Norway/UNEP Chemicals Branch, Geneva, Switzerland. vi + 263 pp.
- L. Zhang, P. Blanchard, D. Gay, E. Prestbo, M. Risch, D. Johnson, J. Narayan, R. Zsolway, T. Holsen and E. Miller, Atmos. Chem. Phys., 2012, 12, 4327–4340 CAS.
- L. Zhang, P. Blanchard, D. Johnson, A. Dastoor, A. Ryzhkov, C. J. Lin, K. Vijayaraghavan, D. Gay, T. M. Holsen, J. Huang, J. A. Graydon, V. L. St Louis, M. S. Castro, E. K. Miller, F. Marsik, J. Lu, L. Poissant, M. Pilote and K. M. Zhang, Environ. Pollut., 2012, 161, 272–283 CrossRef CAS PubMed.
- A. J. Hynes, D. L. Donohoue, M. E. Goodsite and I. M. Hedgecock, in Mercury Fate and Transport in the Global Atmosphere, Springer, 2009, pp. 427–457 Search PubMed.
- J. J. Tokos, B. o. Hall, J. A. Calhoun and E. M. Prestbo, Atmos. Environ., 1998, 32, 823–827 CrossRef CAS.
- H. A. Wiatrowski, S. Das, R. Kukkadapu, E. S. Ilton, T. Barkay and N. Yee, Environ. Sci. Technol., 2009, 43, 5307–5313 CrossRef CAS PubMed.
- P. R. Kim, Y. J. Han, T. M. Holsen and S. M. Yi, Atmos. Environ., 2012, 61, 94–102 CrossRef CAS.
- M. Subir, P. A. Ariya and A. P. Dastoor, Atmos. Environ., 2012, 46, 1–10 CrossRef CAS.
- P. Ariya, J. Sun, N. Eltouny, E. Hudson, C. Hayes and G. Kos, Int. Rev. Phys. Chem., 2009, 28, 1–32 CrossRef CAS.
- C. R. Usher, A. E. Michel and V. H. Grassian, Chem. Rev., 2003, 103, 4883–4940 CrossRef CAS PubMed.
- E. Journet, K. V. Desboeufs, S. Caquineau and J. L. Colin, Geophys. Res. Lett., 2008, 35, L07805 CrossRef.
- P. K. Mogili, P. D. Kleiber, M. A. Young and V. H. Grassian, J. Phys. Chem. A, 2006, 110, 13799–13807 CrossRef CAS PubMed.
- Y. Dupart, S. M. King, B. Nekat, A. Nowak, A. Wiedensohler, H. Herrmann, G. David, B. Thomas, A. Miffre, P. Rairoux, B. D'Anna and C. George, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20842–20847 CrossRef CAS PubMed.
- M. Ndour, M. Nicolas, B. D'Anna, O. Ka and C. George, Phys. Chem. Chem. Phys., 2009, 11, 1312–1319 RSC.
- H. Zhang, Recent Developments in Mercury Science, 2006, pp. 37–79 Search PubMed.
- R. Bhardwaj, X. Chen and R. D. Vidic, J. Air Waste Manage. Assoc., 2009, 59, 1331–1338 CAS.
- J.-E. Jung, D. Geatches, K. Lee, S. Aboud, G. E. Brown and J. Wilcox, J. Phys. Chem. C, 2015, 119, 26512–26518 CAS.
- T. Liu, L. Xue, X. Guo, J. Liu, Y. Huang and C. Zheng, Environ. Sci. Technol., 2016, 50(24), 13585–13591 CrossRef CAS PubMed.
- S. Lafon, I. N. Sokolik, J. L. Rajot, S. Caquineau and A. Gaudichet, J. Geophys. Res.: Atmos., 2006, 111, D21207 CrossRef.
- B. Gilbert, C. Frandsen, E. R. Maxey and D. M. Sherman, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035108 CrossRef.
- G. Snider, F. Raofie and P. A. Ariya, Phys. Chem. Chem. Phys., 2008, 10, 5616–5623 RSC.
- A. Bouzaza and A. Laplanche, J. Photochem. Photobiol., A, 2002, 150, 207–212 CrossRef CAS.
- J. Li, N. Yan, Z. Qu, S. Qiao, S. Yang, Y. Guo, P. Liu and J. Jia, Environ. Sci. Technol., 2009, 44, 426–431 CrossRef PubMed.
- J. H. Sienfeld and S. N. Pandis, Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, J. Wiley, New York, 1st edn, 1998 Search PubMed.
- A. R. Ravishankara, Science, 1997, 276, 1058–1065 CrossRef CAS.
- P. K. Mogili, P. D. Kleiber, M. A. Young and V. H. Grassian, J. Phys. Chem. A, 2006, 110, 13799–13807 CrossRef CAS PubMed.
- R. Massart, IEEE Trans. Magn., 1981, 17, 1247–1248 CrossRef.
- J. Adams, D. Rodriguez and R. Cox, Atmos. Chem. Phys., 2005, 5, 2679–2689 CrossRef CAS.
- S. Q. Liu, Environ. Chem. Lett., 2012, 10, 209–216 CrossRef CAS.
- D. M. Sherman, Geochim. Cosmochim. Acta, 2005, 69, 3249–3255 CrossRef CAS.
- M. F. Silva, L. A. de Oliveira, M. A. Ciciliati, L. T. Silva, B. S. Pereira, A. A. W. Hechenleitner, D. M. Oliveira, K. R. Pirota, F. F. Ivashita and A. Paesano Jr, J. Appl. Phys., 2013, 114, 104311 CrossRef.
- T. K. Townsend, E. M. Sabio, N. D. Browning and F. E. Osterloh, Energy Environ. Sci., 2011, 4, 4270–4275 CAS.
- D. E. Moore, in Photostability of drugs and drug formulations, ed. H. H. Tonnesen, CRC Press, Boca Raton, 2nd edn, 2004, ch. 2, pp. 9–37 Search PubMed.
- H. Z. Zhang, M. Bayne, S. Fernando, B. Legg, M. Q. Zhu, R. L. Penn and J. F. Banfield, J. Phys. Chem. C, 2011, 115, 17704–17710 CAS.
- A. G. Tamirat, J. Rick, A. A. Dubale, W.-N. Su and B.-J. Hwang, Nanoscale Horiz., 2016, 1, 243–267 RSC.
- F. Kong, J. Qiu, H. Liu, R. Zhao and Z. Ai, J. Environ. Sci., 2011, 23, 699–704 CrossRef CAS.
- O. Hamdaoui and E. Naffrechoux, J. Hazard. Mater., 2007, 147, 381–394 CrossRef CAS PubMed.
- G. Snider and P. Ariya, Chem. Phys. Lett., 2010, 491, 23–28 CrossRef CAS.
- R. Grau-Crespo, A. Y. Al-Baitai, I. Saadoune and N. H. De Leeuw, J. Phys.: Condens. Matter, 2010, 22, 255401 CrossRef PubMed.
- P. Mazellier and M. Bolte, J. Photochem. Photobiol., A, 2000, 132, 129–135 CrossRef CAS.
- B. Ahmmad, K. Leonard, M. S. Islam, J. Kurawaki, M. Muruganandham, T. Ohkubo and Y. Kuroda, Adv. Powder Technol., 2013, 24, 160–167 CrossRef CAS.
- C. Baumanis, J. Z. Bloh, R. Dillert and D. W. Bahnemann, J. Phys. Chem. C, 2011, 115, 25442–25450 CAS.
- A. Fujishima, T. N. Rao and D. A. Tryk, J. Photochem. Photobiol., C, 2000, 1, 1–21 CrossRef CAS.
- D. Bauer, L. D'Ottone, P. Campuzano-Jost and A. J. Hynes, J. Photochem. Photobiol., A, 2003, 157, 247–256 CrossRef CAS.
- B. Show, N. Mukherjee and A. Mondal, RSC Adv., 2016, 6, 75347–75358 RSC.
- M. M. Rahman, A. Jamal, S. B. Khan and M. Faisal, J. Nanopart. Res., 2011, 13, 3789–3799 CrossRef CAS.
- L. Tang, H. Feng, J. Tang, G. Zeng, Y. Deng, J. Wang, Y. Liu and Y. Zhou, Water Res., 2017, 117, 175–186 CrossRef CAS PubMed.
- S. A. Styler and D. J. Donaldson, Environ. Sci. Technol., 2012, 46, 8756–8763 CrossRef CAS PubMed.
- H. A. Al-Abadleh, RSC Adv., 2015, 5, 45785–45811 RSC.
- B. Aguila, Q. Sun, J. A. Perman, L. D. Earl, C. W. Abney, R. Elzein, R. Schlaf and S. Ma, Adv. Mater., 2017, 1700665 CrossRef PubMed.
- B. Li, Y. Zhang, D. Ma, Z. Shi and S. Ma, Nat. Commun., 2014, 5, 5537 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07401h |
| This journal is © The Royal Society of Chemistry 2017 |