 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unexpected stable stoichiometries and superconductivity of potassium-rich sulfides†‡
Ying Li ,
Xilian Jin
,
Xilian Jin *,
Tian Cui
*,
Tian Cui *,
Quan Zhuang,
Die Zhang,
Xing Meng,
Kuo Bao,
Bingbing Liu
*,
Quan Zhuang,
Die Zhang,
Xing Meng,
Kuo Bao,
Bingbing Liu and
Qiang Zhou
and
Qiang Zhou
College of Physics, State Key Laboratory of Superhard Materials, Jilin University, Changchun, 130012, People’s Republic of China. E-mail: jinxilian@jlu.edu.cn; cuitian@jlu.edu.cn
First published on 20th September 2017
Abstract
Alkali metal compounds exhibit novel characteristics under pressure, such as antimetallization in CLi4, high superconductivity at 80 K in highly compressed Li3S, and the existence of unexpected stable stoichiometries of sodium chlorides, etc., which have greatly prompted us to explore KxS compounds at pressure. We found several stable structures with a variety of stoichiometries and proposed a phase diagram on the K-rich side first. Chemical rules established at ambient pressure are frequently violated when high pressure is applied, Na3Cl and NaCl3 as unusual stoichiometries of sodium chloride have been reported in high-pressure conditions. However, KS, with its counterintuitive chemical formula, has been discovered theoretically even at ambient pressure, and possesses the same stability as K2S. The mechanism of superconductivity in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S is deeply investigated, comparing with the reported Pm
m K3S is deeply investigated, comparing with the reported Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Li3S. The weak electron–phonon coupling mainly contributes to the weak superconductivity in K3S, which is fully in contrast to the mechanism of interstitial charge localization which dominates the low Tc in the reported Li3S.
m Li3S. The weak electron–phonon coupling mainly contributes to the weak superconductivity in K3S, which is fully in contrast to the mechanism of interstitial charge localization which dominates the low Tc in the reported Li3S.
Introduction
Recently, alkali metal compounds have revived the interest of the scientific community to explore their novel structures and characteristics upon compression. Different Na–Cl compounds such as Na3Cl, Na2Cl, Na3Cl2, NaCl3, and NaCl7 are thermodynamically stable at nonambient pressure conditions which contrasts the familiar rules of chemistry.1,2 The compound of helium and sodium, Na2He, reported recently has changed the hitherto bare field of helium chemistry, providing new twists to the chemistry of noble gases.3 Antimetallization is predicted in the dense lithium-rich compound CLi4 (ref. 4) which means that this phenomenon is expected in not only alkali metals Li5–7 and Na8 but also multiple compounds. Interestingly, superconductivity is predicted in alkali metal compounds such as a Li–S system, and Tc has risen to 80 K in highly compressed Li3S.9Alkali metal sulfides are characterized by their high ionic conductivity and large band gap. They appear to be promising candidates for technological applications in solid state batteries, fuel cells and solid state gas-detectors.10,11 The properties of alkali metal sulfides of X2S (X = Li, Na, K, or Rb) have been explored thoroughly, including phase sequence, elastic properties, electronic structure, optical properties, etc.12–20 The conventional superconductivity in the phase diagram of the Li–S system has been explored by ab initio methods for crystal structure prediction and linear response calculations for electron–phonon coupling.9 Most of these phases are metallic, but they exhibit no or low-Tc superconductivity, except for the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group of Li3S with a Tc of 80 K at 500 GPa. In contrast to the low-Tc of Pm
m space group of Li3S with a Tc of 80 K at 500 GPa. In contrast to the low-Tc of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Li3S, it is concluded that interstitial charge localization due to avoiding core overlap can be a fundamental limiting factor for conventional superconductivity.
m Li3S, it is concluded that interstitial charge localization due to avoiding core overlap can be a fundamental limiting factor for conventional superconductivity.
In this work, various stoichiometric structures of KxS (x = 1–4) systems are widely investigated up to 100 GPa. We found six thermodynamically stable structures with the stoichiometries of KS, K3S and K4S under these conditions and proposed a phase diagram on the K-rich side first. KS, the totally counterintuitive chemical formula with extraordinary bonding and electronic properties, is predicted to be stable at atmospheric pressure in KxS compounds. The mechanism of superconductivity in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S is deeply investigated and compared with the reported Pm
m K3S is deeply investigated and compared with the reported Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Li3S. The low Tc is attributed to a weak interaction of electron–phonon coupling in the K3S compound instead of interstitial charge localization like in the reported Li3S compound.9
m Li3S. The low Tc is attributed to a weak interaction of electron–phonon coupling in the K3S compound instead of interstitial charge localization like in the reported Li3S compound.9
Computational methods
The structural prediction for the KxS compounds at different pressures was performed by the ELocR code.21 The high accuracy structural relaxations and electronic localization functions (ELF) were performed using density functional theory with the Vienna ab initio simulation package (VASP).22 The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)23 was selected for the exchange–correlation function. The partial augmented wave (PAW)24 method was adopted with the PAW potentials where s2p4 and 3s3p4s are treated as valence electrons. Brillouin zone sampling used a grid spacing of 2π × 0.03 Å−1 and the plane-wave cutoff energy was 600 eV.The electronic projected density of states and the electronic band structure were calculated by the CASTEP25 code with a cutoff energy of 720 eV, norm-conserving pseudopotentials, GGA-PBE exchange–correlation functional, and Brillouin zone sampling grid with a spacing of 2π × 0.04 Å−1. The dynamic properties, three-dimensional Fermi surfaces and electron–phonon coupling calculations were studied in the QUANTUM-ESPRESSO package.26 The Troullier–Martins-type norm-conserving pseudopotentials were used, and convergence tests provided a suitable value of 60 Ry for the kinetic energy cutoff. The q-point meshes in the first Brillouin zone of 8 × 8 × 8 for Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Li3S) and 4 × 4 × 4 for Pm
m (Li3S) and 4 × 4 × 4 for Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S) were used for phonon and electron–phonon calculations.
m (K3S) were used for phonon and electron–phonon calculations.
Results and discussion
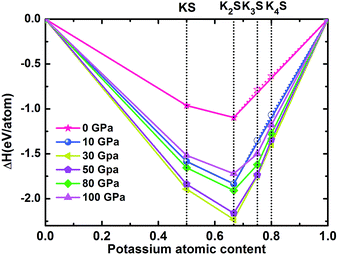
We have systematically studied the chemical stabilities of various KxS (x = 1–4) compounds by calculating the enthalpies of formation up to 100 GPa. The thermodynamical stability of different compounds with respect to elemental K and S solids at each pressure is calculated using the equation below:| ΔH(KxS) = [[H(KxS) − xH(K) − H(S)]/(x + 1)] |
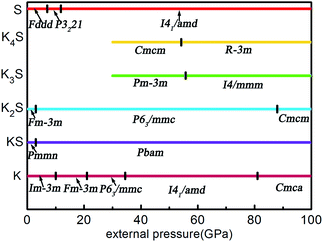
According to the hull data, a compound lying on the convex hull is thermodynamically stable with respect to decomposition into other K–S compounds or elemental K and S solids, and thus it is experimentally synthesizable. However, those located above the convex hull indicated by dashed lines are either unstable or metastable. In order to obtain clear information for the structures at ambient conditions and 10 GPa, the independent convex hull is shown in Fig. S1.‡ Moreover, the phase diagram for the KxS crystals is presented in Fig. 2.
Under ambient conditions, the stable phase of KS crystallizes in the orthorhombic structure of Pmmn and remains stable until 3 GPa as shown in Fig. 3(a). There are three nonequivalent atoms, and the nearest distance between K and S is 3.16 Å. K atoms occupy the crystallographic 2b position with mm2 symmetry on the top and bottom sides, and the other nonequivalent K atoms occupy the crystallographic 2a position with mm2 symmetry in the middle of the crystal. S atoms occupy the crystallographic 4f position with .m. symmetry. Elevating the pressure above 3 GPa, another orthorhombic phase with Pbam symmetry emerges which is stable until 100 GPa, as depicted in Fig. 3(b). There are two nonequivalent atoms in the crystal lattice, and they consist of one KS unit. K atoms occupy the crystallographic 4h position with ..m symmetry, and S atoms occupy the crystallographic 4g position with ..m symmetry. The nearest distance between K and S is 2.558 Å. As for K3S and K4S, they are thermodynamically metastable under normal conditions until 30 GPa. With increasing pressure, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, the face-centered cubic phase, is energetically preferred from 30 GPa to 55.7 GPa. The layer stacking sequence in every axis can be denoted by the repeated AB stacking. K atoms occupy the crystallographic 3c position with 4/mm.m symmetry sitting at the center of each cube face. S atoms occupy the crystallographic 1a position with m
m, the face-centered cubic phase, is energetically preferred from 30 GPa to 55.7 GPa. The layer stacking sequence in every axis can be denoted by the repeated AB stacking. K atoms occupy the crystallographic 3c position with 4/mm.m symmetry sitting at the center of each cube face. S atoms occupy the crystallographic 1a position with m![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry around the cube corners as shown in Fig. 3(c). Each K atom is surrounded by the four nearest S atoms and the distance is 2.779 Å. The calculated structural parameters and Wyckoff positions for each phase are summarized in Table S1.‡ The mechanical property is one of the basic criteria when considering the structure stability. According to the mechanical stability criteria, the crystal deformation energy is positive which means the determinants of the elastic constants matrix Cij should be positive.27 It is noteworthy that negative values are not prohibited for Cij.28 To evaluate the mechanical stability of Pmmn, Pbam, Pm
m symmetry around the cube corners as shown in Fig. 3(c). Each K atom is surrounded by the four nearest S atoms and the distance is 2.779 Å. The calculated structural parameters and Wyckoff positions for each phase are summarized in Table S1.‡ The mechanical property is one of the basic criteria when considering the structure stability. According to the mechanical stability criteria, the crystal deformation energy is positive which means the determinants of the elastic constants matrix Cij should be positive.27 It is noteworthy that negative values are not prohibited for Cij.28 To evaluate the mechanical stability of Pmmn, Pbam, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, I4/mmm, Cmcm and R
m, I4/mmm, Cmcm and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, the elastic constants were calculated and are listed in Table S2.‡ They all satisfy the Born–Huang criterion,29 representing the stability of the mechanical property.
m, the elastic constants were calculated and are listed in Table S2.‡ They all satisfy the Born–Huang criterion,29 representing the stability of the mechanical property.
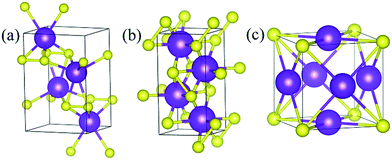 | ||
Fig. 3 Stable structures of KxS: (a) Pmmn KS at ambient pressure, (b) Pbam KS at 100 GPa, and (c) Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S at 50 GPa. The purple and yellow atoms are K and S, respectively. m K3S at 50 GPa. The purple and yellow atoms are K and S, respectively. | ||
KS and K2S are thermodynamically stable compounds throughout the entire pressure range we explored. At ambient pressure, K2S is the familiar stoichiometry in the KxS system. We have predicted its phase sequence successfully by the ELocR21 code, and account for the experimental results effectively.20 Pressure can efficiently modify the compositional landscape, leading to materials with unprecedented stoichiometries that would not be expected from conventional wisdom based on chemical rules at ambient pressure. For instance, at ambient conditions, sodium chloride (NaCl) is the archetypical ionic compound in chemistry textbooks. Under pressure, different Na–Cl compounds such as Na3Cl, Na2Cl, Na3Cl2, NaCl3, and NaCl7, which are clearly against our conventional wisdom, become thermodynamically stable.1,2 Some other examples are seen in Li–B,30,31 Ca–H,32 and Si–C33 systems at high pressure conditions. Interestingly, the unusual stoichiometry (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) KS compound is even stable thermodynamically and mechanically at ambient conditions. In order to judge its dynamical stability, the phonon band structure and partial phonon density of states (PHDOS) were calculated as shown in Fig. S2.‡ The absence of imaginary frequency modes in the entire Brillouin zone indicates the dynamic stability of Pmmn (KS). Hence, KS, the totally counterintuitive chemical formula, may exist in nature theoretically.
1) KS compound is even stable thermodynamically and mechanically at ambient conditions. In order to judge its dynamical stability, the phonon band structure and partial phonon density of states (PHDOS) were calculated as shown in Fig. S2.‡ The absence of imaginary frequency modes in the entire Brillouin zone indicates the dynamic stability of Pmmn (KS). Hence, KS, the totally counterintuitive chemical formula, may exist in nature theoretically.
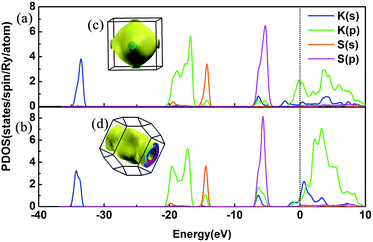
We have discussed the mechanical and thermodynamical stability of the proposed phases and confirmed that they are all stable at the relevant pressure range. To understand the electronic properties of the various KxS compounds, the electronic band structures, partial density of states (PDOS) and three-dimensional Fermi surfaces were calculated as depicted in Fig. 4 and S3.‡ From the band structures we found that all the stable phases at the different pressures are metallic due to several bands crossing the Fermi level, except for Pmmn and Pbam. At ambient pressure, the band gap in Pmmn is 1.432 eV, which reveals its nonmetallic character. Elevating the pressure above 3 GPa, the Pbam structure appears with nonmetallic features until 100 GPa. For K3S, from the partial density of states (PDOS) in Fig. 4(a) and (b), the metallic character of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and I4/mmm is confirmed by the high level of total electronic density distribution at the Fermi level. The majority of the occupied states come from the K(p) state, whereas the contribution from K(s), S(s) and S(p) to the states around the Fermi level is quite small in K3S. This complex electronic band structure near the Fermi energy brings the rich and multiple Fermi surface feature, as displayed in Fig. 4(c) and (d).
m and I4/mmm is confirmed by the high level of total electronic density distribution at the Fermi level. The majority of the occupied states come from the K(p) state, whereas the contribution from K(s), S(s) and S(p) to the states around the Fermi level is quite small in K3S. This complex electronic band structure near the Fermi energy brings the rich and multiple Fermi surface feature, as displayed in Fig. 4(c) and (d).
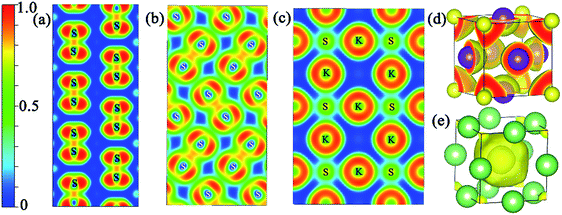
In addition, the electron localization function (ELF) was calculated to analyze the nature of the chemical bonding and the unusual distribution of the valence electron localization function in the proposed structures at the relevant pressure range. It is a ratio from 0 to 1, and the values equal 1.0 and 0.5, reflecting the extremely strong localization and homogeneous electron distribution, respectively.34,35 Fig. S4‡ shows the isosurface value of 0.65 for the proposed structures. The valence electron localization around interstitial regions is found in Pmmn (KS), Pbam (KS), I4/mmm (K3S), Cmcm (K4S), and R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K4S), and is not found in Pm
m (K4S), and is not found in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S). Fig. 5(a) and (b) show the two dimensional electron location function (2D ELF) of Pmmn (KS) and Pbam (KS). The values around the positions of the S2 units are close to 0.75, revealing the covalent bond character. From the 2D ELF of Pm
m (K3S). Fig. 5(a) and (b) show the two dimensional electron location function (2D ELF) of Pmmn (KS) and Pbam (KS). The values around the positions of the S2 units are close to 0.75, revealing the covalent bond character. From the 2D ELF of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S) displayed in Fig. 5(c), we can see that the conductivity comes from connected regions where the value of ELF is about 0.5 between the K and S atoms. The ELF of Pm
m (K3S) displayed in Fig. 5(c), we can see that the conductivity comes from connected regions where the value of ELF is about 0.5 between the K and S atoms. The ELF of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Li3S) at 500 GPa is calculated to compare with K3S as shown in Fig. 5(e). Obviously, charges accumulate in the open interstitial regions in Li3S. However, this phenomenon is not observed in Pm
m (Li3S) at 500 GPa is calculated to compare with K3S as shown in Fig. 5(e). Obviously, charges accumulate in the open interstitial regions in Li3S. However, this phenomenon is not observed in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S as displayed in Fig. 5(d).
m K3S as displayed in Fig. 5(d).
To explore the potential superconductivity of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S, the electron–phonon coupling (EPC) strength λ and logarithmic average phonon frequency ωlog have been investigated at 50 GPa by QUANTUM-ESPRESSO.26 The Eliashberg phonon spectral function α2F(ω) can be obtained as below. It is described as:
m K3S, the electron–phonon coupling (EPC) strength λ and logarithmic average phonon frequency ωlog have been investigated at 50 GPa by QUANTUM-ESPRESSO.26 The Eliashberg phonon spectral function α2F(ω) can be obtained as below. It is described as:
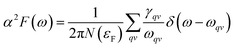 | (1) |
| γqv = λqvπN(εF)ωqv2 | (2) |
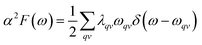 | (3) |
In this work, α2F(ω) is obtained by the integration of ωqv in the whole Brillouin zone. The heavier K atom from the low-frequency vibrational modes below about 8 THz contributes more to the total λ as shown in Fig. 6. Phonon-mediated superconductors are accurately described by the Migdal–Eliashberg theory,36,37 and Tc can be estimated by the Allen–Dynes formula:38
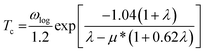 | (4) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase and high-Tc (80 K) in the Fm
m phase and high-Tc (80 K) in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase, and it attributed the difference to interstitial charge localization, i.e., charge localizing in the interstitial region is a limiting factor to conventional superconductivity.9 K3S has the same stoichiometry, space group and Tc as Li3S, however, the mechanism of superconductivity is totally different. We attribute the low Tc to weak electron–phonon coupling. As expected, in K3S and Li3S, Tc is dominated by λ. Then the variation of λ is analysed using the rigid-muffin-tin (RMT) theory of Gaspari and Gyorffy.40 McMillan’s strong coupling theory defines an electron–phonon coupling constant by
m phase, and it attributed the difference to interstitial charge localization, i.e., charge localizing in the interstitial region is a limiting factor to conventional superconductivity.9 K3S has the same stoichiometry, space group and Tc as Li3S, however, the mechanism of superconductivity is totally different. We attribute the low Tc to weak electron–phonon coupling. As expected, in K3S and Li3S, Tc is dominated by λ. Then the variation of λ is analysed using the rigid-muffin-tin (RMT) theory of Gaspari and Gyorffy.40 McMillan’s strong coupling theory defines an electron–phonon coupling constant by
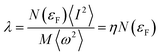 | (5) |
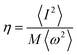 . N(εF) is the density of states (DOS) at the Fermi level, M is the atomic mass, 〈ω2〉 is a weighted average of the square of the phonon frequency, and 〈I2〉 is an average over the Fermi surface of the electron–phonon matrix element. From Table 1, η plays an important role in λ which further influenced the low Tc in Li3S and K3S. With regard to η, it is believed that η is a factor about the lattice and its value is influenced by interstitial charge localization in Li3S,9 i.e. charge localizing in the interstitial region led to a smaller η. The value of η in K3S is smaller than that in Li3S, nevertheless, there is no charge localizing in the interstitial region as shown in Fig. 5(c). We attribute the small η to the electron–ion matrix element 〈I2〉. In conclusion, the low Tc in K3S is mainly influenced by electron–phonon coupling which is fully in contrast to the mechanism of interstitial charge localization which dominates the low Tc in the reported Li3S.9
. N(εF) is the density of states (DOS) at the Fermi level, M is the atomic mass, 〈ω2〉 is a weighted average of the square of the phonon frequency, and 〈I2〉 is an average over the Fermi surface of the electron–phonon matrix element. From Table 1, η plays an important role in λ which further influenced the low Tc in Li3S and K3S. With regard to η, it is believed that η is a factor about the lattice and its value is influenced by interstitial charge localization in Li3S,9 i.e. charge localizing in the interstitial region led to a smaller η. The value of η in K3S is smaller than that in Li3S, nevertheless, there is no charge localizing in the interstitial region as shown in Fig. 5(c). We attribute the small η to the electron–ion matrix element 〈I2〉. In conclusion, the low Tc in K3S is mainly influenced by electron–phonon coupling which is fully in contrast to the mechanism of interstitial charge localization which dominates the low Tc in the reported Li3S.9
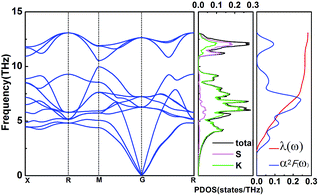 | ||
Fig. 6 Phonon dispersion curves, partial phonon density of states (PDOS), Eliashberg spectral function α2F(ω), and the EPC λ for Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S) at 50 GPa. m (K3S) at 50 GPa. | ||
| Phase | P (GPa) | Tc | ωlog | λ | N(εF) | η | 〈ω2〉1/2 | 〈I2〉 | |
|---|---|---|---|---|---|---|---|---|---|
| Present work | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S) m (K3S) |
50 | 0.069 | 285.569 | 0.280 | 2.107 | 0.133 | 40.698 | 2.884 |
| Present work | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Li3S) m (Li3S) |
500 | 0.044 | 814.923 | 0.250 | 0.668 | 0.375 | 141.074 | 25.120 |
| Other calculations | Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (Li3S)9 m (Li3S)9 |
500 | 0 | 702 | 0.25 | 0.67 | 0.37 |
Conclusions
In conclusion, a high-pressure phase diagram of K-rich KxS systems was built from structure prediction simulations and first-principles calculations. KS, the totally counterintuitive chemical formula with extraordinary bonding and electronic properties, is predicted to be stable at atmospheric pressure. All of the S atoms of KS are in the form of S2 units with covalent bond character from the analyses of the electronic localization function. Further electron–phonon coupling calculations revealed that the Tc of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (K3S) is approximately near to 0 K at 50 GPa. The mechanism of superconductivity in Pm
m (K3S) is approximately near to 0 K at 50 GPa. The mechanism of superconductivity in Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m K3S was deeply investigated and compared with the reported Pm
m K3S was deeply investigated and compared with the reported Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m Li3S. We attribute the low Tc to weak electron–phonon coupling in the K3S compound.
m Li3S. We attribute the low Tc to weak electron–phonon coupling in the K3S compound.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51632002, 51572108, 11634004, 11174102, 11774119), the Program for Changjiang Scholars and Innovative Research Team in University (No. IRT_15R23), the 111 Project (No. B12011), the National Fund for Fostering Talents of Basic Science (No. J1103202), and the Development Program of Science and Technology of Jilin Province, China (No. 20150312002ZG). Parts of the calculations were performed in the High Performance Computing Center (HPCC) of Jilin University.References
- W. Zhang, A. R. Oganov and A. F. Goncharov, et al., Science, 2013, 342, 1502–1505 CrossRef CAS PubMed.
- J. I. Insa, Science, 2013, 342, 1459–1460 CrossRef CAS PubMed.
- X. Dong, A. R. Oganov and A. F. Goncharov, et al., Nat. Chem., 2017, 9, 440–445 CrossRef CAS PubMed.
- X. Jin, X. J. Chen, T. Cui, H. K. Mao, H. Zhang, Q. Zhuang, K. Bao, D. Zhou, B. Liu, Q. Zhou and Z. He, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2366–2369 CrossRef CAS PubMed.
- J. B. Neaton and N. W. Ashcroft, Nature, 1999, 400, 141–144 CrossRef CAS.
- T. Matsuoka and K. Shimizu, Nature, 2009, 458, 186–189 CrossRef CAS PubMed.
- Y. Yao, S. T. John and D. D. Klug, Phys. Rev. Lett., 2009, 102, 115503 CrossRef PubMed.
- Y. Ma, M. Eremets and A. R. Oganov, et al., Nature, 2009, 458, 182–185 CrossRef CAS PubMed.
- C. Kokail, C. Heil and L. Boeri, Phys. Rev. B, 2016, 94, 060502 CrossRef.
- P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J. Tarascon, Nat. Mater., 2012, 11, 19–29 CrossRef CAS PubMed.
- H. Momida, T. Yamashita and T. Oguchi, J. Phys. Soc. Jpn., 2014, 83, 124713 CrossRef.
- H. Khachai, R. Khenata and A. Bouhemadou, Solid State Commun., 2008, 147, 178–182 CrossRef CAS.
- R. D. Eithiraj, G. Jaiganesh and G. Kalpana, Phys. Status Solidi A, 2007, 244, 1337–1346 CrossRef CAS.
- J. C. Schön, Ž. Čančarević and M. Jansen, J. Chem. Phys., 2004, 121, 2289 CrossRef PubMed.
- H. Khachai, R. Khenata and A. Bouhemadou, J. Phys., 2009, 21, 095404 CAS.
- E. Zintl, A. Harder and B. Dauth, Z. Elektrochem. Angew. Phys. Chem., 1934, 40, 588–593 CAS.
- A. Grzechnik, A. Vagas, K. Syassen, L. Loa, M. Hanfland and M. Jansen, J. Solid State Chem., 2000, 154, 603–611 CrossRef CAS.
- A. Vegas, A. Grzechnik, K. Syassen, L. Loa, M. Hanfland and M. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 151–156 CrossRef CAS.
- D. Santamaria-Perez, A. Vegas, C. Muehle and M. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 109–115 CAS.
- Y. Li, X. Jin, T. Cui, Q. Zhuang, Q. Lv, G. Wu, X. Meng, K. Bao, B. Liu and Q. Zhou, RSC Adv., 2017, 7, 7424–7430 RSC.
- The code for crystal structural prediction and analysis is based on the evolutional local random computational method, and is developed by our group. Some details have been provided in the ESI.‡.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 77, 3865–3868 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- S. J. Clark, M. D. Segall and C. J. Pickard, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. F. Nye, Physical properties of crystals: their representation by tensors and matrices, Oxford Univ. Press, Oxford, 1985, pp. 142–143 Search PubMed.
- J. P. Perdew and K. Burke, Phys. Rev. Lett., 1997, 77, 3865–3868 CrossRef PubMed.
- Z. Wu, E. Zhao and H. Xiang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- F. Peng, M. Miao, H. Wang, Q. Li and Y. Ma, J. Am. Chem. Soc., 2012, 134, 18599–18605 CrossRef CAS PubMed.
- A. Hermann, A. McSorley, N. W. Ashcroft and R. Hoffmann, J. Am. Chem. Soc., 2012, 134, 18606–18618 CrossRef CAS PubMed.
- H. Wang, S. T. John, K. Tanaka, T. Iitaka and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6463–6466 CrossRef CAS PubMed.
- G. Gao, N. Ashcroft and R. Hoffmann, J. Am. Chem. Soc., 2013, 135, 11651–11656 CrossRef CAS PubMed.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- J. K. Burdett and T. A. McCormick, J. Phys. Chem. A, 1998, 102, 6366–6372 CrossRef CAS.
- A. B. Migdal, J. Exp. Theor. Phys., 1958, 34, 996 Search PubMed.
- G. M. Eliashberg, J. Exp. Theor.Phys., 1960, 11, 696 Search PubMed.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- N. W. Ashcroft, Phys. Rev. Lett., 2004, 92, 187002 CrossRef CAS PubMed.
- G. D. Gaspari and B. L. Gyorffy, Phys. Rev. Lett., 1972, 28, 801–805 CrossRef CAS.
Footnotes |
| † Dedicated to Prof. Guangtian Zou on the occasion of his 80th birthday. |
| ‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07455g |
| This journal is © The Royal Society of Chemistry 2017 |

![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) m
m