Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optimized PAMAM coated magnetic nanoparticles for simultaneous hyperthermic treatment and contrast enhanced MRI diagnosis†
A. Boni *a,
A. M. Basinib,
L. Capolupoa,
C. Innocentic,
M. Cortib,
M. Cobianchid,
F. Orsinib,
A. Guerrinic,
C. Sangregorioce and
A. Lascialfarib
*a,
A. M. Basinib,
L. Capolupoa,
C. Innocentic,
M. Cortib,
M. Cobianchid,
F. Orsinib,
A. Guerrinic,
C. Sangregorioce and
A. Lascialfarib
aCenter for Nanotechnology Innovation @NEST, Istituto Italiano di Tecnologia, Piazza San Silvestro, 12 – 56127 Pisa, Italy. E-mail: adriano.boni1@virgilio.it
bDipartimento di Fisica and INSTM, Università degli studi di Milano, Italy
cDepartment of Chemistry “Ugo Shiff”, University of Florence and INSTM, via della Lastruccia 3 – 50019 Sesto F. no, Firenze, Italy
dDipartimento di Fisica and INSTM, Università degli studi di Pavia, Italy
eCNR-ICCOM and INSTM, via Madonna del Piano, 50019 Sesto F. no, Firenze, Italy
First published on 12th September 2017
Abstract
We report the synthesis and characterization of multi-functional monodisperse superparamagnetic Magnetic NanoParticles, MNPs, able to act as contrast agents for magnetic resonance and Magnetic Fluid Hyperthermia (MFH) mediators. The investigated samples are constituted of a magnetic core of magnetite and a biocompatible PAMAM coating. We studied two samples with the same magnetic volume but different shape, i.e. spherical and faceted. Despite the relatively large size (MNPs of 20 nm diameter) that generally leads to particles' aggregation and instability, the resulting samples were very stable. For faceted MNPs, the efficiency in contrasting Magnetic Resonance images, i.e. the nuclear transverse 1H NMR relaxivity r2, reached values of about 250/300 mM−1 s−1 at clinical frequencies f > 5 MHz, i.e. 2.5/3 times higher than the commercial compound Endorem, while the Specific Absorption Rate at Hac ∼ 10 kA m−1 and frequency f < 300 kHz (i.e. within the physiological limits) reaches 900 W g−1, suggesting this system as a potentially useful mediator for MFH. The experimental data strongly indicate the new synthesized MNP systems as good candidates for theranostic applications.
1. Introduction
Local control of tumors is a major challenge because of the cells' rapid proliferation and the possible diffusion of tumor cells in the whole body with consequent metastases. In the current local treatments of tumors by means of radiotherapy (RT) and chemotherapy (ChT), and related refined techniques (like cyber-knife and gamma-knife), the side-effects are severe. For many tumor sites,1–3 the effectiveness of RT and ChT is significantly enhanced when combined with hyperthermia (HT), i.e. raising tissue temperature up to 43–45 °C. Indeed, HT has been shown to improve the clinical outcome when added to RT and ChT4–6 or alone.7 In addition to a reduction in tumor bulk and analgesia requirements, the thermal treatment as coadjuvant treatment improves quality of life with decreased pain and preserves patient's function and appearance. Further advantages include a reduction in procedural costs, avoidance of complex repetitive surgeries, and the ability to visualize the area during the treatment.Among various methods of hyperthermia, Magnetic Fluid Hyperthermia (MFH) has drawn considerable attention.8–10 In MFH, fluids containing magnetic nanoparticles (MNPs) (generally iron oxide based systems) are delivered to the cancer and then heated by on external alternating magnetic field, resulting in hyperthermic treatment of cancer tissue. Magnetic nanoparticles based therapy has been investigated for many types of tumors, including those of the central nervous system.11,12 Clinical trials (Phase I and II) on glioblastoma multiforme and prostate cancers have already been performed13 and, at present, Phase III clinical study on the first is going on. Concerning glioblastoma, the survival time of patients has been increased by a factor 1.5/2 after MFH application. This result stimulated a lot of multidisciplinary research all over the world involving physicists, chemists, engineers, biologists and physicians, often starting from basic proprieties of novel nanoparticles to experimental tests on cells cultures and animal models.
MNPs have also been proposed as complimentary or alternative Magnetic Resonance Imaging (MRI) contrast agents with respect to the paramagnetic Gadolinium-Based Contrast Agents (GBCAs), thanks to their ability to increase the transverse relaxation rate (r2) and bring negative contrast.14 The general idea about MNPs is to obtain a nanosystem that can work as therapeutic MFH agent due to its heat release capacity, and as diagnostic agent because of the contrast efficiency in the MR images. Other functionalities, like fluorochromes for optical imaging or carrier for drug loading, can be additionally envisaged.
On this purpose, some of us recently developed a new class of iron oxide nanoparticles coated with lipid modified Poly(AMidoAMine) (PAMAM) dendrimers.15,16 This approach for the coating of MNPs, which occurs through hydrophobic interaction of the C12 chains of the dendrimer with the oleic acid coating, presents important advantages over existing strategies. Firstly, in many cases17 the coating may interact with the surface atoms of the magnetic core to form a nonmagnetic layer, reducing its effective size and the total amount of magnetic phase. The PAMAM based procedure does not require harsh conditions, thus preserving magnetic and structural properties of the iron oxide nanoparticles, which can be finely tuned by synthesizing the nanoparticles with the decomposition of organometallic precursors. Moreover, the possibility of performing the coating process directly in water/pentane makes possible to avoid toxic solvents such as dimethyl sulfoxide and N,N-dimethyl formamide, which are difficult to remove, thus reducing the safety risks deriving from their presence in traces in the final injectable solution. Finally, the mild temperatures required by this method make possible to use dendrimers modified with thermally unstable moieties through the surface amino residues, thus extending the range of functional groups that can be conjugated to MNPs for targeting or sensing. In vitro cell viability tests, performed by administration to bEND 5 cells and measurement of metabolic activity, the poor toxicity of this material was proved at least up to 1000 ng mL−1 of iron, obtaining results similar to those of widely used coatings, such as 3-aminopropyltriethoxysilane (APTES) over a wide size range (4–14 nm).18 Further on, Dynamic Light Scattering (DLS) measurements of hydrodynamic size and relaxometric mesurements repeated on the same sample over weeks provided evidence of a high colloidal stability both in water and in biological media, such as human plasma. Additionally, these MNPs demonstrated to induce a strong reduction in the MR signals in the rat liver after injection, suggesting their potential use as T2 MRI contrast agents with enhanced sensitivity.
In this work we aim to investigate the possibility to tune the properties of PAMAM coated MNPs to obtain a material which can simultaneously provide hyperthermic efficacy and increase the contrast in MRI imaging. In order to achieve this goal and maximize both the hyperthermic and relaxometric efficacy, we decided to synthesize samples, having the highest diameter obtainable with this method (ca. 20 nm), of two different shapes (spheres and faceted-like) and we performed a full structural, magnetic and relaxometric characterization. As a final test, we measured the Specific Absorption Rate (SAR).
2. Experimental
2.1 Sample preparation
In the preparations, iron pentacarbonyl (Fe(CO)5, 99.5%), oleic acid (OA), dioctyl ether, trimethylamine N-oxide, toluene, ethanol, anhydrous dimethylsulfoxide (DMSO), anhydrous N,N-dimethylformamide (DMF), PAMAM-C12 generation 4 (methanol solution) were purchased from Sigma-Aldrich. Oleic acid coated samples were prepared according to the reported method: 0.2 mL of iron pentacarbonyl were decomposed in 20 mL of dioctyl ether in the presence of oleic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Fe/oleic acid molar ratio). Further addition of iron oleate, prepared by decomposition of 0.2 mL of iron pentacarbonyl at 130 °C in the presence of oleic acid (1
3 Fe/oleic acid molar ratio). Further addition of iron oleate, prepared by decomposition of 0.2 mL of iron pentacarbonyl at 130 °C in the presence of oleic acid (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 Fe/oleic acid molar ratio), in dioctylether at solvent reflux temperature for 3 hours allowed growing the particle size. Oxidation with trimethyl amine N-oxide was performed before and after the growth step (A1) or only at the end of the growth (A2).
3 Fe/oleic acid molar ratio), in dioctylether at solvent reflux temperature for 3 hours allowed growing the particle size. Oxidation with trimethyl amine N-oxide was performed before and after the growth step (A1) or only at the end of the growth (A2).
The coating modification was performed according to the reported method:15 NP-OAs (13 mg, 83 μmol Fe, 30 μmol OA) were added to a solution of 0.25 mL of PAMAM-C12 generation 4 (methanol solution, 20 mg, 1 μmol) in 10 mL of water. After 16 hours stirring, solvents were removed under vacuum and replaced by water. 30 minutes of sonication facilitated the dispersion of the powder in water solution, which became orange. Recovery with a magnet allowed removing the unreacted dendrimers and other residues of the reaction.
2.2 Structural and magnetic characterization
The measurement of iron content in the samples was performed by an Inductively Coupled Plasma-Mass Spectrometry technique (ICP-MS, Agilent Technologies Inc., 7700 series, USA). DLS measurements were performed on a Beckman & Coulter Delsa Max instrument at 298 K. Conventional TEM micrographs and electron diffraction patterns were obtained with a Zeiss Libra 120 TEM operating at 120 kV and equipped with in column Omega filter for Electron-Energy Loss Spectroscopy (EELS). The MNP size distribution histogram was determined using enlarged TEM micrographs taken at magnification of 100 K on a statistical sample of ca. 200 MNPs. Magnetization data were collected on dry powder with a Quantum Design Ltd. SQUID magnetometer working in the temperature range of 1.8–350 K and the magnetic field range of 0–5 T.2.3 Relaxometry
Water 1H NMR relaxation measurements at fixed frequency 10 < ν < 60 MHz were collected by means of a Stelar SpinMaster Spectrometer (Stelar S.n.c., Mede (PV), Italy) on water solution of PAMAM-magnetic particles. Water proton T1 data were obtained by means of the Inversion-Recovery technique (16 experiments, 2 scans). Water proton T2 data were obtained by means of the CPMG sequence with the following parameters: 8 scans, 2048 data points, delay time equal to 5 times T1, applying a phase cycle on the pulses. Data were fitted with a monoexponential function.1H-NMRD (Nuclear Magnetic Relaxation Dispersion) profiles for 10 kHz < ν < 10 MHz (i.e. magnetic field strengths in the range 2.4 × 10−4 to 0.23 T) were recorded at 37 °C on a StelarSpinmaster-FFC field-cycling relaxometer (StelarS.n.c., Mede (PV), Italy) by measuring the water proton longitudinal and transverse relaxation rates with the use of FFC proper sequences.
Phantoms consisting of PAMAM–USPIO solution in vials were used to acquire Magnetic Resonance images through an ESAOTE Artoscan system operating at a fixed magnetic field of 0.2 Tesla, i.e. ∼8.5 MHz. The longitudinal (T1) relaxation time of the solutions was measured using a T1-weighted MRI sequence based on a standard Inversion Recovery (IR) with the following parameters: TR = 160 ms, TE = 26 ms, slice thickness = 3 mm. The used T2-weighted sequence was a spin-echo with experimental parameters: TE = 80 ms, TR (Repetition Time) = 5000 ms and TH (slice thickness) = 3 mm.
2.4 Calorimetric measurements
The hyperthermic efficiency was evaluated with a Magnetherm system by nanoTherics Ldt., which allows investigating frequencies in the range 100–1000 kHz with applied alternating magnetic fields of intensity 4–20 mT. An optical fiber by Optocon AG was used to measure the temperature with 1 s recording time. For all the experiments, the initial temperature was approximately 21/22 °C (laboratory conditions).The initial slopes of the temperature kinetics curves, T(t), were obtained by using the Box–Lucas fit reported in eqn (1):
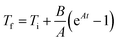 | (1) |
Before the measurements, the samples were sonicated for 5 minutes and then thermalized to the laboratory temperature before starting the experiment.
3. Results and discussion
3.1 Synthesis and structural characterization
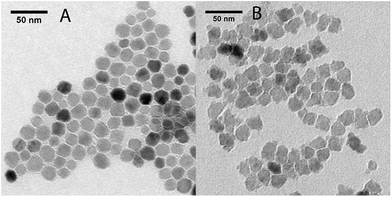
Iron oxide nanoparticles were synthesized according to the method proposed by Hyeon and coworkers.20 The obtained nanoparticles were grown by further reaction with iron oleate. In the case of sample A1, the nanoparticles were oxidized twice, before and after the growth step by addition of trimethyl amine N-oxide, while in the case of sample A2 the nanoparticles were oxidized only after the growth step.The final products were characterized by TEM analysis (Fig. 1). A1 consisted of a dispersion of regular-shaped particles, approximated by spheres, while A2 showed an irregular and faceted shape. The size distribution over ca. 200 nanoparticles for each sample have been fitted to a Gaussian to obtain the mean diameters, which are reported in Table 1 (distribution graphs are reported in ESI, Fig. S1†).
| Sample | dcore (nm) | dhyd (nm) | TB (K) | μ0HC (Oe) | MR/MS | MS@2.5 K (emu g−1) | MS@300 K (emu g−1) | K (104 J m−3) |
|---|---|---|---|---|---|---|---|---|
| A1(S1) | 19.5 ± 1.8 | 30.2 ± 3.3 | 270 | 324 | 0.28 | 77.2 | 69.8 | 2.61 |
| A2(S2) | 19.7 ± 0.8 | 33.7 ± 3.8 | >300 | 442 | 0.33 | 91.2 | 78.8 | 4.20 |
The coating procedure was performed on the samples A(1–2) by means of the reaction with lipid-modified PAMAM dendrimers of generation 4, which allowed us to obtain stable water dispersions for both samples, which were re-named S(1–2), respectively. The final water dispersions were characterized by DLS, TEM and ICP-MS. From the DLS mass distributions (see ESI, Fig. S2†), it was observed that the average hydrodynamic diameter was about 10 nm higher than the pristine magnetic core A(1–2) size (cfr dcore and dhyd in Table 1). By considering that the molecular diameter of the used generation 4 PAMAM on the surface is 4.5 nm,21 this result is consistent with TEM analysis on S(1–2), which did not show evidences of consistent aggregates formation (see ESI, Fig. S3†). Further DLS measurements repeated over weeks did not report changes in mean hydrodynamic diameter and confirmed the dispersions stability. In conclusion, the morphological and structural analysis on S(1–2) allowed verifying that the coating step did not alter the main properties of the samples, as already demonstrated in our previous work.15
3.2 Magnetic characterization
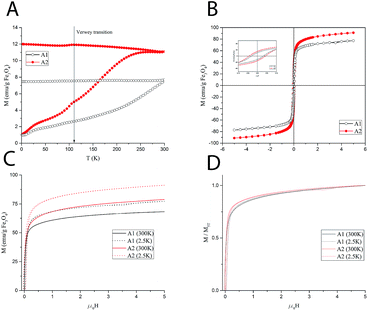
In order to establish the magnetic behavior of the MNP dispersions, which strongly influence their relaxometric performance, a full set of magnetic measurements was performed on the solid (dry powders) samples A1–A2. The main magnetic parameters obtained from the measurements are summarized in Table 1. The zero-field cooled/field cooled (ZFC/FC) magnetization curves, collected with a probe field of 5 mT in the 5–300 K temperature range, are reported in Fig. 2A.The curves represent the typical behavior of a set of single domain MNPs. Sample A1 also displays a smoothed peak at ca. 110 K, which can be associated to the Verwey transition, whose characteristic temperature for bulk magnetite (120 K), is often reduced in nanosized systems. This transition is typical of magnetite and its absence in the ZFC/FC curve of A2 can be ascribed to a certain degree of oxidation to maghemite. The average blocking temperature, TB, commonly associated to the temperature at which the ZFC curve reaches its maximum, is about 270 K for A2, while it could not be estimated accurately for A1 as it is above the temperature range of the instrument. According to the Néel model for non-interacting MNPs, TB is proportional to the anisotropy energy barrier ΔE = KV, where K is the anisotropy constant of the material and V the mean magnetic volume of the NPs. Thus, the observed difference may be ascribed to a difference in anisotropy and/or magnetic volume between the two samples.
The magnetization as a function of the applied field, M(H), was measured at 300 K and 2.5 K (Fig. 2C) up to 5 T. The magnetization curves rapidly approach the saturation. However, as the magnetization curves do not completely saturate, an estimate of the saturation value, MS, was obtained by fitting the high field magnetization data to the empirical law M = MS + b/H + c/H2.22 At high temperature, the saturation values are 69.8 and 78.8 emu g−1 of iron oxide for A1 and A2, respectively.
Hysteresis was observed at low temperature (Fig. 2B), while no coercivity is present at 300 K, as expected for superparamagnetic nanoparticles. The remanent magnetization, MR, and the coercive field, HC, are slightly higher for sample A2. The magnetic anisotropy constant, K, can be estimated from the low temperature coercive field HC as, for an ensemble of randomly oriented NPs at a finite temperature, is given by μ0HC = 0.96(K/MS)[1 − (T/TB)0.77]. In our case, since the temperature-dependent term is negligible for all samples (TB is much larger than T = 2.5 K), the anisotropy constant can be simply estimated by K = HCMS/0.96 where MS is the value at 2.5 K. The results reported in Table 1 show a higher anisotropy for A2. Hence, in principle, the higher TB of A1 should be associated with a higher average magnetic volume. Furthermore, in the normalized magnetization curves (Fig. 2D), a faster approach to saturation can be observed for sample A1. This suggests a higher susceptibility, which is commonly associated to a higher magnetic volume. Nevertheless, the mean volume foreseen by the Nèel simple model to compensate the anisotropy difference should be too large to be realistic. A more complex model including other factors (size distribution and interparticle interactions) should be envisaged to account for TB findings, which is beyond the purpose of the present work.
The magnetic measurements were repeated on a lyophilized sample of S2 to test the effect of the PAMAM coating on the magnetic behavior. The comparison between A2 and S2 (see ESI, Fig. S4†) shows small differences, which can be ascribed to the change of the interparticle interactions rather than to an intrinsic modification of the particle surface during the coating procedure. In particular, the decreased dipolar interactions due to the larger interparticle distance provided by the coating layer can account for the small reduction of the blocking temperature of S2 (253 K).
The superparamagnetic behavior at room temperature of both samples, particularly evidenced for sample A2, together with the high MS values of the material, prefigures the use of these nanoparticles as negative contrast agents for MRI, as this allows a fast response to the applied magnetic field and a large and constant magnetic moment for single particles.23
3.3 1H NMR relaxometric characterization
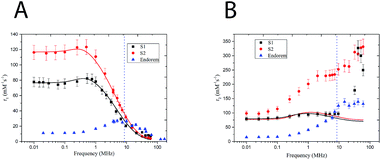
A relationship between the dynamic and static magnetic properties of the samples has been evaluated through the relaxometric behavior of the 1H nuclei present in the nanoparticle solution (i.e. water's hydrogens). The nuclear magnetic relaxation properties of a compound are ideally obtained by the study of its Nuclear Magnetic Resonance Dispersion (NMRD) profile. These curves give the relaxivity evolution of the nuclear spins of the 1H versus the external magnetic field, and constitute an interesting tool to optimize the parameters of the nanoparticle synthesis24 for having better MRI contrast agents. The relaxivity ri (i = 1, 2) is defined as the increase of the relaxation rate (ri, the inverse of the relaxation time Ti) of the hydrogen nuclei of H in the solvent (water in this case) induced by 1 mM of magnetic center (iron in this case). The capability of the nuclear spin of 1H to exchange energy with the giant electronic spin of the nanoparticles increases the nuclear spin relaxivity and gives information about the local electronic spin dynamics. Two different phenomena can be distinguished with respect to the direction of the external static magnetic field. The relaxation of the longitudinal nuclear magnetization is mainly due to the interaction between the lattice and the nuclear spins and T1 is the time of equilibrium recovery. The relaxation of the nuclear transverse competition (T2) is the result of the spin–spin interaction. In Magnetic Resonance Imaging (MRI) the signal is contrasted, with different efficacies, by introducing contrast agents that reach specific sites and change locally the relaxivities of the 1H nuclei contained in the human tissues. The T1 and T2 relaxivities depend on the magnetic field whose typical values in MRI apparatus of hospital are between 0.2 T (8.5 MHz) and 3 T (120 MHz). It is worth to notice that in this range of field the MNPs display quite high r1 but very high r2 so that they can be helpful mainly to increase the T2 negative contrast (i.e. local dispersion of signal) in MRI images. For these reasons from now on, we will refer to r2 as the contrast efficiency. Fig. 3 shows the longitudinal (A) and transversal (B) relaxometric profiles of samples S(1–2). All the measured samples present a dispersion curve strongly dominated by the effects of superparamagnetic relaxation, characterized by a low field plateau followed by a smoothed peak in the 0.5–1 MHz range, referred to as the Curie peak, and by a decrease at high fields (i.e. high Larmor frequencies). It can be noticed that sample S1 presents an irregular r2 profile with respect to S2; the difference is of uncertain origin. The NMRD profiles the two samples present very different MRI contrast efficiency (i.e. r2 especially at high fields), in particular S2 displaying higher r2 with respect to S1. If it is assumed that the r2 value is dominated by the effect of the giant magnetic moment, these data are in agreement with the magnetic measurements, where A2 displayed a higher MS compared with A1. It is worth to notice that sample S2 presents a transversal relaxivity more than two times higher than the commercial contrast agent Endorem, while the longitudinal relaxivities for f > 10 MHz are comparable. From the relaxometric analysis we can then conclude that the study of local spin dynamics confirms the superparamagnetic regime at room temperature and demonstrates that S2 is a promising T2 contrast agent.To obtain further information on the microscopic features and the Néel relaxation time of our nanostructures, we fitted the r1 and r2 profiles by using a heuristic model developed by Roch, Muller and Gillis.25 This RMG model considers the nuclear relaxation composed by different contributions: the first due to hyperfine field fluctuations at the nuclear sites caused by the diffusion of solvent protons into the inhomogeneous magnetic field created by the large magnetic moments of the MNP (named Curie relaxation) and the second due to the fluctuations of the magnetic moment of each particle induced by the Néel relaxation with typical correlation time τN (low f). The model presents a very complicate formula to fit the experimental data (see ref. 25), which is not useful to be reported here. However, the parameters of our interest (reported in Table 2) can be summarized as follows: τN is the Néel relaxation time, dNMR is the minimum approach distance (i.e. the capacity of water molecules to permeate the coating) and P and Q are weighting factors, bonded by the constraint P + Q = 1 and related to the magnetic anisotropy (the two limit cases are P = 1 for null anisotropy energy and Q = 1 for anisotropy energy tending to infinite). From the fitting of the longitudinal relaxivity r1 with RMG model (Fig. 3A, solid lines), we obtained that: (i) the P/Q ratio decreases with increasing anisotropy, coherently with magnetic anisotropy constant data obtained by magnetometric measurements (Table 2); (ii) the values of the Néel relaxation times at room temperature, τNMRN, are in the typical range of SPM compounds reversal time; (iii) the distance of minimum approach dNMR is intermediate between the magnetic core diameter as determined by TEM and the hydrodynamic diameter dhyd, a result suggesting that our samples' coating is partially penetrated by the water. On the other hand, the experimental r2 profile cannot be fitted to the RMG model, the bigger disagreement being in the high field (frequency) region (Fig. 3B, solid lines). A similar mismatch has previously been observed26,27 and attributed to one or more physical mechanisms not included in the model itself. On this respect, it should be observed that the RMG model describes systems in the so called motional averaging regime (in short MAR, corresponding to fast motions) while our systems are out of the limit of the MAR regime. In particular they can be considered between the MAR and the SDR (static dephasing regime, slow motions regimes).28 In fact, by using the approximated model of Vuong et al.,28 one can easily guess that our r2 experimental data at frequencies between 20 and 60 MHz fall in between the predictions of the different regimes (rMAR2 ∼ 72 s−1 mM−1, rSDR2 ∼ 780–800 s−1 mM−1). The discussion on further details of the physical mechanisms responsible for the high values of r2 in our samples is out of the scope of the present manuscript (Table 3).
| Sample | P/Q | τNMRN 300 K | r2/r1 (60 MHz) | dNMR (nm) | dhyd (nm) |
|---|---|---|---|---|---|
| S1 | 2.62 | 1.57 × 10−7 | 35.04 | 24.8 ± 2.0 | 30.2 |
| S2 | 1.17 | 2.77 × 10−7 | 87.23 | 25.1 ± 0.4 | 33.7 |
| Sample | r1 (s−1 mM−1) at 8.5 MHz | r2 (s−1 mM−1) at 8.5 MHz | r1 (s−1 mM−1) at 60 MHz | r2 (s−1 mM−1) at 60 MHz |
|---|---|---|---|---|
| S1 | 27(2) | 96(8) | 9.0(0.7) | 249(20) |
| S2 | 37(3) | 245(19) | 3.8(0.3) | 331(26) |
| Endorem | 26(2) | 114(9) | 11(1) | 106(8) |
3.4 MR-imaging
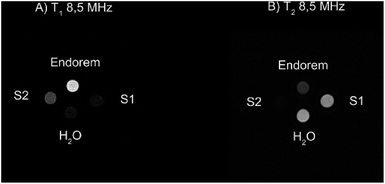
To validate the previous results regarding the high r2 contrast efficiency of S1 and S2, we collected MRI images at a field intensity of 0.2 T (∼8.5 MHz), commonly used by clinical scanners for the investigation of diseases in articulations. As described in the Experimental section, the vials containing different samples at the same Fe concentration were placed in the center of the detection coil. Fig. 4 shows the T1 and T2-weighted images of the prepared samples compared to the commercial contrast agent (CA) Endorem and to water. We expect positive bright contrast in the T1-weighted image and negative dark contrast in the T2-weighted image.Fig. 4A shows that Endorem is the best T1-CA among the analyzed samples, while Fig. 4B confirms the best r2 performance for S2, thus being a better T2-CA in comparison with Endorem, as rS-22 (8.5 MHz) ∼ 254 s−1 mM−1 > rEndorem2 (8.5 MHz) ∼ 106 s−1 mM−1 > rS-12 (8.5 MHz) ∼ 95 s−1 mM−1.
3.5 Hyperthermic efficacy
The heating mechanism in magnetic materials is related to the capability to adsorb energy from an external alternating magnetic field (AMF) and to dissipate it in the environmental medium. For MNPs superparamagnetic MNPs, as in our case, the energy losses are due to the lag of the magnetization with respect of the field oscillation which can be related to the an effective relaxation time, τeff (see the definition below). The energy loss power per unit volume (Specific Loss Power, SLP) for randomly oriented superparamagnetic nanoparticles, can be thus represented as in eqn (2):
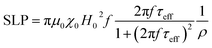 | (2) |
The effective time τeff is given by τeff = 1/τN + 1/τB, where τN and τB are the characteristic times of the Néel and Brown mechanisms concurring to the magnetization relaxation, given by:
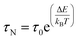 | (3) |
| τB = 3ηVH/KkBT | (4) |
The MNPs such as ferrite nanoparticles have shown promising results as potential heating mediators in magnetic hyperthermia due to their efficiency in conversion of magnetic energy into heat even at low concentrations. Magnetic energy dissipation in a ferrofluid sample is measured by calorimetric experiments using the thermodynamic relationship reported in eqn (5):
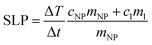 | (5) |
We measured the temperature kinetics curve T(t) for several of the combinations field-frequency allowed by the experimental set up. We must note that they exceeds the clinical safety limit (fH < 4.58 × 108 A m−1 s−1)29 commonly accepted for whole-body exposure, but all of them are within the less restrictive threshold (5 × 109 A m−1 s−1) allowed when the region of the body exposed to the AMF is small.
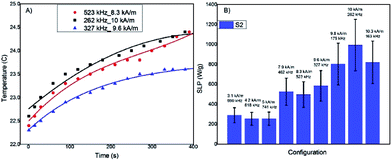
In Fig. 5A three examples of T(t) curves acquired for the most promising sample, S2, (data not shown for sample S1) with different fH combinations are reported, showing a temperature increase of a few Celsius degrees after 5 minutes of exposition to the AFM field. The low temperature increase is due to the low MNP concentration used for reducing the interparticles interactions. The SLP values have been evaluated using the Box–Lucas function, T(t) = A(1 − eBt), the most appropriate model when the temperature increment is small, as in this case (examples of the best-fitting curves are shown in Fig. 5A). The SLP results for all the considered fH combinations are reported in Fig. 5B. The SLP values clearly show an increment when the field is increased. The maximum SLP values, about 900 W g−1, was obtained for field intensities of the order of 10 kA m−1 in the frequency range 100–300 kHz. The high SLP values demonstrate that the new synthetized MNPs are promising hyperthermic agents.
4. Conclusions
In this work, we synthesized stable suspensions of MNPs with d ∼ 20 nm diameter by decomposition of iron pentacarbonyl and further growth with iron oleate. By tuning the reaction conditions, we have been able to prepare two samples having a similar size but a different shape, almost spherical (A/S1) and faceted (A/S2). Further on, transferring the MNPs in water phase by PAMAM coating, at room temperature, preserved the structural properties of the inorganic core. The MNPs have been fully characterized by SQUID magnetometry, displaying a high magnetization, especially for the faceted sample, S2. In addition, the transverse relaxivities of this sample – r2 ∼ 300 mM−1 s−1 at 60 MHz (corresponding to the clinical field 1.5 Tesla) and r2 ∼ 250 mM−1 s−1 at 8.5 MHz (corresponding to the field 0.2 Tesla)-are higher than S1 and about 2.5–3 times higher than the corresponding ones of the commercial compound Endorem. Thus, the faceted MNPs underwent calorimetric measurements aimed to verify their possible application in Magnetic Fluid Hyperthermia. The SLP was recorded for several combinations of amplitude and frequency of the applied field and very high values were found at any field intensity and frequency, reaching 900 W g−1 at 262 kHz and 10 kA m−1 (within the tolerance limit for H*f ∼ 2.6 × 109 A m−1 s−1), a value indicating these materials among the most promising ones for application in this field. Faceted MNPs being very effective both as MRI negative CAs and hyperthermic mediators, can be envisaged for a future application as theranostic agents, capable of diagnosing cancer, treating it and monitoring the response to treatment. Future investigations will be needed to transfer these results in vivo and, possibly, to properly functionalize the MNPs surface thus addressing specific molecular targets (like e.g. tumour antigenes). Their use as targeting agents will require the achievement of sufficiently long lifetime in the human circulatory system and reduction of doses. The selective delivery to malignant tumor tissues will be pursued through the conjugation with nucleic acids (aptamers), peptides, and natural molecules. On this purpose, the flexibility displayed by the coating chosen for this work seems to offer a quite wide range of possibilities.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We wish to thank Fondazione Cassa di Risparmio di Firenze for funding this work. The COST European projects RADIOMAG (TD 1402) and EURELAX (CA 15209) are gratefully acknowledged.Notes and references
- M. Franckena, L. J. A. Stalpers, P. C. M. Koper, R. G. J. Wiggenraad, W. J. Hoogenraad, J. D. P. van Dijk, C. C. Wárlám-Rodenhuis, J. J. Jobsen, G. C. van Rhoon and J. van der Zee, Int. J. Radiat. Oncol., Biol., Phys., 2008, 70, 1176–1182 CrossRef PubMed.
- E. L. Jones, J. R. Oleson, L. R. Prosnitz, T. V. Samulski, Z. Vujaskovic, D. Yu, L. L. Sanders and M. W. Dewhirst, J. Clin. Oncol., 2005, 23, 3079–3085 CrossRef PubMed.
- J. van der Zee, D. González, G. C. van Rhoon, J. D. P. van Dijk, W. L. J. van Putten and A. A. M. Hart, Lancet, 2000, 355, 1119–1125 CrossRef CAS.
- M. Amichetti, M. Romano, L. Busana, A. Bolner, G. Fellin, G. Pani, L. Tomio and R. Valdagni, Radiother. Oncol., 1997, 45, 155–158 CrossRef CAS PubMed.
- Y. Hua, S. Ma, Z. Fu, Q. Hu, L. Wang and Y. Piao, Int. J. Hyperthermia, 2011, 27, 180–186 CrossRef PubMed.
- N. G. Huilgol, S. Gupta and R. Dixit, Int. J. Hyperthermia, 2010, 26, 21–25 CrossRef CAS PubMed.
- M. E. Sharafinski, R. L. Ferris, S. Ferrone and J. R. Grandis, Head Neck, 2010, 32, 1412–1421 CrossRef PubMed.
- S. Dutz and R. Hergt, Nanotechnology, 2014, 25, 452001 CrossRef PubMed.
- R. Ivkov, S. J. DeNardo, W. Daum, A. R. Foreman, R. C. Goldstein, V. S. Nemkov and G. L. DeNardo, Clin. Cancer Res., 2005, 11, 7093s–7103s CrossRef CAS PubMed.
- P. Moroz, S. K. Jones and B. N. Gray, Int. J. Hyperthermia, 2002, 18, 267–284 CrossRef CAS PubMed.
- S. Müller, Nanomedicine, 2009, 5, 387–393 CrossRef PubMed.
- J. M. Provenzale and G. A. Silva, Am. J. Neuroradiol., 2009, 30, 1293–1301 CrossRef CAS PubMed.
- K. Maier-Hauff, F. Ulrich, D. Nestler, H. Niehoff, P. Wust, B. Thiesen, H. Orawa, V. Budach and A. Jordan, J. Neuro-Oncol., 2011, 103, 317–324 CrossRef PubMed.
- Y. Jin, C. Jia, S.-W. Huang, M. O'Donnell and X. Gao, Nat. Commun., 2010, 1, 41 Search PubMed.
- A. Boni, L. Albertazzi, C. Innocenti, M. Gemmi and A. Bifone, Langmuir, 2013, 29, 10973–10979 CrossRef CAS PubMed.
- A. Boni, D. Ceratti, A. Antonelli, C. Sfara, M. Magnani, E. Manuali, S. Salamida, A. Gozzi and A. Bifone, Contrast Media Mol. Imaging, 2014, 9, 229–236 CrossRef CAS PubMed.
- Y. Yuan, D. Rende, C. L. Altan, S. Bucak, R. Ozisik and D.-A. Borca-Tasciuc, Langmuir, 2012, 28, 13051–13059 CrossRef CAS PubMed.
- A. Boni, G. Bardi, A. Bertero, V. Cappello, M. Emdin, A. Flori, M. Gemmi, C. Innocenti, L. Menichetti, C. Sangregorio, S. Villa and V. Piazza, Nanoscale, 2015, 7, 7307–7317 RSC.
- A. Cervadoro, C. Giverso, R. Pande, S. Sarangi, L. Preziosi, J. Wosik, A. Brazdeikis and P. Decuzzi, PLoS One, 2013, 8, e57332 CAS.
- T. Hyeon, S. S. Lee, J. Park, Y. Chung and H. B. Na, J. Am. Chem. Soc., 2001, 123, 12798–12801 CrossRef CAS PubMed.
- A. Tomalia Donald, S. Uppuluri, R. Swanson Douglas and J. Li, Journal, 2000, 72, 2343 Search PubMed.
- A. H. Morrish, The Physical Principles of Magnetism, John Wiley and Sons, New York, 1965 Search PubMed.
- A.-H. Lu, E. L. Salabas and F. Schüth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244 CrossRef CAS PubMed.
- A. Ouakssim, S. Fastrez, A. Roch, S. Laurent, Y. Gossuin, C. Piérart, L. Vander Elst and R. N. Muller, J. Magn. Magn. Mater., 2004, 272–276, E1711–E1713 CrossRef CAS.
- A. Roch, R. N. Muller and P. Gillis, J. Chem. Phys., 1999, 110, 5403–5411 CrossRef CAS.
- M. Basini, T. Orlando, P. Arosio, M. F. Casula, D. Espa, S. Murgia, C. Sangregorio, C. Innocenti and A. Lascialfari, J. Chem. Phys., 2017, 146, 034703 CrossRef CAS PubMed.
- T. Orlando, M. Albino, F. Orsini, C. Innocenti, M. Basini, P. Arosio, C. Sangregorio, M. Corti and A. Lascialfari, J. Appl. Phys., 2016, 119, 134301 CrossRef.
- Q. L. Vuong, J.-F. Berret, J. Fresnais, Y. Gossuin and O. Sandre, Adv. Healthcare Mater., 2012, 1, 502–512 CrossRef CAS PubMed.
- D. Ortega and Q. A. Pankhurst, in Nanoscience: Volume 1: Nanostructures through Chemistry, The Royal Society of Chemistry, 2013, vol. 1, pp. 60–88 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07589h |
| This journal is © The Royal Society of Chemistry 2017 |