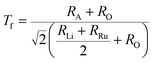Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Origin of the optical anisotropy and the electronic structure of Ru-based double perovskite oxides: DFT and XPS studies†
Anup Pradhan Sakhya *a,
D. P. Raib,
Md. Sariful Sheikha,
Manabendra Mukherjeec,
Alo Duttad and
T. P. Sinhaa
*a,
D. P. Raib,
Md. Sariful Sheikha,
Manabendra Mukherjeec,
Alo Duttad and
T. P. Sinhaa
aDepartment of Physics, Bose Institute, 93/1 Acharya Prafulla Chandra Road, Kolkata 700009, India. E-mail: npshakya31@gmail.com
bDepartment of Physics, Pachhunga University College, Aizawl 796001, Mizoram, India
cSaha Institute of Nuclear Physics, 1/AF, Bidhan Nagar, Kolkata 700064, India
dDepartment of Condensed Matter Physics and Material Sciences, S. N. Bose National Centre for Basic Sciences, Block-JD, Sector-III, Salt Lake, Kolkata-700098, India
First published on 8th September 2017
Abstract
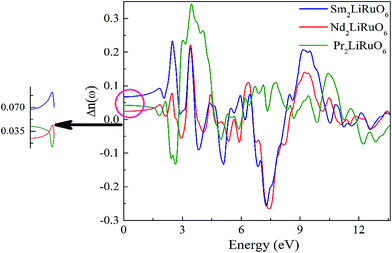
Experimental and theoretical studies of the electronic structure of Pr2LiRuO6 (PLR), Nd2LiRuO6 (NLR) and Sm2LiRuO6 (SLR) crystals are reported. The linear optical properties of these compounds have been investigated using density functional theory calculations. The optical anisotropy in these compounds is revealed from their computed optical properties, such as their complex dielectric functions and refractive indices. The calculations show that SLR has a relatively large birefringence (Δn = 0.06) compared to NLR and PLR, which is important for mid-infrared nonlinear optical applications. We propose that the O 2p to Ru 4d transition is primarily responsible for the origin of optical activity in these materials while the origin of the optical anisotropy in these materials results from the asymmetrically oriented Ru–O bonds in the RuO6 octahedra of the unit cell. The evolution of the Ru 3d core-level signals as obtained from the X-ray photoemission spectroscopy measurements provide confirmation of a dynamic increment in the electron correlations as we move from PLR and NLR to SLR.
1. Introduction
The structural and the physical properties of double perovskite oxides with the general formula A2BB′O6 and distinct transition metal ions at the B and B′ sites have been an active area of research because of the diverse physical properties and structural chemistry exhibited by this family of oxides.1 Recently, the electronic properties of mixed-metal oxides containing ruthenium, particularly those which adopt the perovskite structure, have gained tremendous interest. This interest has been stimulated due to developments in a number of fields such as colossal magnetoresistance2,3 and superconductivity.4 Complex oxides with ruthenium show diverse properties, for example, rutile type RuO2 is a normal metal and the density of states (DOS) obtained from band structure calculations is in good agreement with its photoemission spectra.5 Bi2Ru2O7 is a Pauli-paramagnetic metal whereas pyrochlore-type Y2Ru2O7 is an insulator and exhibits a local-moment behaviour.6 Further, Sr2RuO4 has attracted interest due to its unusual electronic and magnetic properties such as non-s-wave superconductivity,7 orbital ordering in La4Ru2O10 (ref. 8) and non-Fermi-liquid behaviour in La4Ru6O19.9 SrRuO3 is a rare example of a 4d ferromagnet (Tc ≈ 165 K).10 This change in the electronic behaviour has been attributed to the change in the electron–electron correlation as suggested by Kim et al.11 The conclusion has been made based on the fits of the experimental core level X-ray photoemission (XP) spectra. Recently, Makowski et al. have reported the structural and magnetic properties of the Ln2LiRuO6 double perovskites where Ln = Pr, Nd, Sm, Eu, Gd, Tb using synchrotron X-ray, neutron powder diffraction, and magnetic susceptibility measurements for the first time.12 Beyond this, not much is known about these materials. The motivation behind this paper is twofold. Firstly, we want to study the linear optical properties of these materials and see if these materials are birefringent. Birefringent materials are very important and interesting in optical communications and laser industry as they can modulate the polarization of light and are vital crystalline materials in producing optical devices such as optical isolators, circulators, polarization beam splitters and photo storage devices.13–17 The birefringence value of a material can be obtained by measuring the refractive index by using the minimum deviation method. However, large size crystals of good optical quality are needed which is very difficult to synthesize. Hence density functional theory (DFT) calculations play a very important role to predict the birefringence value which is very significant in choosing optical materials with suitable birefringence.17,18 Additionally, birefringence is necessary for phase matching conditions during the optical second harmonic experiments.19 Secondly, we have made an attempt to understand the electronic structure of these materials using XP spectroscopy and DFT calculations. A detailed theoretical understanding of the intrinsic physical properties of these materials will be very significant not only for fundamental research but also for technological applications.2. Experiment
A2LiRuO6 (A = Pr, Nd, Sm) compounds have been synthesized by the solid-state reaction method. For the synthesis of A2LiRuO6, the reagent grades of Pr2O3 (Sigma Aldrich), Sm2O3 (Alfa Aesar), Nd2O3 (Alfa Aesar) (prefired at 1000 °C for 12 h), RuO2 (Alfa Aesar) (pre-fired at 450 °C for 12 h) and 20 mol% excess of Li2CO3 (Loba Chemie) (pre-fired at 80 °C for 12 h) are taken in stoichiometric ratio and mixed in the acetone medium. The resultant mixture is then dried and calcined at 980 °C for 12 h and brought to room temperature by cooling at the rate of 100 °C h−1. The material is then mixed again in the acetone medium with an additional 20 mol% excess of Li2CO3 and then finally heated at 980 °C for 12 h (cooled at the rate of 100 °C h−1). The excess Li2CO3 has been added because of the volatilization of Li and is essential for the preparation of pure samples.12 The calcined powders are pelletized into discs (8 mm diameter and 1.5 mm thickness) using polyvinyl alcohol as a binder. These discs are then sintered at 1080 °C for 10 h and cooled to room temperature at the rate of 1 °C min−1. The X-ray diffraction (XRD) pattern of the synthesized samples have been taken at the room temperature using Rigaku Miniflex-II X-ray powder diffractometer in the 2θ range from 10° to 80° by scanning at 0.02° per step. The Rietveld refinement of the XRD pattern has been carried out using FULLPROF20 method. In the refinement process, the background is fitted with sixth order polynomial, while the peak shapes are described by pseudo-Voigt profiles. During the refinement, scale factor, zero correction, background, half width parameters, lattice parameters, positional coordinates and isotropic thermal parameters (Biso) are varied. No correlation between the positional and the thermal parameters are observed during refinement and as such, it is possible to refine all the parameters together. XP core-level spectra are taken with an Omicron Multiprobe (Omicron Nanotechnology GmbH., UK) spectrometer fitted with an EA125 hemispherical analyzer. A monochromated 1486.7 eV X-ray source operated at 150 W has been used for the experiments. The analyzer pass energy is kept fixed at 40 eV for all the scans. As the samples are insulating in nature, a low energy electron gun (SL 1000, Omicron) with a large spot size has been used to neutralize the samples. The potential of the electron gun is kept fixed at −3 eV for all the samples with respect to the ground. The binding energy (BE) has been determined with reference to the C 1s line at 284.8 eV.3. Computational details
In this study, two computational methods within the framework of density functional theory (DFT) have been used in a complementary manner. The structural optimization and dielectric tensor are obtained by using the projector augmented wave (PAW)21,22 method as implemented in the VASP.23 The electronic structure and the optical properties have been calculated using WIEN 2k code.24 For more details on computational parameters see Section S1 in ESI.†4. Results and discussion
4.1. Structural study
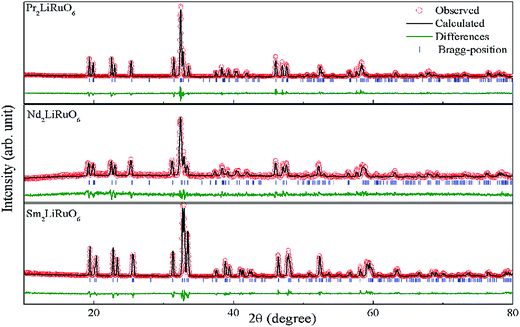
The stability of A2LiRuO6 to a first approximation is determined by the ratio of A–O, Li–O, Ru–O bond lengths, which can be expressed as the tolerance factor given bywhere RA, RO, RLi, and RRu denote the ionic radii of A, O, Li and Ru ions respectively. The tolerance factor calculated using the ionic radius of Pr (1.179 Å), Nd (1.27 Å), Sm (1.24 Å), Li (0.76 Å), Ru (0.62 Å) and O (1.4 Å) are found to be 0.87, 0.90 and 0.89 for PLR, NLR and SLR respectively. Usually a cubic perovskite structure is obtained for Tf close to unity, whereas it can be lower symmetrical structure (orthorhombic, monoclinic) for lower value of tolerance factor. This value of the tolerance factor suggests that the room temperature crystal structure of A2LiRuO6 should have a lower symmetry than cubic structure. The distortion from the ideal cubic double perovskite structure is a result of the tilting of the LiO6 and RuO6 octahedra, while maintaining their corner-sharing connectivity. This is commonly observed for compositions that include an A-cation which is too small to fill the 12-fold coordination site and would result in reduced eight-fold coordination environment. To verify the same, we have performed the Rietveld refinement of the room-temperature XRD patterns of A2LiRuO6 using the Fullprof software.20 The XRD patterns of A2LiRuO6 are shown in Fig. 1. A good agreement between the observed (symbols) and refined (lines) data suggests that the compounds are crystallized in the monoclinic perovskite structure with space group P21/n. As both the A–O and (Li, Ru)–O bond lengths are limited to a narrow range; for a double perovskite structure, the only way to accommodate smaller A-cations is by distorting the Li–O–Ru bond angles. This feature of the rotated octahedron, common among all P21/n ordered double perovskites, requires that the (Li, Ru)–O6 octahedrons have different tilt angles as a result of the differences in the size and the distortion of the two polyhedron. Consequently, the β angle of a monoclinic unit cell can be viewed as a measure of the structural distortion. The lattice parameters, atomic positions, reliability factors, bond lengths and bond angles for the different constituent ions are listed in (Table S4 and Table S5 respectively in ESI†). In these materials Pr, Nd and Sm have co-ordination number 8 instead of 12. The co-ordination number of these cations has been reduced because some of the anions move too far away from the A-cation for lower symmetry double perovskite oxides (DPOs) due to the octahedral tilting which causes the first coordination sphere about the A cation to change. It has been proposed by Woodward25 that any anion more than 3.00 Å away from the A-cation of DPOs may be considered to be outside the coordination sphere. A schematic presentation of the A2LiRuO6 cell is shown in Fig. S1 in ESI,† with the distribution of ions at crystallographic positions 4e for A ions, 2d for Li ions, 2c for Ru ions and 4e for O ions as given in Table S4 in ESI.† Each Li and Ru ions are surrounded by six O ions, constituting LiO6 and RuO6 octahedra, respectively.
4.2. Spin polarized electronic band structure and density of states
The spin-polarized band structures of A2LiRuO6 (A = Pr, Nd, Sm) compounds along the high-symmetry directions in the Brillouin zone are shown in Fig. 2, where similarities in the energy bands are evident. For the clarity of the figures, the energy bands in the region from −6 eV to 6 eV are shown in Fig. 2(a)–(c). In these calculations, the zero of the energy scale is taken at the top of the valence band (VB). It is clear that the spin-up/down channels of PLR possesses an indirect energy band gap as the valence band maximum (VBM) is located at the Γ symmetry point of the Brillouin zone (BZ) for spin up/down, while the conduction band minimum (CBM) is situated at the R symmetry point for spin up (↑) and at the Γ point for spin down (↓). NLR also possesses an indirect energy band gap as the VBM is located at the Γ symmetry point for spin up (↑) and Σ symmetry point for spin down (↓), while the CBM is located at the Σ symmetry point for spin up (↑) and Γ symmetry point for spin down (↓). SLR however shows a direct band gap as the VBM is located at the Γ symmetry point of the Brillouin zone (BZ) for both spin up (↑)/down (↓) whereas the CBM is situated at the Γ symmetry point of the Brillouin zone (BZ) for both spin up (↑)/down (↓). The spin-polarized electronic band structure of A2LiRuO6 (A = Pr, Nd, Sm) reveals that all the compounds are insulators. The calculated band gaps are 3.1 eV (↑) and 1.6 eV (↓) for PLR, 3.12 eV (↑) and 1.7 eV (↓) for NLR and 2.2 eV (↑) and 1.8 eV (↓) for SLR. It is observed that the energy gap of spin down (↓) is noticeably lower than that of spin up (↑). This is attributed to the fact that the location of Ru d states at the lower part of the conduction band (CB) for the spin down (↓) pushes the CBM towards the Fermi level (EF) resulting in the reduced energy gap value for all these compounds. However, for the spin up (↑), the Ru d states as well as A f states are shifted towards higher energies resulting in the increased spin up (↑) band gap.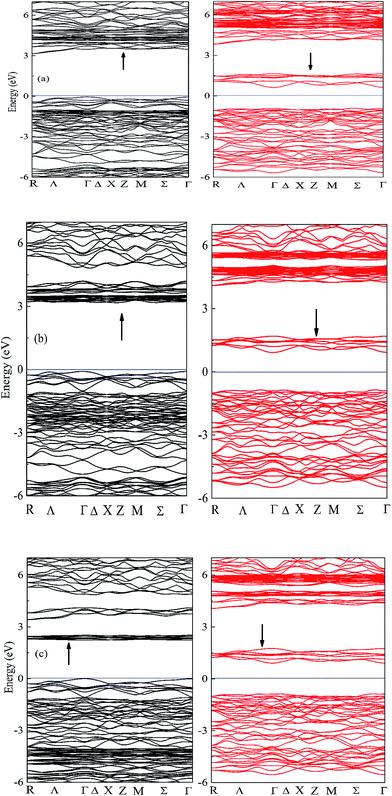 | ||
| Fig. 2 Band structure of (a) PLR (b) NLR and (c) SLR within GGA + U. Bands in black (red) indicate the spin up (down) channel. | ||
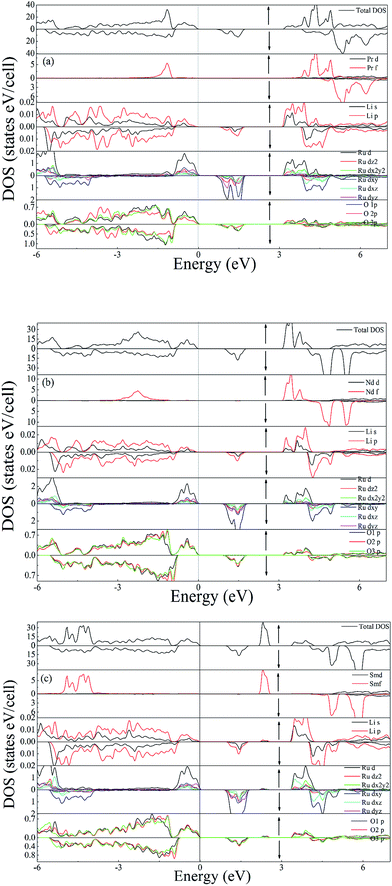
The calculated DOS for the investigated compounds are shown in Fig. 3(a)–(c), which are helpful in identifying the character of band states at different energy levels. In the case of PLR, in the up-spin channel (shown by ↑ in [Fig. 3(a)]) the VB and the CB is mainly dominated by Pr f and Ru d states hybridized with O p and Li p states. The existence of Pr f states in the upper VB and lower CB have a significant effect on the energy band gap dispersion. The Ru d states lie near the EF in the energy range from −1.4 eV to 0 eV and in the lower part of the VB from −4.5 eV to −5.1 eV, while the remaining states of VB are dominated by O p character. In the down spin channel (shown by ↓ in [Fig. 3(a)]), the VB is mainly dominated by O p and Li p orbitals. Since the valency of Pr ion in PLR compound is +3 ([Xe]4f2), its energy states in the spin up channel are partially filled up and lies in the VB region whereas the energy states of Pr ion in the down spin channel (shown by ↓ in [Fig. 3(a)]), are completely empty and lies in the CB region. In the case of NLR, from the partial density of states (PDOS) plots, one can see that there exists a strong hybridization between the Ru d states and the O p states in the up-spin channel (↑) from −1 eV up to EF. In the VB the contribution of Nd 4f states lies in between the energy range from −1.3 eV to −2.9 eV hybridized with the O p states. The CB in the up-spin channel is mainly composed of Ru d states and Nd f states. In the down spin channel (shown by (↓) in [Fig. 3(b)]), the VB is mainly composed of O p and Li s states. The band extending from 4 to 5.9 eV in the CB is mainly occupied by the anti-bonding states of Nd 4f. There is no contribution of Nd 4f states in the down spin channel, which is in conformity with the electronic configuration of Nd3+ ([Xe]4f3) in NLR. The spin up channel of Nd (↑) is not completely filled up, so some part of Nd states lies in the VB while the spin down channel is completely empty and lies in the CB. For SLR, in the up-spin channel (shown by (↑) in [Fig. 3(c)]), the VB consists mainly of Sm f, Ru d and O p orbitals. The states near the EF have contributions mainly from Ru d states hybridized with O p states. The Sm f states lie in the energy region from −3.8 eV to −5 eV and are strongly localized. The CB in the up-spin channel is mainly composed of the anti-bonding states of Ru d and Sm f in the energy region from 3.3 eV to 4.2 eV and 2.1 to 2.6 eV respectively. The VB in the down spin channel (shown by (↓) in [Fig. 3(c)]), is mainly composed of O p and Li p states. Since the valency of Sm ion in SLR is +3 ([Xe]4f5), it contains five electrons in the spin up channel so the major part of the Sm states lies in the VB while the spin down channel is completely empty and lies in the CB.
4.3. Linear optical properties
The investigated compound crystallizes in the monoclinic phase with P21/n space group. This symmetry group has two dominant components of the dielectric tensor. These dielectric functions are ε2∥(ω) and ε2⊥(ω), corresponding to the electric field direction parallel and perpendicular to the crystallographic c axis respectively (see Section S2 in ESI†). The calculated dispersive part ε1(ω) and the absorptive part ε2(ω) of the complex dielectric function ε(ω) of A2LiRuO6 as a function of the photon energy are shown in Fig. 4(a)–(f). The imaginary part of the dielectric function illustrates the optical transition mechanism. The structures observed in the optical spectra originate from the transitions between the occupied and the unoccupied electronic energy states. The solid red and black lines in Fig. 4 represent the result along the ε⊥(ω) and ε∥(ω) polarization direction respectively. It can be seen from Fig. 4(b), (d) and (f) that the threshold energy for ε2(ω) occurs at around 1.6, 1.7 and 1.8 eV for peak A of PLR, NLR and SLR respectively. This point is Γv–Γc splitting which gives the threshold for optical transitions between the highest VB and the lowest CB. This is known as the fundamental absorption edge. Beyond these points, the curve increases rapidly. This is because of the fact that the number of transitions from the VB to the CB which contributes toward ε2(ω) curve increases rapidly. The peaks appearing in the imaginary part of the dielectric function are labelled as A, B and C. It should be stated that for the interpretation of a structure (peak) in the optical spectra of the systems, it does not seem realistic to give a single transition assignment resembling the energy of the peak since numerous transitions between the occupied and the unoccupied energy bands for a particular structure can be satisfied. In the case of PLR, the peak A mainly corresponds to the transitions from Ru d states lying at the top of the VB to the Pr f states in the CB. The peak B arises due to the transitions between the middle region of O 2p in the VB and Ru d states in the CB. The peak C originates due to the transitions from the semi-core Ru d states to Pr f states as well as from the lowermost O 2p states in the VB to the Ru d states in the CB. For SLR, the transitions from the topmost Ru d states to Sm f states are responsible for the peak A whereas the peak B corresponds to the transitions from the O 2p states lying in the middle of the VB to Ru d states in the CB. The peak C arises due to the transitions from Ru d states lying at the semi-core region to Sm f states in the CB and also for the transitions between the O 2p states at the lowermost VB to Ru d states. Similarly, for NLR, the peak A may be due to the transitions from Ru d to Nd f, the peak B due to the transitions from O 2p to Ru d states and the peak C due to the transitions from semi-core Ru d states to Nd f states (may also be due to the O 2p in the lowermost VB to Ru d states). It is clear from Fig. 4 that there is a considerable anisotropy between ε1⊥(ω) and ε1∥(ω) for A2LiRuO6 compounds [see Fig. 4(a), (c) and (e)]. In the low-frequency limit (ω → 0); the magnitude of the dielectric response ε1(0) corresponds to the static optical dielectric constant (εs). The calculated static values of the dielectric function ε1⊥(0) and ε1∥(0) for these compounds are given in Table S6 in ESI.† The obtained values indicate a considerable anisotropy26 of the dielectric function for these compounds. The uniaxial anisotropy is calculated using the following expression| [δε = (ε0∥ − ε0⊥)/εtotal0] |
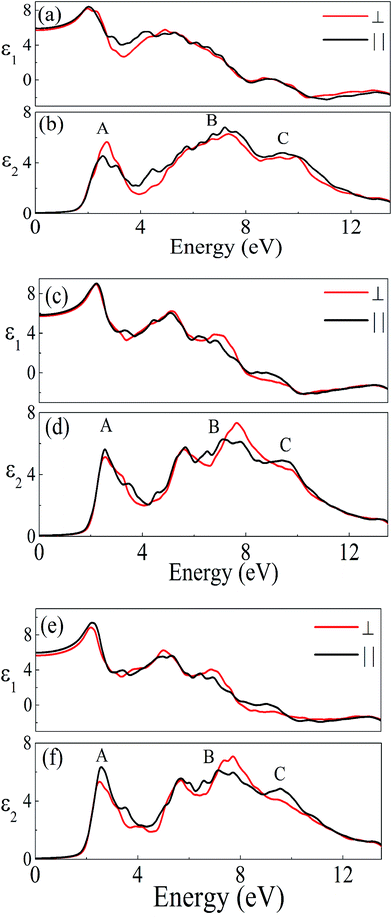 | ||
| Fig. 4 Real ε1(ω) and imaginary ε2(ω) parts of the complex dielectric constant of (a and b) PLR (c and d) NLR and (e and f) SLR. | ||
4.4. X-ray photoemission spectroscopy study
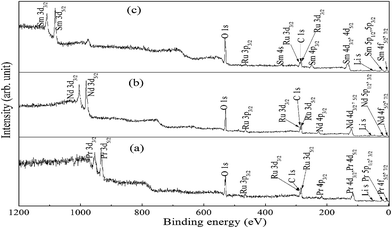
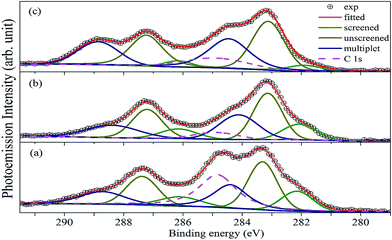
Fig. 6 shows the XP spectrum of A2LiRuO6 in the energy window of 0 to 1200 eV. The profile of the XP spectra are identified and indexed. The curve fitting of A 3d and Ru 3d core level peaks are performed to isolate the contribution of the various species to the total signal envelope. The high-resolution core-level spectrum of Ru 3d is shown in Fig. 7. The XP data for each spectrum has been normalized (zero-clipping) and plotted. The Ru 3d spectrum is complex and could be best fitted using a function with three sets of doublets which have been assigned as screened, unscreened and multiplet peaks.31 The six components are necessary to obtain a fit of good quality. These features have been observed in many other ruthenates and shown to be associated with different final state effects in photoemission process arising due to the screening of core hole by valence electrons.32–35 Thus, we have fitted the experimental spectrum with three pairs of spin orbit peaks using XPSPEAK software.36 The Shirley method37 is used to subtract the background and then the experimental spectra are numerically fitted using the sum of the Lorentzian–Gaussian model. A typical peak fit performed on the compounds is depicted in Fig. 7.The fitting parameters are given in Table 1. The spin orbit separation between the two Ru 3d peaks as shown in Table 1 corresponds well to the expected value of 4.17 eV.38 It is observed that the full-width at half-maximum (FWHM) of the Ru 3d3/2 components is always larger than the Ru 3d5/2 components. The comparison between Ru 3d spectra in these materials reveals that the degree of localized character for Ru is different for PLR, NLR, and SLR. Panaccione et al.31 suggested that with the increase of U i.e., electron correlation the intensity of the screened peak decreases. Similar results have been obtained for the Ru 3d evolution as we move from PLR to SLR. The U value is in the order of Sm > Nd > Pr (Table S1†), so accordingly the screened peak intensity is in the order of Pr > Nd > Sm (Table 1).
| Material | Peak | BE (eV) | FWHM (eV) | Doublet separation (eV) | BE (eV) | FWHM (eV) | Doublet separation (eV) | BE (eV) | FWHM (eV) | Doublet separation (eV) |
|---|---|---|---|---|---|---|---|---|---|---|
| PLR | Ru 3d5/2 | 282.1 | 1.251 | 4 | 283.31 | 1.152 | 4.066 | 284.39 | 1.357 | 4.332 |
| Ru 3d3/2 | 286.1 | 1.670 | 287.376 | 1.247 | 288.722 | 1.806 | ||||
| NLR | Ru 3d5/2 | 282.067 | 1.337 | 4.07 | 283.14 | 1.13 | 4.07 | 284.122 | 1.538 | 4.26 |
| Ru 3d3/2 | 286.141 | 1.440 | 287.21 | 1.19 | 288.379 | 2.064 | ||||
| SLR | Ru 3d5/2 | 282.2 | 1.38 | 4.1 | 283.227 | 1.229 | 4.04 | 284.533 | 1.438 | 4.33 |
| Ru 3d3/2 | 286.304 | 1.4444 | 287.264 | 1.238 | 288.864 | 1.563 |
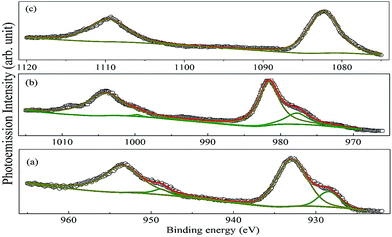
The core-level XP spectra of Pr 3d, Nd 3d and Sm 3d of the investigated compounds are shown in Fig. 8. Each of the spectra is split into two components due to the spin–orbit interaction having a lower J (=l − s) value component in the higher energy side and a higher J (=l + s) component in the lower energy side. The high intensity peaks at 932.93 and 953.47 eV in PLR, 981.6 and 1004.1 eV in NLR and 1082 eV and 1109 eV in SLR correspond to the A 3d5/2 and A 3d3/2 levels. This splitting is equal to 20.5, 22.5 and 27 eV for Pr, Nd, and Sm respectively. In addition to this, the Pr 3d and Nd 3d profiles show interesting features and are fitted to locate the positions of the main and the screened peaks. At the low-binding-energy side of the main lines of the 3d5/2 and 3d3/2, the peaks at 928.43 and 948.77 eV for PLR and 977.75 and 999.69 eV for NLR are observed which is known to account for the screened Pr 3d94f3 and Nd 3d94f4 final states.39,40 It is observed from Fig. 8 that the intensity of the screened peaks is less than that of the 3d main peaks. The origin of these peaks can be attributed to life time effects and the exchange interaction between the 3d hole and the partially filled 4f shell of Pr3+ and Nd3+ ion.41–43 It has been observed that the screened peaks are well separated from the main 3d peaks in the case of PLR and NLR, however, no significant peaks are observed in SLR. Hillerbrecht and Fuggle41 found similar results for LnPd3 (Ln = La, Ce, Pr, Nd, and Sm) compounds. According to Hillerbrecht et al. the observation of these screened peaks is due to the hybridization of 4f levels with the extended CB states41,44 in LnPd3 (Ln = La, Ce, Pr, Nd, and Sm). Further, based on the XP spectroscopy of these compounds they have concluded that the hybridization in LnPd3 decreases in the order La > Ce > Pr > Nd > Sm. So, this may be the reason that no screened peaks have been observed for SLR.
In order to verify the electronic structure calculations experimentally, we have performed the VB-XP spectroscopy measurements of these compounds. The VB-XP spectrum of PLR, NLR and SLR are shown in Fig. 9(a)–(c) respectively (solid red lines). We have generated the VB spectrum of PLR, NLR and SLR using the calculated DOS in a standard way by adding the partial DOS of Pr 4f, Nd 4f, Sm 4f, Li p, Ru 4d and O 2p (multiplied with their respective photo-emission cross-section for 1486.6 eV) weighted by the atomic cross sections for photon scattering.45 The added DOS is convoluted with a Lorentzian of 0.55 eV, 0.86 eV and 0.9 eV FWHM for PLR, NLR and SLR respectively. The calculated VB-DOS spectrum is compared with the experimental XP VB spectra, as shown in Fig. 9. The VB spectra of these materials from the Fermi level (EF) to ∼2.5 eV below it mainly consists of Ru 4d states and the contribution of O 2p states lies from below ∼2.5 eV to ∼12 eV below EF. In order to align the major peak obtained theoretically with the experimental XP spectra, the theoretical DOS has been shifted. This shift has been performed because, in the experiment, the energy zero is taken as the “middle of the gap”, while, in theory, it is taken at the top of the VB.46 Further, according to Ong et al.,46 there may be a “homogeneous charging” problem for insulators which can shift the entire spectrum rigidly without any distortion of broadening and without changing the relative positions of the various spectroscopic features. The calculated DOS for all of the studied materials show sharper peaks than the experimental spectrum, which may be due to the fact that in the DFT calculations the lifetime broadening is not taken into account.
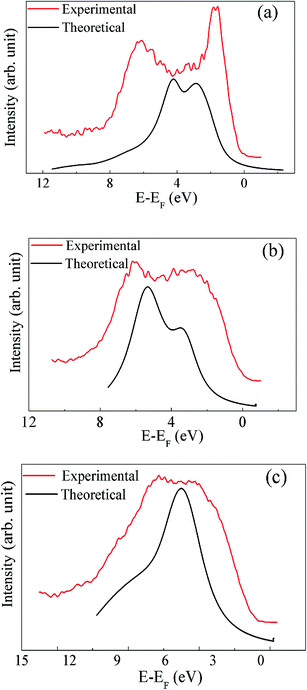 | ||
| Fig. 9 The XP spectrum in the valence band region are compared with the theoretically calculated spectrum for (a) PLR, (b) NLR and (c) SLR. | ||
4.5. Dielectric tensor
The contribution of the electronic and the ionic dielectric constant has been calculated from the Born effective charges (BECs) of the constituent atoms of the system. The calculated electronic and ionic parts of static dielectric tensor for A2LiRuO6 are given in section S3 in ESI.† The calculated dielectric tensors for all these materials are anisotropic reflecting the low-symmetric structure. The average value of the electronic and the ionic dielectric constant is found to be 6.86 and 19 for PLR, 5.97 and 23.2 for NLR, 5.73 and 17.1 for SLR respectively. The obtained results clearly indicate that the dielectric constant value is dominated by the ionic component. Thus, the total static dielectric constant value obtained by summing up the mode contributions and the electronic dielectric constant are 25.86, 29.2 and 22.8 for PLR, NLR and SLR respectively.5. Conclusion
The double perovskite A2LiRuO6 (A = Pr, Nd, Sm) compounds have been synthesized by the solid-state reaction method. The Rietveld refinement of the XRD data indicates that the room-temperature crystal structure of A2LiRuO6 is monoclinic with the space group P21/n, which contains an ordered array of alternate LiO6 and RuO6 octahedra. The calculated bond distances and bond angles show good agreement with the experimental data. The optical properties of these materials have been predicted by the first-principles calculations and all these crystals exhibit positive uniaxial anisotropy. The observed anisotropy in these materials primarily arises from the asymmetrically oriented Ru–O bonds in RuO6 octahedra in the unit cell. The interband contributions to ε2(ω) of these materials are explained using the band structures. The evolution of Ru 3d spectra in these materials suggests that the electron-correlation strength is minimum in PLR and maximum in SLR among these materials. The VB-XP spectra are obtained and compared with the calculated DOS spectra in the VB region. It has been established that the O 2p states hybridize with the Ru d states and occupy the VB maximum. The calculated dielectric constant values are dominated by the ionic component. The orientationally averaged dielectric constant has been calculated and is found to be the highest for NLR among these materials which suggests that NLR may be used as a high dielectric constant material for microwave applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Anup Pradhan Sakhya and Md. Sariful Sheikh acknowledges Department of Science and Technology for providing the financial support through Inspire Fellowship. Alo Dutta thanks the Department of Science and Technology of India for providing the financial support through DST Fast Track Project under grant no. SB/FTP/PS-175/2013. D. P. Rai acknowledges a Start-Up Grant from UGCBSR, FRPS, Lett. No. F.30-52/2014.References
- R. H. Mitchell, Perovskites: Modern and Ancient, Almaz Press, Ont., Canada, 2002 Search PubMed.
- C. Martin, A. Maignan, M. Hervieu, B. Raveau and J. Hejtmanek, Eur. Phys. J. B, 2000, 16, 469–474 CrossRef CAS.
- B. Raveau, A. Maignan, C. Martin, R. Mahendiran and M. Hervieu, J. Solid State Chem., 2000, 151, 330 CrossRef CAS.
- Y. Maeno, H. Hashimoto, K. Yoshida, S. Nishizaki, T. Fujita, J. G. Bednorz and F. Lichtenberg, Nature, 1994, 372, 532–534 CrossRef CAS.
- K. M. Glassford and J. R. Chelikowsky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1732–1741 CrossRef CAS.
- T. Yamamoto, R. Kanno, Y. Takeda, O. Yamamoto, Y. Kawamoto and M. J. Takano, Solid State Chem., 1994, 109, 372–383 CrossRef CAS.
- Y. Maeno, H. Hashimoto, K. Yoshida, S. Nishizaki, T. Fujita, J. G. Bednorz and F. Lichtenberg, Nature, 1994, 372, 532–534 CrossRef CAS.
- P. Khalifah, R. Osborn, Q. Huang, H. W. Zandbergen, R. Jin, Y. Liu, D. Mandrus and R. J. Cava, Science, 2002, 297, 2237–2240 CrossRef CAS PubMed.
- P. Khalifah, K. D. Nelson, R. Jin, Z. Q. Mao, Y. Liu, Q. Huang, X. P. A. Gao, A. P. Ramirez and R. J. Cava, Nature, 2001, 411, 669–671 CrossRef CAS PubMed.
- L. Klein, J. S. Dodge, C. H. Ahn, J. W. Reiner, L. Mieville, T. H. Geballe, M. R. Beasley and A. Kapitulnik, J. Phys.: Condens. Matter, 1996, 8, 10111–10126 CrossRef CAS.
- H. D. Kim, H. J. Noh, K. H. Kim and S. J. Oh, Phys. Rev. Lett., 2004, 93, 126404 CrossRef PubMed.
- S. J. Makowski, J. A. Rodgers, P. F. Henry, J. P. Attfield and J. W. G. Bos, Chem. Mater., 2009, 21, 264–272 CrossRef CAS.
- S. Ghosh, W. H. Wang, F. M. Mendoza, R. C. Myers, X. Li, N. Samarth, A. C. Gossard and D. D. Awschalom, Nat. Mater., 2006, 5, 261–264 CrossRef CAS PubMed.
- K. Aoki, H. T. Miyazaki, H. Hirayama, K. Inoshita, T. Baba, K. Sakoda, N. Shinya and Y. Aoyagi, Nat. Mater., 2003, 2, 117–121 CrossRef CAS PubMed.
- S. J. Goncher, N. E. Sveum, D. T. Moore, N. D. Bartlett and D. M. Neumarka, J. Chem. Phys., 2006, 125, 224304 CrossRef PubMed.
- H. Zhang, M. Zhang, S. Pan, Z. Yang, Z. Wang, Q. Bian, X. Hou, H. Yu, F. Zhang, K. Wu, F. Yang, Q. Peng, Z. Xu, K. B. Chang and K. R. Poeppelmeier, Cryst. Growth Des., 2015, 15, 523–529 CAS.
- Q. Bian, Z. Yang, L. Dong, S. Pan, H. Zhang, H. Wu, H. Yu, W. Zhao and Q. Jing, J. Phys. Chem. C, 2014, 118, 25651–25657 CAS.
- A. P. Sakhya, D. P. Rai, Md. S. Sheikh, A. Dutta, R. K. Thapa and T. P. Sinha, RSC Adv., 2016, 6, 59988–59997 RSC.
- A. H. Reshak, H. Kamarudin, I. V. Kityk and S. Auluck, J. Phys. Chem. B, 2012, 116, 13338–13343 CrossRef CAS PubMed.
- J. R. Carvaja, Physica B, 1993, 192, 55–69 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz and K. Schwarz, An augmented plane wave plus local orbitals program for calculating crystal properties, Wien2K User's Guide, Techn. Universitat Wien, Wien, 2008 Search PubMed.
- P. M. Woodward, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 44–66 CrossRef.
- A. H. Reshak, Ph.D. thesis, Indian Institute of Technology Rookee, India, 2005.
- A. H. Reshak, RSC Adv., 2016, 6, 51675–51682 RSC.
- S. Cabuk, Philos. Mag., 2016, 96, 190–207 CrossRef CAS.
- Y. Noguchi, M. Soga, M. Takahashi and M. Miyayama, Jpn. J. Appl. Phys., 2005, 44, 6998–7002 CrossRef CAS.
- A. Roy, R. Prasad, S. Auluck and A. Garg, J. Appl. Phys., 2014, 115, 133509–133516 CrossRef.
- G. Panaccione, U. Manju, F. Offi, E. Annese, I. Vobornik, P. Torelli, Z. H. Zhu, M. A. Hossain, L. Simonelli, A. Fondacaro, P. Lacovig, A. Guarino, Y. Yoshida, G. A. Sawatzky and A. Damascelli, New J. Phys., 2011, 13, 053059 CrossRef.
- K. Maiti, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235110 CrossRef.
- K. Maiti, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 212407 CrossRef.
- P. A. Cox, R. G. Egdellt, J. B. Goodenough, A. Hamnett and C. C. Naishj, J. Phys. C: Solid State Phys., 1983, 16, 6221 CrossRef CAS.
- H.-D. Kim, H.-J. Noh, K. H. Kim and S.-J. Oh, Phys. Rev. Lett., 2004, 93, 126404 CrossRef PubMed.
- R. W. M. Kwok, see http://www.phy.cuhk.edu.hk/%7Esurface/XPSPEAK%20for%20XPS%20Peak%20Fitting%20Program%20Version%204.1, 2000.
- D. A. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 5, 4709–4714 CrossRef.
- J. F. Moulder, W. F. Strickle, P. E. Sobol and K. D. Bomben, Handbook of X-ray Photoelectron Spectroscopy, Perkin-Elmer Corporation: Physical Electronics Division, Eden Prairie, MN, 1992 Search PubMed.
- J. C. Fuggle, F. U. Hillebrecht, Z. Żołnierek, R. Lässer, C. H. Freiburg, O. Gunnarsson and K. Schönhammer, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 7330–7341 CrossRef CAS.
- A. Szytuła, B. Penc and A. Jezierski, Mater. Sci.-Pol., 2008, 26(3), 759–765 Search PubMed.
- F. U. Hillerbrecht and J. C. Fuggle, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 25(6), 3550–3556 CrossRef.
- J. C. Fuggle and S. F. Alvarado, Phys. Rev. A, 1980, 22(4), 1615–1624 CrossRef CAS.
- J. C. Fuggle, M. Campagna, Z. Zolnierek, R. Lasser and A. Platau, Phys. Rev. Lett., 1980, 45(19), 1597–1600 CrossRef CAS.
- B. V. Kumar, R. Velchuri, G. Prasad, B. Sreedhar, K. Ravikumar and M. Vithal, Ceram. Int., 2010, 36, 1347–1355 CrossRef CAS.
- J. J. Yeh and I. Lindau, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS.
- K. P. Ong, P. Blaha and P. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 073102–073104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra07712b |
| This journal is © The Royal Society of Chemistry 2017 |