Open Access Article
Open Access ArticleA controllable mechanistic transition of charge transfer in helical peptides: from hopping to superexchange
Jingxian Yu*,
John R. Horsley and
Andrew D. Abell *
*
ARC Centre of Excellence for Nanoscale BioPhotonics (CNBP), Department of Chemistry, The University of Adelaide, Adelaide, SA 5005, Australia. E-mail: jingxian.yu@adelaide.edu.au; andrew.abell@adelaide.edu.au
First published on 1st September 2017
Abstract
Understanding the electronic properties inherent to peptides is crucial for controlling charge transfer, and precursory to the design and fabrication of bio-inspired next generation electronic components. However, to achieve this objective one must first be able to predict and control the associated charge transfer mechanisms. Here we demonstrate for the first time a controllable mechanistic transition in peptides resulting directly from the introduction of a side-bridge. High level computational studies on two similar 310-helical hexapeptides, one further constrained into this geometry by linking the i to i + 3 residues with a lactam side-bridge, highlight the effects of the bridge on electron transfer parameters, i.e. thermodynamic driving forces, reorganization energies, and electronic coupling factors. The additional backbone rigidity imparted by the bridge significantly alters the molecular dynamics of the peptide to such an extent as to induce a mechanistic transition from hopping in the linear peptide, to superexchange in the constrained peptide. This exciting finding not only advances our fundamental knowledge of the mechanisms governing charge transfer in peptides, but also reveals novel approaches to design and develop new functional devices that are tailored for applications in molecular electronics.
1. Introduction
A fundamental understanding of electron transfer in complex biomolecules such as proteins and DNA is central to the design and development of bio-inspired molecular electronic components.1 However, the vast complexities of such systems is somewhat limiting to progress, with model synthetic peptides presenting as ideal candidates in this context. Synthetic peptides can be designed to conform to specific secondary structures, such as helices and β-strands, to allow the dynamics and mechanisms of electron transfer to be studied in a controlled and defined environment.2 In addition, they can be specifically functionalized along their backbone to enable precision-branching, analogous to three-dimensional molecular circuitry.3 Such molecular electronics provide an opportunity to begin to redefine integrated circuit technologies and revolutionize modern computing.4 However, one must first understand and subsequently be able to predict and control the associated charge transfer mechanisms.5 Two main modes, superexchange (tunnelling) and thermally activated hopping, are widely accepted.6 The superexchange mechanism of electron transfer involves direct molecule-mediated tunnelling, where the intervening peptide chain between electron donor and acceptor takes on a virtual role. In this one-step process the electron transfer rate constant decreases exponentially with increasing distance between the donor and acceptor.7 The alternative hopping mechanism operates in a helical peptide by using sites on the peptide chain that are coupled to each other electronically for electron transfer, resulting in shorter and therefore faster sequential steps.8 In this multi-step process electrons reside on the peptide chain for a finite time, with molecular conductance obeying ohmic behavior with increasing distance between donor and acceptor, enabling efficient long-range electron transfer.9 This charge transfer process can be explained by the ordered coupling of amide groups within the backbone of α/310-helical peptides.10–12 Specifically, the 2p-π orbital overlap between the oxygen atoms of the adjacent carbonyl groups is thought to provide potential hopping sites for electrons (or holes) along the peptide chain.13,14A mechanistic transition between one-step superexchange and multi-step hopping has been previously observed in DNA,15,16 and peptides of increasing lengths,6,17,18 where superexchange operates in short sequences and hopping over longer sequences. Temperature dependence measurements have revealed switching between the two mechanisms in peptides/proteins,1,19 where superexchange operates at low temperatures and hopping at higher temperatures. Notably, a controllable transition between superexchange and hopping in peptides with similar lengths, at room temperature, would no doubt provide significant benefits for advancing the design and development of functional single-molecule electronic components.20 Here, we aim to demonstrate such a mechanistic transition using two 310-helical peptides of similar length at room temperature, that differ essentially in the presence (or absence) of a lactam side-bridge constraint.
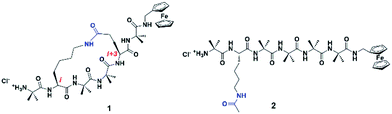
We and others have previously demonstrated that the addition of a tether linking the side-chains of peptides via Huisgen cycloaddition,21–23 ring closing metathesis,24–27 or lactamization,28–30 fixes the structural conformation into a well-defined helical geometry. The resulting decrease in backbone flexibility leads to a reduction of torsional motion necessary for facile electron transfer through the peptide via a hopping mechanism, which in turn impacts the associated electron transfer dynamics and hence their electronic properties. We have recently reported the synthesis of two closely related 310-helical hexapeptides (see Fig. 1), one further constrained into this geometry by way of a lactam side-bridge.28 An electrochemical study of the two peptides found the electron transfer rate constant in the constrained peptide 1 to be approximately one order of magnitude lower than that of the linear counterpart 2, with a corresponding and significant increase in the formal potential. Complementary quantum transport (ballistic scattering) simulations, using density functional theory (DFT) coupled with the non-equilibrium Green's function (NEGF)31 were performed. Anti-resonance peaks were found in both cases, with discontinuous eigenchannel wave functions32 indicative of the occurrence of destructive quantum interference. The calculated conductance for both peptides was found to be remarkably similar, contrasting the approximate ten-fold difference in the electron transfer rate constants observed in the electrochemical study.28 Similar results were also recently reported in helical peptides based on the same theoretical approach.13 This suggests that different charge transfer mechanisms may be operating in these helical peptides, which cannot be determined using ballistic scattering transport simulations.
It is thus critical to determine whether the additional rigidity generated by the lactam side-bridge is sufficient to inhibit the electron transfer dynamics of the peptide backbone, thereby altering the associated electron transfer mechanism. This ability to define the mechanism then has wider consequences for the design and development of bio-inspired molecular devices. We have previously shown, through the application of a side-chain tether, that the reorganization energy for each sequential electron transfer step increases by as much as 0.3 eV, relative to the untethered counterpart,21 using Marcus theory of electron transfer.33 However, it is not known if this increased energy barrier is substantial enough to induce a transition in the charge transfer mechanism. In light of this, Marcus theory will now be used in conjunction with the latest constrained density functional theory (cDFT)34 to elucidate this fundamental issue. The charge constraints on arbitrary molecular fragments in cDFT provide a natural way to define diabatic states for electron transfer, and calculate the properties of individual states using the basic machinery of the Kohn–Sham SCF procedure.35 The cDFT states, together with the couplings between these states, can be exploited to construct complex charge transfer models. In this computational study, we will show that charge transfer mechanisms can be modulated through the application of a lactam side-bridge constraint, specifically where the presence/absence of the constraint represents gate-assisted on/off states.
2. Computational details
The model peptides used for this computational study (3 and 4, see Fig. 2) are analogues of 1 and 2, albeit with redox-active ferrocene units at both termini to act as electron donor and acceptor21,36 to maximize the similarity with these synthetic peptides.28 All initial geometries of peptides 3 and 4 were prepared using the GaussView 5.0 package by modifying the related side-chains of Z-(Aib)10-OH homopeptide crystal structure37 (accession code CCDC 1430000). The lowest energy conformers for all uncharged peptide models were determined in gas phase using the Gaussian 09 package,38 with tight convergence criteria using a hybrid B3LYP method with 6-31G** basis set for all C, H, N, O atoms, and Lanl2dz basis set for Fe atom in order to define the backbone conformations. Conformational analysis, including dihedral angles, total molecular lengths and intramolecular hydrogen bond lengths, was conducted using the GaussView 5.0 package.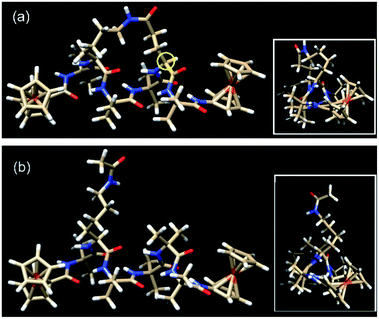 | ||
| Fig. 3 The lowest energy conformers for (a) the constrained helical peptide 3 with the link for the lactam side-bridge located on the i + 3 residue (circled in yellow), and (b) the direct linear analogue 4. Insets: top view looking down the helices, showing the triangular void indicative of a 310-helix.25 | ||
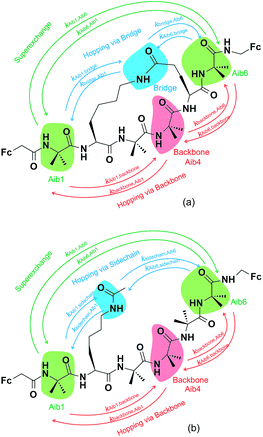
Three key charge transfer pathways are depicted in Fig. 2. One particular pathway involves one-step elastic tunnelling between the first and last residues (Aib1 and Aib6, see Fig. 2, green arrows). The others are two-step sequential hopping pathways originating at Aib1, either passing through the peptide backbone (Aib4, see Fig. 2, red arrows) or the amide-containing side-bridge/side-chain (see Fig. 2, blue arrows), terminating at Aib6. In order to obtain quantitative information about electron transfer kinetics, diabatic states were constructed by individually localizing an overall charge of +1 on the amino acids Aib1, Aib4, and Aib6 in both peptide models, and on the amide bonds located in the side-bridge of 3 and the side-chain of 4 (see Fig. 2).10,39,40 The geometry of each diabatic state was optimized with the excess charge constrained to the indicated part of the molecule using cDFT as implemented in the NWChem 6.1 package41 with the hybrid B3LYP density functional and 6-31G** basis set for all C, H, N, O atoms and Lanl2dz basis set for Fe atom, starting from the lowest energy conformer of their corresponding uncharged molecular model. Both electronic coupling matrix elements (Hab) and diabatic potential energy surfaces were computed for these diabatic states36,42 using the NWChem 6.1 package. Diabatic potential profiles were determined by assuming that, during a charge transfer step, the nuclear configuration changes smoothly between the optimized geometries of the diabatic states in which the excess charge is localized before and after electron transfer.10,43 Thus, the energy of each of the two diabatic states along the electron transfer reaction coordinate was taken as the energy for geometries linearly interpolated between the optimized geometries of the two diabatic states, with the excess charge localized to the part of the molecule corresponding to the diabatic state in question.
The energy gap (ΔE) and inner sphere reorganization energy (λ)inner,ij between two neighboring states along an electron transfer pathway extracted from the diabatic potential profiles,44 allows the elementary electron transfer rate constant (kET)ij from one diabatic state (i) to the neighboring diabatic state (j) to be estimated based on the semi-classical Marcus theory expression:33,44
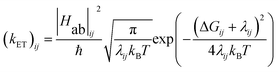 | (1) |
The outer-sphere reorganization energy (λ)outer,ij from the diabatic state (i)to the neighboring diabatic state (j) is given by45
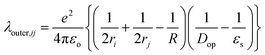 | (2) |
3. Results and discussion
3.1. Conformational analysis
Peptides 1 and 2 are rich in geminally di-substituted α-aminoisobutyric acid (Aib) residues which are known to stabilize a 310-helical conformation.25 Peptide 1 is further constrained into this geometry by linking the side-chains of the i and i + 3 residues with an amide bond to form a lactam bridge, while peptide 2 is a direct linear counterpart. The geometries of both peptides were confirmed as 310-helical using 1H NMR, 2D NMR, and IR spectroscopy.28 The lowest energy conformers for peptides 3 and 4, determined by molecular modelling using a hybrid B3LYP method, reveal that the distances from the first to last carbonyl carbons (backbone lengths) are the same for both peptides (11.99 Å, see Table 1). In addition, the distances between the two Fe centres in the two peptides are also remarkably similar, differing by only 0.05 Å. The mean intramolecular hydrogen bond length of the constrained 3 is 2.13 Å, only 0.02 Å longer than that of its linear counterpart 4 (see Table 1). The molecular models also demonstrate that each of these peptides adopts a 310-helical conformation. Specifically, the mean dihedral angles in the peptide backbone for residues 1–6 of peptide 3 were determined to be (−60.17° for Φ) and (−25.01° for Ψ), deviating from an ideal 310-helix by 3.2° (Φ) and 5.0° (ψ), whilst the mean dihedral angles in the peptide backbone for residues 1–6 of peptide 4 deviated by only 0.4° and 2.6° respectively from an ideal 310-helix (see Table 1).| 3 | 4 | |||
|---|---|---|---|---|
| Φ | ψ | Φ | ψ | |
| a The dihedral angles in bold (residue 5 in peptide 3) differ greatly from an ideal 310-helix (−57° Φ, −30° ψ),47 revealing the constrictive effect from the tether at this site. | ||||
| Residue 1 | −60.24° | −31.93° | −60.40° | −31.61° |
| Residue 2 | −62.48° | −18.41° | −61.03° | −21.21° |
| Residue 3 | −50.82° | −33.28° | −53.46° | −28.11° |
| Residue 4 | −55.45° | −30.52° | −54.13° | −28.40° |
| Residue 5 | −72.36° | −7.33° | −55.19° | −28.01° |
| Residue 6 | −59.69° | −28.61° | −60.28° | −26.75° |
| Average | −60.17° | −25.01° | −57.42° | −27.35° |
| Differing from ideal 310 helix | 3.17° | 4.99° | 0.42° | 2.65° |
| Distance (Å) | ||
|---|---|---|
| From first to last carbonyl carbon | 11.99 | 11.99 |
| Fe–Fe | 16.32 | 16.37 |
| Mean intramolecular H-bond length | 2.13 | 2.11 |
The actual dihedral angles proximal to the i + 3 residue in the constrained peptide 3 differ from an ideal 310-helix by 15.4° (Φ) and 22.7° (ψ), clearly showing the constrictive effect from the tether at this site (see Table 1). A comparison with other related 18-membered macrocyclic 310-helical hexapeptides constrained i to i + 3 by a hydrocarbon linker (alkane, 4.6° Φ, 10.0° ψ; and alkene, 10.1° Φ, 16.7° ψ),24 shows that the lactam bridge imparts the largest deviation from an ideal structure at this location. The resulting constriction generated by the lactam side-bridge at the i + 3 residue contributes additional rigidity to the peptide backbone, which in turn increases the reorganization energy,21 and is reflected by the highest observed formal potential (0.924 V for 1) and lowest electron transfer rate constant (9.34 s−1 for 1)28 when compared with other forms of cyclization discussed here. As such these studies demonstrate that the two molecular structures have essentially the same conformations, such that they differ only in the presence (or absence) of the constraint and the associated effect that this has on backbone rigidity.
3.2. Electron transfer mechanisms
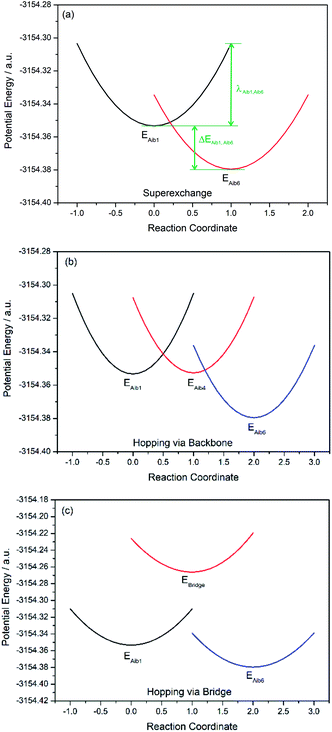
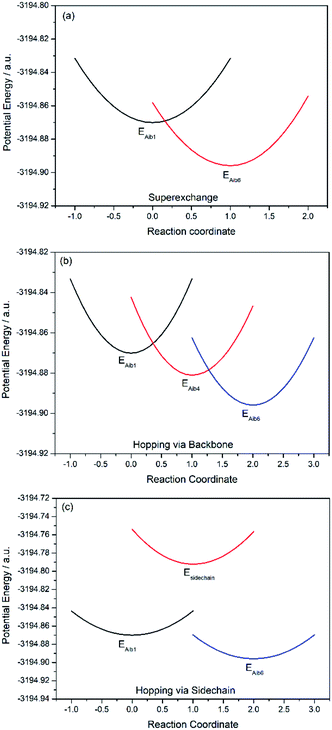
Charge transfer in linear 310-helical peptides such as 2 is understood to proceed via a hopping mechanism,18,48 however very little is known about electron transfer in constrained peptides.49 Here, Marcus theory33,50,51 was used in combination with the latest constrained density functional theory (cDFT)34 to model the diabatic states in 310-helical models 3 and 4 (see Fig. 2a and b) in order to provide an insight into the electron transfer pathway and mechanism(s).52 As mentioned, three key electron transfer pathways are considered in the theoretical simulations, with Fig. 4 and 5 showing the diabatic potential profiles for the superexchange and two sequential hopping pathways in peptides 3 and 4 respectively. The inner sphere reorganization energy (λ)inner and the energy gap (ΔE) between two neighboring diabatic states were estimated from the diabatic potential profiles, as indicated schematically in Fig. 4a. The calculated (λ)inner and (ΔE) values are given in Tables 2 and 3 for the constrained 3 and the linear counterpart 4 respectively, together with the strength of the electronic coupling (Hab)ij calculated from the electronic structures of neighboring diabatic states.36| Elementary step | ΔEij (eV) | λinner,ij (eV) | (Hab)ij (eV) | (kET)ij (s−1) |
|---|---|---|---|---|
| Superexchange pathway | ||||
| Aib1 → Aib6 | −0.71 | 1.35 | 0.02 | 7.53 × 1010 |
| Aib6 → Aib1 | 0.71 | 1.22 | 0.02 | 2.03 × 10−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Sequential hopping pathway via backbone | ||||
| Aib1 → Aib4 | 0.02 | 1.30 | 0.29 | 4.33 × 108 |
| Aib4 → Aib1 | −0.02 | 1.22 | 0.29 | 2.12 × 109 |
| Aib4 → Aib6 | −0.73 | 1.23 | 0.04 | 9.29 × 1011 |
| Aib6 → Aib4 | 0.73 | 1.17 | 0.04 | 6.51 × 10−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Sequential hopping pathway via side-bridge | ||||
| Aib1 → bridge | 2.35 | 1.17 | 0.04 | 3.07 × 10−30 |
| Bridge → Aib1 | −2.35 | 1.08 | 0.04 | 2.47 × 109 |
| Bridge → Aib6 | −3.05 | 1.26 | 0.01 | 3.43 × 104 |
| Aib6 → bridge | 3.05 | 1.10 | 0.01 | 1.73 × 10−50 |
| Elementary step | ΔEij (eV) | λinner,ij (eV) | (Hab)ij (eV) | (kET)ij (s−1) |
|---|---|---|---|---|
| Superexchange pathway | ||||
| Aib1 → Aib6 | −0.70 | 1.04 | 0.03 | 1.58 × 1012 |
| Aib6 → Aib1 | 0.70 | 1.02 | 0.03 | 2.63 × 100 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Sequential hopping pathway via backbone | ||||
| Aib1 → Aib4 | −0.29 | 0.10 | 2.73 | 2.36 × 1017 |
| Aib4 → Aib1 | 0.29 | 1.04 | 2.73 | 1.42 × 109 |
| Aib4 → Aib6 | −0.40 | 0.93 | 19.60 | 7.36 × 1016 |
| Aib6 → Aib4 | 0.40 | 0.90 | 19.60 | 1.65 × 1010 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Sequential hopping pathway via side-chain | ||||
| Aib1 → sidechain | 2.11 | 0.72 | 0.04 | 7.73 × 10−30 |
| Sidechain → Aib1 | −2.11 | 1.03 | 0.04 | 3.61 × 1010 |
| Sidechain → Aib6 | −2.81 | 0.96 | 2.66 | 5.04 × 106 |
| Aib6 → sidechain | 2.81 | 0.71 | 2.66 | 1.15 × 10−48 |
In all potential profiles the energy of diabatic state Aib1 is greater than that of diabatic state Aib6, as shown in Fig. 4 and 5. The negative energy difference (ΔEAib1,Aib6) provides a necessary driving force to move the cationic (+1) charge from Aib1 (N-terminal) to Aib6 (C-terminal), due to the large dipole moment in helical peptides with a negative C-terminal and a positive N-terminal.53–55 This is in accordance with experimental observations where the dipole moment can facilitate charge transfer if the charge propagation (in the form of hole transfer) follows the same direction as the dipole moment in helical peptides.12,56 Since each of the forward superexchange charge transfer steps has a negative energy difference (ΔEAib1,Aib6), it is therefore energetically more favorable for the transference of cationic (+1) charge from the states Aib1 to Aib6, than the backward superexchange charge transfer step (Aib6 → Aib1), which is energetically unfavorable according to the Arrhenius' equation. Notably, there is a positive energy gap (ΔEAib1,Aib4) in 3 (approx. 0.02 eV) for the sequential hopping pathway via the backbone, whilst this energy gap (ΔEAib1,Aib4) is negative in 4 (−0.29 eV), thus favoring the forward charge transfer step (Aib1 → Aib4) in 4. We believe that the clamp-like lactam bridge of 3 contributes to the additional potential energy which is required for the cationic (+1) charge to move from the unbridged (Aib1) to bridged (Aib4) state. Consequently, this bridge favours a more negative (ΔEAib4,Aib6) in 3 than in 4 (−0.73 eV and −0.40 eV respectively), when the cationic charge moves from the bridged (Aib4) to the unbridged (Aib6) state.
The mean reorganization energy (λ) between the states Aib4 and Aib1 (or Aib6) in peptide 3 is estimated to be 1.24 eV (see Table 2), which is approximately 25% higher than that of 4 (0.97 eV, see Table 3). A significant contribution to the higher λ values between Aib4 and the neighboring states is believed to be due to the additional steric strain induced by the lactam side-bridge. It has also been reported that a fast interconversion in a homo-Aib hexapeptide takes place between 310-helix and several other conformations in the nanosecond time scale.57 The presence of the lactam bridge in 3 reduces the dynamic property of the peptide backbone by stabilizing the 310-helical structure. Furthermore, the (Hab) values for each of the elementary electron transfer steps in 3 are considerably lower than that of 4. Specifically, the (Hab) value between the states Aib4 and Aib6 in the constrained 3 was found to be 500 times lower than that in the linear 4. This relates to the tethered site (i + 3), and is further supported by the large deviation from an ideal 310-helical structure at this location, as indicated by the dihedral angles for residue 5 (see Table 1). The coupling between the states Aib4 and Aib6 in 3 would have to contend with the lactam side-bridge rigidifying the backbone in these states, whereas a more flexible backbone of 4 may reposition these states, allowing for a much stronger coupling between them. Clearly, the presence of the lactam bridge influences the molecular dynamics of the peptide, resulting in significant changes to the thermodynamic driving force, inner sphere reorganization energy, and electronic coupling between the diabatic states.
A considerable energy gap (ΔE) in the sequential hopping pathways for bridge–Aib1 (2.35 eV), bridge–Aib6 (3.05 eV) in 3, and sidechain–Aib1 (2.11 eV), sidechain–Aib6 (2.81 eV) in 4 was noted (see Fig. 4c, 5c, Tables 2 and 3). The intramolecular electrostatic interaction energy Eelec between atom pairs was estimated using,
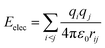 | (3) |
The elementary electron transfer rate constants (see Tables 2 and 3) were calculated using the semi-classical Marcus theory expression. For the superexchange pathway (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) in peptide 3, the backward charge transfer rate constant is negligible (kAib6,Aib1 = 2.03 × 10−1 s−1), hence the overall superexchange electron transfer rate constant ksuper is represented by the forward reaction (kAib1,Aib6 = 7.53 × 1010 s−1), namely ksuper = 7.53 × 1010 s−1. For the sequential electron transfer pathway via the backbone (Aib1
Aib6) in peptide 3, the backward charge transfer rate constant is negligible (kAib6,Aib1 = 2.03 × 10−1 s−1), hence the overall superexchange electron transfer rate constant ksuper is represented by the forward reaction (kAib1,Aib6 = 7.53 × 1010 s−1), namely ksuper = 7.53 × 1010 s−1. For the sequential electron transfer pathway via the backbone (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib4
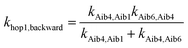
Aib4 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) in 3, the elementary rate constant (kAib6,Aib4) is also negligible. An overall forward hopping electron transfer rate constant via the backbone was calculated as khop1,forward = 4.32 × 108 s−1, using the kinetic model that assumes steady-state occupation probability for different diabatic states,10
Aib6) in 3, the elementary rate constant (kAib6,Aib4) is also negligible. An overall forward hopping electron transfer rate constant via the backbone was calculated as khop1,forward = 4.32 × 108 s−1, using the kinetic model that assumes steady-state occupation probability for different diabatic states,10
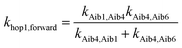 | (4) |
 | (5) |
The overall hopping electron transfer rate constant via the backbone is equal to khop1,forward, namely khop1 = 4.32 × 108 s−1. For the sequential electron transfer pathways via the side bridge (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) bridge
bridge ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) in 3, the elementary rate constants kAib1,bridge and kAib6,bridge are extremely low. These exceptionally low overall electron transfer rate constants (khop2,forward = 4.26 × 10−35 s−1 and khop2,backward = 1.73 × 10−50 s−1) further demonstrate that the sequential electron transfer pathway via the side-bridge in 3 is clearly not possible.
Aib6) in 3, the elementary rate constants kAib1,bridge and kAib6,bridge are extremely low. These exceptionally low overall electron transfer rate constants (khop2,forward = 4.26 × 10−35 s−1 and khop2,backward = 1.73 × 10−50 s−1) further demonstrate that the sequential electron transfer pathway via the side-bridge in 3 is clearly not possible.
For the superexchange pathway (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) in peptide 4, the overall superexchange electron transfer rate constant ksuper is dominated by the forward reaction (kAib1,Aib6 = 1.58 × 1012 s−1), namely ksuper = 1.58 × 1012 s−1, since the electron transfer rate in the backward reaction is negligible (kAib6,Aib1 = 2.63 × 100 s−1). For the sequential electron transfer pathways via the backbone (Aib1
Aib6) in peptide 4, the overall superexchange electron transfer rate constant ksuper is dominated by the forward reaction (kAib1,Aib6 = 1.58 × 1012 s−1), namely ksuper = 1.58 × 1012 s−1, since the electron transfer rate in the backward reaction is negligible (kAib6,Aib1 = 2.63 × 100 s−1). For the sequential electron transfer pathways via the backbone (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib4
Aib4 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) in 4, the overall hopping electron transfer rate constant via the backbone was represented by an overall forward hopping electron transfer rate constant, estimated to be khop1 = 2.36 × 1017 s−1, while the overall hopping electron transfer rate constant (khop2) through the side-chain (Aib1
Aib6) in 4, the overall hopping electron transfer rate constant via the backbone was represented by an overall forward hopping electron transfer rate constant, estimated to be khop1 = 2.36 × 1017 s−1, while the overall hopping electron transfer rate constant (khop2) through the side-chain (Aib1 ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) side-chain
side-chain ![[left over right harpoons]](https://www.rsc.org/images/entities/char_21cb.gif) Aib6) is exceptionally low (1.08 × 10−33 s−1).
Aib6) is exceptionally low (1.08 × 10−33 s−1).
A comparison of the overall electron transfer rate constants (ksuper, khop1 and khop2) reveals that the superexchange pathway is the most favorable in the constrained peptide 3, with an overall electron transfer rate constant of 7.53 × 1010 s−1, compared with hopping along the peptide backbone (khop1 = 4.32 × 108 s−1). Conversely, the hopping pathway via the backbone is favored in the linear peptide 4 as expected, with an overall electron transfer rate constant of 2.36 × 1017 s−1, compared with the superexchange pathway (ksuper = 1.58 × 1012 s−1). Charge transfer through two similar 310-helical hexapeptides has not only been shown to proceed at significantly different rates, but most notably by utilizing two different mechanisms. We have also definitively ruled out the possibility of charge transfer through the lactam side-bridge of 3, and the side-chain of 4, with exceptionally low computed rate constants, khop2 = 4.26 × 10−35 s−1 and 1.08 × 10−33 s−1, respectively. For the first time, a clear transition from hopping to superexchange has been demonstrated through the application of a side-bridge. This result is perhaps not surprising as the pronounced effect on the dihedral angles arising from the lactam constraint located on the i + 3 residue (see Fig. 3) is expected to further increase backbone rigidity, so reducing the torsional motion necessary for the hopping mechanism to operate in helical peptides of this type. These data reinforce experimental observations where the linear peptide 2 (analogue of 4) has been shown to exhibit the lowest formal potential and the highest electron transfer rate constant relative to the constrained 1 (ref. 28) (analogue of 3). This suggests that in the constrained peptide 1, the energetically unfavorable oxidation/reduction of the ferrocene moiety is due to the slow charge transfer proceeding via a superexchange mechanistic pathway. In contrast, oxidation/reduction of the ferrocene moiety in the linear peptide 2 is governed by multiple shorter and therefore faster sequential steps via a hopping mechanism.
Thus, we infer that the lactam side-bridge restricts the molecular dynamics of the peptide, impeding the specific internal rotations of the amide bonds within the peptide backbone to such an extent as to result in a mechanistic transition from hopping to superexchange between the linear and constrained helical species. These findings underscore the ubiquitous nature and importance of structural fluctuations to charge transport in peptides. We have also shown that both mechanisms potentially operate in the same peptide, for example ksuper = 7.53 × 1010 s−1 and khop1 = 4.32 × 108 s−1 in the constrained 3, with one favored over the other. These discoveries not only add considerable weight to the belief that electron transfer utilizes both the superexchange and hopping mechanisms,59,60 depending on such factors as the nature of the peptide architecture; they also challenge the widely accepted hypothesis that the mechanisms responsible for electron transfer in peptides are solely distance-dependent. Collectively, these developments provide fundamental advances in our understanding of the associated dynamics and mechanisms, further supporting the notion that conformation and function are inextricably linked when defining charge transfer in peptides. Understanding the dynamic effects associated with backbone conformation is also of wider significance, for instance in the design and exploitation of side-bridge stabilized peptides as biological probes and enzyme inhibitors.61–63
4. Conclusions
High level computational studies conducted on two similar 310-helical hexapeptides, one further constrained into this geometry by linking the i to i + 3 residues to form a lactam bridge and the other a direct linear analogue, show electron transfer to proceed at significantly different rates and, most notably, by utilizing two different mechanisms (hopping and superexchange). These findings unveil a new pragmatic approach for controlling the mechanisms responsible for charge transfer in helical peptides through the introduction of a side-bridge. Such an ability to judiciously change the behavior of the system is strategic to the design of stable building blocks for future three-dimensional peptide-based circuitry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Australian Research Council (ARC) Centre of Excellence for Nanoscale BioPhotonics (CNBP), the University of Adelaide, for the financial support of this work. The computational aspects of this work were supported by an award under the National Computational Merit Allocation Scheme (NCMAS) for JY on the National Computing Infrastructure (NCI) National Facility at the Australian National University.Notes and references
- N. Amdursky, D. Marchak, L. Sepunaru, I. Pecht, M. Sheves and D. Cahen, Adv. Mater., 2014, 26, 7142–7161 CrossRef CAS PubMed.
- L. Sepunaru, S. Refaely-Abramson, R. Lovrincic, Y. Gavrilov, P. Agrawal, Y. Levy, L. Kronik, I. Pecht, M. Sheves and D. Cahen, J. Am. Chem. Soc., 2015, 137, 9617–9626 CrossRef CAS PubMed.
- G. Maruccio, Nat. Nanotechnol., 2012, 7, 147–148 CrossRef CAS PubMed.
- A. G. Wardrip, A. Mazaheripour, N. Husken, J. M. Jocson, A. Bartlett, R. C. Lopez, N. Frey, C. B. Markegard, G. Kladnik, A. Cossaro, L. Floreano, A. Verdini, A. M. Burke, M. N. Dickson, I. Kymissis, D. Cvetko, A. Morgante, S. Sharifzadeh, H. D. Nguyen and A. A. Gorodetsky, Angew. Chem., Int. Ed., 2016, 55, 14265–14269 CrossRef PubMed.
- J. Juhaniewicz, J. Pawlowski and S. Sek, Isr. J. Chem., 2015, 55, 645–660 CrossRef CAS.
- H. S. Mandal and H.-B. Kraatz, J. Phys. Chem. Lett., 2012, 3, 709–713 CrossRef CAS PubMed.
- O. S. Wenger, Acc. Chem. Res., 2011, 44, 25 CrossRef CAS PubMed.
- J. Watanabe, T. Morita and S. Kimura, J. Phys. Chem. B, 2005, 109, 14416 CrossRef CAS PubMed.
- M. Wang, J. Gao, P. Muller and B. Giese, Angew. Chem., Int. Ed., 2009, 48, 4232–4234 CrossRef CAS PubMed.
- J. Yu, D. M. Huang, J. G. Shapter and A. D. Abell, J. Phys. Chem. C, 2012, 116, 26608–26617 CAS.
- E. W. Schlag, S. Y. Sheu, D. Y. Yang, H. L. Selzle and S. H. Lin, Angew. Chem., Int. Ed., 2007, 46, 3196–3210 CrossRef CAS PubMed.
- M. Lauz, S. Eckhardt, K. M. Fromm and B. Giese, Phys. Chem. Chem. Phys., 2012, 14, 13785–13788 RSC.
- S. Y. Sheu and D. Y. Yang, Sci. Rep., 2017, 7, 39792 CrossRef CAS PubMed.
- E. Gatto and M. Venanzi, in Peptide Materials: From Nanostructures to Applications, ed. C. Alemán, A. Bianco and M. Venanzi, John Wiley & Sons, Ltd., 2013 Search PubMed.
- B. Giese, J. Amaudrut, A. K. Kohler, M. Spormann and S. Wessely, Nature, 2001, 412, 318 CrossRef CAS PubMed.
- Y. Q. Li, L. M. Xiang, J. L. Palma, Y. Asai and N. J. Tao, Nat. Commun., 2016, 7, 11294 CrossRef CAS PubMed.
- R. A. Malak, Z. N. Gao, J. F. Wishart and S. S. Isied, J. Am. Chem. Soc., 2004, 126, 13888 CrossRef CAS PubMed.
- J. Yu, O. Zvarec, D. M. Huang, M. A. Bissett, D. B. Scanlon, J. G. Shapter and A. D. Abell, Chem. Commun., 2012, 48, 1132–1134 RSC.
- L. Sepunaru, N. Friedman, I. Pecht, M. Sheves and D. Cahen, J. Am. Chem. Soc., 2012, 134, 4169–4176 CrossRef CAS PubMed.
- X. S. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z. Y. Xiao, W. J. Hong, C. J. Lambert and S. X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176 CrossRef CAS PubMed.
- J. Yu, J. R. Horsley, K. E. Moore, J. G. Shapter and A. D. Abell, Chem. Commun., 2014, 50, 1652 RSC.
- A. D. Pehere, M. Pietsch, M. Guetschow, P. M. Neilsen, D. S. Pedersen, S. Nguyen, O. Zvarec, M. J. Sykes, D. F. Callen and A. D. Abell, Chem.–Eur. J., 2013, 19, 7975–7981 CrossRef CAS PubMed.
- D. S. Pedersen and A. Abell, Eur. J. Org. Chem., 2011, 2011, 2399–2411 CrossRef.
- J. R. Horsley, J. Yu, K. E. Moore, J. G. Shapter and A. D. Abell, J. Am. Chem. Soc., 2014, 136, 12479–12488 CrossRef CAS PubMed.
- A. K. Boal, I. Guryanov, A. Moretto, M. Crisma, E. L. Lanni, C. Toniolo, R. H. Grubbs and D. J. O'Leary, J. Am. Chem. Soc., 2007, 129, 6986–6987 CrossRef CAS PubMed.
- K. C. H. Chua, M. Pietsch, X. Z. Zhang, S. Hautmann, H. Y. Chan, J. B. Bruning, M. Gutschow and A. D. Abell, Angew. Chem., Int. Ed., 2014, 53, 7828–7831 CrossRef CAS PubMed.
- H. C. Lin, Y. X. Jiang, Q. Z. Zhang, K. Hu and Z. G. Li, Chem. Commun., 2016, 52, 10389–10391 RSC.
- J. Yu, J. R. Horsley and A. D. Abell, Mol. Syst. Des. Eng., 2017, 2, 67–77 CAS.
- A. D. de Araujo, H. N. Hoang, W. M. Kok, F. Diness, P. Gupta, T. A. Hill, R. W. Driver, D. A. Price, S. Liras and D. P. Fairlie, Angew. Chem., Int. Ed., 2014, 53, 6965–6969 CrossRef CAS PubMed.
- C. J. White and A. K. Yudin, Nat. Chem., 2011, 3, 509–524 CrossRef CAS PubMed.
- M. Brandbyge, J. L. Mozos, P. Ordejon, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401 CrossRef.
- M. Paulsson and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 15117 CrossRef.
- R. A. Marcus, Annu. Rev. Phys. Chem., 1964, 15, 155–196 CrossRef CAS.
- T. Van Voorhis, T. Kowalczyk, B. Kaduk, L. P. Wang, C. L. Cheng and Q. Wu, Annu. Rev. Phys. Chem., 2010, 61, 149–170 CrossRef CAS PubMed.
- B. Kaduk, T. Kowalczyk and T. Van Voorhis, Chem. Rev., 2012, 112, 321–370 CrossRef CAS PubMed.
- F. Z. Ding, H. B. Wang, Q. Wu, T. Van Voorhis, S. W. Chen and J. P. Konopelski, J. Phys. Chem. A, 2010, 114, 6039–6046 CrossRef CAS PubMed.
- R. Gessmann, H. Bruckner and K. Petratos, J. Pept. Sci., 2016, 22, 76–81 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- E. G. Petrov, Y. V. Shevchenko, V. I. Teslenko and V. May, J. Chem. Phys., 2001, 115, 7107–7122 CrossRef CAS.
- E. W. Schlag, S. Y. Sheu, D. Y. Yang, H. L. Selzle and S. H. Lin, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 1068–1072 CrossRef CAS.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- Q. Wu and T. Van Voorhis, J. Chem. Phys., 2006, 125, 164105 CrossRef PubMed.
- A. Farazdel, M. Dupuis, E. Clementi and A. Aviram, J. Am. Chem. Soc., 1990, 112, 4206–4214 CrossRef CAS.
- Q. Wu and T. Van Voorhis, J. Phys. Chem. A, 2006, 110, 9212–9218 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1957, 26, 872–877 CrossRef CAS.
- M. L. Tan, E. A. Dolan and T. Ichiye, J. Phys. Chem. B, 2004, 108, 20435–20441 CrossRef CAS.
- O. Jacobsen, H. Maekawa, N. H. Ge, C. H. Gorbitz, P. Rongved, O. P. Ottersen, M. Amiry-Moghaddam and J. Klaveness, J. Org. Chem., 2011, 76, 1228 CrossRef CAS PubMed.
- Y. Arikuma, H. Nakayama, T. Morita and S. Kimura, Angew. Chem., Int. Ed., 2010, 49, 1800 CrossRef CAS PubMed.
- H. Sasaki, M. Makino, M. Sisido, T. A. Smith and K. P. Ghiggino, J. Phys. Chem. B, 2001, 105, 10416–10423 CrossRef CAS.
- X. Chen, G. Ma, W. Sun, H. Dai, D. Xiao, Y. Zhang, X. Qin, Y. Liu and Y. Bu, J. Am. Chem. Soc., 2014, 136, 4515–4524 CrossRef CAS PubMed.
- R. Nissim, C. Batchelor-McAuley, M. C. Henstridge and R. G. Compton, Chem. Commun., 2012, 48, 3294–3296 RSC.
- G. Kastlunger and R. Stadler, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 125410 CrossRef.
- N. P. A. Monney, T. Bally and B. Giese, J. Phys. Chem. B, 2015, 119, 6584–6590 CrossRef CAS PubMed.
- P. Gobbo, S. Antonello, I. Guryanov, F. Polo, A. Solda, F. Zen and F. Maran, ChemElectroChem, 2016, 3, 2063–2070 CrossRef CAS.
- M. Zhang, J. Zhao, H. Yang, P. Liu and Y. Bu, J. Phys. Chem. B, 2013, 117, 6385–6393 CrossRef CAS PubMed.
- A. J. Wain, H. N. L. Do, H. S. Mandal, H. B. Kraatz and F. M. Zhou, J. Phys. Chem. C, 2008, 112, 14513–14519 CAS.
- B. Pispisa, A. Palleschi, L. Stella, M. Venanzi and C. Toniolo, J. Phys. Chem. B, 1998, 102, 7890–7898 CrossRef CAS.
- D. C. Young, Computational Chemistry: A Practical Guide for Applying Techniques to Real World Problems, John Wiley & Sons, Inc., 2001 Search PubMed.
- C. Lambert, G. Noll and J. Schelter, Nat. Mater., 2002, 1, 69–73 CrossRef CAS PubMed.
- E. G. Petrov, Y. V. Shevchenko and V. May, Chem. Phys., 2003, 288, 269–279 CrossRef CAS.
- P. A. Sanchez-Murcia, M. Ruiz-Santaquiteria, M. A. Toro, H. de Lucio, M. A. Jimenez, F. Gago, A. Jimenez-Ruiz, M. J. Camarasa and S. Velazquez, RSC Adv., 2015, 5, 55784–55794 RSC.
- N. E. Shepherd, H. N. Hoang, V. S. Desai, E. Letouze, P. R. Young and D. P. Fairlie, J. Am. Chem. Soc., 2006, 128, 13284–13289 CrossRef CAS PubMed.
- K. H. Khoo, Y. Chen, S. Li and S. Y. Quek, Phys. Chem. Chem. Phys., 2015, 17, 77–96 RSC.
| This journal is © The Royal Society of Chemistry 2017 |