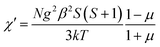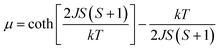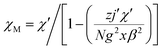The diversities of magnetic behaviors appearing simultaneously in three isomorphs based on 1H-tetrazolyl-acetic acid ligand

Abstract

Three isomorphous metal–organic complexes with 1H-tetrazolyl-acetic acid (TAA), namely [M(TAA)₂]_n (M = Mn^II, 1, Co^II, 2 and Ni^II, 3), have been synthesized under hydrothermal conditions. All the compounds were fully characterized by X-ray crystallography, elemental analysis, IR spectroscopy, thermal analysis and magnetic studies. The single crystal X-ray analyses show that the 1D chains of [M(COO⁻)₂]_n (M = Mn^II, 1, Co^II, 2 and Ni^II, 3) are further joined by tetrazolyl spacers to form a 3D network. Based on the topological perspective, the complexes can be simplified into a (3,6)-connected 2-nodal net with (4².6)₂(4⁴.6².8⁸.10) “ant” topology. The magnetic measurements reveal different magnetic exchange-coupling interactions: antiferromagnetic for 1 and ferromagnetic for 2 and 3. Furthermore, the magnetic measurements confirm that spin glass behaviour occurs in 3 but not in 2.

---

1. Introduction

Metal–organic complexes have been attracting considerable attention in the field of crystal engineering owing to their intriguing architectures and topologies and potential applications.^1–8 Molecular magnetic materials are an important part of the research concerning the application of metal–organic complexes and to date, we have attained impressive advancement in their synthesis, design and characterization. These materials are of great theoretical interest in fields such as quantum tunnelling of magnetization (QTM) and potential technological applications such as qubits for quantum computing etc.^9–12 However, the design and preparation of magnetic materials such as single molecular magnets (SMMs) or single-chain magnets (SCMs) with bulk magnetic behaviors or special magnetic phenomena are still a challenge. So far, researchers have placed particular emphasis not only on designing new SMMs or SCMs, but also on exploiting other unique magnetic phenomena and behaviors. The selection of metals and ligands for the magnetic materials is extremely important. Usually, the preparation of magnetic materials is focused on the use of paramagnetic metal and bridging ligands because of their abilities in efficient transfer of magnetic exchange interactions.^13,14 Therefore, the proper choice of ligands is considerably important and it may provide us with the new structures and types as desired. 1H-Tetrazolyl-acetic acid (TAA) is a good candidate as it exhibits a variety of coordination abilities and diverse coordination modes.^15–21 Bai and colleagues reported a 3D mixed-valence iron complex based on the TAA ligand, which shows spin-crossover behaviour.¹⁵ The Liu research group reported an Mn(II) compound {[Mn(TAA)₂(HTAA)₂]·2H₂O} grounded on TAA, and the magnetic data displayed that a weak AF interaction exists between the two Mn centers.²²

In addition, 3D isomorphous organic–inorganic hybrid frameworks with diverse magnetic properties haven been relatively rarely reported in literature. The Kitagawa group²³ reported two isomorphous 3D networks of Mn(II) and Co(II) based on naphthalene-1,4-dicarboxylic acid (1,4-napdcH₂), showing metamagnetic behaviour (T_C = 5.5 K) for Co(II) and a weak antiferromagnetic interaction for Mn(II). Two isomorphous 3D complexes based on Co^II/Ni^II, with the Co^II system exhibiting spin-canted antiferromagnetism were reported by Bu and co-workers.²⁴ Other examples based on the lanthanide(III) state with diverse magnetic properties were reported.^25,26 Herein, we report three isostructural coordination compounds of the type [M(TAA)₂]_n based on TAA ligand and three different metal ions: Mn^II for 1, Co^II for 2 and Ni^II for 3, in which the metal ions are bridged via the carboxyl groups to give an eight-membered ring infinite chain with pillared μ-1-tetrazolyl groups generating a 4,6-connected 3D structure. These compounds were synthesized under hydrothermal conditions. The magnetic susceptibility properties of all complexes were measured, and the alternating current (ac) magnetic susceptibility measurements of 2 and 3 were carried out. In addition, thermal stabilities and the IR spectra of the complexes were studied.

2. Experimental

2.1 Materials and methods

All chemicals were commercially available and used without further purification. Elemental analysis (C, H, N) was performed using an ElementarVario ELIII analyzer. Magnetic susceptibility data of the crystalline samples were obtained using a Quantum Design MPMS-XLSQUID magnetometer. The variable-temperature susceptibility measurements were performed in the temperature range of 2–300 K under an applied field of 1000 Oe. Alternating current (ac) susceptibility measurements were performed with a 2.5 Oe ac oscillating field in an operating frequency range of 10–997 Hz under a dc field of 0 or 1000 Oe. Thermogravimetric analysis (TGA) data were collected using a simultaneous SDT thermal analyzer at a heating rate of 10 °C min⁻¹ under a N₂ atmosphere (N₂ flow rate = 0.06 L min⁻¹). Fourier transform infrared (FT-IR) spectra were recorded with a Nicolet iS10 Near/Mid-IR Std spectrophotometer using the pressed KBr pellet in the range of 400–4000 cm⁻¹.

2.2 Synthesis of complex 1

A mixture of MnCl₂·4H₂O (0.2 mmol) and TAA (0.4 mmol) was dissolved in 10 mL of acetonitrile, and the mixture was sealed in a Teflon-lined autoclave and heated at 130 °C for 3 days. Moccasin-block crystals were collected and washed sequentially by acetonitrile. Yield: ∼55% based on TAA. Anal. calcd (%) for C₆H₆MnN₈O₄ (309.13): C, 23.31; H, 1.96; N, 36.25. Found (%): C, 22.94; H, 2.32; N, 35.70.

2.3 Synthesis of complex 2

The synthesis method used for compound 2 was similar to that of 1 except that MnCl₂·4H₂O was used instead of Co(NO₃)₂·6H₂O. Orange red-block crystals were collected and washed sequentially with acetonitrile. Yield: ∼75% based on TAA. Anal. calcd (%) for C₆H₆CoN₈O₄ (313.12): C, 23.02; H, 1.93; N, 35.79. Found (%): C, 22.81; H, 2.23; N, 35.02.

2.4 Synthesis of complex 3

The synthesis method for compound 3 is similar to that of 1 except that MnCl₂·4H₂O was used instead of Ni(NO₃)₂·6H₂O. Spring green-block crystals were collected and washed sequentially with acetonitrile. Yield: ∼79% based on TAA. Anal. calcd (%) for C₆H₆NiN₈O₄ (312.90): C, 23.03; H, 1.93; N, 35.82. Found (%): C, 22.97; H, 2.19; N, 35.06.

2.5 Crystallographic data collection and refinement

The selected suitable single-crystal was used for the X-ray diffraction analyses. Crystallographic data were collected with graphite-monochromated Mo-Kα radiation (λ = 0.71073 Å) on Bruker Smart APEX II CCD at 293 K. Empirical absorption corrections were carried out using the SADABS program.²⁷ The structures were solved using direct methods and then refined on F² by the full-matrix least-squares technique using SHELXL-97 software.^28,29 All of the non-hydrogen atoms were located using difference Fourier syntheses and were then refined with anisotropic displacement parameters. All the hydrogen atoms of the organic ligands were located using geometrical considerations and isotropically refined with fixed U values using a riding model. Crystallographic data and refinement parameters for complexes 1–3 are summarized in Table 1. The main bond lengths and angles are presented in Tables S1–S3.†

Table 1 Crystal data for 1–3

a R1 = Σ||Fo| − |Fc||/Σ|Fo|.b wR2 = [Σw(Fo^2 − Fc^2)^2/Σw(Fo^2)^2]^1/2.
Compound	1	2	3
Empirical formula	C6H6MnN8O4	C6H6CoN8O4	C6H6NiN8O4
Fw	309.13	313.12	312.90
Crystal system	Monoclinic	Monoclinic	Monoclinic
Space group	C2/c	C2/c	C2/c
a/Å	14.7220(15)	14.4184(16)	14.285(2)
b/Å	8.4723(9)	8.3825(8)	8.3073(14)
c/Å	9.6326(10)	9.4836(9)	9.4700(16)
β (°)	119.0620(10)	118.5310(10)	118.178(2)
V/Å^3	1050.19(19)	1007.01(18)	990.6(3)
Z	4	4	4
Dc/g cm^−3	1.955	2.065	1.991
2θ range for data collection	5.76 to 56.52	5.82 to 56.58	5.88 to 56.66
μ/mm^−1	1.287	1.736	1.287
Reflections collected	3286	4191	2986
Unique reflections	1174	1174	1150
F(000)	620.0	628.0	632.0
Rint	0.0165	0.0165	0.0165
GOF on F^2	1.001	1.002	0.997
R1^a, wR2^b [I > 2σ(I)]	0.0234, 0.0634	0.0230, 0.0617	0.0271, 0.0694
R1^a, wR2^b [all data]	0.0243, 0.0641	0.0236, 0.0623	0.0319, 0.0727

---

3. Results and discussion

3.1 Crystal structure analysis

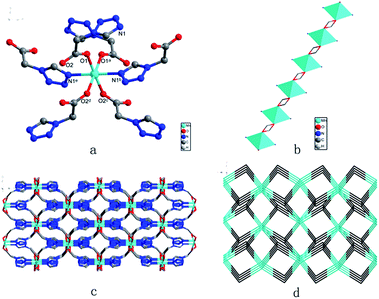
X-ray diffraction analysis indicates that the three compounds are isomorphous with the reported Zn/Cd compounds.^19,29 They crystallized in the monoclinic space group C2/c. Herein, we only describe the crystal structure of 1 in detail as an example.

The asymmetric unit of 1 is crystallographically independent with one Mn(II) and one TAA ligand. As shown in Fig. 1a, the Mn^II ions localize the two fold axis and the crossing point of the mirror plane, which exhibits a distorted octahedral geometry, completed by the four O atoms from the carboxyl groups in the equatorial plane and two tetrazolyl N atoms at axial positions with Mn–O distances slightly shorter than the Mn–N distances. Each TAA ligand acts as a tridentate-N, O, O′ mode ligand coordinated to three Mn^II ions through two 1, 1 − μ₂ carboxyl oxygen atoms bridging the intrachain Mn^II ions to form a 1D chain (Fig. 1b) and the tetrazolyl nitrogen atom linking the third Mn^II ions in the adjacent chain. The Mn^II ions are spanned via two syn–anti carboxylate oxygen atoms simultaneously composed of [Mn₂(COO⁻)₂] 8-membered ring chain structure with Mn⋯Mn distances of 4.865 Å (4.786 Å for 2 and 4.785 Å for 3, respectively). The dihedral angle between the two tetrazolyl rings of the TAA ligands coordinated to the same Mn^II ions is 79.3° (80.67° for 2 and 80.41° for 3), while the two tetrazolyl rings coordinated to the adjacent bridged Mn^II ions are parallel with each other. Such [Mn₂(COO⁻)₂] 8-member ring chains are further pillared via tetrazolyl spacers to form a 3D network, where the shortest Mn⋯Mn interchain separation is 7.451 Å (7.371 Å for 2 and 7.314 Å for 3) (Fig. 1c). To better understand the structure, topological analysis was undertaken. The Mn^II ions can be simplified as a 6-connected node and the TAA ligand can be regarded as a 3-connected vertex, which link three nodes to form a (3,6)-connected “ant” network with the point symbol of (4².6)₂(4⁴.6².8⁸.10) (Fig. 1d). It is a seldom reported topological net and the reported center material (Zn/Cd) is not the same.^20,22

Fig. 1 (a) Coordination environment of Mn(II) ion in complex 1 with hydrogen atoms omitted for clarity (symmetry codes: (a) 2 − x, y, 1.5 − z; (b) 2.5 − x, 0.5 − y, 2 − z; (c) x, −y, −0.5 + z; (d) 2 − x, −y, 2 − z; (e) −0.5 + x, 0.5 − y, −0.5 + z). (b) The 1D chain of [Mn(COO⁻)]_n. (c) The 3D network of complex 1 down the c axis. (d) View of simplified network in the complex 1 structure with the point symbol (4².6)₂(4⁴.6².8⁸.10).

It is worth nothing that the three are isomers reported for complexes 1 and 2 by Dong.²⁰ Comparing complex 1/2 and iso-1/2 indicates remarkable differences, which results in visible structures and different space groups. The difference between the complexes can be attributed to the discrimination of the N–M–O angles (θ₁), the N–M–N angles (θ₂), the C–C–N angles (θ₃), the dihedral angle (θ₄) between the plane A and B, the dihedral angle (θ₅) between the two tetrazolyl planes and the modes of the two TAA ligands linked by the central metal (Scheme 1). The angles in Table S4† indicate that the atoms N, M, N of the iso-1/2 are almost on a line; the N–M–N angles θ₂ in complex 1/2 are 179.45(6)° and 179.11(6)°. The N–M–N angles θ₂ are nearly the same as the difference values are about 0.3° for complex 1 and 0.2° for complex 2. The difference is very apparent when the dihedral angles θ₄ and θ₅ are contrasted with the angles θ₂ and θ₃. The dihedral angles θ₄ between the plane A and B are 84.486(32)° for 1 and 86.176(34)° for 2, and the angles of θ₄ are 73.202(29)° in iso-1 and 76.814(46)° in iso-2. The dihedral angles (θ₅) between the two tetrazolyl planes are 79.307(53)° in complex 1 and 80.667(45)° in complex 2, and the two tetrazolyl planes are parallel in iso-1 and 2. The metal atoms are linked by the TAA ligand in a similar syn–anti tridentate coordination mode; in contrast, the modes of the two TAA ligands linked by the central metal are different, which is mode I: syn–syn coordination in complexes 1 and 2, and mode II: syn–anti coordination in iso-1 and 2.

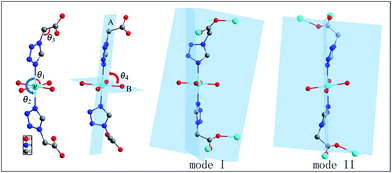Scheme 1 The four N–M–O angles θ₁, N–M–N angles θ₂, C–C–N angles θ₃, dihedral angle between planes (A) and (B) and modes of two TAA ligands linked by central metal.

3.2 Magnetic properties

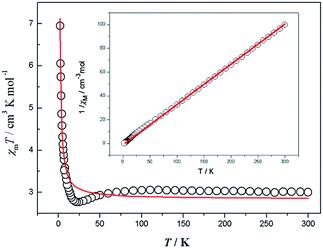
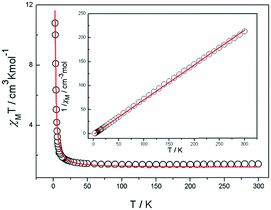
Magnetic susceptibility data were collected on powdered crystalline samples of the complexes 1, 2 and 3 at an applied magnetic field of 1 kOe in the temperature range of 2–300 K, which are shown as χ_MT and 1/χ_M versus T plots in Fig. 2 for 1, Fig. 3 for 2 and Fig. 4 for 3.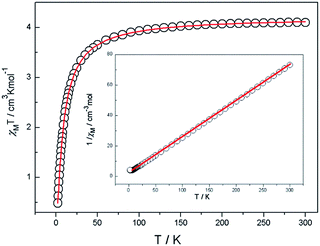

Fig. 2 Temperature dependence of the magnetic susceptibility for complex 1 and 1/χ_M vs. T curve for complex 1. The red line represents the best-fit curves.

Fig. 3 Temperature dependence of the magnetic susceptibility for complex 2 and 1/χ_M vs. T curve for complex 2. The red line represents the best-fit curves.

Fig. 4 Temperature dependence of the magnetic susceptibility for complex 3 and 1/χ_M vs. T curve for complex 3. The red line represents the best-fit curves.

For 1, the χ_MT value at 300 K is equal to 4.10 cm³ mol⁻¹ K, which is compatible with the expected spin Mn^II (S = 5/2, g = 2, 4.37 cm³ kmol⁻¹) anions. With the decrease in temperature, the χ_MT decreases slowly to 45 K and then decreases sharply to 2 K. In the temperature range of 5–300 K, the data can be fitted to the Curie–Weiss law χ_M = C/(T − θ) expression with a Curie constant C = 4.311 cm³ mol⁻¹ K and the Weiss constant θ = −9.47 K, which further suggests the existence of an overall antiferromagnetic exchange interaction between Mn^II ions.

In the case of 2, the value of 4.56 cm³ mol⁻¹ K χ_MT at room temperature exceeds the spin only value of 3.75 cm³ mol⁻¹ K as expected for two uncoupled high-spin Co^II (S = 3/2) ions with g = 2. Thus, it indicates that an important orbital contribution exists due to the distorted octahedral ions of Co^II. The χ_MT first decreases smoothly to a rounded minimum of 2.76 cm³ mol⁻¹ K at 25 K along with the possible antiferromagnetic interactions between the Co^II ions. At lower temperatures the χ_MT plot rises rapidly to a maximum of 6.94 cm³ mol⁻¹ K at 2 K. The magnetic data above 25 K obey the Curie–Weiss law with C = 3.097 and a high Weiss constant θ of −1.97 K, which further suggest the existence of an overall ferromagnetic exchange interaction between Co^II ions.

For complex 3, the χ_MT value is equal to 1.40 cm³ mol⁻¹ K at room temperature. Overall, the χ_MT value slowly increases with decreasing temperature from 300 K to 20 K. However, a dramatic increase in the value to 10.79 cm³ mol⁻¹ K at 2 K was observed. The magnetic behavior of the complex 3 follows the Curie–Weiss law in the entire range of temperature with Curie constants and Weiss temperatures of 1.38 cm³ mol⁻¹ K and 2.57 K, respectively. It suggests ferromagnetic exchange interactions.

According to the structural features of the complexes, the magnetic interaction between metal(II) ions can be estimated by simple chain models, and the mean-field, zj′, is also introduced. The simplified equation³⁰ is as follows:

where the values of S are 5/2 for complex 1, 3/2 for complex 2, and 1 for complex 3. The best fits to the experimental data give g = 1.96, J = −0.79 cm⁻¹, zj′ = −0.025 cm⁻¹, and R = 1.3 × 10⁻⁵ for complex 1, g = 2.46, J = 0.57 cm⁻¹, zj′ = −0.025 cm⁻¹, and R = 1.3 × 10⁻⁵ for complex 2, and g = 2.52, J = 4.97 cm⁻¹, zj′ = 0.15 cm⁻¹, and R = 1.3 × 10⁻⁵ for complex 3 (R value is defined as Σ[(χ_M)_obs − (χ_M)_calcd]²/Σ(χ_M)_obs²). The fitting results confirm that weak antiferromagnetic coupling exists in 1, and weak ferromagnetic coupling exists in 2 and 3.

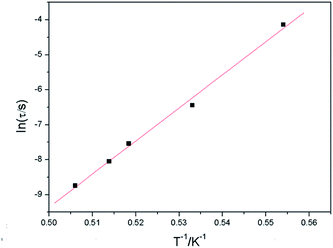
In order to confirm the existence of special magnetic behavior in complexes 2 and 3, alternating current (ac) magnetic susceptibility measurements were carried out (Fig. S5 for 2 and S6† for 3). However, there was no frequency dependence for both the in-phase (χ′_M) and out-of phase (χ′′_M) susceptibility signals of complex 2. Furthermore, the ac susceptibility measurements of 3 were performed in the temperature range of 1.80–2.95 K under a zero static field oscillating at various frequencies (10–997 Hz). As revealed in Fig. 5, both in-phase (χ′_M) and out-of phase (χ′′_M) susceptibility signals were obviously frequency dependent with a maximum between 2.0–2.2 K and 1.8–2.0 K, respectively. This was accompanied by an increase in peak temperature as well as a decrease in peak height of χ′_M with increasing temperature, while the maximum of the χ′′_M peaks shifted to the lower temperature region with decreasing frequencies. 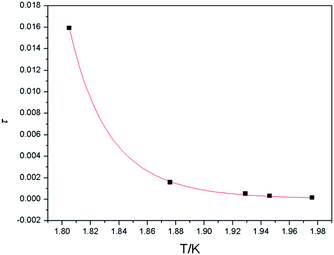Such a shift in temperature of the maximum of χ′_M and χ′′_M with frequency is the positive signature of single molecule magnets (SMMs), single chain magnets (SCMs), and spin glass or a superparamagnetic behavior.^31–33 The frequency dependence is measured by a parameter ϕ = (ΔT_p/T_p)/Δ(log f) = 0.06, in which T_p is the temperature at which χ′ reaches a maximum. This is the typical value for spin-glass magnets (ϕ < 0.1).³³ In order to gain insight into the real magnetic behavior of 3, we first tried to determine the relaxation time. The relaxation time τ(T) data obtained from the χ′′_M peaks follow the Arrhenius equation τ = τ_o exp(Δτ/T), resulting in the relaxation time τ_o = 2.3 × 10⁻²⁵ s and the energy barrier Δτ = 94.7 K (Fig. 6). The rather small value of τ_o is obtained beyond the normal range of typical SMMs or SCMs (10⁻⁷–10⁻¹² s),³⁴ locating in the usual range for spin-glass dynamics in case of 3.³³ Moreover, another quantitative measurement in a spin-glass system is also determined by fitting the frequency dependence maxima in χ′′_M using the conventional critical scaling law of the spin dynamics, τ = τ_o[(T_p − T_f)/T_f]^−zv (T_f and zv represent the freezing temperature and the critical exponent, respectively),^35,36 with τ_o = 5.1 × 10⁻⁸ s, zν = 9.4, and T_f = 1.5 K (Fig. 7). The obtained zν value just falls in the typical range (4–12) of the conventional spin glasses.^32,33 As shown above, all ac measurements and the deduced results are indicative of the canonical spin glass characteristic for 3, which is ascribed to be a ferromagnetic-like layer with spin-glass dynamic relaxation. Although slow relaxation has been observed in SMMs, SCMs and some magnetic frustration systems, three-dimensional compounds comprising ferromagnetic chains/layers and showing slow magnetic relaxation are very scarce.^36–39

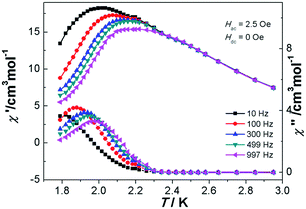Fig. 5 Temperature dependence of the in-phase (χ′) and out-of-phase (χ′′) ac susceptibilities in the range of 10–997 Hz at H_ac = 2.5 Oe for complex 3 measured without an applied dc field.

Fig. 6 Plots of ln τ vs. T⁻¹ of complex 3.

Fig. 7 Temperature dependence of the relaxation time of 3.

3.3 FT-IR spectra and thermal stability

The IR spectra of the complexes are shown in Fig. S7.† The thermogravimetric analysis (TGA), as shown in Fig. S8,† was performed for complexes 1–3 to examine their stability. Caution: the complexes are easy to explode when heated. Complex 1 remains stable up to ca. 285 °C, finally leading to the formation of the stoichiometric amount of MnO₂ as a residue. For complexes 2 and 3, the framework structure began to decompose form 270 °C and 200 °C, respectively.

4. Conclusions

We used a newly developed tetrazolate carboxylic acid ligand as the bridging ligand in three isomorphous 3D Mn^II, Co^II and Ni^II coordination polymers and they were observed to possess totally different magnetic properties. Framework 1 shows simple antiferromagnetic interactions. Framework 2 combines canted antiferromagnetic exchange, whereas framework 3 shows spin glass behavior between the Ni^II ions bridged by the syn–anti carboxyl. Herein, we provide evidence for the existence of diversity in magnetic properties of three isomorphous frameworks with a simple difference of metal ions and thereby demonstrate the importance of engineering metal–organic coordination polymers in the field of molecular-based magnetic materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported financially by the National Natural Science Foundation of China (No. 21461029, 21561033) and the Natural Science Foundation of YunNan province (Project 2016FB023).

Notes and references

1. X. Y. Dong, B. Li, B. B. Ma, S. J. Li, M. M. Dong, Y. Y. Zhu, S. Q. Zang, Y. Song, H. W. Hou and T. C. Mak, J. Am. Chem. Soc., 2013, 135, 10214–10217.
2. D. N. Dybtsev, H. Chun, S. H. Yoon, D. Kim and K. Kim, J. Am. Chem. Soc., 2004, 126, 32–33.
3. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
4. Y. Kondo, K. Kon-i, A. Iwasaki, T. Ooi and K. Maruoka, Angew. Chem., Int. Ed., 2000, 39, 414–416.
5. Y. W. Zhao, F. Q. Zhang and X. M. Zhang, ACS Appl. Mater. Interfaces, 2016, 8, 24123–24130.
6. P. Verma, K. D. Vogiatzis, N. Planas, J. Borycz, D. J. Xiao, J. R. Long, L. Gagliardi and D. G. Truhlar, J. Am. Chem. Soc., 2015, 137, 5770–5781.
7. K.-J. Chen, R.-B. Lin, P.-Q. Liao, C.-T. He, J.-B. Lin, W. Xue, Y.-B. Zhang, J.-P. Zhang and X.-M. Chen, Cryst. Growth Des., 2013, 13, 2118–2123.
8. Z. Z. Lu, R. Zhang, Y. Z. Li, Z. J. Guo and H. G. Zheng, J. Am. Chem. Soc., 2011, 133, 4172–4174.
9. Y. Tian, W. Wang, Y. Chai, J. Cong, S. Shen, L. Yan, S. Wang, X. Han and Y. Sun, Phys. Rev. Lett., 2014, 112, 017202.
10. Y. Dong, P. Yan, X. Zou, T. Liu and G. Li, J. Mater. Chem. C, 2015, 3, 4407–4415.
11. T. N. Nguyen, W. Wernsdorfer, M. Shiddiq, K. A. Abboud, S. Hill and G. Christou, Chem. Sci., 2016, 7, 1156–1173.
12. K. R. Vignesh, S. K. Langley, K. S. Murray and G. Rajaraman, Chem.–Eur. J., 2017, 23, 1654–1666.
13. A. K. Boudalis, B. Donnadieu, V. Nastopoulos, J. M. Clemente-Juan, A. Mari, Y. Sanakis, J.-P. Tuchagues and S. P. Perlepes, Angew. Chem., Int. Ed., 2004, 43, 2266–2270.
14. T. Gong, X. Lou, J.-J. Fang, E.-Q. Gao and B. Hu, Dalton Trans., 2016, 45, 19109–19116.
15. Y. L. Bai, J. Tao, R. B. Huang, L. S. Zheng, S. L. Zheng, K. Oshida and Y. Einaga, Chem. Commun., 2008, 1753–1755.
16. Y.-B. Lu, S. Jin, F.-M. Jian, Y.-R. Xie and G.-T. Luo, J. Mol. Struct., 2014, 1061, 14–18.
17. X.-Q. Zhang, Q. Yu, H.-D. Bian, X.-G. Bao and H. Liang, J. Coord. Chem., 2009, 62, 2108–2117.
18. D. Ding, M. Zhang, L. Li, Y. Fan and H. Hou, J. Coord. Chem., 2009, 62, 2675–2681.
19. Q. Yu, X. Zhang, H. Bian, H. Liang, B. Zhao, S. Yan and D. Liao, Cryst. Growth Des., 2008, 8, 1140–1146.
20. W.-W. Dong, J. Zhao and L. Xu, Cryst. Growth Des., 2008, 8, 2882–2886.
21. W.-W. Dong, J. Zhao and L. Xu, J. Solid State Chem., 2008, 181, 1149–1154.
22. D.-S. Liu, W.-T. Chen, Y.-P. Xu, P. Shen, S.-J. Hu and Y. Sui, J. Solid State Chem., 2015, 226, 186–191.
23. T. K. Maji, W. Kaneko, M. Ohba and S. Kitagawa, Chem. Commun., 2005, 4613–4615.
24. J. R. Li, Q. Yu, Y. Tao, X. H. Bu, J. Ribas and S. R. Batten, Chem. Commun., 2007, 2290–2292.
25. Y. L. Wang, Y. L. Jiang, Z. J. Xiahou, J. H. Fu and Q. Y. Liu, Dalton Trans., 2012, 41, 11428–11437.
26. X.-W. Liu, R. Guo, H. Liu, Y.-Q. Yu, X.-W. Qi, J.-Y. Xu and C.-Z. Xie, RSC Adv., 2015, 5, 15059–15068.
27. G. M. Sheldrick, Program for Empirical Absorption Correction of Area Detector Data, Germany, 1996.
28. G. M. Sheldrick, SHELX-97, University of Göttingen, Germany, 1997.
29. G. M. Sheldrick, SHELX-97, University of Göttingen, Germany, 1997.
30. A. Das, G. M. Rosair, M. S. El Fallah, J. Ribas and S. Mitra, Inorg. Chem., 2006, 45, 3301–3306.
31. Z. X. Wang, X. L. Li, T. W. Wang, Y. Z. Li, S. Ohkoshi, K. Hashimoto, Y. Song and X. Z. You, Inorg. Chem., 2007, 46, 10990–10995.
32. D. Li, L. Zheng, Y. Zhang, J. Huang, S. Gao and W. Tang, Inorg. Chem., 2003, 42, 6123–6129.
33. J. A. Mydosh, Nurs. Times, 1993, 78, 654.
34. R. Clérac, H. Miyasaka, M. Yamashita and C. Coulon, J. Am. Chem. Soc., 2002, 124, 12837–12844.
35. Y. Z. Zheng, M. L. Tong, W. X. Zhang and X. M. Chen, Angew. Chem., Int. Ed., 2006, 45, 6310–6314.
36. X. J. Li, X. Y. Wang, S. Gao and R. Cao, Inorg. Chem., 2006, 45, 1508–1516.
37. X. N. Cheng, W. X. Zhang, Y. Z. Zheng and X. M. Chen, Chem. Commun., 2006, 3603–3605,  10.1039/b606765d.
38. X. M. Zhang, P. Li, W. Gao, J. P. Liu and E. Q. Gao, Dalton Trans., 2015, 44, 511–514.
39. J. Liu, J. Luo, Q. Han, J. Cao, L. Chen, Y. Song and J. Zhao, J. Mater. Chem. C, 2017, 5, 2043–2055.

---

Footnotes

† Electronic supplementary information (ESI) available: TGA and IR spectra. CCDC: 725886 for 1, 725885 for 2, 725887 for 3. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra07997d

‡ These authors contributed equally to this paper.

---