Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revealing phase relations between Fe2B7 and FeB4 and hypothetical Fe2B7-type Ru2B7 and Os2B7: first-principles calculations†
Yunkun Zhanga,
Biao Wanab,
Lailei Wu*ac,
Zhiping Lic,
Zhibin Wang c,
Jingwu Zhang*a,
Huiyang Gou
c,
Jingwu Zhang*a,
Huiyang Gou *bc and
Faming Gaoc
*bc and
Faming Gaoc
aKey Laboratory of Metastable Materials Science and Technology, College of Material Science and Engineering, Yanshan University, Qinhuangdao 066004, China. E-mail: wll@ysu.edu.cn; zjw@ysu.edu.cn
bCenter for High Pressure Science and Technology Advanced Research, Beijing 100094, China. E-mail: huiyang.gou@gmail.com
cKey Laboratory of Applied Chemistry, College of Environmental and Chemical Engineering, Yanshan University, Qinhuangdao 066004, China
First published on 19th September 2017
Abstract
Investigation of new materials recovered using high pressure can foresee the unobservable structures and bonding of crystals. Employing first-principles calculations, we aim to provide an atomic understanding of the origin of multiple phases and mutual intergrowth for metastable iron borides. The competing FeB4 and Fe2B7 in the experiment are compared by their enthalpy and structural features. The closely similar enthalpy of Fe2B7 + B and Fe2B8 (FeB4) may explain the coexistence and tight mutual intergrowth of these two phases. The hypothetical Ru2B7 and Os2B7 are also suggested by the stability evaluations. The stable Ru2B7 and Os2B7 show an interesting metallic property and a great mechanical property due to the hybridization of metal-d and B-p orbitals and B–B covalent bonding.
1 Introduction
Over the decades, transition metal (TM) borides have attracted much attention due to their great promise for hard, wear-resistant, chemically inert coatings' applications.1–4 Extensive experimental and theoretical studies have been performed with a focus on the synthesis and physical property characterizations of transition metal borides. Thus far, a variety of transition metal borides, e.g. OsB2,5 RuB2,2 ReB2,2,6–10 WB4,2,11–13 and CrB4,14,15 have been successfully synthesized in experiments, enabling the discovery of structural complexity, unique chemical bonding and exotic properties. Subsequently, the Os–B, Ru–B and W–B systems were investigated by first-principles calculations and the stable phases with different stoichiometry were identified, providing a road map for exploring design and synthesis strategies for new osmium, ruthenium and tungsten borides.16,17 Recently, FeB4 with Pnnm symmetry was synthesized to be a phonon mediated superconductor.18 Computational structure simulations of the energy landscape did expedite the exploration for the discovery of FeB4.19 Interestingly, Fe2B7 was found to coexist with FeB4 in experiments. This stoichiometry was not previously identified in any 3d metal boron systems. Aided by single-crystal X-ray diffraction, Bykova et al.20 identified Fe2B7 to have an orthorhombic symmetry of Pbam, with lattice parameters of a = 16.9699(15) Å, b = 10.6520(9) Å, and c = 2.8938(3) Å. However, the understanding of this compound is lacking to date, although Fe2B21 and FeB2 (ref. 22) in the Fe–B system have been theoretically reported. Moreover, an experimental determination of the phase stability of Fe2B7 and FeB4 has not been characterized. Furthermore, FeB4 is found to exhibit great incompressibility along the b axis.18 Due to the intergrowth of Fe2B7 and FeB4, Fe2B7 may exhibit interesting physical properties. In view of the similarity of these two borides, there is a lack of understanding of the mechanical and electronic properties of this phase. Knowledge about these properties is essential to the understanding of the fundamental phase behaviors of this compound and offers the potential to discover new phases in transition metal borides.It is found that chemically related compounds usually share similar crystallographic structure.23 OsB2 and RuB2 crystallize in the orthorhombic Pmmn structure.24,25 Furthermore, OsN2 and RuN2 are also formed in the same marcasite structure.26,27 In addition, IrN2 was predicted to have the IrP2-type structure by Wang et al.28 It is thus reasonable to expect the existence of Ru2B7 and Os2B7 with the same crystal symmetry of Fe2B7. Inspired by the potential of investigating the rich phase space of metal borides, we carried out a systematic study of Fe2B7, Ru2B7 and Os2B7 based on first-principles density functional calculations. We elucidated their phase relations and discussed their thermodynamic stability and mechanical and electronic properties. The results may provide guidance for further experimental and theoretical studies of these phases.
2 Computational details and methods
The structural optimizations were performed within CASTEP code.29 Exchange and correlation functional was treated by the generalized gradient approximation with Perdew–Burke–Ernzerhof (GGA-PBE).30 An energy cutoff of 500 eV and dense k-point grids within the Monkhorst–Pack scheme31 were adopted for the Brillouin zone sampling, yielding excellent convergence for total energies (within 1 meV per atom). By calculating the individual elastic constants of crystals, Cij, bulk modulus, B, and shear modulus, G, were obtained using the Voight–Reuss–Hill (VRH) approximation.32 The theoretical Vickers hardness was estimated using Chen's empirical model,33 Hv = 2.0(k2G)0.585 − 3.0, and Tian's empirical model,34 Hv = 0.92k1.137G0.708, where k = G/B. In the enthalpy calculations, α-B and γ-B are adopted as the reference structure below 20 GPa and 20–50 GPa for boron, respectively.Formation enthalpy was calculated by the following formula:
| ΔH = [H(TM2B7) − 2H(TM) − 7H(B)]/(2 + 7) | (1) |
3 Results and discussion
Motivated by the tight mutual intergrowth of FeB4 and Fe2B7 in the experiment, we initially examined the structural stability by calculating the relative enthalpy as a function of pressure, shown in Fig. 1. In the pressure range from 0 to 50 GPa, both Fe2B7 + B and Fe2B8 (FeB4) are found to be favored with respect to element Fe and B phases. Moreover, the enthalpy of Fe2B7 + B is very similar to that of Fe2B8 (FeB4) in the entire pressure range considered (the enthalpy difference is 9–14 meV per atom), which confirms the coexistence of Fe2B7 and FeB4 during the synthesis process. Orthorhombic FeB was also obtained independent of pressure in their high-pressure experiments, and hence the relative enthalpy of Fe2B2 + 6B (FeB + B) is also shown for comparison. In the entire pressure range, the enthalpy of Fe2B2 + 6B (FeB + B) is lower than that of 2Fe + 8B, but higher than that of Fe2B7 + B and Fe2B8 (FeB4). The larger enthalpy difference between Fe2B2 + 6B (FeB + B) and Fe2B8 (FeB4) may explain why they are not in tight mutual intergrowth.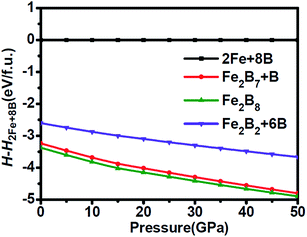 | ||
| Fig. 1 Relative enthalpy of Fe2B7 + B, Fe2B8 and Fe2B2 + 6B with respect to 2Fe + 8B as a function of pressure. | ||
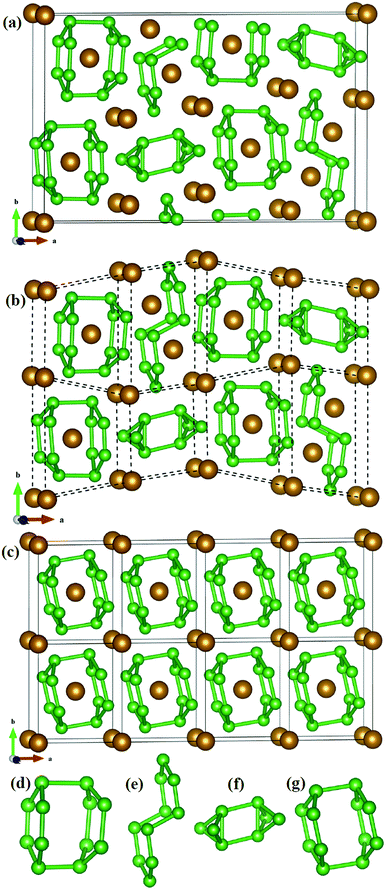
The structural characteristic of Fe2B7 with FeB4 may give the clue of the phase competition of Fe2B7 and FeB4 during synthesis. As shown in Fig. 2a, the structure of Fe2B7 consists of B12, B10 and B8 units (see Fig. 2d–f), with Fe atoms situated among or inside these units. Therefore, each unit cell of Fe2B7 can be viewed as eight small distorted cells (see Fig. 2b). Compared with Fe2B7, FeB4 (see Fig. 2c) consists of only B12 units (see Fig. 2g) with Fe atoms located inside. In Fe2B7, the length of B–B bonds is 1.616–2.028 Å in the B12 units, 1.666–1.771 Å in the B10 units, and 1.669–1.896 Å in the B8 units. For FeB4, the length of B–B bonds is between 1.694 and 1.880 Å in the B12 units, which is close to the lengths of B–B bonds in B12, B10 and B8 units in Fe2B7. Between the two structures, moreover, we can find some close correlation that the size of the unit cell of Fe2B7 is closely similar to the size of the 4 × 2 × 1 supercell of FeB4. Therefore, we can speculate that the small cells with B12 units in Fe2B7 may transform to a unit cell of FeB4 through compression, and on adding more B in the experiment, the small cells with B10 and B8 units in Fe2B7 may also transform to FeB4 through diffusion and deformation (high pressure and temperature may be needed). Hence, it is reasonable to consider that FeB4 may be synthesized by reacting Fe2B7 and B under certain conditions.
It is known that RuB2 and OsB2 crystallize in the same orthorhombic structure.24,25 Similarly, RuN2 and OsN2 in experiment adopt an identical marcasite-type structure.26,27 In addition, IrP3,35 IrAs3,36 IrSb3,36 CoP3,35 and RhP3 (ref. 35) with cubic skutterudite CoAs3-type structure were synthesized in experiments. Corresponding nitrides IrN3,37 CoN3 (ref. 38) and RhN3 (ref. 38) with the same type structure were also suggested by first-principles calculations. Thus, it is expected that Ru2B7 and Os2B7 adopt a similar crystallographic structure to Pbam-Fe2B7. The lattice parameters of Fe2B7, Ru2B7 and Os2B7 obtained from geometric optimization are listed in Table 1 in comparison with available experiment data. The calculated lattice parameters of Pbam-Fe2B7 are in good agreement with the experimental data within a maximum error of 1.4%, which confirms the reliability of our calculations.
| a | b | c | Ref. | |
|---|---|---|---|---|
| Fe2B7 | 16.732 | 10.538 | 2.893 | 20 |
| 16.9699 | 10.6520 | 2.8938 | ||
| Ru2B7 | 17.965 | 11.061 | 2.984 | |
| Os2B7 | 18.322 | 11.101 | 2.989 |
In order to check the possibility of the existence of Ru2B7 and Os2B7, we calculated the formation enthalpy of the two phases. The computed formation enthalpy is −0.071 eV per atom for Ru2B7 and 0.058 eV per atom for Os2B7. However, at a pressure of 100 GPa, the formation enthalpy for Os2B7 becomes negative, with the value of −0.027 eV. The negative formation enthalpy indicates that Ru2B7 may exist at ambient pressure, while Os2B7 should be favored with high pressure.
The mechanical stability of the proposed Ru2B7 and Os2B7 is checked by calculating their individual elastic constants, as listed in Table 2. The calculated elastic constants fully satisfy Born–Huang stability criteria,37 suggesting their mechanical stability. For comparison, the elastic constants of Fe2B7 are also given in Table 2, together with the bulk modulus B, shear modulus G, Young's modulus E, Poisson's ratio ν and Vickers hardness Hv. We can see that as the atomic number of TM (TM = Fe, Ru and Os) increases, the elastic constants C11, C22 and C33 decrease. The C22 value for Fe2B7 is 691 GPa, slightly lower than that of Pnnm-FeB4 (717 GPa).39 For all three compounds TM2B7 (TM = Fe, Ru and Os), C22 is much larger than C11 and C33, similar to that in VB4,40 CrB4,14 FeB4 (ref. 39) and MnB4,41 as the shortest B–B bonds are almost parallel to the [010] direction. The calculated bulk modulus of Fe2B7 is 274 GPa, which is consistent with the experiment value of 268.9 GPa,20 and higher than the experiment value of Pnnm-FeB4 (252 GPa).18 Although the valence electron density of element Ru and Os is higher than that of Fe, the bulk modulus of Ru2B7 and Os2B7 is only 264 GPa and 272 GPa, respectively, suggesting that the valence electron density is not a predominant factor accounting for the bulk moduli of TM2B7 (TM = Fe, Ru and Os) but the boron network. Moreover, Fe2B7 exhibits the highest shear modulus (197 GPa) and hardness (26.9 GPa), comparable to the theoretical value of Pnnm-FeB4 (197.97 GPa/28.4 GPa). The G/B ratio, proposed by Pugh,42 is correlated with the brittleness and ductility of materials (G/B > 0.57 corresponds to brittle and G/B < 0.57 to ductile behavior). Fe2B7 and Ru2B7 are brittle with G/B values of 0.72 and 0.60, while Os2B7 is ductile with a G/B ratio of 0.50. Poisson's ratio, ν, is an important parameter to describe the directional degree of covalent bonds in a material.43 For Fe2B7, Ru2B7 and Os2B7, ν values are 0.21, 0.25 and 0.28, respectively, indicating their directional covalent bonding.
| C11 | C22 | C33 | C44 | C55 | C66 | C12 | C13 | C23 | B | G | G/B | E | v | Hv (Chen) | Hv (Tian) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fe2B7 | 396 | 691 | 432 | 240 | 205 | 237 | 148 | 172 | 183 | 274 | 197 | 0.72 | 477 | 0.21 | 26.9 | 26.6 |
| Ru2B7 | 378 | 614 | 404 | 161 | 201 | 160 | 209 | 154 | 155 | 264 | 159 | 0.60 | 397 | 0.25 | 18.4 | 18.7 |
| Os2B7 | 359 | 575 | 377 | 148 | 194 | 134 | 242 | 190 | 166 | 272 | 136 | 0.50 | 350 | 0.28 | 12.7 | 13.6 |
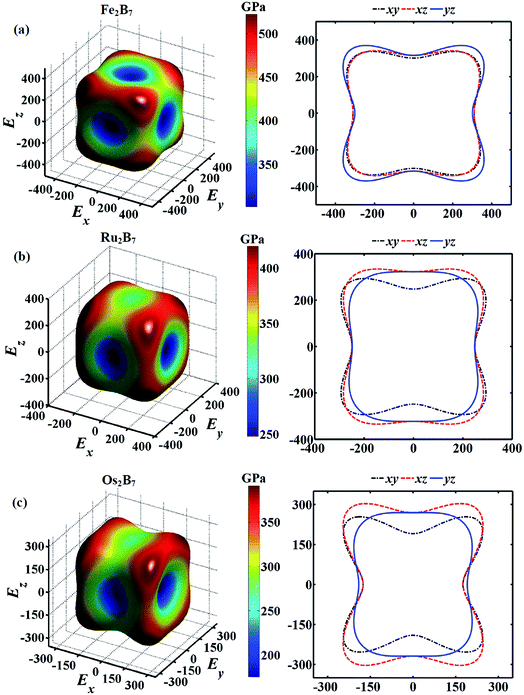
Young's modulus (E) is an important mechanical parameter to measure of the stiffness of a solid material. To get a better understanding of the direction oriented Young's modulus, a 3D representation and corresponding two dimensional (2D) projections of Young's modulus for Fe2B7, Ru2B7 and Os2B7 as a function of the crystallographic direction44 are calculated and presented in Fig. 3. The shape deviation from a sphere indicates the degree of anisotropy in the system. Clearly, they all exhibit a slight elastic anisotropy, and the elastic anisotropy increases as the atomic radius of TM (TM = Fe, Ru and Os) increases. For Fe2B7, the 2D projections of Young's modulus in the xy, xz and yz planes have similar profiles, and the lowest Young's modulus values are along the [010] direction. For Ru2B7, the 2D projection of Young's modulus in the xy plane exhibits greater anisotropy than that in the xz and yz planes. For Os2B7, the lowest Young's modulus values are along the [100] direction, with the 2D projection of Young's modulus in the xy and xz planes showing larger anisotropy than in the yz plane.
The dynamical stability of the newly proposed Ru2B7 and Os2B7 is checked by calculating the phonon spectra (see ESI Fig. S1†). Both compounds are dynamically stable with no imaginary frequency found throughout the Brillouin zone.
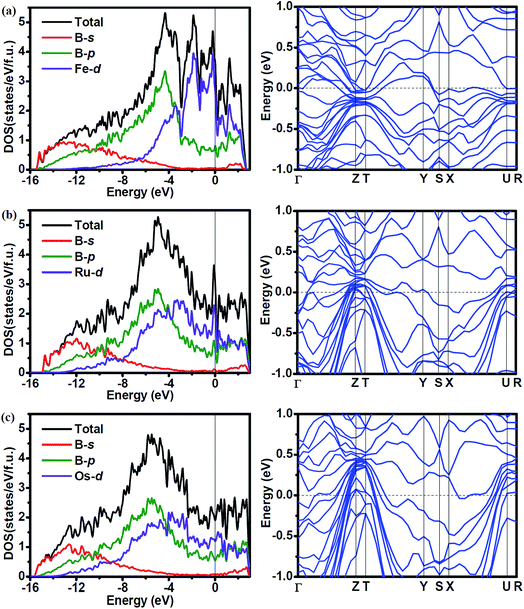
To investigate the effect of the atomic radius of TM (TM = Fe, Ru and Os) on the electronic properties, we calculated the density of states (DOS) and band structure of Fe2B7, Ru2B7 and Os2B7, and the results are shown in Fig. 4. Due to the similarity of the crystal structure, the DOS profile of the three compounds is quite similar to each other, the valence band is dominated by B-s states at low energy part, B-p states in the middle range, and TM (TM = Fe, Ru and Os)-d states at the higher energies. We observe the gradual shift of the main peak in the DOS to a lower energy region as the atomic radius of TM (TM = Fe, Ru and Os) increases. All three compounds exhibit metallic features due to the finite values at the Fermi level (EF), which is mainly contributed by TM (TM = Fe, Ru and Os)-d state. The DOSs of TM (TM = Fe, Ru and Os)-d and B-p show a similar profile from the bottom of the valence band to the Fermi level, indicating the covalent hybridization between TM (TM = Fe, Ru and Os) and B atoms. Note that a pseudogap near the Fermi level is observed for all three compounds, enhancing their structural stability. In the band structure of these compounds, the large dispersion bands cross the Fermi level, also revealing their metallic character.
To gain a more detailed insight into the bonding characters of these compounds, we plot the valence electron density distribution for Fe2B7, Ru2B7 and Os2B7 in (001) and (002) planes in Fig. 5. We can see that there is a charge density maxima located between neighboring B atoms, which correspond to strong directional nonpolar σ covalent B–B bonding. However, between the TM (TM = Fe, Ru and Os) atom and the B atom, the valence electrons are more localized around the B atoms due to the electronegativity difference, corresponding to polar covalent bonding, which mainly originates from the hybridization between TM (TM = Fe, Ru and Os)-d and B-p orbitals.
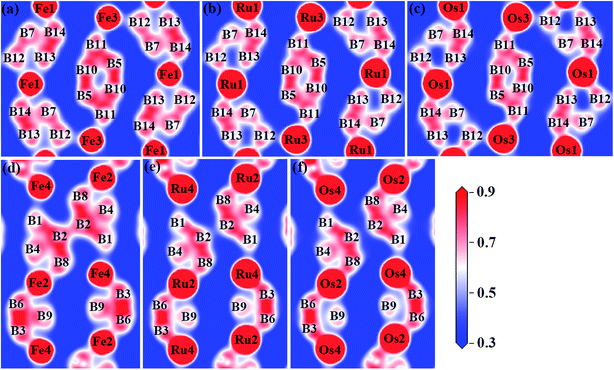 | ||
| Fig. 5 Valence electron density distribution of (a) Fe2B7 in (002) and (d) in (001) planes, (b) Ru2B7 in (002) and (e) in (001) planes, (c) Os2B7 in (002) and (f) in (001) planes. | ||
The relative bond strength between boron atoms can be evaluated by the calculated Mulliken overlap populations (MOP). The bond distances and MOP of B–B bonds in Fe2B7, Ru2B7 and Os2B7 are listed in Table 3. The strongest B–B bond in all three compounds is the B3–B6 bond, which is located in the (001) plane with MOP values of 0.98, 1.00 and 0.94, respectively. The strong B3–B6 bond, nearly parallel to the b axis, is responsible for their high incompressibility along this direction. The MOP of B6–B9/B3–B9 is 0.58/0.55 in Fe2B7, 0.52/0.49 in Ru2B7, and 0.39/0.41 in Os2B7, indicating a decrease in the B6–B9/B3–B9 bond strength as TM (TM = Fe, Ru and Os) moves down in group from Fe to Os. A similar trend can be found in the B2–B2 bond, with MOP of 0.68 in Fe2B7, only 0.30 in Ru2B7, and merely 0.16 in Os2B7. For B1–B2, B2–B4 and B2–B8 bonds, MOP is found to be 0.81, 0.46 and 0.90 in Fe2B7, 0.87, 0.53 and 0.89 in Ru2B7, and 0.83, 0.47 and 0.71 in Os2B7. In the (002) plane, MOP for B10–B11, B5–B10 and B5–B11 is between 0.70 and 0.89 in Fe2B7, between 0.75 and 0.82 in Ru2B7, and between 0.71 and 0.78 in Os2B7. As TM (TM = Fe, Ru and Os) moves down in group from Fe to Os, the B13–B14/B7–B12 bond strength decreases, with a MOP value of 0.94/0.8 in Fe2B7, 0.91/0.67 in Ru2B7, and 0.86/0.46 in Os2B7. As for the B7–B14 bond, MOP is found to be 0.53, 0.61 and 0.60 in Fe2B7, Ru2B7 and Os2B7, respectively.
| Fe2B7 | Ru2B7 | Os2B7 | ||||
|---|---|---|---|---|---|---|
| d | MOP | d | MOP | d | MOP | |
| B3–B6 | 1.616 | 0.98 | 1.644 | 1.00 | 1.649 | 0.94 |
| B13–B14 | 1.691 | 0.94 | 1.733 | 0.91 | 1.726 | 0.86 |
| B2–B8 | 1.666 | 0.90 | 1.692 | 0.89 | 1.689 | 0.71 |
| B10–B11 | 1.728 | 0.89 | 1.800 | 0.82 | 1.792 | 0.78 |
| B1–B2 | 1.714 | 0.81 | 1.740 | 0.87 | 1.727 | 0.83 |
| B7–B12 | 1.773 | 0.8 | 1.884 | 0.67 | 1.991 | 0.46 |
| B5–B11 | 1.747 | 0.74 | 1.800 | 0.76 | 1.817 | 0.72 |
| B5–B10 | 1.669 | 0.70 | 1.682 | 0.75 | 1.687 | 0.71 |
| B2–B2 | 1.771 | 0.68 | 2.117 | 0.30 | 2.206 | 0.16 |
| B6–B9 | 1.834 | 0.58 | 1.991 | 0.52 | 2.101 | 0.39 |
| B3–B9 | 1.847 | 0.55 | 1.986 | 0.49 | 2.034 | 0.41 |
| B7–B14 | 1.859 | 0.53 | 1.884 | 0.61 | 1.880 | 0.60 |
| B2–B4 | 1.811 | 0.46 | 1.838 | 0.53 | 1.859 | 0.47 |
The electron transfer from TM (TM = Fe, Ru and Os) to B atoms is found to be 1.49 e for Fe1, 1.61 e for Fe2, 1.24 e for Fe3 and Fe4 in Fe2B7; 1.11 e for Ru1, 1.26 e for Ru2, 0.85 e for Ru3, and 0.93 e for Ru4 in Ru2B7; 1.02 e for Os1, 1.09 e for Os2, 0.76 e for Os3, and 0.80 e for Os4 in Os2B7. The valence charge transfer from TM (TM = Fe, Ru and Os) to B atoms indicates the partial ionic character of the TM-B (TM = Fe, Ru and Os) bonds.
4 Conclusions
In conclusion, Fe2B7, Ru2B7 and Os2B7 have been studied by first-principles calculations based on density functional theory. Our calculations indicate that the enthalpy of Fe2B7 + B is closely similar to that of Fe2B8 (FeB4), which is responsible for the coexistence and the tight mutual intergrowth of the two phases in the experiments. Ru2B7 and Os2B7 are thermodynamically (Os2B7 at 100 GPa) and mechanically stable and can be synthesized experimentally. In addition, the bulk modulus of Fe2B7, Ru2B7 and Os2B7 is higher than that of FeB4, and the hardness of Fe2B7 is comparable to that of FeB4. The electronic structure calculations indicate that Fe2B7, Ru2B7 and Os2B7 are metallic, which is mainly attributed to the Fe/Ru/Os-d states. The B–B bonding in the three compounds is covalent, and Fe/Ru/Os–B interactions have partial covalent and partial ionic character.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) under Grants No. 51201148 and U1530402. L. Wu thanks the foundation of China Postdoctoral Science Foundation (2016M601280). Z. Li thanks Hebei Natural Science Foundation (No. B2015203096) and the Autonomic Research Project of Yanshan University under Grant No. 14LGA017.References
- H.-Y. Chung, M. B. Weinberger, J.-M. Yang, S. H. Tolbert and R. B. Kaner, Appl. Phys. Lett., 2008, 92, 261904 CrossRef.
- Q. Gu, G. Krauss and W. Steurer, Adv. Mater., 2008, 20, 3620–3626 CrossRef CAS.
- M. B. Weinberger, J. B. Levine, H.-Y. Chung, R. W. Cumberland, H. I. Rasool, J.-M. Yang, R. B. Kaner and S. H. Tolbert, Chem. Mater., 2009, 21, 1915–1921 CrossRef CAS.
- J. B. Levine, S. H. Tolbert and R. B. Kaner, Adv. Funct. Mater., 2009, 19, 3519–3533 CrossRef CAS.
- R. B. Kaner, J. J. Gilman and S. H. Tolbert, Science, 2005, 308, 1268 CrossRef CAS PubMed.
- H.-Y. Chung, M. B. Weinberger, J. B. Levine, A. Kavner, J.-M. Yang, S. H. Tolbert and R. B. Kaner, Science, 2007, 316, 436–439 CrossRef CAS PubMed.
- J. B. Levine, S. L. Nguyen, H. I. Rasool, J. A. Wright, S. E. Brown and R. B. Kaner, J. Am. Chem. Soc., 2008, 130, 16953–16958 CrossRef CAS PubMed.
- A. Latini, J. V. Rau, D. Ferro, R. Teghil, V. R. Albertini and S. M. Barinov, Chem. Mater., 2008, 20, 4507–4511 CrossRef CAS.
- J. Qin, D. He, J. Wang, L. Fang, L. Lei, Y. Li, J. Hu, Z. Kou and Y. Bi, Adv. Mater., 2008, 20, 4780–4783 CrossRef CAS.
- N. Orlovskaya, Z. Xie, M. Klimov, H. Heinrich, D. Restrepo, R. Blair and C. Suryanarayana, J. Mater. Res., 2011, 26, 2772–2779 CrossRef CAS.
- R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10958–10962 CrossRef CAS PubMed.
- C. Liu, F. Peng, N. Tan, J. Liu, F. Li, J. Qin, J. Wang, Q. Wang and D. He, High Pres. Res., 2011, 31, 275–282 CrossRef CAS.
- M. Xie, R. Mohammadi, Z. Mao, M. M. Armentrout, A. Kavner, R. B. Kaner and S. H. Tolbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064118 CrossRef.
- H. Niu, J. Wang, X.-Q. Chen, D. Li, Y. Li, P. Lazar, R. Podloucky and A. N. Kolmogorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144116 CrossRef.
- A. Knappschneider, C. Litterscheid, D. Dzivenko, J. A. Kurzman, R. Seshadri, N. Wagner, J. Beck, R. Riedel and B. Albert, Inorg. Chem., 2013, 52, 540–542 CrossRef CAS PubMed.
- Y. Wang, T. Yao, L.-M. Wang, J. Yao, H. Li, J. Zhang and H. Gou, Dalton Trans., 2013, 42, 7041–7050 RSC.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2013, 110, 136403 CrossRef PubMed.
- H. Gou, N. Dubrovinskaia, E. Bykova, A. A. Tsirlin, D. Kasinathan, W. Schnelle, A. Richter, M. Merlini, M. Hanfland and A. M. Abakumov, Phys. Rev. Lett., 2013, 111, 157002 CrossRef PubMed.
- A. N. Kolmogorov, S. Shah, E. R. Margine, A. F. Bialon, T. Hammerschmidt and R. Drautz, Phys. Rev. Lett., 2010, 105, 217003 CrossRef CAS PubMed.
- E. Bykova, H. Gou, M. Bykov, M. Hanfland, L. Dubrovinsky and N. Dubrovinskaia, J. Solid State Chem., 2015, 230, 102–109 CrossRef CAS.
- S. Deng, J. Zhao, S. Wei, C. Zhu, J. Lv, Q. Li and W. Zheng, RSC Adv., 2016, 6, 73576–73580 RSC.
- I. Harran, H. Wang, Y. Chen, M. Jia and N. Wu, J. Alloys Compd., 2016, 678, 109–112 CrossRef CAS.
- R. Yu, Q. Zhan and X.-F. Zhang, Appl. Phys. Lett., 2006, 88, 051913 CrossRef.
- B. Aronsson, Acta Chem. Scand., 1963, 17, 2036–2050 CrossRef CAS.
- R. B. Roof Jr and C. P. Kempter, J. Chem. Phys., 1962, 37, 1473–1476 CrossRef.
- R. Yu, Q. Zhan and L. C. De Jonghe, Angew. Chem., Int. Ed., 2007, 46, 1136–1140 CrossRef CAS PubMed.
- K. Niwa, K. Suzuki, S. Muto, K. Tatsumi, K. Soda, T. Kikegawa and M. Hasegawa, Chem.–Eur. J., 2014, 20, 13885–13888 CrossRef CAS PubMed.
- Y. X. Wang, M. Arai, T. Sasaki and C. Z. Fan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104110 CrossRef.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- X.-Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS.
- Y. Tian, B. Xu and Z. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS.
- S. Rundquist and N. O. Ersson, Ark. Kemi, 1968, 30, 103 Search PubMed.
- A. Kjekshus and G. Pedersen, Acta Crystallogr., 1961, 14, 1065–1070 CrossRef CAS.
- Z.-J. Wu, E.-J. Zhao, H.-P. Xiang, X.-f. Hao, X.-j. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115 CrossRef.
- Z. Wu and J. Meng, Comput. Mater. Sci., 2008, 43, 495–500 CrossRef CAS.
- Y. Zhang, L. Wu, B. Wan, Y. Zhao, R. Gao, Z. Li, J. Zhang, H. Gou and H.-k. Mao, Phys. Chem. Chem. Phys., 2016, 18, 2361–2368 RSC.
- L. Wu, B. Wan, Y. Zhao, Y. Zhang, H. Liu, Y. Wang, J. Zhang and H. Gou, J. Phys. Chem. C, 2015, 119, 21649–21657 CAS.
- M. Yang, Y. C. Wang, J. L. Yao, Z. P. Li, J. Zhang, L. L. Wu, H. Li, J. W. Zhang and H. Y. Gou, J. Solid State Chem., 2014, 213, 52–56 CrossRef CAS.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CrossRef CAS.
- J. Haines, J. M. Leger and G. Bocquillon, Annu. Rev. Mater. Res., 2001, 31, 1–23 CrossRef CAS.
- J. F. Nye, Physical properties of crystals, Oxford university press, 1985 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra08134k |
| This journal is © The Royal Society of Chemistry 2017 |