Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy level alignment at semiconductor–water interfaces from atomistic and continuum solvation models†
Lars Blumenthal *ad,
Juhan Matthias Kahkbd,
Ravishankar Sundararamanc,
Paul Tangneyabd and
Johannes Lischnerabd
*ad,
Juhan Matthias Kahkbd,
Ravishankar Sundararamanc,
Paul Tangneyabd and
Johannes Lischnerabd
aImperial College London, Department of Physics, South Kensington Campus, London SW7 2AZ, UK. E-mail: lars.blumenthal11@imperial.ac.uk
bImperial College London, Department of Materials, Royal School of Mines, South Kensington Campus, London SW7 2AZ, UK
cDepartment of Materials Science and Engineering, Rensselaer Polytechnic Institute, 110 8th St, Troy, New York 12180, USA
dThomas Young Centre for Theory and Simulation of Materials, UK
First published on 11th September 2017
Abstract
Accurate and efficient methods for predicting the alignment between a semiconductor's electronic energy levels and electrochemical redox potentials are needed to facilitate the computational discovery of photoelectrode materials. In this paper, we present an approach that combines many-body perturbation theory within the GW method with continuum solvation models. Specifically, quasiparticle levels of the bulk photoelectrode are referenced to the outer electric potential of the electrolyte by calculating the change in electric potential across the photoelectrode–electrolyte and the electrolyte–vacuum interfaces using continuum solvation models. We use this method to compute absolute energy levels for the prototypical rutile (TiO2) photoelectrode in contact with an aqueous electrolyte and find good agreement with predictions from atomistic simulations based on molecular dynamics. Our analysis reveals qualitative and quantitative differences of the description of the interfacial charge density in atomistic and continuum solvation models and highlights the need for a consistent treatment of electrode–electrolyte and electrolyte–vacuum interfaces for the determination of accurate absolute energy levels.
1 Introduction
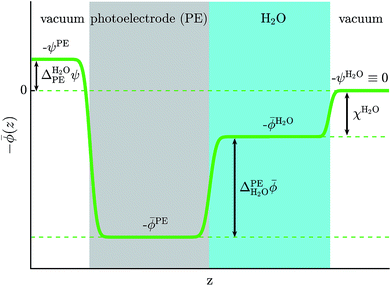
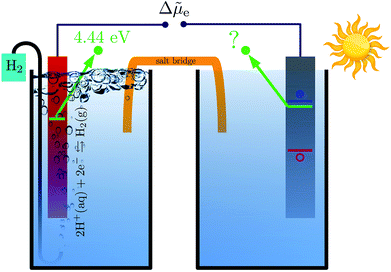
Photocatalysts enable the conversion of solar energy into chemical fuels and there is currently much interest in the search for new materials for water splitting or carbon dioxide reduction.1–4 An important criterion for photocatalyst materials is the favorable alignment of their electrons' quasi electrochemical potential with the redox potential of the desired chemical reaction.5 For example, a photocathode can only drive the hydrogen evolution reaction (HER) if the quasi electrochemical potential of its electrons is above the reduction potential of water, see Fig. 1. Accurate methods to calculate electronic energy levels and align them with redox potentials are therefore needed to enable the computational search for new photocatalysts and their in silico design.Redox potentials are conventionally reported relative to a reference electrode, such as the standard hydrogen electrode (SHE).6,7 Trasatti proposed to determine absolute redox potentials by computing the work needed to bring an electron from the SHE to a point in the vacuum above an ideal aqueous electrolyte.8 By performing the same calculation for an electron from the photoelectrode, a direct comparison between the redox potentials of interest and the photoelectrode's electronic energy levels is possible.
Many computational studies have used density functional theory (DFT) to calculate the Kohn–Sham energy levels of a photoelectrode. Often, these levels are then referenced to the vacuum outside the photoelectrode and the effect of the electrolyte is ignored.9–12 Except for the energy of the highest occupied state, the Kohn–Sham energies do not have the physical meaning of electron addition or removal energies and Stevanović and coworkers employed many-body perturbation theory within the GW method to compute accurate quasiparticle energy levels.13 After aligning the GW-corrected energy levels to the vacuum outside the photoelectrode, they concluded that, on average, an additional shift of 0.5 ± 0.3 eV towards the vacuum level was needed to bring the computed energy levels into agreement with electrochemical measurements at semiconductor–electrolyte interfaces. However, it has become clear that such a rule of thumb is only of limited value for the search for new photoelectrodes as the effect of the electrolyte can vary significantly across different semiconductors. For example, while the reduction of the ionization energy and the electron affinity by 0.5 eV yields good agreement with electrochemically measured band edges at flat band conditions for the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0) surface of ZnO, other materials like TiO2, CdS, and SnO2 show a shift of 1 eV or more, while the shift for Fe2O3 and NiO is only 0.2 eV.13
0) surface of ZnO, other materials like TiO2, CdS, and SnO2 show a shift of 1 eV or more, while the shift for Fe2O3 and NiO is only 0.2 eV.13
To explicitly capture the effect of the electrolyte, several groups carried out ab initio molecular dynamics (AIMD) simulations of the photoelectrode–electrolyte and the electrolyte–vacuum interface.3,14–18 By averaging the electric potential of many structural configurations, the difference between the inner electric potential of the photoelectrode and the outer electric potential of the electrolyte was determined.6 This potential difference was then used to obtain absolute photoelectrode energy levels. Unfortunately, the computational expense of such simulations is very high as large unit cells and long simulation times are needed for precise thermodynamic averages. As a consequence, such methods cannot easily be used in high-throughput computational searches for photocatalyst materials.
Continuum solvation models are computationally inexpensive alternatives to atomistic simulations of liquids at solid–liquid interfaces.19,20 Within this category exists a wide range of approaches, from simple polarizable continuum models (PCMs) to classical density functional theory (CDFT).21–24 Many of these approaches are often based on or at least inspired by the work of Fattebert and Gygi.25 Continuum solvation models directly yield averages of properties, such as number densities of atoms or electric potentials, and avoid the computationally expensive sampling of atomic configurations. Furthermore, in many cases they enable the use of much smaller supercells compared to atomistic solvation models which reduces the computational cost even further. It has been shown that the free energy of solid–liquid interfaces can be obtained by means of joint density functional theory (JDFT) which combines a CDFT treatment of the liquid with an electronic structure DFT approach to the solid.26 JDFT partitions the free energy of the solid–liquid interface into three contributions: one contribution depends only on the electron density of the solid, another contribution depends only on the atomic site density of the liquid and the final contribution, which captures the interaction between the solid and the liquid, depends both on the electron density of the solid and the atomic site density of the liquid. Other successful attempts of directly linking continuum solvation models to DFT include those by Anderson et al., Liu et al. and Marzari et al.27–30 The former has been employed to calculate reversible potentials for redox reactions in solution and at the surface of metal electrodes.31 The latter two have been used to study reaction mechanisms at metal–water interfaces.29,32
Ping and coworkers recently employed a sophisticated PCM to study band edge positions of several well-known photoelectrodes. By modelling the photoelectrode–electrolyte interfaces, they referenced the photoelectrodes' electronic energy levels to the inner electric potential of the electrolyte. Despite this being a different reference point than the outer electric potential of water, which is the one used to calculate the absolute SHE potential, they reported good agreement of their results with experimental data.33 However, so far no explanation for this quantitative agreement despite choosing inconsistent reference points has been given. This demonstrates that the determination of absolute electronic energy levels, which is well established for atomistic solvation models, is qualitatively different and much less well understood for continuum solvation approaches.
In this paper, we rigorously explain the above observation by directly comparing approaches for calculating absolute energy levels of photoelectrodes based on atomistic and continuum solvation models using both a PCM and CDFT. To reference GW quasiparticle energies of bulk photoelectrodes to the outer electric potential of water, we compute the electric potential across both the photoelectrode–water interface and the water–vacuum interface. As will be shown, the two approaches yield significantly different results for the change in electric potential across the individual interfaces, but their predictions for the absolute positions of the electrode's electronic energy levels agree closely with each other. We explain the observed disagreement for the individual interfaces by analyzing how the different approaches describe the interfacial charge distribution. As a test system, we investigate a prototypical rutile (TiO2) photoelectrode as this material has been extensively studied and there exists a wide range of experimental and theoretical reference data.
In the following, we first outline the methods and computational details that were used to align the photoelectrode's electronic energy levels with the SHE potential. Next, we present our results for the electronic structure of bulk rutile, and the structure of the rutile(110)–water and water–vacuum interfaces. Finally, the main differences between atomistic and continuum solvation models are discussed.
2 Methods
2.1 Electronic energy level alignment at photoelectrode–electrolyte interfaces
Aligning electronic energy levels across photoelectrode–electrolyte interfaces requires the choice of a common energy reference point.16 Redox potentials of chemical reactions are conventionally expressed on a scale whose zero is the potential of the SHE.7 By computing the work required to bring electrons from the SHE and a photoelectrode to the same reference point in space, it is possible to compare their electrochemical potentials. Trasatti proposed a reference point in the vacuum located far enough above an ideal aqueous electrolyte so that effects of image charges are negligible.8 By analysing the associated Born–Haber cycle and using experimental values for the involved energy differences, he determined the work required to bring an electron from the SHE to this point to be 4.44 ± 0.02 eV.8 The electric potential the electron experiences at this reference point is the outer electric potential of the aqueous electrolyte, ψH2O, and the associated potential energy is the zero of Trasatti's absolute scale.To express the electronic energy levels in the photoelectrode on this absolute scale, we follow a two-step procedure. First, the energy levels of the bulk photoelectrode are calculated using the GW method.34–36 In this approach, the electron self-energy, which determines the quasiparticle energy levels via the Dyson equation, is expanded in a power series in the screened Coulomb interaction, W, and only the first term is retained; G denotes the one-electron Green's function. In the second step of the alignment procedure, the quasiparticle energies of the bulk photoelectrode—most importantly, the valence band maximum (VBM) and the conduction band minimum (CBM)—are referenced to the outer electric potential of the aqueous electrolyte, ψH2O. For this, we first reference the quasiparticle energies to the average electric potential in the bulk of the photoelectrode, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) PE, with the electric potential being here calculated as
PE, with the electric potential being here calculated as
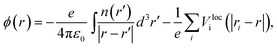 | (1) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) (z), as
(z), as
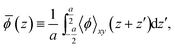 | (2) |
After referencing the quasiparticle energies to ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) PE, the difference between
PE, the difference between ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) PE and ψH2O is computed. In principle, this requires a unit cell containing a slab with a photoelectrode layer, an electrolyte layer and a vacuum layer, see Fig. 2.16,17 In practice, first-principles calculations for such systems are extremely challenging because of the large system size and the need for configurational averages.
PE and ψH2O is computed. In principle, this requires a unit cell containing a slab with a photoelectrode layer, an electrolyte layer and a vacuum layer, see Fig. 2.16,17 In practice, first-principles calculations for such systems are extremely challenging because of the large system size and the need for configurational averages.
As the water surface should be independent of the chosen photoelectrode material, the calculation of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) PE − ψH2O is usually split into two parts. First, the inner electric potential difference
PE − ψH2O is usually split into two parts. First, the inner electric potential difference
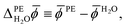 | (3) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) H2O denotes the average electric potential in the ideal aqueous electrolyte, is calculated using a unit cell that does not contain any vacuum but only a slab of the photoelectrode whose periodic images are separated by the electrolyte. In the second step, the surface potential of water,
H2O denotes the average electric potential in the ideal aqueous electrolyte, is calculated using a unit cell that does not contain any vacuum but only a slab of the photoelectrode whose periodic images are separated by the electrolyte. In the second step, the surface potential of water,
χH2O ≡ ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) H2O − ψH2O, H2O − ψH2O,
| (4) |
Finally, the outer electric potential difference is defined as
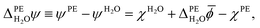 | (5) |
![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) PE − ψPE denotes the surface potential of the photoelectrode. Note that
PE − ψPE denotes the surface potential of the photoelectrode. Note that 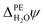 is experimentally measurable, for example by two-photon photoemission, and relates electronic energy levels referenced to the vacuum above the photoelectrode, e.g. the electron affinity (EA) and ionization energy (IE), to absolute energy levels referenced to ψH2O.38 For example, the absolute value of the CBM is given by
is experimentally measurable, for example by two-photon photoemission, and relates electronic energy levels referenced to the vacuum above the photoelectrode, e.g. the electron affinity (EA) and ionization energy (IE), to absolute energy levels referenced to ψH2O.38 For example, the absolute value of the CBM is given by
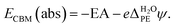 | (6) |
For a detailed discussion, see the work of Cheng et al.16
The computational details of each of these steps are outlined below. We emphasize that we perform GW calculations only for the bulk photoelectrode, but not for the photoelectrode–water or the water–vacuum interfaces. The goal of our work is to align energy levels of bulk states which are unaffected by surface phenomena, such as mutual polarization effects.3,16 For non-ideal photoelectrode–electrolyte interfaces, where surface states are important, GW calculations of the full interface will be needed.
2.2 Electronic energy levels of bulk rutile
We first determined the atomic structure of bulk rutile TiO2 using DFT with the PBEsol exchange–correlation functional (PBEsol-DFT).39 Calculations employed a plane-wave basis and Garrity–Bennett–Rabe–Vanderbilt (GBRV) ultrasoft pseudopotentials with kinetic energy cutoffs of 200 Ry and 40 Ry for the electron density and the wave functions, respectively.40 The Brillouin zone was sampled with a 5 × 5 × 7 Monkhorst–Pack grid, which was shifted by half a grid step in each principal direction.41 Lattice parameters and atomic positions were obtained through a variable-cell geometry optimization using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. All calculations were carried out using the Quantum Espresso software package.42Next, quasiparticle corrections to the DFT band structure were determined using the GW method. For this, we first computed DFT energies and wavefunctions using the PBE exchange–correlation functional (PBE-DFT) and Optimized Norm-Conserving Vanderbilt (ONCV) pseudopotentials with a kinetic energy cutoff of 80 Ry for the wave functions.43–45 For titanium, the valence electrons comprised the 3s, 3p, 3d, and 4s states. For the GW calculations, we employed a one-shot G0W0 correction with a plane wave cutoff of 50 Ry for the dielectric matrix. The frequency dependence of the screened Coulomb interaction was treated within the Hybertsen–Louie generalized plasmon-pole model.46 Empty state summations employed an explicit set of 2875 conduction states and an additional static remainder correction.47 All GW calculations were performed using the BerkeleyGW software package.48
To establish the accuracy of our GW calculations, the resulting EA and first IE of a rutile(110) surface were determined following the method of Fall et al., originally developed for the accurate calculation of electron work functions.49 Hence, DFT calculations on relaxed rutile(110) slabs were performed to reference the GW energy levels to the vacuum level, ψTiO2. In these calculations, a shifted 8 × 4 × 1 k-point sampling was used and the results were carefully converged with respect to the thickness of the rutile slab and the vacuum region. This resulted in a final slab thickness of 15 TiO2-layers and a vacuum thickness of 10 Å. Note that for consistency with our bulk calculations, we used GBRV pseudopotentials and the PBEsol functional for structure relaxations and ONCV pseudopotentials and the PBE functional to determine electronic properties of the optimized surface structures. In fact, PBEsol was chosen for the structural relaxations as it greatly improves the convergence of rutile's surface properties with respect to the slab thickness compared to PBE. The PBE exchange–correlation functional was used for the electronic structure calculations for the sake of easing comparison with previous work on rutile.
2.3 Rutile(110)–water interface
We calculated the difference between the average electric potentials in the rutile(110) photoelectrode and the aqueous electrolyte, i.e.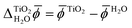 , using both JDFT and classical molecular dynamics combined with subsequent DFT calculations (MD+DFT).
, using both JDFT and classical molecular dynamics combined with subsequent DFT calculations (MD+DFT).
For the JDFT calculations, the water was described using both CDFT and a PCM. We note that the results of solvation calculations can depend on the details of the continuum model which is used to describe the solvent.33,50 Below, we describe the physical content of the employed continuum approaches. For a full description of the models, we refer the interested reader to the original papers.21,24,26,51–53
In the JDFT-CDFT method, the free energy of the photoelectrode–electrolyte system, AJDFT[n,{Nα}], is expressed as
| AJDFT[n,{Nα}] = ADFT[n] + Alq[{Nα}] + ΔA[n,{Nα}], | (7) |
For the JDFT-PCM calculation, we employed the recently developed SaLSA model, which is derived from the linear response limit of the ScalarEOS CDFT functional.21 Its free energy functional of the photoelectrode–electrolyte interface depends only on n(r), which determines the induced polarization response of the electrolyte through its non-local susceptibility.
In addition, we carried out JDFT-CDFT and JDFT-PCM calculations of rutile(110)–water interfaces with an explicit monolayer of water molecules adsorbed to the fivefold-coordinated titanium atoms exposed at the rutile(110) surface. The initial configurations of the water molecules, which were assumed to be those found by Patel et al., were relaxed using the BFGS algorithm.54 In reality, the water molecules of the first monolayer at the rutile(110) surface are very likely to be at least partially dissociated.55 However, as the focus of this work is on the comparison between atomistic and continuum solvation models, we only require consistency between these two methods. Therefore, any possible dissociation of the water molecules was ignored in both cases for the sake of simplicity.
All JDFT calculations employed GBRV ultrasoft pseudopotentials and the PBEsol exchange–correlation functional and were carried out using the JDFTx software package.53,56–58 To avoid inconsistencies due to the choice of the pseudopotentials and to make use of the potential-subtraction method implemented in JDFTx, we ran JDFT calculations with and without the liquid electrolyte to first determine the difference 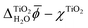 which was then added to χTiO2 =
which was then added to χTiO2 = ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) TiO2 − ψTiO2 as calculated with ONCV pseudopotentials and PBE-DFT to obtain the final inner electric potential difference between rutile(110) and water.59
TiO2 − ψTiO2 as calculated with ONCV pseudopotentials and PBE-DFT to obtain the final inner electric potential difference between rutile(110) and water.59
For comparison, MD+DFT simulations of the rutile(110)–water interface were performed using the interaction potentials of Předota et al.60,61 In these calculations, a rutile(110) slab comprising 3 × 2 rutile(110) surface unit cells with a thickness of 7 TiO2-layers separated by 72 water molecules was used. To be consistent with the JDFT calculations, the geometry of the TiO2 slab was relaxed in the presence of an adsorbed monolayer of water molecules using PBEsol-DFT and then frozen during the MD simulations so that only the water molecules were free to move. The calculations were performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).62 A time step of 1.2 fs and a Nose–Hoover thermostat with a damping parameter of 0.1 ps were used. After equilibrating the system for 1 ns within a canonical ensemble at 300 K, 30 Snapshots of the atomic configurations were taken every 20 ps and PBE-DFT calculations employing ONCV pseudopotentials were carried out for these snapshots to obtain the associated average electric potentials.
2.4 Water–vacuum interface
Referencing the photoelectrode's electronic energy levels to the outer electric potential of water also requires the calculation of the water surface potential, χH2O. Again, both JDFT and MD+DFT simulations were utilized to study the water–vacuum interface. As before, both CDFT and PCM approaches were employed for the JDFT calculations. In the continuum models, the water slab was constrained to a 45 Å wide region using an artificial electron density which acted as a hard wall. Note that electrostatic interactions of the liquid with this electron density were cancelled using a coincident positive charge density.For the MD+DFT calculations, the water surface was modelled as a slab comprising 256 water molecules in a 15 × 15 × 100 Å3 simulation cell. Using the SPC/E model, the water was equilibrated for 2 ns at 300 K using the CSVR thermostat in CP2K, a time constant of 10 fs, and a time step of 0.5 fs before 80 snapshots of atomic configurations were obtained from simulations in a microcanonical ensemble at a temperature of 308.4 K every 20 ps.63–67 Finally, PBE-DFT calculations employing ONCV pseudopotentials were carried out for these snapshots to compute the average electric potential. Due to the asymmetric nature of the water slab configurations, a dipole correction was used for the latter.68
3 Results
3.1 Electronic energy levels of bulk rutile
The converged PBEsol-DFT lattice parameters of rutile are a = 4.5944 Å and c = 2.9404 Å, comparing well with the experimental estimates of a = 4.5937 Å and c = 2.9587 Å.69 For the converged structure, PBE-DFT predicts a Kohn–Sham band gap of Eg = 1.95 eV. The GW correction significantly increases this value to 3.42 eV in good agreement with experimental values which range from 3.3 ± 0.5 eV to 4.0 ± 0.2 eV.70–75 By combining photoemission spectroscopy and inverse photoemission spectroscopy results, Rangan et al. obtained a presumably very accurate estimate of rutile's fundamental electronic band gap of 3.6 ± 0.2 eV.73 Previous GW studies reported a wide range of values for the band gap of rutile. For example, Patrick et al. carried out G0W0 calculations on top of a PBE+U mean-field calculation with U chosen to minimize the GW self-energy correction.76 However, the resulting band gap Eg = 2.85 eV is significantly smaller than the experimentally measured gap. In contrast, a quasiparticle self-consistent GW calculation by van Schilfgaarde et al. yielded Eg = 3.78 eV.77To determine the IE and EA of rutile(110), we first calculated the rutile surface potential finding χTiO2 = 12.70 ± 0.02 V. Table 1 shows the resulting values of the IE and EA from PBE-DFT, GW and photoemission experiments. The increase in the GW band gap is mostly caused by a shift of the VBM—measured relative to the average electric potential ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) TiO2—to lower energies, while the CBM increases by only 0.28 eV. The experimental estimate of the EA was obtained by adding the fundamental band gap, which was assumed to be 3.5 eV, to the experimentally measured IE. While our GW results agree well with experiment, there is a significant discrepancy of 1.0 eV between PBE-DFT and experiment for the IE.
TiO2—to lower energies, while the CBM increases by only 0.28 eV. The experimental estimate of the EA was obtained by adding the fundamental band gap, which was assumed to be 3.5 eV, to the experimentally measured IE. While our GW results agree well with experiment, there is a significant discrepancy of 1.0 eV between PBE-DFT and experiment for the IE.
| Method | IE | EA |
|---|---|---|
| DFT (PBE) | 7.18 | 5.23 |
| G0W0 (PBE) | 8.37 | 4.95 |
| Experiment | 8.2 ± 0.3 | 4.7 ± 0.3 |
3.2 Rutile(110)–water interface
Fig. 3 shows the electric potential profiles from MD+DFT snapshots of the rutile(110)–water interface and the associated average electric potential. The resulting inner electric potential difference is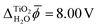 .
.
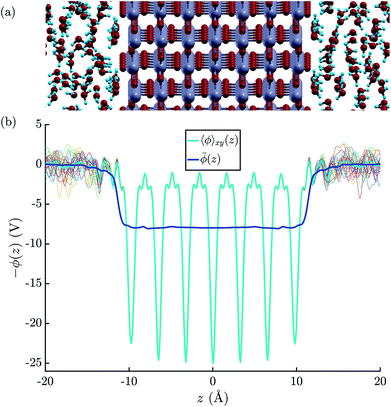 | ||
| Fig. 3 (a) Illustration of the atomic structure of the rutile(110)–water interface.79 Note that we assumed a fully molecular rather than a (partially) dissociated structure of the first monolayer of water molecules. (b) Electric potential profiles at the rutile(110)–water interface based on the atomic configurations obtained by the means of MD+DFT. The thin colourful lines represent that planar average electric potentials of the individual atomic configurations. | ||
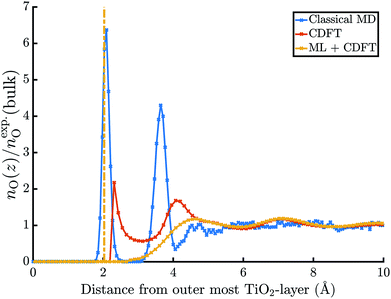
The electric potential profiles of the rutile(110)–water interface from JDFT-CDFT and JDFT-PCM are shown in Fig. 4 and the resulting potential differences are summarized in Table 2. JDFT-CDFT yields 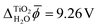 for the pristine rutile(110) surface, somewhat larger than the MD+DFT result. Explicitly including the first monolayer of water molecules reduces this value by 0.29 V. Fig. 5 shows the oxygen number density nO(Z) of water at the rutile(110)–water interface. The MD prediction of nO(Z) exhibits two large peaks corresponding to two water layers which are strongly bound to the rutile surface. The JDFT-CDFT density profile also exhibits several peaks at the interface, but with a significantly smaller height and a wider spacing between them reflecting the inability of the ScalarEOS approximation to describe strongly adsorbed water molecules. Inclusion of an explicit monolayer of water molecules in JDFT leads to a better description of the interface.
for the pristine rutile(110) surface, somewhat larger than the MD+DFT result. Explicitly including the first monolayer of water molecules reduces this value by 0.29 V. Fig. 5 shows the oxygen number density nO(Z) of water at the rutile(110)–water interface. The MD prediction of nO(Z) exhibits two large peaks corresponding to two water layers which are strongly bound to the rutile surface. The JDFT-CDFT density profile also exhibits several peaks at the interface, but with a significantly smaller height and a wider spacing between them reflecting the inability of the ScalarEOS approximation to describe strongly adsorbed water molecules. Inclusion of an explicit monolayer of water molecules in JDFT leads to a better description of the interface.
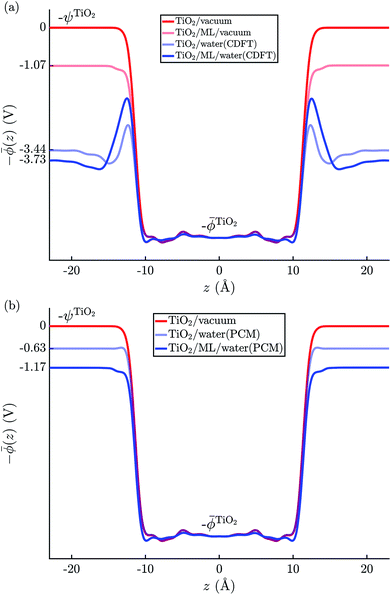 | ||
| Fig. 4 Average electric potential profiles at the rutile(110)–water interface from (a) JDFT-CDFT and (b) JDFT-PCM. | ||
| MD+DFT | JDFT | JDFT + ML | Exp.38,80 | |||
|---|---|---|---|---|---|---|
| PCM | CDFT | PCM | CDFT | |||
| a Note that any PCM is unsuitable for describing the water–vacuum interface as a perturbing electric field that could induce a response in the PCM is missing. The resulting absence of any surface charge leads to χH2O = 0. Nevertheless, in the case of water, this happens to be in fair agreement with the expected value, cf. Section 4. | ||||||
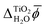 |
8.00 | 12.07 | 9.26 | 11.53 | 8.97 | — |
| χH2O | 3.46 | 0a | 2.93 | 0a | 2.93 | — |
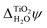 |
1.24 | 0.63 | 0.51 | 1.17 | 0.80 | 0.95 |
| ECBM(abs) | −3.71 | −4.32 | −4.44 | −3.78 | −4.15 | −4.10 |
In contrast, JDFT-PCM yields a significantly larger value of 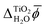 than MD+DFT and JDFT-CDFT, namely
than MD+DFT and JDFT-CDFT, namely 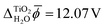 . This value is reduced by 0.54 V when an explicit monolayer of water is included in the calculation. The large discrepancy between JDFT-PCM calculations and the MD+DFT and JDFT-CDFT results is further analyzed in Section 4.
. This value is reduced by 0.54 V when an explicit monolayer of water is included in the calculation. The large discrepancy between JDFT-PCM calculations and the MD+DFT and JDFT-CDFT results is further analyzed in Section 4.
We also carried out DFT calculations with an adsorbed monolayer of water molecules and no additional description of the electrolyte, see Fig. 4(a). This yields a surface potential of 11.63 V, i.e. a reduction of χTiO2 by 1.07 V compared to the pristine surface.
3.3 Water–vacuum interface
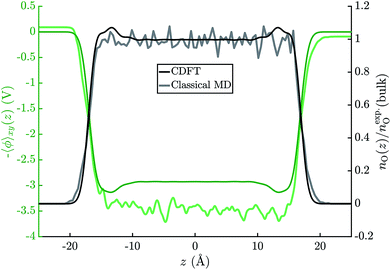
Fig. 6 shows the average electric potential of the water–vacuum interface from MD+DFT. From this, the resulting water surface potential is χH2O = 3.46 ± 0.03 V. This value is similar to previous results by Pham et al. and Leung who reported χH2O = 3.75 ± 0.10 V and χH2O = 3.63 ± 0.04 V, respectively.15,81 Note that value of χH2O depends on the pseudopotential, see eqn (1). Furthermore, the average electric potential obtained by the means of JDFT-CDFT and a comparison of the normalised oxygen site densities are also shown in the same figure. For the water surface potential, CDFT yields χH2O = 2.93 V. The decay of the oxygen site density profile agrees well between CDFT and MD indicating the absence of any spurious features due to the confining potential described in Section 2.4.Lastly, the JDFT-PCM yields χH2O = 0 as there is no external perturbation which induces any polarization response in the liquid.
3.4 Absolute electronic energy levels
Table 2 shows the resulting absolute values of rutile's CBM. MD+DFT yields ECBM(abs) = −3.7 eV, significantly higher than the results of both JDFT-CDFT and JDFT-PCM. Again, the agreement is improved when an explicit monolayer of adsorbed water molecules is included in the JDFT calculations.Experimental measurements suggest that ECBM(abs) = −4.1 ± 0.1 eV.80,82 Specifically, Chandra et al. obtained ECBM(abs) = −4.35 ± 0.05 eV at pH = 1 using electrochemical techniques.80 Using the Nernst law to adjust this value to pH = 5.5 ± 0.5, which corresponds to the point of zero charge of the rutile(110) surface, yields ECBM(abs) = −4.1 ± 0.1 eV.61,80,83,84 A similar value was also found in measurements of the flatband potential of a reduced rutile(110) surface by Nakamura et al.82
In addition to the absolute energy levels, it is also possible to measure 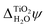 . Using two-photon photoemission, Onda et al. found
. Using two-photon photoemission, Onda et al. found 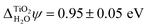 .38 This value is in agreement with
.38 This value is in agreement with 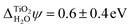 obtained from eqn (6) when the experimental EA and ECBM(abs) are used. Table 2 shows that JDFT-PCM and JDFT-CDFT significantly underestimate the experimental two-photon photoemission value of
obtained from eqn (6) when the experimental EA and ECBM(abs) are used. Table 2 shows that JDFT-PCM and JDFT-CDFT significantly underestimate the experimental two-photon photoemission value of 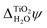 by almost 0.5 V, while MD+DFT overestimates it by 0.3 V. For both JDFT methods, the agreement with experiment is improved by including an explicit monolayer of adsorbed water molecules.
by almost 0.5 V, while MD+DFT overestimates it by 0.3 V. For both JDFT methods, the agreement with experiment is improved by including an explicit monolayer of adsorbed water molecules.
4 Discussion
The results presented in Section 3 show good agreement between the absolute electronic energy levels of rutile calculated with atomistic models and those calculated with continuum solvation models. There is also good agreement with experimental measurements. However, in our calculations we assumed an ideal stoichiometric rutile surface, whereas real rutile photoelectrodes can have a variety of surface structures, morphologies, chemistries, defects, and impurities.87 Furthermore, as mentioned previously, the structure of the first monolayer of water molecules at the interface may differ from the one assumed here.54,55 Direct comparison with experiment requires careful consideration of these issues and we emphasise that our focus is not on comparison with experiment, but on the comparison between atomistic and continuum solvation models of the electrolyte.Despite the good agreement between different models for the absolute electronic energy levels, there is a substantial discrepancy of several volts in the values of 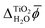 and χH2O calculated from MD+DFT, JDFT-CDFT and JDFT-PCM, see Table 2. Interestingly, these differences almost cancel when
and χH2O calculated from MD+DFT, JDFT-CDFT and JDFT-PCM, see Table 2. Interestingly, these differences almost cancel when 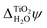 and the absolute energy levels are calculated. This can, at least partially, be explained by differences in how these models describe the charge distributions in water at interfaces, as we now explain.
and the absolute energy levels are calculated. This can, at least partially, be explained by differences in how these models describe the charge distributions in water at interfaces, as we now explain.
There has been much discussion in the literature about how to define, and to calculate, the change in potential across an interface, with particular interest in the water surface potential.37,81,88–91 However, a consensus has yet to emerge and we are not aware of any rigorous theory—one that would be equally applicable to a molecular liquid and to a crystalline solid. We do not attempt to propose such a theory here, but we note that χH2O can be written as a sum containing terms that are the same for all water interfaces, which we refer to as the “bulk” and the “frozen interface” contributions, and a term that is different for each water interface, which we call the “interface relaxation” contribution. These three contributions are depicted schematically in Fig. 7.
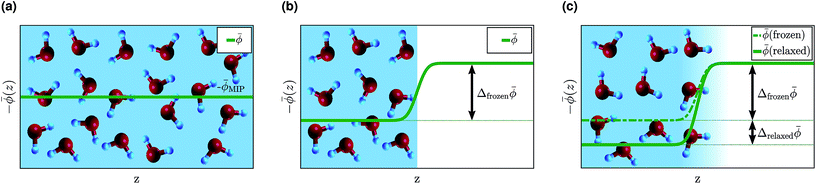 | ||
Fig. 7 Contributions to the inner electric potential of water at an aqueous interface: (a) the mean inner potential (MIP) is due to the microscopic charge density in the bulk of water.85 There is an electric potential step due to the non-zero average charge density at a “frozen” interface (b) and a “relaxed” interface (c). The sum of ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) MIP and Δfrozen MIP and Δfrozen![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is uniquely defined and its value is the same for any interface with water, see Section 4 for details.86 is uniquely defined and its value is the same for any interface with water, see Section 4 for details.86 | ||
The bulk contribution arises from the microscopic charge density in the bulk of water and is that which, in the context of electron wave refraction, is often referred to as the mean inner potential (MIP).85 It is the time average of the potential one would calculate by solving Poisson's equation for the instantaneous microscopic bulk charge density, if one neglected boundary terms. The MIP was analyzed in the context of crystalline solids by Bethe who showed that, for a hypothetical crystal composed of spherically-symmetric atoms, it can be expressed in terms of the spherical second moment of the electron density.92 Because MD+DFT simulations provide the microscopic charge density everywhere in the electrolyte, they include this bulk contribution denoted by ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) MIP. By contrast, continuum models of liquids can only predict a time-averaged charge density which is zero in bulk water. Consequently continuum models do not describe
MIP. By contrast, continuum models of liquids can only predict a time-averaged charge density which is zero in bulk water. Consequently continuum models do not describe ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) MIP.
MIP.
To understand the interface contributions depicted in Fig. 7(b) and (c), it is useful to imagine creating an interface from bulk water in two steps. First, a surface is created by inserting a plane and removing all of the charge on one side of it. The remaining semi-infinite bulk can be placed in contact with the semi-infinite bulk of another phase to create a hypothetical unrelaxed, or “frozen”, interface. The change in the average electric potential across this unrelaxed interface is what we refer to as the frozen interface contribution, Δfrozen![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) . This contribution is described by both the MD+DFT calculations and the JDFT-CDFT approach. The JDFT-PCM approach does not capture Δfrozen
. This contribution is described by both the MD+DFT calculations and the JDFT-CDFT approach. The JDFT-PCM approach does not capture Δfrozen![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) as this method only describes changes in the charge density induced by an external potential. Recall that JDFT-CDFT reconstructs the electron density from the average nuclear densities and therefore does not require an external perturbation to predict a non-zero surface charge density, see Section 2.3. Due to the liquid nature of the aqueous electrolyte, and the associated lack of long-range order, Δfrozen
as this method only describes changes in the charge density induced by an external potential. Recall that JDFT-CDFT reconstructs the electron density from the average nuclear densities and therefore does not require an external perturbation to predict a non-zero surface charge density, see Section 2.3. Due to the liquid nature of the aqueous electrolyte, and the associated lack of long-range order, Δfrozen![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is the same for any interface of liquid water with another phase. Therefore, it can also be considered a property of the bulk since it is interface independent. Indeed, as Finnis has shown, neither the frozen interface contribution nor the bulk contribution to the electric potential is well defined because each one depends sensitively on the precise position of a notional boundary plane separating “interface” from “bulk” regions. However their sum is independent of the position of this plane and is well defined.86
is the same for any interface of liquid water with another phase. Therefore, it can also be considered a property of the bulk since it is interface independent. Indeed, as Finnis has shown, neither the frozen interface contribution nor the bulk contribution to the electric potential is well defined because each one depends sensitively on the precise position of a notional boundary plane separating “interface” from “bulk” regions. However their sum is independent of the position of this plane and is well defined.86
The second step in creating an aqueous interface is to allow the nuclei and electrons to relax. The resulting change in the interfacial charge density gives rise to the interface-specific relaxation contribution to the inner electric potential, Δrelaxed![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , see Fig. 7(c). This contribution is captured by the MD+DFT simulation and also by the JDFT-CDFT and JDFT-PCM methods.
, see Fig. 7(c). This contribution is captured by the MD+DFT simulation and also by the JDFT-CDFT and JDFT-PCM methods.
We have decomposed χH2O into three terms to make it clear that different models of the electrolyte yield different electric potential profiles across an interface and that this is not only due to inaccurate formulations or parametrizations of these models. It is also a consequence of different levels of detail in their descriptions of the charge density. Differences in the effective charge density are also partially responsible for the different values of χH2O obtained by electrochemical measurements and electron holography experiments because protons, or H3O+ ions, sample space on a different time scale to electrons and thus experience a different charge density. In addition to this, the sampling of space by high energy electrons is relatively unbiased, whereas ions do not sample space close to nuclei.37 However, it is important to remember that the determination of absolute quasiparticle energy levels requires the simulation of two aqueous interfaces, the photoelectrode–water and the water–vacuum interface. As both these interfaces need to be crossed when going from the interior of the electrode to the vacuum above the electrolyte, the bulk contribution, ![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) MIP, and the frozen interface contribution, Δfrozen
MIP, and the frozen interface contribution, Δfrozen![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) , to the inner electric potential of water precisely cancel when absolute energies are calculated. In contrast, the relaxed interface contributions to the electric potential are very different for the rutile(110)–water and the water–vacuum interface. In particular, Fig. 5 and 6 suggest that the alignment of water molecules is much weaker at the water–vacuum interface than at the rutile(110)–water interface. Indeed, according to the MD+DFT calculations and the value of
, to the inner electric potential of water precisely cancel when absolute energies are calculated. In contrast, the relaxed interface contributions to the electric potential are very different for the rutile(110)–water and the water–vacuum interface. In particular, Fig. 5 and 6 suggest that the alignment of water molecules is much weaker at the water–vacuum interface than at the rutile(110)–water interface. Indeed, according to the MD+DFT calculations and the value of 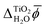 predicted by JDFT-PCM when the first monolayer of water molecules is explicitly accounted for, Δrelaxed
predicted by JDFT-PCM when the first monolayer of water molecules is explicitly accounted for, Δrelaxed![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) is only a very small part of χH2O, see Table 2.
is only a very small part of χH2O, see Table 2.
The above discussion explains why JDFT-PCM predictions for absolute energy levels agree with atomistic and JDFT-CDFT results despite JDFT-PCM's incomplete description of the charge density. The small value of Δrelaxed![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) for the water–vacuum interface and the fact that the bulk and frozen interface contributions to the electric potential, which JDFT-PCM does not capture, would cancel are also the reasons why Ping et al. obtained accurate results for the absolute electronic energy levels of photoelectrodes when using JDFT-PCM even though they did not include the water surface.33
for the water–vacuum interface and the fact that the bulk and frozen interface contributions to the electric potential, which JDFT-PCM does not capture, would cancel are also the reasons why Ping et al. obtained accurate results for the absolute electronic energy levels of photoelectrodes when using JDFT-PCM even though they did not include the water surface.33
Previously it has also been noted that the shift of rutile's electronic energy levels due to an aqueous electrolyte is numerically very similar to that observed when only a monolayer of adsorbed water molecules is considered.93 The latter is 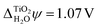 , in good agreement with experiment, see Fig. 4(a) and Table 2. While it is at first surprising that a single monolayer of water molecules can capture the combined effect of the rutile(110)–water and the water–vacuum interface, our analysis might offer an explanation for this as well. The monolayer of water molecules adsorbed to the pristine rutile(110) surface is structurally very similar to that at the actual rutile(110)–water interface, see Fig. 5. The strong alignment of the water molecules in this first monolayer suggests that they should be responsible for the main part of Δrelaxed
, in good agreement with experiment, see Fig. 4(a) and Table 2. While it is at first surprising that a single monolayer of water molecules can capture the combined effect of the rutile(110)–water and the water–vacuum interface, our analysis might offer an explanation for this as well. The monolayer of water molecules adsorbed to the pristine rutile(110) surface is structurally very similar to that at the actual rutile(110)–water interface, see Fig. 5. The strong alignment of the water molecules in this first monolayer suggests that they should be responsible for the main part of Δrelaxed![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) across the rutile(110)–water interface. Thus, this interface contribution is reasonably well described by the single monolayer of adsorbed water molecules and, as before, Δrelaxed
across the rutile(110)–water interface. Thus, this interface contribution is reasonably well described by the single monolayer of adsorbed water molecules and, as before, Δrelaxed![[small phi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d6.gif) from the water surface can be numerically neglected due to its small value.
from the water surface can be numerically neglected due to its small value.
5 Conclusions
In summary, we introduced a new approach for determining absolute electronic energy levels of photoelectrodes by combining GW calculations of bulk quasiparticle energies with JDFT simulations of electrode–electrolyte and electrolyte–vacuum interfaces. We applied this method to rutile (TiO2) photoelectrodes and obtained good agreement with experimental results when an explicit monolayer of adsorbed water molecules was included in the JDFT calculations. We also compared our results to atomistic MD+DFT simulations of the interfaces. Again, good agreement for the absolute energy levels was found despite observing significant discrepancies for the electric potential differences at the individual interfaces. This paradoxical situation was resolved by analyzing the interfacial potential differences in terms of interface and bulk contributions. Specifically, we find that the different methods yield very different values for the bulk contributions, which, however, cancel when the effects of both water interfaces are combined to calculate the absolute electronic energy levels.The presented workflow can now be employed for the efficient study of complex photoelectrochemical systems and high-throughput searches for novel photoelectrode materials. We note, however, that additional work is needed to develop better liquid functionals and coupling functionals which can capture the effect of strongly adsorbed water molecules in order to avoid the need to include any explicit water in the JDFT calculations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Jason Riley, Nicholas Harrison and Michiel Sprik for helpful discussions. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk). This work was supported through a studentship in the Centre for Doctoral Training on Theory and Simulation of Materials at Imperial College London funded by the EPSRC (EP/L015579/1). We acknowledge the Thomas Young Centre under grant number TYC-101.References
- I. Roger, M. A. Shipman and M. D. Symes, Nature Reviews Chemistry, 2017, 1, 0003 CrossRef.
- J. Hofkens and M. B. J. Roeffaers, Nature, 2016, 530, 36–37 CrossRef CAS PubMed.
- T. A. Pham, Y. Ping and G. Galli, Nat. Mater., 2017, 16, 401–408 CrossRef CAS PubMed.
- M. Grätzel, Nature, 2001, 414, 338–344 CrossRef PubMed.
- R. Memming, Semiconductor electrochemistry, Wiley-VCH-Verl, Weinheim, 2nd edn, 2015 Search PubMed.
- IUPAC Compendium of Chemical Terminology: Gold Book, ed. M. Nič, J. Jirát, B. Košata, A. Jenkins and A. McNaught, IUPAC, Research Triangle Park, NC, 2nd edn, 2009 Search PubMed.
- P. W. Atkins and J. De Paula, Atkins' Physical chemistry, Oxford University Press, Oxford ; New York, 9th edn, 2010 Search PubMed.
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CAS.
- D. W. Davies, K. T. Butler, A. J. Jackson, A. Morris, J. M. Frost, J. M. Skelton and A. Walsh, Chem, 2016, 1, 617–627 CAS.
- J. Buckeridge, K. T. Butler, C. R. A. Catlow, A. J. Logsdail, D. O. Scanlon, S. A. Shevlin, S. M. Woodley, A. A. Sokol and A. Walsh, Chem. Mater., 2015, 27, 3844–3851 CrossRef CAS.
- H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238 CrossRef CAS.
- A. K. Singh, K. Mathew, H. L. Zhuang and R. G. Hennig, J. Phys. Chem. Lett., 2015, 6, 1087–1098 CrossRef CAS PubMed.
- V. Stevanović, S. Lany, D. S. Ginley, W. Tumas and A. Zunger, Phys. Chem. Chem. Phys., 2014, 16, 3706 RSC.
- T. A. Pham, D. Lee, E. Schwegler and G. Galli, J. Am. Chem. Soc., 2014, 136, 17071–17077 CrossRef CAS PubMed.
- T. A. Pham, C. Zhang, E. Schwegler and G. Galli, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 060202 CrossRef.
- J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245 RSC.
- M. Otani, I. Hamada, O. Sugino, Y. Morikawa, Y. Okamoto and T. Ikeshoji, J. Phys. Soc. Jpn., 2008, 77, 024802 CrossRef.
- N. Kharche, J. T. Muckerman and M. S. Hybertsen, Phys. Rev. Lett., 2014, 113, 075140 CrossRef PubMed.
- P. Tarazona, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 2672–2679 CrossRef CAS.
- W. A. Curtin and N. W. Ashcroft, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2909–2919 CrossRef CAS.
- R. Sundararaman, K. A. Schwarz, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2015, 142, 054102 CrossRef PubMed.
- J. Lischner and T. A. Arias, J. Phys. Chem. B, 2010, 114, 1946–1953 CrossRef CAS PubMed.
- K. Letchworth-Weaver and T. A. Arias, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075140 CrossRef.
- R. Sundararaman and T. A. Arias, Comput. Phys. Commun., 2014, 185, 818–825 CrossRef CAS.
- J.-L. Fattebert and F. Gygi, J. Comput. Chem., 2002, 23, 662–666 CrossRef CAS PubMed.
- S. A. Petrosyan, A. A. Rigos and T. A. Arias, J. Phys. Chem. B, 2005, 109, 15436–15444 CrossRef CAS PubMed.
- R. Jinnouchi and A. B. Anderson, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245417 CrossRef.
- A. B. Anderson, Phys. Chem. Chem. Phys., 2012, 14, 1330–1338 RSC.
- H.-F. Wang and Z.-P. Liu, J. Phys. Chem. C, 2009, 113, 17502–17508 CAS.
- O. Andreussi, I. Dabo and N. Marzari, J. Chem. Phys., 2012, 136, 064102 CrossRef PubMed.
- R. Jinnouchi and A. B. Anderson, J. Phys. Chem. C, 2008, 112, 8747–8750 CAS.
- L. Sementa, O. Andreussi, W. A. Goddard III and A. Fortunelli, Catal. Sci. Technol., 2016, 6, 6901–6909 CAS.
- Y. Ping, R. Sundararaman and W. A. Goddard III, Phys. Chem. Chem. Phys., 2015, 17, 30499–30509 RSC.
- Y. Ping, D. Rocca and G. Galli, Chem. Soc. Rev., 2013, 42, 2437 RSC.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. Lett., 1985, 55, 1418–1421 CrossRef CAS PubMed.
- L. Hedin and S. Lundqvist, in Solid State Physics, Elsevier, 1970, vol. 23, pp. 1–181 Search PubMed.
- S. M. Kathmann, I.-F. W. Kuo, C. J. Mundy and G. K. Schenter, J. Phys. Chem. B, 2011, 115, 4369–4377 CrossRef CAS PubMed.
- K. Onda, B. Li and H. Petek, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 045415 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- M. Schlipf and F. Gygi, Comput. Phys. Commun., 2015, 196, 36–44 CrossRef CAS.
- M. S. Hybertsen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 5390–5413 CrossRef CAS.
- J. Deslippe, G. Samsonidze, M. Jain, M. L. Cohen and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165124 CrossRef.
- J. Deslippe, G. Samsonidze, D. A. Strubbe, M. Jain, M. L. Cohen and S. G. Louie, Comput. Phys. Commun., 2012, 183, 1269–1289 CrossRef CAS.
- C. J. Fall, N. Binggeli and A. Baldereschi, J. Phys.: Condens. Matter, 1999, 11, 2689–2696 CrossRef CAS.
- R. Sundararaman and K. Schwarz, J. Chem. Phys., 2017, 146, 084111 CrossRef PubMed.
- R. Sundararaman, K. Letchworth-Weaver and T. A. Arias, J. Chem. Phys., 2014, 140, 144504 CrossRef PubMed.
- K. Letchworth-Weaver, PhD Dissertation, Cornell University, Ithaca, New York, U.S., 2016.
- R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler, Y. Ozhabes and T. A. Arias, arXiv:1708.03621 [cond-mat.mtrl-sci], 2017.
- M. Patel, G. Mallia, L. Liborio and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045302 CrossRef.
- M. Patel, F. F. Sanches, G. Mallia and N. M. Harrison, Phys. Chem. Chem. Phys., 2014, 16, 21002–21015 RSC.
- R. Sundararaman, K. Letchworth-Weaver, K. A. Schwarz, D. Gunceler and T. A. Arias, JDFTx, http://jdftx.sourceforge.net, 2016 Search PubMed.
- S. Ismail-Beigi and T. Arias, Comput. Phys. Commun., 2000, 128, 1–45 CrossRef CAS.
- T. A. Arias, M. C. Payne and J. D. Joannopoulos, Phys. Rev. Lett., 1992, 69, 1077–1080 CrossRef CAS PubMed.
- R. Sundararaman and Y. Ping, J. Chem. Phys., 2017, 146, 104109 CrossRef PubMed.
- A. V. Bandura and J. D. Kubicki, J. Phys. Chem. B, 2003, 107, 11072–11081 CrossRef CAS.
- M. Předota, A. V. Bandura, P. T. Cummings, J. D. Kubicki, D. J. Wesolowski, A. A. Chialvo and M. L. Machesky, J. Phys. Chem. B, 2004, 108, 12049–12060 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- P. G. Kusalik and I. M. Svishchev, Science, 1994, 265, 1219–1221 CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- G. Bussi and M. Parrinello, Comput. Phys. Commun., 2008, 179, 26–29 CrossRef CAS.
- L. Bengtsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 12301–12304 CrossRef CAS.
- C. J. Howard, T. M. Sabine and F. Dickson, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 462–468 CrossRef.
- Y. Tezuka, S. Shin, T. Ishii, T. Ejima, S. Suzuki and S. Sato, J. Phys. Soc. Jpn., 1994, 63, 347–357 CrossRef CAS.
- R. G. Breckenridge and W. R. Hosler, Phys. Rev., 1953, 91, 793–802 CrossRef CAS.
- A. Frova, P. J. Boddy and Y. S. Chen, Phys. Rev., 1967, 157, 700–708 CrossRef CAS.
- S. Rangan, S. Katalinic, R. Thorpe, R. A. Bartynski, J. Rochford and E. Galoppini, J. Phys. Chem. C, 2010, 114, 1139–1147 CAS.
- H. Waff and K. Park, Phys. Lett. A, 1970, 32, 109–110 CrossRef CAS.
- P. J. Hardman, G. N. Raikar, C. A. Muryn, G. van der Laan, P. L. Wincott, G. Thornton, D. W. Bullett and P. A. D. M. A. Dale, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 7170–7177 CrossRef CAS.
- C. E. Patrick and F. Giustino, J. Phys.: Condens. Matter, 2012, 24, 202201 CrossRef PubMed.
- M. van Schilfgaarde, T. Kotani and S. Faleev, Phys. Rev. Lett., 2006, 96, 226402 CrossRef CAS PubMed.
- K. Schierbaum, S. Fischer, M. Torquemada, J. de Segovia, E. Román and J. Martín-Gago, Surf. Sci., 1996, 345, 261–273 CrossRef CAS.
- A. Kokalj, Comput. Mater. Sci., 2003, 28, 155–168 CrossRef CAS.
- S. Chandra and R. K. Pandey, Phys. Status Solidi A, 1982, 72, 415–454 CrossRef CAS.
- K. Leung, J. Phys. Chem. Lett., 2010, 1, 496–499 CrossRef CAS.
- R. Nakamura, N. Ohashi, A. Imanishi, T. Osawa, Y. Matsumoto, H. Koinuma and Y. Nakato, J. Phys. Chem. B, 2005, 109, 1648–1651 CrossRef CAS PubMed.
- G. A. Parks, Chem. Rev., 1965, 65, 177–198 CrossRef CAS.
- J. Cheng and M. Sprik, J. Chem. Theory Comput., 2010, 6, 880–889 CrossRef CAS PubMed.
- A. Sanchez and M. A. Ochando, J. Phys. C: Solid State Phys., 1985, 18, 33–41 CrossRef CAS.
- M. W. Finnis, Phys. Status Solidi A, 1998, 166, 397–416 CrossRef CAS.
- U. Diebold, Surf. Sci. Rep., 2003, 48, 53–229 CrossRef CAS.
- M. A. Wilson, A. Pohorille and L. R. Pratt, J. Phys. Chem., 1987, 91, 4873–4878 CrossRef CAS PubMed.
- M. A. Wilson, A. Pohorille and L. R. Pratt, J. Chem. Phys., 1988, 88, 3281–3285 CrossRef CAS PubMed.
- L. R. Pratt, J. Phys. Chem., 1992, 96, 25–33 CrossRef CAS.
- J. R. Cendagorta and T. Ichiye, J. Phys. Chem. B, 2015, 119, 9114–9122 CrossRef CAS PubMed.
- H. Bethe, Ann. Phys., 1928, 392, 55–129 CrossRef.
- P. Deák, J. Kullgren, B. Aradi, T. Frauenheim and L. Kavan, Electrochim. Acta, 2016, 199, 27–34 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra08357b |
| This journal is © The Royal Society of Chemistry 2017 |

![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) e
e