Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Alloying effects of Ag on grain boundaries and alumina interfaces in copper: a first principles prediction
F. Tengab,
G. Q. Lanc,
Y. Jiang *bde,
M. Songde,
S. J. Liude,
C. P. Wub and
D. Q. Yiab
*bde,
M. Songde,
S. J. Liude,
C. P. Wub and
D. Q. Yiab
aLight Alloys Research Institute, Central South University, Changsha 410083, China
bKey Lab of Nonferrous Materials of Ministry of Education, School of Materials Science and Engineering, Central South University, Changsha 410083, China. E-mail: yjiang@csu.edu.cn
cDepartment of Mining and Materials Engineering, McGill University, Montréal, Québec H3A 0C5, Canada
dShenzhen Research Institute of Central South University, Shenzhen, 518057, China
eNational Key Laboratory for Powder Metallurgy, Central South University, Changsha 410083, China
First published on 13th October 2017
Abstract
The mechanical properties of oxide dispersion-strengthened copper are largely dictated by its internal interfaces, i.e. the oxide interfaces and the grain boundaries (GBs). Here we present a systematic first-principles study for evaluating the potential impact of Ag alloying on adhesion of Cu/α-Al2O3 interfaces and Cu grain boundaries as well. The results suggest that, in contrast to the strong segregation of S that is always detrimental, Ag only slightly segregates to the Al2O3 interfaces, strengthens the weak stoichiometric interface, and slightly weakens the strong Al-rich interface. Ag cannot pin S inside the matrix. The co-segregation of Ag with S modestly negates the detrimental influence of S on adhesion, but can hardly occur. Ag segregation to most of the GBs is found also to be weak, and reduces the adhesion slightly. The only one exception is on the Σ9 GB. Based on the gained insights, we suggest that Ag alloying has only limited benefits but can still be encouraged.
1. Introduction
The alumina dispersion-strengthened copper (ADSC) alloys, also called alumina particle-reinforced copper matrix composites Cu(Al2O3)p, have excellent comprehensive properties of high electrical/thermal conductance and high strength. They are highly advantageous for uses in many electrical applications at elevated temperatures, such as electrical connectors, spot-welding electrodes, heat sink devices, and high pressure heat exchangers for power generations.1 ADSC alloys are often fabricated by in situ internal oxidation. During fabrication, a small number of solute Al atoms are first pre-alloyed with solvent Cu atoms. The mixture is heat-treated, either by using Cu2O powder as an internal oxidizer or by directly heating in an oxygen-rich gaseous atmosphere, followed by densification in vacuum. During the process, Al atoms are preferentially oxidized in situ, forming ultra-fine Al2O3 dispersoids with a uniform distribution inside the Cu matrix. Performance and reliability of such alloys are largely determined by the oxide interfaces as well as grain boundaries. Both interfaces can be significantly affected by trace amount of impurities and alloying elements.It is known from the literature that S segregation not only significantly degrades the grain boundary adhesion in Ni,2–4 but also provokes the spallation of the protective alumina scales from Ni and Fe substrates.5–8 The so-called “sulfur effect” has long been of both fundamental and technological interest to the materials research society.7–12 Our previous studies have suggested13,14 that S also strongly segregates to Cu/α-Al2O3 interface, degrading the adhesion and further reducing the size stability of Al2O3 dispersoids in Cu. To improve the performance and reliability of ADSC alloys, it is natural to consider the alloy design strategy, i.e. designing appropriate alloying elements to directly enhance the oxide interface binding, and/or to prevent S segregation to the interfaces.10–12,15,16 Ag, with the same superior electrical/thermal conductance as Cu, can be considered as a good candidate for such alloying elements. However, there was only one single report that alloying with Ag increases the macroscopic hardness of ADSC alloys.17 This, as a hypothesis, has been ascribed to Ag segregation to internal oxide interfaces (Cu/Al2O3) which presumably enhanced the interface adhesion. Direct evidence from microscopic characterizations still lacked, leaving this hypothesis with many uncertainties. Meanwhile, a recent experimental characterization on a Cu bicrystal with only the well-defined Σ5(310) grain boundary (GB)18,19 suggested that Ag has a noticeably strong segregation tendency to this GB, as compared to many other high-angle GBs in polycrystalline Cu. Thus, there appears to be a competition between GB segregation and oxide-interface segregation (if possible) for Ag in Cu. In other words, in the case of strong GB segregation, the potential impact of segregation to oxide interfaces would be greatly limited, and vice versa.
First principles calculations provide a useful tool to test all aspects of interface segregation at an electronic–atomic scale. One successful example is on the thermally-grown coating interface of Ni/α-Al2O3.11–13,15,16,20–23 Encouraged by these efforts, we apply the similar first-principles strategy to evaluate the potential impact of Ag segregation on the oxide interface of Cu/α-Al2O3, and Cu grain boundaries as well. In this work, we first constructed a series of oxide interfaces with different interfacial stoichiometries and coordinations, along with a series of low-Σ symmetric tilted grain boundaries (STGBs) using the structural-unit (SU) model. The following calculations and analyses were further performed. (1) The heats of segregation (ΔGseg) for Ag and S from inner Cu matrix to the most relevant interfaces, and correspondingly, the most possible segregation paths. (2) The work of separation (Wsep), as a measurement of adhesion strength, for both the clean and S/Ag-contaminated interfaces.
2. Computational methods
To construct a heterogeneous metal/oxide interface model, we choose the Cu(111) and the α-Al2O3(0001) surfaces, each with the lowest surface energy in its bulk, to yield an interface orientation of Cu(111) (√3 × √3)/α-Al2O3(0001) (1 × 1). This orientation was employed for it has the lowest strains to commensuration: the Cu(111) lattice was stretched and the Al2O3(0001) was compressed by the same amount, only 3.8%. It is also consistent with the high resolution transmission electron microscopy (HRTEM) observations for Cu/α-Al2O3.24 Stacking such an Al2O3 and two Cu blocks together with a sufficient vacuum thickness, one obtains a Cu/Al2O3/Cu sandwich hexagonal supercell, with a = 4.62 Å and c = 51.08 Å, that can be regarded as a more appropriate atomistic model of the Cu(111)/α-Al2O3(0001) interface. Nevertheless, TEM and HRTEM cannot provide all detailed information that is needed for an atomistic modeling of the interface. Ascertaining interfacial stoichiometry and atomic coordination must be resorted to energetic calculations. Upon the local chemical activity of Al or O, the interface structure can be stoichiometric, Al-rich, or O-rich. Under each stoichiometry, interfacial Cu atoms may sit at Al-top, O-top, or hollow sites of Al2O3. Among different stoichiometry or coordination types, the associated formation energy and adhesion strength could vary by several folds.12 In our previous studies,13,14 we have evaluated the thermodynamic equilibrium interface structures and energies of Cu/α-Al2O3 as a function of both aAl and pO2. The results have been used to construct the interface phase diagram. According to the phase diagram, at T = 1000 K, the equilibrium interface structure of practical interest still resides in the Al-rich phase regime, but is near the transition between the Al-rich and the stoichiometric phases, especially when considering the prediction uncertainty of Al activity. Therefore, it is practically possible for both types of interfaces to coexist. All the ensuing interface calculations were hence carried out for both the Al-rich and the stoichiometric phases.The GB structure models are rather diverse, being mostly the coincident-site-lattice (CSL) model25 and the structural-unit (SU) model.26,27 The CSL model is constructed by rotating one grain lattice against the other about a rotation axis by a certain angle, so as to achieve a number of coincident lattice sites. The degree of fit (Σ) of a GB is measured as the reciprocal of the ratio of coincidence sites to the total number of sites. A lower Σ boundary corresponds to a higher density of coincident sites, and thus generally a more stable GB structure. While in the SU model, a GB is constructed using a serial of “favored” structural units (SUs). Each SU typically has a low Σ value, and thus can be seen as a favored symmetric tilt grain boundary (STGB). In this sense, a GB with a long period can be treated as a combination of SUs comprising one or several neighboring favored boundaries with shorter periods.28 In our previous work,23,29 the SU model has been suggested to be more appropriate for describing low-Σ GBs of Fe and Cu, and thus was employed in the ensuing calculations of GBs in this work. All SU-modeled GBs were calculated using “sandwich” supercells with periodic boundary conditions. Each supercell hosts two identical GB interfaces which are separated by a sufficient thickness of one grain lattice to preclude any possible spatial interaction. This sandwich model avoids the necessity of vacuum and two extra free surfaces, enabling a good balance between computational efficiency and accuracy (as long as a full relaxation can be carefully performed both on supercell shape and volume).
All the ensuing structural relaxation and energetic calculations were performed using the density functional theory (DFT) code-VASP (Vienna Ab initio Simulation Package, version 5.3)30,31 with plane-wave basis sets. The electron–core interaction was described by the Blöchl projector augmented wave method (PAW) within the frozen-core approximation32 as implemented in VASP. The plane-wave basis sets were generated with valence configurations of Cu-3p63d104p1, Al-3s23p1, and O-2s22p4. The validation of the exchange–correlation (XC) functional was performed by fitting the energy–volume data of crystalline Cu and Al2O3 to the universal equation of state33 and comparing the predicted bulk properties with experiments.34,35 The PAW-PW91 functional was finally chose for all subsequent calculations, for it yielded the best predictions for bulk Cu and Al2O3.13 The interface calculations were performed using a Cu/Al2O3/Cu sandwich configuration with a vacuum thickness of at least 12 Å and a 3 × 3 × 1 M–P k-mesh. In the sandwich model, each Cu block consists of seven atomic layers (with a total of twenty-one Cu atoms), and the alumina consists of four O-layers and eight Al-layers (with a total of twelve O and eight Al atoms for the stoichiometric case). All ground-state configurations were optimized using a high energy cutoff of 550 eV for the plane-wave basis set, until the total energy was a minimum and the total force on each ion converged to within 0.02 eV Å−1.
3. Results and discussion
3.1. Interface segregation and adhesion
In our previous studies,13,14 we have shown the strong dependence of interface energy on interface structure, both of which are dictated by local thermodynamic conditions (T and aAl). For a given interface structure, we further computed and compared the heat of segregation ΔGseg of Ag from inside the (unstrained) matrix to various interfacial sites.The heat of segregation (ΔGseg) is defined as the energy difference associated with a solute atom segregating from the ground-state, unstrained bulk Cu to a possible interstitial or substitutional sites in the interface. For Ag segregation,
| ΔGseg = Gintf + GAgCu − (GAgintf + GCu), | (1) |
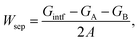 | (2) |
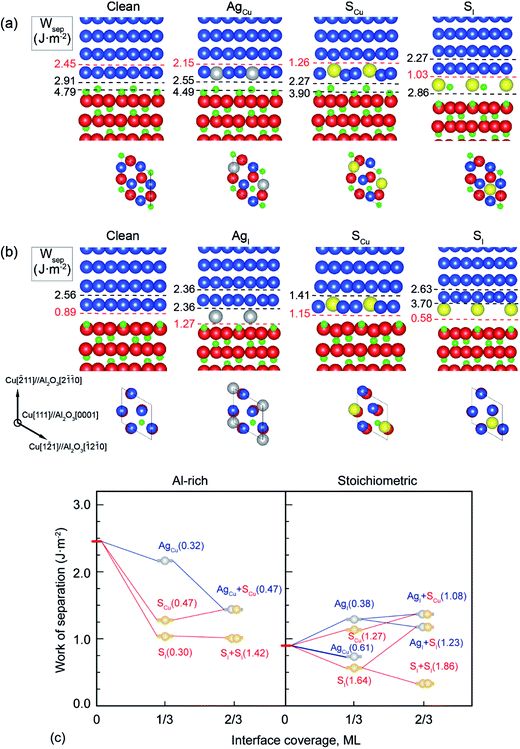
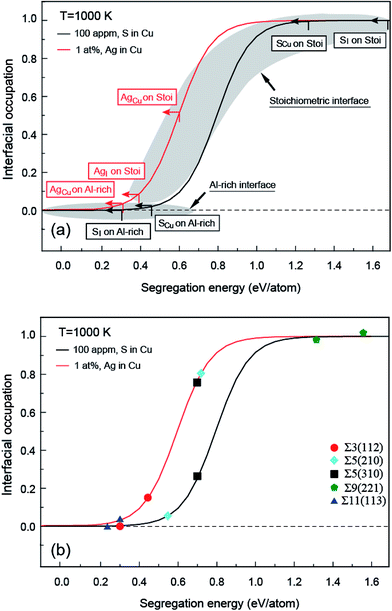
It is shown in Fig. 1a and b that the clean Al-rich interface has a significantly higher adhesion strength (2.45 J m−2), about three times that of the stoichiometric counterpart (0.89 J m−2). Segregated elements strongly affect the interface adhesion. Fig. 1c reveals the segregation trends and sites of Ag and S, as well as their impacts on adhesion. Please note that values in parentheses represent the heats of segregation associated with each segregation step (in units of eV per atom). It is clear that segregated Ag and S have a site competition at both interfaces. For the strong Al-rich interface, the segregation of Ag and S are rather weak and closely comparable. Ag only segregates to Cu substitutional (AgCu) sites with ΔGseg = 0.32 eV per atom. When impurity S presents, it can segregate to interstitial (SI) and Cu substitutional (SCu) sites, lowering the energy of the system by ΔGseg = 0.30 and 0.47 eV per atom, respectively. Co-segregation of Ag and S can hardly occur due to the low energy driving force, 0 or 0.15 eV per atom when refers to single SCu or AgCu. For the weak stoichiometric interface, Ag segregates to interfacial interstitial (AgI) and Cu substitutional (AgCu) sites, with ΔGseg = 0.38 and 0.61 eV per atom, respectively. These heat of segregation values are way below those of S, i.e. ΔGseg = 1.64 eV per atom for interstitial (SI) and 1.27 eV per atom for Cu substitutional (SCu) sites. Similarly as seen for the Al-rich interface, co-segregation of Ag with S can hardly occur, due to the strong segregation of single S.
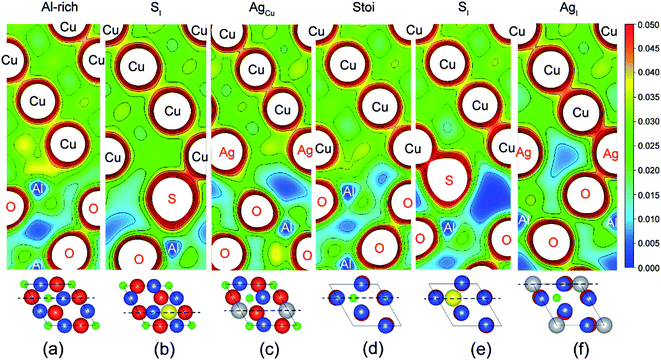
Fig. 2 provides electron density contours for these interfaces. The Al-rich interface results are found in Fig. 2a–c, while the stoichiometric interface results are in Fig. 2d–f. For the strong Al-rich interface, Fig. 2a reveals strong metallic character in the bonding between Cu and the extra Al on the Al-rich Al2O3 surface, corresponding to a high Wsep of 2.45 J m−2. Good electrical conductance can be also expected at this interface. Segregated S and Ag both reduce the interfacial electron density. Fig. 2b reveals a directed partially-ionic, partially-covalent bond between Cu and S atoms across the Al-rich interface, which significantly decreases Wsep from 2.45 J m−2 down to 1.03 J m−2. Fig. 2c reveals a slightly weaker metallic bonding between the substitutional Ag and Cu than that between Cu and Cu. Correspondingly, the adhesion is slightly reduced by ∼12%, down to 2.15 J m−2. For the weak stoichiometric interface, S segregation to interstitial sites is strong and decreases Wsep from 0.89 to 0.58 J m−2 (Fig. 2e). This happens because the interfacial covalent–ionic Cu–O bonds (Fig. 2d) tend to be replaced with much weaker ionic S–Al bonds (Fig. 2e). Compared to Al-rich interface, there are certain benefits of Ag on the stoichiometric. When at an interstitial site (AgI), the valence electron density between the Ag and the surface O in Fig. 2f is obviously higher than that between the Cu and the O in Fig. 2d, knitting Cu and α-Al2O3 together and increasing Wsep by ∼40%, up to 1.27 J m−2.
When co-segregation of Ag and S occurs, Wsep may further decrease to 1.29 J m−2 (AgCu + SCu) on the Al-rich interface and to 1.21 J m−2 (AgI + SI) on the stoichiometric interface (Fig. 1c), making the two interfaces are comparable in adhesion. Nevertheless, the lowest value is still above that for a clean stoichiometric interface (0.89 J m−2) and well in excess of that with 2/3 monolayer (ML) of S (0.32 J m−2). Evidently, when any unpinned S reach the interface, Ag counteracts the deleterious effects of S at the interface and hence the seriously reduced Wsep by a higher coverage of S can be modestly negated.
3.2. GB segregations
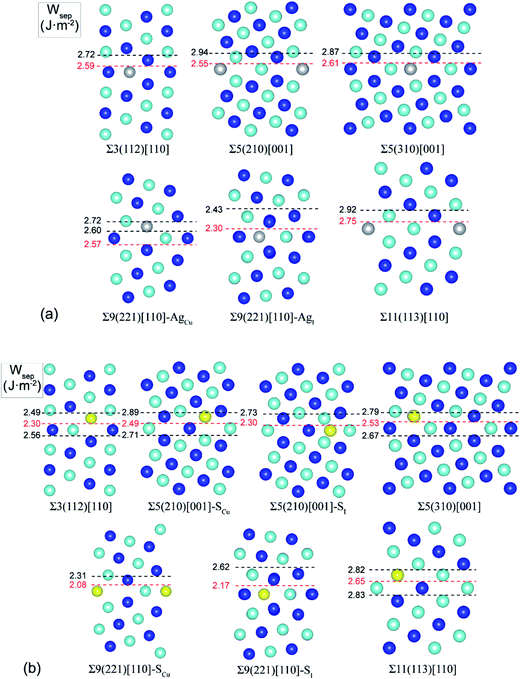
Extensive calculations were further performed to evaluate Ag and S segregation to various interfacial sites, including both substitutional and interstitial sites, of a group of low-Σ STGBs (Σ ≤ 11) within the 〈100〉 and 〈110〉 tilt systems. Fig. 3 plots the most energy-favored structures of those GBs after segregation. The resulting works of separation are labeled on the side. The corresponding segregation energies are compared in Table 1.| Grain boundary | θ (deg) | N | Wsep (J m−2) | Ag segregation | S segregation | ||
|---|---|---|---|---|---|---|---|
| ΔGseg (eV per atom) | Wsep (J m−2) | ΔGseg (eV per atom) | Wsep (J m−2) | ||||
| Σ3(111)[110] | 190.47 | 96 | 2.53 | −0.04 | — | −0.03 | — |
| Σ3(112)[110] | 70.53 | 102 | 2.71 | 0.30 | 2.59 | 0.44 | 2.30 |
| Σ5(210)[100] | 53.13 | 160 | 2.67 | 0.54 | 2.55 | 0.73(SCu), 0.41(SI) | 2.49, 2.30 |
| Σ5(310)[100] | 36.87 | 152 | 2.66 | 0.69 | 2.61 | 0.68 | 2.53 |
| Σ9(221)[110] | 141.06 | 102 | 2.39 | 1.12(AgCu), 0.54(AgI) | 2.57, 2.30 | 0.44(SCu), 1.57(SI) | 2.08, 2.17 |
| Σ11(113)[110] | 50.48 | 132 | 2.86 | 0.23 | 2.75 | 0.30 | 2.65 |
It is seen that, except for the Σ9(221) GB, Ag segregation is generally weak and has undesired effects on GB adhesion. For the Σ3(112), Σ5(210), Σ5(310), or Σ11(113), Ag only weakly segregates to Cu substitutional (AgCu) sites on the GB interface layer (with ΔGseg = 0.23–0.69 eV per atom), slightly reducing Wsep by 2–5% only. While for the Σ9(221) GB, Ag can strongly segregate to Cu substitutional (AgCu) sites on the first sub-interface layer (ΔGseg = 1.12 eV per atom) and increase Wsep from 2.39 to 2.57 J m−2. Meantime, Ag may also weakly segregate to interfacial interstitial (AgI) sites (ΔGseg = 0.54 eV per atom) and slightly decrease Wsep to 2.30 J m−2.
S segregation always reduces GB adhesion. S weakly segregates to Cu substitutional (SCu) sites in the first sub-interface layers of Σ3(112), Σ5(310), and Σ11(113), with ΔGseg = 0.3–0.7 eV per atom. Besides SCu sites, S may also segregate to interfacial interstitial (SI) at the Σ5(210) and Σ9(221), and in particular, S segregation to the Σ9(221) is fairly strong, with ΔGseg = 1.57 eV per atom.
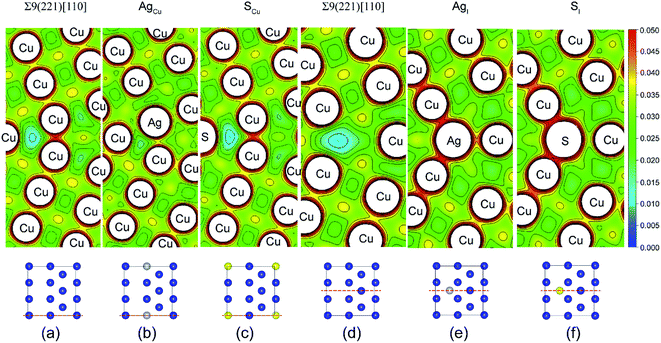
Fig. 4 shows the calculated valence charge density distributions for the clean and segregated Σ9(221) GBs. The charge density distributions in the (0–10) plane of Σ9(221) GB are found in Fig. 4a–c, while the (010) plane results are in Fig. 4d–f. As seen from the (0–10) plane contour of the GB, the strong segregation of Ag to a Cu substitutional (AgCu) site (ΔGseg = 1.12 eV per atom) increases the interfacial charge density in Fig. 4b. This is consistent with an increase of Wsep from the initial value of 2.39 to 2.57 J m−2 (Table 1 and Fig. 3a). In contrast, the weak segregation of S to a Cu substitutional (SCu) site (ΔGseg = 0.44 eV per atom) induces almost no changes in the interfacial charge density in Fig. 4c, but an obvious reduction of ∼13% in Wsep (from 2.39 to 2.08 J m−2). Similarly, the segregated Ag or S at the interstitial sites corresponds to a high interfacial charge density (Fig. 4e and f), as compared to the clean interface, and Wsep is also reduced slightly to 2.30 (AgI) and 2.17 J m−2 (SI). The reduction in Wsep for SCu, SI, and AgI, shall refer to the even stronger adsorption of S or Ag on Cu surface after interface separation (Fig. 5).
Given a temperature, the interfacial occupancy of a segregant not only depends on segregation energy, but also on the initial bulk concentration. Ag, as an alloying element, far outnumbers impurity S in the matrix, normally by ∼2 orders of magnitude. Based on McLean's equation,36 the interfacial occupation of Ag and S under the thermodynamic equilibrium can be estimated by
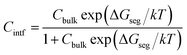 | (3) |
To assess the potential of Ag pinning S, we further evaluated the pair affinity of Ag–S in Cu as
| ΔGg(Ag–S) = (Gperf + GAg–S) − (GAg + GS), | (4) |
Based on the knowledge gained in this work, a joint design strategy can be suggested for achieving high quality ADSC alloys: (1) alloying with Ag, for its segregation can directly enhance the weak stoichiometric oxide interfaces, and has only minimal influence on the strong Al-rich oxide interfaces and most GBs (except to enhance the Σ9) (2) introducing certain desulfurization processes during fabrication, such as hydrogen-based annealing, to substantially reduce S content in Cu matrix, for Ag cannot pin S effectively in Cu, and (3) alloying with other reactive elements, to effectively bind S in the matrix. In one our earlier study, rare-earth elements Ce, Y, and Hf have been predicted effective in pinning S in Ni alloys.16 Their effectiveness in Cu alloys awaits our further studies.
4. Conclusions
The structure and adhesion of the Cu/α-Al2O3 interfaces in Cu and Cu grain boundaries, along with the potential impact of alloying with Ag, have been thoroughly studied using DFT calculations. The Al-rich Cu/α-Al2O3 interface has a significantly lager Wsep than its stoichiometric counterpart. Segregation of S to the interfaces degrades adhesion by up to 64%. Ag itself segregates to the interfaces, can slightly weaken the strong Al-rich interface, but greatly enhance the weak stoichiometric interface. Ag cannot pin S in Cu matrix, thus cannot prevent S segregation to the interfaces. Co-segregation of Ag with S at both interfaces only modestly negates the detrimental influence of any S that reaches the interfaces, but can still hardly occur. As for the GBs, Ag has a weak segregation tendency to most GBs and reduces the adhesion slightly. The only one exception is on the Σ9 GB. Ag can strongly segregate to the Σ9(221) GB and directly enhance the adhesion. Based on the gained insights, we proposed that Ag alloying has limited benefits but can be still encouraged, especially when the impurity S in Cu can be effectively eliminated.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This paper is based upon work supported by the National Science Foundation of China (No. 51471189, 51474244, 51601225), and partially by the Shenzhen Science and Technology Project (JCYJ20140509142357196) and the National Basic Research Program of China (sub-contract No. 2014CB644001-2). The computational resource at the High Performance Computing Center of Central South University is also gratefully acknowledged.References
- V. Rajkovic, D. Bozic and M. T. Jovanovic, Properties of copper matrix reinforced with nano-and micro-sized Al2O3 particles, J. Alloys Compd., 2008, 459(1), 177–184 CrossRef CAS.
- M. Yamaguchi, M. Shiga and H. Kaburaki, Grain boundary decohesion by impurity segregation in a nickel-sulfur system, Science, 2005, 307(5708), 393–397 CrossRef CAS PubMed.
- J. K. Heuer, P. R. Okamoto, N. Q. Lam and J. F. Stubbins, Disorder-induced melting in nickel: implication to intergranular sulfur embrittlement, J. Nucl. Mater., 2002, 301(2), 129–141 CrossRef CAS.
- J. R. Rice and J. S. Wang, Embrittlement of interfaces by solute segregation, Mater. Sci. Eng., A, 1989, 107, 23–40 CrossRef.
- D. R. Sigler, The influence of sulfur on adherence of Al2O3 grown on Fe-Cr-Al alloys, Oxid. Met., 1988, 29(1–2), 23–43 CrossRef CAS.
- J. G. Smeggil, A. W. Funkenbusch and N. S. Bornstein, A relationship between indigenous impurity elements and protective oxide scale adherence characteristics, Metall. Trans. A, 1986, 17(6), 923–932 CrossRef.
- A. W. Funkenbusch, J. G. Smeggil and N. S. Bornstein, Reactive element-sulfur interaction and oxide scale adherence, Metall. Trans. A, 1985, 16(6), 1164–1166 CrossRef.
- P. Y. Hou, Segregation phenomena at thermally grown Al2O3/alloy interfaces, Annu. Rev. Mater. Res., 2008, 38, 275–298 CrossRef CAS.
- D. G. Lees, On the reasons for the effects of dispersions of stable oxides and additions of reactive elements on the adhesion and growth-mechanisms of chromia and alumina scales-the “sulfur effect”, Oxid. Met., 1987, 27(1–2), 75–81 CrossRef CAS.
- Y. Jiang and R. Liu, Gettering of S in Ni from first principles, Scr. Mater., 2010, 62(10), 782–785 CrossRef CAS.
- Y. Jiang, J. R. Smith and A. G. Evans, First principles assessment of metal/oxide interface adhesion, Appl. Phys. Lett., 2008, 92(14), 141918 CrossRef.
- J. R. Smith, Y. Jiang and A. G. Evans, Adhesion of the γ-Ni(Al)/α-Al2O3 interface: a first-principles assessment, Int. J. Mater. Res., 2007, 98(12), 1214–1221 CrossRef CAS.
- G. Lan, Y. Jiang, D. Yi and S. Liu, Theoretical prediction of impurity effects on the internally oxidized metal/oxide interface: the case study of S on Cu/Al2O3, Phys. Chem. Chem. Phys., 2012, 14(31), 11178–11184 RSC.
- G. Lan, Y. Jiang, D. Yi and S. Liu, Theoretical prediction of microstructure evolution during the internal oxidation fabrication of metal-oxide composites: the case of Cu–Al2O3, RSC Adv., 2013, 3(36), 16136–16143 RSC.
- Y. Jiang and J. R. Smith, Pt effects in γ-Ni(Al)/α-Al2O3 adhesion, J. Mater. Sci., 2009, 44(7), 1734–1740 CrossRef CAS.
- G. Lan, Y. Wang, Y. Jiang, H. Zhou and D. Yi, Effects of rare-earth dopants on the thermally grown Al2O3/Ni(Al) interface: the first-principles prediction, J. Mater. Sci., 2014, 49, 2640–2646 CrossRef CAS.
- Y. Xiao, S. Liu, J. Wu and X. Qu, Effect of trace alloying elements addition on microstructure and hardness of alumina dispersion strengthened copper alloys, Fenmo Yejin Jishu, 2012, 30(4), 260–265 Search PubMed.
- S. V. Divinski, H. Edelhoff and S. Prokofjev, Diffusion and segregation of silver in copper Σ5(310) grain boundary, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(14), 144104 CrossRef.
- T. Frolov, S. V. Divinski, M. Asta and Y. Mishin, Effect of interface phase transformations on diffusion and segregation in high-angle grain boundaries, Phys. Rev. Lett., 2013, 110(25), 255502 CrossRef CAS PubMed.
- K. M. Carling and E. A. Carter, Effects of segregating elements on the adhesive strength and structure of the α-Al2O3/β-NiAl interface, Acta Mater., 2007, 55(8), 2791–2803 CrossRef CAS.
- W. Zhang, J. R. Smith and A. G. Evans, The connection between ab initio calculations and interface adhesion measurements on metal/oxide systems: Ni/Al2O3 and Cu/Al2O3, Acta Mater., 2002, 50(15), 3803–3816 CrossRef CAS.
- W. Zhang, J. R. Smith, X. G. Wang and A. G. Evans, Influence of sulfur on the adhesion of the nickel/alumina interface, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(24), 245414 CrossRef.
- J. Xu, J. Liu, S. Li, B. Liu and Y. Jiang, Self-healing properties of nanocrystalline materials: a first-principles analysis of the role of grain boundaries, Phys. Chem. Chem. Phys., 2016, 18, 17930–17940 RSC.
- G. Dehm, M. Rühle, G. Ding and R. Raj, Growth and structure of copper thin films deposited on (0001) sapphire by molecular beam epitaxy, Philos. Mag. B, 1995, 71(6), 1111–1124 CrossRef CAS.
- M. L. Kronberg and F. H. Wilson, Secondary recrystallization in copper, Trans. Metall. Soc. AIME, 1949, 185, 501–514 Search PubMed.
- G. H. Bishop and B. Chalmers, A coincidence—Ledge—Dislocation description of grain boundaries, Scr. Metall., 1968, 2(2), 133–139 CrossRef.
- G. H. Bishop and B. Chalmers, Dislocation structure and contrast in high angle grain boundaries, Philos. Mag., 1971, 24(189), 515–526 CrossRef CAS.
- M. A. Tschopp, K. N. Solanki, F. Gao, X. Sun, M. A. Khaleel and M. F. Horstemeyer, Probing grain boundary sink strength at the nanoscale: Energetics and length scales of vacancy and interstitial absorption by grain boundaries in α-Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(6), 064108 CrossRef.
- J. Xu, Y. Jiang, L. Yang and J. Li, Assessment of the CSL and SU models for bcc-Fe grain boundaries from first principles, Comput. Mater. Sci., 2016, 122, 22–29 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented- wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758 CrossRef CAS.
- P. Vinet, J. H. Rose, J. Ferrante and J. R. Smith, Universal features of the equation of state of solids, J. Phys.: Condens. Matter, 1989, 1(11), 1941 CrossRef CAS.
- H. M. Otte, Lattice Parameter Determinations with an X-Ray Spectrogoniometer by the Debye-Scherrer Method and the Effect of Specimen Condition, J. Appl. Phys., 1961, 32(8), 1536–1546 CrossRef CAS.
- L. W. Finger and R. M. Hazen, Crystal structure and compression of ruby to 46 kbar, J. Appl. Phys., 1978, 49(12), 5823–5826 CrossRef CAS.
- D. McLean, Grain Boundaries in Metals, Oxford University Press, London, 1957, p. 116 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |