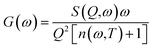DOI:
10.1039/C7RA09049H
(Paper)
RSC Adv., 2017,
7, 47801-47805
Higher-order glass-transition singularities in nano-confined states†
Received
16th August 2017
, Accepted 15th September 2017
First published on 11th October 2017
Abstract
The dynamic processes of 2-biphenylmethanol (BPM) confined in carbon and silica pores with different sizes have been studied using the quasi-elastic neutron scattering (QENS) technique. A β-relaxation process following a logarithmic decay was found in both the nano-confined states. The peculiar features of the observed dynamic processes strongly agree with the predictions of the mode-coupling theory (MCT) for higher-order glass-transition singularities. The MCT critical temperature (Tc) of BPM, when confined in carbon and silica pores, was evaluated. The Tc was significantly low in the nano-confined states as compared to the bulk states. Furthermore, when comparing BPM confined in similar pore-sized carbon and silica materials, it was observed that the Tc was much lower for BPM confined in nano-porous silica materials. The generalized vibrational density-of-states of confined BPM indicated that the interactions of BPM with the silica pores is hydrophobic, whereas the interactions with the carbon surfaces is more hydrophilic. The different lowering of Tc for BPM depending on whether it is confined in carbon or silica materials is due to the different nature of the interactions between BPM and the confining surfaces of silica and carbon.
Introduction
Understanding the behaviour of fluids in nano-confined states is of great importance in many scientific and technological fields. For instance, about 50–65% of the human body consists of water. However, water within the human body does not exist in its bulk form; instead, it is confined in crowded environments. Furthermore, interfacial water molecules control mineral dissolution, which is very important in earth science. Furthermore, water diffusion along the nanoscopic channels of polymer electrolyte membranes is central to the operation of hydrogen fuel cells. It is well-known that the properties of fluids confined in nano-scale dimensions differ from their corresponding bulk states.1–4 For example, water crystallizes at 273 K in its bulk state. However, water confined in carbon nanotubes with a pore diameter of about 20 Å or less could be supercooled down to 190 K and upon further cooling, water transforms to an amorphous solid state.5,6 This is due to the fact that the reduced dimensionality leads to enhanced surface effects.7 In general, liquids confined in nano-pores can be supercooled well below their melting point, and the degree of supercooling has been found to be higher in hydrophobic pores than in hydrophilic pores.8 This phenomenon allows us to study the properties of supercooled liquids, particularly the molecular relaxation processes occurring in supercooled glass-forming liquids.9 The molecular relaxation processes occurring in bulk glass-forming liquids have been extensively investigated in the recent years.10 In viscous glass-forming liquids, the molecules undergo two types of relaxation processes: (i) the fast β-relaxation, in which the molecules rattle inside a cage formed by neighbouring molecules and (ii) the slow α-relaxation, which consists of a long-range diffusion process.11 In most liquids, the fast β-relaxation process follows a simple exponential decay.12 However, recently, a logarithmic decay has been observed for the fast β-relaxation in 2-biphenylmethanol (BPM), phenyl salicylate (salol), ortho-terphenyl (OTP) and benzophenone (BZP) in their supercooled states by Optical-Kerr-Effect (OKE) experiments,13–15 and in RNA and proteins by quasi-elastic neutron scattering (QENS).16,17 However, the origin of such a complex relaxation process is not yet fully understood. Herein, we report the study by QENS of the effect of nano-scale confinement on a relaxation process characterized by a logarithmic decay.
Experimental methods
BPM (C13H12O, Tm = 320 K, Tg ∼239 K) was obtained from Sigma-Aldrich. The materials used for confinement of BPM were nano-porous carbon with pore sizes of 39 ± 1 Å and 56 ± 1 Å, and nano-porous silica gel with pore sizes of 40 ± 1 Å and 60 ± 1 Å, which were purchased from ACS materials and Sigma-Aldrich, respectively. The Raman, FTIR and X-ray photoelectron spectra showed that there was no hydroxyl, carboxyl or silanol groups on the carbon or silica pore surfaces.18 BPM was loaded onto the nano-porous carbon and silica materials via incipient wetness impregnation method, and the materials were 100% filled with BPM. The amount of BPM needed to completely fill the pores of 1 g of nanoporous carbon or silica powder was calculated, and this amount was dissolved in deuterated acetone (D-acetone). The carbon or silica powder was completely immersed in this liquid mixture and the system was kept open until D-acetone had evaporated. Subsequently, the BPM-loaded powder was heated at 80 °C overnight in a vacuum oven to completely evaporate residual D-acetone from the pores, leaving only BPM.
The QENS experiments were performed using a FOCUS time-of-flight neutron scattering spectrometer at the Paul Scherrer Institute, Switzerland.19 We chose a neutron wavelength of 5.75 Å, which afforded an energy resolution of ∼53 μeV (full-width at half-maximum). The accessible Q range at this wavelength was 0.4 Å−1 to 1.8 Å−1, and this experimental set-up covered the dynamical time window from 0.1 ps to ∼15 ps. The QENS data were collected at 4 different temperatures: 300 K, 320 K, 340 K and 360 K. Since the incoherent neutron cross-section of hydrogen is the highest (80.26 barn), and the BPM molecule contains 12 hydrogen atoms, the scattering signals were mainly due to incoherent scattering processes. In addition, the samples were measured at 35 K in order to determine the instrumental resolution function. Empty sample containers were also measured at each temperature, and the scattering signal from a vanadium sample with a similar geometry to that of the test samples was applied to normalize the BPM scattering signals. The obtained raw data were converted into equidistant energy and momentum transfer steps using the Data Analysis and Visualization Environment (DAVE) software package.20
The QENS experiments for bulk BPM were performed using a MARS high-resolution indirect time-of-flight backscattering spectrometer (∼13 μeV) at SINQ, Switzerland.19 The scattered neutrons were filtered by a mica analyzer using the (0 0 6) reflection at a neutron wavelength of 6.61 Å. The accessible Q range was 0.4 Å−1 to 1.7 Å−1. The QENS data were collected at 5 different temperatures: 303 K, 313 K, 323 K, 333 K and 343 K. The bulk BPM sample was also measured at 10 K in order to determine the instrumental resolution function.
Results and discussion
The measured QENS intensity data were corrected for detector efficiency by normalizing it with the Vanadium data and subtracting the scattering contribution of empty sample containers and confining materials to obtain the incoherent dynamic structure factor, S(Q,ω) (Fig. 1). S(Q,ω) provides information on the dynamic processes within the sample and indicates the energy changes that occur during the scattering process as a function of momentum transfer.21 The generalized vibrational density-of-states, G(ω), of the confined BPM molecules were then calculated from the dynamic structure factor, S(Q,ω), measured at 35 K using the standard equation:| |
 | (1) |
where n(ω,T) is the Bose population factor. The resultant generalized vibrational density-of-states for the BPM molecules confined in carbon pores (39 ± 1 Å) and silica pores (40 ± 1 Å), shown in Fig. 2, were normalized with the weighted macroscopic scattering neutron cross-section of BPM on the neutron beam. The peak at around 5 meV is associated with translational vibrational motions (boson peak). This peak is more pronounced for BPM confined in 40 ± 1 Å silica pores as compared to that obtained for BPM confined in 39 ± 1 Å carbon pores. This indicates that the interaction of BPM with silica is more hydrophobic than the interaction of BPM with carbon. The self-intermediate scattering function, Φ(Q,t), was determined by Fourier transform of S(Q,ω) and convoluted with a resolution function. In a semi-logarithmic representation, the Φ(Q,t) decays linearly with time (Fig. 3). This is a clear indication that the relaxation process occurring in this time domain follows a logarithmic decay. The bulk BPM was found to exhibit a logarithmic decay relaxation process,15 as shown in the ESI (Fig. 1S†). Our experiments showed that the logarithmic decay relaxation process persisted in the nano-confined states. This indicated that the complex β-relaxation process was not influenced by confinement in nano-scale dimensions with different surface interactions.
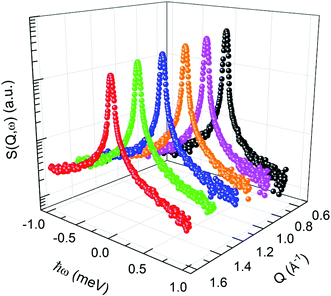 |
| | Fig. 1 Dynamic structure factor of BPM confined in silica pores (60 ± 1 Å) at 360 K in a semi-logarithmic representation. | |
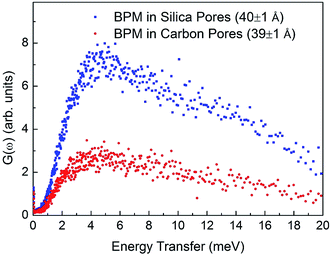 |
| | Fig. 2 Generalized vibrational density-of-states of BPM confined in carbon pores (39 ± 1 Å) and silica pores (40 ± 1 Å) measured at 35 K. | |
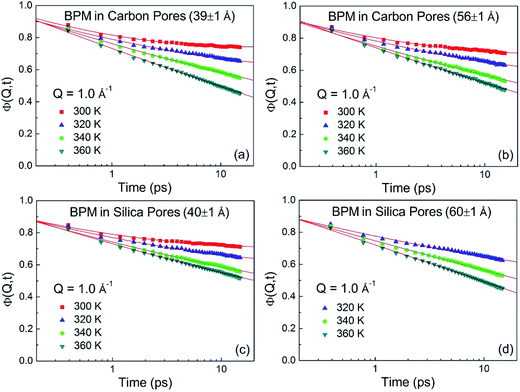 |
| | Fig. 3 Self-intermediate scattering functions of BPM confined in carbon pores (39 ± 1 Å) (a), carbon pores (56 ± 1 Å) (b), silica pores (40 ± 1 Å) (c) and silica pores (60 ± 1 Å) (d) at different temperatures. The error bars are within the symbols. The solid lines are fitting with eqn (2). | |
According to the mode-coupling theory (MCT), dynamic arrest occurs at a temperature well above the calorimetric glass-transition temperature, Tg. At the temperature where dynamic arrest occurs, also called the dynamic singularity point, the transport mechanism changes from molecular motions such as those in liquids to activated hopping processes such as those occurring in glass.22 The MCT describes different types of singularities in the equations of motion for the density correlation functions. The equations can be classified as Al, where l = 2, 3,… and l = 2 is the simplest singularity. It has been shown that in some systems with inter-particle potentials having hard-core repulsive and short-range square-well attractive components, dynamic arrest may occur via a different mechanism associated with higher order singularities such as A3 or A4. In these systems, the density correlation function for the fast β-relaxation process exhibits a logarithmic time dependence, and the following asymptotic formula derived from the MCT can be used for expressing the Φ(Q,t) corresponding to the β-relaxation process:23–26
| | |
Φ(Q,t) ≈ [f(Q,T) − H1(Q,T)ln(t/τβ(T)) + H2(Q,T)ln2(t/τβ(T))]
| (2) |
where
f(
Q,
T) is the Debye–Waller factor,
f(
Q,
T) = exp[−
A(
T)
Q2], and
τβ(
T) is the characteristic β-relaxation time, which is
Q independent.
H1(
Q,
T) and
H2(
Q,
T) represent the first- and second-order logarithmic decay parameters, respectively. The fitting-parameters,
f(
Q,
T),
H1(
Q,
T),
H2(
Q,
T) and
τβ(
T), were obtained by fitting the curves in the measured time range. The
Q dependence of
H1(
Q,
T) parameter is shown in
Fig. 4. The solid lines are the fitting lines as obtained by
H1(
Q,
T) =
B1(
T)
Q. The fitted
B1(
T) values are plotted as a function of the temperature in
Fig. 5. The
Q and temperature dependence plots of
H2(
Q,
T) and
τβ(
T) are provided in the ESI (Fig. 2S and 3S
†). The plot corresponding to the temperature dependence of
B1(
T) (
Fig. 5) was consistently extrapolated to obtain the MCT critical temperature,
Tc. The
Tc of bulk BPM was determined to be 282 ± 2 K, which is in good agreement with the value obtained in previous studies (290 ± 4 K).
14,15 This
Tc value is approximately 1.2
Tg (
Tg ∼239 K), which is universally observed. The
Tc of confined BPM in nanoscale carbon pores with diameters of 39 ± 1 Å and 56 ± 1 Å was found to be 191 ± 2 K and 185 ± 2 K, respectively. Furthermore, the
Tc of confined BPM in silica nanopores with diameters of 40 ± 1 Å and 60 ± 1 Å was 159 ± 2 K and 174 ± 2 K, respectively (see
Fig. 5). For BPM confined in carbon nanopores,
Tc was not substantially affected by pore size, despite the fact that the difference in pore diameter was nearly 20 Å. In contrast, for BPM confined in silica,
Tc was found to be about 15 K lower in the 40 ± 1 Å pores as compared to that obtained for 60 ± 1 Å pores. Under confinement in a nanoscale environment, the properties of liquid molecules are mostly affected by the finite size of their environment and their interactions with the interfaces or the confining surfaces. The carbon nano-pores provide walls with strongly attractive interactions, while the silica nano-pores provide walls with relatively weak attractive interactions. Herein, the difference in the
Tc values for BPM when confined in silica or carbon nanoporous materials agrees with a universally observed behaviour: liquids can be supercooled to a much lower temperature in hydrophobic environments than in hydrophilic environments.
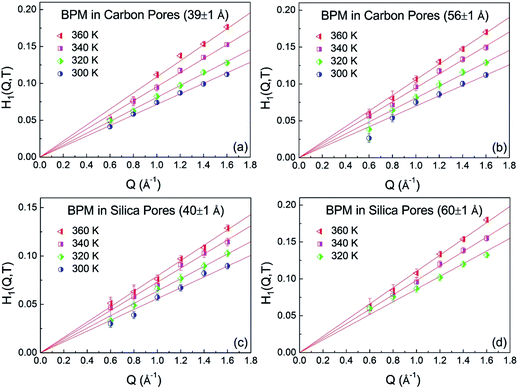 |
| | Fig. 4 Q dependence of fitting parameter H1(Q,T) for BPM confined in carbon pores (39 Å) (a), carbon pores (56 ± 1 Å) (b), silica pores (40 ± 1 Å) (c) and silica pores (60 ± 1 Å) (d) at different temperatures. | |
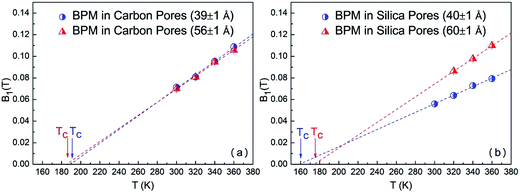 |
| | Fig. 5 Temperature dependence of B1(T) for BPM confined in carbon pores (39 ± 1 Å and 56 ± 1 Å) (a), and silica pores (40 ± 1 Å and 60 ± 1 Å) (b). The linear fitting lines were extrapolated to obtain the mode-coupling critical temperature, Tc. | |
Conclusions
In summary, we have carried out QENS studies on 2-biphenylmethanol confined in carbon and silica nano-pores. A logarithmic decay for β-relaxation was observed in both nano-confined states within the time scale of the QENS data acquisition. The anomalous features of the dynamic processes are consistent with the mode-coupling theory predictions for higher-order glass transition singularities. The critical temperature values obtained from the analysis of the QENS data showed that Tc is significantly lower in the nano-confined states than in the bulk state. However, the decrease in Tc was found to be larger for BPM confined in silica nano-pores as compared to carbon nano-pores. The generalized vibrational density-of-states of confined BPM indicated that the interaction between BPM molecules and silica pores is hydrophobic, whereas the interaction with the carbon surfaces is more hydrophilic. The different nature of the interaction between BPM molecules and pore surfaces of carbon and silica results in a different value for the Tc depending on whether it is confined in carbon or silica.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research has been supported by Science, Technology and Innovation Committee of the Shenzhen Municipality, and the Basic Research Program under project no. JCYJ20140827151540605. All authors thank the Paul Scherrer Institute (Switzerland) for providing beam time on the time-of-flight neutron scattering FOCUS instrument.
References
- P. Huber, J. Phys.: Condens. Matter, 2015, 27, 103102 CrossRef PubMed.
- S.-H. Chen, F. Mallamace, C.-Y. Mou, M. Broccio, C. Corsaro, A. Faraone and L. Liu, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12974–12978 CrossRef CAS PubMed.
- J. C. Saint Remi, A. Lauerer, C. Chmelik, I. Vandendael, H. Terryn, G. V. Baron, J. F. M. Denayer and J. Kärger, Nat. Mater., 2016, 15, 401–406 CrossRef PubMed.
- N. C. Osti, T. N. Etampawala, U. M. Shrestha, D. Aryal, M. Tyagi, S. O. Diallo, E. Mamontov, C. J. Cornelius and D. Perahia, J. Chem. Phys., 2016, 145, 224901 CrossRef CAS PubMed.
- X. Q. Chu, A. I. Kolesnikov, A. P. Moravsky, V. Garcia-Sakai and S. H. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 1–6 CrossRef PubMed.
- S. M. Chathoth, E. Mamontov, A. I. Kolesnikov, Y. Gogotsi and D. J. Wesolowski, EPL, 2011, 95, 56001 CrossRef.
- V. Teboul and C. A. Simionesco, J. Phys.: Condens. Matter, 2002, 14, 5699–5709 CrossRef CAS.
- R. Richert, Annu. Rev. Phys. Chem., 2011, 62, 65–84 CrossRef CAS PubMed.
- C. Alba-Simionesco, B. Coasne, G. Dosseh, G. Dudziak, K. E. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, J. Phys.: Condens. Matter, 2006, 18, R15–R68 CrossRef CAS PubMed.
- C. A. Angell, K. L. Ngai, G. B. McKenna, P. F. McMillan and S. W. Martin, J. Appl. Phys., 2000, 88, 3113 CrossRef CAS.
- S. M. Chathoth, B. Damaschke, M. M. Koza and K. Samwer, Phys. Rev. Lett., 2008, 101, 37801 CrossRef CAS PubMed.
- A. Toelle, Rep. Prog. Phys., 2001, 64, 79 Search PubMed.
- G. Hinze, D. D. Brace, S. D. Gottke and M. D. Fayer, Phys. Rev. Lett., 2000, 84, 4783 CrossRef CAS.
- H. Cang, V. N. Novikov and M. D. Fayer, Phys. Rev. Lett., 2003, 90, 197401 CrossRef PubMed.
- H. Cang, V. N. Novikov and M. D. Fayer, J. Chem. Phys., 2003, 118, 2800–2807 CrossRef CAS.
- X. Chu, M. Lagi, E. Mamontov, E. Fratini, P. Baglioni and S.-H. Chen, Soft Matter, 2010, 6, 2623 RSC.
- X. Chu, E. Mamontov, H. O'Neill and Q. Zhang, J. Phys. Chem. Lett., 2013, 4, 936–942 CrossRef CAS PubMed.
- P. A. Bazuła, A.-H. Lu, J.-J. Nitz and F. Schüth, Microporous Mesoporous Mater., 2008, 108, 266–275 CrossRef.
- P. L. W. Tregenna-Piggott, F. Juranyi and P. Allenspach, Neutron News, 2008, 19, 20–24 CrossRef.
- R. T. Azuah, L. R. Kneller, Y. Qiu, P. L. W. Tregenna-Piggott, C. M. Brown, J. R. D. Copley and R. M. Dimeo, J. Res. Natl. Inst. Stand. Technol., 2009, 114, 341–358 CrossRef CAS PubMed.
- K. S. Singwi and A. Sjölander, Phys. Rev., 1960, 119, 863–871 CrossRef CAS.
- W. Götze and L. Sjögren, Transp. Theory Stat. Phys., 1995, 24, 801–853 CrossRef.
- W. Götze and M. Sperl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 11405 CrossRef PubMed.
- C. Chen, K. Wong, R. A. Mole, D. Yu and S. M. Chathoth, Sci. Rep., 2016, 6, 33374 CrossRef CAS PubMed.
- M. Lagi, P. Baglioni and S.-H. Chen, Phys. Rev. Lett., 2009, 103, 108102 CrossRef PubMed.
- M. Sperl, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 31405 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09049h |
|
| This journal is © The Royal Society of Chemistry 2017 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Kaikin Wonga,
Rithin P. Krishnana,
Jan P. Embs
a,
Kaikin Wonga,
Rithin P. Krishnana,
Jan P. Embs b and
Suresh M. Chathoth
b and
Suresh M. Chathoth *ac
*ac