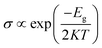Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theoretical insights into the structural, relative stable, electronic, and gas sensing properties of PbnAun (n = 2–12) clusters: a DFT study†
Gaofeng Libc,
Xiumin Chen *abc,
Zhiqiang Zhouabc,
Fei Wangbc,
Hongwei Yangbc,
Jia Yangbc,
Baoqiang Xu
*abc,
Zhiqiang Zhouabc,
Fei Wangbc,
Hongwei Yangbc,
Jia Yangbc,
Baoqiang Xu bc,
Bin Yangbc and
Dachun Liubc
bc,
Bin Yangbc and
Dachun Liubc
aState Key Laboratory of Complex Nonferrous Metal Resources Clear Utilization, Kunming University of Science and Technology, Kunming 650093, PR China. E-mail: chenxiumin9@hotmail.com
bNational Engineering Laboratory for Vacuum Metallurgy, Kunming University of Science and Technology, Kunming 650093, PR China
cYunnan Provincial Key Laboratory for Nonferrous Vacuum Metallurgy, Kunming University of Science and Technology, Kunming 650093, PR China
First published on 25th September 2017
Abstract
Recently, Au-based clusters have been provoking great interest due to their potential applications in nanotechnology. Herein, the structural, relative stable, electronic, and gas sensing properties of PbnAun (n = 2–12) clusters were systematically investigated using density functional theory together with scalar relativistic pseudopotential. The ground state structures, average binding energies, dissociation energies, second order energy differences, HOMO–LUMO gaps, and average Mulliken charges of PbnAun (n = 2–12) clusters were calculated. The results revealing that the PbnAun (n = 4, 6, and 8) clusters are more relatively stable than their neighboring clusters. Furthermore, charges are always transferred from the Pb atoms to Au atoms based on Mulliken charge analysis. Furthermore, through the investigations of CO or NO molecule adsorption onto PbnAun (n = 4, 6, and 8) clusters, it is found that CO or NO molecule can chemisorb on those clusters with high sensitivity, and the charges are transferred from PbnAun (n = 4, 6, and 8) clusters to the gas molecules. According to the analysis of the electric conductivity, PbnAun (n = 4, 6, and 8) clusters can be served as potential gas sensors in CO and NO molecules detection.
1. Introduction
In recent years, clusters have drawn considerable attention from all over the world. The mesoscopic or macroscopic properties of clusters can be investigated at an atomic or molecular level,1–3 which are governed by geometrical structure, cluster size and chemical composition.2,4–7 In particular, Aun clusters and Au-based clusters have been extensively studied using theoretical calculations and experimental investigations since they have been found to serve as potential applications in nanostructured materials,8 electronic devices,9 optical limiting materials,10 sensor technologies,9,11 and nano-catalytic systems,12–15 etc.The investigations of Aun clusters are important to the deep investigations of Au-based clusters, because the fundamental investigations of Aun clusters may provide some valuable guidance for that of Au-based clusters. Overall, pure Aun clusters have been more systematically investigated than Au-based clusters. It is well known that the properties of Aun clusters are very sensitive to both size n and geometrical structure. According to the theoretical calculations,16–22 the ground-state structures of Aun clusters demonstrate a transition from two-dimensional structures to three-dimensional structures due to the strong relativistic effects in Au atoms.23,24 In general, Aun (n = 3–13) clusters favor planar structures, whereas those Aun clusters exhibit three-dimensional structures when the size n is larger than 13. In order to uncover the structural, energetic and electronic properties of Aun (n = 3–14) clusters, Li et al.19 carried out systematical calculations by density functional theory, the results show that those Aun clusters with even numbers of atoms are more stable than their neighboring clusters, and the two-dimensional to three-dimensional transition occurs at n = 12. De Bas et al.25 employed a combination of empirical potentials and first principles method to further explore the low energy structures of the large Aun (n = 3–38) nanoclusters. It is found that the Aun clusters are disordered and could be stable at room temperature. However, the promising applications of Aun clusters are also particularly interesting to scholars. For example, Gautam et al.18 systematically investigated the C2H2 activation and hydrogenation of C2H2 activated on small Aun (n = 3–10) clusters using DFT calculations. Zhou et al.26 performed ultrafast spectroscopic investigations on atomically precise thiolate-protected Aun nanoparticles, the Aun nanoparticles show three distinct states, including metallic, transition regime and non-metallic or excitonic states and their catalytic properties were obviously changed.
Nowadays, bimetallic clusters have drawn more considerable attention than monatomic clusters. Bimetallic clusters exhibit more intriguing properties than both pure clusters due to the synergetic effects between the two different atoms in bimetallic clusters,13 which provide a new technological and fundamental point of view as well as wide range of applications in nanotechnology. First of all, fundamental investigations of bimetallic clusters are crucial to the further applications. There are many evidences. For the sake of discovering electronic and magnetic properties of MAu6− (M = Ti, V, Cr) clusters, Li et al.27 applied a combination of density functional theory and photoelectron spectroscopy (PES) scheme, with the results indicating that all the anionic and neutral clusters possess planar structures and large magnetic moments, in which the doped transition atom lies in the center of the Au6 ring. Wen et al.28,29 investigated the structures of AuxS0,±1 (x = 2–10) clusters by means of theoretical calculations and experimental study, it is found that the transition of 1D-to-2D-to-3D was observed owing to the strong S–Au covalent bond, delocalized Au–Au bond, strong relativistic effects of Au and electronegativity between Au and S. The 3D assignment of structures of Au8M (M = Si, Ge, Sn) anion clusters were investigated by Liu et al.,30 it is found that the ground state structures of anion Au8Ge cluster and anion Au8Sn cluster are different from the results in previous studies. Furthermore, the promising applications of bimetallic Au-based clusters have been receiving great interest ever before. Mondal et al.12 investigated the structure and chemical reactivity of Au19Pt binary cluster within density functional theory, the results show that the tetrahedral structures of Au19Pt clusters are particularly stable, and CO molecule adsorption on the bare Pt site are favorable in tetrahedral Au19Pt clusters. Kauffman et al.31 investigated Au25−xAgx binary cluster by computational and experimental characterization, the results demonstrate that the Ag atom preferentially occupy the surface of the cluster, resulting Au25−xAgx cluster as a candidate in photo-mediated charge-transfer event. Yong et al.11 theoretically investigated the potential applications of Ag7Au6 cluster in gas sensing, it is found that the Ag7Au6 cluster show good chemisorbing characteristic of CO, HCN and NO molecules, which may has a promising gas sensor applications in CO, HCN and NO gases detection.
To the best of our knowledge, no systematical work has been reported on the PbnAun clusters. In this work, the structural, relative stable, electronic, and gas sensing properties of PbnAun (n = 2–12) clusters were systematically studied by density functional theory to explore the fundamental characters and promising applications of PbnAun (n = 2–12) clusters. It is well known that bimetallic Au-based novel clusters may have great novel properties, and the development of the functional nanomaterials based on earth-abundant and alternative cheap metal elements to replace the novel elements for functionally Au-based cluster catalysis are promising. Additionally, the toxic CO and NO gas molecules have become an increasing urgent environment problem owing to mainly combustion of fossil fuel, which have been posing great threats to humans' health. Hence, the toxic gases monitoring are extremely important with regard to the serious environment at present. Therefore, we firmly believe that this systematically theoretical investigation of PbnAun (n = 2–12) clusters would help us to uncover the fundamental characteristic of these clusters and their promising applications in gas detection.
2. Computational details
In the present work, all the calculations were carried out using spin-polarized density functional theory (DFT) as implemented in the DMol3 package.11,32,33 Initially, the GGA-PW91 functional,11,34 GGA-PBE functional,12,35 and GGA-BLYP36 functional were employed to treat the exchange and correlation energy for Pb2 dimer, Au2 dimer and PbAu cluster. The results demonstrate that the GGA-PW91 functional yields the parameters of the dimers which are closer to the experimental data, as shown in Table S1 (ESI†). Therefore, the GGA-PW91 functional was chosen in all the following calculations. All electron relativistic pseudopotentials were employed to treat the strong relativistic effects for PbnAun clusters due to the energetically close between the destabilization of the 5d10 orbitals and stabilization of the 6s1 orbit in Au atom.23,32 The double-numerical basis set plus d polarization functions (DNP)33 was chosen in this work. The extensive isomers were generated using ab initio molecular dynamics in which time step is 1 fs, total simulation time is 100 ps, temperature is 300 K, ensemble is NVT37 with constant temperature and constant volume. Possible spin multiplicities (singlet, triplet, quintet and septet were used to treat those PbnAun clusters with closed-shell electronics, whereas double, quartet, sextet and octet were chosen to treat those PbnAun clusters with open-shell electronics) were also taken into account during the geometry optimization processes because the polarization may have potential effects on the structures of PbnAun clusters. It is interesting to point out that all optimized geometries were found to adopt the corresponding lowest spin states. The same results during the geometry optimization processes of the bimetallic M2-doped Aun (M = Cu, Ag; n = 1–10) clusters were also found by Zhao et al.8 The SCF threshed is 10−6 Ha on the total energy. Convergence tolerance: 10−5 Ha, 0.002 Ha Å−1 and 0.005 Å are for energy, maximum force and maximum displacement, respectively. The smearing (0.005 Ha) was used to achieve good convergence results. Harmonic vibration frequencies were calculated to verify no imaginary frequency in the ground-state structures of PbnAun clusters. It is indispensable to mention that the density of states (DOS) were calculated using DFT Semi-core Pseudopotentials (DSPPs) with fitting all-electron relativistic DFT calculations. We are confident that the calculation methods in this work are reliable and accurate enough for investigating the PbnAun (n = 2–12) clusters, because our calculated results are in excellent agreement with the experimental data, as shown in Table S1 (ESI†).3. Results and discussion
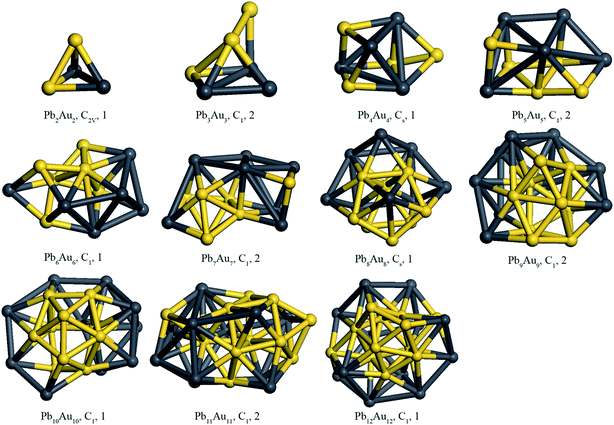
3.1. The ground-state structures and growth pattern of PbnAun (n = 2–12) clusters
We initially built the structure of PbnAun cluster which was optimized using geometry optimization calculations. Then the optimized structure was served as the initial structure of ab initio molecular dynamics calculations. The isomers of PbnAun clusters were generated using ab initio molecular dynamics calculations, then the obtained low-lying isomers were optimized, and then the ground state structures of PbnAun clusters were achieved by comparing the energies of the optimized low-lying isomers. Fig. 1 shows the lowest energy structures of the PbnAun (n = 2–14) clusters after the ab initio molecular dynamics simulations and geometry optimizations of local minimum isomers of PbnAun clusters, whereas the second lowest energy structures are shown in Fig. S1 (ESI†). As we can see from the Fig. 1, the Pb2Au2 cluster is a triangular pyramid with C2V symmetry, which yields a huge difference to the Pb4 cluster and Au4 cluster since the Pb4 cluster and the Au4 cluster prefer planar geometries.19,38 The Pb3Au3 cluster is a rectangular pyramid which is capped by an additional Au atom, and shows no symmetry. For the Pb4Au4 cluster, its geometrical structure seems to be complicated, exhibiting Cs symmetry, and the Au atoms evenly distributed on the surface of the cluster. The Pb5Au5 cluster is composed of two parts which are a distorted quadrangular and a triangular prism, and shows no symmetry. The ground state structure of the Pb6Au6 cluster is the 3D configuration without any symmetry, in which the six gold atoms bond together and occupy on the side of the cluster. The most stable structure of the Pb7Au7 cluster is distorted with no symmetry, and only six gold atoms bond together but the rest of the Au atoms is separated by two Pb atoms. From n = 8 to n = 12, we clearly see that those PbnAun clusters show a difference to those PbnAun (n = 2–7) clusters, which gold atoms aggregate together and occupy the central sites of the clusters. Moreover, all the PbnAun (n = 8–12) clusters are no symmetry except for the Pb8Au8 cluster is the 3D configuration with Cs symmetry. The aggregation effects of gold atoms in the central sites of PbnAun clusters are originated from the atomic radius of Au atom (1.44 Å) is smaller than that of Pb atom (1.75 Å). The similar phenomenon was also found by other researchers.39–41 It is interesting to note that the PbnAun (n = 2–12) clusters don't exhibit distinct rule of symmetry due to the equal ratio of Pb atoms and Au atoms for PbnAun clusters and the Jahn–Teller effects. Additionally, the cluster with a lower symmetry can decrease its total energy to some extent based on the Jahn–Teller theory.42 Particularly, it is concluded that Au atoms have strong interactions with the Pb atoms, because the Pbn clusters and Aun clusters are in favor of planar structures when the cluster size n is small while the PbnAun (n = 2–12) clusters are in favor of three dimensional structures.16,18,38,433.2. Average binding energies and stabilities of PbnAun (n = 2–12) clusters
In order to predict the relative stabilities of the ground state structures of PbnAun (n = 2–12) clusters, the average binding energies (Eb), the fragmentation energies (ΔE), and the second order energy differences (Δ2E) of PbnAun (n = 2–12) clusters are calculated. For PbnAun clusters, the Eb, ΔE, and Δ2E are defined using the following formulas36,44,45| Eb(PbnAun) = [nE(Pb) + nE(Au) − E(PbnAun)]/2n |
| ΔE(PbnAun) = E(Pbn−1Aun−1) + E(PbAu) − E(PbnAun) |
| Δ2E(PbnAun) = E(Pbn−1Aun−1) + E(Pbn+1Aun+1) − 2E(PbnAun) |
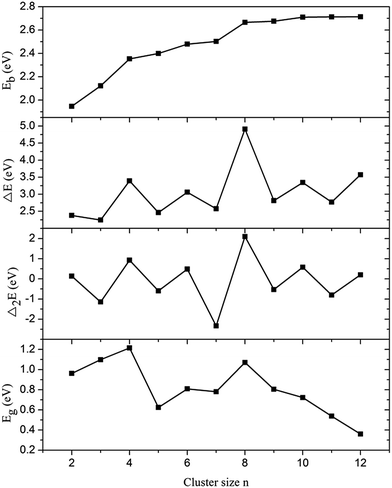 | ||
| Fig. 2 Average binding energies (Eb), fragmentation energies (ΔE), and second order energy differences (Δ2E) of PbnAun (n = 2–12) clusters versus the cluster size n. | ||
In order to further study the stabilities of the ground state structures of PbnAun clusters, we will also discuss the fragmentation energies and second order energy differences of PbnAun (n = 2–12) clusters. From the given formulas mentioned above, a higher value of fragmentation energy corresponding to a higher stability of the cluster due to more energy is needed if the PbnAun cluster dissociates into a smaller PbAu cluster and a smaller Pbn−1Aun−1 cluster. Moreover, the definition of second order energy difference is similar to that of fragmentation energy, the second order energy differences can reflect the relative stabilities of neutral clusters compared to their neighbors. It is suggested that the cluster is more stable with a higher value of second order energy difference. As shown in Fig. 2, the size dependence of the fragmentation energies and second order energy differences show obvious odd–even alternation phenomena, and the general trends are in good agreement with each other. Therefore, it is interesting to find that the cluster with even number of electrons is more stable than their neighbors with odd number of electrons. In addition, four obvious peaks are observed at n = 4, 6, 8, and 10, revealing that the Pb4Au4 cluster, Pb6Au6 cluster, Pb8Au8 cluster, and Pb10Au10 cluster are more stable than their neighbors.
3.3. HOMO–LUMO gaps and Mulliken charge analysis
The HOMO–LUMO gap (Eg) is of great interest due to its reflection of the kinetic stability, chemical stability, and electrical conductivity of the cluster.46,47 HOMO–LUMO gap demonstrates the energy gap between the highest occupied orbit and the lowest unoccupied orbit for a cluster. A higher value of HOMO–LUMO gap corresponds to a high energy required for electrons jump from the occupied orbit to unoccupied orbit. In a word, a smaller value of HOMO–LUMO gap represents a higher chemical reactivity, whereas a higher value of HOMO–LUMO gap indicates a weaker chemical reactivity. HOMO–LUMO gaps of PbnAun (n = 2–12) clusters are listed in Table 1, and the relationship between the HOMO–LUMO gaps and the corresponding cluster size n are shown in Fig. 2. As presented in the Fig. 2, it is seen that the HOMO–LUMO gaps show a general decreasing tendency with the increasing cluster size n, which means the chemical reactivity of the PbnAun clusters decrease with the increasing cluster size n. In addition, the Pb4Au4 cluster, Pb6Au6 cluster and Pb8Au8 cluster are found with relatively higher values of HOMO–LUMO gaps than their neighbouring clusters. Therefore, we draw a conclusion that the PbnAun (n = 4, 6, and 8) clusters have relatively stable chemical reactivity. It is in well agreement with the analysis of fragmentation energies and second-order energy in differences mentioned above. To further analyse the electronic structures of the Pb4Au4 cluster, Pb6Au6 cluster, and Pb8Au8 cluster, it is important to find that valence electrons of the Pb4Au4 cluster, Pb6Au6 cluster, and Pb8Au8 cluster are 20 electrons, 30 electrons and 40 electrons, respectively. The electron configurations of the PbnAun (n = 4, 6, and 8) clusters are in excellent agreement with the Jellium model that the cluster with distinct close-shell electronics is particularly chemical stable.48,49 We can further conclude that the chemical stabilities of the Pb4Au4 cluster, Pb6Au6 cluster, and Pb8Au8 cluster are enhanced. Therefore, the Pb4Au4 cluster, Pb6Au6 cluster, and Pb8Au8 cluster may be the stable building blocks, and can be used in novel nanomaterials. The potential adsorption properties of the stable clusters will be further investigated in this work.| PbnAun cluster | HOMO–LUMO gap (eV) | Average Mulliken charge (e) | |
|---|---|---|---|
| Pb atoms | Au atoms | ||
| n = 2 | 0.961 | 0.272 | −0.272 |
| n = 3 | 1.098 | 0.247 | −0.247 |
| n = 4 | 1.214 | 0.291 | −0.291 |
| n = 5 | 0.624 | 0.261 | −0.261 |
| n = 6 | 0.808 | 0.228 | −0.228 |
| n = 7 | 0.780 | 0.235 | −0.235 |
| n = 8 | 1.070 | 0.232 | −0.232 |
| n = 9 | 0.804 | 0.189 | −0.189 |
| n = 10 | 0.722 | 0.200 | −0.200 |
| n = 11 | 0.538 | 0.254 | −0.254 |
| n = 12 | 0.360 | 0.223 | −0.223 |
To unravel the reliable charge transfer information of PbnAun (n = 2–12) clusters, the average Mulliken charges were calculated, the results are given in Table 1. The values of average Mulliken charges for Pb atoms in PbnAun clusters are positive and that of for Au atoms in PbnAun clusters are negative, indicating that the charges always transfer from Pb atoms to Au atoms in PbnAun clusters since the electronegativity of Au (2.54 for Au, according to Pauling) is larger than that of that Pb (2.33 for Pb, according to Pauling). This interesting phenomenon is in excellent agreement with our previous work about PbnCun clusters36 and other scholars' results.8,47,50 Therefore, we can conclude that the Pb atoms act as the electron donors while Au atoms act as the electron acceptors in PbnAun clusters. The electron accumulation of Au atoms in PbnAun clusters may be the most active sites during the catalytic and adsorption processes.
3.4. Gas adsorption properties of the Pb4Au4 cluster, Pb6Au6 cluster and Pb8Au8 cluster
According the detailed discussions on PbnAun (n = 2–12) clusters mentioned above, the Pb4Au4 cluster, Pb6Au6 cluster and Pb8Au8 cluster are relatively more stable than other PbnAun clusters, and may serve as the building blocks for the design of cluster-assemble nanomaterials due to their chemically stable reactivity. Then, we will investigate the feasibility of CO or NO molecule adsorption on the ground-state structures of the three clusters with tailored properties. For PbnAun–CO (n = 4, 6, and 8) and PbnAun–NO (n = 4, 6, and 8) complexes, the adsorption energy (Eads) of CO molecule (or NO) molecule on PbnAun clusters can be defined as follows11,18| Eads = E(PbnAun–CO) − E(PbnAun) − E(CO) |
| Eads = E(PbnAun–NO) − E(PbnAun) − E(NO) |
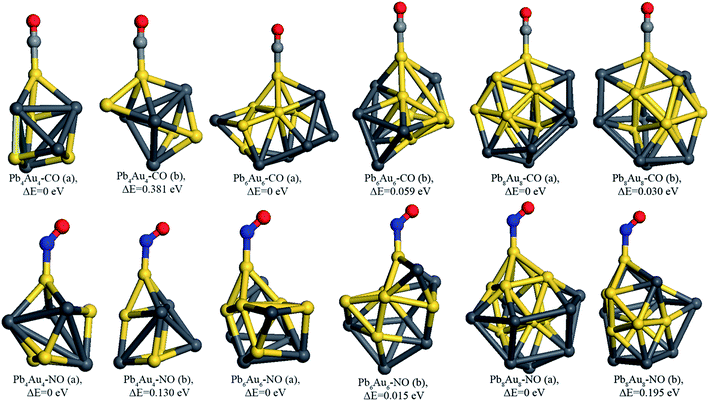
In this work, every possible adsorption sites (all the bare Pb atoms and Au atoms) were taken into consideration. Moreover, the orientation of C atom pointing to adsorption site and that of O atom pointing to adsorption site for CO molecule adsorption on PbnAun (n = 4, 6, and 8) clusters were also taken into consideration. After full geometry relaxation of all possible initial configurations, C or N atom directly binds to Au atoms of PbnAun (n = 4, 6, and 8) clusters are energetically favorable, which means Au atoms are the active sites for molecule adsorption. Interestingly, it is worthy to note that the active sites of PbnAun clusters are in well agreement with the analysis of the average Mulliken charges discussed above. The most stable and second stable configurations of CO molecule adsorption on Pb4Au4, Pb6Au6, and Pb8Au8 clusters are shown in Fig. 3.
According to the most stable configurations of CO molecule adsorption on PbnAun clusters (n = 4, 6, and 8), the CO molecule prefers the orientation of the C atom directly binding to the PbnAun clusters and C atom of CO molecule is located on the top of Au atom, which is consistent with the work reported by other literature.11,51,52 Moreover, the CO molecule almost in the straight line with absorbed Au atom and the Au–C–O angles are in the range of 175.418–179.007°. The distances between the C atom and active Au atoms are in the range of 1.875–1.902 Å, as shown in Table 2, revealing that the adsorption processes are enhanced compared to the distances between C atom and Ag atom (or Au atom) of Ag7Au6–CO complexes are in the range of 2.099–2.002 Å.11 It is concluded that the configurations of PbnAun–CO (n = 4, 6, and 8) complexes do not show big differences when CO molecule adsorption on the different adsorption sites of PbnAun (n = 4, 6, and 8) clusters. The adsorption energies are in the range of −1.062–1.498 eV, as shown in Table 2, indicating that CO molecule is chemisorbed onto the PbnAun (n = 4, 6, and 8) clusters. The adsorption energies are larger than that of CO molecule adsorbed onto the Ag7Au6 cluster, the contributions of Pb atoms in PbnAun (n = 4, 6, and 8) clusters may be responsible for the enhanced chemical adsorption. Moreover, it is found that charges are always transferred from the PbnAun clusters to CO molecule, as shown in Table 2. The charges were calculated using Hirshfeld method due to the Hirshfeld method can obtain more reliable results than Mulliken, Bader, and Weinhold methods.11 This trend of electron transfer is similar to the previous work reported by Yong et al.11 In order to unravel the charges transfer from the PbnAun (n = 4, 6, and 8) clusters to the CO molecule, we calculated the vibrational frequencies of the –CO moieties in the PbnAun–CO (n = 4, 6, and 8) complexes, and the vibrational frequency of the isolated CO molecules in the gas phase, as shown in Table 3. From the table, we can see that the vibrational frequencies of the –CO moieties in the PbnAun–CO (n = 4, 6, and 8) complexes are decreased as compared to the vibrational frequency of the isolated CO molecule in the gas phase. Obviously, the red shifts of the vibrational frequencies of –CO moieties are achieved. It can be used to explain the charges transfer from the PbnAun clusters to CO molecule.
| Configuration | Eads (eV) | D (Å) | QT (e) | Eg (eV) | ΔEg (eV) |
|---|---|---|---|---|---|
| Pb4Au4–CO(a) | −1.443 | 1.878 | 0.029 | 0.992 | 0.222 |
| Pb4Au4–CO(b) | −1.062 | 1.902 | 0.045 | 1.057 | 0.157 |
| Pb6Au6–CO(a) | −1.498 | 1.875 | 0.044 | 0.546 | 0.262 |
| Pb6Au6–CO(b) | −1.439 | 1.875 | 0.032 | 0.577 | 0.209 |
| Pb8Au8–CO(a) | −1.355 | 1.885 | 0.057 | 0.721 | 0.349 |
| Pb8Au8–CO(b) | −1.325 | 1.884 | 0.045 | 0.719 | 0.315 |
| System | υa (cm−1) | υb (cm−1) | Δυa (cm−1) | Δυb (cm−1) |
|---|---|---|---|---|
| CO | 2119.91 | |||
| NO | 1893.46 | |||
| Pb4Au4–CO | 2038.65 | 2028.11 | 81.26 | 91.8 |
| Pb6Au6–CO | 2054.94 | 2045.35 | 64.97 | 74.56 |
| Pb8Au8–CO | 2031.63 | 2069.86 | 88.28 | 50.05 |
| Pb4Au4–NO | 1640.74 | 1632.55 | 252.72 | 260.91 |
| Pb6Au6–NO | 1649.30 | 1633.92 | 244.16 | 259.54 |
| Pb8Au8–NO | 1652.42 | 1635.32 | 241.04 | 258.14 |
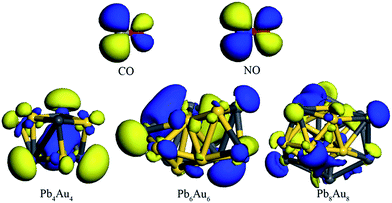
In order to uncover the reaction mechanisms that charges always transfer from PbnAun clusters to CO molecule when CO molecule adsorption onto PbnAun (n = 4, 6, and 8) clusters. The energy levels of HOMOs and LUMOs for CO molecule and PbnAun clusters were calculated, respectively, as listed in Table 4. The energy differences between LUMO of CO molecule and HOMOs of PbnAun (n = 4, 6, and 8) clusters are in the range of 2.564–2.645 eV, whereas that of HOMO of CO molecule and LUMOs of PbnAun (n = 4, 6, and 8) clusters are in the range of 5.411–5.636 eV. It is obvious that the energy gaps of HOMO–LUMO (PbnAun → CO) are smaller than that of HOMO–LUMO (CO → PbnAun), and HOMOs of PbnAun (n = 4, 6, and 8) clusters overlap well with LUMO of CO molecule, as shown in Fig. 4. Therefore, PbnAun clusters are the electron donors and CO molecule is the electron acceptor on the basis of the frontier molecular orbital theory.53,54 Wang et al.16 also yielded the similar results on HCl molecule adsorption on Aun–C2H2 complexes based on the frontier molecular orbital theory. Moreover, it is also interesting to find that the HOMOs are mainly located on the Au atoms of PbnAun (n = 4, 6, and 8) clusters and the LUMO is mainly located on the C atom of CO molecule should be responsible for the orientation of C atom of CO molecule directly adsorbed on the Au atoms of PbnAun (n = 4, 6, and 8) clusters.
| System | HOMO | LUMO | HOMO–LUMO (PbnAun → CO) | HOMO–LUMO (CO → PbnAun) | HOMO–LUMO (PbnAun → NO) | HOMO–LUMO (NO → PbnAun) |
|---|---|---|---|---|---|---|
| CO | −8.951 | −1.965 | ||||
| NO | −11.089 | −4.44 | ||||
| Pb4Au4 | −4.529 | −3.315 | 2.564 | 5.636 | 0.089 | 7.774 |
| Pb6Au6 | −4.543 | −3.735 | 2.578 | 5.216 | 0.103 | 7.354 |
| Pb8Au8 | −4.61 | −3.54 | 2.645 | 5.411 | 0.17 | 7.549 |
The most stable and second stable configurations of NO molecule binding to PbnAun (n = 4, 6, and 8) clusters were also investigated, as shown in Fig. 3. The initial adsorption configurations of PbnAun–NO (n = 4, 6, and 8) complexes are similar to that of PbnAun–CO (n = 4, 6, and 8) complexes. It is found that the NO molecule binds to PbnAun (n = 4, 6, and 8) clusters by means of N atom (Au–N model), which adopt the similar adsorption configurations with that of NO molecule adsorption onto Ag7Au6 clusters.11,55 The lowest distances between NO molecule and PbnAun (n = 4, 6, and 8) clusters are in the range of 1.933–1.977 Å, as shown in Table 5, which are larger than the distances between CO molecule and PbnAun (n = 4, 6, and 8) clusters. The Au–N–O bond angles are in the range of 129.464–135.899°, which shows NO doesn't vertically adsorption onto PbnAun (n = 4, 6, and 8) clusters. The adsorption energies are in the range of 0.957–1.125 eV, which shows that NO adsorption onto PbnAun clusters are also chemical processes, as listed in Table 5. The charges are also transferred from the PbnAun (n = 4, 6, and 8) clusters to NO molecule, which shows the same trend with that of PbnAun–CO (n = 4, 6, and 8) complexes discussed above. In order to unravel the charges transfer from the PbnAun (n = 4, 6, and 8) clusters to the NO molecule, we calculated the vibrational frequencies of the –NO moieties in the PbnAun–NO (n = 4, 6, and 8) complexes, and the vibrational frequency of the isolated NO molecules in the gas phase, as shown in Table 3. From the table, we can see that the vibrational frequencies of the –NO moieties in the PbnAun–NO (n = 4, 6, and 8) complexes are decreased as compared to the vibrational frequency of the isolated NO molecule in the gas phase. Obviously, the red shifts of the vibrational frequencies of –NO moieties are achieved. It can be used to explain the charges transfer from the PbnAun clusters to NO molecule in PbnAun–NO (n = 4, 6, and 8) complexes. In addition, according to the analysis of PbnAun–CO (n = 4, 6, and 8) complexes, similarly, the HOMOs of PbnAun (n = 4, 6, and 8) clusters match the LUMO of CO molecule should be responsible for the configurations of PbnAun–NO complexes and the charges transfer mechanism on the basis of frontier molecular orbital theory. The energy levels of the HOMOs and LUMOs are listed in Table 4, and the diagrams of the HOMOs and LUMOs are shown in Fig. 4.
| Configuration | Eads (eV) | D (Å) | QT (e) | Eg (eV) | ΔEg (eV) |
|---|---|---|---|---|---|
| Pb4Au4–NO(a) | −1.125 | 1.943 | 0.135 | 0.120 | 1.094 |
| Pb4Au4–NO(b) | −0.995 | 1.977 | 0.151 | 0.270 | 0.944 |
| Pb6Au6–NO(a) | −1.076 | 1.933 | 0.132 | 0.442 | 0.366 |
| Pb6Au6–NO(b) | −1.061 | 1.948 | 0.112 | 0.551 | 0.257 |
| Pb8Au8–NO(a) | −1.152 | 1.944 | 0.098 | 0.611 | 0.459 |
| Pb8Au8–NO(b) | −0.957 | 1.939 | 0.134 | 0.237 | 0.833 |
3.5. The promising applications of PbnAun (n = 4, 6, and 8) clusters for CO and NO molecules detection
It is well known that the nanoclusters are widely used in nanotechnology, especially in the toxic gas sensing. Herein, we will explore the sensitivity of CO and NO molecule adsorption onto PbnAun (n = 4, 6, and 8) clusters. However, there are two main parameters to judge a nanocluster as an ideal gas sensor:56 (1) the gas molecules should chemiadsorp onto the nanocluster with a large adsorption energy, because the large adsorption energy can prevent the gas molecule spontaneous desorption from the nanocluster, (2) the gas molecules have a great influence on the electric conductivity of the nanoclusters owing to the sufficient charges transfer between gas molecule and the nanocluster. According to the results and discussion mentioned above, the CO and NO molecules can chemiadsorp onto the PbnAun clusters (n = 4, 6, and 8), it agrees well with the second condition under which a nanocluster is judged as an ideal gas sensor. Then we will focus on the changes of electric conductivity of the systems before and after the CO or NO molecule adsorption onto the PbnAun (n = 4, 6, and 8) clusters. The definition of electric conductivity (σ) can be described as the following formula11,52,57where Eg, K, and T are the band energy gap of configuration, the Boltzmann's constant, and the thermodynamic temperature, respectively. From the equation, it is find that Eg is responsible for the electric conductivity of the gas molecule before and after adsorption onto the nanocluster. Our results indicating that the HOMO–LUMO gaps of PbnAun clusters are obviously changed after the CO and NO molecules adsorption onto PbnAun clusters. The ΔEg are in the range of 0.157–1.094 eV, as shown in Tables 2 and 5. Hence, the results suggest that the miniaturized sensors based on PbnAun (n = 4, 6, and 8) clusters can be used to detect the CO and NO molecules by calculating the electric conductivity changes of PbnAun clusters before and after the molecules adsorption onto the clusters, because the resistance of the system can be easily detected. Moreover, it is possible for CO and NO molecules desorption from the PbnAun (n = 4, 6, and 8) clusters, which is originated from that PbnAun clusters are less chemically stable than the PbnAun–CO and PbnAun–NO (n = 4, 6, and 8) complexes because the HOMO–LUMO gaps of PbnAun clusters are larger than that of PbnAun–CO and PbnAun–NO complexes. In addition, we will calculate the recovery time τ for gas desorption from PbnAun (n = 4, 6, and 8) clusters. According the transition state theory, the recovery time τ in terms of adsorption energy Ead can be expressed as58
| τ = υ0−1e(−Ead/KT) |
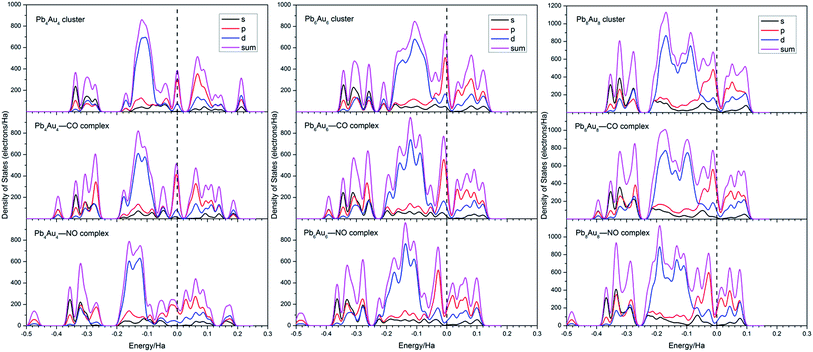
3.6. Density of states
The density of states (DOS) near the fermi levels of the most stable configurations of PbnAun (n = 4, 6, and 8) clusters, PbnAun–CO (n = 4, 6, and 8) complexes, and PbnAun–NO (n = 4, 6, and 8) complexes were carried out, in order to further investigate the increased conductance of PbnAun–CO (n = 4, 6, and 8) and PbnAun–NO (n = 4, 6, and 8) complexes, as shown in Fig. 5. The HOMO–LUMO gaps of PbnAun (n = 4, 6, and 8) clusters are don't obviously reduced when CO molecule is adsorbed on the PbnAun (n = 4, 6, and 8) clusters, as shown in Table 2. But the HOMO–LUMO gaps of PbnAun–NO (n = 4, 6, and 8) complexes are obviously reduced compared to that of PbnAun clusters, as summarized in Table 5. From Fig. 5, the DOS of PbnAun (n = 4, 6, and 8) clusters do not show distinct changes before and after CO molecule adsorption on the PbnAun (n = 4, 6, and 8) clusters. It may be attributed to the little charges transfer between the CO molecule and the PbnAun clusters. However, there are some little changes near the Fermi levels, the DOS above the Fermi levels are slightly shrank and weakly shift toward more negative energy levels. It can be used to explained the decreased HOMO–LUMO gaps of PbnAun–CO (n = 4, 6, and 8) complexes. According to the Fig. 5, the DOS of PbnAun–NO (n = 4, 6, and 8) complexes are significantly shift towards to more negative energy levels compared to that of bare PbnAun (n = 4, 6, and 8) clusters, and the DOS above the Fermi level become more nonlocalized. In other words, the Fermi levels of PbnAun–NO (n = 4, 6, and 8) complexes shift towards more positive energy levels. Those changes near the Fermi levels should be responsible for the increased conductivities of PbnAun–NO (n = 4, 6, and 8) complexes.4. Conclusions
In summary, the ground state structures, average binding energies, fragmentation energies, second order energy differences, HOMO–LUMO gaps, gas sensing, density of states of PbnAun clusters were systematically investigated on the basis of density functional theory as implemented in DMol3 package. Based on the structural growth pattern of the ground state structures of PbnAun (n = 2–12) clusters, the Au atoms tend to aggregate together and occupy the geometrical centers of PbnAun clusters. The average binding energies show a generally increasing tendency to be stable at the beginning of cluster size n = 10. The fragmentation energies and second order energy differences show obvious odd–even alternations, indicating that the PbnAun clusters with close shell electrons are more stable than their neighboring clusters with open shell electrons. Pb4Au4, Pb6Au6 and Pb8Au8 clusters are the magic clusters with chemically stable reactivity. Moreover, PbnAun (n = 4, 6, and 8) have great potential in CO and NO molecules detection. The gas sensing properties of PbnAun clusters will be further verified by experimental results.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was financially supported by the Regional Foundation of the NSFC (51664032), the Foundation of the State Key Laboratory of Complex Nonferrous Metal Resources Clear Utilization (CNMRCUTS1503), the Joint Foundation of the NSFC-Yunnan province (U1502271), the Leader in Science and Technology of Yunnan Province (2014HA003), the Program for Nonferrous Metals Vacuum Metallurgy Innovation Team of Ministry of Science and Technology (2014RA4018), the National Key Research and Development Program of China (2016YFC0400404) and the Program for Innovative Research Team in University of Ministry of Education of China (No. IRT_17R48).References
- I. M. L. Billas, A. Châtelain and W. A. de Heer, Science, 1994, 265, 1682 CAS.
- H. Yang, Y. Wang, X. Chen, X. Zhao, L. Gu, H. Huang, J. Yan, C. Xu, G. Li, J. Wu, A. J. Edwards, B. Dittrich, Z. Tang, D. Wang, L. Lehtovaara, H. Häkkinen and N. Zheng, Plasmonic twinned silver nanoparticles with molecular precision, Nat. Commun., 2016, 7, 12809 CrossRef CAS PubMed.
- T. Zhou, J. J. Goings and Z. Lin, J. Phys. Chem. A, 2016, 120, 8485 CrossRef CAS PubMed.
- P.-C. Chen, Y.-C. Li, J.-Y. Ma, J.-Y. Huang, C.-F. Chen and H.-T. Chang, Sci. Rep., 2016, 6, 24882 CrossRef CAS PubMed.
- A. P. Alivisatos, Science, 1996, 271, 933 CAS.
- M. C. Daniel and D. Astruc, Chem. Rev., 2004, 104, 293 CrossRef CAS PubMed.
- Q. Y. Lin, Z. Li, K. A. Brown, M. N. O'Brien, M. B. Ross, Y. Zhou, S. Butun, P. C. Chen, G. C. Schatz and V. P. Dravid, Nano Lett., 2015, 15, 4699 CrossRef CAS PubMed.
- Y.-R. Zhao, X.-Y. Kuang, B.-B. Zheng, Y.-F. Li and S.-J. Wang, J. Phys. Chem. A, 2011, 115, 569 CrossRef CAS PubMed.
- C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Phys. Rev. Lett., 1997, 79, 1873 CrossRef CAS.
- S. H. Yau, O. Varnavski and T. Goodson, Acc. Chem. Res., 2013, 46, 1506 CrossRef CAS PubMed.
- Y. Yong, C. Li, X. Li, T. Li, H. Cui and S. Lv, J. Phys. Chem. C, 2015, 119, 7534 CAS.
- K. Mondal, A. Banerjee and T. K. Ghanty, J. Phys. Chem. C, 2014, 118, 11935 CAS.
- Y. Chen, H. Wang, C.-J. Liu, Z. Zeng, H. Zhang, C. Zhou, X. Jia and Y. Yang, J. Catal., 2012, 289, 105 CrossRef CAS.
- Z. Y. Li, N. P. Young, M. Di Vece, S. Palomba, R. E. Palmer, A. L. Bleloch, B. C. Curley, R. L. Johnston, J. Jiang and J. Yuan, Nature, 2008, 451, 46 CrossRef CAS PubMed.
- D. R. Kauffman, D. Alfonso, C. Matranga, H. Qian and R. Jin, J. Am. Chem. Soc., 2012, 134, 10237 CrossRef CAS PubMed.
- Y. Wang, M. Zhu, L. Kang and B. Dai, RSC Adv., 2014, 4, 38466 RSC.
- H. S. De, S. Krishnamurty, D. Mishra and S. Pal, J. Phys. Chem. C, 2011, 115, 17278 CAS.
- S. Gautam and A. D. Sarkar, Phys. Chem. Chem. Phys., 2016, 18, 13830 RSC.
- X. B. Li, H. Y. Wang, X. D. Yang, Z. H. Zhu and Y. J. Tang, J. Chem. Phys., 2007, 126, 084505 CrossRef PubMed.
- B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306 CrossRef PubMed.
- H. Haekkinen, B. Yoon, U. Landman, X. Li, H. J. Zhai and L. S. Wang, J. Phys. Chem. A, 2003, 107, 6168 CrossRef CAS.
- B. Assadollahzadeh and P. Schwerdtfeger, J. Chem. Phys., 2009, 131, 064306 CrossRef PubMed.
- H. Häkkinen, M. Moseler and U. Landman, Phys. Rev. Lett., 2002, 89, 033401 CrossRef PubMed.
- X. Gu, M. Ji, S. H. Wei and X. G. Gong, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205401 CrossRef.
- B. S. de Bas, M. J. Ford and M. B. Cortie, J. Mol. Struct.: THEOCHEM, 2004, 686, 193 CrossRef.
- M. Zhou, C. Zeng, Y. Chen, S. Zhao, M. Y. Sfeir, M. Zhu and R. Jin, Nat. Commun., 2016, 7, 13240 CrossRef CAS PubMed.
- X. Li, B. Kiran, L.-F. Cui and L.-S. Wang, Phys. Rev. Lett., 2005, 95, 253401 CrossRef PubMed.
- H. Wen, Y. R. Liu, T. Huang, K. M. Xu, W. J. Zhang, W. Huang and L. S. Wang, J. Chem. Phys., 2013, 138, 174303 CrossRef PubMed.
- H. Wen, Y.-R. Liu, K.-M. Xu, T. Huang, C.-J. Hu, W.-J. Zhang and W. Huang, RSC Adv., 2014, 4, 15066 RSC.
- Y. R. Liu, T. Huang, Y. B. Gai, Y. Zhang, Y. J. Feng and W. Huang, Sci. Rep., 2015, 5, 17738 CrossRef CAS PubMed.
- D. R. Kauffman, D. Alfonso, C. Matranga, H. Qian and R. Jin, J. Phys. Chem. C, 2013, 117, 7914 CAS.
- M. Zhang, L.-M. He, L.-X. Zhao, X.-J. Feng and Y.-H. Luo, J. Phys. Chem. C, 2009, 113, 6491 CAS.
- M. Zhang, H. Zhang, L. Zhao, Y. Li and Y. Luo, J. Phys. Chem. A, 2012, 116, 1493 CrossRef CAS PubMed.
- G. Mills, M. S. Gordon and H. Metiu, Chem. Phys. Lett., 2002, 359, 493 CrossRef CAS.
- W. Zhang, D. Cheng and J. Zhu, RSC Adv., 2014, 4, 42554 RSC.
- G. Li, J. Wang, X. Chen, Z. Zhou, H. Yang, B. Yang, B. Xu and D. Liu, Comput. Theor. Chem., 2017, 1106, 21 CrossRef CAS.
- S. Nosé, Mol. Phys., 2002, 52, 255 CrossRef.
- B. Wang, J. Zhao, X. Chen, D. Shi and G. Wang, Phys. Rev. A, 2005, 71, 033201 CrossRef.
- M. Hu, D. P. Linder, M. B. Nardelli and A. Striolo, J. Phys. Chem. C, 2013, 117, 15050 CAS.
- C. Rajesh and C. Majumder, J. Chem. Phys., 2008, 128, 024308 CrossRef PubMed.
- H. Xie, Z. Qin, X. Wu, Z. Tang and L. Jiang, J. Chem. Phys., 2012, 137, 064318 CrossRef PubMed.
- M. E. Eberhart, R. C. O'Handley and K. H. Johnson, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1097 CrossRef CAS.
- C. Rajesh and C. Majumder, J. Chem. Phys., 2007, 126, 244704 CrossRef PubMed.
- J.-Q. Wen, J.-M. Zhang, G.-X. Chen, X.-Z. Zhang and Z.-Y. Wen, J. Phys. Chem. Solids, 2016, 96–97, 68 CrossRef CAS.
- R. Trivedi and D. Bandyopadhyay, Int. J. Hydrogen Energy, 2016, 41, 20113 CrossRef CAS.
- L. R. Radovic and B. Bockrath, J. Am. Chem. Soc., 2005, 127, 5917 CrossRef CAS PubMed.
- Z. Mahdavifar and M. Haghbayan, Appl. Surf. Sci., 2012, 263, 553 CrossRef CAS.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141 CrossRef CAS.
- M. L. Cohen, M. Y. Chou, W. D. Knight and W. A. De Heer, J. Phys. Chem., 1987, 91, 3141 CrossRef CAS.
- X. Huang, Y. Su, L. Sai, J. Zhao and V. Kumar, J. Cluster Sci., 2015, 26, 389 CrossRef CAS.
- K. Mondal, D. Manna, T. K. Ghanty and A. Banerjee, Chem. Phys., 2014, 428, 75 CrossRef CAS.
- Y. Yong, H. Jiang, X. Li, S. Lv and J. Cao, Phys. Chem. Chem. Phys., 2016, 18, 21431 RSC.
- K. N. Houk, Acc. Chem. Res., 1975, 8, 361 CrossRef CAS.
- K. Fukui, Recognition of Stereochemical Paths by Orbital Interaction, 1971, pp. 244–251 Search PubMed.
- R. Q. Wu, M. Yang, Y. H. Lu, Y. P. Feng, Z. G. Huang and Q. Y. Wu, J. Phys. Chem. C, 2015, 112, 15985 Search PubMed.
- J. Kong, N. R. Franklin, C. Zhou, M. G. Chapline, S. Peng, K. Cho and H. Dai, Science, 2000, 287, 622 CrossRef CAS PubMed.
- A. Ahmadi, N. L. Hadipour, M. Kamfiroozi and Z. Bagheri, Sens. Actuators, B, 2012, 161, 1025 CrossRef CAS.
- S. Peng, K. Cho, P. Qi and H. Dai, Chem. Phys. Lett., 2004, 387, 271 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09286e |
| This journal is © The Royal Society of Chemistry 2017 |