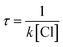Theoretical study of the Cl-initiated atmospheric oxidation of methyl isopropenyl ketone

Abstract

The Cl-initiated atmospheric oxidation mechanism of methyl isopropenyl ketone (MIK) has been investigated at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level of theory. Two reaction types initiated from Cl-addition and H-abstraction, respectively, and the key intermediates involved, IM1, IM2 (obtained from Cl-addition) and IM6 (obtained from H-abstraction), are presented and discussed. The calculated results supported the experimental results that Cl addition dominates the initial reactions of MIK with Cl atoms, and the most energetically favorable pathway is the Cl addition to the terminal carbon of C=C bond. Among the four proposed H abstraction processes, our study clearly indicated that the H-abstraction by Cl only takes place at the methyl linking to the internal alkenfinic carbon rather than the one at the methyl linking to the carbonyl carbon, which resolves the uncertainty of H-abstraction encountered in experiment. In addition, the isomerization processes involved in the Cl addition mechanism (1,4-H shift isomerization of IMa3 and 1,5-H shift isomerization of IMb3) were proposed in this work and found to be feasible. Both the major products experimentally detected and those derived from our theoretical study have been identified. The rate constants of the initial reactions over the atmospheric temperature range of 180–380 K have been determined using the MESMER program on the basis of Rice–Ramsperger–Kassel–Marcus (RRKM) theory. One the basis of the kinetic data we obtained, the Arrhenius formula of the total rate constant has been deduced: k_tot = (5.31 × 10⁻¹¹)exp(−335.24/T) cm³ per molecule per s. The atmospheric lifetime of MIK in the presence of Cl atoms is calculated to be about 170.01 h.

---

1. Introduction

Methyl isopropenyl ketone (MIK, H₂C=C(CH₃)C(O)CH₃) is an important α,β-unsaturated ketone and has been observed from anthropogenic sources (plants, solvent use, biomass burning, fossil fuel combustion, etc.).^1–4 In addition, MIK has been found to be an intermediate product in synthesis and in the catalysis industry.⁵ It is reported that MIK can be widely used in the polymer manufacturing industry.⁶ MIK is highly toxic, and can cause eye, nose, throat, and skin irritation. Exposure to excessive vapor concentration may cause severe damage to eyes, possibly leading to some permanent impairment of vision.⁷ Due to its high vapor pressure (42 mmHg, at 298 K), MIK is mainly released into the environment as a vapor under general atmospheric conditions.⁸ The atmospheric concentration of MIK is increasing year by year because of the increasing industrial dosage. It will undergo chemical transformation or degradation to produce some secondary pollutants that have a potential contribution to air quality on regional and global scales.⁹ To assess the atmospheric behavior of pollutants, it is crucial to understand their atmospheric reactions.

Once in the atmosphere, MIK can undergo photolysis and gas-phase reactions initiated by oxidants like OH and NO₃ radicals, O₃ molecules or Cl atoms, which leads to its removal from the atmosphere. Photodissociation appears to be insignificant for α,β-unsaturated ketones, since they do not absorb radiation at actinic wavelengths.¹⁰ Although the reaction of MIK with OH radicals is generally considered to be the predominant degradation pathway among these various species, the reaction of MIK with Cl atoms also represents a significant loss process in some special regions, such as coastal regions, the marine boundary layer and some polluted mid-continental regions with high chlorine emissions.^11–13 According to Chang's report, the average concentration of Cl atoms is estimated to be as high as 3 × 10⁵ molecules per cm³ or more in the marine boundary layer.¹⁴ In addition, the Cl atoms reactions with organic compounds have been reported to be much faster than OH-participated reactions.¹⁵ Thus, it is necessary to study the Cl-initiated oxidation of MIK in order to assess its potential impact to the atmosphere.

To date, only two experimental studies have been conducted concerning the gas-phase oxidation of MIK. In 2005, Canosa-Mas et al. performed the kinetic study on NO₃-initiated reactions of a series of α,β-unsaturated ketones using the relative-rate technique at 298 ± 2 K and 760 ± 5 Torr. In their study, the rate constant for reaction of NO₃ with MIK was given as (8.27 ± 6.44) × 10⁻¹⁵ cm³ per molecule per s.¹⁶ In 2015, Wang et al. determined the rate constants and products for the gas-phase reactions of atomic Cl and O₃ with MIK in a 100 L Teflon chamber at the conditions of 293 ± 1 K and atmospheric pressure. The obtained rate constants were (2.38 ± 0.26) × 10⁻¹⁰ and (1.18 ± 0.21) × 10⁻¹⁷ cm³ per molecule per s, respectively. Several reaction products were identified by means of proton-transfer-reaction mass spectrometry (PTR-MS).¹⁷ Furthermore, possible reaction mechanism for the reaction of Cl atoms with MIK was tentatively proposed based on the observed products.¹⁷ However, several important questions are not solved in the experimental work. Firstly, the H-abstraction occurring at C₄ or C₅ is uncertain (see Fig. 1A). Secondly, the alkoxy radical isomerization processes should be probed although not considered experimentally. Thirdly, the rate coefficients were not studied over the general range of temperatures (for instance, 180–380 K) in the troposphere. Quantum calculations have been proven to be especially suitable for calculating the geometrical structures of the reactants, intermediates, transition states and products involved in the detailed reaction mechanism, establishing the feasibility of a reaction pathway, and investigating the kinetic properties of reactions. In this paper, the comprehensive kinetic and mechanistic studies concerning the Cl-initiated atmospheric reaction of MIK are carried out using theoretical methods.

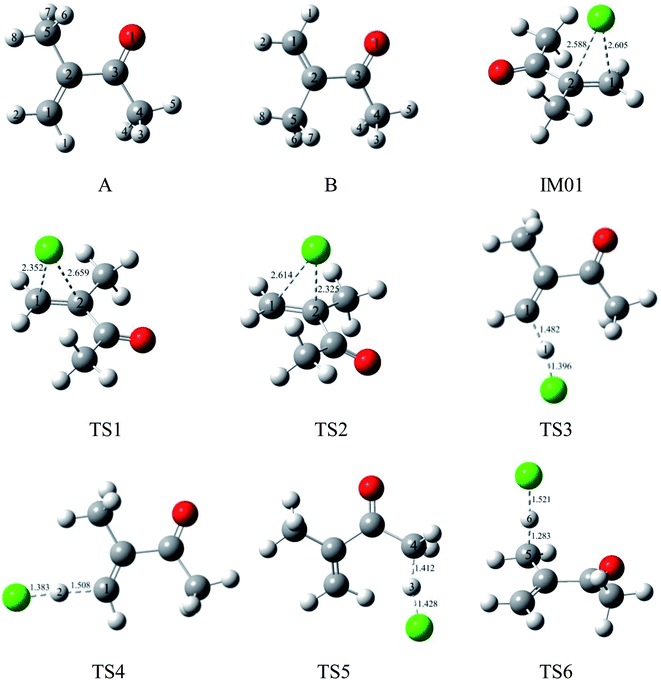Fig. 1 Optimized geometries for reactants, pre-complexes, and transition states in the initial reaction of MIK with Cl atoms at the MP2/6-311G(d,p) level. Bond lengths are given in Å.

2. Computational methods

All the quantum chemical calculations reported in this paper are performed using the Gaussian 09 program operated in a Linux system.¹⁸ The geometric parameters of the stationary points including reactants (R), intermediates (IM), transition states (TS), and products (P) are fully optimized using the second-order Møller–Plesset perturbation theory (MP2) with standard 6-311G(d,p) basis set.^19–21 This MP2 method has been used successfully in previous studies on the similar reaction systems.^22–25 The zero point vibrational energy (ZPE), the Gibbs free energy, the enthalpy, the entropy and the harmonic vibrational frequencies of various species are obtained at the MP2/6-311G(d,p) level (see Tables S1 and S2†). Each transition state is verified to connect the designated reactants and products by performing an intrinsic reaction coordinate (IRC)^26,27 analysis. To obtain more accurate energetic data, the single-point energy calculations are carried out at the coupled-cluster singles and doubles plus perturbative triples CCSD(T) method with 6-311++G(d,p) basis set.²⁸ Unless otherwise specified, the energies in this paper include the zero-point energy (ZPE) corrections and scaled by a scaling factor 0.95.²⁹ In other word, these Δ(E + ZPE) values at CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) + 0.95 × ZPE level were used for the reaction mechanism analysis and kinetic calculations. Furthermore, the T1 diagnostic values have been calculated at the CCSD(T)/6-311++G(d,p) level (see Table S3†) and the values of all the species are less than 0.045,^30,31 which implies that the energy data obtained from single-determinant wave function of CCSD(T) are reasonably reliable for this reaction system.

The calculations of rate constants at several temperatures for the primary reactions are performed by employing Rice–Ramsperger–Kassel–Marcus (RRKM) theory with the open source MESMER program.^32,33 The RRKM reaction rate constants are calculated using the following equation:

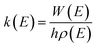where, W(E) is the rovibrational sum of states at the transition state, ρ(E) is density of states of reactants, and h is Planck's constant. The canonical rate constant k(T) is calculated using the following equation:where, Q(T) is the reactant partition function and β = 1/k_BT, where k_B is the Boltzmann's constant and T is the temperature.

3. Results and discussion

As shown in Fig. 1, two different conformers, labeled as A and B, are considered due to the internal rotation around the C₂–C₃ single bond of MIK. According to our calculation, the relative energy of conformer A is 1.95 kcal mol⁻¹ lower than that of B. Therefore, the more stable conformer, A, is chosen for the following investigation.

3.1 Initial reactions of MIK with Cl atoms

For the convenience of discussion, the atomic number in MIK (conformer A) is labeled in Fig. 1. Apparently, there exist C=C and C–H bonds in the molecular structure of MIK. Thus, the initial reactions of MIK with Cl atoms can be classified as two types: Cl addition to C=C bond and H abstraction from the C–H bonds. The two types of reactions can be supported by Wang's recent experimental work.¹⁷ Here the channels of Cl addition to the C=C double bond and H abstraction from the C–H bonds will be studied in detail. The reaction schemes embedded with the potential barriers ΔE^≠ and reaction heats ΔH are presented in Fig. 2.

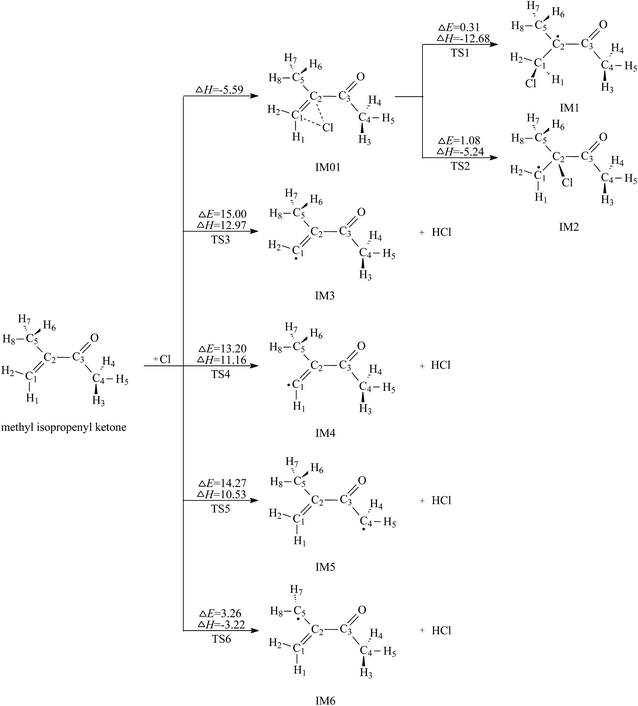Fig. 2 Cl addition pathways and H abstraction pathways embedded with the potential barriers ΔE^≠ (kcal mol⁻¹) and reaction heats ΔH (kcal mol⁻¹).

As seen in Fig. 2, the Cl-addition reactions would proceed through two distinct reaction pathways due to the unequivalence of C₁ and C₂ positions in the double bonds of MIK. For both reaction pathways, the first step leads to the formation of the same pre-reaction complex IM01. In IM01, the distances of C₁–Cl (chlorine atom) and C₂–Cl are 2.605 and 2.588 Å, respectively. The energy of IM01 are 5.59 kcal mol⁻¹ lower than the total energy of the separated reactants (MIK and Cl). Subsequently, IM01 transfers to two radical adducts (IM1 and IM2) via transition states TS1 and TS2 with the imaginary frequencies of 416.70i and 430.14i cm⁻¹, respectively. IRC calculations show that TS1 and TS2 do connect IM01 with IM1 and IM2, respectively. The energy barrier and exothermic heat of the two pathways are 0.31, 12.68 and 1.08, 5.24 kcal mol⁻¹, respectively. Evidently, both Cl-addition pathways are energetically favorable and can readily occur under the general atmospheric conditions.

In MIK molecule structure, the eight H atoms linked to different carbon atoms fall into six species according to their different chemical environment. Therefore, six possible processes are identified: H-abstractions of H₁, H₂, H₃, H₅, H₆ and H₈ atoms. The H-abstractions of H₃ and H₅ atoms occur through the same transition state since the C₃–C₄ bond is rotatable. Similarly, H₆ and H₈ abstraction processes proceed via the same transition state due to the rotation of C₂–C₅ bond. Hence, only four H abstraction pathways are considered and depicted in Fig. 2. Four transition states (TS3, TS4, TS5, and TS6) are located, and each one is identified with only one imaginary frequency. Furthermore, the validity of each transition-state structure is determined by IRC calculations. The geometrical parameters of the four transition states are presented in Fig. 1. Following H abstraction, four intermediate radicals IM3, IM4, IM5, and IM6 are generated. As given in Fig. 2, the energy barriers of the four H abstraction processes are 15.00, 13.20, 14.27 and 3.26 kcal mol⁻¹, respectively. The H abstraction in C₅–H₆ bond is exothermic by 3.22 kcal mol⁻¹, while the other three channels are endothermic by 12.97, 11.16, and 10.53 kcal mol⁻¹. The energy values mentioned above show that the H abstraction from C₅ position is both thermodynamically and kinetically favorable and is easy to occur under the general conditions. In the experimental investigation reported by Wang et al.,¹⁷ it is uncertain whether the H-abstraction process occurs at C₄ or C₅ positions of MIK only according to the experimental measurement. Obviously, our theoretical calculation provides a solid conformation for the feasibility of the H abstraction from C₅ position. Thus, the combination of experiment and theoretical calculation is a wonderful method to obtain more accurate conclusions in this investigation.

Comparing the two Cl-addition pathways and the four H abstraction processes, we can know that the two addition paths are more favorable than H abstraction channels and they dominate the reaction of MIK with Cl atoms. Also, Cl addition to C₁ (terminal carbon) atom is preferred over that to C₂ because the former has a lower energy barrier and exothermicity. From the analysis of the molecular geometry, Cl addition to C₂ has the greater steric hindrance than Cl addition to C₁ (terminal carbon). This conclusion agrees well with the previous experimental study about the reaction of MIK with atomic Cl.¹⁷ For the four H abstraction reactions, the H abstraction from C₅ position is easy to occur due to its low barrier and exothermicity, while the other three H abstraction processes can hardly to take place as they have higher potential barriers and are endothermic.

3.2 Secondary reactions

On the basis of the above discussion, it is shown that both addition and H abstraction from C₅ processes are the dominant pathways for the Cl-initiated atmospheric reaction of MIK. The corresponding products, IM1, IM2, and IM6 are important radical intermediates and their further reactions will be discussed step by step in this section.

3.2.1. Atmospheric reaction pathway of IM1. As an open-shell and highly reactive radical, IM1 can react readily with O₂ molecule to form an organic peroxy intermediate IMa1. This process is barrier-free with 37.29 kcal mol⁻¹ exothermicity. In the troposphere, IMa1 will react immediately with ubiquitous NO. An energy of 23.88 kcal mol⁻¹ is released to produce an excited intermediate IMa2. The geometric structures of IMa1 and IMa2 are depicted in Fig. S2.† IMa2 will undergo unimolecular decomposition which proceeds via the rupture of O₂–O₃ bond, leading to the oxyl radical IMa3 and NO₂. TSa1 represents the transition state for this decomposition process. The O₂–O₃ distance in TSa1 is 1.794 Å, which is 0.368 Å longer than that in IMa2. The potential barrier of this process is calculated to be 7.86 kcal mol⁻¹. IMa3 is an activated alkoxy radical and its further reaction is inevitable in the atmosphere. Two decomposition reactions and one isomerization reaction are found and displayed in Fig. 3.

Fig. 3 Secondary reaction pathways of IM1 with the potential barriers ΔE^≠ (kcal mol⁻¹) and reaction heats ΔH (kcal mol⁻¹).

One decomposition reaction is the cleavage of C₁–C₂ bond to generate 2,3-butanedione (Pa1) and IMa4 by passing transition state TSa2 with the energy barrier value of 6.34 kcal mol⁻¹. The reaction heat of this process is −4.03 kcal mol⁻¹. Subsequently, IMa4 can be further oxidized by O₂ and nitric oxide through two barrier-free steps to produce IMa6. Both association processes are highly exothermic by 23.82 and 17.68 kcal mol⁻¹, respectively. Then, energy-rich IMa6 will promptly decompose to IMa7 and NO₂ via the scission of the O₁–O₂ bond. This dissociation process has a very low energy barrier of 0.93 kcal mol⁻¹. Further reaction from IMa7 is the direct H abstraction by O₂ molecule via the transition state TSa4 with the barrier height of 8.35 kcal mol⁻¹. This H abstraction process leads to the formation of formyl chloride (Pa2) and HO₂ radical with 32.81 kcal mol⁻¹ heat released.

The other decomposition reaction is finished by the rupture of C₂–C₃ bond, leading to chloroacetone (Pa3) and a radical intermediate, denoted IMa8. The transition state of this process is TSa5, in which the C₂–C₃ distance is 1.860 Å (see Fig. S7†). This reaction has a low potential barrier of 2.87 kcal mol⁻¹ and is exothermic by 2.80 kcal mol⁻¹, which means the decomposition reaction is energetically favorable under atmospheric condition. IMa8 has high reactivity and can easily further react via the fission of C₃–C₄ bond to produce CO and IMa9, with the transition state TSa6. The energy barrier and reaction heat of the process are 13.87 and −4.31 kcal mol⁻¹, respectively. The subsequent reactions of IMa9 with O₂/NO proceeds through three elementary steps to generate IMa12. Then, formaldehyde (Pa4) and HO₂ are produced from the reaction of IMa12 with O₂. It can be seen from Fig. 4 that the highest barrier of these four elementary reactions is 11.40 kcal mol⁻¹. Consequently, this formation pathway of Pa4 is energetically favorable in the atmosphere, which provides a theoretical conformation for the formation of Pa4 in experiment.

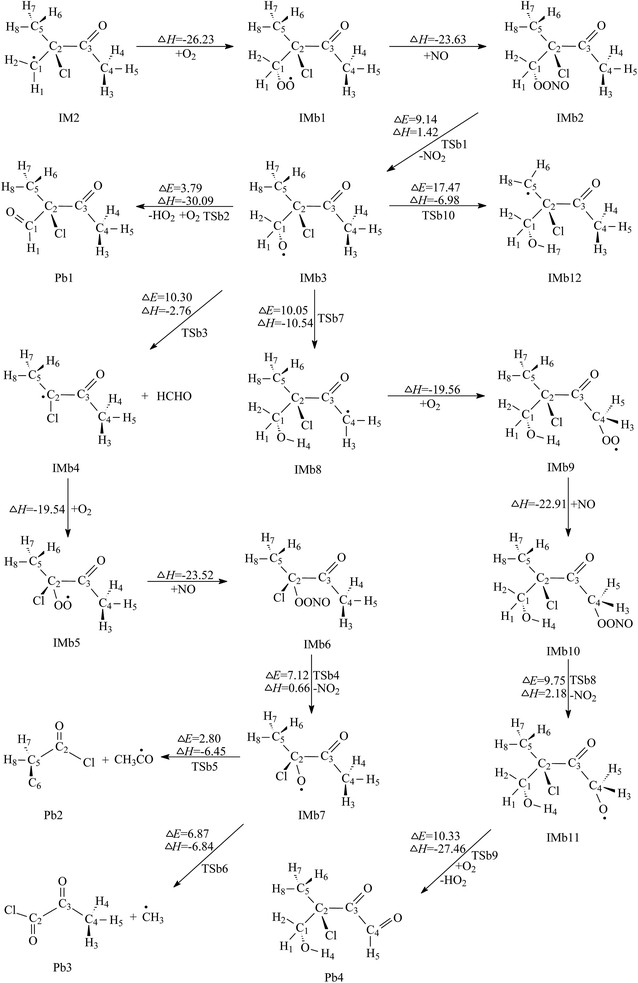Fig. 4 Secondary reaction pathways of IM2 with the potential barriers ΔE^≠ (kcal mol⁻¹) and reaction heats ΔH (kcal mol⁻¹).

The 1,4-H shift isomerization of IMa3 to IMa13 takes place via a five-membered ring transition state, TSa9, with a potential barrier of 7.87 kcal mol⁻¹. The C₄–H₄ and H₄–O₂ distances in TSa9 are 1.235 and 1.295 Å, respectively. Also, the intrinsic reaction coordinate calculation verifies the synchronism of the breakage of C₄–H₄ bond and the generation of O₂–H₄ bond. The geometric structure of TSa9 is presented in Fig. S3.† Further reaction of IMa13 that results in the product of 4-chloro-3-hydroxy-3-methyl-2-oxobutanal (Pa5) involves four elementary processes: two free-barrier processes with high exothermicity and two elementary processes with low energy barriers. Accordingly, these elementary steps are both thermodynamically and kinetically favorable under atmospheric conditions. The product of Pa5 should be present in photochemical smog. Unfortunately, Pa5 was not detected in the experimental study by Wang et al.¹⁷ Further experimental observation would be anticipated to confirm the formation of Pa5.

Comparing three further reactions of intermediate IMa3, we can find that the decomposition by the cleavage of C₂–C₃ bond is the most favorable pathway. Pa3 and Pa4 are the dominant products. The 1,4-H shift isomerization pathway is favorable in thermodynamics and kinetics.

3.2.2. Atmospheric reaction pathway of IM2. As depicted in Fig. 4, IM2 firstly reacts with O₂ and NO in turn to form the peroxy radical IMb2. 26.23 and 23.63 kcal mol⁻¹ are the corresponding exothermic energies of the two barrierless processes. Then, energy-rich IMb2 breaks down to IMb3 and NO₂ is removed via TSb1, respectively with the energy barrier of 9.14 kcal mol⁻¹ and endothermic heat of 1.42 kcal mol⁻¹. There are four possible reaction pathways for further reaction of the oxyl radical IMb3.

The first one is the reaction of IMb3 with O₂ molecule. In this process, H₂ atom linked to C₁ is directly abstracted by O₂ to form 2-chloro-2-methyl-3-oxobutanal (Pb1) and HO₂. TSb2 is the transition state in which the distances of C₁–H₂ and O₄–H₂ are 1.226 and 1.351 Å, respectively. Calculations indicate that this process has a low potential barrier of 3.79 kcal mol⁻¹ and is strongly exothermic of 30.09 kcal mol⁻¹, which suggests that this O₂ direct abstraction can occur readily. The product of Pb1 was detected in the reaction chamber of the Cl-initiated atmospheric reaction of MIK.¹⁷

The second channel is unimolecular decomposition that is initiated from the C₁–C₂ bond breakage through the transition state TSb3. The formation of Pa4 and IMb4 is an exothermic process by releasing 2.76 kcal mol⁻¹ heat quantities, with the energy barrier of 10.30 kcal mol⁻¹. The intermediate IMb4 then combines with O₂ and NO sequentially, forming IMb6. Both free-barrier processes are exothermic by 19.54 and 23.52 kcal mol⁻¹. Then IMb6 will be changed to IMb7 by releasing NO₂. This process should overcome 7.12 kcal mol⁻¹ energies and absorb 0.66 kcal mol⁻¹ heat quantities. For IMb7, two reaction channels are taken into account. The first one is the decomposition of IMb7 via C₂–C₃ bond scission to generate acetyl chloride (Pb2) and IMa8. The barrier height is very low, only 2.80 kcal mol⁻¹. This process is exothermic by 6.45 kcal mol⁻¹. The second channel proceeds through the C₂–C₅ bond rupture to produce 2-oxopropanoyl chloride (Pb3) and IMa9. The energy barrier and the exothermic heat of this process is calculated to be 6.87 and 6.84 kcal mol⁻¹, respectively. Thus, the decomposition pathways of IMb7 to Pb2 or Pb3 are energetically favorable. Comparing the energy barriers of the two decomposition channels, the first decomposition is more favorable than the second one, which is revealed for the first time.

The third channel of IMb3, called 1,5-H shift isomerization, occurs via a six-membered ring transition state, TSb7, to yield IMb8. In the structure of TSb7, the breaking C₄–H₄ bond is elongated by 12.42% with respect to the equilibrium value of 1.095 Å in IMb3, while the forming H₄–O₂ bond is shortened by 30.83% with respect to the equilibrium value of 0.960 Å in IMb8. The structure of TSb7 is illustrated in Fig. S3.† The energy barrier and the exothermic heat of this process are 10.05 and 10.54 kcal mol⁻¹, respectively. The subsequent reaction of resulting radical intermediate IMb8 can generate 3-chloro-4-hydroxy-3-methyl-2-oxobutanal (Pb4) via the different mechanisms which include O₂ addition, NO addition, breakage of O–ONO bond and H abstraction by O₂. The calculated profiles of the potential energy surface show that these elementary steps are easy to occur due to lower potential barriers and strong exothermicity. This indicates that the product Pb4 should be a secondary pollutant present in the experiment chamber. Unluckily, this whole isomerization pathway form IMb3 to Pb4 was not considered in previous experimental study.¹⁷ Hence, this is the first time to report the feasible isomerization pathway of IMb3 and its conformation needs further more experimental investigations. The fourth channel of IMb3 takes place via H₇ migration to form IMb12. A five-membered ring transition state, TSb10, is identified as being associated with this 1,4-H shift isomerization process. The distances for the breaking C₅–H₇ and the forming H₇–O₂ are 1.248 and 1.297 Å, respectively. This isomerization process overcomes a high potential barrier of 17.47 kcal mol⁻¹, and releases an energy of 6.98 kcal mol⁻¹ to the surroundings. It can be inferred that this isomerization reaction is not expected to be important as it has a much higher energy barrier than the above three channels. Consequently, further reaction of IMb10 can be ignored.

Comparison of the calculated results reveals that the first channel (O₂ direct abstraction reaction) is preferred over the other three ones due to the lowest energy barrier. Both the second and the third channels are competitive. Pb1 and Pb2 are the dominant products for further reaction of IMb3.

3.2.3. Atmospheric reaction pathway of IM6. IM6 is the primary intermediate produced from the hydrogen abstraction pathways of MIK by atomic Cl. Fig. 5 exhibits the possible reaction routes from IM6. Similar to IM1 and IM2, IM6 can also react with O₂/NO through three elementary steps to form NO₂ and an alkoxy radical, IMc3. The geometric parameters of IMc3 are depicted in Fig. S2.† The following reaction of IMc3 will proceed via three different paths under the atmospheric conditions. The first path is the O₂ direct H-abstraction, which occurs via TS10, followed by the loss of HO₂, to produce 2-methylene-3-oxobutanal (Pc1), with a potential barrier of 7.08 kcal mol⁻¹. This process is strongly exothermic by up to 29.04 kcal mol⁻¹. Thus, Pc1 should be the product for further reaction of IM6. The second path of IMc3 is the cleavage of C₂–C₅ bond and IMc4 + HCHO are produced via the transition state TSc3 with a high energy barrier of 28.64 kcal mol⁻¹. Both the reaction heat and Gibbs free energy change are positive values, 22.74 and 11.65 kcal mol⁻¹, respectively, which indicates that this decomposition process is unlikely to occur spontaneously under the atmospheric conditions. The third path is the isomerization of IMc3 via 1,5-H shift, which leads to IMc5. A six-membered ring transition state, TSc5, is identified with a potential barrier of 15.12 kcal mol⁻¹. This process is found to be an endothermic process, with an absorption heat of 10.65 kcal mol⁻¹. Moreover, the Gibbs free energy change is 10.30 kcal mol⁻¹, which is far greater than zero. It can be inferred that this isomerization process can not take place spontaneously.

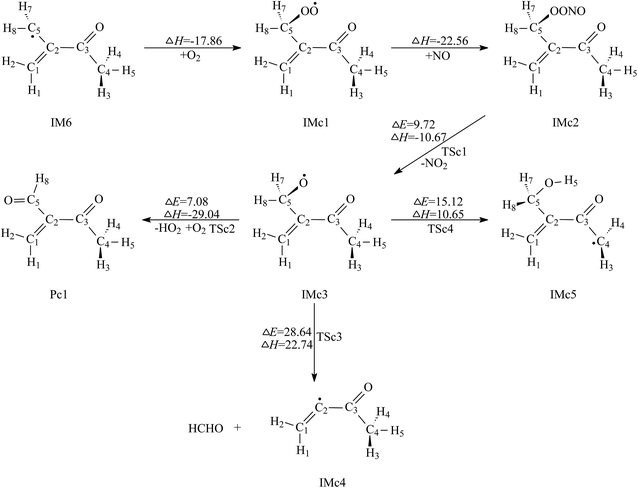Fig. 5 Secondary reaction pathways of IM6 with the potential barriers ΔE^≠ (kcal mol⁻¹) and reaction heats ΔH (kcal mol⁻¹).

Comparison of the above calculated data reveals that the second and the third paths, i.e. decomposition via C₂–C₅ bond fission and 1,5-H shift isomerization, can be ignored, while the first path, i.e. O₂ abstracting reaction, will be the dominant removal pathway of IMc3. Pc1 and HO₂ are the products for further reaction of IM6.

3.3 Rate constant calculations

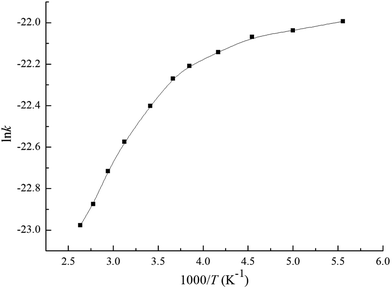
Based on the above thermodynamic results, the individual and overall rate constants for the primary reactions including the Cl additions and the H abstractions are calculated with the Rice–Ramsperger–Kassel–Marcus (RRKM) theory. A suitable temperature range of 180–380 K is selected to study the relationship between the temperature and rate constant. The rate constants k₁ and k₂ are for Cl addition to C₁ and C₂ atoms, while k₃ to k₆ correspond to H abstraction from C₁–H₁, C₁–H₂, C₄–H₃, and C₅–H₆, respectively. The overall rate constant of OH-addition channels and H-abstraction reactions are denoted as k_add, and k_abs, respectively. The total rate constant for the reaction of MIK with Cl atoms is labeled as k_tot, where k_add = k₁ + k₂, k_abs = k₃ + k₄ + 3k₅ + 3k₆, then k_tot = k_add + k_abs.

The individual and overall rate constants are calculated in the temperature range of 180–380 K and they are fitted in the two-parameter Arrhenius formula k = A exp(−E_a/RT). The calculated rate constants and the Arrhenius formulas are given in Table 1. Under the pressure of 760 Torr and at 293 K, the calculated total rate constant is 1.87 × 10⁻¹⁰ cm³ per molecule per s. This value matches well with available experimental value ((2.38 ± 0.26) × 10⁻¹⁰ cm³ per molecule per s) with a maximum relative deviation of less than two times, which indicates that our calculation in this work is thought as reasonable. The ln k_tot versus 1000/T are depicted in Fig. 6. We can clearly see that k_tot shows negative temperature dependence over the studied interval. The Arrhenius equation of the total rate coefficient over the temperature of 180–380 K is fitted as k_tot = (5.31 × 10⁻¹¹)exp(−335.24/T). It is evident from Table 1 the overall rate constant of Cl-addition reactions (1.83 × 10⁻¹⁰ cm³ per molecule per s) is about two orders of magnitude higher than that of H-abstraction reactions (3.48 × 10⁻¹² cm³ per molecule per s) under the same conditions, which means that the Cl-addition reactions are easier to take place than the H-abstraction reactions. For the addition pathways, k₁ is nearly an order of magnitude higher than k₂, which indicates that the more favorable pathway is the Cl addition to the terminal carbon (C₁) of the C=C bond. Compared all the possible H abstraction channels, we can see that the rate constants are k₆ > k₄ > k₅ > k₃. Moreover, k₆ is more than ten orders of magnitude higher than k₃, k₄, and k₅. Hence, Cl abstracting the H atom from C₅ position is predominant in the abstraction reactions and the other three channels can be neglected.

Table 1 Rate constants k (cm³ per molecule per s) at 293 K and Arrhenius formulas for the reaction of MIK with Cl atoms over the temperature range of 180–380 K^a

Reactions	Arrhenius formulas	k293 K
a At 293 K, kadd = 1.83 × 10^−10, kabs = 3.48 × 10^−12, ktot = 1.87 × 10^−10.
MIK + Cl → IM1	k1(T) = 4.18 × 10^−10 exp(−373.34/T)	1.61 × 10^−10
MIK + Cl → IM2	k2(T) = 8.36 × 10^−11 exp(−352.33/T)	2.19 × 10^−11
MIK + Cl → IM3 + HCl	k3(T) = 9.52 × 10^−15 exp(−6445.13/T)	2.61 × 10^−24
MIK + Cl → IM4 + HCl	k4(T) = 1.62 × 10^−15 exp(−4996.08/T)	9.19 × 10^−23
MIK + Cl → IM5 + HCl	k5(T) = 4.02 × 10^−15 exp(−5804.12/T)	2.05 × 10^−23
MIK + Cl → IM6 + HCl	k6(T) = 1.58 × 10^−13 exp(−573.59/T)	1.16 × 10^−12

---

Fig. 6 Rate constants for the reaction of MIK with Cl at different temperatures and 760 Torr.

The atmospheric lifetime of MIK can be calculated using the following expression:

Here k is the total rate constant obtained in this work and [Cl] is the atmospheric concentration of Cl which is 1.0 × 10⁴ molecules per cm³.³⁴ The calculated atmospheric lifetime of MIK determined by the concentration of Cl atoms is approximately 148.54 h, which is in good agreement with the observed value of 116.71 h. In the coastal marine boundary layer and some industrial areas, the average daytime concentration of Cl atoms is as high as 3.0 × 10⁵ molecules per cm³.¹⁴ Under the circumstances, atmospheric lifetime of MIK with Cl is only 4.95 h, which suggests that Cl-initiated oxidation of MIK could compete with the corresponding hydroxylation reaction (3.86 h).³⁵ This implies that Cl-initiated reaction of MIK plays an important role in the marine boundary layer and some special areas.

3.4 Discussion of structure impact on reaction activity

In order to evaluate the effect of structure on reaction reactivity of this series of unsaturated aldehydes and ketones, rate constants of Cl-initiated acrolein (ACR, CH₂=CHCHO), methacrolein (MACR, CH₂=C(CH₃)CHO), and methyl vinyl ketone (MVK, CH₂=CHC(O)CH₃) were calculated at 298 K and 760 Torr. As displayed in Table 2, all the kinetic data are in accord with their corresponding experimental values previously reported.^36–40 Compared all the addition channels of these four compounds, we can see that the rate constants of addition channels are k_add-MACR > k_add-ACR > k_add-MIK > k_add-MVK. Also, the total rate constants are k_tot-MACR > k_tot-ACR > k_tot-MIK > k_tot-MVK. This phenomenon can be explained from the electron-donating effects of methyl group and the electron-withdrawing properties of ketone group in the concerned molecules. The inductive effect of methyl group (in methacrolein and methyl isopropenyl ketone) increases the reactivity due to the electron-donating inductive effect of the methyl group attached to the double bond. On the contrary, the adjacent ketone group (in methyl vinyl ketone and methyl isopropenyl ketone) decreases the reactivity because the oxygen has the electron-withdrawing properties.

Table 2 The overall rate constant of addition channels and the total rate constant for the reaction of ACR, MACR, MVK, MIK with Cl atoms at 298 K and 760 Torr

Compound	Rate constant/10^−10 cm^3 per molecule per s
	kadd	ktot	kexp
Acrolein	1.94	1.96	2.5 ± 0.7 (ref. 36)
			2.0 ± 0.3 (ref. 37)
			2.2 ± 0.3 (ref. 38)
Methacrolein	2.38	2.42	2.9 ± 0.8 (ref. 36)
			3.2 ± 0.5 (ref. 39)
Methyl vinyl ketone	1.59	1.59	2.0 ± 0.5 (ref. 36)
			2.0 ± 0.2 (ref. 40)
			2.1 ± 0.5 (ref. 39)
Methyl isopropenyl ketone	1.82	1.86

---

4. Conclusions

The atmospheric oxidation reaction of MIK initiated by atomic Cl was investigated using quantum chemical methods. The conclusions are drawn as follows:

(1) Two types of reactions, Cl additions and H abstractions, involved in the initial reactions of MIK with Cl atoms, are considered based on the experimental data. Our calculations show that Cl-addition pathways are favored over H-abstraction channels and Cl addition to terminal carbon C₁ in C=C bond is the most energetically favorable pathway, which supports the experimental results. Among the four possible H abstraction processes, only the H abstraction from C₅ position is confirmed to be feasible by our study. This resolves the uncertainty of H-abstraction encountered in experiment.

(2) Four alkoxy radical isomerization processes are proposed and investigated theoretically in our work. The calculated results indicate that the two processes (1,4-H shift isomerization of IMa3 and 1,5-H shift isomerization of IMb3) can take place under atmospheric conditions. The formation of the corresponding isomerization products, 4-chloro-3-hydroxy-3-methyl-2-oxobutanal and 3-chloro-4-hydroxy-3-methyl-2-oxobutanal, needs further experimental observation. In addition, our study clearly indicated that 2-methylene-3-oxobutanal is the only product formed from the H abstractions.

(3) The calculated total rate constants match the experimental values well at the same temperature and pressure. The Arrhenius equation of the total rate coefficient over the temperature range of 180–380 K is fitted as k_tot = (5.31 × 10⁻¹¹)exp(−335.24/T). The atmospheric lifetime of MIK in the presence of Cl is estimated to be 197.01 h.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Shandong Province Natural Science Foundation (No. ZR2017MB050, ZR2017QB001), National Natural Science Foundation of China (No. 21473100, 21702119, 21207078) and Qufu Normal University Research Fund (No. XJ201206).

References

1. S. K. Akagi, R. J. Yokelson, I. R. Burling, S. Meinardi, I. Simpson, D. R. Blake, G. R. McMeeking, A. Sullivan, T. Lee, S. Kreidenweis, S. Urbanski, J. Reardon, D. W. T. Griffith, T. J. Johnson and D. R. Weise, Atmos. Chem. Phys., 2013, 13, 1141–1165.
2. J. D. McDonald, B. Zielinska, E. M. Fujita, J. C. Sagebiel, J. C. Chow and J. G. Watson, Environ. Sci. Technol., 2000, 34, 2080–2091.
3. D. E. Seizinger and B. Dimitriades, J. Air Pollut. Control Assoc., 1972, 22, 47–51.
4. M. Dicke, Plant, Cell Environ., 2009, 32, 654–665.
5. P. G. N. Mertens, H. Poelman, X. Ye, I. F. J. Vankelecom, P. A. Jacobs and D. E. De Vos, Catal. Today, 2007, 122, 352–360.
6. U. S. Coast Guard, Department of Transportation, CHRIS-Hazardous Chemical Data. Manual Two, U.S. Government Printing Office, Washington, DC, Oct 1978.
7. Industrial Hygiene and Toxicology: Volume II: Toxicology, ed. F. Patty, Interscience Publishers, New York, 2nd edn, 1963, p. 1753.
8. Patty's Industrial Hygiene and Toxicology: Volume 2A, 2B, 2C: Toxicology, ed. G. D. Clayton and F. E. Clayton, John Wiley Sons, New York, 3rd edn, 1981–1982, p. 4722.
9. A. Mellouki, G. Le Bras and H. Sidebottom, Chem. Rev., 2003, 103, 5077–5096.
10. A. Mellouki, T. J. Wallington and J. Chen, Chem. Rev., 2015, 115, 3984–4014.
11. E. Galán, I. González and B. Fabbri, Atmos. Environ., 2002, 36, 5289–5298.
12. L. H. Mielke, F. Amanda and H. D. Osthoff, Environ. Sci. Technol., 2011, 45, 8889–8896.
13. J. A. Thornton, J. P. Kercher, T. P. Riedel, N. L. Wagner, C. Julie, J. S. Holloway, W. P. Dubé, G. M. Wolfe, P. K. Quinn and A. M. Middlebrook, Nature, 2010, 464, 271–274.
14. C. T. Chang, T. H. Liu and F. T. Jeng, Environ. Res., 2004, 94, 67–74.
15. R. Atkinson, D. L. Baulch, R. A. Cox and J. N. Crowley, Atmos. Chem. Phys., 2006, 6, 3625–4055.
16. C. E. Canosa-Mas, M. L. Flugge, M. D. King and R. P. Wayne, Phys. Chem. Chem. Phys., 2005, 7, 643–650.
17. J. Wang, L. Zhou, W. Wang and M. Ge, Phys. Chem. Chem. Phys., 2015, 17, 12000–12012.
18. M. Frisch, G. Trucks, H. B. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, revision A. 02, Gaussian. Inc., Wallingford, CT, 2009, vol. 270, p. 271.
19. C. Mǿller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
20. G. D. Fletcher, A. P. Rendell and P. Sherwood, Mol. Phys., 1997, 91, 431–438.
21. EMSL Basis Set Library, http://www.emsl.pnl.gov/forms/basisform.html.
22. H. Xie, F. Ma, Y. Wang, N. He, Q. Yu and J. Chen, Environ. Sci. Technol., 2015, 49, 13246–13255.
23. X. Wang, F. Bai, Y. Sun, R. Wang, X. Pan and F. Tao, J. Phys. Chem. A, 2017, 121, 226–237.
24. W. Zhang and D. Zhang, Mol. Phys., 2012, 110, 2901–2917.
25. P. Biswas, J. Theor. Comput. Chem., 2015, 14, 1550010.
26. C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161.
27. C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527.
28. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975.
29. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
30. T. J. Lee and P. R. Taylor, Int. J. Quantum Chem., Quantum Chem. Symp., 1989, 23, 199–207.
31. J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer III, J. Phys. Chem. A, 2000, 104, 9823–9840.
32. P. J. Robinson and K. A. Holbrook, Unimolecular Reactions, John Wiley & Sons, 1972.
33. D. R. Glowacki, C. H. Liang, C. Morley, M. J. Pilling and S. H. Robertson, J. Phys. Chem. A, 2012, 116, 9545–9560.
34. M. B. Blanco, I. Bejan, I. Barnes, P. Wiesen and M. A. Teruel, Environ. Sci. Pollut. Res., 2009, 16, 641–648.
35. D. Grosjean and E. L. Williams, Atmos. Environ., Part A, 1992, 26, 1395–1405.
36. W. H. Wang, M. J. Ezell, A. A. Ezell, G. Soskin and B. J. Finlayson, Phys. Chem. Chem. Phys., 2002, 4, 1824–1831.
37. M. Ullerstam, E. Ljungström and S. Langer, Phys. Chem. Chem. Phys., 2001, 3, 986–992.
38. C. E. Canosa-Mas, E. S. N. Cotter, J. Duffy, K. C. Thompson and R. P. Wayne, Phys. Chem. Chem. Phys., 2001, 3, 3075–3084.
39. C. E. Canosa-Mas, H. R. Hutton-Squire, M. D. King, D. J. Stewart, K. C. Thompson and R. P. Wayne, J. Atmos. Chem., 1999, 34, 163–170.
40. B. J. Finlayson-Pitts, C. J. Keoshian, B. Buehler and A. A. Ezell, Int. J. Chem. Kinet., 1999, 31, 491–499.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09445k

---