Open Access Article
Open Access ArticleRheological reversibility and long-term stability of repulsive and attractive nanoemulsion gels†
Vivek Vardhan Erramreddy,
Sylvana Tu and
Supratim Ghosh *
*
Department of Food and Bioproduct Sciences, University of Saskatchewan, Saskatoon, Saskatchewan, Canada. E-mail: supratim.ghosh@usask.ca; Fax: +306-966-8898; Tel: +306-966-2555
First published on 10th October 2017
Abstract
In this research, the stability of sodium dodecyl sulfate (SDS)-stabilized canola oil nanoemulsion gels was investigated as a function of repeated rotational shear, oscillatory strain and storage time. Nanoemulsion gels, termed nanogels, were formed from oil-in-water nanoemulsions, prepared with various concentrations of SDS to get a range of droplet sizes, interdroplet interactions, and gel strengths. Repulsive nanogels were formed with 0.5, 1 and 2 times the critical micelle concentration (CMC), while attractive nanogels were prepared with 5, 10 and 15 times the CMC of SDS. No change in droplet size of the nanoemulsions was observed over a period of 90 days and an accelerated gravitation study indicated extremely high stability against creaming. All nanogels showed a remarkable recovery in viscosity and gel strength during repeated shear and strain sweep experiments, respectively. Interestingly, the elastic storage moduli (G′) for the repulsive nanogels significantly decreased, converting the nanogels into flowable weak gels. For attractive nanogels, the decrease in G′ was less. It was proposed that generation of surface active components due to lipid oxidation may alter the interfacial composition and ultimately reduce the thickness of the charge cloud leading to a reduction in G′ in the repulsive nanogels. For attractive nanogels, the uptake of lipid oxidation products in the excess micelles and their inter-droplet transfer led to a decrease in the attractive depletion interactions and charge cloud, with subsequent loss of the gel structure. The nanogels possess great potential for use in food and related soft materials provided the loss of gel strength with time could be prevented.
Introduction
Emulsions exhibit a broad range of different rheological properties, ranging from low viscosity liquids (e.g., milk, lotion) to viscoelastic solids (margarine, butter and other related soft materials).1 Recently gelation in nanoemulsions has also garnered much attention due to their unique properties such as gelation at a much lower oil volume fraction compared to conventional emulsions, and extremely high stability.2–4Rheological properties of emulsions and nanoemulsions provide information that helps to understand structural organization and interactions within emulsions and their shelf-life. It depends on many factors such as packing or volume fraction (ϕ) of the dispersed phase droplets, properties of the continuous phase, and the type, size and strength of interactions between the dispersed droplets.1,5–7 Emulsions' rheological behaviour can transform from liquid to viscoelastic solid depending on the ϕ. In dilute emulsions (ϕ < 0.05) the droplets do not interact with each other, as they are sufficiently far apart. Such emulsions exhibit relatively low viscosity, which is dominated by the influence of the continuous phase. As the emulsion becomes more concentrated (0.05 < ϕ < 0.49), interactions between the droplets through collisions, hydrodynamic interactions become appreciably higher hindering their movement within the continuous phase resulting in an increase in emulsion viscosity.8,9 With a increase in ϕ, viscosity increases and for 0.58 < ϕ < 0.64, the movement of droplets become severely restricted as each droplet is caged between the neighbors and separated by a thin layer of continuous phase between them.10 These systems are known as colloidal glasses where the droplets can only vibrate in the cage, but cannot move past each other. When ϕ is close to 0.64 dramatic increase in viscosity and viscoelastic behaviour of emulsions is observed.1,11–13 For monodispersed emulsions at ϕ = 0.64 droplets surface touch with each other and when ϕ is higher than 0.64 droplets become compressed and deformed. This deformation leads to an increase in interfacial area, which results in energy stored in the droplets that manifest as elasticity (G′ > G′′).10,14 Many simulations and experimental works done by different researcher groups have found jamming transition of monodispersed droplets at ϕ = 0.64, commonly known as random close packing (RCP) or the point of maximal random jamming (MRJ).2,15 For polydisperse emulsions jamming transition usually occurs at a higher values of ϕ as smaller droplet can fit in the interstices of larger droplets.
Another major factor that influences the rheological properties of emulsions is the interactions (repulsive or attractive) between the dispersed droplets.1,7,16,17 Electrostatic interactions arise due to the surface charge caused by adsorption of ionic emulsifiers on the droplets and their surrounding counter ions in the continuous phase. It plays a significant role in preventing droplets from aggregation. Part of the counterion charge cloud around the droplets are strongly associated and prevents close approach of other droplets with their charge cloud resulting in an increase of effective droplet size and corresponding effective droplet volume fraction (ϕeff). This increase in ϕeff due to charge cloud, however, strongly dependent on the dispersed phase droplet size below a critical level. In conventional emulsions the thickness of the charge cloud (δ) has negligible influence on the effective droplet size and ϕeff, however, in nanoemulsions, with average droplet radius (r) less than 100 nm, the thickness of the charge cloud becomes similar order of magnitude to the actual droplet size. In this case, ϕeff becomes significantly larger than the actual volume fraction (ϕcore) according to:
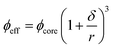 | (1) |
From eqn (1) it can be seen that as r decreases, the thickness of the interfacial layer (δ) significantly contributes to the ϕeff. As a consequence, rheological properties of such repulsive emulsions with a high value of ϕeff would be similar to that of highly concentrated emulsions.17 Recently we have shown that sodium dodecyl sulfate (SDS)-stabilized 40 wt% canola oil-in-water repulsive nanoemulsions transformed from fluids (G′ < G′′) at droplet size >250 nm to weakly gelled glassy state (G′ > G′′) at around 224 nm to strongly viscoelastic jammed state below 200 nm (G′ ≫ G′′).18
In some emulsions, long-range attractive interaction such as depletion force leads to extensive droplet aggregation and formation tenuous network which entraps continuous phase and forms a colloidal gel.7 These emulsions exhibit yield stress, and elastic properties similar to that of highly concentrated emulsions even at very low ϕ (ϕ ≪ ϕMRJ).7 The flow and viscoelastic properties of these emulsions are characterized by the droplet size, strength of attractive interactions and the interdroplet network structure. We found a rapid increase in gel strength in SDS-stabilized 40 wt% oil-in-water attractive nanoemulsion (depletion attraction in the presence of excess SDS micelles) when the droplet size decreased from 143 nm to 130 nm, which was explained by a combined effect of ϕeff increase and the formation of stronger fractal network with a higher number of nano-scale droplets.18
In this work, we are interested in understanding the long-term stability of the SDS-stabilized canola oil nanoemulsion gels, termed as nanogels, with a range of gel strength and interdroplet interactions. It should be noted that the term nanogel is also referred to nanoscale hydrogel particles.19 In the present case, the term nanogel is referred to the whole system where a nanoemulsion is transformed into a nano-particulate gelled material. The nanogels were formed from nanoemulsions, which were prepared with SDS concentrations ranging from 0.5 to 15 times critical micelle concentration (CMC) giving rise to a range of repulsive and attractive interactions among the nanodroplets. For these nanogels to find suitable application in food and related industry it is important that their gel-stability remain unaffected under long-term storage condition. Properties of out-of-equilibrium colloids such as repulsively jammed and attractive gels are known to evolve slowly towards equilibrium with time; a behaviour known as aging.20,21 In other words, they exhibit-ultra slow relaxation during which their viscoelasticity evolve.22 The effect of aging mechanism on the viscoelasticity of glasses and gels has been studied by few researchers.23,24 However, most of the studies investigated the aging on the time scale of minutes to hours if not days.21 In the current study we have aged the nanogels over a period of 3 months (90 days) and determined their elasticity as a function of time.
Also important is to investigate how the elasticity of these nanogels varies with repeated application of shear. It is desired that the nanogels gain their elasticity after removal of external shear, so that their behaviour remains unaffected. The yielding behaviour of repulsive glasses and attractive colloidal gels have been extensively studied. It was found that repulsive glasses yield by cage-breaking process where distortions of neighbouring droplets lead to breakdown of elastic behaviour.25,26 Attractive colloidal gels, on the other hand, goes through a series of process during yielding, starting from breaking the attractive bonds between the droplet clusters, which in turn break the network, resulting in smaller clusters of droplets which can flow past each other and finally breakdown of the small clusters into individual particles leading to a viscous flow.27 Similar observation based on the rheological experiments on attractive gels have been made by Datta et al.7
In this work, rheological reversibility of the SDS-stabilized canola oil nanogels in both the repulsive and attractive regimes was tested using repeated shear and strain sweep analysis. An estimation of the long-term stability of the nanogels was also obtained under accelerated gravitation. Finally, the evolution in visual observation in flow behaviour, droplet size and viscoelastic behaviour of the nanogels was determined as a function of time for 90 days and the results were explained using a proposed change in inter-droplet interactions and lipid chemical reactivity.
Materials and methods
Materials
Canola oil was purchased from a local grocery store and stored at room temperature in the dark. De-ionized water (conductivity of 8.2 μS cm−1) was used for the aqueous phase. Sodium dodecyl sulfate (SDS) (>99% purity) and mineral oil (O-121) were purchased from Fisher Scientific (Nepean, ON, Canada). All other chemicals were purchased from Sigma-Aldrich (St. Louise, MO, USA).Nanoemulsion preparation
O/W nanoemulsions were prepared by pre-mixing 40 wt% oil phase with aqueous phase containing different amounts of SDS emulsifier in a rotor–stator mixer (Polytron, Brinkmann instruments, Ontario, Canada) for 30 seconds at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm, followed by high-pressure homogenization (EmulsiFlex-C3, Avestin Inc., Ottawa, ON, Canada) at a pressure of 20
000 rpm, followed by high-pressure homogenization (EmulsiFlex-C3, Avestin Inc., Ottawa, ON, Canada) at a pressure of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 psi (137.9 MPa) for 7 passes. Emulsification was performed at room temperature (25.5 °C ± 0.5 °C), although the temperature of the product increased to 60 °C during homogenization. Emulsifier concentrations were chosen based on the critical micelle concentration (CMC) of SDS (CMC = 8.3 mM). Six different emulsifier concentrations were used: 0.5, 1, 2, 5, 10 and 15 times SDS CMC (ranged from 4.15 to 124.5 mM). Based on our previous work, nanoemulsions stabilized with 0.5, 1 and 2 times SDS CMC were in the repulsive regime where repulsive electrostatic interaction exists between the nanodroplets.18 In contrast, nanoemulsions with 5, 10 and 15 times SDS CMC were in the attractive regime, where excess SDS micelles in the continuous phase induced depletion attraction among the nanodroplets.18 A part of the sample was stored for 90 days at room temperature in 40 mL glass vials for visual observation, and the rest was stored in 120 mL glass bottles (VWR International, Edmonton, AB, Canada) for further analysis.
000 psi (137.9 MPa) for 7 passes. Emulsification was performed at room temperature (25.5 °C ± 0.5 °C), although the temperature of the product increased to 60 °C during homogenization. Emulsifier concentrations were chosen based on the critical micelle concentration (CMC) of SDS (CMC = 8.3 mM). Six different emulsifier concentrations were used: 0.5, 1, 2, 5, 10 and 15 times SDS CMC (ranged from 4.15 to 124.5 mM). Based on our previous work, nanoemulsions stabilized with 0.5, 1 and 2 times SDS CMC were in the repulsive regime where repulsive electrostatic interaction exists between the nanodroplets.18 In contrast, nanoemulsions with 5, 10 and 15 times SDS CMC were in the attractive regime, where excess SDS micelles in the continuous phase induced depletion attraction among the nanodroplets.18 A part of the sample was stored for 90 days at room temperature in 40 mL glass vials for visual observation, and the rest was stored in 120 mL glass bottles (VWR International, Edmonton, AB, Canada) for further analysis.
Droplet size distribution
Droplet sizes distribution of the nanoemulsions were measured as a function of time for 90 days by a static laser diffraction particle size analyzer (Mastersizer 2000, Malvern Instruments, Montreal, QC, Canada) with a relative refractive index of the dispersed vs. continuous phases as 1.465. Nanoemulsion average droplet size was characterized by surface area mean diameter (d32).Apparent viscosity
All rheology experiments were performed using an AR G2 rheometer (TA Instrument, New Castle, DE, USA) at room temperature. Nanoemulsions were gently transferred onto the lower stationary plate of the rheometer by a spatula so that the gel structure was not disturbed. A 40 mm diameter cross-hatched geometry plate was used to apply shear on the samples to avoid any wall slip effect (geometry gap 1000 μm). Samples were equilibrated for 30 s before applying any shear. Influence of repeated shearing on the viscosity of the nanoemulsions was determined in three steps, first as a function of increasing shear from 0.01 to 1000 s−1, followed by decreasing shear from 1000 to 0.01 s−1 and then repeating the first step again. There was no equilibration or residence time after reaching both the limits of applied shear rate.Viscoelasticity
Reversibility in the viscoelastic behaviour of the nanoemulsions was determined by repeated strain sweep measurements within the frequency independent region using the same AR G2 rheometer and geometry settings as in viscosity measurements. Initially, strain sweep experiments were done at a range of frequencies to find the frequency independent viscoelastic behaviour. An example data is given in Fig. S1 of the ESI data.† Then a three-steps (ascending, descending and second ascending) strain sweep measurement was performed in the range 0.01 to 100% strain and at a constant frequency of 1 Hz (6.28 rad s−1). For all experiments, storage (G′) and loss (G′′) moduli of the nanoemulsions were recorded and further data analysis was done using the Rheology Advantage software (TA Instrument, New Castle, DE, USA). To assess the long-term stability of the gel network, strain-sweep viscoelastic behaviour of the nanoemulsions was also recorded as a function time on day 15, 30, 60 and 90.Freeze fracture scanning electron microscopy (FE-SEM)
The FE-SEM analysis of the nanogels was performed at the University of Guelph, ON, Canada. Samples (3 mm3) were mounted on a copper holder designed for the Emitech 1250× Cryo-preparation unit (Ashford, Kent, UK). A cryo-mounting gel (Tissue-Tek®), was used to ensure that the samples were affixed to the holder. The copper holders were plunged into liquid nitrogen slush (−207 °C) which was prepared by pulling a vacuum on the liquid nitrogen (thereby forming a mixer of solid and liquid nitrogen). After freezing, the copper holder was withdrawn from the freezing chamber through argon to prevent frost forming on the surface of the samples. Once into the transfer device the samples are put under vacuum and transferred frozen into the preparation chamber of the cryo unit where the frozen samples were fractured to provide a fresh surface free of frost. After that the samples were coated with <30 nm of gold in the Emitech cryo-preparation system at <−135 °C. Next, the sample holder was transferred, frozen and under vacuum, onto the cold stage in the SEM (Hitachi S-570 at the Department of Food Science, University of Guelph, ON). The temperature was maintained at <−150 °C. Images were captured digitally using Quartz PCI imaging software (Quartz Imaging Corp. Vancouver, BC).Accelerated shelf-life study
The accelerated shelf-life of the nanoemulsions were determined using a photocentrifuge (LUMiSizer, LUM Americas, Boulder, CO, USA). The software calculates the creaming rate of O/W emulsion droplets under centrifugal force by measuring near infra-red light transmission (865 nm) as a function of length of emulsion in transparent cuvettes.28 400 μl of freshly prepared samples were transferred into 8 mm × 2 mm rectangular polycarbonate cuvettes, centrifuged at different rpm for 20 h and the transmission data were collected after every 72 s (1000 profiles). The relative centrifugal force (RCF) was calculated using the equation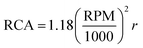 , where r is the distance from the centre of the centrifuge to the mid point of the sample in the cuvette, and expressed as times earth gravitation (g). The bigger droplets would cream faster compared to the smaller droplets and as the droplets cream, the bottom of the cuvette would transmit more lasers as it gets devoid of oil droplets with time. The transmission profiles as a function of the length of the cuvette and centrifugation time was recorded by the SEPView® software. For each run at different RCF the position of the cream layer in the cuvette in mm was plotted as a function of time, the slope of which gave the creaming velocity (in mm per hour) of the droplets at a RCF (Front Tracking analysis in the software). By plotting the creaming velocity against RCF and extrapolating to one (1) RCF, which is equivalent to earth gravitation, an estimation of creaming rate of emulsion at normal storage condition can be obtained.28
, where r is the distance from the centre of the centrifuge to the mid point of the sample in the cuvette, and expressed as times earth gravitation (g). The bigger droplets would cream faster compared to the smaller droplets and as the droplets cream, the bottom of the cuvette would transmit more lasers as it gets devoid of oil droplets with time. The transmission profiles as a function of the length of the cuvette and centrifugation time was recorded by the SEPView® software. For each run at different RCF the position of the cream layer in the cuvette in mm was plotted as a function of time, the slope of which gave the creaming velocity (in mm per hour) of the droplets at a RCF (Front Tracking analysis in the software). By plotting the creaming velocity against RCF and extrapolating to one (1) RCF, which is equivalent to earth gravitation, an estimation of creaming rate of emulsion at normal storage condition can be obtained.28
Statistics
All experiments were conducted with at least three replicates, and the statistical significance was analyzed using Microsoft Excel 2007.Results and discussions
Average droplet size of nanogels
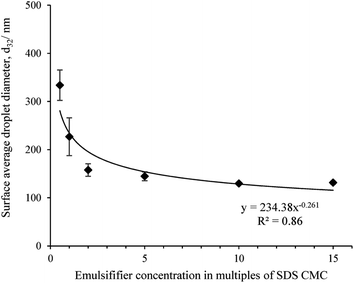
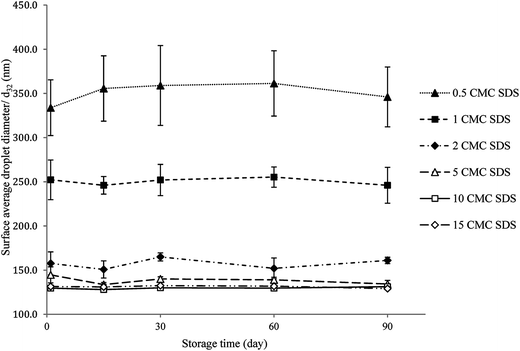
Fig. 1 shows the surface average droplet diameter (d32) of all freshly made nanoemulsions as a function of emulsifier concentration. As a control particle size of SDS solutions were also determined but no measurable signal was obtained as SDS micelles size is beyond the instrument limit. The d32 decreased from 333.8 ± 31.6 nm for 0.5 CMC SDS to 131.4 ± 3.2 nm for 15 CMC SDS concentration in a power law fashion, similar to what was observed before.18,29 The value of the power law exponents is also similar to what we observed before (0.2) and also by Meleson et al.29 (0.33). All nanoemulsion except the one prepared with 0.5 CMC SDS showed a monomodal droplet size distribution (shown in ESI data Fig. S2†). The droplet size distribution became narrower and shifted towards smaller size with increase in SDS concentration (Fig. S2†). Nevertheless, from Fig. 1 beyond 10 times SDS CMC no significant decrease in droplet size was observed (p > 0.05), which could be ascribed to increase in emulsion viscosity reducing the flow behaviour and the limitation in homogenizer efficiency.Reversibility in nanogel viscosity using repeated shear
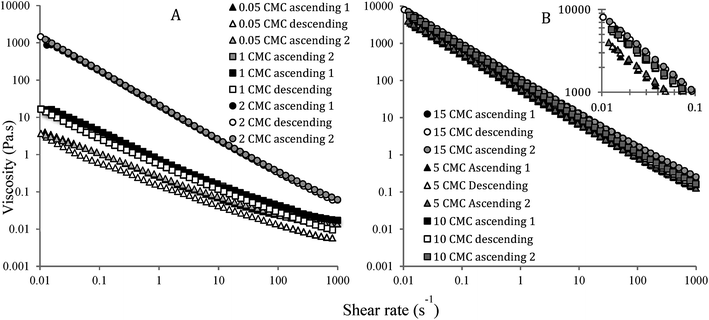
Effect of repeated shear (ascending, descending and again ascending) on nanoemulsions' viscosity is plotted in Fig. 2. Overall, the viscosity of nanoemulsions decreased with an increase in shear rate, indicating pseudoplastic behaviour due to the loss of close packing and breakdown of the inter-droplet network for repulsive and attractive nanogels, respectively. A high-shear plateau in viscosity was observed for the nanogels with 0.5 and 1 CMC SDS, indicating a complete breakdown of repulsive jammed structure into a Newtonian fluid-like behaviour. On the other hand, repulsive nanogels with 2 CMC SDS and all the attractive nanogels showed strong pseudoplastic behaviour even at the end of 1000 s−1 shear rate, meaning that some structure remains intact even at such a high shear rate. Viscosity of nanoemulsions increased with increase in emulsifier concentration, for example, at 1 s−1 shear rate average apparent viscosity for 0.5, 1, 2, 5 and 10 times SDS CMC nanoemulsions were 0.04, 0.73, 19.7, 51.7, 82.4, and 98.0 Pa s, respectively. In the repulsive regime, we previously explained this behaviour by the proximity of the ϕeff towards random jamming.18 In the attractive regime (5 to 15 times CMC), however, increase in attractive depletion interaction due to the presence of excess SDS micelles was proposed for such an increase in viscosity.18 Nevertheless, in spite of their difference in viscosity and the nature of inter-droplet interactions, almost complete reversibility in the viscosity as a function of ascending and descending shear was observed for all nanoemulsions (Fig. 2). The nanoemulsion with 0.5 and 1 CMC SDS appeared to have lost a fraction of their viscosity when the descending shear started at 1000 s−1 shear rate (Fig. 2A), however, during re-application of ascending shear they followed the almost same path as in the first cycle of shear. It appears that with a reduction in shear, the repulsive nanogels instantaneously went back to their original dense droplet structure. For attractive nanoemulsions, a network of droplet aggregates broke down during an increase in shear. However, removal of or decrease in shear instantaneously re-formed the inter-droplet network thereby completely recovering their structure.Reversibility in nanogel elasticity during repeated oscillatory strain sweep
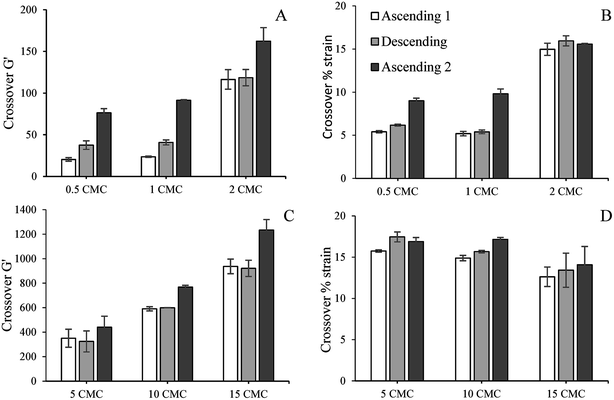
We previously studied the gelation behaviour of similar SDS-stabilized nanoemulsions and found that for all nanoemulsions G′ > G′′ and the gel strength increased with SDS concentration.18 For all freshly prepared nanogels except the two with 0.5 and 1 CMC SDS, G′ and G′′ were independent of strain below 2%, showing the existence of linear viscoelastic region (LVR) (Fig. 3). Within the LVR G′ was significantly greater than G′′, reflecting their dominant elastic nature. Nanoemulsions with 0.5 and 1 CMC SDS also showed G′ > G′′ below 2% strain, but failed to exhibit LVR and can be considered as weak gels (Fig. 3A and B). The values of G′ in the low-strain region, indicating gel strength of the nanogels, increased with SDS concentration from repulsive to attractive regimes. In the repulsive regime, gel strength scaled by polydispersity of the droplets increased with ϕeff, which indicates their proximity towards random jamming.18 In the attractive regime, gel strength increased with SDS micelle-induced depletion attraction strength.18 Similar strain sweep viscoelastic behaviour for colloidal gels was also observed by others.2,7Here we further examined whether the gel strength of the nanogels would be affected by repeated ascending and descending strain sweeps to better understand their yielding behaviour, recoverability of the elasticity and suitability for potential application in various foods, cosmetics, and related products. The values of G′ and % strain at the crossover were also calculated from Fig. 3 for all cycles of strain sweep for all nanogels and plotted in Fig. 4. Irrespective of gel strength and interdroplet interactions, all nanogels showed remarkable recovery in gel strength (Fig. 3). Repulsive nanoemulsions with 0.5 and 1 times SDS CMC (Fig. 3A and B) were weak gels where the droplets were in a loosely bound cage. As strain increased, G′ sharply dropped at yield strain and the system yielded by cage escape. At the same time, G′′ rose, formed a peak indicating relaxation in the nanogel structure. The peak in G′′ is also where it crossed the G′ curve indicating loss of gelled structure and liquid-like behaviour. When the strain was reversed from 100%, G′ traced very similar path in the high-strain regime, however, below the yield strain, G′ rose further than the initial cycle and ultimately gained more than 10 times the initial G′ in the low-strain regime. During the second ascending strain sweep the recovered nanogels showed perfect linear viscoelastic regions (LVR) and both yield strain and crossover strain shifted towards higher values indicating stronger gel (Fig. 4). Overall, repeated strain sweep of repulsive nanogels (0.5 and 1 CMC SDS) increased the gel strength and shifted the crossover G′ and strain towards higher values. For 2 CMC repulsive nanogel no significant change was observed in the crossover G′ in the first two cycles and the crossover strain in all the cycles of 2 CMC nanogels (Fig. 4A and B). Largest increase in gel strength upon descending strain sweep was observed for the two weakest nanogels (0.5 and 1 CMC). For 2 CMC nanogel a near perfect LVR appeared during the first ascending strain sweep, indicating it has already reached a jammed state in which nanodroplets along with their charge cloud do not have enough space to rearrange to significantly increase the gel strength during the repeated strain sweep. Recovery of gel strength in this nanogels was due to simple re-localization of nanodroplets in the jammed state during the descending strain sweep. This behaviour is similar to Shao et al.,27 who found complete reversible strain sweep rheology for repulsive microgel suspension. It should also be noted that we did not use any pre-shear while Shao et al.27 used 1000 s−1, which may have impacted starting viscoelasticity of their microgel suspension.
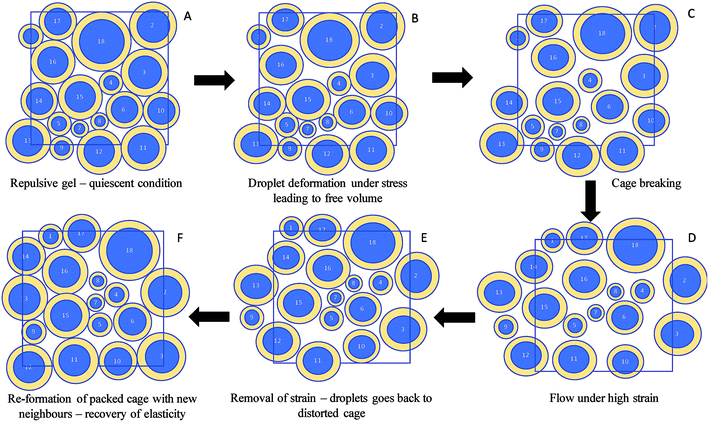
This recovery of gel strength in repulsive nanogels can be explained by the concept of droplet deformability25 and cage elasticity.26,30 Pham et al.26 in their creep and flow experiments observed that the repulsive glasses recover the strain as the applied stress is removed. Caged particles in colloidal glasses are isotropic under no external stresses. At an applied stress below the yield point cage distortion occurs in which the particles above and below the central particle of the cage move in opposite directions causing the particles to be anisotropic. This results in an internal anisotropic osmotic pressure, which balances the applied stress. When the applied stress is removed, the distorted cages relax back to their original state resulting in strain recovery. Under external shear stresses greater than yield stress, as the system flows the particles escape out of cages. In the present case the nanoemulsion droplets along with their charge cloud are deformable when they are close-packed. Mason et al.10 proposed that perfectly packed spherical emulsion droplets must deform under external stress before yielding. However, the deformation would generate free volume for the droplets to move or exchange positions25 which facilitate energy dissipation by cage breaking leading to liquid-like flow behaviour. Upon removal of stress the droplets will find them in maximally distorted cages with new neighbours and the system gets back to isotropy, regains un-deformed state of the droplets and recovers its elasticity.26 A schematic diagram of the proposed colloidal interaction discussed above during reversibility of the repulsive nanogels is given in Fig. 5. Petekidis et al.30 also observed that as the flow ceases the sterically-stabilized repulsive hard sphere glasses recover a strain whose magnitude is independent of the flow rate. However, in their research the hard sphere glasses recovered only a fraction of the total strain. In the present case, perhaps the deformable soft nature of the droplets along with their charge cloud could have contributed to the higher recovery of gel strength by forming a close-packed structure that expands to a higher volume fraction and gains greater elasticity compared to the quiescent nanogel (Fig. 5).
Attractive nanogels (5, 10 and 15 CMC SDS) also showed reversibility in viscoelastic behaviour with repeated strain sweeps (Fig. 3D–F). During descending strain sweep these nanogels were also able to recover their gel strength and their plateau G′ (G′p) became higher than the initial ascending strain sweep. From Fig. 4C and D it can also be seen that the crossover G′ and crossover strain during the second ascending strain sweep was always higher than the initial value, indicating that after structural recovery during the repeated strain sweep the nanogels became stronger and more force was required to break their inter-droplet network structure. Overall, the attractive nanogels showed much higher crossover G′ compared to the repulsive nanogels (Fig. 4C vs. 4A), while the crossover strain values of the attractive nanogels (Fig. 4D) were comparable only to the 2 CMC repulsive nanogels (Fig. 4B).
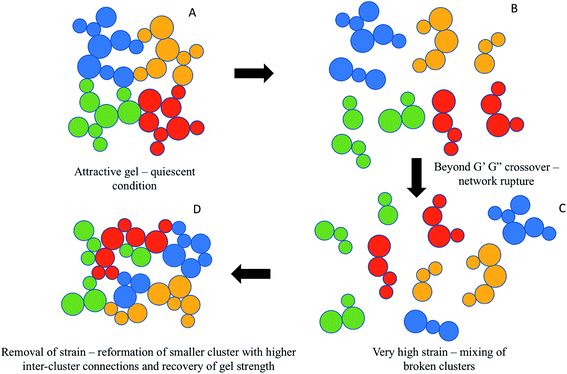
The recovery of gel strength for attractive nanogels in the present case is in stark contrast with Shao et al.,27 who showed a significant drop in gel strength for the attractive microgel suspension during descending strain sweep. It was proposed that the initial strong attractive bonds between the particles broke down due to application of strain (between 10 to 100%) beyond the first peak in G′′ leading to a ruptured network of broken clusters. Further application of strain (up to 1000%) densified the broken clusters and improved its compactness, which broke down into individual particles leading to a second peak in G′′.31 During descending strain sweep the initial reversibility at high strain was assigned to reformation of dense clusters, which however, could not re-form the original network of droplets and the gel strength decreased in the low-strain regime. The gel forming dense clusters could not form a space-filling network of droplets as in the initial quiescent gel. Quite interestingly, Shao et al.27 also reported that the application of an intermediate pre-shear, which transformed the initial system into a gel made up with densified clusters, although decreased the initial gel strength, led to a near complete recovery during descending strain sweep. It was proposed that the pre-sheared gels, formed by the dense clusters of particles, can be reversibly transformed into a fine dispersion of individual particles during ascending and descending strain sweep. In the present case, no pre-shear was applied and even then, complete recovery of initial quiescent gel strength was observed. Here, the viscoelastic behaviour of the nanogels showed only one peak in G′′ during crossover and continuous drop in both G′ and G′′ beyond crossover (we, however, studied up to a strain range of 100%). This suggests that the strongly attractive nanodroplet network was not completely broken down into individual droplets, rather broken smaller clusters were formed. A similar formation of broken cluster due to bond breakup was also confirmed by Masschaele et al.32 using direct visual observation of yielding behaviour in a two-dimension colloidal gels. During descending strain sweep the smaller clusters were aggregated forming an even stronger space-filling network such that in the low-strain regime G′ surpluses the initial values. The stronger space-filling network could be a result of homogeneous restructuring by re-forming smaller size clusters with a greater number of inter-cluster connections with new neighbouring droplets as the attractive interactions dominated when the strain rate was reduced below the yield strain during the experiment.33 A schematic diagram of the proposed colloidal interaction discussed above during reversibility of the attractive nanogels is given in Fig. 6. Application of strain during the second ascending strain sweep has similar behaviour and the descending curves were retraced, although at slightly higher values (Fig. 4D–F). It is remarkable that even such a strongly attractive gel could recover its gel strength during descending strain sweep, indicating that the applied strain was below the complete disintegration of the clusters and the clusters were able to reform the gel network. Perhaps a charged layer of ionic SDS emulsifier at the nanodroplet surface was better in preventing very strong interdroplet bonding such that reversibility was possible.
The 15 CMC nanogels showed a bit different behaviour. Its crossover G′ values were much higher than the others (Fig. 4C), but the crossover happened at a lower% strain compared to 5 and 10 CMC nanogels (Fig. 4D), indicating brittleness in gel structure.34 The attractive depletion interaction in the 15 CMC nanogels was strongest of all gels considered here, and the application of strain could be accommodated by lengthening or stretching the clusters of droplets. Gisler et al.35 showed that stretching of cluster backbones would increase the stiffness of the gel, resulting in strain hardening and increase in elasticity and brittleness until it breaks.
Creaming stability of the nanogels under accelerated gravitation
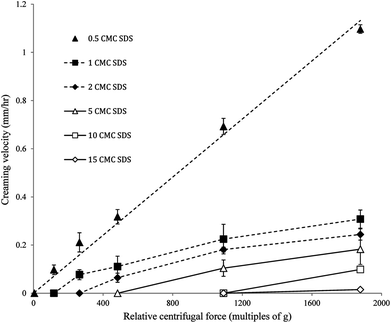
The nanoemulsions developed in the present study were extremely stable against gravity induced separation. Hence, it was impossible to measure whether there was any difference in creaming rates among these highly stable nanoemulsions within the experimental timeframe. However, using an accelerated gravitation we will be able to observe differences in creaming rates among these highly stable nanoemulsions, which could be used to explain any change in flowability and gel strength with time. Photocentrifuge LUMiSizer® is one such instrument where the rate of creaming can be calculated during centrifugation at different relative centrifugal force (RCF) as multiples of earth's gravitation (g). Also, by calculating the creaming rates under accelerated gravity a comparison of the gel stability of the nanogels can be done. Fig. 7 shows the creaming velocities of the nanogels obtained at different RCF using the photocentrifuge. The nanoemulsion with 0.5 CMC SDS showed a linear increase in creaming velocity as a function of RCF and can be fitted with an equation y = mx, where m is the slope of the straight line. By extrapolating the equation to earth's gravity (1 × g, or RCF = 1), we can predict the creaming velocity of the nanoemulsion as 6.03 × 10−4 mm h−1 or 5.28 mm per year. From Fig. 7 it can also be seen that, for all other nanogels except 0.5 CMC, creaming velocity reached a zero value before RCF = 1. According to this, the droplets of these nanogels would not cream at all at earth's gravity. In other words, no creaming was observed for these nanoemulsions until a critical RCF was reached and thereafter creaming velocity increased almost linearly as a function of RCF (Fig. 9). The minimum RCF at which droplet creaming started can also be considered as the yield point of the gel. Correlation between centrifugal separation and gel yield point was also observed by Kuentz et al.36 while determining clarification of gum dispersions. As expected, the minimum RCF required for creaming of nanodroplets also increased with the increase in gel strength. This indicates that the jammed state of droplets (in the repulsive nanogels) or their inter-droplet network (in the attractive nanogels) was preventing them from creaming under accelerated gravitation. From Fig. 7 it can also be seen that with an increase in SDS concentration the creaming velocity decreased at a constant RCF. For example, at 1092 × g RCF the creaming velocity decreased from 0.22 mm h−1 for 1 CMC SDS nanoemulsions to 0.10 mm h−1 for 5 CMC SDS nanoemulsions. For 10 and 15 CMC SDS nanogels, no creaming was observed at this RCF. The extreme stability of the nanogels against creaming could be the result of two factors. First, as mentioned above, the repulsive jamming or attractive network of droplets forming the gel structure may prevent any movement of the droplets. Second, the extreme stability against creaming can also be a direct result of small droplet size according to Stokes law, which states that the creaming velocity of emulsion droplet is inversely proportional to the square of their radius. Studying nanogels or nanoemulsions under accelerated gravity could be a quicker and novel way to predict their stability under long-term storage.Stability and gelation behaviour of nanogels under long-term storage
Mechanism of loss of gel strength under long-term storage of nanogels
In a patent on nanoemulsion gelation Graves et al.17 showed that G′p of 40 wt% polydimethylsiloxane (PDMS) silicone oil nanoemulsions stabilized with 116 mM SDS (equivalent to 14 times CMC) did not change significantly over a period of 461 days. In the present case, we only studied the nanogels for 90 days, but within that time frame we have seen a significant drop in gel strength for all nanogels. The only different between Graves and co-workers' nanogel and our nanogel is in the types of oil used. While silicone oil is an organic polymer which does not undergo chemical reactions such as oxidation, canola oil (mostly made up of triacylglycerols) used in our research is susceptible to lipid oxidation and hydrolysis reactions. The nanogels in the present work were stored at room temperature, which could also promote lipid oxidation upon long-term storage. Moreover, extremely small droplet size of the nanoemulsions means a very high oil interfacial area in the presence of surrounding aqueous phase and hence, a greater chance of lipid oxidation. In fact, after 90 days of storage at room temperature rancid smell was obtained from all the nanogels indicating extensive lipid oxidation. It has been proposed that lipid oxidation in emulsion may induce changes in interfacial composition as the hydroperoxides (primary oxidation products) and broken down aldehyde and ketones (secondary oxidation products) are surface active.37,38 As lipid undergoes oxidation in droplets, the oxidized products move toward the interface and may also get desorbed from the interface into the aqueous phase leading to reorganization and even desorption of some emulsifier from the oil droplet interface.39 Desorbed emulsifiers may also help solubilization of oxidation products by forming micelles in the aqueous phase.40,41 We hypothesized that these changes in interfacial dynamics and the presence of ionizable oxidation products in the aqueous phase might lead to a reduction in charge cloud (EDL) around the droplets which would negatively impact effective oil phase volume fraction and hence gelation in the repulsive nanogels. This changes in the charge cloud due to lipid oxidation was not detected by the zeta potential analyzer for 1 and 2 CMC nanogels, possibly due to necessary dilution of the nanogels in DI water prior to zeta potential analysis. Dilution removes the effect of surface-active lipid oxidation products in the aqueous phase as well as any change in interfacial dynamics, hence we were unable to prove this using direct measurement.
In order to support this hypothesis, the extent of lipid oxidation was quantitatively determined using peroxide value (PV) and p-anisidine value (AV) of the oil phase of the nanogels. The PV gives an estimation of primary oxidation products while the AV measures presence of secondary oxidation products in the oil. Both methods were performed according to the Official Methods of American Oil Chemists' Society (Cd 8-53 for PV and Cd 18-90 for AV). An estimation of total oil oxidation was obtained from TOTOX value where TOTOX = 2PV + AV.42 The oils were separated from the nanogels using repeated freeze/thaw cycles, which completely destabilized the nanogels. The free oil collected from the destabilized nanogels were used for PV and AV analysis, although this approach neglected the oxidized products migrated into in the aqueous phase. Three to four fold increase in TOTOX values were found in the oil phase of the repulsive nanogels (TOTOX ranged from 24–34) after 90 days of storage at room temperature compared to the canola oil purchased from the grocery store and stored under similar condition for 90 days (TOTOX = 8 units). It should be noted that the oxidized products in the nanogels that diffused into the aqueous phase were not measured in this test, hence the actual level of lipid oxidation might be much higher than that is measured. This result indicates that the oils in the nanogels were severely oxidized, which could impact the gel strength as discussed before.
Another indirect proof of our hypothesis that lipid oxidation in canola oil was responsible for loss of gel strength in repulsive nanogels was obtained from similar nanogels prepared with mineral oils (O-121, Fisher Scientific, Nepean, ON, Canada). The mineral oil consisted of linear alkanes with a molecular weight 394 g mol−1 and had a viscosity 33.5 mPa s at 40 °C. As a comparison the canola oil used in the present research had a viscosity of 33.2 mPa s at 40 °C. As there is no unsaturation on the alkane chain, the mineral oil is not oxidizable. Therefore, if our hypothesis of lipid oxidation-induced loss of gel strength is true, then the gel strength of the nanogels prepared with the mineral oil with similar concentration of SDS should not change as a function of time. The mineral oil nanogels were prepared using the same protocol as in case of canola oil nanogels with 1, 2, 5 and 10 CMC SDS in the aqueous phase. The droplet size of the mineral oil nanogels ranges from 326 ± 40.5 nm for 1 CMC SDS to 181.5 ± 10.5 nm for 10 CMC SDS and their size distributions were similar to the canola oil nanogels (see ESI data Fig. S4† for a comparison of droplet size distribution and average droplet size between canola oil and mineral oil nanogels). The gel strengths of the mineral oil nanogels as a function of time were plotted in Fig. 10B. Although the initial gel strength of the mineral oil nanogels were lower than that of canola oil nanogels (due to larger average droplet size as shown in Fig. S4 in ESI data†), it can be seen that for repulsive mineral oil nanogels (with 1 and 2 times SDS CMC) G′ did not change as a function time over a period of 90 days, which proves our hypothesis on the importance of lipid oxidation for the loss of gel strength for canola oil nanogels. Therefore, the most probable reason for the loss of gel strength of the canola oil nanogels could be lipid oxidation-induced changes in the interfacial behaviour.
The lipid oxidation hypothesis proposed to explain the loss of gelation in repulsive nanogels should also be applied to attractive nanogels. In this case presence of excess micelles in the continuous phase of the nanoemulsions would facilitate removal of surface active oxidation products from the droplets.41 Micelles are highly dynamic system and the time scale of molecule exchange among the interfacial emulsifier, free emulsifier in the aqueous phase and the micelles are in the range of micro to milliseconds.50 Therefore diffusion of oxidized products into micelles and their and distribution would be much faster compared to the rate of lipid oxidation.51 It may also promote the transfer of hydroperoxides from one droplet to another by micelles leading to enhanced lipid oxidation in the droplets.37 In fact, evidence of higher lipid oxidation in attractive nanogels (TOTOX = 30–38 in the oil separated from the 15 CMC nanogels after 90 days of storage at room temperature) was seen. Therefore, the EDL around the droplets and corresponding ϕeff of attractive nanogels would also be affected by diffusion of oxidation products through the droplet interface. Moreover, changes in micelle dynamics due to the uptake of lipid oxidation products may also alter their charge and size leading to a change in attractive depletion interactions as a function of time. We propose that these two factors could also be partially responsible for the loss of gel strength in attractive nanogels. It should also be noted that when attractive nanogels were prepared with mineral oil (5 and 10 times SDS CMC), no change in gel strength was observed (Fig. 10B) which also highlights the importance of lipid oxidation-induced loss of gel strength in attractive nanogels.
Nanostructure of the nanogels and nanoemulsions
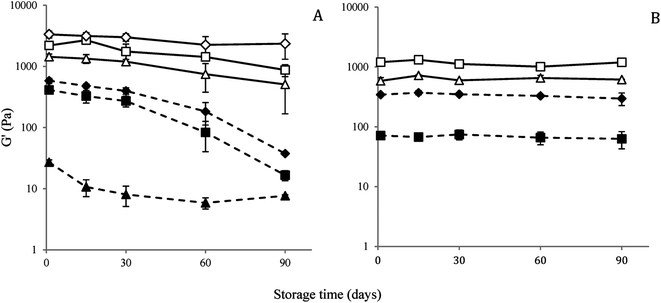
To understand the change in nanostructure responsible for loss of gel strength under long-term storage of the nanogel, nanostructure of the 10 CMC SDS-stabilized attractive canola oil nanogels were recorded using a freeze-fracture cryo-scanning electron microscope before and after 90 days storage (Fig. 11). From the visual observation, we have seen that the 10 CMC SDS nanogel convert from a strong non-flowable gel to a weakly flowable gel (Fig. 9) where the G′ values changed from 2205.2 ± 12.0 Pa for freshly prepared nanogel to 280.2 ± 192.6 Pa after 90 days storage (Fig. 10). SEM images revealed that the freshly nanogel was made by aggregating clusters of nanodroplets (Fig. 11A), where the clusters were themselves made by strong aggregation among the nanodroplets (Fig. 11B). After 90 days of storage, the nanostructure of the same sample looked flat (Fig. 11C) without the presence of fractal clusters as seen in Fig. 11A. The nanodroplets were still close-packed as seen in Fig. 11D after 90 days, which explains their gelation behaviour, but the gel strength was considerably weaker compared to the freshly prepared sample.Conclusions
In this research, the stability of SDS-stabilized canola oil nanogels was investigated as a function of repeated rotational shear, oscillatory strain and storage time. Nanogels were formed from oil-in-water nanoemulsions, prepared with various concentration of SDS to get a range of droplet size, interdroplet interactions and gel strength. No change in droplet size of the nanoemulsions was observed over a period of 90 days and accelerated gravitation study indicated extremely high stability of the nanoemulsions against creaming. Irrespective of gel strength and interdroplet interactions, all nanogels showed recovery in viscosity and gel strength during repeated shear and strain sweep experiments, respectively. It was proposed that for repulsive nanogels, where gelation happens due to close packing of nanodroplets along with their charge cloud, external stress induced deformation of soft oil droplets led to the generation of free volume for droplet movement thereby facilitating energy dissipation by cage breaking and liquid-like flow behaviour. Upon removal of stress the droplets would re-form the cages with new neighbours and the system regains un-deformed state of the droplets to recover its elasticity. For attractive nanogels, during yielding, the bond between the droplets broke down due to the application of strain leading to a ruptured network of broken clusters, however, the smaller clusters were not broken down into individual droplets in the strain rate studied. Upon reducing the strain, a stronger space-filling network (higher gel strength) was formed by smaller clusters with a greater number of inter-cluster connections.Interestingly, despite high stability in droplet size and creaming behaviour, the elastic storage moduli (G′) of most of the nanogels significantly decreased with time during storage. For repulsive nanogels (0.5, 1 and 2 CMC SDS) a large decrease in G′ was observed converting the strong gels into flowable weak gels. For attractive nanogels with 5, and 10 CMC SDS decrease in G′ was less, although significant. Gel strength of the strongly attractive nanogel with 15 CMC SDS did not change significantly within 90 days, although given enough time they would also show drop in gel strength. It was proposed that generation of surface active components due to extensive lipid oxidation may alter the interfacial composition and ultimately reduce the thickness of the charge cloud leading to a reduction in gel strength in repulsive nanogels. Lipid oxidation was also believed to be the main destabilization mechanism for the loss of gel strength in attractive nanogels. It was proposed that the presence of excess micelles in the continuous phase could have facilitated the transfer of the surface-active lipid oxidation products from droplets towards micelles or other droplets leading to a decrease in the charge cloud and attractive depletion interactions. The vegetable oil-based nanogels with extremely stable droplet size, creaming stability and low oil volume fraction possess great potential for use in low-fat foods and related soft materials provided loss of gel strength with time could be prevented.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Dr Alexandra Smith of the Department of Food Science, University of Guelph for her work on the SEM. Financial support for this work is provided by NSERC Discovery Grant, Canada Foundation for Innovation (CFI) Leaders Opportunity Fund and the Saskatchewan Innovation and Science Fund (ISF). Technical help from Amy Liu, Kunal Kadiya and Aakash Patel is also acknowledged.References
- D. J. McClements, Food emulsions: principles, practices, and techniques, CRC Press, Boca Raton, 2nd edn, 2005 Search PubMed.
- J. N. Wilking and T. G. Mason, Phys. Rev. E, 2007, 75, 041407 CrossRef PubMed.
- J. N. Wilking, S. M. Graves, C. B. Chang, K. Meleson, M. Y. Lin and T. G. Mason, Phys. Rev. Lett., 2006, 96, 015501 CrossRef CAS PubMed.
- T. G. Mason, J. N. Wilking, K. Meleson, C. B. Chang and S. M. Graves, J. Phys.: Condens. Matter, 2007, 19, 079001 CrossRef.
- T. G. Mason, M. D. Lacasse, G. S. Grest, D. Levine, J. Bibette and D. A. Weitz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 3150–3166 CrossRef CAS.
- J. Mewis, Colloidal suspension rheology, Cambridge University Press, Cambridge, 2012 Search PubMed.
- S. S. Datta, D. D. Gerrard, T. S. Rhodes, T. G. Mason and D. A. Weitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 041404 CrossRef PubMed.
- M. Ochowiak, L. Broniarz-Press and J. Rozanski, J. Dispersion Sci. Technol., 2012, 33, 177–184 CrossRef CAS.
- A. Sun and S. Gunasekaran, Int. J. Food Prop., 2009, 12, 70–101 CrossRef.
- T. G. Mason, J. Bibette and D. A. Weitz, Phys. Rev. Lett., 1995, 75, 2051–2054 CrossRef CAS PubMed.
- T. G. Mason and F. Scheffold, Soft Matter, 2014, 10, 7109–7116 RSC.
- F. Scheffold, F. Cardinaux and T. G. Mason, J. Phys.: Condens. Matter, 2013, 25, 502101 CrossRef CAS PubMed.
- J. Weiss and D. J. McClements, Langmuir, 2000, 16, 2145–2150 CrossRef CAS.
- I. Masalova and A. Y. Malkin, Appl. Rheol., 2007, 17, 42250 Search PubMed.
- T. M. Truskett, S. Torquato and P. G. Debenedetti, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 993 CrossRef CAS.
- C. L. A. Berli, D. Quemada and A. Parker, Colloids Surf., A, 2003, 215, 201–204 CrossRef CAS.
- S. M. Graves, T. G. Mason, K. Meleson and J. N. Wilking, US Pat. US20100010105A1, 2008.
- V. V. Erramreddy and S. Ghosh, Langmuir, 2014, 30, 11062–11074 CrossRef CAS PubMed.
- J. Oh, R. Drumright, D. J. Siegwart and K. Matyjaszewski, Prog. Polym. Sci., 2008, 33, 448–477 CrossRef CAS.
- Y. M. Joshi, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 181–202 CrossRef CAS PubMed.
- L. Cipelletti, L. Ramos, S. Manley, E. Pitard, D. A. Weitz, E. E. Pashkovski and M. Johansson, Faraday Discuss., 2003, 123, 237–251 RSC.
- S. Jabbari-Farouji, R. Zargar, G. H. Wegdam and D. Bonn, Soft Matter, 2012, 8, 5507–5512 RSC.
- C. Derec, A. Ajdari, G. Ducouret and F. Lequeux, C. R. Acad. Sci., Ser. IV: Phys., Astrophys., 2000, 1, 1115–1119 CrossRef CAS.
- L. C. E. Struik, Physical Aging in Amorphous Polymers and Other Materials, Elsevier Scientific Publishing Company, 1978 Search PubMed.
- Z. Zhou, J. V. Hollingsworth, S. Hong, H. Cheng and C. C. Han, Langmuir, 2014, 30, 5739–5746 CrossRef CAS PubMed.
- K. N. Pham, G. Petekidis, D. Vlassopoulos, S. U. Egelhaaf, W. C. K. Poon and P. N. Pusey, J. Rheol., 2008, 52, 649–676 CrossRef CAS.
- Z. Shao, A. S. Negi and C. O. Osuji, Soft Matter, 2013, 9, 5492–5500 RSC.
- D. Lerche and T. Sobisch, J. Dispersion Sci. Technol., 2011, 32, 1799–1811 CrossRef CAS.
- K. Meleson, S. Graves and T. G. Mason, Soft Mater., 2004, 2, 109–123 CrossRef CAS.
- G. Petekidis, D. Vlassopoulos and P. N. Pusey, J. Phys.: Condens. Matter, 2004, 16, S3955–S3963 CrossRef CAS.
- N. Koumakis and G. Petekidis, Soft Matter, 2011, 7, 2456–2470 RSC.
- K. Masschaele, J. Fransaer and J. Vermant, J. Rheol., 2009, 53, 1437–1460 CrossRef CAS.
- E. Moghimi, A. R. Jacob, N. Koumakis and G. Petekidis, Soft Matter, 2017, 13, 2371–2383 RSC.
- J. A. Lucey, C. Teo and P. A. Munro, J. Dairy Res., 1997, 64, 591–600 CrossRef CAS.
- T. Gisler, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 1999, 82, 1064 CrossRef CAS.
- M. Kuentz and D. Röthlisberger, Eur. J. Pharm. Biopharm., 2003, 56, 355–361 CrossRef CAS PubMed.
- C. D. Nuchi, P. Hernandez, D. J. McClements and E. A. Decker, J. Agric. Food Chem., 2002, 50, 5445–5449 CrossRef CAS PubMed.
- A. Abousalham, F. Fotiadu, G. Buono and R. Verger, Chem. Phys. Lipids, 2000, 104, 93–99 CrossRef CAS PubMed.
- C. C. Berton-Carabin, M.-H. Ropers and C. Genot, Compr. Rev. Food Sci. Food Saf., 2014, 13, 945–977 CrossRef CAS.
- C. C. Berton-Carabin, J. N. Coupland, C. Qian, D. J. McClements and R. J. Elias, Colloids Surf., A, 2012, 412, 135–142 CrossRef CAS.
- C. C. Berton-Carabin, R. J. Elias and J. N. Coupland, Colloids Surf., A, 2013, 418, 68–75 CrossRef CAS.
- E. N. Frankel, Prog. Lipid Res., 1980, 19, 1–22 CrossRef CAS PubMed.
- S. A. Shah, Y.-L. Chen, K. S. Schweizer and C. F. Zukoski, J. Chem. Phys., 2003, 119, 8747–8760 CrossRef CAS.
- V. Trappe, V. Prasad, L. Cipelletti, P. N. Segre and D. A. Weitz, Nature, 2001, 411, 772–775 CrossRef CAS PubMed.
- N. Katsuyoshi, in Progress in colloida and polymer science, ed. T. Masayuki and N. Katsuyoshi, Springer Science & Business Media, 2009, vol. 136, ch. XII, pp. 87–94 Search PubMed.
- S. Ramakrishnan, Y. L. Chen, K. S. Schweizer and C. F. Zukoski, Phys. Rev. E, 2004, 70, 040401 CrossRef CAS PubMed.
- L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 2000, 84, 2275–2278 CrossRef CAS PubMed.
- C. R. Seager and T. G. Mason, Phys. Rev. E, 2007, 75, 011406 CrossRef PubMed.
- S. Babu, J. C. Gimel and T. Nicolai, Eur. Phys. J. E, 2008, 27, 297–308 CrossRef CAS.
- A. Patist, J. R. Kanicky, P. K. Shukla and D. O. Shah, J. Colloid Interface Sci., 2002, 245, 1–15 CrossRef CAS PubMed.
- L. S. Romsted and C. Bravo-Diaz, Curr. Opin. Colloid Interface Sci., 2013, 18, 3–14 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09605d |
| This journal is © The Royal Society of Chemistry 2017 |