Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Regulation of coin metal substituents and cooperativity on the strength and nature of tetrel bonds†
Yuanxin Wei,
Jianbo Cheng,
Wenzuo Li and
Qingzhong Li *
*
The Laboratory of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Yantai University, Yantai 264005, People's Republic of China. E-mail: liqingzhong1990@sina.com; Fax: +86 535 6902063; Tel: +86 535 6902063
First published on 29th September 2017
Abstract
Ab initio calculations have been performed for the tetrel-bonded dyad MCN⋯TF4 (M = Cu, Ag, and Au; T = C, Si, Ge, and Sn). A coin metal substituent greatly strengthens the tetrel bond, depending on the nature of the coin metal and tetrel atoms. The Ag substituent has the largest enhancing effect with the interaction energy approaching −16 kcal mol−1. The strength of the tetrel bond in MCN⋯TF4 can be further regulated by the cooperative effect with a π⋯metal interaction. It is strengthened in C2H4⋯MCN⋯TF4 but is weakened in C2(CN)4⋯MCN⋯TF4. The interaction energy of the tetrel bond amounts to about −16 kcal mol−1 in C2H4⋯CuCN⋯SiF4, becoming a strong interaction. The nature of the tetrel bond is changed due to the metal substituents and cooperativity.
1. Introduction
By plotting molecular electrostatic potential (MEP) maps of halogen-containing molecules, Clark et al., found a positive MEP on the outermost portion of the halogen's surface, named the σ-hole.1 This σ-hole is helpful in explaining the formation of a halogen bond and its directionality.2 Such a σ-hole is also observed on many covalently-bonded atoms of Groups IV–VI.3–5 The corresponding intermolecular interactions are called tetrel,6 pnicogen,7 and chalcogen bonds.8 These intermolecular interactions have a uniform name: σ-hole bonding.9 Very recently, Grabowski and Sokalski performed a comparative study on some Lewis acid–Lewis base complexes linked by different σ-hole bonds and proposed that they have numerous correlations similar to hydrogen-bonded systems.10 More importantly, these σ-hole bonds have similar applications with hydrogen bonds in crystal materials, chemical reactions, and biological systems.6,7,11–15Recently, much attention has been paid to tetrel bonding16–26 since Bauzá et al., pointed out that it might serve as a new possible molecular linker in supramolecular materials.6 In addition, tetrel bonding is also confirmed to be important in chemical reactions14,15 and molecular recognition.27,28 Tetrel atoms are usually tetravalent in tetrel bonding, thus the formation of tetrel bonding suffers steric constraints if the tetrel atom is adjoined with steric groups. It is natural to understood that TH4, TH3X, and TF4 (where T refers to a tetrel atom and X is an electron-withdrawing atom or group) are often used as the tetrel donors in studying tetrel bonds. When a strong Lewis base attacks the tetravalent tetrel atom, the three covalent bonds facing the Lewis base are repelled to reduce steric constraints, and a trigonal bipyramid structure is finally favorable. This shows that deformation of a tetravalent tetrel molecule is crucial in stabilizing strong tetrel-bonded complexes.26
For tetrel bonds, there is a tendency to be strengthened as the T atom moves down this column of the periodic table since the σ-hole on the T atom is enlarged.29 CH4 seldom participates in tetrel bonding due to the absence of a σ-hole on the carbon atom. However, it can do if the carbon atom binds with an electron-withdrawing atom or group.16 Scheiner performed a systematic study of factors that influence the strength of tetrel bonds.30 With NH3 as a universal Lewis base, unsubstituted TH4 molecules form the weakest tetrel bonds, and this bonding is strengthened gradually from TH3F through THF3 to TF4.30 Additionally, this influence is also dependent on the nature of the T atom.30 HCN is a weaker Lewis base than NH3, while LiCN is a stronger Lewis base than NH3 in forming a tetrel bond due to the strong electron-donating ability of Li atom.14 This indicates that metal substituents in the Lewis bases are effective in strengthening tetrel bonds like that in halogen bonds.31
In most cases, the applications of tetrel bonds in crystal materials and molecular recognition are reached by cooperative effect with itself and other interactions. The addition of a phenyl ring to a single imidazolium perturbs the binding very little with halide anions, while placement of a second imidazolium on the benzene connector group markedly enhances binding energies.32 Some supramolecular assemblies involving lead(II) complexes have been constructed by means of tetrel bonding and other interactions.33–35 Therefore, there are many theoretical studies reported for cooperativity involving tetrel bonds.22,36–44 F2CX (X = Se and Te) can simultaneously form a tetrel bond with the carbon atom and a chalcogen bond with the X atom, thus both interactions display anticooperativity.22 Both anion–π and tetrel-bond interactions are enhanced in the same multicomponent complex of X⋯pyrazine/1,4-dicyanobenzene⋯TH3F/F2TO.44 In all, the strength of tetrel bonding can be tuned by cooperative effect.
Interestingly, Grabowski14 claimed that tetrel bond is not formed in F4Si⋯NCH due to the small 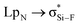 orbital interaction and negligible charge transfer. This means that the tetrel bond in F4Si⋯NCH is weak with interaction energy of −2.8 kcal mol−1.14 We plan to strengthen the tetrel bond in F4Si⋯NCH by using MCN (M is a coin metal including Cu, Ag, and Au) and we also compare the effect of different coin metals on the strength of tetrel bonding. AuCN⋯TF4 (T = C, Si, Ge, and Sn) is used to analyze the dependence of coin metal effect on the nature of the tetrel atom. To further strengthen the tetrel bond in MCN⋯TF4, we introduce a third molecule C2H4 to bind with the coin metal in this complex. For comparison, C2H2⋯AuCN⋯SiF4 is also studied. In the π⋯coin metal interaction, the π-electrons transfer from the occupied π-orbital into the empty σ-type metal orbital, while there is also a π-electron back-donation from the occupied d orbital of metal into the empty π anti-bonding orbital.45 To regulate the role of coin metals in the π⋯coin metal interaction and its effect on the strength of tetrel bond, the four hydrogen atoms in C2H4 are replaced by strong electron-withdrawing group CN.
orbital interaction and negligible charge transfer. This means that the tetrel bond in F4Si⋯NCH is weak with interaction energy of −2.8 kcal mol−1.14 We plan to strengthen the tetrel bond in F4Si⋯NCH by using MCN (M is a coin metal including Cu, Ag, and Au) and we also compare the effect of different coin metals on the strength of tetrel bonding. AuCN⋯TF4 (T = C, Si, Ge, and Sn) is used to analyze the dependence of coin metal effect on the nature of the tetrel atom. To further strengthen the tetrel bond in MCN⋯TF4, we introduce a third molecule C2H4 to bind with the coin metal in this complex. For comparison, C2H2⋯AuCN⋯SiF4 is also studied. In the π⋯coin metal interaction, the π-electrons transfer from the occupied π-orbital into the empty σ-type metal orbital, while there is also a π-electron back-donation from the occupied d orbital of metal into the empty π anti-bonding orbital.45 To regulate the role of coin metals in the π⋯coin metal interaction and its effect on the strength of tetrel bond, the four hydrogen atoms in C2H4 are replaced by strong electron-withdrawing group CN.
2. Theoretical methods
The structures of complexes and monomers were fully optimized using the Moller–Plesset perturbation (MP2) theory. The basis set adopted was aug-cc-pVTZ for the respective atoms except Sn and coin metal atoms, for which aug-cc-pVTZ-PP was used to account for relativistic effects.46 Harmonic frequency calculations at the same level were carried out to confirm that the structures obtained corresponded to energy minima. The interaction energies using supermolecular method (difference between the energy of the complex and the energies of the monomers with their geometries within the complex) were corrected for the basis set superposition error (BSSE) by the counterpoise method of Boys and Bernardi.47 All calculations were performed using the Gaussian 09 package.48The MEP analysis at the molecular surface was performed by the Wave Function Analysis-Surface Analysis Suite (WFA-SAS) program.49 The bonding characteristics were analyzed at the MP2/aug-cc-pVDZ(PP) level by means of Atoms-in-Molecules (AIM) theory50 with the help of AIM 2000 software.51 The second-order perturbation energy and charge transfer was obtained at the HF/aug-cc-pVTZ level with natural bond orbital (NBO) method52 implemented in Gaussian 09. Interaction energy was decomposed using the LMOEDA method53 at the same level by the GAMESS program.54
3. Results and discussion
3.1. Substituent effect of coin metal
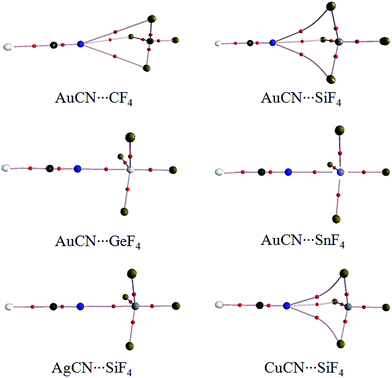
Fig. 1 shows the diagrams of some dyads studied, and the corresponding interaction energies are given in Table 1. The strength of tetrel bond has great dependence on the nature of tetrel atom since its interaction energy extensively varies from −1.32 kcal mol−1 in AuCN⋯CF4 to −26.96 kcal mol−1 in AuCN⋯SnF4. Clearly, the interaction energy of tetrel bond is more negative with the increase of the tetrel atomic mass, consistent with the magnitude of σ-hole on the tetrel atom (Fig. 2). Compared with HCN⋯TF4, the tetrel bond is stronger in AuCN⋯TF4 with the more negative interaction energy. The electron-donating nature of metal atom results in an increase of the negative MEP on the nitrogen atom in MCN relative to HCN (Fig. 2) and thus MCN forms a stronger tetrel bond with TF4 than HCN. It is obvious that the enhancing effect of coin metal on the tetrel bond is related with the nature of the tetrel atom. Generally, the heavier the tetrel atom, the larger the enhancing effect of coin metal on the tetrel bond. The interaction energy of tetrel bond in AuCN⋯SnF4 is more than doubled, becoming a very strong tetrel bond. On the other hand, the enhancing effect of coin metal is also dependent on the nature of coin metal. The increased percentage of tetrel bonding interaction energy is larger in the order Au < Cu < Ag. The Ag substituent makes the interaction energy of tetrel bond increase from −3.45 kcal mol−1 in HCN⋯SiF4 to −15.80 kcal mol−1 in AgCN⋯SiF4. Clearly, a strong tetrel bond is formed in AgCN⋯SiF4. Moreover, the negative MEP on the nitrogen atom is largest in AgCN and smallest in AuCN (Fig. 2). Au has the greatest electronegativity among three coin metal elements, thus its electron-donating power is smallest. Additionally, Au–CN bears strong covalence interaction,55 which also reduces the negative charge density on the nitrogen atom. However, Ag–CN bears stronger ionic interaction than Au–CN,55 which is partly responsible for the larger negative MEP on the nitrogen atom of AgCN. For HCN⋯SiF4, our value (−3.45 kcal mol−1) of interaction energy is more negative than that in the previous value (−2.8 kcal mol−1)14 since our calculations were obtained on base of the geometries of the monomers in the complexes. This shows that deformation has some important contributions to the stability of tetrel-bonded complexes.| Dyads | ΔE | ΔΔE | % | R |
|---|---|---|---|---|
| a Note: data in parentheses are from HCN⋯TF4 dyads. ΔΔE is the difference of ΔE in between MCN⋯TF4 dyads and the corresponding HCN dyads. % is the percentage of ΔΔE to the ΔE of HCN⋯TF4 dyads. | ||||
| AuCN⋯CF4 | −1.32(−1.09) | −0.23 | 21.10 | 3.3268 |
| AuCN⋯SiF4 | −4.95(−3.45) | −1.50 | 43.48 | 2.8598 |
| AuCN⋯GeF4 | −19.60(−10.70) | −8.90 | 83.18 | 2.1818 |
| AuCN⋯SnF4 | −26.96(−12.94) | −14.02 | 108.35 | 2.2343 |
| AgCN⋯SiF4 | −15.80 | −12.35 | 357.97 | 2.2812 |
| CuCN⋯SiF4 | −6.12 | −2.67 | 77.39 | 2.6338 |
| C2H4⋯SiF4 | −1.93 | — | — | 3.4880 |
| C2H4⋯SiH3F | −2.68 | — | — | 3.2473 |
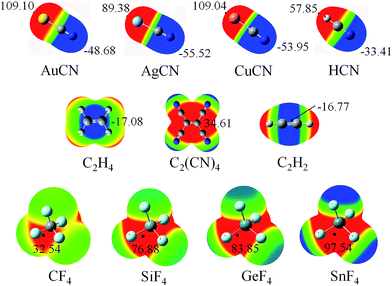 | ||
| Fig. 2 MEP maps of the monomers studied, color ranges, in kcal mol−1, are: red, greater than 9.5; yellow, between 9.5 and 0; green, between 0 and −9.5; blue, smaller than −9.5. | ||
The N⋯C distance in AuCN⋯CF4 is 3.3268 Å, which almost equals to the sum of the van der Waals (vdW) radii of both atoms. Although both molecules arrange in a line in AuCN⋯CF4, this complex can be taken as a van der Waals complex. The separation in other complexes is smaller than the sum of vdW Radii of the corresponding atoms. The N⋯Si distance in MCN⋯SiF4 is smaller in the sequence AuCN > CuCN > AgCN, consistent with the change of the interaction energy.
Fig. 3 is the AIM diagrams of MCN⋯TF4. In the weak complexes of AuCN⋯CF4 and AuCN⋯SiF4, the tetrel bond is characterized with three N⋯F paths. The N⋯F path is linear in AuCN⋯CF4 but is curve in AuCN⋯SiF4. The similar path is also found in CuCN⋯SiF4. When the tetrel bond is strong enough, the N⋯F paths are changed to be a linear N⋯T path in AgCN⋯SiF4, AuCN⋯GeF4, and AuCN⋯SnF4. Three fluorine atoms in the strong tetrel-bonded complexes are far away from the nitrogen atom in MCN. The topological parameters at these paths are listed in Table 2. The electron density at the N⋯C BCP is very small in AuCN⋯CF4. Besides, the charge transfer and orbital interaction are also very small in this complex (Table 3). Thus the interaction in AuCN⋯CF4 is not a tetrel bond. The electron density at the N⋯Si BCP is increased in AuCN⋯SiF4, and its Laplacian and energy density are positive. So the tetrel bond in AuCN⋯SiF4 is a purely close-shell interaction according to the classification for intermolecular interactions by Arnold and Oldfield.56 With the enhancement of tetrel bond, the electron density at the N⋯T BCP grows up and the similar result is found for the corresponding Laplacian. At the same time, the energy density is changed to be negative. These results show that the tetrel bond is a partially covalent interaction in CuCN⋯SiF4, AgCN⋯SiF4, AuCN⋯GeF4, and AuCN⋯SnF4.
| Dyads | ρb | ∇2ρb | Gb | Vb | Hb |
|---|---|---|---|---|---|
| a Note: the bond path is N⋯F in AuCN⋯CF4, AuCN⋯SiF4, and CuCN⋯SiF4, N⋯T in AuCN⋯GeF4, AuCN⋯SnF4, and AgCN⋯SiF4, and C⋯F in C2H4⋯SiF4. All are average values for the N⋯F and C⋯F paths. | |||||
| AuCN⋯CF4 | 0.0036 | 0.0270 | 0.0047 | −0.0038 | 0.0010 |
| AuCN⋯SiF4 | 0.0108 | 0.0438 | 0.0109 | −0.0070 | 0.0040 |
| AuCN⋯GeF4 | 0.0527 | 0.1853 | 0.0573 | −0.0683 | −0.0110 |
| AuCN⋯SnF4 | 0.0600 | 0.2805 | 0.0736 | −0.0771 | −0.0035 |
| AgCN⋯SiF4 | 0.0314 | 0.1024 | 0.0319 | −0.0382 | −0.0063 |
| CuCN⋯SiF4 | 0.0166 | 0.0524 | 0.0152 | −0.0153 | −0.0001 |
| C2H4⋯SiF4 | 0.0057 | 0.0208 | 0.0044 | −0.0035 | 0.0010 |
 orbital interactions in the tetrel-bonded dyadsa
orbital interactions in the tetrel-bonded dyadsa
| Dyads | QCT | E(2) |
|---|---|---|
a Note: QCT is the sum of charge on all atoms of TF4. E(2) corresponds to the  orbital interactions. E(2) in CuCN⋯SiF4 is not shown owing to the abnormal value in the NBO analysis. orbital interactions. E(2) in CuCN⋯SiF4 is not shown owing to the abnormal value in the NBO analysis. |
||
| AuCN⋯CF4 | 0.0015 | 0.09 |
| AuCN⋯SiF4 | −0.0010 | 3.23 |
| AuCN⋯GeF4 | −0.1001 | 72.17 |
| AuCN⋯SnF4 | −0.1090 | 82.27 |
| AgCN⋯SiF4 | −0.0616 | 40.16 |
| CuCN⋯SiF4 | −0.0113 | — |
| C2H4⋯SiF4 | −0.0006 | 0.97 |
The charge transfer in AuCN⋯CF4 is not only very small but also it moves from CF4 to AuCN. This further confirms no formation of a tetrel bond in AuCN⋯CF4. In other complexes, the charge transfer moves from MCN to TF4. The charge transfer in AuCN⋯SiF4 is still small and the single 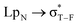 orbital interaction is not large. Thus this charge transfer interaction has a small contribution to the enhancement of tetrel bond in AuCN⋯SiF4. The charge transfer and orbital interaction have a larger increase in AgCN⋯SiF4 and CuCN⋯SiF4, indicating that charge transfer contribution cannot be ignored in strengthening the tetrel bond. The charge transfer amounts to about 0.1e in AuCN⋯GeF4 and AuCN⋯SnF4, and the corresponding orbital interaction is also very large.
orbital interaction is not large. Thus this charge transfer interaction has a small contribution to the enhancement of tetrel bond in AuCN⋯SiF4. The charge transfer and orbital interaction have a larger increase in AgCN⋯SiF4 and CuCN⋯SiF4, indicating that charge transfer contribution cannot be ignored in strengthening the tetrel bond. The charge transfer amounts to about 0.1e in AuCN⋯GeF4 and AuCN⋯SnF4, and the corresponding orbital interaction is also very large.
The weak interaction in AuCN⋯CF4 is still dominated by electrostatic energy and dispersion energy is more than half of electrostatic energy (Table 4). In AuCN⋯SiF4, electrostatic energy has a prominent increase but dispersion energy is almost not changed with respect to AuCN⋯CF4. The easier polarization of silicon atom leads to a relatively large increase of polarization energy in AuCN⋯SiF4. For the strong tetrel bond in AuCN⋯GeF4 and AuCN⋯SnF4, electrostatic energy is very large (>−50 kcal mol−1), and polarization energy is more than half of electrostatic energy. The relatively large polarization energy is mainly responsible for the deformation of TF4 in AuCN⋯GeF4 and AuCN⋯SnF4.54 The similar result is found in AgCN⋯SiF4. The contribution of polarization energy relative to that of electrostatic energy in CuCN⋯SiF4 is smaller than that in AgCN⋯SiF4. The interaction energies in Tables 1 and 4 are almost equal each other for most complexes with an exception in CuCN⋯SiF4, where a difference of 2 kcal mol−1 is found. The main reason is that dispersion energy is obtained by the difference of MP2 and CCSD(T) energies.54 The strong tetrel bond in AuCN⋯GeF4 and AuCN⋯SnF4 brings out a positive dispersion energy, which is primarily caused by the difference in the intra- and intermolecular correlation energy on going from noninteracting to interacting molecules.54
| Dyads | Eele | Eex | Erep | Epol | Edisp | ΔE |
|---|---|---|---|---|---|---|
| AuCN⋯CF4 | −1.89 | −2.82 | 4.87 | −0.40 | −1.09 | −1.33 |
| AuCN⋯SiF4 | −10.64 | −11.86 | 21.48 | −2.67 | −1.30 | −4.99 |
| AuCN⋯GeF4 | −50.58 | −56.10 | 113.75 | −27.93 | 1.17 | −19.69 |
| AuCN⋯SnF4 | −52.16 | −53.59 | 107.96 | −33.03 | 3.75 | −27.08 |
| AgCN⋯SiF4 | −39.56 | −46.01 | 89.66 | −18.81 | −1.41 | −16.13 |
| CuCN⋯SiF4 | −18.72 | −21.16 | 39.31 | −5.90 | −1.66 | −8.12 |
| C2H4⋯SiF4 | −4.54 | −7.22 | 12.96 | −0.68 | −2.44 | −1.92 |
| C2H4⋯SiH3F | −5.32 | −12.4 | 20.7 | −1.99 | −3.71 | −2.72 |
The interaction energy at the same level is −8.13, −8.46, and −6.77 kcal mol−1 in CuCN⋯ClF, AgCN⋯ClF, and AuCN⋯ClF, respectively.57 The interaction energy is −6.12, −15.80, and −4.95 kcal mol−1 in CuCN⋯SiF4, AgCN⋯SiF4, and AuCN⋯SiF4, respectively. A comparative analysis indicates that the dependence of tetrel bond on the coin metal is larger than that for the halogen bond. It is mainly due to the easier polarization of silicon than chlorine caused by the smaller electronegativity and bigger atomic radius of the silicon atom. The Ag substituent causes the interaction energy of halogen bond increased by ∼63% with respect to −5.19 kcal mol−1 in HCN⋯ClF,58 while this atom strengthens the interaction energy of tetrel bond with 358%. Obviously, the Ag substituent is very efficient in enhancing the strength of tetrel bond.
It was demonstrated that C2H4 molecule acts as the π-electron donor to form a π–tetrel bond with SiH3F and the corresponding interaction energy is −2.63 kcal mol−1.59 When SiF4 acts as the σ-hole donor in the π–tetrel bond, the interaction energy is −1.93 kcal mol−1, which is smaller than that in C2H4⋯SiH3F. However, the σ-hole on the silicon atom of SiF4 is larger than that of SiH3F. This inconsistence is mainly attributed to the nonzero dipole moment of SiH3F, which can greatly polarize the C2H4 molecule. In addition, the repulsion force between the π electrons of C2H4 and three fluorine atoms of SiF4 has some contribution to this inconsistence. For the weak π–tetrel bond in C2H4⋯SiF4, both charge transfer and orbital interaction are very small, but dispersion energy is relatively large enough not to be ignored.
3.2. Cooperative effects
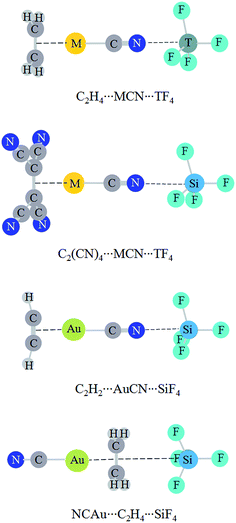
Fig. 4 shows the structures of triads, where both a tetrel bond and a π⋯metal interaction coexist. The interaction in C2H4⋯AuCN is very strong (>−50 kcal mol−1).57 Here we plan to strengthen the tetrel bond by cooperativity with a strong π⋯metal interaction. The weak interaction strength is almost not changed in C2H4⋯AuCN⋯CF4. This implies that a van der Waals interaction is not strengthened prominently even in the presence of a very strong interaction. In C2H4⋯MCN⋯TF4 (T = Si, Ge, and Sn), the tetrel bond is further strengthened, evidenced by the shorter binding distance and the more negative interaction energy (Table 5). The increase of interaction energy is related with the nature of coin metal and tetrel atom in C2H4⋯MCN⋯TF4, and its increase is larger in the order AuCN < AgCN < CuCN and CF4 < SnF4 < SiF4 < GeF4. The former order is like that in halogen bonds.56 The N⋯Si binding distance is shortened up to about 0.4 Å in C2H4⋯CuCN⋯SiF4, and the interaction energy has the largest increase (−9.60 kcal mol−1) in this triad. The interaction energy of tetrel bond amounts to −7.12 kcal mol−1 in C2H4⋯AuCN⋯SiF4, where the strength of tetrel bond is doubled under the combinative influence of metal substituent and cooperativity. The interaction energy of tetrel bond is up to −15.72 kcal mol−1 in C2H4⋯CuCN⋯SiF4, where the tetrel bond varies from a moderate one (CuCN⋯SiF4) to a strong one. The tetrel bond in C2H2⋯AuCN⋯SiF4 has a similar variation with that in C2H4⋯AuCN⋯SiF4. This indicates that the N⋯Si tetrel bond is greatly enhanced by cooperativity. The influence of π⋯metal interaction on the strength of tetrel bond is more prominent than that on halogen bond, where the increased percentage of interaction energy is less than 22%.57 When the four hydrogen atoms in C2H4 are replaced with electron-withdrawing group CN, the tetrel bond is weakened in C2(CN)4⋯MCN⋯SiF4 and the largest weakening is found in C2(CN)4⋯AgCN⋯SiF4. In NCAu⋯C2H4⋯SiF4, where the middle molecule C2H4 plays a double Lewis base in the Au⋯π interaction and π–tetrel bond, a weakening effect is also found.| Triads | RTB | ΔRTB | ΔETB | ΔΔETB |
|---|---|---|---|---|
| C2H4⋯AuCN⋯CF4 | 3.3119 | −0.0149 | −1.34 | −0.02 |
| C2H4⋯AuCN⋯SiF4 | 2.5919 | −0.2679 | −7.12 | −2.17 |
| C2H4⋯AuCN⋯GeF4 | 2.1169 | −0.0649 | −22.27 | −2.67 |
| C2H4⋯AuCN⋯SnF4 | 2.2050 | −0.0293 | −28.34 | −1.38 |
| C2H4⋯AgCN⋯SiF4 | 2.1415 | −0.1397 | −22.23 | −6.43 |
| C2H4⋯CuCN⋯SiF4 | 2.2129 | −0.4209 | −15.72 | −9.60 |
| C2(CN)4⋯AuCN⋯SiF4 | 2.9541 | 0.0943 | −4.41 | 0.54 |
| C2(CN)4⋯AgCN⋯SiF4 | 2.8102 | 0.5290 | −6.37 | 9.43 |
| C2(CN)4⋯CuCN⋯SiF4 | 2.9483 | 0.3145 | −3.31 | 2.81 |
| C2H2⋯AuCN⋯SiF4 | 2.6100 | −0.2498 | −6.92 | −1.97 |
| NCAu⋯C2H4⋯SiF4 | 3.5234 | 0.0354 | −1.65 | 0.28 |
The change in the strength of tetrel bond is also estimated with the electron density at the intermolecular BCP (Table 6). Against the electron density at the N⋯C BCP is almost not changed in C2H4⋯AuCN⋯CF4. The electron density of tetrel bond is increased in C2H4⋯MCN⋯TF4 (M = Cu, Ag, and Au; T = Si, Ge, and Sn) and C2H2⋯AuCN⋯SiF4, while it is decreased in C2(CN)4⋯MCN⋯SiF4 and NCAu⋯C2H4⋯SiF4. With the change of tetrel bonding strength, its nature is also changed. For example, the tetrel bond has a nature of partially covalent interaction in C2H4⋯AuCN⋯SiF4 and C2H2⋯AuCN⋯SiF4, evidenced by the negative energy density, while it is a purely close-shell interaction in C2(CN)4⋯MCN⋯SiF4 and NCAu⋯C2H4⋯SiF4, evidenced by the positive energy density.
| Triads | ρb | Δρb | Hb |
|---|---|---|---|
| a Note: the bond path is N⋯F in most complexes, but N⋯T in C2H4⋯AuCN⋯GeF4, C2H4⋯AuCN⋯SnF4, and C2H4⋯AgCN⋯SiF4, and C⋯F in NCAu⋯C2H4⋯SiF4. All are average values for the N⋯F and C⋯F paths. | |||
| C2H4⋯AuCN⋯CF4 | 0.0052 | 0.0002 | 0.0010 |
| C2H4⋯AuCN⋯SiF4 | 0.0193 | 0.0070 | −0.0005 |
| C2H4⋯AuCN⋯GeF4 | 0.0619 | 0.0092 | −0.0854 |
| C2H4⋯AuCN⋯SnF4 | 0.0647 | 0.0047 | −0.0859 |
| C2H4⋯AgCN⋯SiF4 | 0.0416 | 0.0102 | −0.0073 |
| C2H4⋯CuCN⋯SiF4 | 0.0351 | 0.0170 | −0.0096 |
| C2(CN)4⋯AuCN⋯SiF4 | 0.0105 | −0.0018 | 0.0011 |
| C2(CN)4⋯AgCN⋯SiF4 | 0.0135 | −0.0179 | 0.0008 |
| C2(CN)4⋯CuCN⋯SiF4 | 0.0107 | −0.0074 | 0.0010 |
| C2H2⋯AuCN⋯SiF4 | 0.0187 | 0.0064 | −0.0003 |
| NCAu⋯C2H4⋯SiF4 | 0.0050 | 0.0200 | 0.0011 |
Based on the dominant role of electrostatic interaction in the tetrel bond, it is natural to analyze the change of tetrel bonding strength in the triads with electrostatic potentials. Table 7 presents the most negative MEP on the N atom of MCN in π⋯MCN and on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in NCAu⋯C2H4. This value is more negative in C2H4⋯MCN and C2H2⋯AuCN with respect to MCN but is less negative in C2(CN)4⋯MCN and NCAu⋯C2H4 with respect to MCN and C2H4. This shows that the former is a stronger Lewis base and the latter is a weaker Lewis base. As a result, the former forms a stronger tetrel bond and the latter forms a weaker tetrel bond.
C bond in NCAu⋯C2H4. This value is more negative in C2H4⋯MCN and C2H2⋯AuCN with respect to MCN but is less negative in C2(CN)4⋯MCN and NCAu⋯C2H4 with respect to MCN and C2H4. This shows that the former is a stronger Lewis base and the latter is a weaker Lewis base. As a result, the former forms a stronger tetrel bond and the latter forms a weaker tetrel bond.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in NCAu⋯C2H4 as well as its difference (ΔVmin) relative to the corresponding monomers, all are in kcal mol−1
C bond in NCAu⋯C2H4 as well as its difference (ΔVmin) relative to the corresponding monomers, all are in kcal mol−1
| Dyads | Vmin | ΔVmin |
|---|---|---|
| C2H4⋯CuCN | −57.72 | −3.77 |
| C2H4⋯AgCN | −59.36 | −3.84 |
| C2H4⋯AuCN | −54.58 | −5.90 |
| C2(CN)4⋯CuCN | −43.90 | 10.05 |
| C2(CN)4⋯AgCN | −47.86 | 7.66 |
| C2(CN)4⋯AuCN | −38.88 | 9.80 |
| C2H2⋯AuCN | −54.14 | −5.46 |
| NCAu⋯C2H4 | 18.70 | 35.78 |
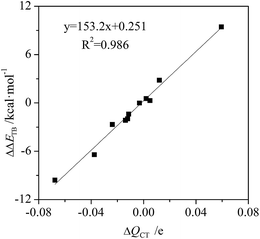
The charge transfer of tetrel bond increases in C2H4⋯MCN⋯TF4 (M = Cu, Ag, and Au; T = Si, Ge, and Sn) and C2H2⋯AuCN⋯SiF4 but decreases in C2(CN)4⋯MCN⋯SiF4 and NCAu⋯C2H4⋯SiF4 (Table S1†). The charge transfer has the largest increase in C2H4⋯CuCN⋯SiF4 and the largest decrease in C2(CN)4⋯AgCN⋯SiF4. The relationship between the change of charge transfer and the change of interaction energy is shown in Fig. 5. They display a good linear relationship with a correlation coefficient of 0.987. This indicates that charge transfer is also responsible for the change of tetrel bonding strength. Similarly, the orbital interaction has a similar change with the charge transfer.
Table S2† presents the energy components of the tetrel bond in the triads to have a further insight into the origin of its interaction energy change. In most interactions, the main attractive contributions are from electrostatic and polarization, thus only their change is depicted in Fig. 6. For C2H4⋯MCN⋯TF4 (M = Cu, Ag, and Au; T = Si, Ge, and Sn) and C2H2⋯AuCN⋯SiF4, both terms are more negative, while they are more positive in C2(CN)4⋯MCN⋯SiF4 and NCAu⋯C2H4⋯SiF4. This indicates that both terms have important contributions in tuning the strength of tetrel bond through cooperativity. In all systems, electrostatic has the larger change than polarization, showing the larger contribution from electrostatic. Both terms are almost not changed in C2H4⋯AuCN⋯CF4 and NCAu⋯C2H4⋯SiF4, consistent with the small change of interaction energy in both triads.
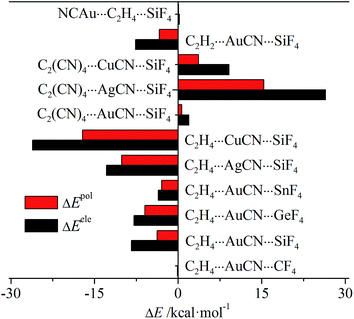 | ||
| Fig. 6 Change of electrostatic and polarization energies in the triads relative to the respective dyads. | ||
4. Conclusions
The triads of C2H4⋯AuCN⋯TF4 (T = C, Si, Ge, and Sn), C2H4⋯MCN⋯SiF4 (M = Cu, Ag, and Au), C2(CN)4⋯MCN⋯SiF4, C2H2⋯AuCN⋯SiF4, and NCAu⋯C2H4⋯SiF4 as well as their dyads have been studied. The following conclusions are reached.(1) Coin metal substituents have a prominent enhancing effect on the strength of tetrel bond. This enhancing effect is related with the nature of coin metal and tetrel atoms, which is larger in the order C < Si < Ge < Sn and Au < Cu < Ag. The tetrel bond varies from a weak interaction in HCN⋯SiF4 (−3.45 kcal mol−1) to a strong one in AgCN⋯SiF4 (−15.80 kcal mol−1).
(2) A π⋯metal interaction can regulate the strength of tetrel bond. The tetrel bond is strengthened in C2H4⋯AuCN⋯TF4 (T = C, Si, Ge, and Sn), C2H4⋯MCN⋯SiF4 (M = Cu, Ag, and Au), and C2H2⋯AuCN⋯SiF4 but is weakened in C2(CN)4⋯MCN⋯SiF4 and NCAu⋯C2H4⋯SiF4. Accompanied with the strengthening/weakening of tetrel bond, its nature could also be changed.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21573188) and the Shandong Province Natural Science Foundation (ZR2016BL11).References
- T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296 CrossRef CAS PubMed.
- P. Politzer, P. Lane, M. C. Concha, Y. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311 CrossRef CAS PubMed.
- J. S. Murray, P. Lane, T. Clark and P. Politzer, J. Mol. Model., 2007, 13, 1033–1038 CrossRef CAS PubMed.
- J. S. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and P. Lane, Int. J. Quantum Chem., 2007, 107, 3046–3052 CrossRef CAS.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Angew. Chem., Int. Ed., 2013, 52, 12317–12321 CrossRef PubMed.
- S. Zahn, R. Frank, E. Hey-Hawkins and B. Kirchner, Chem.–Eur. J., 2011, 17, 6034–6038 CrossRef CAS PubMed.
- W. Z. Wang, B. M. Ji and Y. Zhang, J. Phys. Chem. A, 2009, 113, 8132–8135 CrossRef CAS PubMed.
- P. Politzer, J. S. Murray and P. Lane, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189 RSC.
- S. J. Grabowski and W. A. Sokalski, ChemPhysChem, 2017, 18, 1569–1577 CrossRef CAS PubMed.
- D. P. de Sousa, C. Wegeberg, M. S. Vad, S. Mørup, C. Frandsen, W. A. Donald and C. J. McKenzie, Chem.–Eur. J., 2016, 22, 3810–3820 CrossRef CAS PubMed.
- S. P. Thomas, K. Satheeshkumar, G. Mugesh and T. N. G. Row, Chem.–Eur. J., 2015, 21, 6793–6800 CrossRef CAS PubMed.
- A. R. Voth, F. A. Hays and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2007, 114, 6188–6193 CrossRef PubMed.
- S. J. Grabowski, Phys. Chem. Chem. Phys., 2014, 16, 1824–1834 RSC.
- M. X. Liu, Q. Z. Li, J. B. Cheng, W. Z. Li and H. B. Li, J. Chem. Phys., 2016, 145, 224310 CrossRef PubMed.
- D. Mani and E. Arunan, Phys. Chem. Chem. Phys., 2013, 15, 14377–14383 RSC.
- S. P. Thomas, M. S. Pavan and T. N. G. Row, Chem. Commun., 2014, 50, 49–51 RSC.
- Q. Z. Li, X. Guo, X. Yang, W. Z. Li, J. B. Cheng and H. B. Li, Phys. Chem. Chem. Phys., 2014, 16, 11617–11625 RSC.
- A. Bauzá, T. J. Mooibroek and A. Frontera, Chem. Commun., 2014, 50, 12626–12629 RSC.
- S. Scheiner, J. Phys. Chem. A, 2015, 119, 9189–9199 CrossRef CAS PubMed.
- Q. Z. Li, H. Y. Zhuo, H. B. Li, Z. B. Liu, W. Z. Li and J. B. Cheng, J. Phys. Chem. A, 2015, 119, 2217–2224 CrossRef CAS PubMed.
- X. Guo, Y. W. Liu, Q. Z. Li, W. Z. Li and J. B. Cheng, Chem. Phys. Lett., 2015, 620, 7–12 CrossRef CAS.
- A. Bauzá, A. Frontera and T. J. Mooibroek, Phys. Chem. Chem. Phys., 2016, 18, 1693–1698 RSC.
- V. de P. N. Nziko and S. Scheiner, Phys. Chem. Chem. Phys., 2016, 18, 3581–3590 RSC.
- Q. C. Wei, Q. Z. Li, J. B. Cheng, W. Z. Li and H. B. Li, RSC Adv., 2016, 6, 79245–79253 RSC.
- M. X. Liu, Q. Z. Li and S. Scheiner, Phys. Chem. Chem. Phys., 2017, 19, 5550–5559 RSC.
- S. Scheiner, J. Phys. Chem. A, 2017, 121, 3606–3615 CrossRef CAS PubMed.
- S. Scheiner, Chem.–Eur. J., 2016, 22, 18850–18858 CrossRef CAS PubMed.
- J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548 CrossRef CAS PubMed.
- S. Scheiner, J. Phys. Chem. A, 2017, 121, 5561–5568 CrossRef CAS PubMed.
- J. B. Cheng, R. Li, Q. Z. Li, B. Jing, Z. B. Liu, W. Z. Li, B. A. Gong and J. Z. Sun, J. Phys. Chem. A, 2010, 114, 10320–10325 CrossRef CAS PubMed.
- S. Scheiner, J. Phys. Chem. A, 2017, 121, 3606–3615 CrossRef CAS PubMed.
- G. Mahmoudi, A. Bauzá and A. Frontera, Dalton Trans., 2016, 45, 4965–4969 RSC.
- G. Mahmoudi, A. Bauzá, M. Amini, E. Molins, J. T. Mague and A. Frontera, Dalton Trans., 2016, 45, 10708–10716 RSC.
- M. S. Gargari, V. Stilinović, A. Bauzá, A. Frontera, P. McArdle, D. V. Derveer, S. W. Ng and G. Mahmoudi, Chem.–Eur. J., 2015, 21, 17951–17958 CrossRef PubMed.
- M. X. Liu, Q. Z. Li, W. Z. Li and J. B. Cheng, J. Mol. Graphics Modell., 2016, 65, 35–42 CrossRef CAS PubMed.
- M. X. Liu, L. Yang, Q. Z. Li, W. Z. Li, J. B. Cheng, B. Xiao and X. F. Yu, J. Mol. Model., 2016, 22, 192 CrossRef PubMed.
- Q. J. Tang and Q. Z. Li, Comput. Theor. Chem., 2014, 1050, 51–57 CrossRef CAS.
- M. D. Esrafili, N. Mohammadirad and M. Solimannejad, Chem. Phys. Lett., 2015, 628, 16–20 CrossRef CAS.
- S. Yourdkhani, T. Korona and N. L. Hadipour, J. Comput. Chem., 2015, 36, 2412–2428 CrossRef CAS PubMed.
- M. Marín-Luna, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2016, 120, 648–656 CrossRef PubMed.
- W. Li, Y. Zeng, X. Li, Z. Sun and L. Meng, Phys. Chem. Chem. Phys., 2016, 18, 24672–24680 RSC.
- H. L. Xu, J. B. Cheng, X. Yang, Z. B. Liu, B. Xiao and Q. Z. Li, RSC Adv., 2017, 7, 21713–21720 RSC.
- H. L. Xu, J. B. Cheng, X. Yang, Z. B. Liu, W. Z. Li and Q. Z. Li, ChemPhysChem, 2017, 18, 2442–2450 CrossRef CAS PubMed.
- M. J. S. Dewar and G. P. Ford, J. Am. Chem. Soc., 1979, 101, 783–791 CrossRef CAS.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. A. Yazyev, J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. A. Dapprich, D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- F. Bulat, A. Toro-Labbé, T. Brinck, J. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691 CrossRef CAS PubMed.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, Oxford, 1990 Search PubMed.
- R. F. W. Bader, AIM2000 Program, v. 2.0, McMaster University, Hamilton, Canada, 2000 Search PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- P. F. Su and H. Li, J. Chem. Phys., 2009, 13, 014102 CrossRef PubMed.
- X. Wu, Z. Qin, H. Xie, R. Cong, X. Wu, Z. Tang and H. Fan, J. Phys. Chem. A, 2010, 114, 12839–12844 CrossRef CAS PubMed.
- W. D. Arnold and E. Oldfield, J. Am. Chem. Soc., 2000, 122, 12835–12841 CrossRef CAS.
- M. Gao, J. B. Cheng, X. Yang, W. Z. Li, B. Xiao and Q. Z. Li, J. Chem. Phys., 2015, 143, 054308 CrossRef PubMed.
- W. K. Tian, X. Huang, Q. Z. Li, W. Z. Li, J. B. Cheng and B. A. Gong, J. Mol. Model., 2013, 19, 1311–1318 CrossRef CAS PubMed.
- D. Mani and E. Arunan, J. Phys. Chem. A, 2014, 118, 10081–10089 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra09881b |
| This journal is © The Royal Society of Chemistry 2017 |