Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Intuitionistic study on the critical decomposition energy of ammonium perchlorate by SEM
Jie Liu*,
Xiang Ke ,
Ga-zi Hao,
Lei Xiao,
Wei Jiang and
Feng-sheng Li
,
Ga-zi Hao,
Lei Xiao,
Wei Jiang and
Feng-sheng Li
National Special Superfine Powder Engineering Research Center of China, School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, P. R. China. E-mail: jie_liu_njust@126.com; Tel: +86-025-84315042
First published on 27th October 2017
Abstract
The decomposition course of Ammonium Perchlorate (AP) particles under electron energy is observed using a G2 pro Desktop Scanning Electron Microscope. The state that the AP particle is starting to decompose exhibiting cracks on its surface is observed and recorded using the S-4800II Fielding Emission Scanning Electron Microscope (FESEM), the Image Pro Plus (IPP) System is employed to obtain the projected area of that decomposed AP particle in the FESEM image, and the critical decomposition energy of the AP particle is calculated. Results have shown that the critical decomposition energy is decreased with the reduction of AP particle size. Especially when the AP particle size is approximately under 20 μm, the critical decomposition energy is sharply decreased, and the critical decomposition energy is very small if under 3 μm. This result is very helpful to explain why the burning rate of propellants and the brisance of Fuel Air Explosives (FAE) are enhanced and the sensitivities of those AP-based energetic materials are increased with the reduction of AP particle size. Furthermore, this method can be used to calculate in an intuitionistic way the critical decomposition energies of other crystalline materials.
1. Introduction
Ammonium Perchlorate (AP) is widely used in composite propellants (CP),1–6 composite modified double-based propellants (CMDBP)7–10 and fuel air explosives (FAE)11,12 as an excellent oxidizer. The studies have shown that the burning rate of propellants and the brisance of FAE are enhanced. However, the sensitivities of those AP-based energetic materials are increased, which means worse safety, with the reduction of AP particle size. Burning or an explosion may be easily initiated during researching, producing, storing and applying the materials, which is seriously restricting the large-scale application of the small AP particles (especially the particles under 3 μm) in propellants and FAE.Many researches have focused on why danger happens and how to avoid danger during the application of AP particles in propellants and FAE. So far, the models employed to be as the theoretical explanation are indirectly based on various assumptions and limited. How to intuitionisticly study on the decomposition of AP particles, observe their critical decomposition states and calculate their critical decomposition energies are very expectable and urgent for researchers.
In the philosophy of mathematics, intuitionism is an approach where mathematics is considered to be purely the result of the constructive mental activity of humans rather than the discovery of fundamental principles claimed to exist in an objective reality. That is, logic and mathematics are not considered analytic activities wherein deep properties of objective reality are revealed and applied but are instead considered the application of internally consistent methods used to realize more complex mental constructs, regardless of their possible independent existence in an objective reality.
In this work, the S-4800II Field Emission Scanning Electron Microscope (FESEM) is employed to intuitionisticly research the critical decomposition energy of AP particles. The electron energy is emitted by the FESEM and inflicted on the AP particles, the critical decomposition state is observed and recorded by the FESEM, and the critical decomposition energy is calculated. The result has shown that the critical decomposition energy of AP particle is decreased with the reduction of the particle size, especially when the particle size is approximately under 20 μm, the critical decomposition energy is apparently decreased, and the critical decomposition energy is very small if under 3 μm. It is distinctly claimed that the superfine AP particles will be easily initiated to decompose by very small energy, so the burning rate or brisance of the AP-based energetic materials will be enhanced, and at the same time, their sensitivities to friction, impact and shock will be increased. Furthermore, it is potentially expectable to get the critical decomposition energies of other crystalline materials based on this method.
2. Experimental
2.1 Materials and instruments
The decomposition course of AP particles with an average size of 2.099 μm is observed using the Desktop SEM (G2 pro Desktop Scanning Electron Microscope). The AP particles with the size of 6 μm are selected as an example how to observe the critical decomposition state and calculate the critical decomposition energy. The critical decomposition energies of other five kinds of AP particles, 1 μm, 6 μm, 10 μm, 20 μm, 60 μm and 80 μm, are calculated. The AP particles selected to calculate the critical decomposition energy should be quasi-spherical or with regular shape. All of the researched AP samples are produced by Dalian North Chlorate Company of China.2.2 Observation of decomposition course
The decomposition course of AP particles is observed using the Desktop SEM. The states, that the AP particles are separately affected by the electron energy for 1 second, 11 seconds, 21 seconds and 31 seconds, are observed and recorded. The thermal decomposition properties of two AP samples, which are characterized with the average particle size of 60 μm and 6 μm, respectively, are analyzed by thermogravimetric (TG) analysis and differential scanning calorimetric (DSC) techniques.2.3 Calculation of critical decomposition energy
When AP particles are affected by the electron energy, they will be initiated. The state that the specific sized particle begins to decompose exhibiting with cracks on its surface is defined as the critical decomposition state. Meanwhile, the accepted electron energy is defined as the critical decomposition energy.When the critical decomposition energy is calculated, it is assumed that the affected electron energy is absolutely transformed to be initiation energy. That is, the electron diffraction, the electron transmission, the secondary electron and the characteristic ray won't be considered in this work.
3. Results and discussion
3.1 SEM images of the decomposition course
Fig. 1 shows the total decomposition course of AP particles under electron energy emitted by the Desktop SEM. The state that the AP particles are affected by electron energy for 1 second without decomposing is shown in Fig. 1a. The state that some of the particles begin to crack, bubble and disappear after 11 seconds is shown in Fig. 1b. The state that most of the AP particles have decomposed to be bubbles and disappeared after 21 seconds is shown in Fig. 1c. And, as shown in Fig. 1d, almost all of the AP particles have decomposed and disappeared after 31 seconds. | ||
| Fig. 1 SEM images of AP particles affected by electron energy for various time: (a) 1 s, (b) 11 s, (c) 21 s and (d) 31 s. | ||
As shown in Fig. 1, with the extended time under electron energy, the amount of decomposed AP particles is increased, and the smaller particles begin to decompose earlier. That is, the smaller AP particles are more easily to be initiated.
The corresponding state of AP particles changing from Fig. 1a–d under electron energy is defined as the critical decomposition state. The accepted electron energy in the critical decomposition state is defined as the critical decomposition energy of the specific sized AP particle. The FESEM is employed to observe and record the critical decomposition state of the AP particle and the critical decomposition energy is calculated as shown in the following section.
3.2 Calculation of critical decomposition energy
The aforementioned S-4800II FESEM is employed to observe and record the critical decomposition state of a specific sized AP particle. The size of an AP particle is expressed as the diameter of the isovolumetric sphere. The critical decomposition energy is calculated based on the method and the principle shown in “Section 2.3(b)”. The critical decomposition energy of the 6 μm sized AP particle is selected as the calculation example as below.As shown in Fig. 2, when the 6 μm sized AP particle begins to decompose under electron energy, cracks occur on its surface. Firstly, the electron energy affected on the whole FESEM view can be calculated as the next expression.
| E0 = U × I × t = 15 × 103 × 10 × 10−6 × 3 = 0.45 J; |
Secondly, the effective area of the FESEM image (S0) and the projected 6 μm sized AP particle area (S1) can be calculated by the IPP System. The areas are expressed in pixels, as shown in the next.
| S0 = 1137784; S1 = 218907; |
Then, the critical decomposition energy of the 6 μm sized AP particle can be calculated as follows.
| ΔE = E0 × S1/S0 = 0.45 × 218907 ÷ 1137784 = 0.0866 J. |
3.3 The changing rule of critical decomposition energy with AP particle size
Based on the method demonstrating in “Section 3.2”, the critical decomposition energies of AP particles with different sizes, 1 μm, 6 μm, 10 μm, 20 μm, 60 μm and 80 μm, are calculated and shown in Table 1.| Particle size/μm | 1 | 6 | 10 | 20 | 60 | 80 |
| S0 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 821 821 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 137 137![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784 784 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473 473 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 141 141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 755 755 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
| S1 | 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 170 170 |
218![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 907 907 |
372![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 353 353 |
569![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 218 218 |
840![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535 535 |
1040![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 311 |
| E0/J | 0.45 | 0.45 | 0.45 | 0.45 | 0.45 | 0.45 |
| ΔE/J | 0.0247 | 0.0866 | 0.146 | 0.224 | 0.331 | 0.409 |
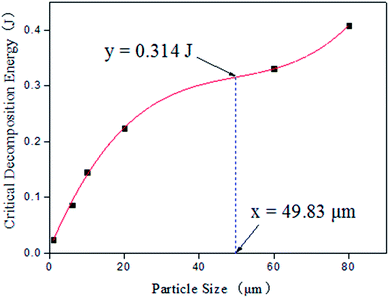
Based on the critical decomposition energy of AP particles as listed in Table 1, the relation curve between critical decomposition energy and particle size is fitted as shown in Fig. 3.
The corresponding function of that curve and its second derivative are shown in formula (1) and formula (2):
| y = 1.98 × 10−6x3 − 2.96 × 10−4x2 + 1.60 × 10−2x + 0.00718 | (1) |
| y′ = 1.188 × 10−5x − 5.92 × 10−4 | (2) |
As shown in Fig. 3, the critical decomposition energy is decreased with the reduction of AP particle size. It can be known from formula (1) and formula (2) that there is an inflexion point existing in that relation curve, and the inflexion point can be calculated, when the second derivative is equal to zero (y′ = 0), to be (y = 0.314, x = 49.83). When AP particle size is above 49.83 μm, the reduction rate of critical decomposition energy is decreased gradually. When AP particle size is under 49.83 μm, the reduction rate of critical decomposition energy is decreased rapidly. Especially when AP particle size is approximately less than 20 μm, the critical decomposition energy is sharply decreased with the reduction of particle size, and the reduction rate is quickly increased. When AP particle size is less than 3 μm, the critical decomposition energy is very small.
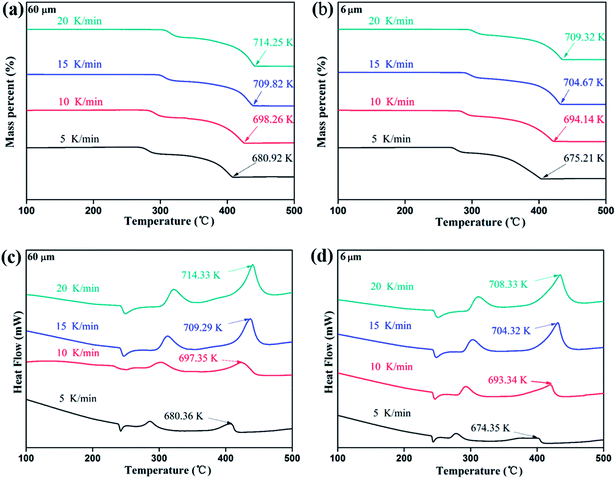
To further verify the variation trend of critical decomposing energy with particle size, TG-DSC test are performed at different heating rate and the activation energy were calculated according to Kissinger,13 Starink14 and Ozawa equation,15 respectively. The selected AP samples are characterized with the average particle size of 60 μm and 6 μm, respectively, and the TG-DSC curves are shown in Fig. 4.
As can be seen from Fig. 4, the ending temperature and high-temperature decomposition (HTD) temperature are gradually decreased with reduction of particle size. The HTD activation energy of AP samples are calculated from exothermic peak temperature dependence as a function of heating rate shown in Fig. 4c and d.
As shown in Table 2, the activation energy of the AP sample with the average particle size of 6 μm is lower than that of the AP sample with the average particle size of 60 μm AP. That is, the AP sample with lower particle size is indicated to be easier to decompose, which is consistent with the variation trend of critical decomposition energy.
| Sample | Activation energy/kJ mol−1 | Average value/kJ mol−1 | ||
|---|---|---|---|---|
| Kissinger equation | Starink equation | Ozawa equation | ||
| 60 μm AP | 148.78 | 148.90 | 152.47 | 150.05 |
| 6 μm AP | 144.44 | 144.57 | 148.24 | 145.75 |
Combined with the results of calculated critical decomposition energy and HTD activation energy, it is clearly demonstrated that the superfine AP particles will be easily initiated to decompose by small stimuli. The propellants or FAE are easily initiated to burn or explode, and then the burning rate and brisance of AP-based energetic materials are enhanced. At the same time, their sensitivities to friction, impact and shock are also increased which means the worse safety.
The changing rule between burning rate, brisance or sensitivities of AP based-energetic materials and AP particle size can be explained based on the intuitionisticly calculated critical decomposition energy. If the inflicted energy on AP particles is controlled under the critical decomposition energy, the safety of AP-based energetic materials during development, production, storage, transportation and application will be guaranteed. It is very helpful for the use of superfine AP particles in energetic materials.
4. Conclusions
The critical decomposition state of AP particles can be observed and recorded using FESEM, and the critical decomposition energy can be intuitionisticly calculated based on the introduced method. The critical decomposition energy is decreased with the reduction of AP particle size, which is consistent with the variation trend of activation energy calculated from the TG-DSC curves. When AP particle size is less than 3 μm, the critical decomposition energy is very small. The changing rule between burning rate, brisance or sensitivities of AP based-energetic materials and AP particle size can be explained based on the intuitionisticly calculated critical decomposition energy. It is potentially expectable to get the critical decomposition energies of other crystalline materials based on this method.In future studies, the electron energy loss will be considered. The statistically average critical decomposition energies of AP particles with different size distributions, as well as other crystalline materials, will be calculated and corresponded to the apparent activation energies, so that the energy bridge between microcosm and macrocosm can be built.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially sponsored by the National Natural Science Foundation of China (NSFC, 51606102) and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD). Many thanks to Wei-dong Zhou and his group, Yangzhou University, for their helpful discussions in the research area.References
- H. Singh, J. Upadhyay, D. Chimurkar, V. Ghorpade, A. Kotbagi, A. Kumar, A. Kumar and M. Gupta, Propellants, Explos., Pyrotech., 2013, 39, 180–184 CrossRef.
- Y. F. Liu, Y. Chen, L. Shi and W. S. Yao, J. Energ. Mater., 2014, 32, 71–79 CrossRef CAS.
- Y. L. Zhu, H. Huang, H. Ren and Q. J. Jiang, J. Energ. Mater., 2014, 32, 16–26 CrossRef CAS.
- K. Kishore, S. Sankaralingam, R. Nagarajan and K. Mohandas, Def. Sci. J., 2013, 45, 243–254 CrossRef.
- K. T. Lu, T. M. Yang, J. S. Li and T. F. Yeh, Combust. Sci. Technol., 2012, 184, 2100–2116 CrossRef CAS.
- C. Franck, F. Yves and E. Charles, Int. J. Energ. Mater. Chem. Propul., 2013, 12, 1–13 Search PubMed.
- X. Han, T. F. Wang, Z. K. Lin, D. L. Han, S. F. Li, F. Q. Zhao and L. Y. Zhang, Def. Sci. J., 2010, 59, 284–293 CrossRef.
- X. Y. Li, X. L. Liu, Y. Cheng, Y. C. Li and X. L. Mei, J. Therm. Anal. Calorim., 2014, 115, 887–894 CrossRef CAS.
- S. N. Asthana, C. N. Divekar, R. R. Khare and P. G. Shrotri, Def. Sci. J., 2013, 42, 201–204 CrossRef.
- M. K. Choudhari, S. S. Dhar, P. G. Shrotri and H. Singh, Def. Sci. J., 2013, 42, 253–257 CrossRef.
- M. L. Chan and G. W. Meyers, U.S. Pat., 6955732, 2005.
- A. A. Borisov, A. A. Sulimov, M. K. Sukoyan, P. V. Komissarov, I. O. Shamshin, R. Kh Ibragimov and Yu. M. Mikhailov, Russ. J. Phys. Chem. B, 2009, 3, 936–944 CrossRef.
- T. Chen, P. Du, W. Jiang, J. Liu, G. Z. Hao, H. Gao, L. Xiao, X. Ke, F. Q. Zhao and C. L. Xuan, RSC Adv., 2016, 6, 83838–83847 RSC.
- M. J. Starink, J. Mater. Sci., 1997, 32, 4061–4070 CrossRef CAS.
- Y. Cheng, Y. Li, S. Yan and C. Huang, J. Math. Chem., 2010, 48, 704–713 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |